Journal of Materials Science and Chemical Engineering
Vol.03 No.01(2015), Article ID:53363,8 pages
10.4236/msce.2015.31009
Transport Properties of Novel Hybrid Cation-Exchange Membranes on the Base of MF-4SC and Halloysite Nanotubes
Anatoly Filippov, Daria Khanukaeva, Denis Afonin, Galina Skorikova, Evgeny Ivanov, Vladimir Vinokurov, Yuri Lvov
Gubkin Russian State University of Oil and Gas, Moscow, Russia
Email: a.filippov@mtu-net.ru


Received December 2014

ABSTRACT
The diffusion permeability through new hybrid materials based on a Nafion-type membrane (MF- 4SC) and nanotubes of halloysite is investigated using the Nernst-Planck approach. A method of quantitative evaluation of physicochemical parameters (averaged and individual diffusion coefficients and averaged distribution coefficients of ion pairs in the membrane) of system “electrolyte solution―ion-exchange membrane―water”, which was proposed earlier, is further developed. The parameters of hybrid membranes on the base of MF-4SC and nanotubes of halloysite (5% wt and 8% wt) are obtained from experimental data on diffusion permeability of NaCl solutions using theoretical calculations. New model of three-layer membrane system can be used for refining calculated results with taking into account both diffusive layers. It is shown that adding of halloysite nanotubes into the membrane volume noticeably affects exchange capacity as well as structural and transport characteristics of original perfluorinated membranes. Hybrid membranes on the base of MF-4SC and halloysite nanotubes can be used in fuel cells and catalysis.
Keywords:
Three Layer Membrane Model, The Nernst-Planck Approach, Diffusion Permeability, Perfluorinated Cation-Exchange Membrane, Hybrid MF-4SC/Halloysite Membrane

1. Introduction
Perfluorinated cation-exchange Nafion membrane produced by DuPont (USA) and its analogues such as MF-4SC (LTD Plastpolymer, Russia), Dow (Dow, USA) are the most widely used in various devices (like fuel cells, electrodialyzers) and investigated ion-exchange materials [1]. Volume and surface modification of such membranes by incorporation of different additives allows to change their properties, in particular, stability and structural characteristics as well as ion and molecular transport [2]. Recently major attention of scientists has been focused on the modeling of species transport across ion-exchange membranes and a number of studies are devoted to the electromigration phenomenon. The practical application of such membranes is often based on the diffusion processes, so diffusion permeability is one of the important characteristics of ionic transport through such ion-exchange membranes [2]-[6]. In hybrid materials obtained via modification of the cation-exchange membrane matrix by inorganic and some organic compounds, dopant nanoparticles are located in the membrane pores and force out electro-neutral solution with the major part of anions [2] [7], while cations are mostly located within the Debye layer (close to the negatively charged walls of the pores) which is not affected by the dopant particle. Thus, in hybrid membranes with low dopant concentration the rate of cation transfer is higher, while the rates of anion transfer are lower than in the initial membrane [8] [9]. In recent years mathematical modeling of ion and molecular transport processes through the membranes is of great interest [10]-[14]. This article is devoted to a theoretical description of the diffusion permeability processes in a hybrid MF-4SC membrane doped by halloysite nanotubes, based on our own experimental data.
2. Theory
A boundary-value problem of diffusion of aqueous solution of a 1:1 electrolyte with concentration 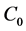 through the ion-exchange membrane into pure water was formulated and solved earlier on the basis of the Nernst-Planck transport equations [12] [15]. However those papers did not take into consideration the difference between the diffusion coefficients of cations and anions of the electrolyte in the membrane, which is crucial. This drawback has been eliminated in our recent article [16], where diffusion permeability through hybrid materials, based on MF-4SC membrane volumetrically modified by silica nanoparticles, is investigated. Meanwhile diffusive layers on both sides of the membrane (Figure 1) can significantly affect diffusion permeability. Besides that, concentration of electrolyte beyond the right diffusive layer is non-zero and slightly growing function of time. The membrane is characterized by thickness h, diffusion coefficients D+, D- (mobilities) of ions in the bulk solution and Dm+, Dm− in the membrane, respectively, absolute value of charge density of the fixed groups ρ > 0, i.e. exchange capacity, which is constant across the entire membrane, distribution coefficients γ+, γ− of cations and anions in it. The distribution coefficients were introduced in [17] to calculate the reverse osmotic separation of electrolyte solutions. They show the level of surface interaction of ions with the membrane material (γ± = exp(γ±), γ± is the interaction potential for each ion in kBT units, where kB is the Boltzmann constant, T - absolute temperature). So, as was mentioned above, we suppose that the same electrolyte with a very low concentration C0/k (k >> 1) is beyond the right side diffusive layer (x > h + δ). In the limiting case, k → ∞, we have got pure water in 4-th region (Figure 1).
through the ion-exchange membrane into pure water was formulated and solved earlier on the basis of the Nernst-Planck transport equations [12] [15]. However those papers did not take into consideration the difference between the diffusion coefficients of cations and anions of the electrolyte in the membrane, which is crucial. This drawback has been eliminated in our recent article [16], where diffusion permeability through hybrid materials, based on MF-4SC membrane volumetrically modified by silica nanoparticles, is investigated. Meanwhile diffusive layers on both sides of the membrane (Figure 1) can significantly affect diffusion permeability. Besides that, concentration of electrolyte beyond the right diffusive layer is non-zero and slightly growing function of time. The membrane is characterized by thickness h, diffusion coefficients D+, D- (mobilities) of ions in the bulk solution and Dm+, Dm− in the membrane, respectively, absolute value of charge density of the fixed groups ρ > 0, i.e. exchange capacity, which is constant across the entire membrane, distribution coefficients γ+, γ− of cations and anions in it. The distribution coefficients were introduced in [17] to calculate the reverse osmotic separation of electrolyte solutions. They show the level of surface interaction of ions with the membrane material (γ± = exp(γ±), γ± is the interaction potential for each ion in kBT units, where kB is the Boltzmann constant, T - absolute temperature). So, as was mentioned above, we suppose that the same electrolyte with a very low concentration C0/k (k >> 1) is beyond the right side diffusive layer (x > h + δ). In the limiting case, k → ∞, we have got pure water in 4-th region (Figure 1).
Inside each of diffusive layers membrane, −δ < x < 0 and h < x < h + δ, the fluxes of ions can be represented in the following form:
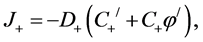 (1)
(1)
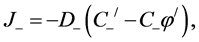 (2)
(2)
Figure 1. A scheme of the diffusion transfer of ions through a charged single layer membrane: 0 and 4―regions of intensive steering with constant concen- tration of solution; 1 and 3―left and right diffusive layers; 2―membrane.
where the bar at the right top of the symbol stands for a derivative in x, and  -is a non-dimensional electric potential in the
-is a non-dimensional electric potential in the 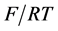 units (F is the Faraday constant, R is the universal gas constant, T-absolute temperature).
units (F is the Faraday constant, R is the universal gas constant, T-absolute temperature).
Inside the membrane, 0 < x < h, the fluxes are:
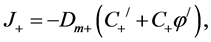 (3)
(3)
 (4)
(4)
The boundary conditions of equality of the electrochemical potentials are written at the interfaces x = 0 and x = h of cation-exchange membrane [12] [13] [18]:
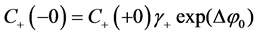 (5)
(5)
 (6)
(6)
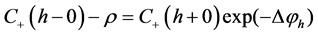 (7)
(7)
 (8)
(8)
where C± are concentrations of ions, 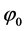 and
and  are drops of the electric potential at the membrane-electrolyte interfaces, x=0 and x=h, accordingly. To close the system of Equations (1)-(8) it should be complemented by the conditions of electroneutrality:
are drops of the electric potential at the membrane-electrolyte interfaces, x=0 and x=h, accordingly. To close the system of Equations (1)-(8) it should be complemented by the conditions of electroneutrality:
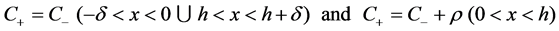 (9)
(9)
as well as the absence of electric current, which for the 1:1 electrolyte reads:
 (10)
(10)
where J is the flux density of ions, and continuities of ion concentrations and electric potential on the external boundaries of diffusive layers:
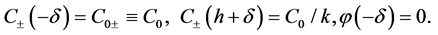 (11)
(11)
For purpose of convenience let us introduce dimensionless parameters:

It should be noticed that two last notations (



where


where notation 
electrolyte, which was first introduced in [17]. In the limit, 


In other limit, 



The behavior of the diffusion permeability of a 1:1 electrolyte, passing through uniformly charged cation- exchange membranes into water, is presented in Figure 2. Usually, for simplicity, we can neglect value 

Note also, that 
so, consequently,
and it is associated with three-layer membrane system. When 


When 

Figure 2. Dependence of the diffusion permeability of a cation-exchange membrane on electrolyte concentration.
which is convenient in order to find preliminary values of effective averaged diffusivity 

It should be noted that parameters
















where 

3. Experiment
Original perfluorinated cation-exchange and two hybrid membranes with pure aluminosilicate (halloysite) nanotubes were prepared by casting method. For the proposed method we used a solution of sulfopolymer of the MF-4SC membrane in lithium form (7.1%wt. in dimethylformamide solution, exchange capacity was 0.98 mg- eq/g).
To modify the polymer solution it was mixed with the sample of halloysite clay nanotubes in an amount of 5 and 8%wt. to the weight of the pure polymer and homogenized by mechanical stirring. Halloysite clay is natural tubule material formed by rolled kaolin sheets. Halloysite is alumosilicate and is chemically identical to kaolin although usually contains minor amount (less than 1 wt%) of iron ions. Typically 10 - 15 alumosilicate layers roll into the cylinder [20] [21]. Surface of halloysite tubes is silica and its innermost is alumina, providing strong negative zeta-potential of approximately −30 mV on the tube surface and +25 mV in the tube innermost in aqueous dispersions at normal pH. Halloysite tubes’ diameter is of 40 - 60 nm with inner lumen diameter of 10 - 15 nm and length of 1500 ± 500 nm.
The suspension of the polymer with halloysite nanotubes was placed in a Petri dish and spreaded uniformly with a rotating table, and dried in air at room temperature for 24 hours, and then in sequence at 100˚C for 1 hour, at 120˚C for 1 hour, at 130˚C for 1 hour, at 140˚C for 1 hour and finally at 120˚C for 4 hours to remove the solvent gradually and form a film of membrane. Thereafter, the film was removed carefully from the surface.
The resultant hybrid membranes were visually homogeneous throughout the sample area but the slight turbidity was observed. The thicknesses of the resultant membranes were 390 (original membrane), 310 (5%wt. of halloysite) and 290 (8%wt. of halloysite) microns. In the analysis of SEM and AFM micrographs it is worthy to notice that the nanotubes are uniformly distributed on the surface of the membrane. The electron and atomic- force microscopy results of synthesized hybrid membranes are shown in Figure 3(a) and Figure 3(b). We can conclude that aluminosilicate nanotubes and micro-cavities are observed on both images. The cavities size inreases as halloysite concentration increases, thus agreeing with Berns [22].
After the synthesis, the membranes were washed with water and then equilibrated with HCl, LiCl, or NaCl solutions at specified concentrations. Following this, its transport characteristics were investigated with experimental methods described in [23]. The specific electrical conductivity of the membranes (

Figure 3. SEM (a) and AFM (b) micrographs of the surface of hybrid MF-4SC membrane obtained by casting method (aluminosilicate nanotubes and micro-cavities are observed on both images).


Figure 4. Experimental (bold points) and theoretical (curves) dependencies of the diffusion permeability of original (a) and hybrid MF-4SC/halloysite membranes with 5% wt; (b) and 8% wt; (c) content of nanotubes.
4. Results and Discussion
Using simplified formula (17) and Mathematica 9 software with the help of least square method from experimental data we found two main physico-chemical parameters of the membranes: effective averaged mobility of Na+ and Cl− ions (

It is clear that 5% wt. hybrid membrane is much better than 8% wt. membrane because it has larger ion-ex- change capacity and lower diffusion permeability even in comparison with original MF-4SC membrane. Probably,
Table 1. Calculated values of physicochemical parameters.
adding 8% wt. of halloysite nanotubes leads to strong irreversible degradation of perfluorinated cation-ex- change membrane. This hypothesis is proved by increase in electrical conductivity (Table 1) and enlargement of microcavities inside the membrane (Figure 3). Since the exchange capacity 



Figure 4 shows good correspondence between experimental and theoretical behavior of diffusion permeability P as function of NaCl electrolyte concentration for all three investigated membranes even in the case of application of simplified Formula (17). Utilizing implicit Equation (13) will allow us to clarify values of physicochemical parameters of the system and find individual diffusivities of ions inside a membrane.
So, in this article we continued to develop a method of quantitative evaluation of physicochemical parameters of the system electrolyte solution―ion-exchange membrane―water (averaged and individual diffusion coefficients and averaged distribution coefficient of ion pairs in the membrane). The parameters of hybrid cation-ex- change MF-4SC membranes with different halloysite concentration were obtained by this method with the use of experimental data on the diffusion permeability of NaCl electrolyte. The results allow us to evaluate the effect of membrane modification and to choose optimal compositions for hybrid membranes.
Acknowledgements
This work is partially supported by the Russian Science Foundation (grant RSF No. 14?19?01045) and CRDF- Global (project # FSAX-14-60158-0).
Cite this paper
Anatoly Filippov,Daria Khanukaeva,Denis Afonin,Galina Skorikova,Evgeny Ivanov,Vladimir Vinokurov,Yuri Lvov, (2015) Transport Properties of Novel Hybrid Cation-Exchange Membranes on the Base of MF-4SC and Halloysite Nanotubes. Journal of Materials Science and Chemical Engineering,03,58-65. doi: 10.4236/msce.2015.31009
References
- 1. Pourcelly, G., Nikonenko, V.V., Pismenskaya, N.D. and Yaroslavtsev, A.B. (2012) Ionic Interactions in Natural and Synthetic Macromolecules. In: Ciferri, A. and Perico, A., Eds., Applications of Charged Membranes in Separation, Fuel Cells and Emerging Processes, John Wiley & Sons Inc., Hoboken, 761-816.
- 2. Yaroslavtsev, A.B. and Nikonenko, V.V. (2009) Ion-Exchange Membrane Materials: Properties, Modification, and Practical Application. Nanotechnologies in Russia, 4, 137-159. http://dx.doi.org/10.1134/S199507800903001X
- 3. Villaluenga, J.P.G., Barragan, V.M., Seoane, B. and Ruiz-Bauza, C. (2006) Sorption and Permeation of Solutions of Chloride Salts, Water and Methanol in a Nafion Membrane. Electrochimica Acta, 51, 6297-6303. http://dx.doi.org/10.1016/j.electacta.2006.04.011
- 4. Izquierdo-Gil, M.A., Barragan, V.M., Godino, M.P., Villaluenga, J.P.G., Ruiz-Bauza, C. and Seoane, B. (2009) Salt Diffusion through Cation-Exchange Membranes in Alcohol-Water Solutions. Separation and Purification Technology, 64, 321-325. http://dx.doi.org/10.1016/j.seppur.2008.10.017
- 5. Ramkumar, J. (2012) Nafion Perfluorosulphonate Membrane: Unique Properties and Various Applications. In: Banerjee, S. and Tyagi, A.K., Eds., Funct. Materials: Preparation, Processes and Applications, Elsevier Ltd., London, 549- 577. http://dx.doi.org/10.1016/B978-0-12-385142-0.00013-1
- 6. Strathmann, H., Grabowski, A. and Eigenberger, G. (2013) Ion-Exchange Membranes in the Chemical Process Industry. Industrial & Engineering Chemistry Research, 52, 10364-10379. http://dx.doi.org/10.1021/ie4002102
- 7. Ahmad, H., Kamarudin, S.K., Hasran, U.A. and Daud, W.R.W. (2010) Overview of Hybrid Membranes for Direct- Methanol Fuel-Cell Applications. International Journal of Hydrogen Energy, 35, 2160-2175. http://dx.doi.org/10.1016/j.ijhydene.2009.12.054
- 8. Takata, K., Yamamoto, Y. and Sata, T. (2000) Modification of Transport Properties of Ion-Exchange Membranes: XIV. Effect of Molecular Weight of Polyethyleneimine Bonded to the Surface of Cation-Exchange Membranes by Acid- Amide Bonding on Electrochemical Properties of the Membranes. Journal of Membrane Science, 179, 101-107. http://dx.doi.org/10.1016/S0376-7388(00)00503-2
- 9. Yaroslavtsev, A.B. (2012) Correlation between the Properties of Hybrid Ion-Exchange Membranes and the Nature and Dimensions of Dopant Particles. Nanotechnologies in Russia, 7, 437-451. http://dx.doi.org/10.1134/S1995078012050175
- 10. Fila, V. and Bouzek, K. (2003) A Mathematical Model of Multiple Ion Transport across an Ion-Selective Membrane under Current Load Conditions. Journal of Applied Electrochemistry, 33, 675-684. http://dx.doi.org/10.1023/A:1025018726112
- 11. Seda, L. and Kosek, J. (2008) Predictive Modeling of Ionic Permse-lectivity of Porous Media. Computers & Chemical Engineering, 32, 125-134. http://dx.doi.org/10.1016/j.compchemeng.2007.03.023
- 12. Filippov, A.N., Starov, V.M., Kononenko, N.A. and Berezina, N.P. (2008) Asymmetry of Diffusion Permeability of Bilayer Membranes. Advances in Colloid and Interface Science, 139, 29-44. http://dx.doi.org/10.1016/j.cis.2008.01.009
- 13. Belashova, E.D., Melnik, N.A., Pismenskaya, N.D., Shevtsova, K.A., Nebavsky, A.V. and Lebedev, K.A. (2012) Overlimiting Mass Transfer Through Cation-Exchange Membranes Modified by Nafion Film and Carbon Nanotubes. Electrochimica Acta, 59, 412-423. http://dx.doi.org/10.1016/j.electacta.2011.10.077
- 14. Romero, V., Vázquez, M.I. and Benavente, J. (2013) Study of Ionic and Diffusive Transport through a Regenerated Cellulose Nanoporous Membrane. Journal of Membrane Science, 433, 152-159. http://dx.doi.org/10.1016/j.memsci.2013.01.012
- 15. Berezina, N.P., Kononenko, N.A., Filippov, A.N., Shkirskaya, S.A., Falina, I.V. and Sycheva, A.A.-R. (2010) Electrotransport Properties and Morphology of MF-4SK Membranes after Surface Modification with Polyaniline. Russian Journal of Electrochemistry, 46, 515-524. http://dx.doi.org/10.1134/S1023193510050010
- 16. Filippov, A.N., Safronova, E.Yu. and Yaroslavtsev, A.B. (2014) Theoretical and Experimental Investigation of Diffusion Permeability of Hybrid MF-4SC Membranes with Silica Nanoparticles. Journal of Membrane Science, 471, 110- 117. http://dx.doi.org/10.1016/j.memsci.2014.08.008
- 17. Martynov, G.A., Starov, V.M. and Churaev, N.V. (1980) Theory of Membrane Separation of Solutions. Colloid J. of the USSR, 42, 547-553.
- 18. Filippov, A.N., Iksanov, R.Kh., Kononenko, N.A., Berezina, N.P. and Falina, I.V. (2010) Theoretical and Experimental Study of Asymmetry of Diffusion Permeability of Composite Membranes. Colloid Journal, 72, 243-254. http://dx.doi.org/10.1134/S1061933X10020158
- 19. Zabolotsky, V.I. and Nikonenko, V.V. (1996) Ion Transport in Membranes. Nauka, Moscow.
- 20. Lvov, Y., Price, R., Gaber, B. and Ichinose, I. (2002) Thin Film Nanofabrication via Layer-by-Layer Adsorption of Tubule Halloysite, Spherical Silica, and Polycations. Colloids and Surfaces: Engineering, 198-200, 375-382.
- 21. Lvov, Y. and Abdullayev, E. (2013) Functional Polymer—Clay Nanotube Composites with Sustained Release of Chemical Agents. Progress in Polymer Sciences, 38, 1690-1719. http://dx.doi.org/10.1016/j.progpolymsci.2013.05.009
- 22. Berns, B.A., Romanovicz, V., de Camargo Forte, M.M. and Carpenter, D.E.O.S. (2013) Development and Characterization of a Polymer Composite Electrolyte to Be Used in Proton Exchange Membranes Fuel Cells. Int. J. of Chemical, Biomolecular, Metallurgical, Materials Science and Engineering, 7, 704-709.
- 23. Berezina, N.P., Kononenko, N.A., Dyomina, O.A. and Gnusin, N.P. (2008) Characterization of Ion-Exchange Membrane Materials: Properties vs Structure. Advances in Colloid and Interface Science, 139, 3-28. http://dx.doi.org/10.1016/j.cis.2008.01.002










