Journal of Materials Science and Chemical Engineering
Vol.03 No.01(2015), Article ID:53349,7 pages
10.4236/msce.2015.31002
Phenomena of Intergranular Liquid Film Formation in Technology
Yu. A. Minaev
Mining and Metallurgy Division, Russian Academy of Natural Science, Moscow, Russia
Email: ymin36@mail.ru


Received November 2014

ABSTRACT
The phenomena of the first order phase transition (two-dimensional melting) of grain boundary at temperatures 0.6 - 0.9 TS0 (of the solid state melting point), discovered by the author (1971), is a fundamental property of solid crystalline materials. This finding leads to a principal revision of the scientific concepts of the solid state of substance. The phenomenological description and justification of the finding are developed. The generalized equation of Clausius-Clapeyron type for two-dimensional phase transition was obtained by applying the mathematical tools of the film thermodynamics. The equation has been used for calculating the grain boundary phase transition(GBPhT) temperature TSf of any metal, which TSf value lies within the range of (0.55 - 0.86) TS0. The investigation outcomes are applied to develop the methodology for more effective hard coating formation by synthesis of nanosize nitrides and carbonitrides in surface layers of steels and nickel alloys using a thermo-chemical processing (TChP). Production of an overall nitrogen concentration gradient from 4% to 0.5% at within surface layers leads to formation of modified coatings with a stepped change in properties. The mechanical behavior of new tools at the industrial tests indicated a higher heat resistance (nickel alloys), high resistance to surface wears and fragile breaks-down (chromium tool steels). A short overview of the results of some graded alloys characterization is presented.
Keywords:
Grain Boundaries, Phase Transition, Nitrided Coatings, Graded Alloys, Hard Metals

1. Introduction
The analysis of a surface layers status had been executed by author and presented in number of publications earlier [1] [2]. The investigations carried out in frame of an atom-vacancy concept in approach of a lattice model. The background of our investigation is the statement of Frenkel that the melting point of a solid state is specified as “jumping” of a vacancy concentration from 10−3 - 10−4 up to 10−1. Within the framework of these rough approaches the concentration of vacancy and the temperature of solid-liquid phase transition of grain boundaries appeared to differ from the volume stated above. According to the concept, applied in the study the formation of the vacancy in a surface layer should be caused by its transfer from the middle of solution both at constant system mass and at constant surface. It was resulted in the equation for vacancy concentration Xv in the surface, which differed from the known one by a factor 2: Xv = Nv exp (2 sAm /RT), where Nv-vacancy concentration in a volume, Am- one mole area in a monolayer, s-surplus interfacial Gibbs energy. The valuation of the vacancy concentrations for some of metals (Cu, W, Ag, Mo, Mg, Na, Al, Ti, Cr, Co, Ni, Fe, Au) gives Xv/Nv = 1000. It means, that near solidification temperature TS0 the vacancy concentration in a surface layers of a solid metals is the same, as in a liquid state [1].
1.1. Phenomenology
Discovery a crystal boundaries two-dimensional melting [1] [2] is based on the known fact of the existence of an excess energy at interfaces. The interfacial tension leads to an excessive stress followed by stretching of the boundaries. The melting point (TS0) increases with the pressure for substances which the bulk density in the liquid state is much less than in the solid state. Hence, TS0 should decrease while tension presents. The surface layer is stretched, so we can assume that its melting point reduced. Situation is similar to changing of the boiling point of the two-dimensional liquid [3]. According to the autoadsorption concept suggested by Frenkel [4], the notion of phase transitions from solid to liquid state in two-dimensional adsorption layers can be extended to pure substances [3]. The rough valuation of the solidification temperature of a surface layer change (due to its stretching) was done on the basis of the Guggenheim and Clausius-Clapeyron equations. The relation for temperature TSσ of grain boundaries phase transition (GBPhT) liquid-solid is following: TSσ = TS0 exp (−sΔAm/QS). Here ΔAm is the change of a surface area in transition (was evaluated by change of density), QS-heat of melting. The valuation for a number of metals (Cu, W, Ag, Mo, Mg, Na, Al, Ti, Cr, Co, Ni, Fe, Au) gives downturn of melting temperature of a surface layer by hundreds of degrees. Here in a certain interval of temperature the surface layers or grain boundaries of solid metal can be considered as liquid or quasi-liquid, i.e. as a separate phase.
We applied the concept considering the grain boundaries as a separate phase in our works from 1968. Later the approach has been applied successfully by other researchers. Slezov [5] showed that within the applied concept Harrisons in polycrystalline may be easily fixed and author got the correct expression for the effective diffusion coefficient in polycrystals at large times [6]. The group of scientists lead by Acad. Kishkin demonstrated that the diffusion width of the grain boundaries is not less than 10 nm [7]. Earlier Ralph in his review of the electron-microscopic studies concluded that the crystallographic boundary consists of clusters of 50 - 250 vacancies and has a size of 2 - 3.5 nm [8]. These preliminary estimates give the possibility to use mathematical methods of films thermodynamics, namely, the system of equations, proposed by Rusanov [9] [10].
1.2. Theoretical Background in Terms of Film Thermodynamics
Let’s take in consideration a polycrystalline structure with the same phase (a) from both sides of a film with a tension g, the equation describing an relation between the changes T, P, g and a composition of a film Xi,k on all components from i up to k may be written as:
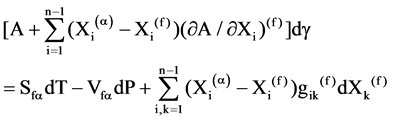 (1)
(1)
Let’s rewrite Equation (1) considering composition and pressure as constant and the following simplifications: since Xi(a) ® 1 and Xi(f) ® 1, therefore (Xi(a) ? Xi(f)) ® 0 and A = const:
A(dg/dT)P = Sfa (2)
Let us express a change of an entropy of phase transition solid - liquid (S ↔ L) in a film using a heat QSL and temperature TSL of this transition: (SfL − SfS) = QSL/TSL and a change of a molar surface at phase transition as: AfL − AfS = DASL, finally we obtain:
(dT/TSL)P = −(DASL/QSL)dg (3)
Let us apply an integration Equation (3) from volume (o) up to a surface (f). The temperature of phase transition (L ↔ S) in a thick film changes from TS0 up to
TSf-GBPhT temperature, and the film tension changes from “zero” in volume up to g » 2sL-surface tension of liquid. Then we get the basic equation for an evaluation of a modification of temperature of GBPhT (on the intergranular boundaries) based on its comparison with a melting point TS0 of a solid body:
TSf = TS0 exp(−2sL DASL/QSL) (4)
Data for TSf of solid-liquid GBPhT of some metals calculated by means of this equation are presented in Table 1. These evaluation data correspond with the experimental data found by Inoko et al. [11], where with use of an electronic microscopy it was shown that TSf was near 0.56 TS0 (melting point) for Cu, Ag, Ni. We based the experimental proofs on the study of diffusion, identifying of the temperature coefficients of surface tension and on experimental data of a vacancies concentration changes with temperature [1] [12]. For example, we obtained the value of the nitrogen effective diffusion coefficient in polycrystalline being equal to: D = 1.1 × 10?5 cm2/sec at 800˚C. The value is the same as in the liquid phase, i.e., direct confirmation of the fact that a grain boundary layer exhibits liquid-phase properties. A value of D = 3× 10−9 cm2/sec is known from publications for Fe-C system (0.5 wt.%) (at 550˚C, i.e., close to the GBPhT temperature―740˚C).
The parameters of GBPhT and characteristics of mass-transfer in interfaces had been used for the development of the nanotechnology for the advanced materials production and effective hard coating formation by synthesis of nanosize nitrides and carbonitrides in surface layers of alloys and hard metals using gaseous nitrogen in thermo-chemical processing (TChP).
2. Characterization Characteristic of Advanced Materials and Hard Coatings after Treatment in Regime of Intergranular Quasi-Liquid Films
2.1. Industrial Tests of Advanced Tools with Hart Coating
We chose the drilling pipes tools for an experimental study, namely the inserts for tongs from steel Fe-0.46C- 0.9Cr %mass (40×) replacing hard metal, and the elements for a forcing-lift of diesel engine from steel Fe-0.18C-2Cr-4Ni-0.3Mo (18X2H4MA) after nitriding. The industrial tests of the tools were carried out on the oil fields and testing stands of autoworks. The mechanical behavior of advance tools was indicated a high resistance to surface wears and fragile breaks-down. Inserts life times improved more then 2 - 3 times. Bench tests of parts of a fuel pump of a diesel engine (plunger pair and feeder), indicated the increase of wear-resistance of the nozzle needle and spraying case by 1.5 - 2 times without coking.
2.2. Structure and Mechanical Properties of Coatings
The improvement of the mechanical properties of inserts from the steel 40× is provided by the combination of a specific stepped change of high micro hardness (650 - 730 Hv) of surface coatings up to 3 mm (enriched of nanosize nitrides) with high impact on the toughness of bulk. The micro hardness of a disperser from steel 18Х2Н4МА has the same specific stepped change due to obtain an isotropic structure zone formation (Figure 1).
Figure 1.Microhardness of nitrated steel: 1 - 40× (max 712Hv); 2-18X2H4MA (max 960Hv).
Table 1. TSf of solid-liquid GBPhT of some metals with surface tension sL at melting point TS0.
The prior thermodynamic analysis based on the temperature dependence of the Gibbs energy and the equilibrium diagram Fe-Cr-C showed, that content of equilibrium nitrogen in an alloy at temperatures 400˚C - 1400˚C can make up to 0.03% - 1.0% at. The measured concentrations of nitrogen gives value of 0.5% - 4.2% at in coating of steel 40× and 0.7% - 1.6% at in coating of 18X2H4MA. The creation of a concentration gradient of summary nitrogen in a layer of chromium steel up to 3 mm from surface results in forming graded coatings with laminated, stepped changes in properties. The graded, staged change of hardness in coatings is connected to formation up to three zones by an expansion 0.4 - 0.8 mm with specific structure. The qualitative and quantitative metallographic analysis methods have shown, that the basic quantity of nitrogen present as a nitride Cr2N (has blue color). For the study we used the optical microscope OLYMPUS PME-3c and the analyzer IA-3001 LECO. For a structure research was applied the X-ray phase analyzer and electron microscope EM-200CX. Zone up to 0.5mm contains residual austenite and nanosize cubic nitrides of chromium of the needle shape (20 - 50 nm). The total of nitrides sharp falls already at the end of the first zone synchronously with fall of nitrogen concentration. The second zone is characterized by the increase of martensite up to 70% and increase of quantity nanosize nitrides (fraction less than 30 nm). Martensite structure and nitrides are found in the third zone. The results are summarized in Table 2.
The solutions with higher then equilibrium level of nitrogen in martensite specify the increase of parameter of a lattice in the α-phase up to 0.2873 nm and is marked by strong eroded diffraction lines (Figure 2).
Increase of hardness in the formed surface layer may be associated with dispersing of the hardening due to the carbonitrides and nitrides formation at high nitrogen concentration and hardening of solid solutions of austenite and martensite by nitrogen. Residual austenite presents in the coatings due stabilization by dissolved nitrogen.
All this factors provide more high wear resistance of the material and decrease sensibility to fragile rupture.
2.3. Nickel Alloy for Aircraft Industry
Nickel alloys are widely used in aircraft and aerospace industry. The ordered structure of cuboids γ'-phase determines the properties of alloys. The γ'-phase in the heat-resistant nickel alloys completely transform into solid solution at temperatures above 950˚C. This process predetermines the softening of alloys [13]. It is known that enlarged threshold of heat resistance temperature is possible way for the inclusion into alloy a refractory compounds in the form of nanosize phases. Nitrides and carbides may remain unchanged up to the melting temperature of the alloy.
2.3.1. Nitrides Hardening Effect on Ni-Cr Alloy
The endogenous introduction into alloy of a nanosize phase of refractory compounds is possible by way of diffusion TChP. Nitrides, along with an ordered structure, similar to carbides by their impact on the strength prop-
Figure 2. Coating structure: a) Microscopy image of martensite in third zone (2 mm, steel 40×); b) microdiffraction <100>.
Table 2. Results of analysis of the coatings with laminated, step changes of properties.
erties. The main effect of the presence of nitride appears at high temperatures. Effect of hardening by the intro- ducing of nitrides is illustrated on the alloy Ni-Cr (20%) where γ'-phase is not formed. In the alloy, after nitriding by gaseous nitrogen, quantity of nitrogen was 0.003% - 0.048% mass and size of nitrides was not more then 20 nm (Figure 3).
The test results under 1100˚C shows change of tensile strength and elongation according to the content of nitrides, what corresponds with the nitrogen content in the alloy (Table 3). The change in the nitrides content caused the pronounced hardening effect (over 40% σb) related to change of nitrogen concentration. Descending change of the plasticity δ indicates the presence of nitrogen in solid solution too.
2.3.2. Nitrides Hardening High-Temperature Alloy
The fullness of ex-solution, size and morphology of the γ'-phase largely determine the properties of the heat-re- sistant alloys such as EI437A (%mass: C-0.08, Cr-20, Ti-2.50, Al-0.7, Ce-0.008, Mn-0.19, Si-0.42, N-0.0032). Introduction of nanosized nitrides by TChP leads to a breaking of grains, grinding and stabilizing of γ'-phase. Size and quantity of the γ'-phase was determined on foils and isolates by method of a contrast extinction of electron microscopy. Composition of the γ'-phase was measured the use of the Auger spectroscopy and emission spectrometer LECO SA-200. The group of alloys was studied including standard industry samples (N- 0.0032% mass), nitrided by TChP (N-0.035) and nitrided alloy with 1.2% mass Nb (N-0.085). Size of the γ'-phase varies as 25.0; 20.0; 18.0 nm and quantity as 10.8%; 12.9%; 13.2% mass. The acceptable heat-resistant characteristics increase on 180˚C (Figure 4).
2.4. Improving of Armour Plate Resistance to Fragile Rupture
The subject of the study was the resistance of the armour plate to heavy impacts in connection to a structure and properties of nitrided steel 40XHMA Plates after TChP have structure with a residual nitriding austenite and Cr2N in needle shape. The heat treatment resulted in the formation of a fine grain martensite, hardened by dispersible Cr2N of a size up to 300 nm. Outcomes of the X-ray phase analysis on a distance 0.25мм: a = 0.2874 nm <211> −α Fe = 54%mаss; a = 0.3616 nm <200> −γ Fe = 46%mаss; Cr2N. The hardness on a surface (up to 1 mm ) achieves 900 - 950 HV, while within a layer of 1 - 3 mm stays at level 700 - 800 HV at a minor drop of impact toughness. Nitrides Cr2N are distributed uniformly within a thickness of 0.3 - 0.4 mm . The summary content of nitrogen changes with thickness from surface to depth: at 0.1 mm - 1.4%mas, 1.0% - 0.98%, 2.5% - 0.75% relatively. The structure of steel formed in conformity with this gradient concentration of nitrogen (Figure 5).
The penetration and breakdown test was carried out using АКМ by a bullet of caliber 7.62 mm . The flattening of a standard bullet took place on the plate. The bullet with the core from W was scattered. Sensibility of the plate to fragile rupture is decreased after TChP with following thermo-treatment.
Figure 3. Image made by extinction contrast method: white inclusions against a dark background-nitrides.
Table 3. Nitrides hardening effect on Ni-Cr alloy.
Figure 4. The tensile strength sharp falls and elongation anomalously increased already at 800˚C for standard alloy (1 - 3); these characteristics displaced on 180˚C in the acceptable heat-resistant area for nitrided alloy (4).

Figure 5. Steel structure after TChP (diffusion nitriding and heat-treatment) at same magnification for (a), (b), (c): (a) surface of plate ( 0.1 mm ) with dispersible Cr2N; (b) distance from surface 1.0 mm?residual austenite, martensite and Cr2N in needle shape; (c) 2.0 mm?hardened Cr2N martensite and ferrite-perlite composition.
3. Conclusions
The fundamental properties of the solid crystalline materials i.e. phenomena of first-order phase transition of grain boundary with formation of two-dimensional quasi-liquid phase have described with means of the fundamental equations of film thermodynamics. The obtained generalized equation had been used for the calculating of the phase transition temperature TSf of grain boundary for some metals. The obtained values found within the range of (0.55 - 0.86) TS0.
The use of phenomena for a modification of process engineering of metals handling allows receiving graded materials with necessary mechanical and rheological properties.
The formation of coatings with laminated, stepped changes of properties provides increase of a hardness as well as wear resistance of the tools.
Cite this paper
Yu. A. Minaev, (2015) Phenomena of Intergranular Liquid Film Formation in Technology. Journal of Materials Science and Chemical Engineering,03,8-14. doi: 10.4236/msce.2015.31002
References
- 1. Minaev, Yu.A. (1972) Surface Layers of Pure Substances. ZhFKh, 46, 1090-1094.
- 2. Kuznetsov, O.A. (Ed.) (2005) Scientific Discoveries: Collection of Short Descriptions of Scientific Discoveries, Scientific Hypotheses, 2004. RAEN, Moscow. (In Russian)
- 3. Flad, A. (1970) Interphase Boundary Gas-Solid. Mir, Moscow, 18. (In Russian)
- 4. Frenkel, Ya.I. (1959) Kinetics Theory of Liquids. RAN USSR, Moscow, Lenin-grad.
- 5. Slezov, V.V. (1981) Effective Coefficient of Grain Boundary Diffusion in Polycrystals. Dokl.AN USSR, 257, 871-875.
- 6. Harrison, L.G. (1961) Influence of Dislocations on Diffusion Kinetics in Solids with Particular Reference to the Alkali Halides. Transactions of the Faraday Society, 57, 1191-1199. http://dx.doi.org/10.1039/tf9615701191
- 7. Bokshtein, S.Z., Kishkin, S.T., Mishin, Y.M. and Razumovsky, I.M. (1985) Theory and Experimental Verification of the Method of Separate Determination of Boundary Diffusion Coefficient and the Diffusion Width of the Grain Boundaries. Dokl.AN USSR, 280, 1125-1128.
- 8. Ralph, B. (1968) Field-Ion Microscopy. Plenum Press, Cambridge.
- 9. Rusnaov, A.I. (1967) Phase Equilibria and Surface Phenomena. Khimiya, Leningrad. (In Russian);
- 10. Krotov, V.V. and Rusanov, A.I. (1999) Physicochemical Hydrodynamics of Capillary Systems. Imperial College Press, London.
- 11. Inoko, F. and Yoshikawa, T. (1996) Deformation, Recrystallization and Premelting in Bicrystals. Materials Science Forum, 204-206, 379-388. http://dx.doi.org/10.4028/www.scientific.net/MSF.204-206.379
- 12. Minaev, Yu.A. (2007) Phase Transitions in Surface Layers of Polycrystalline Solids. ZhFKh, 81, 1-4.
- 13. Kablov, E.N. (2001) Alloy Blade Turbine Engines. Alloys. Technology. Coating. MISiS, Moscow. (In Russian)








