Journal of Materials Science and Chemical Engineering
Vol.03 No.01(2015), Article ID:53348,7 pages
10.4236/msce.2015.31001
Surface Plastic Deformation by Sliding Elliptical Cylinder
Rostislav I. Nepershin
Plastic Deformation Systems Department, Moscow State University of Technology “STANKIN”, Moscow, Russia
Email: nepershin_ri@rambler.ru


Received November 2014

ABSTRACT
Steady state plastic flow of the ideal plastic half-space surface by sliding elliptical cylinder is numerically calculated with account of contact friction effect. Numerical solution of the plane strain hyperbolic differential equations with unknown contact pressure distribution is treated as nonlinear vector equation for the steady state plastic flow condition. Pronounced effect of the ellipse boundary curvature on the plastic flow mode is shown. Engineering application of the computer model is surface plastic deformation technology to improve wear and fatigue resistance of metal parts.
Keywords:
Surface Layer, Plastic Flow, Ideal Plasticity, Sliding; Elliptical Cylinder, Friction

1. Introduction
Surface plastic deformation by rigid tools is used in engineering technology to increase wear and fatigue resistance of metal contact parts. Specification of technology parameters for surface plastic deformation is difficult engineering problem induced by complex elastic-plastic deformation of the surface layer.
Finite element analysis of rigid cylinder rolling along elastic-plastic half space is considered in [1] [2]. But large plastic deformation compared with the elastic one, unknown plastic region boundaries, stress and velocity singularities at the intersection of the toll contact with surface boundary are key problems for accuracy of the finite element elastic-plastic analysis.
Plastic deformation in surface layer, deems, is dominant factor of the surface plastic technology, and models on the base of ideal plasticity theory [3] [4] is reasonable. Steady state ideal plastic flow induced by rolling of rigid cylinder is considered in [5] using a small parameter approach. Approximate analysis related with the rolling friction is given in [6]. Steady state plastic flow of surface layer induced by rolling and sliding of circular cylinder is investigated in [7]-[9].
Present steady state plastic flow model of surface layer is developed for rigid elliptical cylinder sliding with contact friction consideration. Variable curvature and ellipse orientation relative the surface boundary are effective features of the plastic flow mode. Sliding of the wedge [10] and circular cylinder [7]-[9] along the plastic surface are limit cases of the present model.
2. Problem Formulation
Steady state plastic flow of an ideal plastic half-space surface layer induced by sliding of loaded long elliptical cylinder is considered. Plane strain plastic flow on the plane x, y orthogonal to the cylinder axis is assumed with half-space moving velocity V and nonmoving cylinder.
Stresses and velocities in the plastic region, loads and torque applied to the cylinder are non-dimension, using material plastic constant 2k and sliding velocity V as reference units. Elliptical section of the cylinder and scheme of the plastic region are shown in Figure 1.
Steady state plastic region OAB and cylinder are non- moving in coordinates x, y with the origin O at the lower contact point of the cylinder with half-space boundary. First principal axis x1 of the ellipse is inclined at the angle θ0 to the axis x. Minimal half-length of the ellipse axis is assumed as unit reference length, and ellipse form is defined by non-dimensional maximal half-length axis a. Ellipse boundary with the center C can be written in parametric form in principal ellipse coordinates x1, x2
x1 = acosω, y1 = sinω, −π/2 ≤ ω ≤ π/2 (1)
Tangent angle θ to the axis x1 at the point x1, x2 is defined as follows
tgθ = −(ctgω)/a (2)
Coordinates x, y of the ellipse point x1, x2 are defined by shift and rotation transformation of the exses
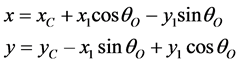 (3)
(3)
Angle θO at the point O is defined from Equation (2) by specified parameter ωO. Coordinates xC, yC of the ellipse center C are found from Equations (1) and (3) with specified ωO using the condition x = y = 0
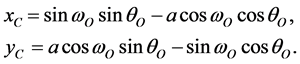 (4)
(4)
Contact boundary OA is defined by specified parameter ωA for the point A. Coordinates x, y of the boundary OA with the tangent angle α to the axis x
α = θ − θO, ωO ≤ ω ≤ ωA (5)
are defined by Equations (1)-(3).
Parameters ωO, ωA and a define ellipse form, the angle θO and contact boundary OA on different segments of the ellipse. Length of the contact boundary lc is defined by integral
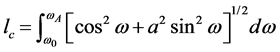 (6)
(6)
Figure 1. Steady state surface plastic region.
Boundary OA with contact pressure and shear stress define loads Q, F and torque M (Figure 1) using static equilibrium of the cylinder.
Plane strain plastic flow of the ideal plastic material [3] [4] is defined by hyperbolic differential Equations with orthogonal ξ and η slip lines
dx/dy = tgφ for ξ, dx/dy = −ctgφ for η, (7)
Henky’s Equations for the mean stress σ and angle φ
dσ − dφ = 0 along ξ, dσ + dφ = 0 along η (8)
where 2k = 1 is used as unit stress, and Geiringer’s Equations for the velocity projections Vξ, Vη on the slip lines
dVξ − Vηdφ = 0 along ξ, dVη + Vξ dφ = 0 along η (9)
Stress and velocity components in coordinates x, y are related with σ, φ, Vξ and Vη variables by Equations
σx = σ − 0.5sin2φ, σy = σ + 0.5sin2φ, τxy = 0.5cos2φ (10)
and
Vx = Vξ cosφ − Vη sinφ, Vy = Vξ sinφ + Vη cosφ (11)
3. Boundary Conditions
Stress free boundary AB (Figure 2) is the stream line of the steady state plastic flow, with the principal stresses σ1 = 0, σ2 = −1 along this boundary, and we have stress and velocity boundary conditions on AB
σ = −0.5, Vξ + Vη = 0 (12)
Friction on the boundary AO is specified by contact shear stress 0 ≤ τc ≤ 0.5, used in technological plasticity problems with large contact pressures [11]. Incline angle γ for the η slip line on the contact boundary (Figure 2(a)) is found from third Equation (10) using specified τc value
γ = 0.5cos−1(2τc) (13)
Angle φ between the ξ slip lines and axis x on the boundary AO with the tangent angles α is defined as
φ = π/2 + γ − α, 0 ≤ α ≤ αA (14)
Zero normal component of the velocity and the angle γ define boundary condition for the velocities Vξ and Vη on the boundary AO
Vξ − Vη tgγ = 0 (15)
Half-space velocities Vx = 1, Vy = 0 are continues on the rigid-plastic boundary OB, and from Equations (11) it follows
Vξ = cosφ, Vη = −sinφ (16)
Mean stress σO at the point O is defined from second Equation (8) for the η slip line, using first boundary condition (12) with φ = π/4 at the point B, and Equation (14) with α = 0 at the point O
σO = −(0.5 + γ + π/4) (17)
Fun angle ψ for the ξ slip lines at the singular point A with tangent angle β on the stress free boundary AB is found using Equation (14) with α = αA
ψ = π/4 + γ − (αA + β) (18)
Angle β is defined during problem solution using condition y = 0 at the point B.

Figure 2. Plastic regions with pressure and plastic. Strain distributions for variants (a) 1; (b) 2 and (c) 3 in Table 1.
Limit value α*A for the steady state plastic flow is found from Equation (18) with ψ = 0
α*A = π/4 + γ − β (19)
Corresponding limit parameter ω*A and contact length lc are found from Equations (5) and (6).
4. Numerical Solution
Numerical solution of the problem with specified parameters a, ωO, ωA and τc begins by initial guess for the angle β with constrain αA < α*A in Equation (19).
Then mean stress σA at the singular point A on the contact boundary AO is found from boundary condition (12) and second Equation (8) for the η slip line
σA = −(0.5 + ψ) (20)
Fan angle ψ is defined by Equation (18) with the angle αA found from Equations (2) and (5) for specified parameters a, ωO and ωA.
Initial mean stress distribution σi is specified at the nodes i = 1, 2, 3,…, N on the contact boundary AO proportional the angles αi, defined by the parameters ωi in the interval ωO ≤ ωi ≤ ωA. Mean stress σi distribution, boundary condition (14) for the angles φi and contact boundary AO, defined by Equations (1) and (3), specify Cauchy’s boundary value problem for differential Equations (7) and (8).
Cauchy’s problem is solved using numerical procedures [11] with the result of slip lines with σ, φ variables calculation in the region AOD (Figure 2(a)). Then σ and φ variables are specified at the singular point A using second Equation (8), followed by numerical solution of Riemann’s problem in the region ADC with known σ, φ variables on the slip line AD. Finally, inverse Cauchy’s problem is solved numerically in the region ACB, using known σ, φ variables on the slip line AC with σ = −0.5 on calculated stress free boundary AB. Then initial guess for the angle β is corrected to satisfy condition y = 0 at the point B.
So, slip lines in the plastic region are calculated for specified stress σ distribution on the contact boundary AO. Next procedure is numerical calculation of the velocity field in the plastic region using conditions (15) on the boundary AO and (16) on the boundary OB. First, velocities Vξ, Vη are calculated in the region AOD by numerical solution of the mixed boundary value problem for Equations (9) with known φ angles at the slip line nodes. Then velocity field is calculated in the region ADC from Riemann’s problem with known Vξ, Vη on the slip lines AD and CD, followed by velocity field calculation in the region ACB, using known Vξ, Vη on the slip lines AC and CB, with the result of Vξ and Vη calculation on the stress free boundary AB.
Velocities Vξ and Vη must satisfy steady state plastic flow condition in Equation (12). If we define specified σi values on the boundary AO as the vector σ in N dimension space and values
fi = (Vξ + Vη)i (21)
at the N nodes of the boundary AB as the vector function f in the same N dimension space, then we have nonlinear vector Equation (22) for the steady state plastic flow problem solution
f(σ) = 0 (22)
because numerical procedures for calculation of the slip lines and velocity field in the plastic region give unique relation between vectors σ and f. Equation (22) with N ≤ 20 was solved using numerical procedures [12] for Broyden’s method [13].
Equation (22) is solved with accuracy max fi ≤ 10−3.
Then contact pressure distribution
pi = −(σi − 0.5sin2γ) (23)
was calculated on the boundary AO, followed by integration of pressure and contact shear stresses to find loads Q, F and torque M (Figure 1).
5. Numerical Results
For numerical solution of the problem FORTRAN program was written with input parameters a, τc, ωO, ωA and output data in the form of tables and graphical mapping of the slip line nodes as pixels on the monitor screen. Stream lines in the plastic region with accumulated plastic strain ep and orthogonal grid distortions were calculated using numerical procedures in [14].
Numerical examples below were calculated for the ellipse parameter a = 2, three variants of the pairs {ωO, ωA} and three typical values τc for practical surface plastic deformation technology to illustrate variable contact curvature and friction effects.
Three variants of the ellipse contact boundary AO, defined by the parameters ωO and ωA, are given in Table 1. Corresponding ellipse incline angle θO, tangent angle αA at the point A , ellipse center C and contact length lc are calculated from Equations (2), (4), (5) and (6). In variants 1 to 3 the incline angles θO and contact angles αA are decreased with decrease of the ellipse curvature and increase of the contact length lc.
Calculated slip lines in the plastic region with distributions of contact pressure p and accumulated plastic strain ep of the material at the exit from the plastic region with shear contact stress τc = 0.1 are shown in Figure 2 for the ellipse boundary variants in Table 1. Curvature decrease of the ellipse contact boundary results in more homogeneous contact pressure distribution and decrease of the gradient and value of the plastic strain distributions through thickness of the surface plastic layer. But mean contact pressure is increased, and for smooth boundary with τc = 0 it is approached to Prandtl’s flat punch value p = 1 + π/2.
Velocity hodographs on the plane Vx, Vy in the plastic regions in Figure 2 are presented in Figure 3 for the same three variants of the ellipse contact boundary (Table 1) and shear contact stress τc = 0.1. Velocities Vx, Vy are calculated using Equations (11) with known variables Vξ, Vη, φ at the slip line nodes and mapped by pixels on the monitor screen.
Unit velocity vector at the point B is decreased along the stress free boundary AB with tangent angle increase to the β at the point A. Then velocity vector direction is rotated at the singular point A to the tangent angle αA at the contact boundary, followed by increase of the vector module tangent to the boundary AO from the point A to the point O where it is unit horizontal vector.
Boundary BCDO of the plastic region on the plane x, y (Figure 2) is mapped to the point BCDO on the hodograph plane (Figure 3), as the result of the velocity continuity with moving half-space given by Equations (16).
Curvature decrease of the ellipse boundary AO from variant 1 to 3 in Table 1, and from (a) to (c) in Figure 2 and Figure 3 results in drastic velocity field non-homogeneous decrease, with homogeneous velocity field Vx = 1, Vy = 0 for the flat sliding Prandtl’s punch.
Initial orthogonal grid distortions with the stream lines for the plastic regions in Figure 2 are shown in Figure 4 for the same variants of the ellipse contact boundaries in Table 1. Plastic boundary OB with the half-space is shown by dash line.
Movement of material point along the stream lines is calculated using steady state velocity fields in Figure 3 for constant horizontal displacement increment dx at the entry to the plastic regions.
Displacement of the material point along the stream lines in the plastic region is calculated using mean velocity vectors in the “time” interval dx, because the half-space velocity is unit.
Final displacement Δx is defined by the slow material point, moving on the path BAO, while the fast material point is moved with unit velocity on horizontal path tangent to the boundary of the plastic region. Calculated positions of the material points on the stream lines are mapped on the monitor screen by pixels at each displacement increments dx.
Increase of the ellipse contact boundary from variant 3 to 1 in Table 1 and from (c) to (a) in Figure 4 results in drastic grid distortion and thickness decrease of the surface plastic layer.
Contact shear stress effect on the pressure at the points O and A, loads Q and F, torque M , surface plastic layer thickness hp and maximum plastic strain ep is given in Table 2 for the three variants of the ellipse contact boundary in Table 1.
Numerical results in Table 2 show essential effect of the ellipse contact curvature on the surface plastic flow. Contact friction decrease results in homogeneous plastic strain distribution through the surface plastic layer.
Table 1. Variants of the ellipse contact boundary.
Table 2. Contact friction effect on the surface plastic deformation by sliding elliptical cylinder.

Figure 3. Velocity hodographs for the plastic regions (a), (b), (c) in Figure 2.

Figure 4. Stream lines with grid distortions for the plastic regions (a), (b), (c) in Figure 2.
Dimensional values of the ellipse center coordinates, contact length and plastic layer thickness are defined by multiplication of non-dimensional values on dimension value of the minor ellipse half-length b. Dimension shear stress τc and pressures p are defined by multiplication of non-dimensional values on double plastic constant 2k, where k = σY/2 for Tresca, or k = σY/√3 for Mises yield criterion. The material yield stress σY should be specified using compression stress-strain curve in the range of mean plastic strains in Figure 2 and in Table 2, to approximate material work hardening effect.
6. Conclusions
Surface steady state plastic deformation by sliding elliptical cylinder with contact friction effect is modeled using hyperbolic differential equations of the plane strain ideal plasticity theory.
Plastic region with curved stress free boundary is calculated by numerical solution of nonlinear vector equation with unknown contact pressure distribution. Numerical results show essential effect of the ellipse contact boundary curvature on the mode of the surface plastic flow. Curvature of the contact boundary can be changed by rotation of the ellipse principal axes relative the surface boundary.
Numerical model is performed by FORTRAN program to investigate effects of the ellipse form, curvature and length of contact boundary and contact friction on the plastic flow of the surface with contact pressure and plastic strain distributions, loads and torque applied to the cylinder. These results, deems, are useful for engineering problems of metal parts surface plastic deformation to increase wear and fatigue resistance.
Acknowledgements
Russian Federation Ministry of Education and Science support by project No. 9.2445.2014/K is gratefully acknowledged.
Cite this paper
Rostislav I. Nepershin, (2015) Surface Plastic Deformation by Sliding Elliptical Cylinder. Journal of Materials Science and Chemical Engineering,03,1-7. doi: 10.4236/msce.2015.31001
References
- 1. Howell, M., Hahn, G.T., Rubin, C.A. and McDowell, D.L. (1995) Finite Element Analysis of Rolling Contact for Non-linear Kinematic Hardening Bearing Steel. Journal of Tribology, 117, 729-736. http://dx.doi.org/10.1115/1.2831544
- 2. Shiratori, M., Ito, M. and Hashimoto, M. (1995) Elastic-Plastic Analysis of Rolling Contact for Surface Hardened Steel. Trans. Jap. Soc. Mech. Eng. A., 61, 1064-1069. http://dx.doi.org/10.1299/kikaia.61.1064
- 3. Hill, R. (1985) The Mathematical Theory of Plasticity. 11th Edition, Oxford University Press, Oxford.
- 4. Ishlinsky, A.Yu. and Ivlev, D.D. (2001) The Mathematical Theory of Plasticity. FIZMATLIT, Moscow.
- 5. Marshall, E.A. (1968) Rolling Contact with Plastic Deformation. Journal of the Mechanics and Physics of Solids, 16, 243-254. http://dx.doi.org/10.1016/0022-5096(68)90032-X
- 6. Collins, I.F. (1972) A Simplified Analysis of the Rolling of Cylinder on a Rigid/Perfectly Plastic Half-Space. International Journal of Mechanical Sciences, 14, 1-14. http://dx.doi.org/10.1016/0020-7403(72)90002-1
- 7. Nepershin, R.I. (2002) On Rolling and Sliding of a Cylinder along a Perfectly Plastic Half-Space with Allowance for Contact Friction. Doklady Physics, 47, 256-259. http://dx.doi.org/10.1134/1.1467875
- 8. Nepershin, R.I. (2003) The Rolling and Slipping of a Cylinder along the Boundary of an Ideally Plastic Half-Space. Journal of Applied Mathematics and Mechanics, 67, 293-301. http://dx.doi.org/10.1016/S0021-8928(03)90015-3
- 9. Nepershin, R.I. (2013) Plastic Deformation of Surface Layer during Rigid Cylinder Rolling and Sliding. Journal of Friction and Wear, 34, 204-207. http://dx.doi.org/10.3103/S1068366613030112
- 10. Nepershin, R.I. (2001) On Sliding of Obtuse Wedge along the Boundary of a Perfectly Plastic Half-Space. Doklady Physics, 46, 885- 887. http://dx.doi.org/10.1134/1.1433536
- 11. Druyanov, B.A. and Nepershin, R.I. (1994) Problems of Technological Plasticity. Elsevier, Amsterdam.
- 12. Dennis, J.E. and Shnabel, R.B. (1983) Numerical Methods for Unconstrained Opti-mization and Nonlinear Equations. Prentice-Hall, Englewood Cliffs.
- 13. Broyden, C.G. (1965) A Class of Methods for Solving Nonlinear Simultaneous Equations. Maths. Comp., 19, 577-593.
- 14. Nepershin, R.I. (2004) Rolling and Sliding of Rigid Cylinder along the Boundary of a Rigid-Plastic Half-Space. Mechanics of Solids, 39, 81-93.









