Vol.3, No.6, 444-455 (2011) Natural Science
http://dx.doi.org/10.4236/ns.2011.36061
Diagnostic of the diurnal cycle of turbulence of the
Equatorial Atlantic Ocean upper boundary layer
Udo T. Skielka1, Jacyra Soares1,*, Amauri P. Oliveira1, Jacques Servain2
1Department of Atmospheric Sciences, University of São Paulo, São Paulo, Brazil; *corresponding author:
2Institut de Recherche pour le Développement (IRD), Paris, France; Visiting scientist at Fundação Cearense de Meteorologia e
Recursos Hídricos (FUNCEME), Fortaleza, Brazil
Received 12 March 2011; revised 4 April 2011; accepted 19 April 2011.
ABSTRACT
This work is an attempt to diagnose the turbu-
lence field of the equatorial Atlantic Ocean dur-
ing the dry period when the mixed layer is more
highly developed using the General Ocean
Turbulence Model (GOTM). A relaxation scheme
assimilates the vertical profiles of in situ ob-
servations (current velocity, sea temperature
and salinity) during simulations. In the absence
of direct turbulence observations and modeling
studies of the equatorial Atlantic Ocean, the
results are compared qualitatively to observed
and simulated results for the equatorial Pacific
Ocean. Similarities are noted between the At-
lantic simulation and previous studies per-
formed in the Pacific Ocean. The mechanism of
nocturnal turbulence production, namely deep-
cycle turbulence, is well captured by GOTM
simulations. This deep nocturnal turbulence
appears rather suddenly during the night in the
simulations and consequently seems to be un-
related to surface wind and radiation forcing.
Keywords: Oceanic Boundary Layer; Oceanic
Turbulence; Tropical Oceanography, Equatorial
Atlantic Ocean
1. INTRODUCTION
The world equatorial region is characterized by the
presence of easterly trade winds that blow almost con-
stantly. Locally, surface wind is responsible for turbu-
lence production in the first depths of the mixed layer
(ML) via shear production, surface wave breaking and
Langmuir circulation [1]. On a large scale, zonal incli-
nation of the sea surface, provided by wind forcing
over the equatorial basin, is responsible for the main-
tenance of the westward equatorial undercurrent (EUC).
The EUC core is located in the thermocline above
which there is a region of intense shear.
The equatorial Pacific Ocean has been the scene of
marine turbulence investigations since the 1980s, with
the first measurements of turbulent kinetic energy dis-
sipation rate (ε) over 140˚W [2,3]. These works showed
the equatorial upper layer as a region of intense and
deep turbulent mixing, with a cycle of turbulence that
may present large diurnal variability. Recently, studies
have been performed to elucidate the physical mecha-
nism of turbulence production and to properly simulate
equatorial upper-ocean flow.
Modeling studies have proven to be very useful and
complementary to laboratory and field experiments
when studying physical processes in situations where
high-resolution observational data is not available.
More recently, large-eddy simulation (LES) has been
used to study the dynamics of the equatorial ML and
turbulent processes in the Pacific Ocean [4-7].
Gregg et al. [3] measured vertical profiles of ε dur-
ing 4.5 days in the equatorial Pacific Ocean and
pointed out the presence of a strong diurnal cycle of the
turbulent upper layer in the equatorial Pacific Ocean.
They verified that at the shallower layer close to the
surface (approximately 10 - 30 m), mixing and stratifi-
cation vary in phase with surface flux. During the day,
turbulence production presents a minimum above 30 m
due to the stable stratification caused by the input of
solar radiation. At this depth, daily fluctuations of ε
vary by a factor of 100. Below this layer (approxi-
mately 30 - 65 m), there is a so-called “upper high-
shear zone”, which is characterized by high turbulent
fluxes and a diurnal fluctuation of ε equivalent to that
found in the ML. Gregg et al. [3] considered some hy-
potheses to explain this deep turbulence, such as 1)
absorption of solar radiation, 2) diurnal cycle in the
EUC shear region and 3) daily modulation of high-
frequency internal waves.
Other measurements of the equatorial Pacific Ocean
*This research was supported by CNPq, Fapesp and IRD.

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 445
confirmed intense diurnal variation in the region be-
tween below the ML base and the EUC [2,8,9].
Using LES, [5] verified a diurnal cycle of ε in the
equatorial Pacific Ocean that was similar to that de-
scribed by [3]. During the day, due to the input of solar
radiation, dynamic stability and decaying turbulence
prevail below the ML. Near sunset, convection begins in
the ML, and turbulence grows. Then, the boundary layer
(BL) deepens, and a turbulence region is verified, reach-
ing more than twice the depth of the ML. At night, while
wind stress tends to maintain a constant shear close to the
surface, convection homogenizes the temperature, result-
ing in a decrease in the gradient Richardson number (Rig).
Wang et al. [5] concluded that the most important cause
of deep-cycle turbulence in their modeling work was the
entrainment associated with the presence of shear, which
is directly linked to local Kelvin-Helmholtz instability,
characterized as direct contact of the ML with the layer
below. However, they also recognized that the model
domain used was unable to reproduce internal waves
generated by large eddies in the nocturnal ML, as sug-
gested by [3], and that these waves might be an important
contributor to deep turbulence production.
Wang and Müller [7] confirmed the hypothesis of [3],
which stated that convection in the mixed layer triggers
shear instability, which in turn radiates gravity waves
downward into the upper thermocline. Local shear in-
stability can be triggered by downward-propagating
internal waves in a marginally stable environment (0.25
< Rig < 0.50).
Despite the role of convection in enhancing turbu-
lence production in the ML, [7] showed that heat flux
cooling variations (variations by a factor of 10) at the
surface do not significantly affect the presence of deep
turbulence and that the shear profile due the presence
of the EUC is the main contributor to mixing at deeper
layers.
However, in the equatorial Atlantic Ocean, oceanic
boundary layer investigations are rarely found in the
literature. During the Seasonal Response of the Equa-
torial Atlantic Program (SEQUAL), [10,11] character-
ized the upper layer of the equatorial Atlantic central
basin (0˚N, 28˚W) using measurements of wind veloc-
ity (surface wind stress) and vertical profiles of tem-
perature and velocity. They studied the annual cycle of
temperature and advection in this upper layer and
found out that advection activity is weaker from Sep-
tember to November. Weisberg and Tang [12] sug-
gested the application of one-dimensional modeling
studies of this region during this period, when the
thermocline has already adjusted to wind stress intensi-
fication and heat input at the surface is in approximate
equilibrium with the entrainment rate at the mixed
layer base. Furthermore, according to [13], the influ-
ence of tropical instability waves diminishes after Au-
gust, allowing better performance of 1D models during
this period.
In the present work, the General Ocean Turbulence
Model (GOTM) [14] was applied to simulate the tur-
bulent field of the equatorial Atlantic Ocean, using data
from an ATLAS buoy (0˚N, 23˚W) of the Prediction
and Research Moored Array in the Tropical Atlantic
(PIRATA) [15,16] to compute surface fluxes and for
relaxation of the mean field in simulations. Comple-
mentary data from the NASA/GEWEX Surface Radia-
tion Budget (SRB) Project was used to close the heat
balance at the surface.
The objective of this work was to diagnose the vertical
structure of the turbulence field of the equatorial Atlantic
Ocean. The chosen period was of the strongest winds and
when the ML is more highly developed (October). A re-
laxation scheme was applied to assimilate the vertical
profiles of in situ observations (current velocity, sea
temperature and salinity). The scheme was used during
the simulations to maintain the model results converging
to the equatorial mean field (mainly thermocline and
EUC variability), so that the turbulence closure may es-
timate the turbulent properties based on realistic equato-
rial features. In the absence of turbulence observations
and modeling studies of the equatorial Atlantic Ocean,
whenever possible, results were qualitatively compared
to studies of the equatorial Pacific Ocean.
Section 2 briefly describes the oceanic turbulence
model and the dataset used in this work. Section 3 pre-
sents the model results, and the main conclusions are
summarized in Section 4.
2. TURBULENCE CLOSURE MODEL
AND DATASET
2.1. The Model Characteristics
Statistical closure turbulence models provide the
complexity needed to simulate boundary layer dynamics
without computational expenses [14]. Moreover, they
allow estimation of turbulent quantities, such as turbu-
lent kinetic energy (k) and its dissipation rate, turbulent
viscosity and tracer diffusivities, which can be compared
to observations.
Burchard et al. [14] developed a computational tool
that compiles different turbulence closure models, which
they called GOTM. This model has been validated and
used in different studies of oceanic ML [15-18]. The
GOTM has, as the most complex turbulent closure, the
k-ε model proposed by [19]. Burchard and Bolding [17]
compared four different second-order closure schemes

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 446
and concluded that the closure scheme of [19] is the
most efficient scheme for simulating the ML in idealized
and applied cases.
The implementation of the GOTM in the laboratory
involved the test of different hydrodynamic cases, ideal-
ized and applied to natural waters, available at the
model’s website (www.gotm.net). Afterwards, the model
was run using the PIRATA dataset.
The model uses dynamic equations to compute k and
ε. Eq.1 describes the terms used to analyze the upper
layer turbulent field, where ∂tk is the local time varia-
tion of k:
tkPBD

 (1)
P is the shear or mechanical production of k:
2
t
PS   (2)
where t

is the turbulent viscosity computed by the
model, and S is the current shear, given by:

222
zz
Suv  (3)
where u and v are the mean zonal and meridional current
velocity, respectively, and z  the vertical derivative. B
is the buoyancy production/dissipation of k:
2
t
BKN (4)
which depends on the turbulent heat diffusivity (Kt)
and the static stability of the water column, given by the
buoyancy frequency (2
N):
2
0
z
g
N


 (5)
where g (9.81 m·s–2) is the acceleration of gravity, ρ is
the density, computed using the UNESCO algorithm
[20], and ρ0 (1027 kg·m–3) is the reference density.
The vertical diffusion of k (D) depends on the Schmidt
number for k (σk), which is an empirical constant:
t
zz
k
Dk



 


(6)
The viscous dissipation rate of turbulent kinetic en-
ergy (ε) is given by Eq.7, which is a linear combination
of the terms of Eq.1 with the semi-empirical parameters
cε1, cε2, cε3 and a vertical diffusion term (Tε). Further de-
tails can be found in [14].

132tcP cB cT
k

 

   (7)
The model uses the eddy viscosity principle, obtaining
the turbulent viscosity and diffusivity using k, ε and a
non-dimensional constant of proportionality called the
stability function, which contains the information of the
second-order closure.
2.2. Dataset
The region investigated was the equatorial Atlantic
central basin, at (0˚N, 23˚W), where an ATLAS mooring
has existed since 1999 as part of the PIRATA backbone
project. The buoy provides high frequency (every 10
minutes) measurements of air temperature and relative
humidity, wind direction and velocity, incoming short-
wave radiation and precipitation at the sea surface and
vertical profiles (0 - 500 m) of temperature and salinity.
Moreover, this PIRATA mooring is the only buoy of the
array that measures the two components of the oceanic
current by an Acoustic Doppler Current Profiler with a
4-m vertical resolution from the surface to approxi-
mately 100 m [21,22].
The surface radiation balance was obtained using ob-
served incoming shortwave radiation from the same PI-
RATA buoy and the other radiation components, upward
shortwave and downward and upward longwave radia-
tions, from the SRB-NASA. The SRB-NASA estimates
radiative parameters globally, with 1˚ X 1˚ resolution,
using satellite products, meteorological inputs from re-
analysis and radiative transfer algorithms (SRB,
http://gewex-srb.larc.nasa.gov). Studies at the Air-Sea
Interaction Research Lab-USP showed good agreement
between the SRB-NASA dataset and the PIRATA in situ
measurements [23]. The climatologic hourly averages of
the SRB-NASA data from 1999 to 2005, the last year of
available satellite data, were computed. Table 1 summa-
rizes the data set used in this work.
The bulk algorithm developed during the TOGA
COARE [24] was used to compute atmospheric turbu-
lent fluxes, with the observed air temperature and hu-
midity, horizontal wind components and SST obtained
using 10-minute averaged values of the PIRATA dataset
Table 1. Dataset used in numerical experiments. Surface tur-
bulent fluxes were computed using the COARE bulk algorithm
with PIRATA measurements.
PIRATA
(0˚N, 23˚W)
(2000-2006)
SRB-NASA
(1999-2005)
Specification on
the model
Air
Wind velocity
Air temperature
Air specific hu-
midity Incoming
shortwave radia-
tion
Upward shortwave
radiation Down-
ward and upward
longwave radia-
tions
Upper boundary
conditions: Sur-
face wind stress
Surface energy
balance
Ocean
column
Vertical profiles
of: Sub-surface
temperature
Salinity Current
velocity
_____________ Relaxation
scheme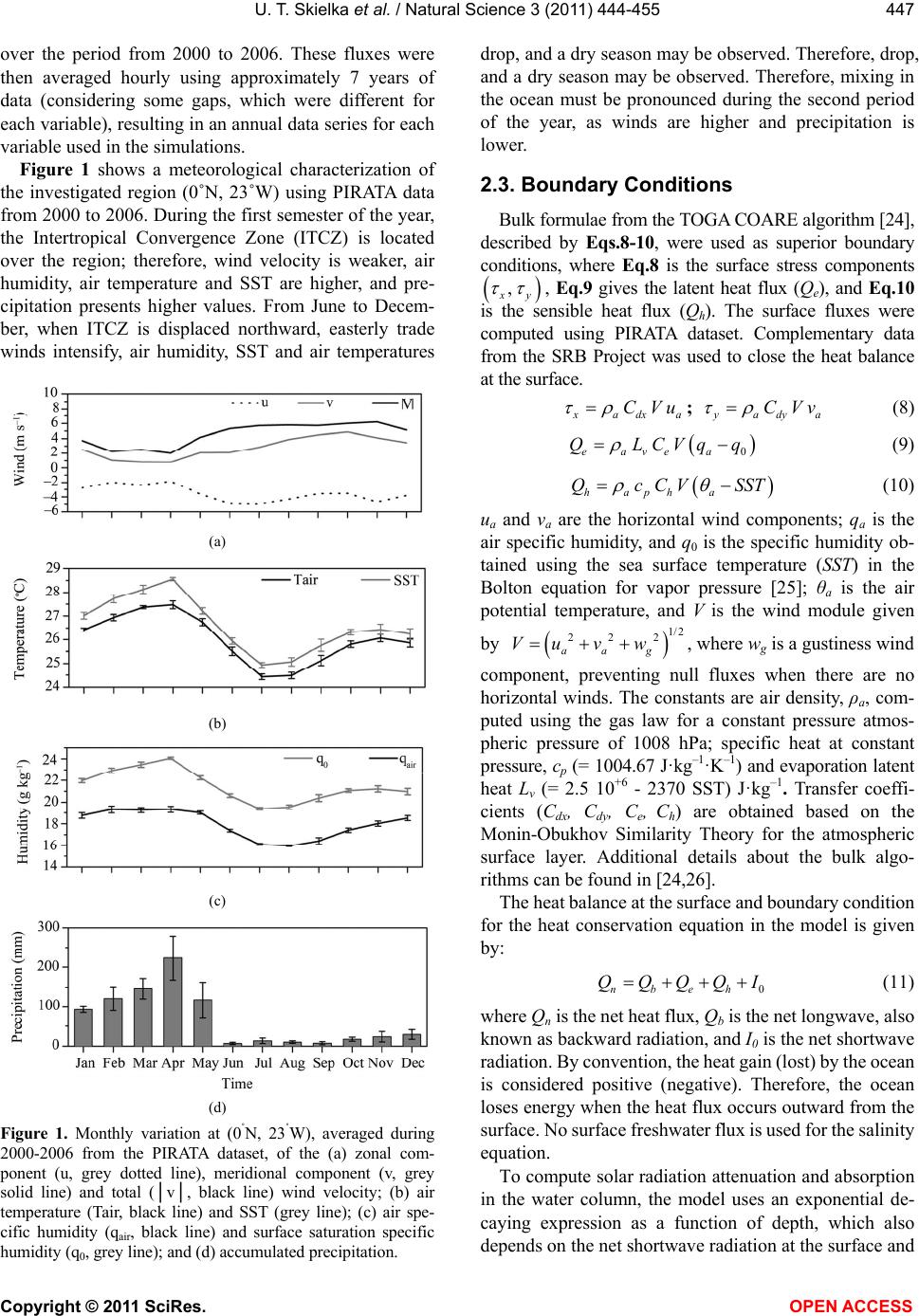

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 447
over the period from 2000 to 2006. These fluxes were
then averaged hourly using approximately 7 years of
data (considering some gaps, which were different for
each variable), resulting in an annual data series for each
variable used in the simulations.
Figure 1 shows a meteorological characterization of
the investigated region (0˚N, 23˚W) using PIRATA data
from 2000 to 2006. During the first semester of the year,
the Intertropical Convergence Zone (ITCZ) is located
over the region; therefore, wind velocity is weaker, air
humidity, air temperature and SST are higher, and pre-
cipitation presents higher values. From June to Decem-
ber, when ITCZ is displaced northward, easterly trade
winds intensify, air humidity, SST and air temperatures
(a)
(b)
(c)
(d)
Figure 1. Monthly variation at (0˚N, 23˚W), averaged during
2000-2006 from the PIRATA dataset, of the (a) zonal com-
ponent (u, grey dotted line), meridional component (v, grey
solid line) and total (│v│, black line) wind velocity; (b) air
temperature (Tair, black line) and SST (grey line); (c) air spe-
cific humidity (qair, black line) and surface saturation specific
humidity (q0, grey line); and (d) accumulated precipitation.
drop, and a dry season may be observed. Therefore, drop,
and a dry season may be observed. Therefore, mixing in
the ocean must be pronounced during the second period
of the year, as winds are higher and precipitation is
lower.
2.3. Boundary Conditions
Bulk formulae from the TOGA COARE algorithm [24],
described by Eqs.8-10, were used as superior boundary
conditions, where Eq.8 is the surface stress components


,
x
y

 , Eq.9 gives the latent heat flux (Qe), and Eq.10
is the sensible heat flux (Qh). The surface fluxes were
computed using PIRATA dataset. Complementary data
from the SRB Project was used to close the heat balance
at the surface.
x
adx a
CVu



;
y
ady a
CVv

 (8)


0eave a
QLCVqq   (9)

haph a
QcC VSST   (10)
ua and va are the horizontal wind components; qa is the
air specific humidity, and q0 is the specific humidity ob-
tained using the sea surface temperature (SST) in the
Bolton equation for vapor pressure [25]; θa is the air
potential temperature, and V is the wind module given
by

1/2
22 2
aa g
Vu v w, where wg is a gustiness wind
component, preventing null fluxes when there are no
horizontal winds. The constants are air density, ρa, com-
puted using the gas law for a constant pressure atmos-
pheric pressure of 1008 hPa; specific heat at constant
pressure, cp (= 1004.67 J·kg–1·K–1) and evaporation latent
heat Lv (= 2.5 10+6 - 2370 SST) J·kg–1. Transfer coeffi-
cients (Cdx, Cdy, Ce, Ch) are obtained based on the
Monin-Obukhov Similarity Theory for the atmospheric
surface layer. Additional details about the bulk algo-
rithms can be found in [24,26].
The heat balance at the surface and boundary condition
for the heat conservation equation in the model is given
by:
0nbeh
QQQQI

 (11)
where Qn is the net heat flux, Qb is the net longwave, also
known as backward radiation, and I0 is the net shortwave
radiation. By convention, the heat gain (lost) by the ocean
is considered positive (negative). Therefore, the ocean
loses energy when the heat flux occurs outward from the
surface. No surface freshwater flux is used for the salinity
equation.
To compute solar radiation attenuation and absorption
in the water column, the model uses an exponential de-
caying expression as a function of depth, which also
depends on the net shortwave radiation at the surface and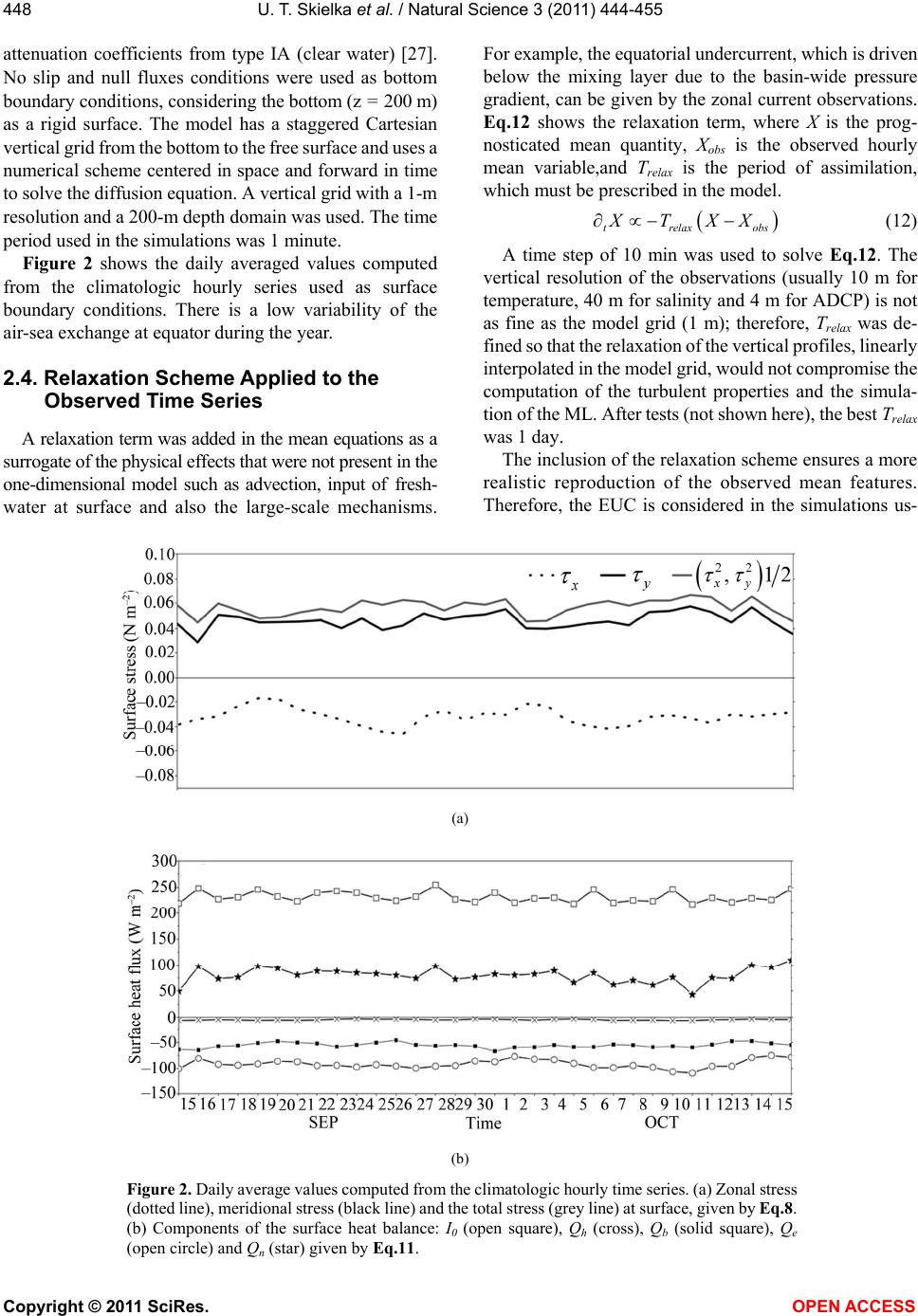

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 448
attenuation coefficients from type IA (clear water) [27].
No slip and null fluxes conditions were used as bottom
boundary conditions, considering the bottom (z = 200 m)
as a rigid surface. The model has a staggered Cartesian
vertical grid from the bottom to the free surface and uses a
numerical scheme centered in space and forward in time
to solve the diffusion equation. A vertical grid with a 1-m
resolution and a 200-m depth domain was used. The time
period used in the simulations was 1 minute.
Figure 2 shows the daily averaged values computed
from the climatologic hourly series used as surface
boundary conditions. There is a low variability of the
air-sea exchange at equator during the year.
2.4. Relaxation Scheme Applied to the
Observed Time Series
A relaxation term was added in the mean equations as a
surrogate of the physical effects that were not present in the
one-dimensional model such as advection, input of fresh-
water at surface and also the large-scale mechanisms.
For example, the equatorial undercurrent, which is driven
below the mixing layer due to the basin-wide pressure
gradient, can be given by the zonal current observations.
Eq.12 shows the relaxation term, where X is the prog-
nosticated mean quantity, X
obs is the observed hourly
mean variable,and Trelax is the period of assimilation,
which must be prescribed in the model.

trelax obs
XTXX (12)
A time step of 10 min was used to solve Eq.12. The
vertical resolution of the observations (usually 10 m for
temperature, 40 m for salinity and 4 m for ADCP) is not
as fine as the model grid (1 m); therefore, Trelax was de-
fined so that the relaxation of the vertical profiles, linearly
interpolated in the model grid, would not compromise the
computation of the turbulent properties and the simula-
tion of the ML. After tests (not shown here), the best Trelax
was 1 day.
The inclusion of the relaxation scheme ensures a more
realistic reproduction of the observed mean features.
Therefore, the EUC is considered in the simulations us-
(a)
(b)
Figure 2. Daily average values computed from the climatologic hourly time series. (a) Zonal stress
(dotted line), meridional stress (black line) and the total stress (grey line) at surface, given by Eq.8.
(b) Components of the surface heat balance: I0 (open square), Qh (cross), Qb (solid square), Qe
(open circle) and Qn (star) given by Eq.11.

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 449
ing the smoothed values of current observations (Figure
3). Comparing the observed zonal current (Figure 3(a))
with the data generated using the model relaxation
scheme (Figure 3(b)), it is possible to see that the
scheme works as an interpolator, reproducing the diurnal
variation of the zonal current.
3. MODEL RESULTS
The model was run from September to October, time
period within the period considered by [10,11] of lowered
contribution of large scale advection processes and
therefore suitable for one-dimensional models. After that,
the boundary layer depth was estimated using as criterion
the turbulent kinetic energy value (by the criterion k >
10–5 m2·s–2) proposed by [17]. The numerical values of k
show that during the day, the ML is shallower due to the
shortwave radiation incident at the surface (Figure 4(a)),
which stratifies the oceanic surface layers, inhibiting tur-
bulence production. According to Figure 4(a), from Sep-
tember 15 to 23, the BL depth varies from 30 to 35 m. On
the following days, the BL deepens, and from day 30 to
the end of the period, the model estimates the most ex-
pressive diurnal variation of the BL depth, reaching
around 70 m during the night on October 02 and shoal-
ing during the day. Therefore, the period of more intense
turbulence is from October 1 to 10, when the boundary
layer depth reaches approximately 60 m.
Direct measurement of the dissipation rate (ε) is not
possible, but estimates can be obtained by different
means, as described by [1]. Therefore, observational
studies of the Pacific equatorial region use the dissipa-
tion rate as a criterion (ε > 10–7 m2·s–3) to consider a re-
gion of turbulent mixing [3]. Using this criterion, the
turbulent layer (Figure 4(b)) shows, as expected, a di-
urnal variation similar to that observed in Figure 4(a).
During the night, the BL entrainment intensifies, reach-
ing its maximum diurnal depth at sunrise.
3.1. Diurnal Cycle of Turbulence
To investigate the diurnal turbulence cycle, a period of
intense turbulence was used (from October 1 to 10; Fig-
ure 4).
The diurnal cycle of the vertical profile of the turbu-
lent dissipation rate (ε), averaged from October 1 to 10,
shows a clear resemblance to the observations [8] and
modeling results [5] of the equatorial Pacific Ocean.
These authors found that when the nighttime mixed layer
depth was approximately 30 m, there was a strong dissi-
pation (ε > 10–7 m
2·s–3) penetrating to a depth of 80 m
and a weaker daytime dissipation immediately below the
(a)
(b)
Figure 3. Temporal variation of the averaged zonal current (m·s–1): (a) from PIRATA observa-
tions and (b) simulated by the model using the relaxation term. Daily values from September 15
to October 15 are averaged during the period from 2000 to 2006.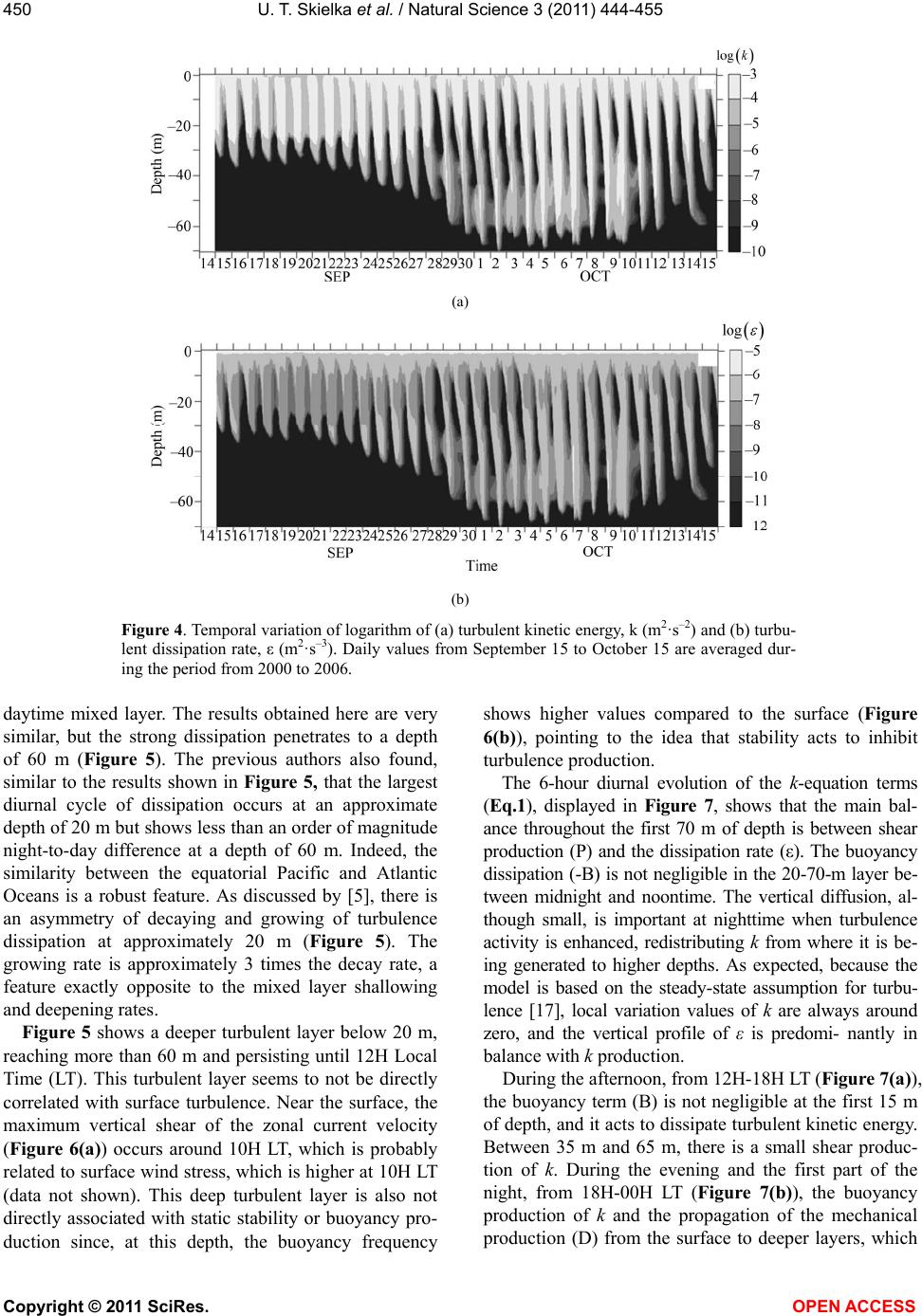

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 450
(a)
(b)
Figure 4. Temporal variation of logarithm of (a) turbulent kinetic energy, k (m2·s–2) and (b) turbu-
lent dissipation rate, ε (m2·s–3). Daily values from September 15 to October 15 are averaged dur-
ing the period from 2000 to 2006.
daytime mixed layer. The results obtained here are very
similar, but the strong dissipation penetrates to a depth
of 60 m (Figure 5). The previous authors also found,
similar to the results shown in Figure 5, that the largest
diurnal cycle of dissipation occurs at an approximate
depth of 20 m but shows less than an order of magnitude
night-to-day difference at a depth of 60 m. Indeed, the
similarity between the equatorial Pacific and Atlantic
Oceans is a robust feature. As discussed by [5], there is
an asymmetry of decaying and growing of turbulence
dissipation at approximately 20 m (Figure 5). The
growing rate is approximately 3 times the decay rate, a
feature exactly opposite to the mixed layer shallowing
and deepening rates.
Figure 5 shows a deeper turbulent layer below 20 m,
reaching more than 60 m and persisting until 12H Local
Time (LT). This turbulent layer seems to not be directly
correlated with surface turbulence. Near the surface, the
maximum vertical shear of the zonal current velocity
(Figure 6(a)) occurs around 10H LT, which is probably
related to surface wind stress, which is higher at 10H LT
(data not shown). This deep turbulent layer is also not
directly associated with static stability or buoyancy pro-
duction since, at this depth, the buoyancy frequency
shows higher values compared to the surface (Figure
6(b)), pointing to the idea that stability acts to inhibit
turbulence production.
The 6-hour diurnal evolution of the k-equation terms
(Eq.1), displayed in Figure 7, shows that the main bal-
ance throughout the first 70 m of depth is between shear
production (P) and the dissipation rate (ε). The buoyancy
dissipation (-B) is not negligible in the 20-70-m layer be-
tween midnight and noontime. The vertical diffusion, al-
though small, is important at nighttime when turbulence
activity is enhanced, redistributing k from where it is be-
ing generated to higher depths. As expected, because the
model is based on the steady-state assumption for turbu-
lence [17], local variation values of k are always around
zero, and the vertical profile of ε is predomi- nantly in
balance with k production.
During the afternoon, from 12H-18H LT (Figure 7(a)),
the buoyancy term (B) is not negligible at the first 15 m
of depth, and it acts to dissipate turbulent kinetic energy.
Between 35 m and 65 m, there is a small shear produc-
tion of k. During the evening and the first part of the
night, from 18H-00H LT (Figure 7(b)), the buoyancy
production of k and the propagation of the mechanical
production (D) from the surface to deeper layers, which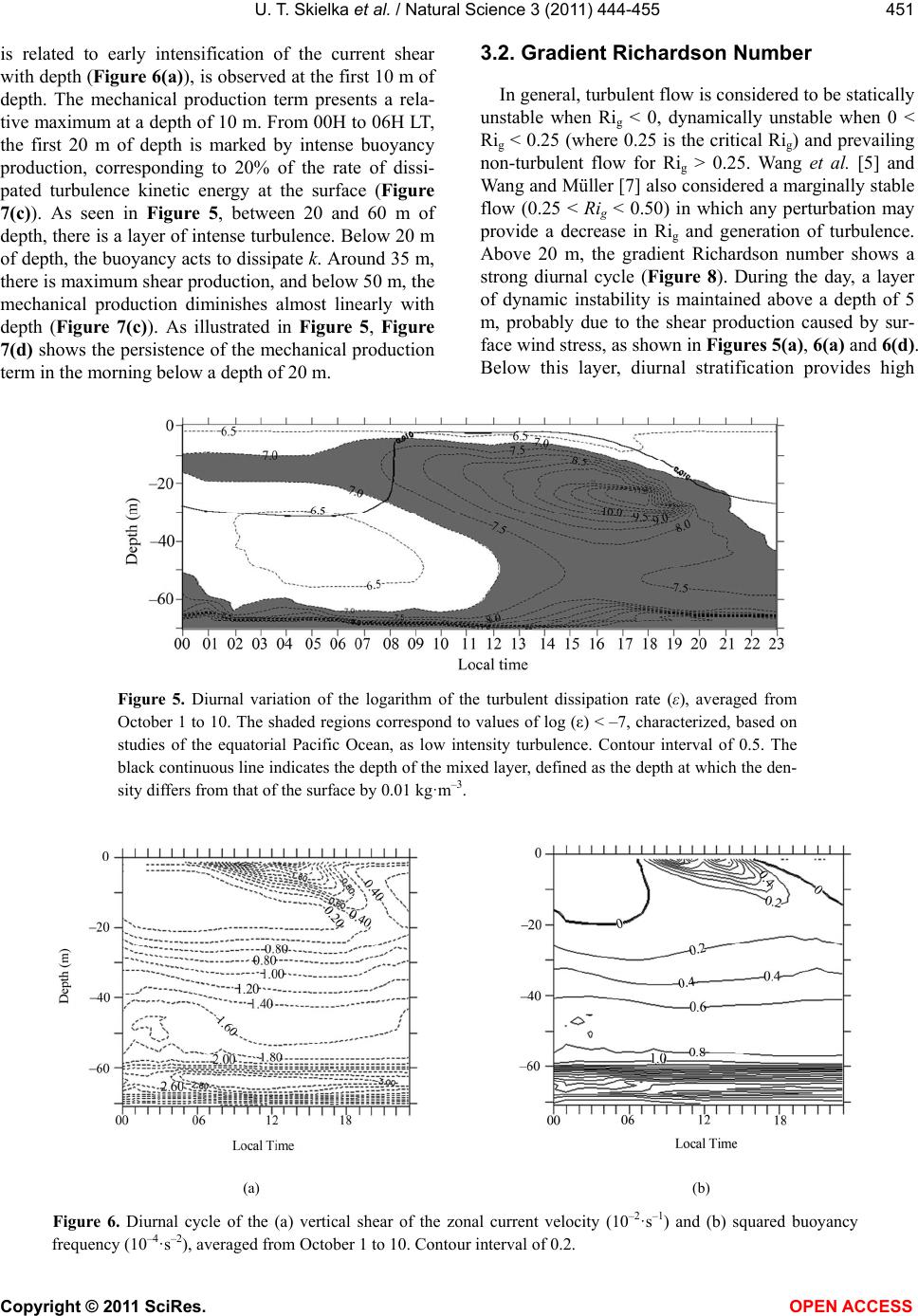

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 451
is related to early intensification of the current shear
with depth (Figure 6(a)), is observed at the first 10 m of
depth. The mechanical production term presents a rela-
tive maximum at a depth of 10 m. From 00H to 06H LT,
the first 20 m of depth is marked by intense buoyancy
production, corresponding to 20% of the rate of dissi-
pated turbulence kinetic energy at the surface (Figure
7(c)). As seen in Figure 5, between 20 and 60 m of
depth, there is a layer of intense turbulence. Below 20 m
of depth, the buoyancy acts to dissipate k. Around 35 m,
there is maximum shear production, and below 50 m, the
mechanical production diminishes almost linearly with
depth (Figure 7(c)). As illustrated in Figure 5, Figure
7(d) shows the persistence of the mechanical production
term in the morning below a depth of 20 m.
3.2. Gradient Richardson Number
In general, turbulent flow is considered to be statically
unstable when Rig < 0, dynamically unstable when 0 <
Rig < 0.25 (where 0.25 is the critical Rig) and prevailing
non-turbulent flow for Rig > 0.25. Wang et al. [5] and
Wang and Müller [7] also considered a marginally stable
flow (0.25 < Rig < 0.50) in which any perturbation may
provide a decrease in Rig and generation of turbulence.
Above 20 m, the gradient Richardson number shows a
strong diurnal cycle (Figure 8). During the day, a layer
of dynamic instability is maintained above a depth of 5
m, probably due to the shear production caused by sur-
face wind stress, as shown in Figures 5(a), 6(a) and 6(d).
Below this layer, diurnal stratification provides high
Figure 5. Diurnal variation of the logarithm of the turbulent dissipation rate (ε), averaged from
October 1 to 10. The shaded regions correspond to values of log (ε) < –7, characterized, based on
studies of the equatorial Pacific Ocean, as low intensity turbulence. Contour interval of 0.5. The
black continuous line indicates the depth of the mixed layer, defined as the depth at which the den-
sity differs from that of the surface by 0.01 kg·m–3.
(a) (b)
Figure 6. Diurnal cycle of the (a) vertical shear of the zonal current velocity (10–2·s–1) and (b) squared buoyancy
frequency (10–4·s–2), averaged from October 1 to 10. Contour interval of 0.2.

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 452
(a) (b)
(c) (d)
Figure 7. Vertical profile of the k-equation terms (Eq.1) normalized by the viscous dissipation rate of k at the surface
(ε0), averaged from October 1 to 10: (a) 12H to 18H LT; (b) 18H to 00H LT; (c) 00H to 06H LT and (d) 06H to 12H LT.
Shear production (P, square); buoyancy production/dissipation (B, circle); local variation (LT, continuous line); verti-
cal diffusion (D, cross) and viscous dissipation rate (ε, triangle).
static stability, inhibiting the generation of turbulence. In
the afternoon, with an increase in shear in the surface
layer provided by wind during the day (Figure 6(a)), the
dynamically unstable layer (shaded area in Figure 8)
extends deeper. After 16H LT, a region of Rig < 0 starts
to develop due to the surface heat lost in the evening,
indicating static instability and the beginning of buo-
yancy production of turbulence, as shown in Figures
6(b), (c). This statically unstable layer reaches its maxi-
mum depth of approximately 20 m at 00H LT and starts
to collapse after sunrise. After sunrise, there is a layer of
stable, non-turbulent flow between approximately 10
and 35 m, where Rig varies between 0.25 and 0.50,
characterizing a marginally stable flow. Below this layer,
the flow is dynamically instable, and after 00H LT, this
unstable flow comprises a layer from 20 to 60 m in
depth, showing the existence of a deeper turbulent flow,
which is apparently decoupled from the turbulence
originated by surface forcing.
4. CONCLUSIONS
Oceanic turbulence in the equatorial Atlantic oceanic
boundary layer was investigated using the General Ocean
Turbulence Model. Boundary conditions and a relaxation
scheme were computed based on time series derived from
the PIRATA buoy dataset located at 0˚N, 23˚W and the
radiation dataset from the NASA/GEWEX Surface
Budget Radiation. The numerical simulation was per-
formed during the dry season (October), when the ther-
mocline is adjusted to the intensified easterly trade winds
and the oceanic ML is deeper.

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 453
Figure 8. Diurnal variation of the gradient Richardson number, averaged from October 1 to
10. The shaded area corresponds to a dynamically unstable flow (0.00 < Rig< 0.25). Dashed
and continuous lines indicate, negative and positive values of Rig, respectively.
It was found that during the day, the ML depth is restricted
to less than 10 m due to buoyancy suppression caused by
solar radiation. In this case, turbulence is maintained by
the shear provided by wind stress. At night, the entrain-
ment rate is positive due to the static instability provided
by the surface heat lost at night, when buoyancy con-
tributes to turbulent kinetic energy production until an
approximate depth of 20 m. Surface turbulence dimin-
ishes after 00H LT due to the diurnal decrease in wind
stress. After sunset, re-stratification of this surface layer
occurs.
At night, the model results indicated the existence of a
deeper turbulence. According to laboratory [28] and
modeling [7] studies, this deeper turbulence is generated
by the breaking of internal waves in the statically stable
region combined with intense shear due to the presence of
the equatorial undercurrent. Linden [28] showed that over
oceanic regions, the energy provided by wind to the
mixed layer may radiate energy to higher depths beyond
the generation of internal waves. In the equatorial ocean,
these waves break when they reach the intense shear
deeper layer, above the equatorial undercurrent core,
inducing dynamical instability of the flow, a feature that
was modeled by [7] using LES. The turbulent closure
scheme used in this work was able to reproduce this
deeper turbulence, based on the mean field provided by
the observed vertical profiles, which appears from depths
of 20 m to more than 60 m. At this layer, the model
identified an enhancement of shear production and a
buoyancy contribution to the dissipation of turbulent
kinetic energy.
The gradient Richardson number also indicated the
presence of a strong diurnal cycle, above 20 m. During
the day, a layer of dynamic instability is maintained
above a depth of 5 m, probably due to the shear produc-
tion caused by surface wind stress. Below this layer,
diurnal stratification provides high static stability, inhib-
iting the generation of turbulence. In the afternoon, with
an increase in shear in the surface layer provided by wind
during the day, the dynamically unstable layer extends
deeper. After 16H LT, a region of instability starts to
develop due to the surface heat loss in the evening. This
statically unstable layer reaches its maximum depth of
approximately 20 m at 00H LT and starts to collapse after
sunrise. After sunrise, there is a layer of stable, non-
turbulent flow between approximately 10 and 35 m. Be-
low this layer, the flow is dynamically instable, and after
00H LT, this unstable flow comprises a layer from 20 to
60 m in depth, showing the existence of a deeper turbu-
lent flow, which is apparently decoupled from the turbu-
lence originated by surface forcing.
The diurnal variation and magnitude of the boundary
layer estimated by the model is in quantitative agreement
with studies performed in the equatorial Pacific Ocean.
Considering the differences related to the applied meth-
odology (using a less complex and general model in this
work) and the differences about the basin scales of the
two oceanic regions, resulting in different equatorial
dynamics [29], the results using GOTM, with relaxation
scheme to assimilate data, showed similarities with pre-
vious studies performed in the Pacific Ocean. Both
mechanisms of nocturnal turbulence production
(deep-cycle turbulence) are captured by GOTM simula-
tions. As shown in the results of this study, deep noctur-
nal turbulence appears to be unrelated to surface forcing
generated turbulence, as it appears rather suddenly dur-
ing the night in the simulations (Figures 5 and 6).
REFERENCES
[1] Thorpe, S.A. (2004) Recent development in the study of
ocean turbulence. Annual Review of Earth and Planetary
Sciences, 32, 91-109.
doi:10.1146/annurev.earth.32.071603.152635
[2] Moum, J.N. and Caldwell, D.R. (1985) Local influences
on the shear-flow turbulence in the equatorial ocean.
Science, 230, 315-316. doi:10.1126/science.230.4723.315

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 454
[3] Gregg, M.C., Peters, H., Wesson, J.C., Oakey, N.S and
Shay, T.J. (1985) Intensive measurements of turbulence
and shear in the equatorial undercurrent. Nature, 318,
140-144.
doi:10.1038/318140a0
[4] Wang, D., Large, W.G. and McWilliams, J.C. (1996)
Large-eddy simulation of the equatorial ocean boundary
layer: Diurnal cycle, eddy viscosity and horizontal
rotation. Journal of Geophysical Research, 101, 3649-
3662.
doi:10.1029/95JC03441
[5] Wang, D., Large, W.G. and McWilliams, J.C. (1998)
Large-eddy simulation of the diurnal cycle of deep
equatorial turbulence. Journal of Physical Oceanography,
28, 129-148.
doi:10.1175/1520-0485(1998)028<0129:LESOTD>2.0.C
O;2
[6] Skyllingstad, E.D., Smyth, W.D., Moum J.N. and
Wijesekera, H. (1999) Upper-ocean turbulence during a
westerly wind burst: A comparison of large-eddy simu-
lation results and microstructure measurements. Journal
of Physical Oceanography, 29, 5-28.
doi:10.1175/1520-0485(1999)029<0005:UOTDAW>2.0.
CO;2
[7] Wang, D. and Müller, P. (2002) Effects of equatorial
undercurrent shear on upper-ocean mixing and internal
waves. Journal of Physical Oceanography, 32, 1041-1057.
doi:10.1175/1520-0485(2002)032<1041:EOEUSO>2.0.C
O;2
[8] Lien, R.-C., Caldwell, D.R., Gregg, M.C. and Moum, J.N.
(1995) Turbulence variability at the equator in the central
Pacific at the beginning of the 1991-1993 El Niño.
Journal of Geophysical Research, 100, 6881-6898.
doi:10.1029/94JC03312
[9] McPhaden, M.J. and Peters, H. (1992) Diurnal cycle of
internal wave variability in the equatorial Pacific Ocean:
Results from moored observations. Journal of Physical
Oceanography, 22, 1317-1329.
doi:10.1175/1520-0485(1992)022<1317:DCOIWV>2.0.
CO;2
[10] Weingartner, T.J. and Weisberg, R.H. (1991) On the
annual cycle of equatorial upwelling in the Central
Atlantic Ocean. Journal of Physical Oceanography, 21,
68-82.
doi:10.1175/1520-0485(1991)021<0068:OTACOE>2.0.
CO;2
[11] Weingartner, T.J. and Weisberg, R.H. (1991) A descrip-
tion of the annual cycle in sea surface temperature and
upper ocean heat in the Equatorial Atlantic. Journal of
Physical Oceanography, 21, 83-96.
doi:10.1175/1520-0485(1991)021<0083:ADOTAC>2.0.
CO;2
[12] Weisberg, T.J. and Tang, T.Y. (1987) Further studies on
the response of the equatorial thermocline in the Atlantic
Ocean to the seasonal varying trade winds. Journal of
Geophysical Research, 92, 3709-3728.
doi:10.1029/JC092iC04p03709
[13] Grodsky, S.A., Carton, J.A., Provost C., Servain, J.,
Lorenzetti, J.A. and McPhaden, M.J. (2005) Tropical
instability waves at 0˚N, 23˚W in the Atlantic: A case
study using PIRATA mooring data. Journal of Geo-
physical Research, 110, C08010.
doi:10.1029/2005JC002941
[14] Burchard, H., Bolding, K. and Villarreal, M. (1999)
GOTM—a general ocean turbulence model. theory, ap-
plications and test cases. European Commission Report
EUR, European Commission.
[15] Burchard, H. and Bolding, K. (2001) Comparative analy-
sis of four second-moment turbulence closure models for
the oceanic mixed layer. Journal of Physical Oceano-
graphy, 31, 1943-1968.
doi:10.1175/1520-0485(2001)031<1943:CAOFSM>2.0.
CO;2
[16] Bolding, K., Burchard, H., Pohlmann, T. and Stips, A.
(2002) Turbulent mixing in the Northern North Sea: A
numerical model study. Continental Shelf Research, 22,
2707-2724.
doi:10.1016/S0278-4343(02)00122-X
[17] Jefrey, C.D., Robinson, I.S., Woolf, D.K. and Donlon C.J.
(2008) The response to phase-dependent wind stress and
cloud fraction of the diurnal cycle of SST and air–sea CO2
exchange. Ocean Modelling, 23, 33-48.
[18] Steiner, N. and Denman, K. (2008) Parameter sensitivities
in a 1-D model for DMS and sulphur cycling in the upper
ocean. Deep-Sea Research, 55, 847-865.
doi:10.1016/j.dsr.2008.02.010
[19] Canuto, V.M., Howard, A., Cheng Y. and Dubovikov M.S.
(2001) Ocean turbulence. Part I: One point closure model,
momentum and heat vertical diffusivities. Journal of Phy-
sical Oceanography, 31, 1413-1426.
doi:10.1175/1520-0485(2001)031<1413:OTPIOP>2.0.C
O;2
[20] Fofonoff, N.P. and Millard, R.C. (1983) Algorithms for
computation of fundamental properties of seawater.
Unesco Technical Papers in Marine Science, 44, 53 pp.
[21] Servain, J., Busalacchi, A.J., McPhaden, M.J, Moura A.D.,
Reverdin, G., Vianna, M. and Zebiak, S.E. (1998) A pilot
research moored array in the Tropical Atlantic (PIRATA).
Bulletin of the American Meteorological Society, 79,
2019-2031.
doi:10.1175/1520-0477(1998)079<2019:APRMAI>2.0.C
O;2
[22] Bourlès, B., Lumpkin, R., McPhaden, M.J., Hernandez,
F., Nobre, P., Campos, E., Yu, L., Planton, S., Busalacchi
A., Moura, A.D., Servain, J. and Trotte, J., (2001) The
PIRATA program: History, accomplishments, and future
directions. Bulletin of the American Meteorological
Society, 89, 1111-1125.
[23] Peres, J.R. (2008) Estudo do balanço de radiação sobre o
oceano Atlântico Tropical na região do Arquipélago de
São Pedro e São Paulo (in portuguese), IAG. USP. 35 pp.
http://www.iag.usp.br/meteo/labmicro/publicacoes/relato
rios_tecnicos/Jean_2008-Estudo_do_balanco_de_radiaca
o_sobre_o_oceano_Atlantico_tropical_na_regiao_do_AS
PSP.pdf
[24] Fairall, C.W., Bradley, E.F., Hare, J.E., Grachev, A.A.
and Edson, J.B. (2003) Bulk parameterization of air-sea
fluxes: updates and verification for the coare algorithm.
Journal of Climate, 16, 571-591.
doi:10.1175/1520-0442(2003)016<0571:BPOASF>2.0.C
O;2
[25] Bolton, D. (1980) The computation of equivalent potential
temperature. Monthly Weather Review, 108, 1046-1053.
doi:10.1175/1520-0493(1980)108<1046:TCOEPT>2.0.C
O;2

U. T. Skielka et al. / Natural Science 3 (2011) 444-455 455
[26] Fairall, C.W., Bradley, E.F., Rogers, D.P., Edson, J.B. and
Young G.S. (1996) Bulk parameterization of air-sea
fluxes for the tropical ocean-global atmosphere coupled-
ocean atmospheric response experiment. Journal of Geo-
physical Research, 101, 3747-3764.
doi:10.1029/95JC03205
[27] Jerlov, N.G. (1968) Optical oceanography. American
Elsevier Publ. Co. Inc., New York.
[28] Linden, P.F. (1975) The deepening of a mixed layer in a
stratified fluid. The Journal of Fluid Mechanics, 71, 385-
405. doi:10.1017/S0022112075002637
[29] Philander, S.G. (1990) El Nino, La Nina and the Southern
Oscillation. Academic Press, San Diego.