 Applied Mathematics, 2011, 2, 705-710 doi:10.4236/am.2011.26093 Published Online June 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM On Eccentric Digraphs of Graphs Medha Itagi Huilgol*, Syed Asif Ulla S., Sunilchandra A. R. Department of Mat hematics, Ba ngal ore University, Bangalore, India E-mail: medha@bub.ernet.in Received March 11, 2011; revised April 9, 2011; accepted April 12, 2011 Abstract The eccentricity e(u) of a vertex u is the maximum distance of u to any other vertex of G. A vertex v is an eccentric vertex of vertex u if the distance from u to v is equal to e(u). The eccentric digraph ED(G) of a graph (digraph) G is the digraph that has the same vertex as G and an arc from u to v exists in ED(G) if and only if v is an eccentric vertex of u in G. In this paper, we have considered an open problem. Partly we have characterized graphs with specified maximum degree such that ED(G) = G. Keywords: Eccentric Vertex, Eccentric Degree, Eccentric Digraph, Degree Sequence,Eccentric Degree Sequence 1. Introduction A directed graph or digraph G consists of a finite nonempty set called vertex set with vertices and edge set of ordered pairs of vertices called arcs; that is represents a binary relation on VG EG EG VG . Throughout this paper, a graph is a symmetric digraph; that is, a digraph G such that implies If is an arc, it is said that u is adjacent to v and also that v is adjacent from u. The set of vertices which are from (to) a given vertex v is denoted ,uv EG vu E G ,. ,uv by and its cardinality is the out-degree NuNu of v [in-degree of v]. A walk of length k from a vertex u to a vertex v in G is a sequence of vertices 012 1 =,,,,,= kk uuuuu uv ,uu such that each pair 1ii is an arc of G. A digraph G is strongly connected if there is a u to v walk for any pair of vertices u and v of G. The distance d(u,v) from u to v is the length of a shortest u to v walk. The eccentricity e(v) of v is the distance to a farthest vertex from v. If ,=distu veuvudi GGGG we say that v is an eccentric vertex of u. We define whenever there is no path joining the vertices u and v. The radius rad(G) and diameter diam(G) are minimum and maximum ec- centricities, respectively. As in [2], the sequential join 123 k of graphs 12 is the graph formed by taking one copy of each of the graphs 12 and adding in additional edges from each vertex of i to each vertex in 1i, for 11 ,=stu v ,,, k GG G ,,, k GG G GG ik . Throughout this paper, means G and H are ='G H isomorphic. The reader is referred to Buckley and Harary [2] and Chartrand and Lesniak [3] for additional, un- defined terms. Buckley [4] defines the eccentric digraph ED G of a graph G as having the same vertex set as G and there is an arc from u to v if v is an eccentric vertex of u. The paper [4] presents the eccentric digraphs of many classes of graphs including complete graphs, complete bipartite graphs, antipodal graphs and cycles and gives various interesting general structural properties of eccentric digraphs of graphs. The antipodal digraph of a digraph G denoted by G, has the vertex set as G with an arc from vertex v in G if and only if v is an antipodal vertex of u in G; that is .m G,=u v dist dia This notion of antipodal digraph of a digraph was introduced by Johns and Sleno [5] as an extension of the definition of the antipodal graph of a graph given by Aravamudhan and Rajendran [6]. It is clear that G is a subgraph of ED G, and = GEDG if and only if G is self centered. In [7] Akiyama et al. have defined eccentric graph of a graph G, denoted by e, has the same set of vertices as G with two vertices u and v being adjacent in e if and only if either v is an eccentric vertex of u in G or u is an eccentric vertex of v in G, that is GG ,=min , GG distu veev *Part of this paper [1] was presented at the International Conference on Emerging Trends in Mathematics and Computer Applications, MEPCO Schlenk Engineering College, Sivakasi, India (Dec. 2010) and had a eared in the Proceedin s of the same. G u. Note that is the underlying graph of e G GED . In [8] Boland and Miller introduced the concept of the  M. I. HUILGOL ET AL. 706 if a eccentric digraph of a digraph. In [9] Gimbert et al. have proved that= e Gnd only if G is self-centered. In the same paper, the authors have characterized eccen- tric digraphs in terms of complement of the reduction of G, denoted by EDG G Given a digraph G of order n, a reduction of G, doted by G, is derived from G by en removing all its arcs incident from vertices with out- degree 1n. Note that )(GED is a subgraph of . G In [9] , Gmbert et al. died on the behaviofihave stuour se . The iterated se- G and t . Basic Results this section we list some results which are quite ph has at least on 2. There exists no directed cycle in an eccen- tr a directed cycle with edge being di dges cther ed quences of iterated eccentric digraphs. Given a positive integer 2k , the th k iterated eccentric digraph of G is writte 1kk DGED EDG , where 0=ED GG entric with the smallest integer numbers 0>p and 0t such that = tp EDGED We cathe period of antities are denoted p(G) and t(G) respectively. In [8,10] Boland et al. have discussed many interesting results about eccentric digraphs. Also they have listed open problems about these graphs. One of these open problems is being discussed mainly in this paper. We have characterized graphs with specified maximum degree such that =EDGG . n asE of ecc il of G; t = 1 ED digra t G. qu and =GED G phs concerns ll p hese quence the ta 2 In evident for eccentric digraphs of graphs. Remark 1. Since every vertex in a gra e vertex at eccentric distance it follows that every vertex in an eccentric digraph will have out degree at least one. Remark ic digraph. Let C be uv e 1 rectedom uv as shown below in Figur . The other ean be bidirectional. If all the o fr ges except uv are bidirectional then a symmetric edge 1 vy indicates the equality of eccentric values of v and ikewise 1 y. L == n eccyecc x 12 ==ecceccyy. Also edge usymmHence, =ecc ueccx eccecc u. This co arc u to tha is existence of etric. 1 the directed . So also, ===veccyecc xtradicts the v as u being tail has less eccentricity as comparedt of . The same argument can be extended to a directed n v cy r a graph to symmetric cycle having a pe cle with more than one directed arc, as the eccen- tricities go on increasing in the same direction. The above two conditions are not sufficient fo be an eccentric digraph. For example consider a ndant vertex adjacent to one of the vertices on the cycle. The pendant vertex having in-degree zero and out-degree one as in Figure 2. Vertex i is at eccentric distance from. Let be u p v adjaceno u and lying on the eccentric ath con- necting u and i t t . All the vertices in the graph except i xare adistanc atmost 1n from u, where n is eccentricity of u. This implies v bng adjacet to u will have eccentricity n. Buv lying on the metric circle can have eccentricity 1n. There- fore the above graph cannot be an eccentriaph. Also we give a counter example for a problem gi t e the sym ei n t c digr ven in 2.2 (p. 41) [2]: If G is self-centered w [2] , as follows: Problem 3, Ex. ith radius 2 , then G is self-centered with radius 2. Counter Exampleonsider 7 C, join the vertice a : Cst distance 2 in . 7 C Let G be tresulting graph with he =2rad G. Considering G, we observe that 7 GC ; that is G is self-centered of radius 3. . Grahs with Isomorphic Eccen3ptric case of undirected graphs, Buckley [4] proved that the Digraph In Figure 1. Directed cycle C. Figure 2. Directed cycle with unidirectional edge u-xi. Copyright © 2011 SciRes. AM  M. I. HUILGOL ET AL.707 ecc - entric digraph of a graph G is equal to its com plement, ()= ,ED GGif and ly if G is either a self-centeradius two or G is the union of 2k complete graphs. In [9], Gimbert et al. have that the eccentric digraph ED G is symmetric if and only if G is self centered. Here we are looking at gr on red graph of aphs which have their ec or which Odd cycles are graphs with minimum nu radius 3, proved centric digraphs isomorphic to themselves. So by Gimbert’s result these graphs are self-centered graphs. In this section we consider self-centered, undirected graphs. The following observations are easily justified. Remark 3. Odd cycles is a class of graphs f =.GG . ED Remark 4 mber of edges and maximum eccentricity on given number of vertices such that =.EDGG Remark 5. For a self-centewithred graph G the complement G is self-centered with radius equ to two. Hence al GG, and GG, and\ ED G is isomorphic to araph o subgf G. F th urther,ing Buckley’s result [4], we can say at by us ==EDGGG . That is if =,ED GED G then G =EDG. k 6. Complete graphs is another class of grRemar aphs for which =EDGG . Remark 7. It is easy to see that for graphs upto order 7, the only graphs for which =EDGG , are 23455677 ,,, ,,,, KKKCKKC ic g . hraphs havRemark 8. Two isomorpe their eccen- tr hown inn Figure 3, we give a pair of raph with ra- di ic digraphs isomorphic, but the converse need not be true always. As an example, as s non-isomorphic, self-centered graphs with same eccentricity having one eccentric digraph. Lemma 9. Let G be a self-centered g us 2, then =EDG if and only if G is self- complementary. Proof. Given self-cente G red graph be self-com- pl G ementary with radius 2. Then by Buckley’s cha- racterization theorem [4], ==DGGG . Conversley, consider a self-centered gra with =EDGG . Then, E ph of radius 2, =,EDGG that is ==GEDG Lemma 10. G . Het. nce tresul with eccen- tr he All self-centered graphs G icity greater than or equal to 3 with Ghaving =1, =1,periodtail satisfies th condition e =ED G a self-centered graph G. with eccen- Proof. Let G be tricity 3.Then G is self-centered graph with eccen- tricity al to 2. nce, equHe ==;EDGGG that is 2 EDGED G. If Gand tail has , that is =1period 1= ED then 2 ED GG 2 ED GGGED . But 2 EDGED G Figure 3. ED(G) = ED(H). 2=ED GEDGEDGG . Hence the result. For connected graph to be isomorphic to G ED G ld not be rathy ce mber of the necessary c shou nique eccentric node as defined by Parthasa and Nandakumar [11], for ssary condition is that thfor ev v of a gr fr o asing order. ondition is that the graph ugraph . Also e th GEDG, the ne- egree say ery vertex of d k, there must exist anoer vertex with k nu eccentric vertices. This can be defined as eccentric degree of a vertex. Definition 11. For a vertex aph G is defined to be the number of vertices at eccentric distance om v. Also the eccentric degree sequencef a graph is defined as a listing of eccentric degrees of vertices written in non-incre So for =ED GG, the eccentric degree sequen of G should be equal to the degree sequence of G. But this condition is not sufficient as seen in the example below, depicted as Figure 4. Here both G and ce ED G have their degree seqence and eccentric degree sequences as 49 3,2 , but ED GG. Next, we consider self-centered graphs with given maximum degree G. By [2], 22,Gpr for a self-centered graph G with radius . Our next result shows that there is no possibility of having a graph with =GEDG, with =22prG . Proposition 12. There does not exist a graph G with =22Gpr , hat such t =G. ED G Proof. Let G be a self-centered graph with =22Gpr Let uVG such that deg u implies =2pr2 . Partitntoion the vertex set i sets lying Copyright © 2011 SciRes. AM  M. I. HUILGOL ET AL. 708 then 1 r will have u as the oy eccentric veex, a ntradiction. imilar contradiction is arrived if 1 r nl rt co S is adjacent to both 2 r and 2 1r Same argum can be appliedn case of ent i Figure 4. G and ED(G) having same eccentric degree se- quence and degre e se quence, but ED(G) ≇ G. at distance fromand name them as i u , 1 i ir . Since 2, =2deg pur 2. As G is 2= 1 rpA self-centered, it cannot contain a cut-vertex and hence 2, 2 i ir. Hence, 22r vertices are needed to onsideration, tices. Hence satisfyh under c with the cnditionsf t t possible to constr o ohe grap t a grap but we have 22=23ppr r ver, it is nouch =EDGG , with =22Gpr. connectecentered graph G with =21Gpr is isomorphic to its eccentric digraph if and only i is of the form 22 21,2 p pr with structure Theorem 13. Ad self- f its degree sequence 121222 2 , pr KFKKHKH KHr times where is the gjoining one vertex of raph obtained by 21 to pr K one vertex of 2 and remaining 2pr vertices to one vertex of 2 , and is the 1 actor removed from successive 22 K. Proo Let G be a self-centered graph with =21Gpr. Let u be a vertex of G with 21p r. As seen in the above Lemma f. each =deg u, i should contain at least two vertices each, for G to satisfy =GEDG, wicenth s self-terednnot ining ess and ma be 22r vertir at least two ie ing unique entric node graph. Since the re e to be ditributed into 1r sets with ach set, it follows that each i ecc ces a n has vertices. Let ththe set k exactly two e vertices in be labelled 1 k and 2 k for all k, 2kr. Since G has no cutvertex, 1 1r be adjacent to at least one vertexr should of , let us say, to 1 r and similarly let 2 1r be adjacent to 2 r . Degree of 1 r is at le 22 ast tw be adj to of o, so it canacent any 1 , rr x or both. 2 r . Therefore, 1 r and 2 r are mutually adjahave degree at least two. There are two ps 1 P an2 ij P where ii cath t be equal to j. r cases are proved as follows: Cla 1: The vertices ent t d o Othe im o 1111 1jx 1 1 11122331 1 11 11111 11 211 =, , , , , , ,,,,,, ,,,,,,,;,=1 kk kk kk rrrrr Puexexexeex ex xexexij and 22 2 2112 ,, , , iji ij Puexe 233 222222 11 11 22222 211 =, , ,, ,,,,,,, ,,,,;2,21, kkkkkk rrrrr xex exexex xexexijpr i need n 1 1k are adjacent to either 1 k 2 k Suppose, 1 r is adjacent to 2 1r , or , bu Proof o x bel t not both; for. f the claimvertex eac verteonging to all : Since , 21kkr G has no cut h k , 21kr, is adjacent to at least one vertex in 1k and 1k . Without loss gene- rality let each vertex 1 1k be adjacent to 1 k , for all , 21krk . Let us cder k onsi , with vertices 1 k and 2 k . Let 1 1k be adjacent to 2 k aloithng w 1 k . Then eccentricity of 1 1k can be at most 1r as any vertex lying on the p 1an be at most at a distance 1rath P or 2 ij P c from 1k 1 . And any vertex on the path ij P2 can be at most at a distance of 2r fr 2 k om . In any case if 1 1k is adjacent to both2 k and 1 k then ceases to be seentered, a contradiction and hence proof of the claim. Claim 2: Each , 2 i G thelf-c 1 kr is independent, that is, , 2 = i K Phe re . roof of the claim: First we prove tsult for 1r . If the verti1 1r ces and 2 1r beloing to1r ng are adjacent then 1 1r will have u as the only eccentric vertex, a contradicti proat on ves th12r =K For any other . k , 2kr2 , if 1 k and 2 k are adjacent then, eccentricity of 1 k and 2 k will t most r − 2 as vertices on P or ij P2 will be at distance at most r − 2 m 1 k be a 1 fro or 2 k and hence for all k, 2i Claim 3: 1 21, =krAK. 2 and 2 2 do not haneve comon ors in m ighb 1 . Proof of the claim: As in case of the veces of 1r rti , the vertices 1 2 and 2 2 of 2 will have their eccentricity equal to 1r ifhey have a common t neighbor in 1 , h 1 ence . th claime Claim 4: 2 is adjacent to 1 1 and 2 2 is adjacent to all er p-othtices of Proof of taim : If 2r ver he clA. 1 1 2 is adjacent to Copyright © 2011 SciRes. AM  M. I. HUILGOL ET AL.709 = 1=1 , 1<<2 ki k k ip r, then two vertices 2 r and 1r 2 have eccentric degree k + 1, but only one vertex 1 2 has del dicgree equa 1k, a contration. If 1 2 to and 2 2 have dege k each ,that is if 2k1 re =2 1pr, then r , r 2 , 1r 1 and 2 1r have eccentric degree equal to+ 1, but only two k vertices1 2 and 2 2 ha Hence, ve de 1 gree k + 1. 2 is adjacent to 1 x1not a and 1 x2 1, 1<<2 i djacent to ip r. Finding the etric degree of all ccenrtices of G we see that, ecc. deg ve 1=2, 11 k kr and ecc.deg 1=2 k y, except for 1 1r , where 11 kk yNx. Silarly, ecc. deg 2= mi2, k 11 kr and ecc.deg 2 y2 gr 2 =2 k, where. Hence, the eccentric de- kk yNx ence of G ee sequence of G is 22 21,2 p pr , which is same as that of degree sequ Claim 5: . 121 = r . Proof Wet for any twvertices AK of the claim: show thao 1 t and 1 where 1,ts are not , 1, 2tsp r eed to consadjacentn. Here we ider two possibilities: Case 1): 1 12 t Nx and 2 2 1 s Nx Case 2): 2 12 t Nx and 1 s 2 2 Nx In case 1), 1 t will have only one eccentric vertex, a contradiction. In case 2), deg 1 t ,deg 13then only the ver- tic 1 s x es r or 2 r of r and 1 1r or 2 1r of 1r the cartof along pa r , si n have ve as ecices 2 ij PA1 nc centric vertices, ths 1 P oe 1 2 and 2 2 t sh co do noare a mmon neighr in 1 bo , as claimed in 3. By Claim 4at 1 , we see th2 is adjacent to 1 1 and 2 x 2th vertis adjacent to all oer pices of 1 − 2r , implies t when degrees t tha of 1 and 1 c a emcedegree other i ve he fof Cgiv m emark 1tices re changed by mak- ing th adjant, thccentriny o vertex of does not change, hence we will not be able to get =E G a contradion pros the claim. Referring all the claims we conclude tat e ef a G DG, ct is of th rm defined in the statement othe theorem. onverse is easy to observe that if G is as en in the statement of the theore, then =GG . In the next result we consider a particular case of graphs with =EDGG , that is, odd cycles. R a labelled 21 ,1 n Cn , two ver ED 4. In , ij v are at eccentric distance in 21n ED C, if and on v ly if ,= 2 Gij dv v or n1n 2 . Remark 15. For unlabelled itti odd cycles,eraons of can be packed into 21n ED C n , 13 1= 22 ns , nED G , whereas, 2 rad Cn 1= n. In case of labelled odd cyclesnce of ED(G)'s e packed into K,pif the permutatumber of the seque can bion on p n defined by vertices 1=1, 2=2, =1,2,3,,; 1=2 2,=1,2,, ffirii r fir iir 23, since there are is a product of three cyclicns of length respectively. permutatio,r1, r, Proposition 16. There exists a self-centered graph G, such that =EDGG , containing an odd cycle. Proof. Let be C be a cycle, whose vertices are labeled as . Let . Define a function onices 1, 2, 3, the setvert ,p of =1,2,3, ,Sp of C as 21 =1, 112.fipiip 1=1, 2=232,112,ffipi ip Now, we partition of set of vertices of C into 123 ,, m S, , SSS ere, wh 12 1 = 2,, 2, SSf S where n is the least positteg 2 1,=2, 2,, 2 n f f ive iner such that 2= 12 n f whereas 2 n f is obtained by applyi ng on n2, times. Similarly, 2 =, , ,, , m m Slflfl fl S S 1 123 1 , m lS S where is the least positive integer such that m = 1m ll . It is clear that 123 = m SSSS S and =, 1,ij j,i jm i SS . Now, for each vertex i S we fine sets of vertices not in of de C by 2 =, ,, i ii ii jj jj Sflflfln for each , and whose adjacencies are to the ertices of i =1,2,3,j v C defined by: If g l, when is adjacent 1lp to h l, then, g ij l is adjacent to glNf , h ij l and h ij l is adjac to , hg i lf lent j; othese, Nf g ij lis adjacent to g Nfl and h rwi ij l is acent to dja h Nfl . So we get a self-ce graph with ntered radius 12p,isfying =ED GG sa vertices t, as l on C and respective , 1 ij m llp , e same distance from ther vertices in the graph. By Remark 15, we get hav o G. Fng is an ee of a self-cente ED G ollow radius own iing i xampl 4, as shn Figure 5, satisfy red graph with ED GG , with 9 C, asSo base. =1,2,S ,9 and 45 ,,SS 12 =,, p VC SS, where 3 S 12 =1,=2,54, =7.SS S 345 ,8, =, =3,6,9S S Copyright © 2011 SciRes. AM 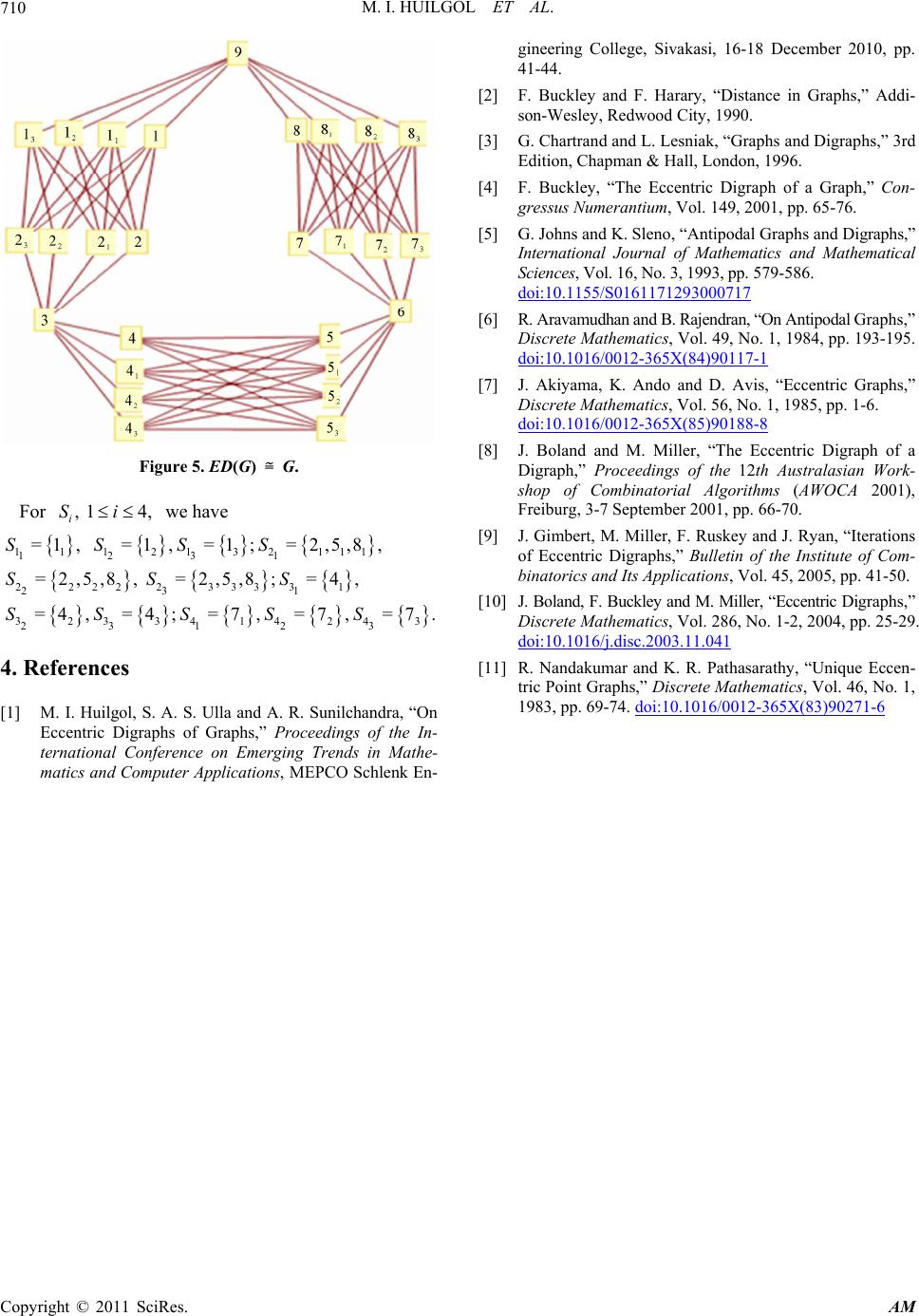 M. I. HUILGOL ET AL. Copyright © 2011 SciRes. AM 710 Figure 5. ED(G) ≅ G. For we have , 14, i Si 1112132111 1 231 2222233331 231 323341424 23123 =1, =1, =1; =2,5,8, =2,5,8 , =2,5,8; =4, =4, =4; =7, =7, =7. SSSS SSS SSSSS 3 4. References . I. Huilgol, Sd A. R. Sunilchandra, “On centric Digraphs of Graphs,” Proceedings of the In- ternational Conference on Emerging Trends in Mathe- matics and Computer Applications, MEPCO Schlenk En ege, Sivakasi, 16-18 December 2010, pp. 41-44. gineering Coll [2] F. Buckley and F. Harary, “Distance in Graphs,” Addi- son-Wesley, Redwood City, 1990. [3] G. Chartrand and L. Lesniak, “Graphs and Digraphs,” 3rd Edition, Chapman & Hall, London, 1996. [4] F. Buckley, “The Eccentric Digraph of a Graph,” Con- gressus Numerantium, Vol. 149, 2001, pp. 65-76. [5] G. Johns and K. Sleno, “Antipodal Graphs and Digraphs,” International Journal of Mathematics and Mathematical Sciences, Vol. 16, No. 3, 1993, pp. 579-586. doi:10.1155/S0161171293000717 [6] R. Aravamudhan and B. Rajendran, “On Antipodal Graphs,” Discrete Mathematics, Vol. 49, No. 1, 1984, pp. 193-195. doi:10.1016/0012-365X(84)90117-1 [7] J. Akiyama, K. Ando and D. Avis, “Eccentric Graphs,” Discrete Mathematics, Vol. 56, No. 1, 1985, pp. 1-6. 8doi:10.1016/0012-365X(85)90188- (AWOCA 2001), e Institute of Com- [8] J. Boland and M. Miller, “The Eccentric Digraph of a Digraph,” Proceedings of the 12th Australasian Work- shop of Combinatorial Algorithms Freiburg, 3-7 September 2001, pp. 66-70. [9] J. Gimbert, M. Miller, F. Ruskey and J. Ryan, “Iterations of Eccentric Digraphs,” Bulletin of th binatorics and Its Applications, Vol. 45, 2005, pp. 41-50. [10] J. Boland, F. Buckley and M. Miller, “Eccentric Digraphs,” Discrete Mathematics, Vol. 286, No. 1-2, 2004, pp. 25-29. doi:10.1016/j.disc.2003.11.041 [11] R. Nandakumar and K. R. Pathasarathy, “Unique Eccen- tric Point Graphs,” Discrete Mathematics, Vol. 46, No. 1, 1983, pp. 69-74. doi:10.1016/0012-365X(83)90271-6 [1] M. A. S. Ulla an Ec -
|