J. Software Engineering & Applications, 2009, 2: 86-95
doi:10.4236/jsea.2009.22013 Published Online July 2009 (www.SciRP.org/journal/jsea)
Lossy-to-Lossless Compression of Hyperspectral Image
Using the 3D Set Partitioned Embedded ZeroBlock
Coding Algorithm
Ying Hou
School of Communication and Information Engineering, Xi’an University of Science and Technology, Xi’an, China.
Received December 28th, 2009; revised March 23rd, 2009; accepted April 22nd, 2009.
ABSTRACT
In this paper, we propose a three-dimensional Set Partitioned Embedded ZeroBlock Coding (3D SPEZBC)
lossy-to-lossless compression algorithm for hyperspectral image which is an improved three-dimensional Embedded
ZeroBlock Coding (3D EZBC) algorithm. The algorithm adopts the 3D integer wavelet packet transform proposed by
Xiong et al. to decorrelate, the set-based partitioning zeroblock coding to process bitplane coding and the con-
text-based adaptive arithmetic coding for further entropy coding. The theoretical analysis and experimental results
demonstrate that 3D SPEZBC not only provides the same excellent compression performances as 3D EZBC, but also
reduces the memory requirement compared with 3D EZBC. For achieving good coding performance, the diverse wave-
let filters and unitary scaling factors are compared and evaluated, and the best choices were given. In comparison with
several state-of-the-art wavelet coding algorithms, the proposed algorithm provides better compression performance
and unsupervised classification accuracy.
Keywords: Image Compression, Hyperspectral Image, 3D Wavelet Packet Transforms, Zeroblock Coding
1. Introduction
Hyperspectral images provide high resolution and valu-
able spectrum information about the Earth’s surface, so
they are a useful tool and extensively applied in military
and civilian fields. However, due to the huge amounts of
data that bring about some problems in data transmission,
storage and processing, more efficient compression tech-
nique becomes an indispensable task and a hot research
topic.
In recent years, some hyperspectral image compression
algorithms based on three-dimensional wavelet transform
[1,2,3,4,5] are particularly interested thanks to their ex-
cellent compression performances and many attractive
properties, such as the three-dimensional Set Partitioning
in Hierarchical Trees (3D SPIHT) [4,5 ], the three-dimen-
sional Set Partitioned Embedded bloCK (3D SPECK) [1],
and the JPEG2000 multi-component (JPEG 2000-MC)
[2,3]. The researches on hyperspectral image compres-
sion schemes can be generally classified into lossless and
lossy techniques [1]. Lossless compression can exactly
reconstruct the original images without losing any infor-
mation. The state-of-the-art lossless compression meth-
ods are able to achieve compression ratios of 2 ~ 3.4 : 1,
which is not enough to meet the actual compression re-
quirements. Lossy compression can achieve higher com-
pression ratio by discarding some information. Never-
theless, thanks to the extraordinary expense to collect
hyperspectral images, sometimes we would not like to
lose important data information that may affect the later
applications. The lossy-to-lossless compression scheme
combines the characteristics of two above-mentioned
compression techniques and gives the option of the re-
constructed image quality (lossy or lossless coding) ac-
cording to the practical demands. The lossy compression
results are obtained when the decoder truncates the loss-
less encoded bit stream at a desired rate. If the hyper-
spectral image is decoded without losing any information,
it can be perfectly reconstructed. Recently, the re-
searches in the lossy-to-lossless compression for hyper-
spectral images have been proposed. Tang and Pearlman
[6] proposed a lossy-to-lossless compression solution to
support random ROI access for hyperspectral image using
the 3D SPECK algorithm. Wu et al. [7] present an asym-
metric transform 3D SPECK (AT-3D SPECK) algorithm
for hyperspectral image lossy-to-lossless compression. In
Reference [8], Penna et al. propose a unified embedded

Lossy-to-Lossless Compression of Hype rspectral Image Using the 3D Set 87
Partitioned Embedded ZeroBlock Coding Algorithm
lossy-to-lossless compression framework based on the
JPEG 2000 standard. Zhang, Fowler and Liu [9] present
a lossy-to-lossless hyperspectral image compression al-
gorithm by using three-dimensional tarp-based coding
with classification for embedding (3D TCE) and integer
Karhunen-Loève transform (KLT).
The motion-compensated Embedded ZeroBlock Cod-
ing (MC-EZBC) [10] coder proposed by Hsiang and
Woods is a successful scalable video compression algo-
rithm and provides higher compression efficiency, lower
computational complexity and some attractive features
such as quality, resolution and temporal scalability. Hy-
perspectral image has higher correlation and not motion
along spectral direction [1]. Thus, the 3D EZBC algo-
rithm without motion compensation can achieve better
coding performance for hyperspectral image compres-
sion. Whereas, because it needs to establish a quadtree
representation structure for each individual 2D subband
before starting the bitplane coding, the amount of mem-
ory required for quadtree structure is prominent and dis-
advantageous for the hyperspectral images compression.
For a hyperspectral image with size 512 512

224, the
memory space of quadtree representation structure needs
about 299.52 Mbytes. So, Hou and Liu take into account
the characteristics of hyperspectral image, the excellent
performance of the 3D EZBC algorithm, as well as the
attractive properties of low memory requirements and
fast encoding/decoding of the 2D SPECK algorithm [11],
and then propose a three-dimensional Set Partitioned
Embedded ZeroBlock Coding (3D SPEZBC) algorithm
which is more suitable for hyperspectral image compres-
sion [12]. Instead of the partitioning coding method
based on the quadtree representation structure in 3D
EZBC, this algorithm adopts the partitioning coding
method based on the set representation structure in 2D
SPECK to process each individual 2D subband, so it can
save higher memory requirements against 3D EZBC
because the quadtree structure can be eliminated. For
512512224 hyperspectral image, 75.52 Mbytes me-
mory space is economized against 3D EZBC.
In this paper, we present a hyperspectral image lossy-
to-lossless compression method based on the 3D SPEZ-
BC algorithm, which adopts the Xiong’s 3D integer wa-
velet packet transform (3D integer WPT) to decorrelate,
the set-based quadtree partitioning zeroblock technique
to process bitplane coding and the context-based adap-
tive arithmetic coding for further entrop y coding. Accor-
ding to the extensive experiments and theoretical analy-
ses, 3D SPEZBC provides the same excellent compressi-
on performances compared with 3D EZBC, saves the
considerable memory requirement against 3D EZBC and
exhibits the speed performance that is slightly worse than
3D EZBC. Furthermore, for achieving good coding per
formance, we also evaluate different wavelet filters and uni-
tary scaling factors based on the 3D integer WPT st ru ct ur e ,
and make the best choices. Compared with several
state-of-the-art wavelet-based coding algorithms, the
experimental results demonstrate that our algorithm can
provide excellent compression performance and unsu-
pervised classification accuracy. So the 3D SPEZBC al-
gorithm is a good candidate for hyperspectral images
lossy-to-lossless compression.
The remainder of this paper is organized as follows:
Section 2 presents an overview of wavelet transform and
Xiong’s 3D integer wavelet packet decomposition struc-
tures with unitary scaling. In Sectio n 3, the 3D SPEZBC
algorithm for hyperspectral image lossy-to-lossless com-
pression is described in detail. Furthermore, the discus-
sions on the coding characteristics and the comparison
between the 3D SPEZBC and 3D EZBC algorithm are
given in Section 4. Section 5 provides the comprehensive
experimental results for hyperspectral image compres-
sion. Finally conclusion is drawn in Section 6.
2. Three-Dimensional Wavelet Transform
The lifting scheme presented by Sweldens is the sec-
ond generation wavelet transform and provides many
attractive advantages. To realize lossy-to-lossless im-
age compression based on wavelet transform, the in-
teger-based lifting scheme [13] is an indispensable
tool. It performs the reversible integer-to-integer
wavelet transform by rounding and truncating each
filter output. Many integer-based lifting wavelet
transforms are proposed [14,15]. In this paper, we
evaluate and compare the lossy-to- lossless compres-
sion performances by using some integer wavelet
transforms, such as S+P(B), (2+2, 2), 5/3, etc.
Hyperspectral images can be viewed as 3D data and
the image coding performance using 3D wavelet trans-
form (WT) obviously outperforms those using 2D WT
in most cases. However, there are diverse 3D WT
structures [1,2,3] according to different decomposition
order in the spatial-horizontal, spatial-vertical, and
spectral-slice directions, namely 3D dyadic wavelet
transform (DWT), 3D wavelet packet transform (WPT)
and Xiong’s 3D integer WPT. In recent years, re-
searches have proven that the statistics of hyperspectral
image are not symmetric along three dimensions and
that higher correlation is exhibited in the spectral direc-
tion [1]. 3D WPT allows different decomposition levels
in the spatial and spectral dimensions, and further per-
forms spatial decomposition even in the higher-fre-
quency spectral subbands. So it can achieve more flexi-
ble decomposition structure and preferable energy con-
vergence in the space-frequency domain. Moreover, 3D
integer WPT proposed by Xiong et al. [15] is capable of
efficiently utilizing the statistical properties to decorre-
late and gaining better compression performance for
lossy-to-lossless coding. In our lossy-to-lossless com-
pression coder, Xiong’s 3D integer WPT is used to
decorrelate hyperspectral images.

88 Lossy-to-Lossless Compression of Hyperspectral Image Using the 3D Set
Partitioned Embedded ZeroBlock Coding Algorithm
2.1 Xiong’s 3D Integer WPT Structure
As shown in Figure 1, Xiong’s 3D integer WPT first
carries out an
s
pectral
L levels 1D WPT in the spec-
tral-slice direction, which needs to further decompose the
high-frequency component at even decomposition level,
and then applies an
s
pectral
L levels 2D DWT to each
resulting spatial image. If we adopt Xiong’s 3D integer
WPT of
s
pectral
L spatial levels and
s
pectral
L spectral lev-
els for the hyperspectral image with F spectral bands,
(3
patial 1) s
K
LF individual 2D subbands can be
generated. For example, Figure 1 shows the Xiong’s 3D
integer WPT structure with 56 2D subbands, as per-
forming two spatial levels and two spectral levels for a
volumetric image with 8 spectral bands.
2.2 Unitary Scaling Factor for 3D Integer Wave-
let Transform
Because the integer-based lifting wavelet transform is not
unitary, it badly compromises integer-based lossy coding
performance [15]. To obtain better lossy coding perform-
ance, some researchers have presented a simple approach
via bit shifting of wavelet coefficients to make the integer
WT approximately unitary. In Reference 1, Tang et al.
adopt Xiong’s 3D integer WPT with unitary scaling [15]
for hyperspectral image lossy-to-lossless compression.
Nevertheless, thanks to fractional scaling factors, bits will
be lost for right shift on the highest-frequency subbands,
so all factors must be multiplied by the correctional times
in order to make them be the nonnegative powers of 2.
The correctional times used by Tang equal to four [1].
Through our experim ental evaluati ons and analysis on the
Figure 1. Xiong’s 3D integer wavelet packet transform struc-
tures of two spectral levels and two spatial levels. The num-
bers on the front upper left corner of all subbands indicate
the list initialization order of the 3D SPEZBC algorithm
compression performances of several 3D integer WT
structures with unitary scaling factor, we found that the
Tang’s unitary scaling structure with the correctional
times can achieve effective integer-based lossy coding
performances, but its lossless compression performance
is degraded. Furthermore, unitary scaling structure
adopted by Wu et al. [7] can obtain slightly better loss-
less performance than Tang’s unitary scaling structure,
but its integer-based lossy coding performance is worse
than that of Tang’s method. So we adopt a unitary scal-
ing structure as in Figure 2’s for hyperspectral image
compression, which can obtain not only better lossless
performance, but also excellent integer-based lossy per-
formance.
3. The 3D SPEZBC Algorithm for Hypersp-
ectral Image Coding
The 3D EZBC algorithm needs to establish a quadtree
representation structure with the hierarchical pyramidal
model for each individual 2D subband before starting the
bitplane coding. This structure provides a fast quadtree
splitting scheme, but its price paid needs much memory
[10]. Especially, the memory cost is prominent and dis-
advantageous in the huge volumetric images compres-
sion, such as hyperspectral images, 3D medical images,
etc. 3D SPEZBC is an embedded zeroblock bitplane cod-
in g algori thm b y effi cientl y util izi ng t h e e n e r g y cluste ring
nature within subbands and the strong dependency across
subbands. It adopts the set-based quardtree partitioning
zeroblock coding and the context-based adaptive arithmetic
(a)
(b)
Figure 2. The unitary scaling factors after Xiong’s 3D
integer WPT of four spatial levels and four spec tral lev-
els. (a) The spatial scaling factors. (b) The spectral scal-
ing factors

Lossy-to-Lossless Compression of Hype rspectral Image Using the 3D Set 89
Partitioned Embedded ZeroBlock Coding Algorithm
Figure 3. Block diagram of the hyperspectral image lossy-to-lossless coding system based on 3D SPEZBC
coding techniques. The block diagram of the hyperspectral
image lossy-to-lossless compression coder based on 3D
SPEZBC is illustrated i n Fi gure 3 and t he complete codi ng
procedure is summarized as the following three steps.
1) Firstly, for the hyperspectral image, a hierarchical
pyramidal structure is obtained by Xiong’s 3D integer
WPT with Figure 2’s unitary scaling factor. In this struc-
ture, many rectangular 2D subbands with different sizes
are generated, and each individual 2D subband is treated
as a code block and defined as an initialization set.
Whereafter, the code blocks are split and the significant
coefficients are located via the set-based quadtree parti-
tioning zeroblock coding t echnique.
2) Before starting the coding process, we define a set
to represent the code block of size l at the
spectral band b, subband k and set partitioning level l, as
shown in Table 1. Where the set partitioning level l de-
notes the splitting depth from current code set to pixel-
level sets (namely s ingle pixel). For a set of size
,[] kb
Sl 22
l

M
M

,
it is defined by
2
loglM
Substantively, l plays the same role as the quadtree level
in 3D EZBC. Moreover, Lk denotes the set partitioning
level of initialization se t (na mely kth 2D subband), where k
is the subband index ordeir (k = 0, 1, …, K-1) and K is the
total number of the 2D subbands in wavelet decomposi-
tion image. At the same time, we define Lmax to be the
maximum set partitioning level among all initialization
subbands. Table 1 lists the relationship among the code
block, set and set partitioning level.
The 3D SPEZBC algorithm adopts the same list strat-
egy used in 3D EZBC, and maintains two arrays of lists:
◆ LIS: List of Insignificant Sets.
◆ LSP: List of Significant Pixels.
In order to effectively use the statistical characteristics
within individual subbands and set partitioning levels,
some lists are separately established, namely LISk[l] (LIS
of the subband k and set partitioning level l ) and LSPk
(LSP of the subband k), where k = 0, 1, …, K-1 and l = 0,
1, …, Lmax. Initially, kth 2D subband at spectral band b is
treated as a Sk,b[Lk] set and added into LISk[Lk] list acc-
ording to the subband index order k of the marked num-
bers in Figure 1. In the coding procedure, the sets are suc-
cessively added into corresponding LISk[l] or LSPk list in
terms of their significance status.
3D SPEZBC adopts the set-based partitioning bitplane
coding to progressively encode the wavelet coefficients of
each subband from the Most Significant Bit (MSB) plane
toward the Least Significant Bit (LSB) plane. In every bit-
plane pass, all sets in LISk (LIS of the subband k) list are
tested and coded from the bo ttom set partitioning level (l = 0
level) to the maximum set partitioning level (l = L
max
level). Therefore, the sets of size 11 (single pixels) are
coded first, and the sets of size 2 are coded next, and
so on. If the set Sk,b[l] contains the significant coefficients,
it is tested significant against the current threshold. So set
Sk,b[l] of size
2
22
ll

at the set partitioning level l is parti-
tioned into four approximately equal subsets ,kb = ([]OS l)

0,[1],
kb
Sl

1,[1Sl],
kb

2,[1Sl],
kb kb of size

[1]
3,
Sl
11
22
ll



at the set partitioning level l-1. Subsequently,
each subset is treated as a new set, and in turn these new
sets ,kb are further tested and processed in the
same way above, as shown in Figure 4(b). Whole parti-
tioning process is recursively executed until the pixel-level
sets are reached, so that all significant pixels in subband
are located and then added into LSPk list for further re-
finement coding. The 3D SPEZBC coding algorithm is
described later in detail.
(OS [])l
3) Finally, in order to further improve the coding per-
formance, 3D SPEZBC makes use of the context-based
adaptive arithmetic coding approach in 3D EZBC to en-
code the significance map, signs and refinement bit-
streams. Although our algorithm gets rid of the quadtree
structure, it can also make use of the set-based partitioning
process to build upon the similar context models with hi-
erarchical pyramidal structure as 3D EZBC. Nevertheless,
unlike the 3D EZBC context models which are built for the
quadtree nodes from different subbands and quadtree levels
[10], 3D SPEZBC build the independent context models
for all sets within individual subbands and set partitioning
levels. And it effectively employs two statistical dependen-
cies — the intra-band correlation among sets at the same
set partitioning level within subband and the inter-band
correlation among set across subbands. For entropy coding
of significance t e s tin g bitstreams, t h e 3 D S PE Z B C c o nt ex t
models registers the significance te sting status of each set,
and the context of every set Sk,b[l] is located as node of the

90 Lossy-to-Lossless Compression of Hyperspectral Image Using the 3D Set
Partitioned Embedded ZeroBlock Coding Algorithm
pyramidal context models at the spectral band b, subband
k and set partitioning level l, as illustrated in Figure 4(c).
Moreover, the sign coding employs the similar scheme of
JPEG 2000, namely the output sign bitstream of the sig-
nificant coefficient is coded according to its sign and sig-
nificance status of its eight neighboring pixels. Finally, the
entropy coding of refinement bitstreams utilizes the same
context models of the significance map coding. The details
about the context models and look-up tables can refer to
Reference 10.
The significance testing function of the set Sk,b[l]
against a certain threshold 2n is defined as follows:
,
1
(, , )[]
,
1,if2max|(,,) |2
([])0, else
kb
nn
ijb Sl
nkb
ci jb
Sl


 









<
where c(i, j, b) denotes the transformed wavelet coeffi-
cient at the coordinate (i, j, b)
Table 1. The relationship of code block, set and set partitioning level
Figure 4. Illustration of the set-based quadtree partitioning procedure and the context models of the 3D SPEZBC algorithm.
(a) The original kth subband of bth spectral band. Initially, two arrays of lists (LISk and LSPk）is maintained for subband k. (b)
The set-based partitioning procedure. (c) The context models for subband k. (d) The Partitioning result for subband k of
spectral band b
Code block Set sizeSet partitionin
level
l
Set
]0[
,bk
S1 x 1 0
]1[
,bk
S 2 x 2 1
]2[
,bk
S 4 x 4 2
]3[
,bk
S 8 x 8 3

Lossy-to-Lossless Compression of Hype rspectral Image Using the 3D Set 91
Partitioned Embedded ZeroBlock Coding Algorithm
therwise
3.1 Initialization
 Output b
2(, , )
log{max|(,,) |}
ijb
ncij



 for 0: 1 kK
 Set


,[], namelysubband,
[] ,o
th
kb k
k
Sl klL
LISl






 Set .
k
LSP


3.2 Sorting Pass
for l = 0 : Lmax
for 0: 1kK
CodeLIS (k, l);
CodeLIS (k, l)
{
For each set,
,[] [] kb k
Sl LISl
 Output , ([])
nkb
Sl; 
 if
,
([])
nkb
Sl1
 if l = 0 ( namely the set Sk,b[l] is a pixel)
Output sign of Sk,b[l], and remove Sk,b[l] to
LSPk;
else
CodeSubSets( Sk,b[l] ), and remove Sk,b[l]
from LISk[l].
}
CodeSubSets ( Sk,b[l] )
{
 Partition Sk,b[l] into four approximately equal
sizes of subsets O ( Sk,b[l] ) ={0,[1]
kb
Sl

,
1,[1]
kb
Sl, 2,[1]
kb
Sl, 3,[1]
kb
Sl}, where
( [])
kb
OSl.
,,
'[1]
kb
Sl
 For each ,
'
[1 ]
kb
Sl
 Output ,
')
;
([
1]
nkb
Sl
 if 
,
'
([1])
nkb
Sl 1
 if l = 1 ( namely the set ,
'[1]
kb
Sl

is a
pixel)
Output sign of , and add
to LSPk;
,
'[1]
kb
Sl
,
'[1]
kb
Sl
else
CodeSubSets ().
,
'[1]
kb
Sl
else
add to .
,
'[1]
kb
Sl[1]
k
LISl
}
3.3 Refinement Pass
for 0: 1kK


CodeLSP ( k );
CodeLSP ( k )
{
 For each pixel set which
correspond to pixel c(i, j, b), output the nth
MSB of | c(i, j, b)|except those included in
the last sorting pass.
,[] kb k
Sl LSP
}
3.4 Quantization Step
Decrement n by 1 and go to step 2.
4. Discussion
The difference between two partitioning mechanism, the
partitioning zeroblock coding based on set representation
structure in 3D SPEZBC and the partitioning zeroblock
coding based on quadtree representation structure in 3D
EZBC, are only the different representation structures
and testing mode for splitting the code block, but their
splitting and coding results are same to each other.
Moreover, our experimental results also show that the
compression performances of 3D SPEZBC and 3D
EZBC are totally the same. However, 3D SPEZBC saves
considerable memory requirement in comparison with
3D EZBC due to the fact that the quadtree representation
structure can be eliminated. For the kth subband of size M
×M, the quadtree depth Dk of 3D EZBC is equal to
2
log
M
. If the transformed wavelet coefficients are stored
as the binary floating-point numbers (4 bytes), its quad-
tree representation structure needs to be allotted
2
00
11
()( )()4
44
k k
DD
ii
ii
MMsizeoffloat M


 

(bytes)
memory usage. The quadtree nodes at the bottom quad-
tree level 0 (namely i = 0) consist of the magnitudes of
the wavelet coefficients in subband, so it can’t be deleted.
Therefore, when using the 3D SPEZBC algorithm,
2
1
1
() 4
4
k
L
i
i
M



 (bytes) memory can be saved for
this subband.
If four spatial levels and four spectral levels 3D WPT
is employed for the hyperspectral image of size 512×
512×224, the pyramidal wavelet structure has 224 bands,
and each band has 4 subbands of size 32×32, 3 subbands
of size 64×64, 3 subbands of size 128×128, and 3 sub-
bands of size 256×256. So the saved memory space in
our algorithm against 3D EZBC is computed as
56
22
11
11
224[4( )3243( )644
44
ii
ii




92 Lossy-to-Lossless Compression of Hyperspectral Image Using the 3D Set
Partitioned Embedded ZeroBlock Coding Algorithm
78
22
11
11
3( )12843( )2564]()
44
79185344()75.52 ()
ii
ii
bytes
bytes Mbytes

  


The quadtree structure of 3D EZBC provides a fast
quadtree splitting scheme by reducing the number of
significance test. Nevertheless, the set-based partitioning
zeroblock coding method of 3D SPEZBC is very simple,
and its 2D code sets are smaller and are processed ac-
cording to the increasing order of set size using the
multi-list structure at the particular set partitioning level,
as well as the 3D SPEZBC algorithm does not need time
to establish quadtree structure, so it also exhibits excel-
lent speed performance that is slightly worse than 3D
EZBC. When our coder compresses four 512×512×224
AVIRIS hyperspectral images (such as Cuprite, Jasper
Ridge, Low Altitude and Lunar Lake) on a AMD Athlon
3800+ CPU 2GHz machine, there are averagely 87.36 s
for encoding and 125.23 s for decoding at 1.0 bpppb,
105.88 s for encoding and 170.74 s for decoding at 2.0
bpppb, as well as 135.10 s for encoding and 209. 42 s for
decoding at 3.0 bpppb , respectively.
5. Experimental Results
We performed coding experiments on four signed 16-bit
radiance AVIRIS hyperspectral images [16], namely
Cuprite scene 1, Jasper Ridge scene 1, Low Altitude
scene 1 and Lunar Lake scene 1. In our experiments, we
extracted the 256×256 lower left corner, so that the di-
mensions of the test image were 256×256×224 pixels.
For lossy compression the rate distortion performance
was compared by means of the signal-to-noise (SNR)
values for a variety of bit rates in bits per pixel per band
(bpppb), and for lossless compression performance we
used those rates to evaluate the size of the compressed
data streams. SNR is defined as2
10
10log
x
M
SE

, where
2
x

is the average squared value (power) of the original
AVIRIS image and MSE is the mean squared error over
the entire sequence.
5.1 Lossless Compression Performance
Table 2 presents the lossless compression results for the
3D SPEZBC algorithm using various integer wavelet
filters, which adopts the four spatial levels and four
spectral levels Xiong’s 3D integer WPT with Figure 2’s
unitary scaling factor. We can see that no certain wavelet
filter is optimal for all test images. The 5/11-A, 13/7-C
and 5/3 integer filters all provide good compression per-
formances. Furthermore, Adams et al. [14] have found
that the 5/3 filter evidently required the least computa-
tion, and experimental results in Subsection 5.2 further
show that the integer-based lossy compression perform-
ance using the 5/3 integer filter clearly outperform that
using the 5/11-A and 13/7-C integer filters at the me-
dium and high bit rates. Therefore, Figure 5 displays the
lossless compression ratios using the 5/3 integer filter in
comparison with several state-of-the-art wavelet-based
algorithms. In our experiments, JPEG2000-MC used the
four spatial levels and four spectral levels 3D integer
WPT and other algorithms used the four spatial levels
and four spectral levels Xiong’s 3D integer WPT with
the unitary scaling factor in Figure 2. For all test images,
the results show that 3D SPEZBC outperforms 3D
SPECK, 3D SPIHT and AT-3D SPIHT, and it is worse
than JPEG2000-MC. The average compression ratio of
3D SPEZBC is 5.70 % lower than 3D SPECK, 7.14 %
lower than 3D SPIHT, 4.96 % lower than AT-3D SPIHT,
and 1.07 % higher than JPEG2000-MC.
5.2 Integer-Based Lossy Compression Performance
The integer-based lossy compression results can be ob-
tained when the decoder truncates the lossless encoded
bitstreams in Subsection 5.1 at a desired bit rate. If we
decode the hyperspectral image without losing any in-
formation, it is perfectly reconstructed. Table 3 shows
the rate distortion results of the 3D SPEZBC algorithm
using various integer wavelet filters for “Cuprite” image.
We can see that these wavelet filters exhibit different
coding performance at various bit rates. The 5/3 integer
filter requires the least computation proved by Adams et
al. [14] and provides excellent compression performance
at medium and high bit rates. Moreover, when we apply
the ISODATA and K-means unsupervised classification
methods in comparison further (in Subsection 5.3), at
more than 1.0 bpppb (16:1 compression ratio) the classi-
fication accuracy is higher than 99%. The experimental
results on “Jasper Ridge”, “Low Altitude” and “Lunar
Lake”
Figure 5. Lossless compression results (bpppb) in com-
parison with the state-of-the-art wavelet-based algorithms
using 5/3 integer filter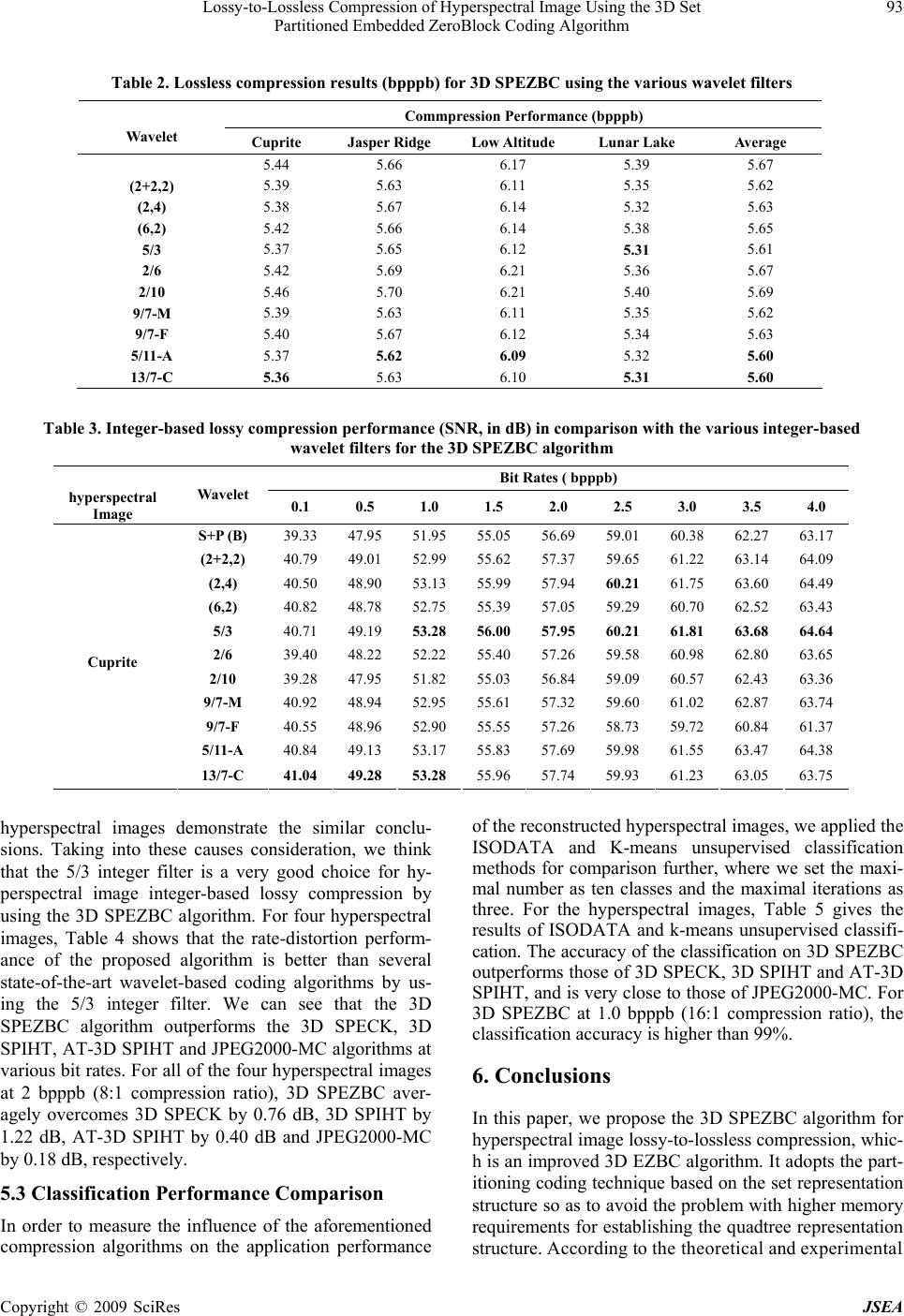

Lossy-to-Lossless Compression of Hype rspectral Image Using the 3D Set 93
Partitioned Embedded ZeroBlock Coding Algorithm
Table 2. Lossless compression results (bppp b) for 3D SPEZBC using the various w avelet filters
Table 3. Integer-based lossy compression performance (SNR, in dB) in comparison with the various integer-based
wavelet filters for the 3D SPEZBC algorithm
Commpression Performance (bpppb)
Wavelet Cuprite Jasper Ridge Low Altitude Lunar Lake Average
5.44 5.66 6.17 5.39 5.67
(2+2,2) 5.39 5.63 6.11 5.35 5.62
(2,4) 5.38 5.67 6.14 5.32 5.63
(6,2) 5.42 5.66 6.14 5.38 5.65
5/3 5.37 5.65 6.12 5.31 5.61
2/6 5.42 5.69 6.21 5.36 5.67
2/10 5.46 5.70 6.21 5.40 5.69
9/7-M 5.39 5.63 6.11 5.35 5.62
9/7-F 5.40 5.67 6.12 5.34 5.63
5/11-A 5.37 5.62 6.09 5.32 5.60
13/7-C 5.36 5.63 6.10 5.31 5.60
Bit Rates ( bpppb)
hyperspectral
Image Wavelet 0.1 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
S+P (B) 39.33 47.9551.9555.05 56.6959.0160.38 62.27 63.17
(2+2,2) 40.79 49.0152.9955.62 57.3759.6561.22 63.14 64.09
(2,4) 40.50 48.9053.1355.99 57.9460.21 61.75 63.60 64.49
(6,2) 40.82 48.7852.7555.39 57.0559.2960.70 62.52 63.43
5/3 40.71 49.1953.2856.00 57.9560.2161.81 63.68 64.64
2/6 39.40 48.2252.2255.40 57.2659.5860.98 62.80 63.65
2/10 39.28 47.9551.8255.03 56.8459.0960.57 62.43 63.36
9/7-M 40.92 48.9452.9555.61 57.3259.6061.02 62.87 63.74
9/7-F 40.55 48.9652.9055.55 57.2658.7359.72 60.84 61.37
5/11-A 40.84 49.1353.1755.83 57.6959.9861.55 63.47 64.38
Cuprite
13/7-C 41.04 49.2853.2855.96 57.7459.9361.23 63.05 63.75
hyperspectral images demonstrate the similar conclu-
sions. Taking into these causes consideration, we think
that the 5/3 integer filter is a very good choice for hy-
perspectral image integer-based lossy compression by
using the 3D SPEZBC algorithm. For four hyperspectral
images, Table 4 shows that the rate-distortion perform-
ance of the proposed algorithm is better than several
state-of-the-art wavelet-based coding algorithms by us-
ing the 5/3 integer filter. We can see that the 3D
SPEZBC algorithm outperforms the 3D SPECK, 3D
SPIHT, AT-3D SPIHT and JPEG2000- MC algorithms at
various bit rates. For all of the four hyperspectral images
at 2 bpppb (8:1 compression ratio), 3D SPEZBC aver-
agely overcomes 3D SPECK by 0.76 dB, 3D SPIHT by
1.22 dB, AT-3D SPIHT by 0.40 dB and JPEG2000-MC
by 0.18 dB, respectiv ely.
5.3 Classification Performance Comparison
In order to measure the influence of the aforementioned
compression algorithms on the application performance
of the reconstructed hyperspectral images, we applied the
ISODATA and K-means unsupervised classification
methods for comparison further, where we set the maxi-
mal number as ten classes and the maximal iterations as
three. For the hyperspectral images, Table 5 gives the
results of ISODATA and k-means unsupervised classifi-
cation. The accuracy of the classification on 3D S PEZBC
outperfor ms those of 3D SPECK, 3D SPIHT and AT-3D
SPIHT, and is very close to those of JPEG2000-MC. For
3D SPEZBC at 1.0 bpppb (16:1 compression ratio), the
classification accuracy is higher than 99%.
6. Conclusions
In this paper, we propose the 3D SPEZBC algorithm for
hyperspectral image lossy-to-lossless compression, whic-
h is an improved 3D EZBC algorithm. It adopts the part-
itioning coding technique based on the set representation
structure so as to avoid the problem with higher memory
requirements for establishing the quadtree representation
structure. According to the theoretical and experimental

94 Lossy-to-Lossless Compression of Hyperspectral Image Using the 3D Set
Partitioned Embedded ZeroBlock Coding Algorithm
Table 4. Integer-based lossy compression performance (SNR, in dB) in comparison with the state-of-the-art
wavelet-based coding algorithms using 5/3 integer filter
Bit Rate ( bpppb)
hyperspectral Image Coding
Methods 0.1 0.5 1.0 1.5 2.0 2.5 3.0
3D SPEZBC 40.71 49.19 53.27 56.00 57.95 60.21 61.81
3D SPECK 39.92 48.62 52.61 55.49 57.57 59.71 61.45
3D SPIHT 38.59 47.79 51.79 54.96 57.35 59.37 61.15
AT-3D SPIHT 40.23 48.93 52.89 55.73 57.80 59.94 61.66
Cuprite
JPEG2000-MC 40.56 49.02 53.18 55.85 57.89 60.01 61.53
3D SPEZBC 30.74 41.03 46.35 50.10 52.91 55.08 57.00
3D SPECK 30.11 40.13 45.50 49.25 52.18 54.27 56.39
3D SPIHT 29.07 39.42 45.14 48.91 51.60 53.86 56.03
AT-3D SPIHT 30.26 40.65 46.05 49.49 52.52 54.51 56.64
Jasper Ridge
JPEG2000-MC 30.62 40.89 46.14 49.78 52.81 54.65 56.58
3D SPEZBC 27.33 37.94 44.33 48.38 51.11 53.52 55.68
3D SPECK 26.74 37.05 43.28 47.42 50.12 52.78 54.69
3D SPIHT 25.84 36.56 42.57 46.82 49.82 52.37 54.40
AT-3D SPIHT 26.76 37.59 43.81 47.82 50.68 53.21 55.10
Low Altitude
JPEG2000-MC 27.18 37.72 44.06 47.99 50.75 53.15 54.91
3D SPEZBC 43.20 50.88 54.76 57.33 59.25 61.35 62.94
3D SPECK 42.41 50.44 54.30 56.94 58.77 60.92 62.73
3D SPIHT 41.11 49.70 53.49 56.31 58.58 60.55 62.39
AT-3D SPIHT 42.59 50.64 54.51 57.14 58.94 61.08 62.81
Lunar Lake
JPEG2000-MC 43.02 50.76 54.68 57.20 59.07 60.98 62.69
Table 5. Overall classification accuracy comparison (in ) based on ISODATA and K_mean at the various bit rates (bpppb)
for lossy compression based on integer wavelet transform
K_mean ISODATA
hyperspectral
Image Coding Methods 0.1 0.5 1.0 1.5 2.0 0.1 0.5 1.0 1.5 2.0
3D SPEZBC 90.88 99.0799.5399.7299.79 92.97 99.28 99.62 99.76 99.78
3D SPECK 90.58 99.0399.4999.7099.7892.7299.2099.58 99.75 99.77
3D SPIHT 87.63 98.8399.4599.6999.7590.3099.1399.56 99.74 99.76
AT-3D SPIHT 90.83 99.0499.5099.7199.79 92.90 99.25 99.59 99.75 99.77
Cuprite
JPEG2000-MC 90.86 99.0699.5299.7199.79 92.9399.2799.61 99.76 99.77
3D SPEZBC 89.74 98.7799.4899.6899.7192.23 99.0899.72 99.80 99.86
3D SPECK 89.63 98.7099.4399.5399.6692.0798.9799.65 99.75 99.84
3D SPIHT 87.53 98.5899.2799.5199.6590.3898.9199.54 99.76 99.83
AT-3D SPIHT 89.69 98.7399.4599.6599.6892.1098.9999.69 99.79 99.84
Jasper Ridge
JPEG2000-MC 89.72 98.7499.4699.6699.71
92.2099.0499.70 99.80 99.85
analysis, our algorithm not only provides the same ex-
cellent compression performance as 3D EZBC, but also
can save considerable memory requirements against 3D
EZBC. For hyperspectral image lossy-to-lossless com-
pression based on 3D SPEZBC, Xiong’s 3D integer
WPT with unitary scaling factor in Figure 2 and the 5/3
integer filter are good options. Compared with several
state-of-the-art wavelet-based coding algorithms, the

Lossy-to-Lossless Compression of Hype rspectral Image Using the 3D Set 95
Partitioned Embedded ZeroBlock Coding Algorithm
experimental results indicate that our coder provides
better compression performance and unsupervised clas-
sification accuracy.
7. Acknowledgments
This work is supported by the Engagement Foundation
of Xi’an University of Science and Technology (Project
No.200722).
REFERENCES
[1] X. Tang and W. A. Pearlman, “Three-dimensional wave-
let-based compression of hyperspectral images,” Hyper-
spectral Data Compression, MA: Kluwer Academic Pub-
lishers, pp. 273-308, 2006.
[2] J. E. Fowler and J. T. Rucker, “3D wavelet-based com-
pression of hyperspectral imagery,” Hyperspectral Data
Exploitation: Theory and Applications, John Wiley &
Sons Inc., Hoboken, NJ, pp. 379-407, 2007.
[3] B. Penna, T. Tillo, E. Magli, and G. Olmo, “Transform
coding techniques for lossy hyperspectral data compres-
sion,” in the Proceedings of IEEE Transactions on Geo-
science and Remote Sensing, Vol. 45, No. 5, pp. 1408
-1421, 2007.
[4] T. W. Fry and S. Hauck, “Hyperspectral image compres-
sion on reconfigurable platforms,” in the Proceedings of
IEEE Symposium on Field-Programmable Custom Com-
puting Machines, pp. 251-260, April 2002.
[5] X. Tang, S. Cho, and W. A. Pearlman, “3D set partition-
ing coding methods in hyperspectral image compres-
sion,” in the Proceedings of IEEE International Confer-
ence on Image Processing, pp. 239-242, September 2003.
[6] X. Tang and W. A. Pearlman, “Lossy-to-lossless block-
based compression of hyperspectral volumetric data,” in
the Proceedings of IEEE International Conference on
Image Processing, pp. 1133-1136, 2006.
[7] J. J. Wu, Z. S. Wu, and C. K. Wu, “Lossy to lossless
compressions of hyperspectral images using three-dimen-
sional set partitioning algorithm,” SPIE Optical Engi-
neering, Vol. 45, No. 2, pp. 0270051-0270058, 2006.
[8] B. Penna, T. Tillo, E. Magli, and G. Olmo, “Embedded
lossy-to-lossless compression of hyperspectral images
using JPEG 2000,” in the Proceedings of IEEE Interna-
tional Geoscience and Remote Sensing Symposium, Vol.
1, pp. 25-29, 2005.
[9] J. Zhang, J. E. Fowler, and G. Z. Liu, “Lossy-to-lossless
compression of hyperspectral imagery using 3D-TCE and
an integer KLT,” IEEE Geoscience and Remote Sensing
Letters, Vol. 4, No. 2, pp. 201-205, 2008.
[10] S. T. Hsiang, “Highly scalable subband/wavelet image
and video coding,” Ph.D dissertation, Rensselaer Poly-
technic Institute, Troy, 2002.
[11] A. Islam and W. A. Pearlman, “An embedded and effi-
cient low-complexity hierarchical image coder,” in the
Proceedings of SPIE Conference on Visual Communica-
tions and Image Processing, Vol. 3653, pp. 294-305, 1999.
[12] Y. Hou and G. Z. Liu, “3D set partitioned embedded zero
block coding algorithm for hyperspectral image compres-
sion,” in the Proceedings of SPIE Symposium on MIPPR,
Vol. 6790, pp. 561-567, 2007.
[13] A. R. Calderbank, I. Daubechies, W. Sweldens, and B. L.
Yeo, “Wavelet transforms that map integers to integers,”
Applied and Computational Harmonic Analysis, Vol. 5,
No. 3, pp. 332-369, 1998.
[14] M. D. Adams and F. Kossentini, “Reversible inte-
ger-to-integer wavelet transforms for image compression:
Performance evaluation and analysis,” IEEE Transactions
on Image Processing, Vol. 9, No. 6, pp. 1010-1024, 2000.
[15] Z. X. Xiong, X. L. Wu, S. Cheng, and J. P. Hua,
“Lossy-to-lossless compression of medical volumetric
data using three-dimensional integer wavelet transforms,”
IEEE Transactions on Medical Imaging, Vol. 22, No. 3,
pp. 459-470, 2003.
[16] http://aviris.jpl.nasa.gov/html/aviris.overview.html.