Component-Oriented Reliability Analysis Based on Hierarchical Bayesian Model for an Open Source Software

doi:10.4236/ajor.2011.12004

Paper Menu >>

Journal Menu >>

American Journal of Oper ations Research, 2011, 1, 25-32

doi:10.4236/ajor.2011.12004 Published Online June 2011 (http://www.SciRP.org/journal/ajor/)

Component-Oriented Reliability Analysis Based on

Hierarchical Bayesian Model for an Open Source Software

Yoshinobu Tamura1, Hidemitsu Takehara2, Shigeru Yamada2

1Graduat e S chool of Sci e n ce and Enginee ring, Yamaguchi University, Ube, Japan

2Graduat e School of Engineering, Tottori University, Tottori, Japan

E-mail: tamura@yamaguchi-u.ac.jp, M09T7016M@edu.tottori-u.ac.jp, yamada@sse.tottori-u.ac.jp

Received March 11, 2011; revised April 10, 2011; accepted May 9, 2011

Abstract

The successful experience of adopting distributed development models in such open source projects includes

GNU/Linux operating system, Apache HTTP server, Android, BusyBox, and so on. The open source project

contains special features so-called software composition by which several geographically-dispersed compo-

nents are developed in all parts of the world. We propose a method of component-oriented reliability as-

sessment based on hierarchical Bayesian model and Markov chain Monte Carlo methods. Especially, we fo-

cus on the fault-detection rate for each component reported to the bug tracking system. We can assess the

reliability for the whole open source software system by using the confidence interval for each component.

Also, we analyze actual software fault-count data to show numerical examples of reliability assessment for

OSS.

Keywords: Open Source Software, Reliability, Bayesian Model, Markov Chain Monte Carlo Method

1. Introduction

Software development environment has changed into new

development paradigms such as concurrent distributed de-

velopment environment and the so- called open source pro-

ject by using network computing technologies [1]. Espe-

cially, such OSS (Open Source Software) systems which

serve as key components of critical infrastructures in the

society are still ever-expanding now [2]. The methodology

of the object-oriented design and analysis is a feature of

distributed development environment and greatly success-

ful in the field of programming-language, simulation, GUI

(graphical user interface), and constructing on database in

the software development. A general idea of the object-

oriented design and analysis is developed as a technique

which can easily construct and maintain the complex sys-

tem. The successful experience of adopting the distributed

development model in such open source projects includes

GNU/Linux operating system [2]. However, the poor han-

dling of the quality and customer support prohibit the pro-

gress of OSS. We focus on the problems in the software

quality, which prohibit the progress of OSS.

Especially, many software reliability growth models

(SRGM’s) [3] have been applied to assess the reliability

for quality management and testing-progress control of

software development. On the other hand, the effective

method of dynamic testing management for a new dis-

tributed development paradigm as typified by the open

source project has only a few presented [4-8]. In case of

considering the effect of the debugging process on entire

system in the development of a method of reliability as-

sessment for OSS, it is necessary to grasp the situation of

registration for bug tracking system, the connection status

of each component, degree of maturation of OSS, and so

on [9,10].

Especially, OSS is composed of several software com-

ponents as a feature of distributed development envi-

ronment. In such cases, it is appropriate to apply the me-

thod of component based reliability assessment rather

than one of reliability assessment based on SRGM’s.

Many SRGM’s are assumed to be suitable for the system

testing phase of software development. On the other h and,

it is difficult to apply SRGM’s to OSS, because OSS

development style has not the typical software develop-

ment environment, i.e., OSS development cycle has no

testing phase. Moreover, OSS is developed under a com-

bination of many software components. Therefore, it is

important for software developers to confirm the static

state of each component in OSS development phase from

the standpoint of reliability assessment [6-8]. The char-

Y. TAMURA ET AL.

acteristics in terms of the reli ability assess ment fo r OSS ’s

are shown as follows [11,12]:

 OSS development cycle has no testing phase;

 The cumulative number of detected faults can not con-

verge to a finite value;

 It is difficult to apply SRGM’s to the development

cycle of OSS;

 OSS is developed under a combination of many

software components;

 Many software components of OSS are developed by

the geographically-dispersed software developers;

 OSS’s are grouped into several categories, i.e., appli-

cation software such as Firefox Web browser, server

software such as Apache HTTP server, embedded sys-

tem software such as Android, operating system soft-

ware s uch as Linux.

In this paper, we focus on an OSS developed under

open source project. We discuss the method of component-

oriented software reliability assessment considering the

fault-detection rate of each component based on Bayesian

theory and Markov chain Monte Carlo methods (MCMC).

It is important to understand the static state of OSS, i.e.,

the connection status of each component. We consider the

method of reliability assessment for the whole OSS sys-

tem by using the data of proportion for fault-detection rate

in terms of the software components. Especially, we esti-

mate the predicted distributions by using MCMC. Then,

we use the data of proportion data for fault-detection rate

in terms of the software components on the bug tracking

system as the sample data. Also, we analyze actual soft-

ware fault-count data to show numerical examples of soft-

ware reliability assessment for the OSS. Especially, we

derive the confidence interval for each component. Then,

we show that the proposed m e t hod can assi st improvement

of quality for OSS. Our method may be useful for the soft-

ware testing manager to assess the static state of the whole

OSS system automatically.

2. Estimation of Predicted Distribution

Based on Bayesian Theory

We apply a Bayesian theory to the data in terms of fault-

detection rate of each OSS components. Let t be the

proportion data of the fault-detection rate in the OSS by

operational time

. Also, t



is the parameter of the

specific distribution at operational time

. We estimate



by using y

. In this case, we use the prior distribu-

tion up to time . As an example, the updated data

is given by the following equation based on Bayesian

theory in case that we hav e knowledge of the prior infor-

mation

(t1)



independently of data .

(|)()

(| )( |)().

(|)()

pD p

pD pDp

pDp d









 (1)

In this paper, we estimate t



by using the data of

proportion for past fault detection rate in order to esti-

mate t



for the sequential data . Then, we can de-

rive the following equation from Equation (1):

12 1

(|, , , )

(|)(|, , , )

(|)(|, , , )d.

tt tt

tt ttt

pyy y

pypy yy

















(2)

According to Equation (2), 12

(|, , , )

pyy y





112

(|, , pyy

is up-

dated on a real-time basis from 1

, )





.

Therefore, we define as follows:

1112 1

12 1

(|, , , )

(|)(|)(|, , , )d

(|)(|, , , )d.

tttttt t

tt ttt

pyy y

pyppy yy

pypy yy



 

 















(3)

Equation (3) means the probab ility at operational time

obtained from

t1t





at operational time . (1)t

Then, we assume the simple case as follows:

tt t









 (4)

where t



is the independent Gaussian noise at opera-

tional time

[13].

3. Hierarchical Bayesian Model

In this paper, we assume the data trend of proportion for

the fault-detection rate as the following probability den-

sity function of normal distribution for simplicity:



() exp,

fx t



















(5)

where



is the mean value and



the standard devia-

tion. We consider the hierarchical Bayesian model based

on the prior distribution and hyper prior distribution

composed of



and



Then, we can obtain the following equation from Equa-

tion (1).

(, |)

(|, )(|)()

(|, )(|)()dd

(|, )(|)().

pDp p





 





 





 (6)

Therefore, we can derive as follows:









12 1

(, |, , , )

(|, )(|)

(|, , , )

(|, )(|)

(|, , , )dd.

tt t

ttt tt

ttt

pyyy

py p

pyy y

py p

pyy yt





 



 















(7)

Y. TAMURA ET AL.

According to Equation (7), 12

(, | , , , )

tt t

pyy







1112

(, |, , ,

Metropolis-Hastings (MH) algorithm in this paper, be is

updated on a real-time basis from 1

)

yy y



 

Therefore, we can obtain as follows: cause MH algorithm has simple structure, and widely

used in many research fields.

The flow of MH algorithm is shown in Figure 1. Also,

the procedures of MH algorithm is as follows:









1121

12 1

(, | , , , )

(|, )(|)

(|)(|, , , )d

(|, )(|)

(|, , , )dd.

tt t

ttt tt

tttt t

ttt tt

tttt

pyyy

py p

ppyyy

py p

pyy y





 

 

 

















(8)

 Generate





by using the applied density (,p )





in case of t





 In case of (, )u







, replace



 by 1t





. In case

of (, )u









, apply 1t



.

 Continue the above mentioned process without the

initial value dependence.

In this paper, we assu me that ()



is (, )





. Al-

so,





means





and



. Therefore, (, )







given by the following equation in this paper:

Equation (8) means the probability at operational time t

obtained from the operational time . We can esti-

mate (1)t



and



at operational time t from Equation (8).

Also, we can derive the confidence interval from the es-

timated mean value ˆ



and standard deviation



ˆ. In

case of the upper side probability 100 %



and the de-

gree of freedom (, we can obtain the upper and

lower confidence limits for the estimated confidence in-

terval as follows:

1)n

(, |, , , ).

(, | , , , )

tt t

pyyy









 (10)

5. Numerical Examples

There are many open source projects around the world. In

particular, we focus on an large scale open source solution

based on the Apache HTTP Server [16]. The fault-count

data used in this paper are collected in the bug tracking

system on the website of each open source pr oject.

1ˆ

ˆ(1 ),







 (9)

where k()t



is the value of distribution in case of

the confidence interval t

(1 )



 at the degree of freedom

. Also, means the total number of data. kn

5.1. The Estimation Results Based on MCMC

4. MCMC

The data of proportion for actual fault-detection rate for

each component in Apache HTTP Server is shown in

Table 1. We use the data from January 2008 to Septem-

ber 2010. Table 1 shows the data of proportion for actual

fault-detection rate for each month. Also, we apply

“Core”, “Documentation”, “mod_ssl”, “mod_proxy”, and

“Build” as the major components. We focus on the data

of all platform for Apache HTTP Server 2 version. We

assume that a unit of time is week, because these results

and computation al times show little chan ge if the unit of

time is day in terms of the software fault data sets.

It is one of the sampling method of the probability dis-

tribution based on Markov chain by the random number

generation. Basically, it is difficult to take a sample of

random variable from the multivariate distribution. How-

ever, we can easily take the probability sample from the

objective probability by using MCMC [14,15]. Several

MCMC algorithms have been proposed by several re-

searchers in order to solve these problems, i.e., Metropo-

lis-Hastings (MH) and Gibbs Sampler. Gibbs Sampler is

the extended method of MH algorith m. We apply the

























1tt















100,0 00t

100,000t



*Regardless of the initial value effect

*Histogram analysis for posterior distrbut ion

Generation





















0,N





Likelihood estimation

Initial value1



configuration

Figure 1. The flow diagram of MH algorithm.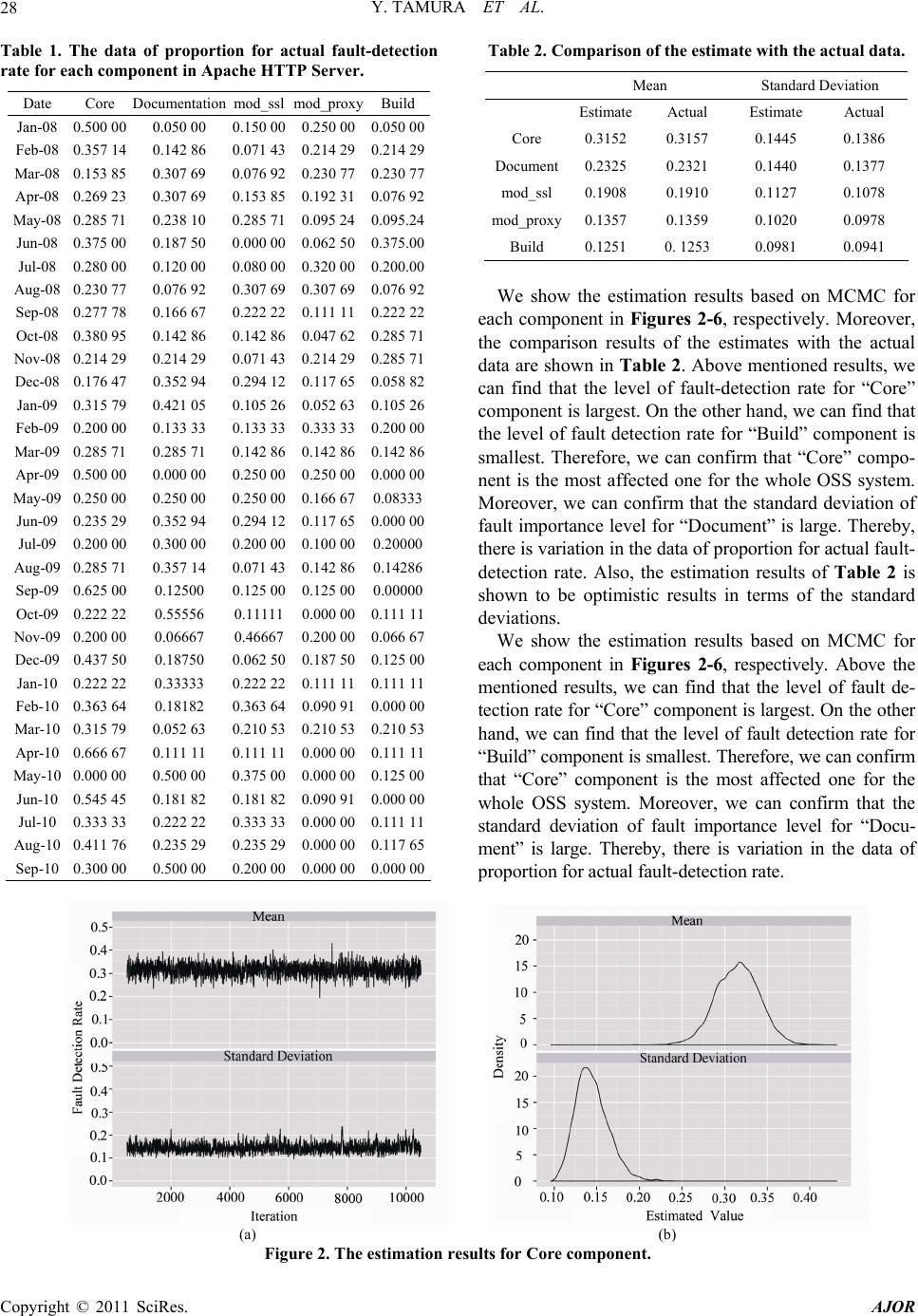

Y. TAMURA ET AL.

Table 1. The data of proportion for actual fault-detection

rate for each component in Apache HTTP Server.

Date Core Documentationmod_ssl mod_proxyBuild

Jan-08 0.500 00 0.050 00 0.150 00 0.250 00 0.050 00

Feb-08 0.357 14 0.142 86 0.071 43 0.214 29 0.214 29

Mar-08 0.153 85 0.307 69 0.076 92 0.230 77 0.230 77

Apr-08 0.269 23 0.307 69 0.153 85 0.192 31 0.076 92

May-08 0.285 71 0.238 10 0.285 71 0.095 24 0.095.24

Jun-08 0.375 00 0.187 50 0.000 00 0.062 50 0.375.00

Jul-08 0.280 00 0.120 0 0 0.080 00 0.320 00 0.200.00

Aug-08 0.230 77 0.076 92 0.307 69 0.307 69 0.076 92

Sep-08 0.277 78 0.166 67 0.222 22 0.111 11 0.222 22

Oct-08 0.380 95 0.142 86 0.142 86 0.047 62 0.285 71

Nov-08 0.214 29 0.214 29 0.071 43 0.214 29 0.285 71

Dec-08 0.176 47 0.352 94 0.294 12 0.117 65 0.058 82

Jan-09 0.315 79 0.421 05 0.105 26 0.052 63 0.105 26

Feb-09 0.200 00 0.133 33 0.133 33 0.333 33 0.200 00

Mar-09 0.285 71 0.285 71 0.142 86 0.142 86 0.142 86

Apr-09 0.500 00 0.000 00 0.250 00 0.250 00 0.000 00

May-09 0.250 00 0.250 00 0.250 00 0.166 67 0.08333

Jun-09 0.235 29 0.352 94 0.294 12 0.117 65 0.000 00

Jul-09 0.200 00 0.300 0 0 0.200 00 0.100 00 0.20000

Aug-09 0.285 71 0.357 14 0.071 43 0.142 86 0.14286

Sep-09 0.625 00 0.12500 0.125 00 0.125 00 0.00000

Oct-09 0.222 22 0.5555 6 0.11111 0.000 00 0.111 11

Nov-09 0.200 00 0.06667 0.46667 0.200 00 0.066 67

Dec-09 0.437 50 0.18750 0.062 50 0.187 50 0.125 00

Jan-10 0.222 22 0.33333 0.222 22 0.111 11 0.111 11

Feb-10 0.363 64 0.18182 0.363 64 0.090 91 0.000 00

Mar-10 0.315 79 0.052 63 0.210 53 0.210 53 0.210 53

Apr-10 0.666 67 0.111 11 0.111 11 0.000 00 0.111 11

May-10 0.000 00 0.500 00 0.375 00 0.000 00 0.125 00

Jun-10 0.545 45 0.181 82 0.181 82 0.090 91 0.000 00

Jul-10 0.333 33 0.222 2 2 0.333 33 0.000 00 0.111 11

Aug-10 0.411 76 0.235 29 0.235 29 0.000 00 0.117 65

Sep-10 0.300 00 0.500 00 0.200 00 0.000 00 0.000 00

Table 2. Comparison of the estimate with the actual data.

Mean Standard Deviation

EstimateActual Estimate Actual

Core 0.3152 0.3157 0.1445 0.1386

Document0.2325 0.2321 0.1440 0.1377

mod_ssl 0.1908 0.1910 0.1127 0.1078

mod_proxy0.1357 0.1359 0.1020 0.0978

Build 0.1251 0. 1253 0.0981 0.0941

We show the estimation results based on MCMC for

each component in Figures 2-6, respectively. Moreover,

the comparison results of the estimates with the actual

data are shown in Table 2. Above mentioned results, we

can find that the level of fault-detection rate for “Core”

component is largest. On the other hand, we can find that

the level of fault detection rate for “Build” component is

smallest. Therefore, we can confirm that “Core” compo-

nent is the most affected one for the whole OSS system.

Moreover, we can confirm that the standard deviation of

fault importance level for “Do cument” is large. Thereby,

there is variation in th e data of propo rtion fo r actual f au lt-

detection rate. Also, the estimation results of Table 2 is

shown to be optimistic results in terms of the standard

deviations.

We show the estimation results based on MCMC for

each component in Figures 2-6, respectively. Above the

mentioned results, we can find that the level of fault de-

tection rate for “Core” component is largest. On the other

hand, we can find that the level of fault detection rate for

“Build” component is smallest. Therefore, we can conf ir m

that “Core” component is the most affected one for the

whole OSS system. Moreover, we can confirm that the

standard deviation of fault importance level for “Docu-

ment” is large. Thereby, there is variation in the data of

proportion for act ual fault -detect i on rat e.

(a) (b)

Figure 2. The estimation results for Core component.

Y. TAMURA ET AL.29

(a) (b)

Figure 3. The estimation results for Documentation component.

(a) (b)

Figure 4. The estimation results for mod_ssl component.

(a) (b)

Figure 5. The estimation results for mod_proxy component.

Y. TAMURA ET AL.

(a) (b)

Figure 6. The estimation results for Build component.

5.2. The Estimation Results Based on MCMC On the other hand, “mod_ssl” and “mod_proxy” compo-

nents decrease in width of the confidence interval, because

the open source project is proceeding without problems

according to be removed the faults of small components.

with Time Variation Considering

Confidence Interval

In this section, we consider the case of 24, 0.95n





Then, 95% confidence interval is given by the following

equation: 6. Concluding Remarks

In this paper, we have focused on the reliability of OSS.

Moreover, we have proposed the method of component-

oriented software reliability assessment based on th e hie-

rarchical Bayesian model and MCMC in order to esti-

mate the predicted distributions for each component of

OSS. Especially, we have assumed the data of proportion

for the fault-detection rate as t he prob ability d ensity f u n c-

tion of normal distribution. Also, we have analyzed ac-

tual software fault-count data to show numerical exam-

ples of component-oriented software reliability assessment

for OSS.

23 ˆ

ˆ(0.05) .





 (7)

The estimation results based on MCMC with time varia-

tion of the data of proportion for each component are

shown in Figures 7-11, respectively. From Figures 7-11,

we can confirm that “Core” component is constant in small

width of the confidence interval. Also, “Core” component

remains in the large value continuously. These results mean

that the open source project keeps a high active state.

Therefore, we consider that the focused OSS system is

stable in terms of the occurrence rate of “Core” component.

Figure 7. The estimation results of confidence interval for Core component.

Y. TAMURA ET AL.31

Figure 8. The estimation results of confidence interval for Documentation component.

Figure 9. The estimation results of confidence interval for mod_ssl component.

Figure 10. The estimation results of confidence interval for mod_proxy component.

Y. TAMURA ET AL.

Figure 11. The estimation results of confidence interval for Build component.

Finally, we have focused on fault-detection rate for

fault importance level of OSS. By us ing our method, th e

software testing manager can assess the static state of

OSS. Our method may be useful as the method of com-

ponent-oriented reliability assessment for OSS.

7. Acknowledgements

This work was supported in part by the Grant-in-Aid for

Scientific Research (C), Grant No. 22510150 from the

Ministry of Education, Cul t ure, Sport s, Sci e nce, and Tech-

nology o f Ja p an.

8. References

[1] L. T. Vaughn, “Client/Server System Design and Imple-

mentation,” McGraw-Hill, New York, 1994.

[2] E-Soft Inc., “Internet Research Reports,” 2010.

http://www.securityspace.com/sspace/

[3] S. Yamada, “Elements of Software Reliability-Modeling

Approach (in Japanese),” Kyoritsu-Shuppan, Tokyo, 2011.

[4] A. D. MacCormack, J. Rusnak and C. Y. Baldwin, “Ex-

ploring the Structure of Complex Software Designs: An

Empirical Study of Open Source and Proprietary Code,”

Informs Journal of Management Science, Vol. 52, No. 7,

2006, pp. 1015-1030.

[5] G. Kuk, “Strategic Interaction and Knowledge Sharing in

the KDE Developer Mailing List,” Informs Journal of

Management Science, Vol. 52, No. 7, 2006, pp. 1031-1042.

[6] Y. Zhoum and J. Davis, “Open Source Software Reliabil-

ity Model: An Empirical Approach,” Proceedings of the

Workshop on Open Source Software Engineering, Vol. 30,

No. 4, 2005, pp. 67-72,

[7] P. Li, M. Shaw, J. Herbsleb, B. Ray and P. Santhanam,

“Empirical Evaluation of Defect Projection Models for

Widely-Deployed Production Software Systems,” Pro-

ceedings of the 12th International Symposium on the

Foundations of Software Engineering, New York, No-

vember 2004, pp. 263-272.

[8] J. Norris, “Mission-Critical Development with Open

Source Software,” IEEE Software Magazine, Vol. 21, No.

1, 2004, pp. 42-49.

[9] Y. Tamura and S. Yamada, “Software Reliability Assess-

ment and Optimal Version-Upgrade Problem for Open

Source Software,” Proceedings of the 2007 IEEE Interna-

tional Conference on Systems, Man, and Cybernetics,

Montreal, 7-10 October 2007, pp. 1333-1338.

doi:10.1109/ICSMC.2007.4413582

[10] Y. Tamura and S. Yamada, “A Method of User-Oriented

Reliability Assessment for Open Source Software and its

Applications,” Proceedings of the 2006 IEEE Interna-

tional Conference on Systems, Man, and Cybernetics,

Taipei, 8-11 October 2006, pp. 2185-2190.

doi:10.1109/ICSMC.2006.385185

[11] D. Bosio, B. Littlewood, L. Strigini and M. J. Newby,

“Advantages of Open Source Processes for Reliability:

Clarifying the Issues,” Proceedings of the Open Source

Software Development Workshop, Newcastle, 25-26

February 2002, pp. 30-46.

[12] F. Zou and J. Davis, “Analyzing and Modeling Open

Source Software Bug Report Data,” Proceedings of the

19th Australian Conference on Software Engineering,

Washington, D.C., 26-28 March 2008, pp. 461-469.

[13] T. Matsumoto, “Implementations of Bayesian Learning

(in Japanese),” Journal of the Institute of Electronics, In-

formation and Communication Engineers, Vol. 92, No.

10, 2009, pp. 853-860.

[14] B. P. Carlin and S. Chib, “Bayesian Model Choice via

Markov Chain Monte Carlo,” Journal of Royal Statistical

Society: Series B (Methodological), Vol. 57, No. 3, 1995,

pp. 473-484.

[15] P. J. Green, “Reversible Jump Markov Chain Monte

Carlo Computation and Bayesian Model Determination,”

Journal of Biometrika, Vol. 82, No. 4, 1995, pp. 711-732.

doi:10.1093/biomet/82.4.711

[16] The Apache HTTP Serve r Projec t, “The Apac he Software

Foundation,” 2010. http://httpd.apache.org/