Int’l J. of Communications, Network and System Sciences, 2011, 4, 372-376
doi:10.4236/ijcns.2011.46043 Published Online June 2011 (http://www.SciRP.org/journal/ijcns)
Low Complexity Discrete Bit-Loading for OFDM Systems
with Application in Power Line Communications
Khalifa S. Al-Mawali, Amin Z. Sadik, Zahir M. Hussain
School of Electrical and Computer Engineering, RMIT University, Melbourne, Australia
Received January 27, 2011; revised February 19, 2011; accepted March 14, 2011
Abstract
Adaptive bit-loading algorithms can improve the performance of OFDM systems significantly. The tradeoff
between the performance of the algorithm and its computational complexity is essential for the implementa-
tion of loading algorithms. In this paper, we present a low complexity non-iterative discrete bit-loading algo-
rithm to maximize the data rate subject to specified target BER and uniform power allocation. Simulation
results show that the proposed algorithm outperforms the equal-BER loading and achieves similar rates to
incremental allocation, yet with much lower complexity.
Keywords: Bit-Loading, OFDM, Power Line Communications
1. Introduction
Power Line Communication (PLC) technology has re-
ceived a great amount of research interest in the last
decade. This technology exploits the already existing and
ubiquitous power line distribution infrastructure to pro-
vide a broadband multimedia connectivity solution to
and within the home or office. Orthogonal Frequency
Division Multiplexing (OFDM) has been a major candi-
date for PLC systems as well as many other broadband
communication systems. This is mainly due to its robust-
ness to multipath, selective fading and different kinds of
interference. Examples of its applications include Digital
Audio Broadcasting (DAB), Terrestrial digital TV
(DVB-T), wireless LANs and Wi-Max.
In a conventional OFDM system, all subcarriers use a
fixed constellation size. Therefore, their overall error
probability is dominated by the subcarriers that have the
worst signal-to-noise ratios (SNR). When channel state
information is available, the performance of OFDM can
be significantly improved by using adaptive modulation
[1]. In adaptive modulation, different parameters including
data rate, transmit power, instantaneous bit-error-rate
(BER), constellation size and channel code or scheme
can be adjusted according to the subchannel fading con-
ditions.
Several bit/power loading algorithm can be found in
the literature [2-15]. Most of these algorithms can be
classified, based on their objective function, into two
categories: margin-adaptive (MA) algorithms (e.g. [7-9])
that strive to minimize the transmitted power subject to
data rate and BER constraints, and rate-adaptive (RA)
algorithms (e.g. [10-14] that strive to maximize the data
rate subject to power and BER constraints. In addition,
some algorithms that have different objectives can also
be found in the literature. For example, the algorithm
proposed by Goldfeld et al. [12] is aimed at minimizing
the probability of error. In all these algorithms, there is
generally a tradeoff between the algorithm performance
and the computational complexity. Optimum bit/power
loading can be achieved by the well-known water-filling
approach. Some loading algorithms can also achieve
near-optimal solutions using incremental allocation (e.g.
[11-14]). However, the cost in terms of computational
complexity associated with both approaches is excessive.
To reduce the complexity of bit allocation, closed-form
expressions for BER or channel capacity approximations
can be exploited. This method, however, requires round-
ing of the constellation size to integer numbers, hence
deviates the allocation from optimality. Wyglinski et al.
[11] proposed an optimum bit-loading with reduced
complexity. However, the method is still rather co mputa-
tionally complex especially when the number of subcar-
riers is large, because it includes an extra iterative algo-
rithm to find the initial p eak BER in addition to th e main
algorithm.
In this paper, we attempt to solve the rate maximiza-
tion problem with target overall BER constraint and uni-

K. S. AL-MAWALI ET AL.
373
form power allocation. A simple discrete bit-loading
algorithm that approaches the maxi mum t hro ughpu t with
minimal complexity is presented. The algorithm per-
formance is verified in a widely-accepted power line
channel model [16].
2. Adaptive Bit Loading
2.1. Problem Formulation
The proposed loading algorithm aims to solve the fol-
lowing rate-adaptive problem given a target mean BER
PT and a fixed energy distribution across all the subcar-
riers:
Maximize subject to
1
N
i
i
b

1
1
N
ii
i
T
N
i
i
bP
P
b




P
(1)
where i and i are the number of bits and BER of
the ith subcarrier respectively. N and
b P
P are the number
of used subcarriers and their mean BER respectively. As
in other studies, it is assumed that perfect knowledge of
the channel gains is available to both the transmitter and
the receiver.
Different loading algorithms trying to solve this prob-
lem have been discussed in the previous section. These
algorithms, however, are either too complex or do not
achieve maximum throughput.
2.2. Proposed Loading Algorithm
The BER of square MQAM with Gray bit mapping can
be approximated [1]:
1.6
0.2exp, 1,2,,
21
i
i
ib
Pi


 


 N
(2)
where 2
2
pH
i
i
i
i


is the ith subchannel SNR, with ,
i
P
i
H
and 2
i

being the signal power, channel gain and
noise power of the ith subcarrier respectively. Accord-
ingly, the number of bits that can be carried in subchan-
nel i is given b y:
2
log1, 1,2,,
i
i
i
bi


 


 N (3)
where i is the SNR gap representing how far the sys-
tem is from achieving capacity and can be defined from
(2) and (3) as:


ln 5, 1,2,,
1.6
i
i
Pi 
 N (4)
The average number of bits per subcarrier in one
OFDM symbol can then be written as:


2
1
2
11
2
1.6 1
log1ln(5 )
1.6 1
= ()log1ln 5
1.6
=log1
ln 5
N
i
ii
N N
i
iii
mc
bNP
NP
P









 
 























 (5)
where mc

is the multichannel SNR which characterizes
the set of N subchannels by an equivalent single AWGN
that achieves the same data rate with the same error
probability [17]. Figure 1 illustrates the concept of the
multichannel SNR. From (5), the multichannel SNR can
be defined by:


(1 )
1
ln 51.6
11
1.6ln 5
N
N
ii
mc
ii
P
P






 



 






 


 (6)
The proposed algorithm initially computes for each
subcarrier the maximum number of bits i that gives a
value of i below T. The resulting overall BER
b
P P
Pwill generally be below T by a large margin. To
exploit this margin, the algorithm then computes the
number of extra bits that can be added to the OFDM
symbol without violating the BER constraint T.The
extra bits are added to the subcarriers that will have the
minimum effect in the overall BER. This is done by
evaluating
P
P
P

for each subcarrier where

iii i
PbP P

 

(7)
and i
P

is the BER of the ith subchannel when the con-
stellation size is shifted to the immediately higher con-
stellation.
The proposed algorithm takes the following steps:
1) Given SNR values i

, find the largest signal con-
stellation for each subcarrier for which is below
. i
bi P
T
P2) Calculate the current values of band P and com-
Figure 1. The conceprt of the multichannel SNR [17].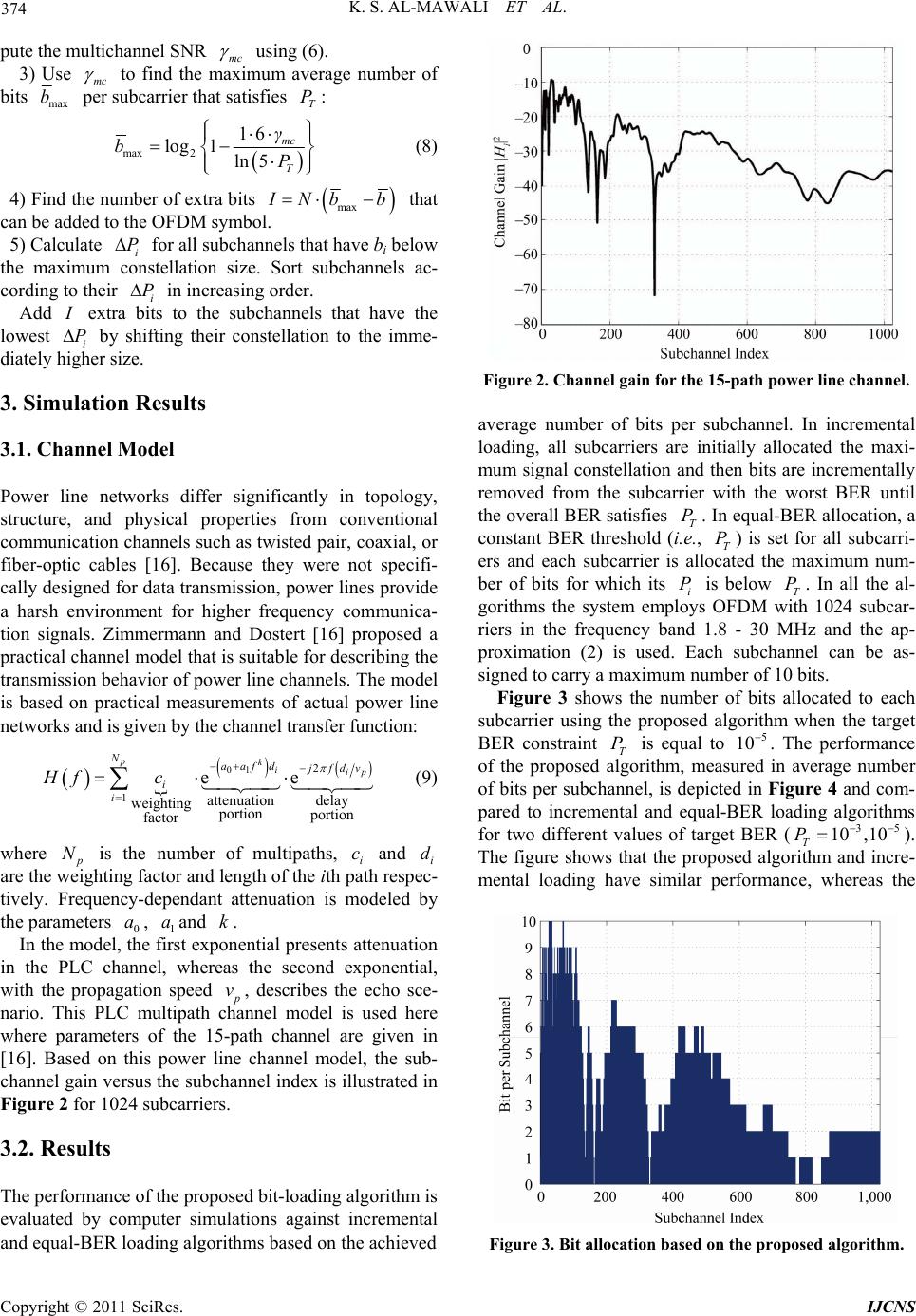

374 K. S. AL-MAWALI ET AL.
pute the multichannel SNR mc

using (6).
3) Use mc

to find the maximum average number of
bits max
b per subcarrier that satisfies :
T
P

max 2
16
log1 ln5
mc
T
γ
bP










(8)
4) Find the number of extra bits

max
I
Nb b that
can be added to the OFDM symbol.
5) Calculate i for all subchannels that have bi below
the maximum constellation size. Sort subchannels ac-
cording to their in increasing order.
P
i
Add P
I
extra bits to the subchannels that have the
lowest i by shifting their constellation to the imme-
diately higher size.
P
3. Simulation Results
3.1. Channel Model
Power line networks differ significantly in topology,
structure, and physical properties from conventional
communication channels such as twisted pair, coaxial, or
fiber-optic cables [16]. Because they were not specifi-
cally designed for data transmission, power lines provide
a harsh environment for higher frequency communica-
tion signals. Zimmermann and Dostert [16] proposed a
practical channel model th at is suitable for describing the
transmission behavior of power line channels. The model
is based on practical measurements of actual power line
networks and is given by the channel transfer function:


  01 2
1attenuation delay
weighting portionportion
factor
ee
pkiip
Naafd

j
fd v
i
i
Hf c

 


 (9)
N
where
p
is the number of multipaths, i c and i
are the weighting factor and length of the ith path respec-
tively. Frequency-dependant attenuation is modeled by
the parameters , and .
d
0 1
In the model, the first exponential pr esents attenuation
in the PLC channel, whereas the second exponential,
with the propagation speed
a ak
p
v, describes the echo sce-
nario. This PLC multipath channel model is used here
where parameters of the 15-path channel are given in
[16]. Based on this power line channel model, the sub-
channel gain versus the sub channel index is illustrated in
Figure 2 for 1024 subcarriers.
3.2. Results
Figure 2. Channel gain for the 15-path power line channel.
average number of bits per subchannel. In incremental
loading, all subcarriers are initially allocated the maxi-
mum signal constellation and then bits are incrementally
removed from the subcarrier with the worst BER until
the overall BER satisfies T. In equal-BER allocation, a
constant BER threshold (i.e., T) is set for all subcarri-
ers and each subcarrier is allocated the maximum num-
ber of bits for which its i is below T. In all the al-
gorithms the system employs OFDM with 1024 subcar-
riers in the frequency band 1.8 - 30 MHz and the ap-
proximation (2) is used. Each subchannel can be as-
signed to carry a maximum number of 10 bits.
P
P
P
P
Figure 3 shows the number of bits allocated to each
subcarrier using the proposed algorithm when the target
BER constraint T is equal to . The performance
of the proposed algorithm, measured in average number
of bits per subchannel, is depicted in Figure 4 and com-
pared to incremental and equal-BER loading algorithms
for two different values of target BER (
P5 10
35
10 ,10
T
P


).
The figure shows that the proposed algorithm and incre-
mental loading have similar performance, whereas the
The performance of the proposed bit-loading algorithm is
evaluated by computer simulations against incremental
and equal-BER loading algorithms based on the achieved Figure 3. Bit allocation based on the proposed algorithm.

K. S. AL-MAWALI ET AL.
375
Figure 4. Performance of the proposed loading algorithm as
compared to incremental and default loading methods in
the 15-path power line channel.
Table1. Mean Computation times (ms) for different values
of SNR (CPU: Intel(R) Core(TM)2 Duo 3 GHz ).
SNR Values
Algorithm 40 dB 50 dB 60 dB 70 dB
Incremental 2.80 2.90 3.30 3.10
Equal-BER 0.30 0.33 0.38 0.40
Proposed 0.60 0.65 0.74 0.76
equal-BER loading achieves lower rates. To compare
the computational complexity of these algorithms, the
computation time (in milli-seconds) taken by each algo-
rithm to reach the final allocation is measured. To insure
fairness, each of those algorithms was implemented us-
ing Matlab and executed 100 times in the same work-
station.
Table 1 illustrates the mean computation times for a
1024-subcarrier OFDM system with T of P5
10

for
different values of SNR. It should be noted that the pro-
posed algorithm is non-iterative, which results in a sig-
nificant reduction in algorithm computational co m- plex-
ity as compared to the iterative incremental loading. Al-
though the computation time of the proposed algorithm
is less than a quarter of that of the incremental loading,
both of these algorithms have indistinguishable per-
formances in terms of average number of bits per sub-
channel. The proposed method tak e s about twice the time
taken by the equal-BER to reach the final allocation.
However, it achieves a considerable improvement of
more than 300 bits per OFDM symbol over the equal-
BER loading method.
4. Conclusions
This paper presents a simple non-iterative discrete
bit-loading algorithm striving to maximize the data rate
subject to target BER constraint and uniform power dis-
tribution. The algorithm was tested in a practically-
proven power line communication channel model using
computer simulations. Results show that the proposed
algorithm improves the data rates achieved by the
equal-BER loading with a small cost in complexity.
When compared to the incremental loading, the proposed
algorithm achieves similar rates, but with much lowers
computational complexity.
5. References
[1] S. T. Chung and A. J. Goldsmith, “Degrees of Freedom in
Adaptive Modulation: A Unified View,” IEEE Trans-
actions on Communications, Vol. 49, No. 9, 2001, pp.
1561-1571. doi:10.1109/26.950343
[2] P. S. Chow, J. M. Cioffi and J. A. C. Bingham, “A Prac-
tical Discrete Multitone Transceiver Loading Algorithm
for Data Transmission over Spectrally Shaped Channels,”
IEEE Transactions on Communications, Vol. 43, No. 234,
2002, pp. 773-775.
[3] Y. George and O. Amrani, “Bit Loading Algorithms for
OFDM,” Proceedings of the International Symposium on
Information Theory (ISIT 2004), Chicago, 2 July 2004, p.
391. doi:10.1109/ISIT.2004.1365428
[4] D. Daly, C. Heneghan and A. D. Fagan, “Power- and
Bit-Loading Algorithms for Multitone System,” Pro-
ceedings of the 3rd International Symposium on Image
and Signal Processing and Analysis, Rome, 18-20 Sep-
tember 2003, pp. 639-644.
doi:10.1109/ISPA.2003.1296355
[5] H. Rohling and C. Fellenberg, “Successive Bit Loading
Scheme,” Electronics Letters, Vol. 45, No. 1, 2009, pp.
214-216. doi:10.1049/el:20093315
[6] E. Guerrini, L. Guerrieri, D. Veronesi, P. Bisaglia and R.
Cappelletti, “LLR-Based Bit Loading Algorithm and its
Applications to HomPlug AV over OPERA Power-Line
Channels with Impulsive Noise,” Journal of Communica-
tions, Vol. 4, No. 7, 2009, pp. 454-462.
[7] S. Nader-Esfahani and M. Afrasiabi, “Simple Bit Loading
Algorithm for OFDM-Based Systems,” IET Communica-
tions, Vol. 1, No. 3, 2007, pp. 312-316.
[8] K. Lui, B. Tang and Y. Lui, “Adaptive Power Loading
Based on Unequal-BER Strategy for OFDM Systems,”
IEEE Communications Letters, Vol. 13, No. 7, 2009, pp.
474-476. doi:10.1109/LCOMM.2009.082158
[9] K. S. Al-Mawali, F. S. Al-Qahani and Z. M. Hussain,
“Adaptive Power Loading for OFDM-Based Power Line
Communications Impaired by Impulsive Noise,” Pro-
ceedings of the IEEE International Symposium on Power
Line Communications and its Applications (IEEE ISPLC
2010), Rio de Janeiro, 28-31 March 2010, pp. 78-182.
doi:10.1109/ISPLC.2010.5479924
[10] A. Leke and J. M. Cioffi, “A Maximum Rate Loading
Algorithm for Discrete Multitone Modulation Systems,”
Proceedings of IEEE GLOBECOM’97, Phoenix, 3-8 No-
vember 1997, pp. 1514-1518.
doi:10.1109/GLOCOM.1997.644387

K. S. AL-MAWALI ET AL.
376
[11] A. M. Wyglinski, F. Lebeau and P. Kabal, “Bit Loading
with BER-Constraint for Multicarrier Systems,” IEEE
Transactions on Wireless Communications, Vol. 4, No. 4,
2005, pp. 1383-1387. doi:10.1109/TWC.2005.850313
[12] L. Goldfeld, V. Lyandres and D. Wulich, “Minimum
BER Power Loading for OFDM in Fading Channel,”
IEEE Transactions on Communications, Vol. 50, No. 11,
2002, pp. 1729-1733.
doi:10.1109/TCOMM.2002.805271
[13] A. M. Wyglinski, F. Labeau and P. Kabal, “An Efficient
Bit Allocation Algorithm for Multicarrier Modulation,”
Proceedings of the 2004 IEEE Wireless Communications
and Networking Conference (IEEE WCNC 2004), Atlanta,
21-25 March 2004, pp. 1194-1199.
doi:10.1109/WCNC.2004.1311358
[14] D. Hugh-Hartog, “Ensemble Modem Structure for Im-
perfect Transmission Media,” U.S. Patent No. 4,679,227
(July 1987), 4,731,816 (March 1988) and 4,833,706 (May
1989).
[15] J. S. Chow, J. C. Tu and J. M. Cioffi, “A Discrete Multi-
tone Transceiver System for HDSL Applications,” IEEE
Journal on Selected Areas in Communications, Vol. 9,
No. 6, 1991, pp. 895-908. doi:10.1109/49.93100
[16] M. Zimmermann and K. Dostert, “A Multipath Model for
the Powerline Channel,” IEEE Transactions on Commu-
nications, Vol. 50, No. 4, 2002, pp. 553-559.
doi:10.1109/26.996069
[17] J. M. Cioffi, “Chapter 4: Multi-Channel Modulation,”
Stanford University website.
http://www.stanford.edu/group/cioffi/book/chap4.pdf [09
Jan. 2011]