Wireless Sensor Network, 2009, 2, 61-121
doi:10.4236/wsn.2009.12015 Published Online July 2009 (h ttp://www.SciRP.org/journal/wsn/).
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
Recurrent Polynomial Neural Networks for Enhancing
Performance of GPS in Electric Systems
Mohammad Reza MOSAVI
Associate Professor, Department of Electrical Engineering,
Iran University of Science and Technology, Narmak, Iran
Received April 2, 2009; revised April 28, 2009; accepted April 30, 2009
Abstract
Global Positioning System (GPS) is a worldwide satellite system that provides navigation, positioning, and
timing for both military and civilian applications. GPS based time reference provides inexpensive but
highly-accurate timing and synchronization capability and meets requirements in power system fault location,
monitoring, and control. In the present era of restructuring and modernization of electric power utilities, the
applications of GIS/GPS technology in power industry are growing and covering several technical and man-
agement activities. Because of GPS receiver’s error sources are time variant, it is necessary to remove the
GPS measurement noise. This paper presents novel recurrent neural networks called the Recurrent Pi-Sigma
Neural Network (RPSNN) and Recurrent Sigma-Pi Neural Network (RSPNN). The proposed NNs have been
used as predictor in GPS receivers timing errors. The NNs were trained using the dynamic Back Propagation
(BP) algorithm. The actual data collection was used to test the performance of the proposed NNs. The ex-
perimental results obtained from a Coarse Acquisition (C/A)-code single-frequency GPS receiver strongly
support the potential of the method using RPSNN to give high accurate timing. The GPS timing RMS error
reduces from 200 to less than 40 nanoseconds.
Keywords: Accurate Timing, GPS, Electric Systems, Neural Networks
1. Introduction
Most descriptions of Global Positioning System (GPS)
focus on its use as a system to provide precise latitude,
longitude and altitude information. Often it is used to
determine speed as well. GPS is depicted as a dynamic
positioning system which provides the raw information
needed to navigate, that is, to find where we are and to
figure how to get from there to some desired place (or,
perhaps, to avoid some undesired place). This is a fun-
damental use for GPS but it is far from the only use of
the system [1].
Continuous access to precise time and frequency, at
low cost and anywhere it is needed, is a revolutionary
development. It allows, for example, improved synchro-
nization and timing of both wired and wireless commu-
nications systems. Users see higher quality (fewer
dropped calls), increased capacity (no delays getting on ),
improved data transmission (low error rates) and new
services (lifetime phone number). Or, consider timing
electrical transients arriving at substations in a geo-
graphically dispersed power delivery system. A fault (a
downed line, for instance) can be precisely located and
crews can be transported to the precise geographic spot
without delay. Similar statements can be made for
wide-area computer networks. GPS allows precise trans-
fer of time between the world’s timing centers ensuring
we all tick on the same clock. In general, wide availabil-
ity of precise time and frequency at low cost will im-
prove many scientific, manufacturing, business, R&D
and just plain fun activities [2,3].
* Tehran 16846-13114
Tel.: [phone]
,
3
,
Fax.: [phone]. GPS provides services for two levels of users. These

M. R. MOSAVI
96
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
are referred to as the Standard Positioning Service (SPS)
and th e Precise Positioning Service (PPS). The latter is
reserved, almost entirely, for the exclusive use of the
DoD. The U.S. DoD states very clearly in the Federal
Radio navigation Plan (FRP) what SPS and PPS provide:
(1) SPS is a positioning and timing serv ice which will be
available to all GPS users on a continuous, worldwide
basis with no direct charge. SPS will be provided on the
GPS L1 frequency which contains a Coarse Acquisition
(C/A) code and a navigation data message. SPS is
planned to provide, on a daily basis, the capability to
obtain timing accuracy within 340nsec (95 percent
probability). The GPS L1 frequency also contains a Pre-
cision (P) code that is reserved for military use and is not
a part of the SPS. Although available during GPS con-
stellation build-up, the P code will be altered without
notice and will not be available to us ers that do not have
valid cryptographic keys. (2) PPS is a highly accurate
military positioning, velocity, and timing service which
will be available on a continuous, worldwide basis to
users authorized by the DoD. PPS will be the data trans-
mitted on GPS L1 and L2 frequencies. PPS was designed
primarily for U.S. military use and will be denied to un-
authorized users by use of cryptography. PPS will be
made available to U.S. Federal and Allied Government
(civilian and military) users through special agreements
with the DoD. Limited, non-Federal Government, civil-
ian use of PPS, both domestic and foreign, will be con-
sidered upon request and authorized on a case-by-case
basis. PPS has timing accuracy with 200nsec [4,5].
For effective use of GPS timing information in power
systems, it is essential to model and predict these errors.
The better the prediction, the smaller the error values
become. Hence, the efficiency of the predictive system
depends highly on the predictor. Linear predictors have
been widely used because of their simple implementation.
In this case, the predicted value is the linear combination
of the previous data elements. Nonlinear predictors pro-
vide better results than the lin ear predicto r; howeve r their
use is limited due to the mathematical complexity of
such predictor structures. NNs provide an alternative to
this problem. The nonlinear nature and the simplicity of
the learning algorithm of the NNs attracted many re-
searchers to use NNs as predictors for GPS receivers
timing errors [6]. This paper is organized as follows.
Section 2 presents GPS applications in power systems.
The proposed prediction methods using Recurrent
Pi-Sigma Neural Network (RPSNN) and Recurrent
Sigma-Pi Neural Network (RSPNN) are described in
Section 3. In Section 4, the experimental tests results are
reported with collected real data. Conclusions are pre-
sented in Section 5.
2. Precise Timing Applications in Power
Systems
Precise timing in power systems is one of the key tech-
nologies that will enable the dev elopment of new control
systems and the monitoring required to maintain them.
Some of these areas of potential development are de-
scribed in the following paragraphs [7-10].
2.1. GPS Traveling Wave Fault Locator
Systems
An important monitoring device is a fault locator. A
short circuit or fault usually can be cleared by momen-
tarily disconnecting the line. Occasionally equipment is
damaged and repair is required. Automatic fault location
is much faster and cheaper than patrolling the entire lin e.
When a line fault occu rs, such as and insulator flashover
or fallen conductor, the abrupt change in voltage at the
point of the fault generates a high frequency electro-
magnetic impulse called a traveling wave which propa-
gates along the line in both directions away from the
fault point at velocities close to that of light (The veloc-
ity is determined by th e distributed parameters of the line
and it varies in the range 295-296m/µs). The fault loca-
tion is determined by accurately time-tagging the arrival
of the traveling wave at each end of the line, and com-
paring the related time difference to the total
propagation time of the line Tp. The equation for calcu-
lating the distance L1 between the fault and the nearest
terminal is as follows [10]:
T
10.5()
p
p
L
LTT
T

(1)
where L is total length of the line. Precise detection of
the arrival time of the traveling wave is critical to the
accuracy of the fault locator. A specially developed Fault
Transient Interface Unit (FTIU) is used for this purpose.
This device couples to the transmission lines by tapping
off an inductive drain coil that is connected in series to
the ground lead of a capacitive voltage transformer. The
FTIU discriminates for a valid traveling wave by meas-
uring the rise time and amplitude of the incoming signal.
A signal whose rise time falls within two predetermined
values (0.7-8.3µs, which corresponds to frequencies in
the range 30-350KHz) and is of sufficient amplitude is
considered to be a valid traveling wave and will cause
the FTIU to produce a trigger pulse that is coincident
with the leading edge of the detected trav eling wave. The
trigger pulse is fed to a GPS time code receiver which
then timestamps the arrival of the traveling wave. The
design goal of the fault location system is an accuracy of
±300 meters (one tower span) which translates to a
time-tagging accuracy of better than 1µs (assuming that
the velocity of the traveling wave is about 300m/µs).
GPS receivers easily fulfill this requirement by providing
a timestamp to within ±0.3µs of Universal Coordinate
Time (UTC).

M. R. MOSAVI
97
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
The marriage of a stable atomic clock and GPS satel-
lite constellation makes possible an instru ment with great
accuracy and stability. It is possible to discipline a local
clock with clocks of greater accuracy resident in the GPS
satellite resulting in both short term and long accuracy
improvements. The timing generator is a very stable and
accurate instrument that has been designed to produce an
accurate time standard with an absolute time accuracy of
±200nsec [11]. It has the capability of maintaining this
accuracy for 24 hours after the total loss of the GPS sig-
nal. Each GPS satellite contains four stable atomic clocks
that are traceable to the National Institute of Standards
and Technology (NIST). There are two cesium beam
clocks and two rubidium clocks aboard each satellite. It
is these atomic clocks which give the GPS satellite the
accuracy to be used as a continual calibration source for
the timing generator rubidium clock.
2.2. Sources of Synchronization
Synchronization signal could be distributed over any of
the traditional communication media currently in use in
power systems. Most communication systems, such as
leased lines, microwave, or AM radio broadcasts, place a
limit on the achievable accuracy of synchronization,
which is too coarse to be of practical use. Fiberoptic
links, where available, could be used to provide high
precision synchronization signals, if a dedicated fiber is
available for this purpose. If a multiplexed fiber channel
is used, synchronization errors of the order of 100 mi-
croseconds are possible, and are not acceptable for power
system measurements. GOES satellite systems have also
been used for synchronization purposes, but their per-
formance is not sufficiently accurate.
The technique of choice at present is the Navstar GPS
satellite transmissions. This systems is designed primar-
ily for navigational purposes, but it furnishes a com-
mon-access timing pulse, which is accurate to within 1
microsecond at any location on earth. The system uses
transmissions from a constellation of satellites in nonsta-
tionary orbits at about 10,000 miles above the earth’s
surface. For accurate acquisition of the timing pulse,
only one of the satellites need be visible to the antenna.
The antenna is small (about the size of a water pitcher),
and can be easily mounted on roof of a substation control
house. The experience with the availability and depend-
ability of the GPS satellite transmission has been excep-
tionally good .
2.3. Phasor Measuring Units
Phasor Measuring Units (PMUs) using synchronization
signals from the GPS satellite system have evolved into
mature tools and are now being manufactured commer-
cially. The GPS receiver provides the 1 Pulse-Per-Second
(PPS) signal, and a time tag, which consist of the year,
day, hour, minute, and second. The time could be the
local time, or the Universal Time Coordinated (UTC).
The 1-PPS signal is usually divided by a phase-locked
oscillator into the required number of pulses per second
for sampling of the analog signals. In most systems being
used at present, this is 12 times per cycle of the funda-
mental frequency. The analog signals are derived from
the voltage and current transformer secondaries, with
appropriate anti-aliasing and su rge filtering.
The microprocessor determines the positive sequence
phasors according to the recursive algorithm described
previously, and the timing message from the GPS, along
with the sample number at the beginning of a window, is
assigned to the phasor as its identifying tag. The com-
puted string of phasors, one for each of the positive se-
quence measurements, is assembled in a message stream
to be communicated to a remote site. The messages are
transmitted over a dedicated communication line through
the modems. A 4800-baud communication line can sup-
port the transmission of the phasor stream at the rate of
about every 2-5 cycles of the fundamental frequency,
depending upon th e number of p ositive sequence p hasors
being transmitted.
2.4. State Estimation
Modern electric utility centers use state estimators to
monitor the state of the power system. The state estima-
tor uses various measurements (such as complex powers
and voltage and current magnitudes) received from dif-
ferent substations, and, through an iterative nonlinear
estimation procedure, calculates the power system state.
The sate (vector) is a collection of all the positive se-
quence voltage phasors of network, and, from the time
the first measurement is taken to the time when the state
estimate is available, several seconds or minutes may
have elapsed. Because of the time skew in the data ac-
quisition process, as well as the time it takes to converge
to a state estimate, the available state vector is at best an
averaged quasi-steady-state description of the power
system. Consequently, the state estimators available in
present-day control centers are restricted to steady-state
applications only.
Now, consider the positive sequence voltages meas-
ured by the synchronized phasor measurement units. If
voltages at all system substations are measured, one
would have a true simultaneous measurement of the
power system state. No estimation of the state vector is
necessary. From a practical point of view, it is sensible to
use the positive sequence currents also, which provide
data redundancy. This leads to a linear estimator of the
power system state, which uses both current and voltage
measurements. The estimate results from the multiplica-
tion, of a constant matrix by the measurement vector, and
is extremely fast.
In addition to a much simplified static state estimator,
synchronized phasor measurements also provide the first

M. R. MOSAVI
98
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
real possibility of providing a dynamic state estimator.
By maintaining a continuous stream of phasor data from
the substations to the control center, a state vector that
can follow the system dynamics can be constructed. With
normal dedicated communication circuits operating at
4800 or 9600 baud, a continuous data stream of one
phasor measurement every 2-5 cycles (33.3-83.33msec)
can be sustained. Considering that the usual power sys-
tem dynamic phenomena fall in the range of 0-2Hz, it is
possible to observe in real-time the power system dy-
namic phenomena with high fidelity at the center.
Another application of directly measured dynamic
phenomena is to validate power system models used in
transient stability studies. For the first time in history,
synchronized phasor measurements have made possible
the direct observation of system oscillations following
system disturbances. By trying to simulate these events,
one can learn a great deal about the models of major
system components, and correct them as needed until the
simulations and observed phenomena match well.
2.5. Improved Control
Power system control elements, such as generation exci-
tation systems, HVDC terminals, variable series capaci-
tors, SVCs, etc., use local feedback to achieve the control
objective. However, often the control objective may be
defined in terms of a remote occurrence. As an example,
consider the task of damping power swings between two
areas by controlling (modulating) the flow on a dc line.
Such a controller must have a built-in mathematical de-
scription (model), which must relate the dc power to the
angle between the two regions. To the extent that the
assumed model is not valid under the prevailing system
conditions, the controller do es not do the job for which it
was intended.
With synchronized phasor measurements being
brought to the controller location, it becomes possible to
provide direct feed-back from the angular difference
between the two systems. Studies of this nature have
shown that improved control performance is achieved
when a model-based controller is replaced by one based
upon feedba ck provided b y the phasor measurement sys-
tem.
2.6. Quasi-Traveling Wave Schemes
Quasi-traveling wave schemes compare only the relative
phase of the charge in impedance at the inception of fault
at the local end with a signal representing the relative
change at the remote end. When a fault occurs, the in-
stantaneous voltage will usually fall and the instantane-
ous current will rise; either quantity may be positive or
negative at that time. The relative change between the
two represents the ch ange in impedance and the direction
of the fault. The relay is triggered by a rate of change in
the voltage and current and sends a directional signal.
Trip decision times are short but must allow for trans-
mission time of the carrier system, relative end-to-end
phasing of the voltage/current is not normally critical.
3. GPS Receivers Timing Errors Modeling
Using Neural Network
The NN concept is used in forecasting, by considering
historical data to be the input to a black box, which con-
tains hidden layers of neurons. These neurons compare
and structure the inputs and known outputs by nonlinear
weightings, which are determin ed by a continuous learn-
ing process (Back-Propagation (BP)). The learning proc-
ess continues until forecast outputs are reasonably close
to known actual outputs. The structure of the black box is
then used for forecasting actual future outputs. For time
series forecasting the inputs are the past observations of
the data series and the output is the future value. The
GPS receiver’s time errors ()
x
t
t
is difference between
the two sequence time at time , i.e., () ()
x
tUTODt

-(1)UTOD t

[12]. The NNs estimate ()
x
t at future
time 1t

.
3.1. Modeling Using Recurrent Pi-Sigma Neural
Network
Similarly to feed-forward PSNN, the RPSNN consists of
three layers, the input layer, the summing units layer and
the output layer. In the output layer, the NN calculates
the product of the we ighted sum of the inputs and passes
the result to a nonlinear transfer function. Then the out-
put of the network is fed back to the inputs. Th e NN has
a regular structure and requires a smaller number of
weights than conventional single-layers, High-Order
Neural Networks (HONNs). The weights from the sum-
ming units to the product unit are fixed at unity, which
implies that the summing units layer is not hidden. The
adoption of the smaller number of weights results in
faster training. The order of the NN corresponds to the
number of

units connected to the unit. Figure 1
shows the architecture of the proposed RPSNN.

Let the number of external inputs to the NN to be
2
M

and the number of outputs to be 1. Let (1)yn

be the output of the network at time and 1n()
j
x
n
be the jth

input to the NN at time n. The overall
inputs to the NN are the concatenation of ()
x
n and
and is referred to as : ()yn ()zn
();1
() 1;1
() ;2
j
j
x
nj
znj M
ynjM


M





(2)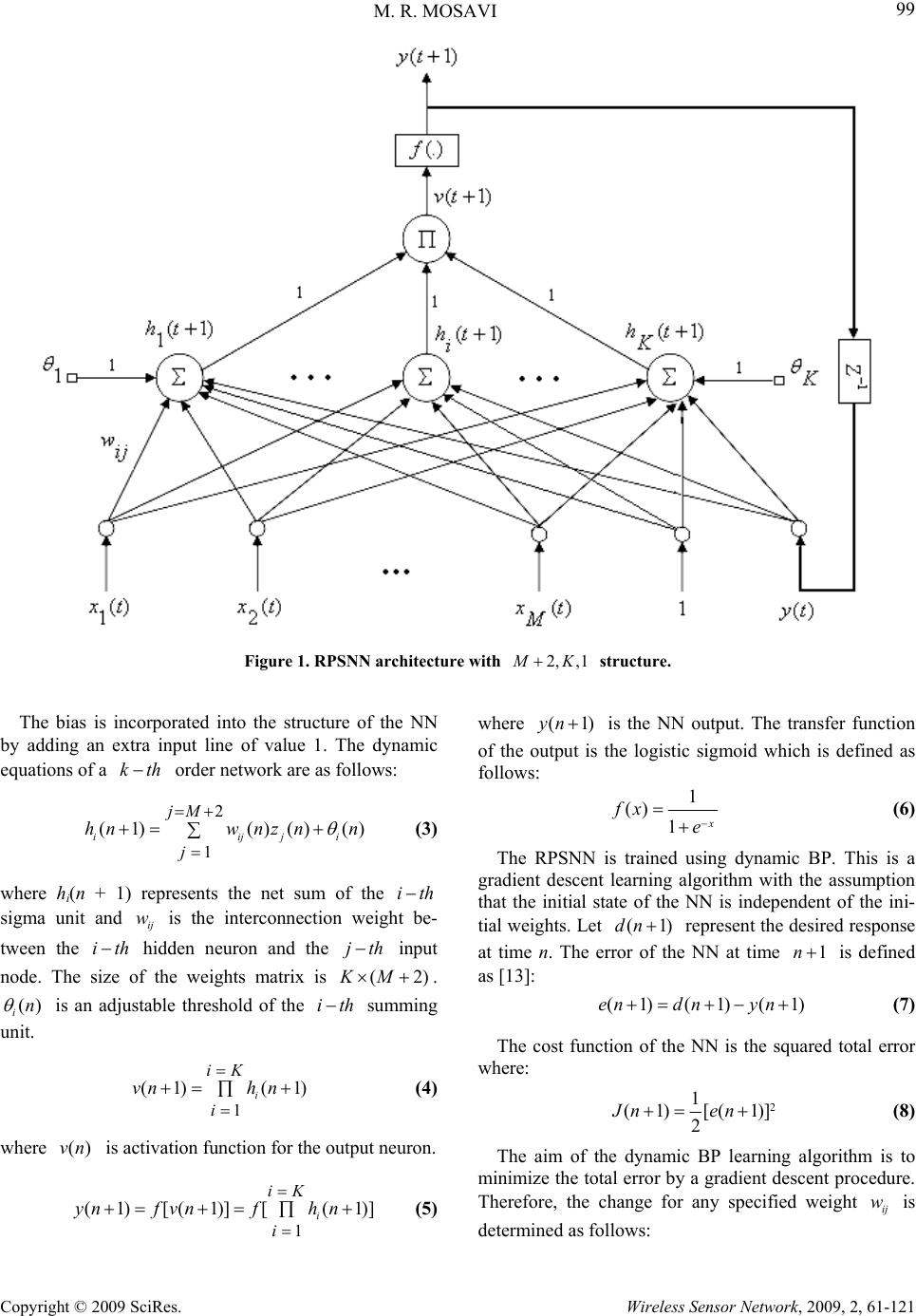

M. R. MOSAVI
99
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
Figure 1. RPSNN architecture with 2, ,1
M
K

structure.
The bias is incorporated into the structure of the NN
by adding an extra input line of value 1. The dynamic
equations of a order network are as follows: kth
where (1)yn

is the NN output. The transfer function
of the output is the logistic sigmoid which is defined as
follows: 1
() 1
x
fx e  (6)
2
1
(1)()() (
iijj
jM
j
hnw nznn 


 
)
i
(3)
The RPSNN is trained using dynamic BP. This is a
gradient descent learning algorithm with the assumption
that the initial state of the NN is independent of the ini-
tial weights. Let (1)dn

represent the desired response
at time n. The error of the NN at time is defined
as [13]: 1n
where hi(n + 1) represents the net sum of the ith

sigma unit and is the interconnection weight be-
tween the hidden neuron and the input
node. The size of the weights matrix is .
ij
w
hitjth
KM
(2)
()
in

is an adjustable threshold of the summing
unit.
ith(1) (1)(1endnyn )

 (7)
The cost function of the NN is the squared total error
where:
1
(1) (1
i
iK
i
vnh n


 
)
]
(4) 2
1
(1) [(1)]
2
Jn en (8)
where is activation function for the output neuron. ()vn The aim of the dynamic BP learning algorithm is to
minimize the total error by a gradient descent procedure.
Therefore, the change for any specified weight is
determined as follows:
ij
w
1
(1)[(1)] [(1)
i
iK
i
ynfvnfhn



 (5)

M. R. MOSAVI
100
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
(1)
(1) (
ij ij
ij
Jn
wn wn
w



) (9)
where

is a positive real number representing the
learning rate and

is the momentum term.
(1) (1)(1)
(1) (1)
ij ijij
Jn enyn
en en
ww
 
 
 w
(10)
In this case, (1)
ij
yn
w

 is found by usin g the chain rule:
(1) (1) (1)
.
(1)i
ij iij
hn yn yn
whnw
  


(11)
By differentiating the dynamic equations of the NN,
(1)
(1)
i
yn
hn


can be obtained as follows:
11;#
(1) '[(1)].[(
(1) ll
i
lK lK
llli
yn fhn hn
hn


 1)]



 (12)
and the value (1)
i
ij
hn
w


 is calculated as follows:
()
2
(1) ()
ijij
ij
yn
iM w
hn zn w
w




 (13)
Let (1)
(1)
ij
ij
yn
Pn w


 , then weights updating rule is:
(1) (1)(1)(
ijij ij
wnen Pnwn)



  (14)
With:
()
2
11;#
'
(1) [(1)].[(1)].[()
ijll j
lK lKPn
iM ij
llli
Pnfhnhnznw



 
 ] (15)
where '(.)
f
is the derivative of the nonlinear transfer
function and is determined as follows:
'()()[1 ()]
f
xfx fx (16)
The change for any specified weight i

is determined
using BP learning algorithm as follows:
(1)
(1) (
ii
i
Jn
nn  



)
 (17)
where (1)
i
Jn


 is obtained as:
(1) (1)
(1)
(1)
(1)
i
i
Jn en
en
yn
en


 



 
(1)
i
yn



 is found by using the chain rule:
(1)
(1) (1)
.
(1)i
ii i
hn
yn yn
hn


 


(19)
The value (1)
i
i
hn



 is calculated as follows:
()
2
(1)
1
i
i
yn
iM i
hn w






 (20)
Let (1)
(1)
i
i
yn
Qn



 , then weights updating rule
is:
(1) (1)(1)()
ii
nenQn i n



  (21)
i
(18)
With:
()
2
'
(1) [(1)].[(1)].[1
11;#
illQn
i
iM
lK lK
Qn fhnhnw
llli 

 

 ]
(22)
3.2. Modeling Using Recurrent Sigma-Pi Neural
Network
The architecture of a RSPNN with 2
M
 inputs and
one output is shown in Figure 2. In this network, hidden
layer neurons output is the product of the input terms and
the network output is the sum of these products. It also
has a single layer of adaptive weights in the second layer.
The RSPNN learning procedure using the BP method
can be summarized as follows: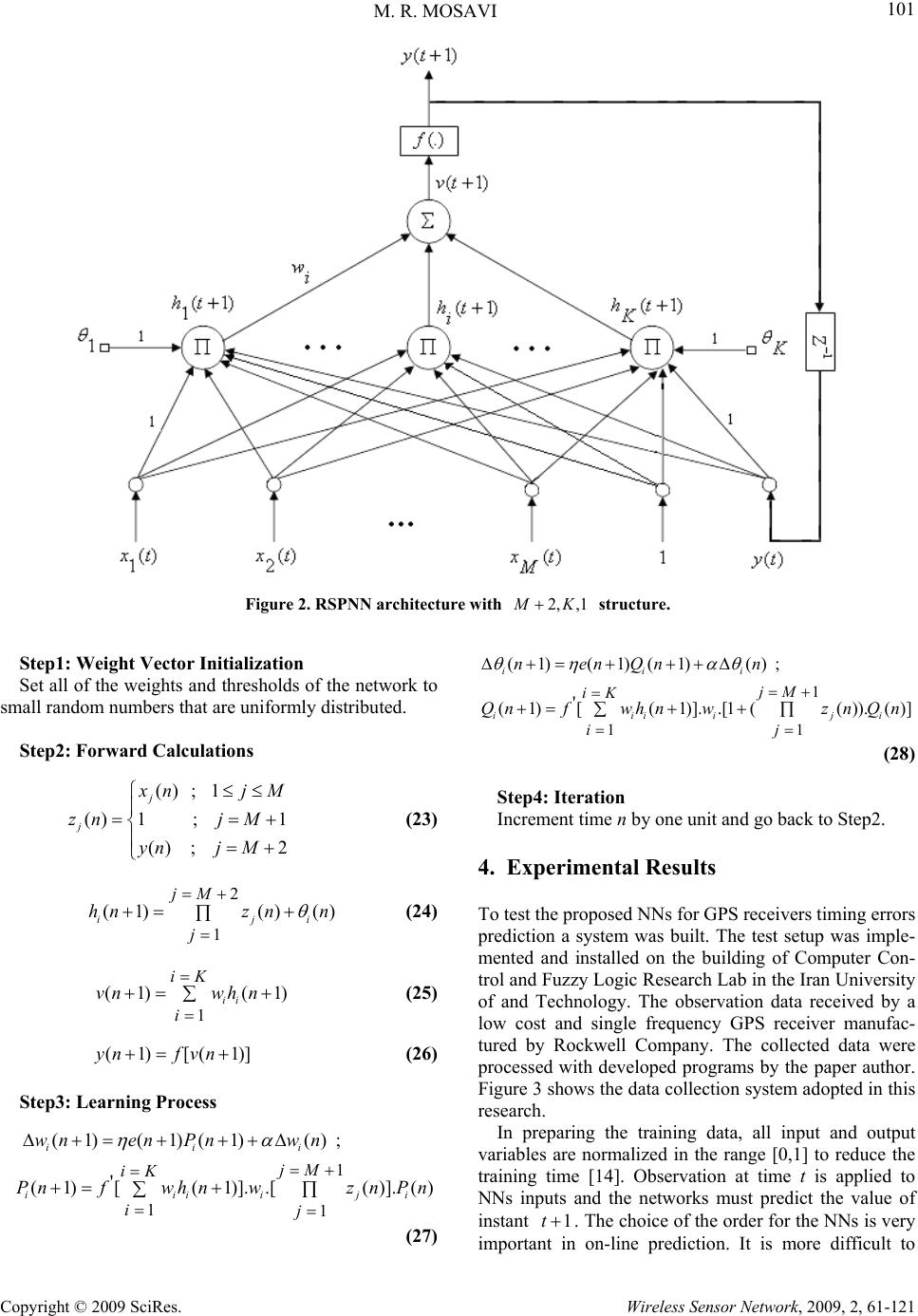

M. R. MOSAVI
101
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
Figure 2. RSPNN architecture with 2, ,1
M
K

structure.
Step1: Weight Vector Initialization
Set all of the weights and thresholds of the network to
small random numbers that are uniformly distributed.
Step2: Forward Calculations
();1
() 1;1
() ;2
j
j
x
nj
znj M
ynjM






M




(23)
2
1
(1)() (
ij
jM
j
hnznn 


 
)
i
]
;
i
(24)
1
(1) (1)
ii
iK
i
vnwh n


 
 (25)
(1) [(1)yn fvn (26)
Step3: Learning Process
(1) (1)(1)()
ii
wnen Pnwn

  
1
11
'
(1) [(1)]..[()].()
iiiij
jM
iK
ij
PnfwhnwznPn



 
i
i
(27)
1
11
(1)(1)(1)();
'
(1)[(1)]..[1(()).()]
iii
iiiij
jM
iK
ij
nenQnn
Qnfwhnwz nQn






 
 

(28)
Step4: Iteration
Increment time n by one unit and go back to Step2.
4. Experimental Results
To test the proposed NNs for G PS r e c e iv ers timing erro rs
prediction a system was built. The test setup was imple-
mented and installed on the building of Computer Con-
trol and Fuzzy Logic Research Lab in the Iran University
of and Technology. The observation data received by a
low cost and single frequency GPS receiver manufac-
tured by Rockwell Company. The collected data were
processed with developed programs by the paper author.
Figure 3 shows the data collection system adopted in th is
research.
In preparing the training data, all input and output
variables are normalized in the range [0,1] to reduce the
training time [14]. Observation at time t is applied to
NNs inputs and the networks must predict the value of
instant 1t

. The choice of the order for the NNs is very
important in on-line prediction. It is more difficult to

M. R. MOSAVI
102
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
formulate the order of a nonlinear model. In this paper,
the order selection is based on the experimental results.
For optimizing NNs structure, various combinations of
input variables were tried. The proposed methods were
implemented and developed by author of this paper using
Microsoft Visual Basic6. These models were validated
using a set of data points.
The RPSNN and RSPNN benefit from both the ad-
vantages of feed-forward HONNs and RNNs. The in-
corporation of higher order terms allows the networks to
make use of nonlinear interactions between the inputs,
thus functionally expanding the input space into a
higher-dimensional space, where linear separability, or
reduction in the dimension of the nonlinearity is possible.
Furthermore, the adaptation of the small number of
weights allows the NNs to be trained faster than HONNs
which suffer from the combinational explosion of the
high-order terms and demonstrate slow learning, when
the order of the NNs becomes excessively high. In con-
trast to fully RNNs that are trained using the RTRL algo-
rithm, the small structure of the RPSNN and RSPNN
accelerates the learning of the NNs using the dynamic
BP.
To evaluate the performance of the presented training
algorithms, they were tested by collected data sets. Six
statistical measures (maximum, minimum, RMS, average,
variance, standard deviation), are used to evaluate pre-
diction results. Table 1 presents statistical measures on
500 test data by using the proposed NNs. In order to
evaluate the prediction accuracy, we used RMS as a
measure of closeness between predicted and observed
values [15]. From Table 1 can be seen that time accuracy
has improved by factor of about 5.
Table 2 shows the comparison of test results of differ-
ent models for GPS timing errors pr ediction. The simula-
tion results demonstrated that RPSNN and RSPNN are
efficient than PSNN,RNN and SPNN,RNN, respectively.
5. Conclusions
Accurate timing using GPS can revolutionize the field of
monitoring, protection, and control of power systems. It
is with great excitement that we look for other applica-
tions, not yet thought of, that can advance the state of the
art in electric power engineering. The past few years
have witnessed increasing interest in synchronized accu-
rate timing and how they may be used for various power
system applications. The development of new types of
computer-based hardware and the completion of the GPS
of satellites provide the components needed for true
synchronized monitoring systems. GPS time synchroni-
zation enables the accurate time tag of each recorded
data sample to better than 1 microsecond accuracy. In
this paper, a RPSNN and RSPNN were implemented and
used as predictor in GPS system. The proposed NNs
were trained using the dynamic BP, which is a gradient
descent learning algorithm. The actual data collection
was used to train the networks. The trained weights of
the NNs were fixed and used to predict GPS receivers
timing errors. Extensive tests have shown that third order
NNs provide the most promising results. The tests results
using the RPSNN predictor have shown an improvement
in the GPS timing accuracy over the linear predictor,
multilayer perceptorns, HONN s, RNNs. The GPS timing
RMS error reduced from 200 to less than 40 nanosec-
onds.
Figure 3. Data collection and processing system.

M. R. MOSAVI
103
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 2, 61-121
Table 1. Performance evaluation of the proposed NNs.
Parameters
Error Values [nsec]
(using RPSNN with
(3,3,1) Structure)
Error Values [nsec]
(using RSPNN with (3,4,1)
Structure)
Max 90.364 101.643
Min -41.784 -20.944
Average -0.224 0.836
Variance 3.137 3.870
Standard Deviation 1.771 1.967
RMS 39.562 43.955
Table 2. Comparison of test results of different models for GPS timing errors prediction.
Model Name RMS
RNN 57.2
PSNN 45.8
RPSNN 39.6
SPNN 50.0
RSPNN 43.9
6. References
[1] K. D. McDonald, “The modernization of GPS: Plans,
new capabilities, and the future relationship to Galileo,”
Journal of Global Positioning System, Vol. 1, No. 1, pp.
1–17, 2002.
[2] W. Lewandowski, J. Azoubib, and W. J. Klepczynski,
“GPS: Primary tool for time transfer,” Proceedings of the
IEEE, Vol. 87, No. 1, pp. 163–172, January 1999.
[3] T. E. Parker and D. Matsakis, “Time and frequency dis-
semination advances in GPS transfer techniques,” GPS
World Magazine, pp. 32–38, November 2004.
[4] K. Mohammadi and M. H. Refan, “A new method for
improving of GPS receivers time accuracy using Kalman
filter,” Journal of Engineering Science, Iran University of
Science and Technology, Vol. 13, No. 1, pp. 11–24,
2002.
[5] M. R. Mosavi, “GPS receivers timing data processing
using neural networks: Optimal estimation and errors
modeling,” Journal of Neural Systems, Vol. 17, No. 5, pp.
383–393, October 2007.
[6] A. J. Hussain and P. Liatsis, “A new recurrent polynomial
neural network for predictive image coding,” IEEE Con-
ference on Image Processing and its Applications, Vol. 1,
No. 465, pp. 82–86, 1999.
[7] K. E. Martin, “Precise timing in electric power systems,”
IEEE Conference on Frequency Control, pp. 15–22, 1993.
[8] A. G. Phadke, “Synchronized phasor measurements in
power systems,” IEEE Computer Applications in Power,
pp. 11–15, April 1993.
[9] M. A. Street, I. P. Thurein, and K. E. Martin, “Global
positioning system applications for enhancing the per-
formance of large power systems,” CIGRE, pp. 1–6, 1994.
[10] H. Lee and A. M. Mousa, “GPS traveling wave fault lo-
cator systems: Investigation into the anomalous meas-
urements related to lighting strikes,” IEEE Transactions
on Power Delivery, Vol. 11, No. 3, pp. 1214–1223, 1996.
[11] M. R. Mosavi, “Modeling of GPS SPS timing error using
multilayered neural network,” IEEE Conference on Sig-
nal Processing, China, November 16–19, 2006.
[12] M. R. Mosavi, “Real time prediction of GPS receivers
timing errors using parallel-structure neural networks,”
Journal of Geoinformatics, Vol. 3, No. 3, pp. 53–61, Sep-
tember 2007.
[13] M. R. Mosavi, “A practical approach for accurate posi-
tioning with L1 GPS receivers using neural networks,”
Journal of Intelligent and Fuzzy Systems, Vol. 17, No. 2,
pp. 159–171, March 2006.
[14] M. R. Mosavi, “Precise real-time positioning with a low
cost GPS engine using neural networks,” Jour nal of Su rvey
Review, Vol. 39, No. 306, pp. 316–327, October 2007.
[15] M. R. Mosavi, “Comparing DGPS correction prediction
using neural network, fuzzy neural network, and Kalman
filter,” Journal of GPS Solutions, Vol. 10, No. 2, pp.
97–107, May 2006.