Intelligent Control and Automation, 2011, 2, 86-94
doi:10.4236/ica.2011.22010 Published Online May 2011 (http://www.SciRP.org/journal/ica)
An Efficient and Cost-Saving Component Scheduling
Algorithm Using High Speed Turret Type Machines for a
Board Containing Multiple PCBs
Wei-Shung Chang, Chiuh-Cheng Chyu
Department of In d ust ri al Engineering and Man a gement, Yuan-Ze University, Chinese Taipei
Received January 6, 2011; revised March 28, 2011; accepted April 2, 2011
Abstract
This paper considers a material constrained component scheduling problem during the high speed surface
mount manufacturing stage in printed circuit board (PCB) assembly, where each piece of board contains an
even number of identical PCBs. To accomplish the production, material requirements must be predetermined
and incorporated as restraints into the scheduling problem, which has the objective of minimizing production
completion time (makespan). A solution procedure is developed based on the following strategies: 1) Each
machine is responsible for the same PCBs of each piece, 2) Components of the same types may use one or
more feeder locations, 3) Component types are clustered based on their suitable placement speeds, 4) A heu-
ristic using a bottom-up approach is applied to determine the component placement sequence and the feeder
location assignment for all machines. Velocity estimate functions of the turret, XY table, and feeder carriage
were derived based on empirical data. An experiment using Fuji CP732E machines was conducted on two
real life instances. Experimental results indicate that our method performs 32.96% and 10.60% better than
the Fuji-CP software for the two instances, in terms of the makespan per piece of board.
Keywords: Printed Circuit Boards Assembly, Surface Mount Technology, Heuristics, Component Placement
Sequence, Feeder Location Assignment
1. Introduction
In printed circuit board (PCB) assembly, surface mount
technology (SMT) is extens ively used to popu late boards
with electronic components. The tools implementing
SMT are generally called surface mount device (SMD)
placement machines. Based on specifications and opera-
tional methods, the SMD are classified into five categories
[1]: dual-delivery, multi-station, turret-type, multi-head
and sequential pick-and-place. High-speed chip place-
ment machines belong to th e turret-type.
In many SMT assembly lines, the SMD processing is
most likely the bottlen eck of production , especially wh en
the number of components on a PCB is large, or when a
piece of board contains several identical PCBs. The most
prevalent analytical approach is to hierarchically de-
compose the problem into a number of more easily
manageable subproblems, and solve each subproblem
one at a time. The solution to the global problem can
then be obtained by integrating the subproblems’ solu-
tions. Several researchers [1] presented similar hierar-
chical classification schemes for the task. Their classifi-
cation is based on the number of machines (one or many)
and the number of board types (one or many) present in
the problem. This paper studies the component place-
ment problem using turret style surface mount placement
machines for PCBs; the problem becomes increasingly
complicated when greater operational efficiency is re-
quired. This problem usually consists of the feeder loca-
tion assignment (FLA), component placement sequence
(CPS), and component retrieval problem (CRP) [2]. The
CRP permits a component type to use more than one
feeder slot, and a retrieval plan must be determined for
such component types before production.
There have been many studies on the component
placement problem using turret style surface mount ma-
chines. Crama et al. [3] and Ohno et al. [4] studied the
CPS problem during PCB assembly on a variety of PCB
types in demand. Klomp et al. [5] extended the study of
Crama [3] and developed a heuristic algorithm which

W.-S. CHANG ET AL.87
focused on the feeder arrangement problem. Their com-
putational results indicate that a retrieval plan may
merely increase inventory cost but not decrease cycle
time. The algorithm by Crama [3] and Klomp [5] is
based on the strategy of determining FLA first and CPS
next. Under this strategy, an estimation procedure was
developed to assess and improve the quality of an FLA
solution. Ellis et al. [6] solved the same case by deter-
mining CPS first and FLA next. Ong et al. [7], Wu and Ji
[8], Chyu and Chang [9] applied the genetic algo rithm to
solve the CPS and FLA prob lems simultaneously on one
machine and one board type case. Kumar and Luo [10]
presented a different approach to optimize the operation
sequence using a generalized-TSP model on the same
problem. Moon [11] proposed 5-in-1 and 3-in-1 working
group assembly methods to solve CPS and FLA prob-
lems simultaneously. His computational results indicate
that the 5-in-1 procedure performs better in the sin-
gle-layered board case, while the 3-in-1 procedure is
more effective for the multiple-layered board. Knuutila
et al. [12], Narayanaswami and Iyengar [13], Salonen et
al. [14] and Jeong [15] presented several grouping PCB
assembly jobs strategies for PCB setup time reduction.
This research was motivated during a consultation
with a PCB manufacturer. One problem often encoun-
tered during PCB assembly is that using leftover com-
ponents will increase the frequency of discontinuing
production process, but disposing them will incur mate-
rial waste cost. Thus, there is a conflict between produc-
tion efficiency and material cost saving. A two-phase
solution procedure is proposed: Phase 1 aims to carefully
plan the material requirements for production scheduling,
and Phase 2 searches for a near optimal solution accord-
ing to Phase 1 results. Phase 2 is a multi-start heuristic
based on the bottom-up strategy, i.e., using CPS first and
FLA second, to solve component scheduling prob lems.
This paper uses Fuji CP 732E machines for the study
example. All relevant information, including th e data for
deriving estimation functions and two real life instances,
was obtained via assistance from the manufacturer.
The remainder of the paper is organized as follows:
Section 2 describes the problem; Section 3 presents the
algorithms; Section 4 presents and discusses the experi-
mental results of the algorithms; Section 5 concludes the
paper.
2. Problem Description
A turret style surface mount placement machine, Fuji CP
732E as shown in Figure 1, consists of th ree elements: a
X-Y table, a feeder rack, and a turret. The X-Y table can
move simultaneously in horizontal direction as well as in
vertical direction with a PCB on it. The feeder rack con-
sists of the so-called slots. A feeder stores components of
a single type and is attached to a slot to the rack. The
turret transports components from the rack to the board.
Throughout this paper, the term feeder carriage and
feeder rack are used interchangeably.
Figure 1 illustrates the operation manner of the ma-
chine. The turret moves clockwise and has 16 placing
heads positioned evenly apart in a circular manner. The
head of the turret at the position of grip station retrieves a
component from a feeder attached in a pre-specified slot
on the feeder rack, while the head of the turret at the
placement station simultaneously mounts a component at
a pre-specified location on the PCB. It should be noted
that the component gripping sequence and the compo-
nent placement sequence are the same but the former is
eight ahead of the latter. The first eight turret rotations
only pick up components, and the movement time for
each pickup is the greater time value between the rota-
tion of turret station and the corresponding shift of the
feeder carriage. On the other hand, the last 8 movements
are only for placing components on the PCB and the
movement time is the maximum value of X-Y table
moving time and turret rotation time. As for the turret
rotations in between, the movement time is the maximum
time value of all three mechanism movements.
Because the PCB table can move both in the vertical
and horizontal axes simultaneously, the distance measure
between two components on the board is a Chebychev
metric, i.e.,


max ,
ijij
x
xyy, where ,
ij
x
x are
the x-coordinates and are the y-coordinates of
components i and j, respective l y.
,
ij
yy
The velocity of the turret has multiple settings. In
general, the velocity setup is between 30% and 100%.
Components of larger size or heavier weight require a
slower velocity to achieve placement accuracy. In practice,
Figure 1. Fuji CP 732E machine.

W.-S. CHANG ET AL. 88
one commonly used feeder arrangement policy is to as-
sign full velocity to the smaller sized component
typeswith a large population. For any velocity setting,
the average velocity increases as the distance traveled
increases, although the relationship does not appear to be
linear. Larger or heavier components are more difficult
to be held accurately during turret rotations; thus, a
slower rotation rate is required for such co mponen ts. The
time for any single turret rotation is determined by the
component transported with the slowest rotation rate.
The machine will perform a grip and a placement opera-
tion at the same time after the three mechanisms com-
plete their individual movements.
In many cases, the production rate is higher when a
component type is allowed to use at least two feeder slots
(feeder duplication). In this situation, a decision so-called
the component retrieval problem occurs as to which
feeder slot should be used to handle the placement job of
each component that uses multiple feeder slots. Some
researchers address different a point of view for feeder
duplication based on inventory cost aspect, even though
the duplication can reduce the cycle time. Rosenblatt and
Lee [16] discussed the trade-off between inventory cost
and throughput rates of the two feeder slot alternatives.
Crama et al. [3] suggested that two feeder slots be used
while necessary. The experimental results in Klomp et al.
[5] indicate that there is no advantage in cycle time re-
duction with the use of feeder duplication.
The global problem with one or more machines can be
described as follows: Firstly, decide which component
types should use feeder duplications; secondly, deter-
mine the feeder location assignment (FLA) and CPS for
each machine. The CPS problem of a machine is a trav-
eling salesman problem (TSP) given an FLA to the ma-
chine. The global problem is NP-hard since its
sub-problem CPS in each machine is NP-hard. The ob-
jective of the problem is to find an FLA and its corre-
sponding CPS for each machine such that the production
time of each PCB is minimized.
The following are notations and decision variables
when a set of components has been assigned to a single
machine. This set can be a subset of components in a
PCB or all components in one PCB.
K: Total number of component types used in the set.
k: Component type index. k = 1,, K.
N: Total number of components in the set.
n: CPS index. n = 1,, N.
n
i
tp: The nth component in the CPS. ()
n
i
(): Component type index for component .
n
i
f
k: Feeder slot number for component type k.
()us: Time for feeder carriage to move s slots leftward
or rightward; .
(0) 0u
1
)
nn
i (,vi : Movement time of X-Y table from com-
ponents to
n
i1n i

.
[
n
trt i] : Turret rotation time for component .
n
i
   




   
 





1
1
1
11
9
87
7
1
7
Max ,Max
,
Max,
Max(, ,
nn q
qn
n
Nnn
n
qnn
nqn
Nqnn
nqN
nN
ftp iftp itrti
uftpif tpi
trtivii
trtiv ii










8



Max
Max
u










(1)
In the case where two or more identical PCBs are as-
signed to one machine, the same FLA will be used. The
machine will process these PCBs one by one using this
FLA alternatively forwards and backwards. The turret
speed changes from fast to slow when processing a PCB
with a forward FLA, and from slow to fast when proc-
essing one with a backward FLA. In general, there is
little difference in processing time between a PCB with
forward FLA and a PCB with a backward FLA, but the
time that the machine needs to move to the start position
of the next PCB needs to be counted.
3. Estimating Velocity Functions
In order to evaluate the performance of our proposed
algorithms, experiments were conducted to develop the
velocity estimate functions of the turret, XY table, and
feeder carriage for the Fuji CP 732E machine. In the ex-
periment for estimating the velocity function of the
feeder carriage, three trials are devised for measuring the
movement speed on each of the three distances, the 1, 3,
and 5 slot [17]. Each trial was performed 80 times back
and forth. The average value of the three trials for each
distance is used as the estimate of the velocity for that
distance. Table 1 displays the results of the experiment.
The average times for the three distances are approxi-
mately 0.1163, 0 .1738, an d 0.1888 second s, respectively.
Figure 2 shows the plot of the average movement times.
It should be noted that the velocity of the feeder carriage
is the slowest among the three mechanisms. Usually, the
production planner will schedule component placements
that require the feeder carriage to shift no more than five
slots in one movement.
Table 1. Experimental results of the feeder carriage move-
ment time (in seconds).
Distance Number of
Movements Movement Time Average Movement Time
1 slot 80 9.3 s. 0.1163 s.
3 slots 80 13.9 s. 0.1738 s.
5 slots 80 15.1 s. 0.1888 s.

W.-S. CHANG ET AL.89
Figure 2. Feeder carriage average movement time data plot.
Based on the data in Table 1, a plot for the feeder car-
riage average velocity ranging from one to five slots is
shown in Figure 2. An estimation formula for the veloc-
ity is given as follows.

0.02880.0875,for 13
0.00750.1513, for 35
f
xx
Vx xx






(2)
To determine the average velocity of the tu rret rotatio n
including pick and place, an experiment was conducted
and the results are shown in Table 2. This experiment
includes eight different turret rotation rate setups, from
the slowest speed of 30% to the full speed of 100%. For
each rate setup experiment, three trials of 80 consecutive
rotations are performed and the average of the three
movement times is taken as the estimate. The experi-
mental results are shown in Table 2 and the velocity plot
is presented in Figure 3.
4. Problem Solving Procedure
This paper focuses on the component scheduling prob-
lem that arises in the high speed surface mount manu-
facturing s t ag e of PCB assembly, where each board piece
contains an even number of identical PCBs and the pro-
duction stage may involve more than one machine. It is
thus reasonable to assume that the number of machines
used in the production line should be a number divisible
by the PCBs in the board. For example, if a board piece
contains two identical PCBs, then the number of ma-
chines can be one or two.
The proposed solution procedure aims to minimize the
production completion time (makespan), where the ma-
terial availability constraints are imposed for cost-saving
purposes. This solution procedure adopts the following
policies: 1) Have each machine be responsible for the
same number of PCBs of each piece, 2) Find the maxi-
mum number of feeder slots that a component type can
use for each machine and, allowing feeder duplications,
calculate all alternatives for the number of feeder slots
used for a machine, 3) Cluster the component types
based on their suitable placement speeds and then proc-
esses the groups one by one with speeds from high to
low, 4) Apply a multi-start local heuristic using nearest
Table 2. Experimental results on the velocity of the turret
rotation involving pick and placement.
Turret Rotation
Rate Setup No. of Rotations Total Time (s.) Average Velocity (rotations/s.)
100% 80 6 13.33
90% 80 7 11.43
80% 80 7 11.43
70% 80 8 10.00
60% 80 9.1 8.79
50% 80 11.1 7.21
40% 80 14 5.71
30% 80 18.1 4.42
Figure 3. XY-Table velocity.
neighbor search with 2-opt or 3-opt to determine the
component placement sequence and the feeder location
assignment for all machines.
When a machine is assigned to manufacture at least
two PCBs in a piece of a board, a promising solution
would be to apply the CPS in forward order on one PCB,
in reverse order on the next PCB, and so forth until all of
the PCBs for which this machine is responsible have
been completed. This strategy has been proven effective
and efficient in simulation and can be applied in practice.
4.1. Feeder Duplication
The use of feeder duplication is subject to two cond itions:
1) material availability and 2) production efficiency. A
feeder duplication of a component type should be used if
it can increase the production rate and enou gh quantity is
provided. In general, if components of a type are distrib-
uted in a scattered manner, then feeder duplication may
reduce the tardiness resulting from the XY table due to
long distance travels. The following discusses some ma-
terial restrictions imposed on the feeder duplication of a
component type:
The number of reels to produce the quantity of PCBs
in the requested order must be divisible by a prime num-
ber. For example, say, we have a PCB type that requires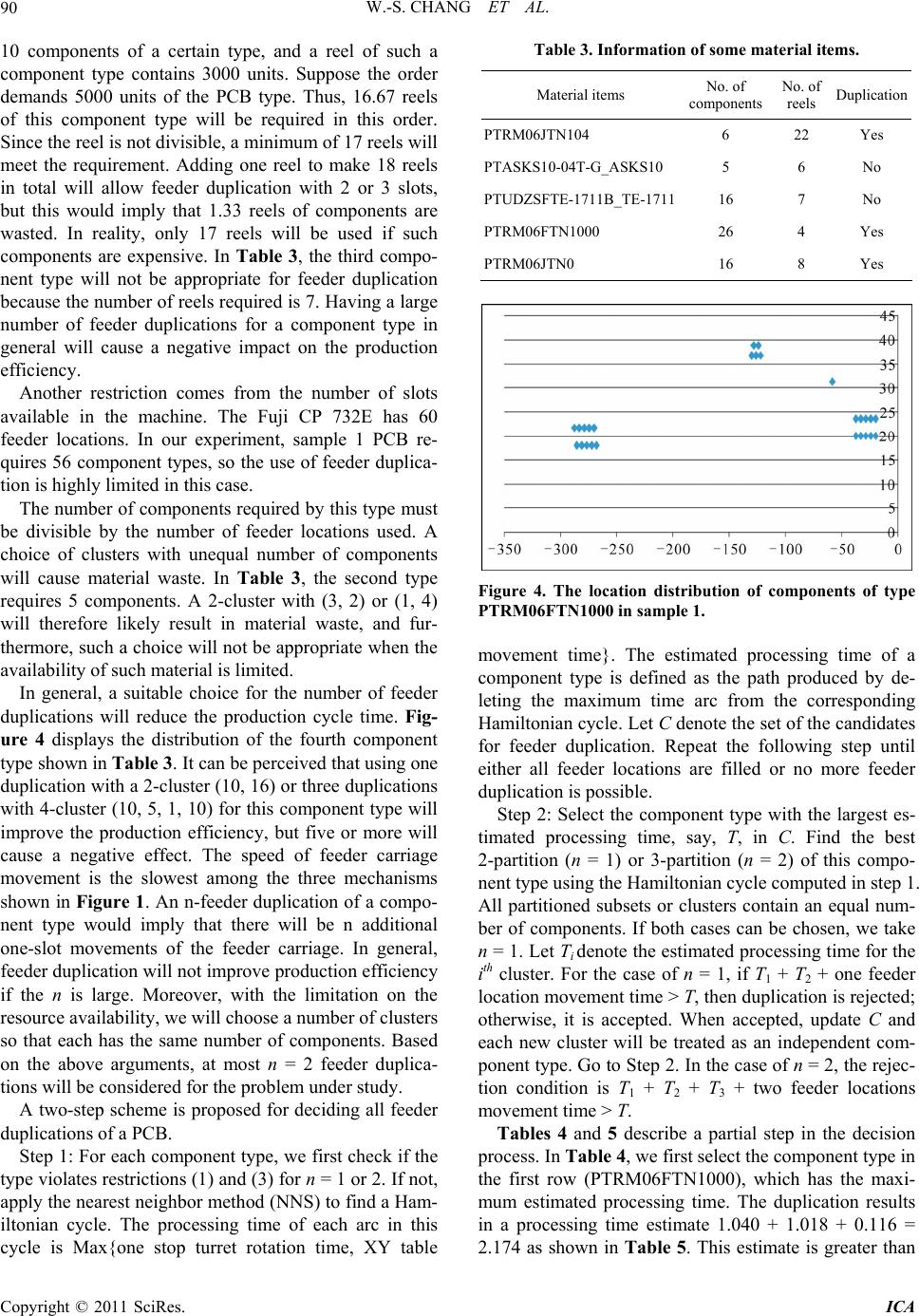

W.-S. CHANG ET AL. 90
10 components of a certain type, and a reel of such a
component type contains 3000 units. Suppose the order
demands 5000 units of the PCB type. Thus, 16.67 reels
of this component type will be required in this order.
Since the reel is not divisible, a minimum of 17 reels will
meet the requirement. Adding one reel to make 18 reels
in total will allow feeder duplication with 2 or 3 slots,
but this would imply that 1.33 reels of components are
wasted. In reality, only 17 reels will be used if such
components are expensive. In Table 3, the third compo-
nent type will not be appropriate for feeder duplication
because the number of reels required is 7. Having a large
number of feeder duplications for a component type in
general will cause a negative impact on the production
efficiency.
Another restriction comes from the number of slots
available in the machine. The Fuji CP 732E has 60
feeder locations. In our experiment, sample 1 PCB re-
quires 56 component types, so the use of feeder duplica-
tion is highly limited in this case.
The number of components required by this type must
be divisible by the number of feeder locations used. A
choice of clusters with unequal number of components
will cause material waste. In Table 3, the second type
requires 5 components. A 2-cluster with (3, 2) or (1, 4)
will therefore likely result in material waste, and fur-
thermore, such a choice will not be appropriate wh en the
availability of such material is limited.
In general, a suitable choice for the number of feeder
duplications will reduce the production cycle time. Fig-
ure 4 displays the distribution of the fourth component
type shown in Table 3. It can be perceived that using one
duplication with a 2-cluster (10, 16) or three duplications
with 4-cluster (10, 5, 1, 10) for this component type will
improve the production efficiency, but five or more will
cause a negative effect. The speed of feeder carriage
movement is the slowest among the three mechanisms
shown in Figure 1. An n-feeder duplicatio n of a compo-
nent type would imply that there will be n additional
one-slot movements of the feeder carriage. In general,
feeder duplication will not improve produ ction efficiency
if the n is large. Moreover, with the limitation on the
resource availability, we will choose a number of clusters
so that each has the same number of components. Based
on the above arguments, at most n = 2 feeder duplica-
tions will be considered for the problem under study.
A two-step scheme is proposed for deciding all feeder
duplications of a PCB.
Step 1: For each component type, we first check if the
type violates restriction s (1) and (3) for n = 1 or 2. If not,
apply the nearest neighbor method (NNS) to find a Ham-
iltonian cycle. The processing time of each arc in this
cycle is Max{one stop turret rotation time, XY table
Table 3. Information of some material items.
Material items No. of
components No. of reels Duplication
PTRM06JTN104 6 22 Yes
PTASKS10-04T-G_ASKS10 5 6 No
PTUDZSFTE-1711B_TE-171116 7 No
PTRM06FTN1000 26 4 Yes
PTRM06JTN0 16 8 Yes
Figure 4. The location distribution of components of type
PTRM06FTN1000 in sample 1.
movement time}. The estimated processing time of a
component type is defined as the path produced by de-
leting the maximum time arc from the corresponding
Hamiltonian cycle. Let C denote the set of the candidates
for feeder duplication. Repeat the following step until
either all feeder locations are filled or no more feeder
duplication is possible.
Step 2: Select the component type with the largest es-
timated processing time, say, T, in C. Find the best
2-partition (n = 1) or 3-partition (n = 2) of this compo-
nent type using the Hamiltonian cycle computed in step 1.
All partitioned subsets or clusters contain an equal num-
ber of components. If both cases can be chosen, we take
n = 1. Let Ti denote the estimated processing time for the
ith cluster. For the case of n = 1, if T1 + T2 + one feeder
location movement time > T, then duplication is rejected;
otherwise, it is accepted. When accepted, update C and
each new cluster will be treated as an independent com-
ponent type. Go to Step 2. In the case of n = 2, the rejec-
tion condition is T1 + T
2 + T3 + two feeder locations
movement time > T.
Tables 4 and 5 describe a partial step in the decision
process. In Table 4, we first select the component type in
the first row (PTRM06FTN1000), which has the maxi-
mum estimated processing time. The duplication results
in a processing time estimate 1.040 + 1.018 + 0.116 =
2.174 as shown in Table 5. This estimate is greater than

W.-S. CHANG ET AL.91
Table 4. Results of the movement time of each component
type in the duplication candidate set.
Material Items No. of
Components Moving Distance (mm) Processing Time (s)
PTRM06FTN1000 26 316.190 2.134a
PTRM06JTN0 16 115.540 1.194
PTRM06JTN104 6 85.960 0.478
PTKC20E1A106MTS 6 56.300 0.429
a: maximum processing t ime.
Table 5. Results of feeder duplications for the selected
component type.
Material Items No. of
Components Moving Distance (mm) Movement Time (s)
PTRM06FTN1000-A 13 137.000 1.040
PTRM06FTN1000-B 13 177.150 1.018
2.134. Thus this component type will be rejected for
feeder duplication. Then we continue on to process the
component type in the second row of Table 4.
4.2. Clustering Component Types
Component types using similar turret speed settings are
clustered into a group. Suppose that there are a total of M
groups, with group m using the mth velocity setting o f the
turret. The speed for the mechanism decreases as m in-
creases, which implies that larger and heavier compo-
nents will be processed with a slower velocity. The
grouping strategy is very time-saving since the turret
velocity will be decreasing in a stepwise manner instead
of having large variation of up-and-downs in the manu-
facturing process.
4.3. Multi-Start Bottom-up Strategy Heuristic
The bottom-up strategy for solving the component
scheduling problem is to find a CPS first while at the
same time determining the corresponding FLA. Under
this strategy, the components of the same type are treated
as an individual group. Then the nearest neighbor search
(NNS) is applied to each group to find the component
placement sequence of that group. In the process, the
choice of the next group is determined by the component
type that is not processed and has a component located
closest to the last component in the last group. Then a
local refinement is applied to improve the component
placement sequence of each group.
The following describes the problem solving proce-
dure, which consists of two ph ases.
4.3.1. Ph as e 1 : Preprocessing
Apply the two-step feeder duplication procedure de-
scribed in Section 4.1 and determine the set of compo-
nent types that will use feeder duplications. For each of
these component types, identify the components in each
subgroup. It should be noted that each subgroup will be
regarded as a different type, even though they are of the
same component type. Let

m be the set of component
types using a rotary tu rret with speed index m = 1,, M.
Feeder location has index r = 1, , R. 
4.3.2. Phase 2: Multi-Start Bottom-up Solution
Procedure
Process the groups of components { 
1,,

M} sequen-
tially. Start with 
1 and r = 1.
Step 1: Process components in 
1.
Step 1.1: Among all components in 
1, select a com-
ponent c1 that is closest to the origin. Starting with com-
ponent c1, compute the CPS for the remaining compo-
nents of type tp(c1) with the NNS method. We denote the
CPS for tp(c1) as CPS_1. Assign component type tp(c1)
to feeder location with index 1. Set r = 2;

1 =

1/tp(c1).
Step 1.2: Seek a component cr in

1, that is closest to
the last component of CPS_r-1. Compute the CPS for the
remaining components of tp(cr) using the NNS method.
Assign component type tp(cr) to feeder location r.

1 =

1/tp(cr). Set r = r + 1.
Step 1.3: If

1 =
 , set m = 2 and proceed to Step 2;
otherwise return to Step 1.2.
Step 2: First, find the component in

m that is closest
to the last component in the CPS for

m-1. Apply the
same procedure used in Steps 1.2 and 1.3 for

m, and
then repeat Step 2 until m = M.
Step 3: For each CPS_r, excluding the first and last
components, apply 2-opt for small-size groups (10
components) and 3-opt for medium to large-size groups
to make additional refinements. Output the final solution
after all the CPS_r have been refine d.
5. Experimental Result
In this section, the performance of the proposed algo-
rithm is tested via two PCB samples. Figure 5 displays
the configuration of sample 1, where each piece of board
contains two identical PCBs, one in the upper part and
the other in the lower part. On the other hand, sample 2
contains four identical PCBs as shown in Figure 6. Ta-
ble 6 presents some information about these two PCB
samples. In sample 1, each PCB has 56 component types
with a total of 175 components, and in sample 2, each
PCB contains 38 component types with a total of 124
components. The algorithm is coded in Microsoft Visual
C++ 6.0 and run on a PC with a 3.0 GHz Pentium IV

W.-S. CHANG ET AL. 92
Figure 5. A sample piece containing two identical PCBs.
Figure 6. A sample piece containing four ide ntic a l PCBs.
Table 6. Number of components and types in the sample
piece.
PCB board Length
(mm) Width (mm) Component Types per PCB Components in Total
Sample 1 351.5 93 56 350 (175 per PCB)
Sample 2 236 116.3 38 496 (124 per PCB)
processor and 1.0 GB DDR RAM. Experiments are con-
ducted with one and two Fuji CP732E placement ma-
chines with 60 feeder slots. The estimation functions for
the velocities of the feeder carriag e, turret, and X-Y table
presented in Section 3 will be used for calculating the
cycle times of both samples.
An experiment using these two sample pieces is con-
ducted in testing the performance of the proposed prob-
lem solving procedure described in Section 4.3. For ei-
ther PCB, the component types are classified into three
categories:

1,

2 and

3, where the components in

1,

2 and

3 are processed at 100%, 80%, and 50% of the
full turret rotation rate, respectively. In sample 1,

1
contains 46 types with a total of 151 components,

2
contains 9 types with a total of 23 components, and 
3
has only one component; In sample 2, 
1 contains 33
types with a total of 112 components, 
2 contains 3
types with a total of 11 components, and 
3 has only one
component.
The experiment contains two cases: one-machine and
two-machine. In the one-machine case, the cycle time of
a solution is measured by two methods and the deviation
is calculated. The two methods are as follows: 1) the
cycle time is calculated using the estimation functions
and 2) the solution is implemented on the machine using
the commercial software, Fuji-CP. The two-machine
case measures the cycle time by the proposed algorithm
using estimation functions, and by directly employing
the Fuji-CP software. The deviation between the two is
then calculated. The results indicate the algorithm out-
performs commercial Fuji-CP software in terms of cycle
time.
Table 7 presents the computationa l results of the algo-
rithm in the one-machine case for both samples based on
the estimation functions. In both samples, feeder dupli-
cation is not applied using the algorithm in Section 4.1.
Table 8 shows the cycle time deviations between com-
puter results and on-line implementation of the solutions
in Table 7. The cycle time deviation is defined as the
subtracted difference divided by the computer simulation
result. From Table 8, we observe that the deviations are
very small for both samples, 0.76% for sample 1 and
0.48% for sample 2. This shows that the computer simu-
lation results can be used to estimate solution perform-
ance for the two real life instances in the two-machine
case.
Both samples in the two-machine case are consecu-
tively solved three times by the multi-start algorithm, and
the average values are used for the further performance
estimation. Table 9 displays the computational results
based on the three runs. As we can perceive from this
table, the processing times are quite close for the ma-
chines, regardless of which sample. Thus, the algorithm
will provide workload-balancing solution. In addition,
small standard deviations indicate that the algorithm is
robust in finding near optimal solutions. Table 10 pro-
vides the estimated processing time for implementing
each sample onto each machine. The estimation is calcu-
lated by adding the deviation.
Table 11 presents the estimated improvements when
these solutions are implemented online. In the two-ma-
chine case, the cycle time of a sample is the maximum
value of the two machines’ processing times. Thus for
sample 1, the cycle time is max{25.10, 20.15} = 25.10
when Fuji-CP software is used and is max{16.827,
16.828} = 16.828 when the proposed algorithm is used,
which results in approximately (25.10 – 16.828)/25.10 =
32.96% improvement. For sample 2, there is an im-
provement of about 10.60%. The result indicates that the
algorithm yields a better production efficiency for a
Table 7. Computer results in single machine using the esti-
mation functions.
PCB Boards Cycle Time CPU Time
Sample 1 34.09 s. 1.963 s.
Sample 2 45.90 s. 1.872 s.

W.-S. CHANG ET AL. 93
Table 8. Deviation between the computer results and online implementations in single machine.
Sample 1 Sample 2
Simulation Implementation Deviation Simulation Implementation Deviation
34.09 s. 34.35 s. 0.76% 45.90 s. 46.12 s. 0.48%
Table 9. Computer results of the algorithm with two machines using the estimation formulae (three runs).
PCB Boards in Machine Minimum Cycle Time Average Cycle TimeStand Deviation Average CPU Time
Sample 1_M1 16.680 s. 16.700 s. 1.06% 12.336 s.
Sample 1_M2 16.681 s. 16.701 s. 1.11% 12.263 s.
Sample 2_M1 22.884 s. 22.913 s. 1.50% 15.234 s.
Sample 2_M2 22.912 s. 22.936 s. 1.54% 15.425 s.
Table 10. Estimation on the cycle times of both samples taking into account the deviation.
M1 M2
PCB Simulation Deviation Estimation Simulation Deviation Estimation
Sample 1 16.700 s. 0.76% 16.827 s. 16.701 s. 0.76 % 16.828 s.
Sample 2 22.913 s. 0.48% 23.023 s. 22.936 s. 0.48% 23.046 s.
Table 11. Estimated improvements for the computed solutions being implemented.
M1 M2
PCB Estimation Fuji-CP Reduction Estimation Fuji-CP Reduction
Sample 1 16.827 s. 25.10 s. 32.96% 16. 828 s . 20.15 s. 16.49%
Sample 2 23.023 s. 24.41 s. 5.68% 23.046 s. 25.78 s. 10.60%
board with anti-symmetrical configuration than a board
with side by side configuration. In contrast to the present
method, the Fuji-CP software adopts a different strategy
to process a piece of board containing several identical
PCBs. Instead of processing its assigned PCBs one at a
time, each machine processes all of its assigned PCBs at
the same time and place components across these PCBs.
6. Conclusions
Surface mount technology (SMT) has been widely used
in PCB assembly for years. In many SMT assembly lines,
high-speed chip placement machines are likely the bot-
tleneck of production. This paper considers a material
constrained component scheduling problem arising at the
high speed surface mount manufacturing stage in printed
circuit board (PCB) assembly, where each piece of board
contains an even number of identical PCBs. A solution
procedure to minimize the makespan was developed us-
ing a strategy which considers the possibility of feeder
duplication and clustering the component types accord-
ing to their suitable velocity setup on turret rotation, to-
gether with a multi-start local heuristic using nearest
neighbor search with 2-opt or 3-opt procedures im-
provement. Velocity estimation functions of the turret,
XY table, and feeder carriage were also derived based on
empirical data. Experiments with one and two Fuji
CP732E machines on two samples demonstrated that the
proposed solution procedure is more effective when
compared to the Fuji-CP software for these particular
instances.
7. References
[1] M. Ayob and G. Kendall, “A Survey of Surface Mount
Device Placement Machine Optimisation: Machine Clas-
sification,” European Journal of Operational Research,
Vol. 186, No. 3, 2008, pp. 893-914.
doi:10.1016/j.ejor.2007.03.042
[2] Y. Crama, O. E. Flippo, J. V. D. Klundert and F. C. R.
Spieksma, “The Component Retrieval Problem in Printed
Circuit Board Assembly,” International Journal of Flexi-

W.-S. CHANG ET AL. 94
ble Manufacturing Systems, Vol. 8, No. 4, 1996, pp.
287-312. doi:10.1007/BF00170016
[3] Y. Crama, O. E. Flippo, J. V. D. Klundert and F. C. R.
Spieksma, “The Assembly of Printed Circuit Boards: A
Case with Multiple Machines and Multiple Board
Types,” European Journal of Operational Research, Vol.
98, No. 3, 1997, pp. 457-472.
doi:10.1016/S0377-2217(96)00228-7
[4] K. Ohno, Z. Jin and S. E. Elmaghraby, “An Optimal As-
sembly Mode of Multi-Type Printed Circuit Boards,”
Computers and Industrial Engineering, Vol. 36, No. 2,
1999, pp. 451-471. doi:10.1016/S0360-8352(99)00142-4
[5] C. Klomp, J. V. D Klundert, F. C. R. Spieksma and S.
Voogt, “The Feeder Rack Assignment Problem in PCB
Assembly: A Case Study,” International Journal of Pro-
duction Research, Vol. 64, No. 1, 2000, pp. 399-407.
[6] K. P. Ellis, F. J. Vittes and J. E. Kobza, “Optimizing the
Performance of a Surface Mount Placement Machine,”
IEEE Transactions on Electronics Packaging Manufac-
turing, Vol. 24, No. 3, 2001, pp. 160-170.
doi:10.1109/6104.956801
[7] N. S. Ong and W. C. Tan, “Sequence Placement Planning
for High-Speed PCB Assembly Machine,” Integrated
Manufacturing Systems, Vol. 13, No. 1, 2002, pp. 35-46.
doi:10.1108/09576060210411495
[8] H. Wu and P. Ji, “A Gene tic Algorithm Approach to Op-
timizing Component Placement and Retrieval Sequence
for Chip Shooter Machines,” International Journal of
Advanced Manufacturing Technology, Vol. 28, No. 5,
2006, pp. 556-560. doi:10.1007/s00170-004-2390-2
[9] C. C. Chyu and W. S. Chang, “A Genetic-Based Algo-
rithm for the Operational Sequence of a High Speed Chip
Placement Machine,” International Journal of Advanced
Manufacturing Technology, Vol. 36, No. 9-10, 2008, pp.
918-926. doi:10.1007/s00170-006-0918-3
[10] R. Kumar and Z. Luo, “Optimizing the Operation Se-
quence of a Chip Placement Machine Using TSP Model,”
IEEE Transactions on Electronics Packaging Manufac-
turing, Vol. 26, No. 1, 2003, pp. 14-21.
doi:10.1109/TEPM.2003.813002
[11] G. Moon, “Efficient Operation Methods for a Component
Placement Machine Using the Patterns on Printed Circuit
Boards,” International Journal of Production Research,
Vol. 48, No. 10, 2010, pp. 3015-3028.
doi:10.1080/00207540802553608
[12] T. Knuutila, M. Hirvikorpi, M. Johnsson and O. Neva-
lainen, “Grouping PCB Assembly Jobs with Feeders of
Several Types,” International Journal of Flexible Manu-
facturing Systems, Vol. 16, No. 2, 2004, pp. 151-167.
doi:10.1023/B:FLEX.0000044838.12637.0e
[13] R. Narayanaswami and V. Iyengar, “Setup Reduction in
Printed Circuit Board Assembly by Efficient Sequenc-
ing,” International Journal of Advanced Manufacturing
Technology, Vol. 26, 2005, pp. 276-284.
doi:10.1007/s00170-003-1634-x
[14] K. Salonen, J. Smed, M. Johnsson and O. Nevalainen,
“Grouping and Sequencing PCB Assembly Jobs with
Minimum Feeder Setups,” Robotics and Computer-Inte-
grated Manufacturing, Vol. 22, No. 4, 2006, pp. 297-305.
doi:10.1016/j.rcim.2005.07.001
[15] I. J. Jeong, “An Entropy Based Group Setup Strategy for
PCB Assembly,” Language and Automata Theory and
Applications, 3982 LNCS, 2006, pp. 698-707.
[16] M. J. Rosenblatt and H. L. Lee, “The Effects of Work-in-
Process Inventory Costs on the Design and Scheduling of
Assembly Lines with Low Throughput and High Com-
ponent Costs,” IIE Transactions, Vol. 28, No. 5, 1996, pp.
405-414. doi:10.1080/07408179608966287
[17] K. P. Ellis, J. E. Kobza and F. J. Vittes, “Development of
a Placement Time Estimator Function for a Turret Style
Surface Mount Placement Machine,” Robotics and Com-
puter-Integrated Manufacturing, Vol. 18, No. 3-4, 2002,
pp. 241-254. doi:10.1016/S0736-5845(02)00015-7