 Journal of Applied Mathematics and Physics, 2014, 2, 1053-1060 Published Online November 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.212120 How to cite this paper: Nakamura, K., Satomi, T. and Takahashi, H. (2014) Improved Model for Soil as a Two-Phase Mixture Based on Smoothed Particle Hydrodynamics (SPH). Journal of Applied Mathematics and Physics, 2, 1053-1060. http://dx.doi.org/10.4236/jamp.2014.212120 Improved Model for Soil as a Two-Phase Mixture Based on Smoothed Particle Hydrodynamics (SPH) Kousuke Nakamura, Tomoaki Satomi, Hiroshi Takahashi Graduate School of Environmental Studies, Tohoku University, Sendai, Japan Email: fy09002@mail.kankyo.tohoku.ac.jp Received Sep te mber 2014 Abstract It is desired to resolve soil contamination with reduced costs. “Insoluble treat ment” is a soil im- provement method for heavy metal containing soil, which uses soil mixers to mix soil and soil im- provement liquid agents. To reduce the costs of this method, soil mixers have to be optimized. However, it is not achieved due to the lack of theoretical knowledge on mixing solid with liquid. Therefore, a numerical model to simulate the dynamic behavior of solid and liquid is on the de- velopment in this study using Smoothed Particle Hydrodynamics (SPH) method. To validate the numerical model, several experiments were carried out and numerically reproduced. The com- parisons of the results showed that the numerical model replicated a liquid flow with an error rate of 2.1% and a seepage flow with an error rate up to 26.1%. Especially, the water distribution in the soil pores was highly improved with absolute gaps in volumetric water content up to 4.4% in the porosity range of 10% - 90%. For the water absorption into dry sand, the simulation result be- came more realistic by concerning soil suction. Keywords Soil Improvement, Water Absorption Test, Saturated and Unsaturated Soil, Smoothed Particle Hydrodynamic s 1. Introduction Soil contamination is a serious environmental issue that can damage living things including human beings through water pollution. One of the actions against this problem is Soil Contamination Countermeasures Act of Japan. According to the investigation under this law, the accumulated volume of contaminated soil from 2004 to 2012 was 10,621,736 m3 and the increased amount of contaminated soil in 2012 was 485,713 m3 [1]. In addition, it is expected that it will continue increasing with investigations with urban redevelopments. Then, it is ideal if soil contamination can be resolved on site with reduced costs. Therefore, optimizations on soil improvement methods are important. “Insoluble treatment” is a soil improvement method that is used against heavy metal containing soil. With this technique, soil is mixed with soil improvement liquid agents using a soil mixer such as a mobile soil recycler.  K. Nakamura et al. This method also have to be optimized about the designs and the operating conditions of soil mixers. Otherwise, environmentally unfriendly combinations of large scale soil mixers that are outside of the site and a lot of dump trucks are necessary to finish the treatment within a limited construction period. Therefore, theoretical know- ledge of mixing solid with liquid in a soil mixer to o ptimize the soil improvement method is needed. There are two categories of theoretical approaches: experimental approaches and numerical approaches. In order to obtain the theoretical knowledge of mixing solid with liquid in a soil mixer, the influences of parame- ters related to soil and soil mixers have to be clarified. If experimental approaches are employed, enormous amounts of experimental materials will be necessary for tests under various conditions, while numerical ap- proaches will not need them. Then, numerical approaches are expected to be proper for this study. Based on the above background, the objective of this study is to develop the simulator that can be used to ac- cumulate the theoretical knowledge of mixing solid with liquid in a soil mixer, which is necessary in optimizing soil mixers for its designs and operating conditions. 2. Selection of the Numerical Method Numerical methods can be broadly classified into two categories: grid-based methods and mesh-free methods [2]. Grid-based methods are usually more simple and faster than mesh-free methods. Mesh-free methods are de- signed to solve complicated problems that cannot be handled by grid-based methods such as the problem in this st udy. Discrete Element Method (DEM) [3] is one of the options for this problem because DEM is a mesh-free me- thod designed for granular material or soil. However, it was found in the previous study [4] that the result was not realistic when DEM wa s used for liquid. In addition, it is known that some of the experimental properties cannot be directly used as DEM parameters [5]. Then, DEM needs time-consuming processes to choose para- meters by trial and error. The other options is Moving Particle Semi-implicit (MPS) method [6] that is a mesh-free method invented for incompressible fluid or liquid. However, it was not suitable for this study because soil is not incompressible. The another option is Smoothed Particle Hydrodynamics (SPH) method [7] [8] that was originally invented to model astrophysical phenomena and later widely extended for applications to the problems of continuum solid and fluid mechanics. It was also used to model a mixture of solid and liquid [9] [10]. In addition, most of the experimental properties can be directly used as parameters in SPH contrary to DEM. Then, the cost to choose parameters can be reduced. Moreover, SPH is said to be simple among mesh-free methods [2]. Judging from the above characteristics of those numerical methods, SPH was expected to be proper for this st udy. 3. Development of the Numerical Model Essential formulations of SPH will be briefly introduced. Further details of them can be found in the references [2] [10]. In addition, the modifications added to the numerical model in this study will be described. 3.1. Kernel Approximation and Particle Approximation The approximation in SPH starts from the integral representation of an arbitrary function in Equation (1). ( )()() d Ù fxfxax xx ′ ′′ = − ∫ (1) where is a function of the three-dimensional coordinate vector , and is the volume of the integral that contains coordinate and is the Dirac delta function. The n, the so-called “kernel approxima- tion” is employed in SPH. In the kernel approximation, a smoothing kernel , which has a wider spread than that of and satisfies number of conditions, replaces . In addition, the kernel approximation operator is marked by the angle bracket <> in the SPH convention. Then, the approximated integral representation is given by ( )()() ,dfxfxWx xhx Ω ′ ′′ = − ∫ (2)  K. Nakamura et al. where is the smoothing length defining the influence area of the smoothing function . The n, the entire system is represented by a finite number of nodes that are called particles and carry individual mass and occupy individual space. This is achieved by the following particle approximation, where the conti- nuous integral representations concerning the kernel approximation in Equation (2) and its derivative can be converted to discretized forms of summation over all the particles in the support domain shown in Figure 1. If the infinitesimal volume in the above integrations at the location of particle is re- placed by the finite volume of the particle , which can be replaced by the mass of the particle divided by , the continuous integral representation for in Equation (2) can finally be written in the following form of discretized particle approximation, where is the number of particles in the support domain of par- ticle . ( ) ( )() 1 , Nj ij ij jj m fxfxWx xh ρ = = − ∑ (3) Equation (3) states that a field value at particle can be approximated using the sum of those field values at all the particles in the support domain of particle weighted by the smoothing kernel . 3.2. Summation Density Approach It should be noted that if the function in Equation (3) is substituted with the density function , the SPH approximation for the density is obtained as follows. This is one of the most popular forms to obtain densi- ty in SPH, and is referred to as the summation density approach. (4) 3.3. Governing Equations for the Interactions inside Liquid and Solid Navier-Stokes equations are employed as the governing equations for the interactions inside liquid. Since Navi- er-Stokes equations require known pressure to be solve d, an equation of state is needed. Then, incompressible flui d is modeled as artificial fluid that is given artificial compressibility, which is larger than that in reality. The equation of state for artificial fluid is written in the following form [11]. (5) where is a constant that is set equal to 7 in most of the circumstances, is the reference density, is a problem dependent parameter that sets a limit for the maximum change of the density. By the way, solid is fixed in space so that the pure interactions between solid and liquid can be easily observed. 3.4. Improved Governing Equations for the Interactions between Solid and Liquid The seepage force and the pore water pressure were e mployed to describe interactions between solid and liquid Figure 1. Particle approximation using particles in the support domain of the smoothing kernel W for particle i.  K. Nakamura et al. [9] [10]. However, they were not fully exact. Then, four improvements were applied on them in this study. The first problem can be described as follows. There are two same bottles filled with liquid and dry soil, re- spectively. In reality, when liquid in the bottle is poured to the bottle filled with dry soil, not whole amount of liquid is used to fill the pores inside dry soil. On the other hand, if the same process is attempted in the previous model, whole amount of liquid can be stored in the bottle filled with soil. To resolve this unphysical behavior, the density, which is used in every SPH equation and pressure calculation, was modified as follows. (6) where is the porosity of solid, and are the density purely calculated by Equation (4) and the cor- rected density, respectively. With Equation (6), corrected density becomes larger when SPH liquid particles approach SPH solid particles. At the same time, the pressure described by Equation (5) becomes larger to sparse the distribution of SPH liquid particles. Finally, the density converges to the reference density . The density of solid can be also corrected by almost the same way by substituting to in Equation (6). The equation generates as soil particle density from as dry density of solid. Then, the volume term in Equation (3) is changed from the bulk volume, which includes the volume of pores, to the exact vo- lume of solid. The second modification was on the seepage force in the following equation. (7) where is the gravitational acceleration, is the density of liquid, is the viscosity of liquid, is the absolute permeability, and are the velocity of liquid and solid respectively. This basic equation yields a volumetric force so that the superficial fluid flow velocity through the medium or solid ap- proaches to . By the way, since the seepage force is a volumetric force, it requires the volume term in Equation (3) to be a bulk volume. However, the first modification changed it into a exact volume of solid, which is smaller by times than the bulk volume. Then, a compensation factor was added to Equation (7) as follows. (8) The third modification was also on the seepage force to reflect the difference between saturated and un- saturated soils by replacing the absolute permeability in Equation (8) with the phase permeability , which changes with local moisture state in reality. Then, the proposed equa tio ns [12] [13 ] as follows, which employ the volumetric water content as a typical field value of local moisture state, were used to describe change in . ( ) 2 1 1 11 S kk ξψ ψ − =Θ− −Θ (9) (10) where is the normalized water content, and are the fitting parameters to represent the water reten- tion curve of soil, and are the saturated water content and the residual water content of a soil respec- tivel y. The fourth modification was on the soil suction , which had not been counted in the previous studies [9] [10] and is a soil characteristic related to the interfacial tension as the following: the more the soil gets dry, the more strongly the soil draws liquid inside. It was implemented by reference to the proposed equations [14] as follows. (11) (12)  K. Nakamura et al. where S is the suction, is the height of a liquid column drawn up by capillary action, C is the parameter re- lated to the shape of soil pores, D10 is the diameter of the 10 percentile grain of the material. 4. Validations for a Seepage Flow inside Saturated Soil In order to validate the numerical model for a seepage flow inside of saturated soil, the following concept was used: the numerical model is valid if input parameters are reproducible by processing simulation results with methods that are used in processing experimental results. Then, the absolute permeability and the volume- tric water content were chosen as parameters that should be reproducible. In addition, a standard falling head permeability test defined in JIS A 1218 was selected as the test content. The input parameters for SPH liquid particles and SPH solid particles are shown in Table 2 and Table 3 respectively. Almost all of the parameters were inherited from the physical properties of water and saturated silica sand No.9. They are shown in Table 1. In addition, the simulations were carried out with and without Equation (6) in the solid porosity range of 10% - 90% to see the effect of this improvement. By the way, Equation (9)-(12) were not used because the soil is satu- rated. The results are shown in Figure 2 and Figure 3. The results without Equation (6) are marked with “Pr evi ous” and the results with Equation (6) are marked with “Improved”. From Figure 2, it can be seen that the saturated volumetric water content, which should be equal to the solid porosity, became close to the solid porosity by the effect of Equation (6). In detail, the maximum gap between volumetric water content and porosity was 4.4%. Fro m Figure 3, it can be seen that the Equation (8) successfully compensated the side effect of Equation (6) but not perfect. The maximum error rate of absolute permeabilit y was 26.1%. 5. Validations for a Water Absorption into Unsaturated Soil In order to validate the numerical model for a seepage flow inside unsaturated soil, an observation of water ab- sorption into unsaturated soil was carried out. The equipment for this test shown in Figure 4. With this transpa- rent tube, almost one-dimensional water absorption can be observed. In addition, the top position and the bottom position of water were recorded to be compared. The specimen was dry silica sand No.9 whose characteristics are shown in Table 1. In the test procedure, water and dry soil are put in the certain position inside the tube. Then, water is allowed to fall down by gravity. the above equipments and procedures were numerically repro- duced with the parameters shown in Table 2 and Table 3. In addition, 4 simulations were carried out with and without phase permeability in Equation (9) and the suction in Equation (11) to see their effect. The results are shown in Figure 5 and Figure 6. The two results with and without phase permeability in Equ- ation (9) are marked with “Absolute” and “Phase” respectively. Similarly, the two results with and without soil suction are marked with “with Suction” and “without Suction” respectively. It can be seen that the two cases with the phase permeability is not close to the experimental result. According the two cases with absolute per- meability, it is found that the soil suction made the simulated phenomena closer to the real one. Therefore, the soil suction seems to be necessary in modeling a unsaturated soil. However, the result of the combination of the absolute permeability and the soil suction is still not very accurate. This is expected be caused by the water retention curve of soil which is a fitting curve and the parameters changes according to the soil property. In this study, the fitting parameters in Table 3 are determined by the previous literature data. Figure 2. Validation on the volumetric water content. 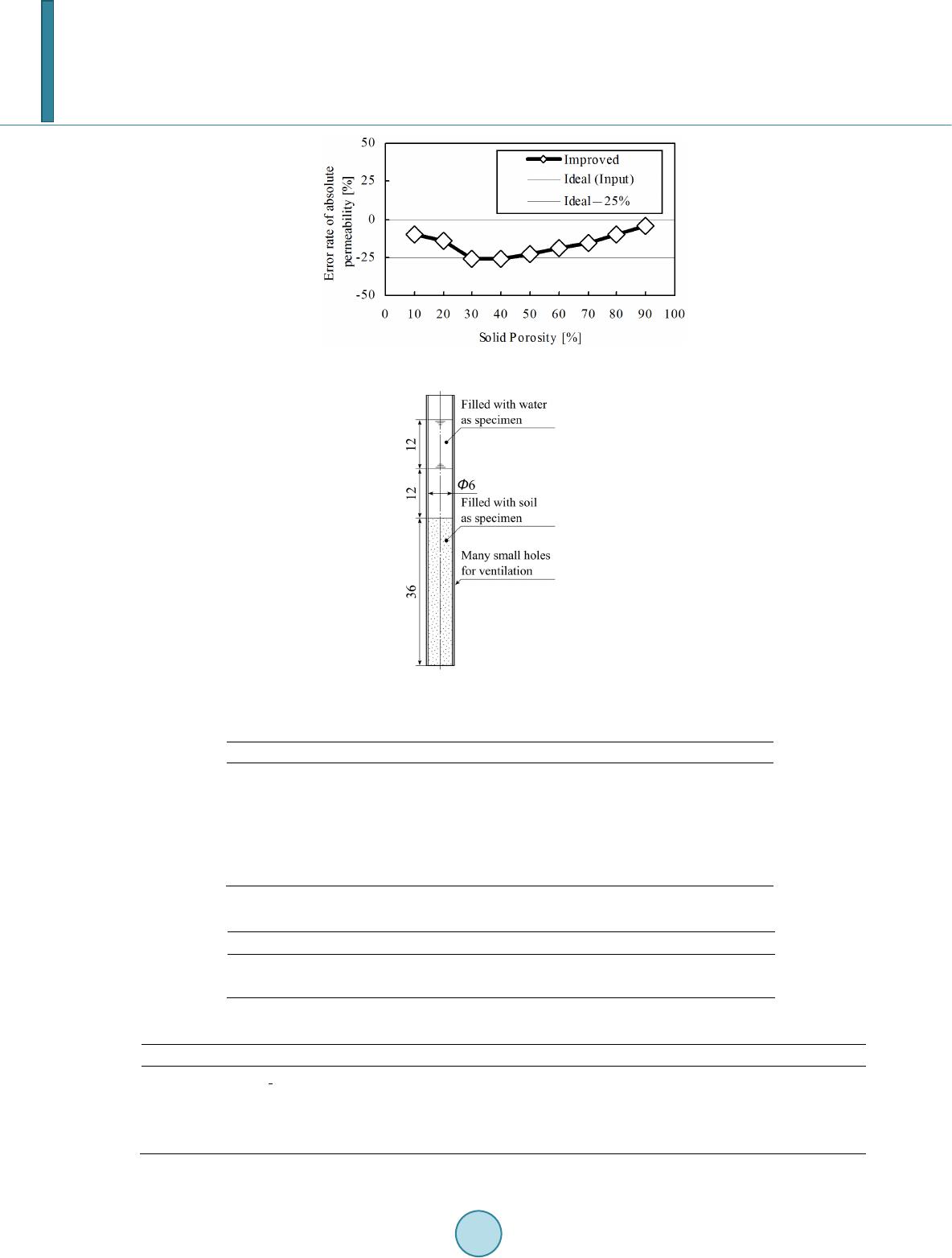 K. Nakamura et al. Figure 3. Validation on the absolute permeability. Figure 4. The water absorption test equipment. Table 1. P hys ical properties of the specimen. Density of soil particles ρs [kg/m ] 2.56 × 10 2.56 × 10 t d Porosity n [-] 0.485 0.485 Water content w [%] 35.6 0 10 percentile grain diameter D 10 Table 2. Parameters for SPH liquid particles. Initial density ρ0 [kg/m3] 1.00 × 103 Incompressible parameter B [MPa ] 1.43 × 10 Viscosity η [Pa・s] 1.00 × 10-3 Table 3. Parameters of SPH solid particles. Soil particle density ρs [kg/m3] 2.56 × 103 Absolute permeability ks [m2] 5.59 × 10-8 Dry density ρd [kg/m3] 1.24 × 103 Porosity n [-] 0.1, 0.2, 0.3, ..., 0.9 Pore characteristics parameter C [m2] 1.5 × 10-5 10 percentile grain diameter D10 [m] 3.84×10-5 Fitting parameter ψ[-] 2.68 Residual water content θr [-] 0.045 Fitting parameter ξ [-] 0.50 Saturated water content θs [-] 0.430 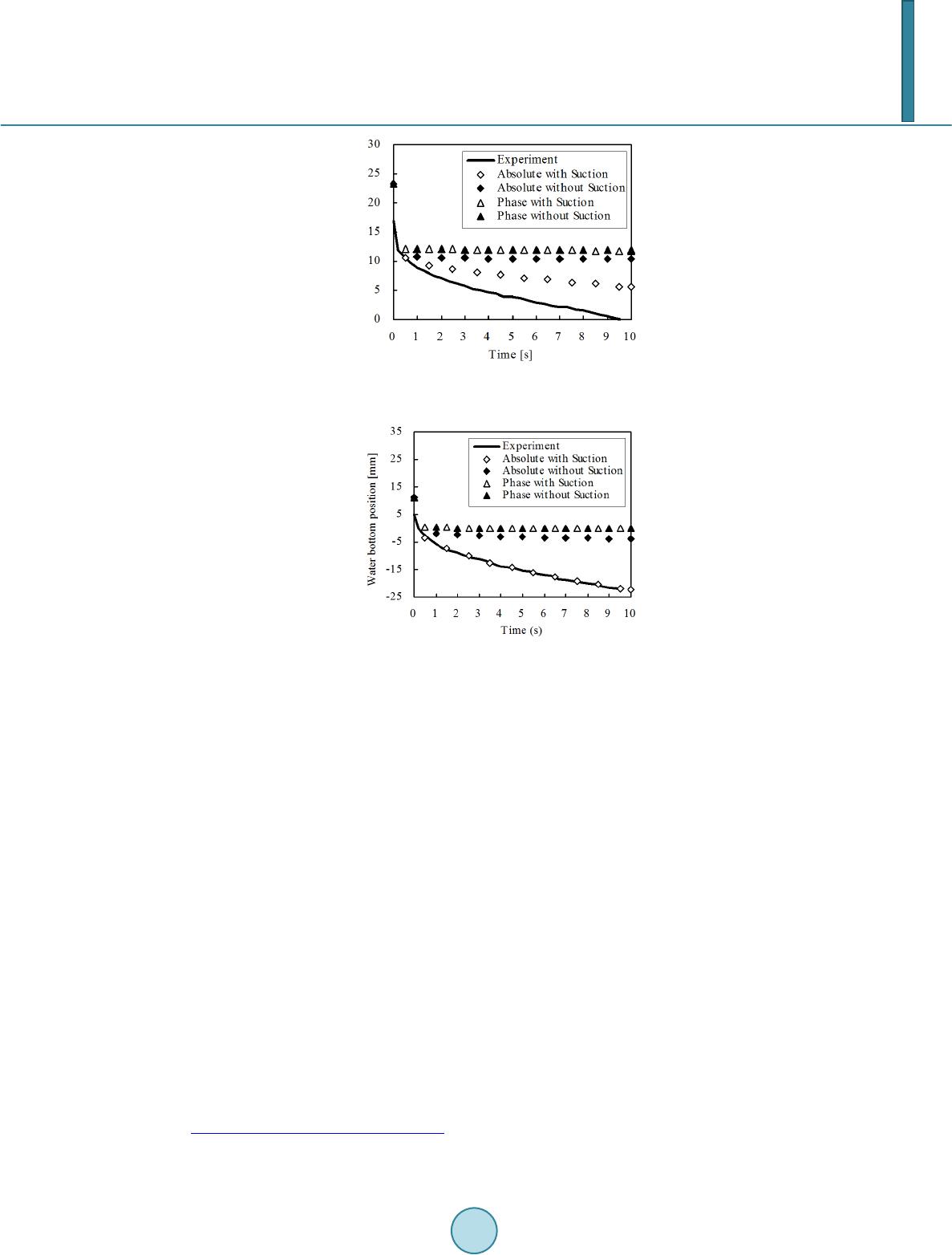 K. Nakamura et al. Figure 5. The results for the upper end position of water in the water absorption test. Figure 6. The results for the lower end position of water in the water absorption test. By the way, the reason why the phase permeability is not suitable for this model is thought to be related to its meaning. It can be obtained for each phase in a two-phase gas-liquid seepage flow through a porous solid and is affected by the difference of the physical properties and the amount between gas and liquid. Then, this is not a parameter that simply represents the drag between single fluid phase and solid phase contrary to the absolute permeability. Therefore, it can be said that it should not be used in the Equation (7) or Equation (8). 6. Conclusion In order to reduce the costs of “insoluble treatment”, a numerical model to simulate the interactions between solid and liquid was developed based on the SPH method. For a seepage flow in a saturated soil, the accuracy of the volumetric water content and the absolute permeability were highly improved by the modifications. For a water absorption into dry silica sand No. 9, it was found that the soil suction makes the simulated phenomena more realistic. On the other hand, the phase permeability was thought to be not suitable for this model because it does not simply represents the drag between single fluid phase and solid phase. References [1] Environmental Management Bureau (2014) The Results of the Survey on the Enforcement Status of the Soil Contami- nation Countermeasures Act & Numbers and Trends of Soil Contamination Investigations and Countermeasu res. Min- istry of the Environment, Japan. [2] Liu , G.R. and Liu, M.B. (2003 ) Smoothed Particle Hydrodynamics: A Meshfree Particle Method. World Scientific Co. Pte. Ltd., Singapore. [3] Cundall, P.A. and Strack, O.D.L. (1979) A Discrete Numerical Model for Granular Assemblies. Geo techn ique, 29, 47- 65. http://dx.doi.org/10.1680/geot.1979.29.1.47 [4] Maruhashi, F. (2004) Study of the Simulator for Mixing Solids and Liquids with Excavated Soils and Liquid Agents in  K. Nakamura et al. a Contaminated Soil Improvement Machine. M. E. Thesis, Tohoku University, Japan. [5] Coet zee, C.J. and Els, D.N.J. (200 9) Calibration of Granular Material Parameters for DEM Modeling and Numerical Verification by Blad e-Granular Material Interaction. Journal of Terramechanics, 46, 15-26. http://dx.doi.org/10.1016/j.jterra.2008.12.004 [6] Koshizuka, S. and Oka, Y. (1996) Moving Particle Semi-Implicit Method for Fragmentation of Incompressible Fluid. Nuclear Science and Engineering, 123 , 421-434. [7] Lu c y, L. B. (1977) A Numerical Approach to the Testing of the Fission Hypothesis. Astronomical Journal, 82, 1013- 1024. http://dx.doi.org/10.1086/112164 [8] Gingold, R.A. and Monaghan, J.J. (1977) Smoothed Particle Hydrodynamics: Theory and Application to Non-Spheri- cal Stars. Monthly Notices of the Royal Astronomical Society, 1 80, 375-389. http://dx.doi.org/10.1093/mnras/181.3.375 [9] Maed a, K. and Sakai, M. (2004) Development of Seepage Failure Analysis Method of the Granular Ground by Smoothed Particle Hydrodynamics. Journal of JSCE (Applied Mechanics), 7, 775-786. [10] Bui, H.H., Sako , K. and Fukagawa, R. (2007) Numerical Simulation of Soil-Water Interaction Using Smoothed Par- ticle Hydrodynamics (SPH) Meth o d . Journal of Terramechanics, 44, 339-346. http://dx.doi.org/10.1016/j.jterra.2007.10.003 [11] Monaghan, J.J. (1994) Simulating Free Surface Flows with SPH. Journal of Computational Physics, 110, 399-406. http://dx.doi.org/10.1006/jcph.1994.1034 [12] van Genuchten, R. (1978) Calculating the Unsaturated Hydraulic Conductivity with a New Closed-Form Analytical Model. Residential Report, Princeton University, Princeton. [13] van Genuchten, M.Th. (1989) A Closed -Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal, 44, 892-898. http://dx.doi.org/10.2136/sssaj1980.03615995004400050002x [14] Ishi hara, K. (2001) Soil Mechanics. 2nd Edition, Maruzen, Japan.
|