 Journal of Applied Mathematics and Physics, 2014, 2, 1023-1030 Published Online November 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.212116 How to cite this paper: Yu, C.J., Kim, D. and Zhao, Y. (2014) Stress Analysis of Membrane Flapping-Wing Aerial Vehicle Based on Different Material Models. Journal of Applied Mathematics and Physics, 2, 1023-1030. http://dx.doi.org/10.4236/jamp.2014.212116 Stress Analysis of Membrane Flapping-Wing Aerial Vehicle Based on Different Material Models Chunjin Yu1,2, Daewon Kim2, Yi Zhao2 1Institute of Flight Vehicle Engineering, Nanchang Hangkong University, Nanchang, China 2Department of Aerospace Engineering, Embry-Riddle Aeronautical University, Daytona Beach, USA Email: 41576503 2@qq.co m Received August 2014 Abstract Recent studies of flapping-wing aerial vehicles have been focused on the aerodynamic perfor- mance based on linear materials. Little work has been done on structural analysis based on non- linear material models. A stress analysis is conducted in this study on membrane flapping-wing aerial vehicles using finite element method based on three material models, namely, linear elastic, Mooney-R ivl in non linear, and composite material models. The purpose of this paper is to under- stand how different types of materials affect the stresses of a flapping-wing. In the finite element simulation, each flapping cycle is divided into twelve stages and the maximum stress is calculated in each stage. The results show that 1) there are two peak stress values in one flapping cycle; one at the beginning stage of down stroke and the other at the beginning of upstroke, 2) maximum stress at the beginning of down stroke is greater than that at the beginning of upstroke, 3) maxi- mum stress based on each material model is different. The composite and the Mooney-Rivlin non- linear models produce much less stresses compared to the linear material model; and 4) the ratio of downstroke maximum stress and upstroke maximum stress varies with different material models. This research is helpful in answering why insect wings are so impeccable, thus providing a possibility of improving the design of flapping-wing aerial vehicles. Keywords Flapping-Wing, Aerial Vehicle, Membrane Wing, Stress Analysis 1. Introduction All flying animals in the nature use flapping-wing flight mode. Compared with the traditional fixed-wing and rotary-wing aerial vehicles, the main characteristics of flapping-wing unmanned aerial vehicle (UAV) include that it can produce the lift and thrust at the same time. Therefore, studying flapping-wing aerial vehicles have a wide application foreground. In the past several years, many researchers have been conducted on flapping-wing using analytical and nu- merical analysis. Kasel et al. [1] used finite element method (FEM) to calculate the models of a dragonfly wing 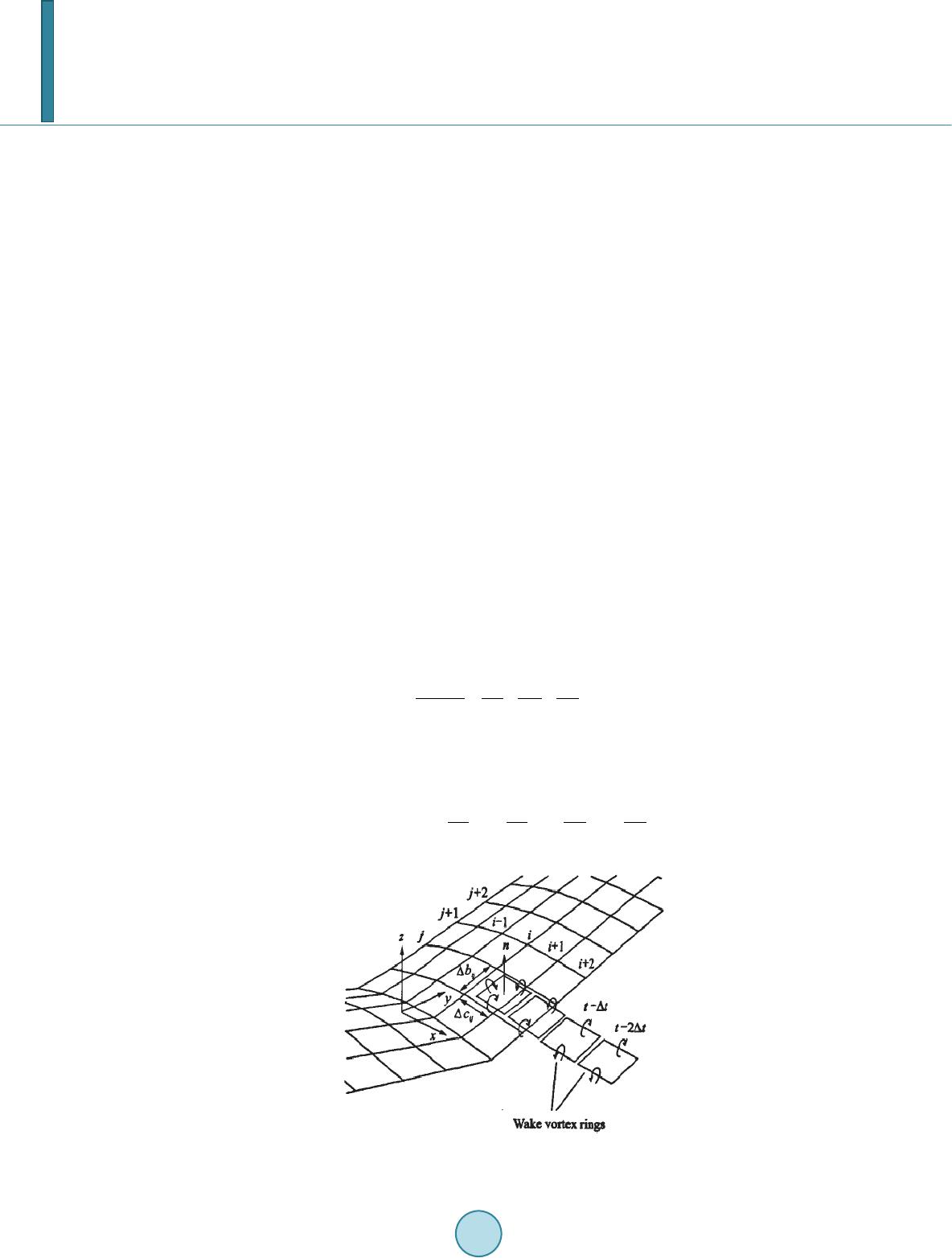 C. J. Yu et al. and of a fly wing. Yu and Ang [2] derived a formula to calculate the aerodynamic force based on three dimen- sional unsteady vortex lattice methods, which calculates the deformation of the flapping-wing using a linear model [3]. Fitzgerald et al. [4] studied the fluid-structure interaction of flexible flapping-wing systems using the direct numerical simulations and unsteady vortex lattice method (UVLM).They found that the UVLM was more suitable in calculating unsteady aerodynamic forces; however, their material model was based on a linear model. Nakata et al. [5] presented a fluid-structure interaction model of insect flapping flight with a flexible wing, using a linear material model. Stewart et al. [6] presented a theory and results of shape variation and structural opti- mization for a plate-like flapping wing. According to this study, the density of a wing material plays a role in the optimal wing design. Vincent [7] found that the material of an insect wing was similar to a composite material. Cho et al. [8] presented a computational approach to simulate a flapping-wing by coupling between c omput a- tional fluid dynamics (CFD) and computational structure dynamics (CSD). A no nlinear structural analysis based on the geometrically exact beam formulation was stud ie d . Mason et al. [9] designed a small unmanned aerial systems to simulate the flapping kinematics of insects and birds, and then used a linear material model to calcu- late the displacement amplitudes. Most work mentioned above have been generally limited to linear materials. In this paper, nonlinear materials are studied for flapping-wing aerial vehicles, especially, a finite element analysis using shell elements is con- ducted to simulate the stresses of a membrane flapping-wing. Three material models, i.e., linear material, com- posite material, and Mooney-Rivlin models are utilized to investigate how material models affect the mechanical behavior of flapping-wing unmanned aerial vehicles. This research can be helpful in answering some questions about impeccable insect wings and also laying the foundation of future design for the flapping-wing unmanned aerial vehicles. 2. Calculation of Aerodynamic Force and Inertial Force Aerodynamic force and the inertial force are both produced when a flapping-wing aerial vehicle flies. Three- dimension unsteady vortex lattice method (UVLM) [2] is utilized here to calculate the aerodynamic forc e s, as shown in Figure 1. The pressures and the loads can be calculated using the unsteady Bernoulli equation shown below. 2 2 ref ref 22 f Pp Q t ν ρ −∂Φ =−+ ∂ (1) where is reference pressure, is pressure of fluid, is flui d d e nsity, is fluid velocity, is reference pressure, is the potential of flow, and is the time. The pressure difference between the flapping-wing upper and lower surfaces is then obtained as 22 22 tt lu ul ul QQ PPP tt ρ ∂Φ ∂Φ ∆= −=−+− ∂∂ (2) Figure 1. Diagrammatic drawing of vortex lattice method [10].  C. J. Yu et al. whe re is the pressure of lower surfaces and is the pressure of upper surfaces. The tangential velocity due to wing vortices have two components on the wing and it can be approximated by two directions, and , on the surface. The velocities of directions due to wing vortices on each element is 1, 2 iji j i ij c τ − Γ −Γ ∂Φ ±=± ∂∆ (3a) ,1 2 iji j j ij b τ − Γ −Γ ∂Φ ±=± ∂∆ (3b) where “ ” represents the upper and lower surfaces, respectively. and are the panel lengths in the i-th and j-th directions. Similarly, and are the panel tangential vectors in the and directions, and is the strength of vortex. Since for this vortex ring model is , (4) Substituting these terms into Equatio n (2) results in ( )( )( ) ( )( )( ) 1, ,1 ,, ,,. iji j ijWWW iij iji j WWW ijij ij ij PUtu Vtv Wtwc Utu Vtv Wtwbt ρτ τ − − Γ −Γ ∆ =+++⋅⋅ ∆ Γ −Γ∂ ++++ ⋅⋅+Γ ∆∂ (5) where , , are respectively the fluid velocities of direction, direction, and di- rection of the inertial coordinates when time is moment. The parameters , , are respectively the velocity of direction, direction, and direction of the body coordinates. The contribution of this panel to the loads is (6) whe re is pressure of element, is area of element. The flapping motion of the present model wing is simplified to a cosine rotation around a fixed axis located at the root. (7) The periodic inertia force, generated from the acceleration and deceleration of the flapping-wing, is one of the main acting loads during each cycle. Its specific load distribution can be predicted as, ( )( )() 22max 2 dcos d i iiii t F tmrmrt t βωβ ω =−= (8) where is the inertial force of element , is the mass of element , is rotational radius of ele- ment , is angular velocity, is time, and is the amplitude of flapping angle. Because the units of the aerodynamic force is , the formula of inertial force can be expressed as follow. ()( )( ) 22 max max cos cos iiis iii FtmrtAtrt ωβωωρβω = = (9) ( )( )( ) 2max cos i i sii i Ft ftt rwt A ωρ β = = (10) where is area of element and is the material density.  C. J. Yu et al. 3. Material Models 3.1. Linear Material Model Mason et al. [9] used finite element method (FEM) to calculate the deformation of a membrane flapping-win g unmanned aerial vehicle and their model was composed of two parts, i.e. leading edge beam and wing mem- brane. The membrane material properties used were 2.47 GPa modulus of elasticity and 0.489 Poisson’s ratio. Yu et al. [11] used a finite element method to design a micro aerial vehicle and the material properties used were 0.02 GPa modulus of elasticity and 0.49Poisson’s ratio. This paper foc us es on a thin, highly flexible membrane with modulus of elasticity of 1.3 GPa and Poisson’s ratio of 0.489. Without any stiffening supports, the membrane of this model would not be able to support forces normal to the membrane plane. The senatorial properties for the membrane may not be easily applicable to pre- dict the wing behavior but it should be necessary to predict aero elasticity as more flexible wings are developed. 3.2. Mooney -Rivlin Model Lia n et al. [12] utilized the M ooney-Rivlin material model to analyze a fl ui d-structure interaction of fixed wing aerial vehicles. In this paper, the authors have applied this model for a flapp ing-wing aerial vehicle. The mem- brane material is ahyperelastic Mooney-Rivlin model for which the strain energy function W can be written as, (11) whe re and are the first and second invariants of the Green deformation tensor, and and are the material property parameters. For the membrane structure of the flapping-wing, we assume that , . [12]. The Money-Rivlin model is one of the most frequently employed hyperelastic models due to its mathematical simplicity and it provides relatively good accuracy for reasonably large strains. 3.3. Composite Material Model The carbon/epoxy composite T300/5208 is used for this analysis, whose properties are shown in Table 1. The 0˚ direction of the fiber is along the x direction. 4. Results and Discussions The structure of an insect wing is very complex and their elastic moduli and thickness are irregular [13] [14]. At the current stage , only simple flapping-wing aerial vehicles can be manufac t ur e d to simulate the motion of the insect wings. Here a membrane flapping-wing aerial vehicle mode is designed and it is composed of a front beam, wing ribs, and a membrane. The front beam and the wing ribs are made of carbon fiber tubes and its beam element is shown in Figure 2. For the membrane structure, its skin thickness is 0.02 mm. The membrane mesh is shown in Figure 3. The detailed parameters used in this model are shown in Table 2. There are eight carbon fiber ribs and the cross section of each rib is 2 mm × 0.2 mm. ANSYS software is used to calculate the internal st res ses during flapping motions. In ANSYS, SHELL63, SHELL181, and SHELL41 element types are adopted for linear, Mooney-Rivlin, and composite material models, respectively. The boundary condition of the fixed support in the body-fixed coordinate system is adopted from [3]. Dur i ng the flapping flight, the flapping-wing must withstand not only aerodynamic forces but also inertial forces. Aerodynamic force of every shell element is calculated from Equation (6), and the inertial force of every ele- ment is calculated from Equati o n (10). Divid i ng the flapping period into twelve segments, the maximum stress curves that adopted the linear material model, the composite T300/5208 model, and the Mooney-Rivlin are respectively shown in Figure 4, Figure 5 and Fi gure 6. From Figures 4-6, one can observe that, regardless of the material models, there are two peak stress values in a single flapping cycle, i.e . fir st peak value occurs at the beginning stage of down stroke and the other peak oc- curs at the beginning stage of upstroke. From the maximum stress curve of linear material model, it is found that the stress peak at the beginning stage is 1.13 Mpa and at the beginning stage of upstroke the stress peak value is 0.97 Mpa. So the former is 16.5%  C. J. Yu et al. Table 1. T300/5208 Material Characteristics. Fiber T300 Carbon G12(GPa) 7.17 Matrix 5208 Epoxy G23(GPa) 3.78 E1(GP a) 181 G13(GPa) 7.17 E2(GP a) 1 0. 3 σ1+(MPa) 1 500 E3(GP a) 1 0.3 σ1 (MPa) 1500 12 v 0.28 2 (M Pa) 40 23 v 0.3 σ2+( MPa ) 2 46 13 v 0.28 τ12(MPa) 68 Table 2. Parameters used in theflapping-wing aerial vehicle model. Semi -span length (m) 0.32 Outer radius of front beam (m) 0.003 Inner radius of front beam (m) Flapping frequency (Hz) 8 Elastic module of front beam (GPa) 40 Flapping angle 45˚ Poisson’s ratio of front beam 0.3 Flight velocity (m/s) 11 Cross section of carbon fiber ribs (mm × mm) 2 × 0.2 Thickness of membrane (mm) Figure 2. Beam element of flapping-wing aerial vehicle. Figure 3. Membrane mesh of flapping-wing aerial vehicle.  C. J. Yu et al. Figure 4. Maximum stress curve of linear material. Figure 5. Maxi mumstress curve of composite material T300/ 5208. Figure 6 . M aximumstress curve of Mooney-Rivlinmater ial. larger than the latter. For the composite T300/5208, the stress peak at the beginning stage of down stroke is 464.8 Pa and the stress peak at the beginning stage of upstroke is 357.7 Pa. So the former is 29.9% larger than the latter. For the Mooney-Rivlin material, at the beginning stage of down stroke the stress peak value is 407.3 Pa and the stress peak at the beginning stage of upstroke is 340.5 Pa. So the former is 19.6% larger than the lat- ter. From the results, the maximum stresses are different per each material model. Much less maximum stress  C. J. Yu et al. values are obtained from the composite and the Mooney-Rivlin material models compared to the linear model. 5. Conclusions Finite element analysis is performed to investigate the membrane stresses of a flapping-wing made of various materials. Stress analysis resu l ts for a flapping motion of a membrane wing using the linear, Mooney-Rivlin, and composite materials models are compared. The following conclusions can be reached based on this study. 1) There are two peak stress values in one flapping cycl e; one at the beginning stage of down stroke and the other at the beginning of upstroke. 2) Maximum stress at the beginning of down stroke is greater than that at the beginning of upstroke. 3) Maximum stress based on each material model is different. The composite and the Mooney-Rivlin nonli- near models produce much less stresses compared to the linear material model. 4) The ratio of down stroke maximum stress and upstroke maximum stress varies with different material models. Mooney-Rivlin material is a hyper elastic material and is generally applied to rubber and many other poly- meric materials. The materials have low stiffness and deficiently high damping, which are advantageous proper- ties for noise reduction and vibration isolation. Composite T300 /52 08 exhibits viscoelastic behavior, and all the insect wings have the viscoelastic behavior [15]. This research is helpful to answer that why insect wings are so immaculate, thus improving the design of flapping-wing aerial vehicle. In the future we will continue the fluid-structure interaction study of flapping-wing aerial vehicles. Acknowledgem ents This work is financially supported by Embry-Riddle Aeronautics University, Jiangxi Provincial Department of Education (GJJ12412) and Doctorate Research Foundation of Nanchang Hangkong University (EA201006045). References [1] Kesel, A. B., Ph ilippiand, U. and Nachtigall, W. (1998) Biomechanical Aspects of the Insect Wing: An Analysis Using the Finite Element Method. Computers in Biology and Medicin e, 28, 423-437. http://dx.doi.org/10.1016/S0010-4825(98)00018-3 [2] Yu, C., Ang, H., Chen, Q., et al. (2008) Th ree-Dimension Unsteady Vortex Lattice Method for Flexible Structure Flap- ping-Wing Aerial Vehicl e. Journal of Nanjing University of Aeronautics and Astronautics, 40, 451-455. [3] Yu, C., Ang , H., Yi, K., et al. (2009) The Study of Deformation for Membrane Flapping-Wing Aerial Vehicles. Chi- nese Journal of Computational Mechanics, 26, 935-941. [4] Fi tzgerald , C., V al dez, M. and Balachan dran , B. (2011) A Comparison of Computational Models for Fluid -Structure Interaction Studies of Flexible Flapping Wing Systems. The 49th AIAA Aerospace Sciences Meeting, Orlando, 4-7 January 2011. [5] Nakata, T. and Liu, H. (2012) A Fl u id-Structure Interaction Model of Insect Flight with Flexible Wings. Journal of Computational Physics, 231 , 1822-1847 . http://dx.doi.org/10.1016/j.jcp.2011.11.005 [6] St ewart, E., Patil, M., Canfield, R. and Snyder, R. (2014) Aeroelastic Shape Optimization of a Flapping Wing. The 10th AIAA Multidisciplinary Design Optimization Conference, National Harbor, 13-17 January 2014. http://dx.doi.org/10.2514/6.2014-0469 [7] V in cent, J.F. (1980) Insect Cuticle: A Paradigm for Natural Composites. Symposia of the Society for Experimenta l Bi- ology, 34 , 183-21 0. [8] Cho, H., Kwa k , J. and Shin, S. (2014) Computational Analysis for Flapping Wing by Coupling the Geometrically Ex- act Beam and Preconditioned Navier-Stokes Solution. The 55th AIAA/ASME/ASCE/AHS/SC Structures, Structural Dynami cs, and Materials Conference, National Harbor, 13-17 January 2014. [9] Mason, J., Jennings, A. and Black, J. (2013) Validation of a Finite Analysis of a Flapping Wing against Inertial and Aeroelastic Responses. The 54 th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Confe- rence, Boston, 8-11 Apri l 2013 . [10] He, H., Zhou, X., Long, Y. and Yu, C. (2010) Improved UVLM for Flapping-Wing Aerodynamics Computation. Transactions of Nanjing University of Aeronautics & Astronautics, 27, 205-212. [11] Yu, Y., Yang, Q. and Wang, X. (2013) Finite Element Analysis of Fluid-Structure Interaction for the Design of MAV  C. J. Yu et al. Aerodynamic Shape. Computers & Fluids, 76, 50-57. http://dx.doi.org/10.1016/j.compfluid.2013.01.026 [12] Lian, Y. and Shyy, W. (2003) Thr e e-Dimensional Fluid-Struture Interactions of a Membrane Wing for Micro Air Ve- hicle Applications. Th e 44th AIAA/ASME/ASCE/AHS Structures, Structural Dynamics, and Materials Conference, Norfolk, 7-10 April 2003. [13] Combes, S.A. and Daniel, T. L. (2003) Flexural Stiffness in I nsect win gs: I. Scaling and the Influence of Wing Venation. Journal of Experimental Biology, 206, 2979-29 87 . http://dx.doi.org/10.1242/jeb.00523 [14] Combes, S.A. and Daniel, T.L. (2003) Flexural Stiffness in Insectwings: II. Spatial Distribution and Dynamic Wing Bending. Journal of Experimental Biology, 206, 2989-2997. http://dx.doi.org/10.1242/jeb.00524 [15] Bao, L., Hu, J., Yu, Y., et al. (2006) Viscoelastic Constitutive Model Related to Deformation of Insect Wing under Loading in Flapping Motion. Applied Mathematics and Mechanics, 27, 741-748. http://dx.doi.org/10.1007/s10483-006-0604-1
|