Engineering, 2011, 3, 517-524
doi:10.4236/eng.2011.35060 Published Online May 2011 (http://www.SciRP.org/journal/eng)
Analytical Solution for Bending Stress Intensity Factor
from Reissner’s Plate Theory
Lalitha Chattopadhyay
National Aerospace Laboratories, Bangalore, India
Received December 30, 2010; revised January 27, 2011; accepted April 7, 2011
Abstract
Plate-type structural members are commonly used in engineering applications like aircraft, ships nuclear re-
actors etc. These structural members often have cracks arising from manufacture or from material defects or
stress concentrations. Designing a structure against fracture in service involves consideration of strength of
the structure as a function of crack size, dimension and the applied load based on principles of fracture me-
chanics. In most of the engineering structures the plate thickness is generally small and in these cases though
the classical plate theory has provided solutions, the neglect of transverse shear deformation leads to the
limitation that only two conditions can be satisfied on any boundary whereas we have three physical bound-
ary conditions on an edge of a plate. In this paper this incompatibility is eliminated by using Reissner plate
theory where the transverse shear deformation is included and three physically natural boundary conditions
of vanishing bending moment, twisting moment and transverse shear stress are satisfied at a free boundary.
The problem of estimating the bending stress distribution in the neighbourhood of a crack located on a single
line in an elastic plate of varying thickness subjected to out-of-plane moment applied along the edges of the
plate is examined. Using Reissner’s plate theory and integral transform technique, the general formulae for
the bending moment and twisting moment in an elastic plate containing cracks located on a single line are
derived. The thickness depended solution is obtained in a closed form for the case in which there is a single
crack in an infinite plate and the results are compared with those obtained from the literature.
Keywords: Reissner Plate Theory, Integral Transform, Stress Intensity Factor, Singular Integral Equation.
1. Introduction
In the classical theory of bending of thin plates, it is pos-
sible to satisfy stress-free conditions at an edge only in
an approximate way, since only two boundary conditions
may be enforced in connection with the bi-harmonic dif-
ferential equation. It is the purpose of this paper to ex-
amine the crack problem by using the theory of bending
of elastic plates developed by Reissner[1] in which the
three physically natural boundary conditions of vanish-
ing bending moment, twisting moment and transverse
shear stress must be satisfied at a free boundary.
The present problem is concerned with the problem of
an infinite plate under uniform uniaxial bending far from
the crack (Figure 1). In the present work the complete
solution is obtained for bending stresses in the vicinity of
a crack tip in a plate taking transverse shear deformation
into account through the use of Reissner’s plate theory.
Using Reissner’s theory and integral transform tech-
niques, the general formulae for the bending mo-
ment,twisting moment and bending stress distribution in
an elastic plate containing cracks located on a single line
are derived.
The procedure employed here is to formulate the
problem in terms of Reissner’s equations. The stress in-
tensity factor is obtained for the case in which there is a
single crack in an infinite plate and the results are com-
pared with those given in the literature.
The mechanical behavior near the crack tip is modeled
using Reissner’s plate theory in the case of an elastic
plate in [2,3].Effect of plate thickness on the bending
stress distribution is included by Hartranft and Sih [2].
The general solution for bending stress in the vicinity of
a crack tip in a plate taking shear deformation into ac-
count through the use of a sixth order plate bending the-
ory of Reissner’s theory is developed by Viswanath [3].

L. CHATTOPADHYAY 518
Figure 1. Plate containing a single crack and subjected to
symmetric bending load.
The solution of the thin plate-bending problem was pio-
neered by Williams [4], who made use of the eigen func-
tion expansion technique and determined the stress dis-
tribution in the neighborhood of a crack. Sih et al. [5]
applied a complex variable method for evaluating the
strength of stress singularities at crack tips in plate ex-
tension and bending problems. The general solution for
finite number of cracks using anisotropic elasticity is
presented by Krenk[6]. Alwar and Ramachandran [7]
showed that the stress intensity factor is nearly linear
through the thickness for thin plates, in the absence of
crack closure. Using finite element method, Mark et al.
[8], Alberto Zucchini et al. [9] computed stress intensity
factors for thin cracked plates. Using complex variable
method Zehnder et al. [10] calculated stress intensity
factor for a finite crack in an infinite isotropic plate. The
present method uses an integral transform technique and
does not assume any symmetry about the co-ordinate
axes. Also the constants appearing in the solution of the
governing differential equations are obtained from the
displacement boundary conditions by defining the de-
rivative of the displacement discontinuities on the crack
surfaces apart from the moment boundary conditions and
continuity conditions. In the present study, the general
formulae for the stress distribution in an infinite elastic
plate containing cracks are derived and the stress inten-
sity factor is determined in a closed form in the case of a
single crack when the plate is subjected to out-of-plane
moments and the results are compared with those from
the literature.
2. Formulation of the Problem
Let us consider the cases of bending or twisting actions
of an infinite plate by moments that are uniformly dis-
tributed along the edges of the plate containing collinear
cracks. We take xy-plane to coincide with the middle
plane of the plate before deformation. The z-axis is as-
sumed to be perpendicular to the middle plane. We de-
note the bending moment per unit length about x-axis by
Myy and about y-axis by Mxx and the twisting moment per
unit length by Mxy. Let Qxand Qy be the shear forces
components. The thickness of the plate is h and we con-
sider it to be small in comparison with other dimensions.
Let us assume that during bending, the plate undergoes
the displacement w perpendicular to xy-plane. In the
present analytical method, we consider the problem in
which an infinite elastic plate, contains cracks located on
a single line is acted upon by applied moments. Let the
co-ordinate system be so chosen that the x-axis coincides
with the line on which the cracks are located. Let L de-
note the union of intervals occupied by the cracks on the
x-axis and M is the interval not occupied by the cracks.
Suppose that a thin plate containing a crack is subjected
to uniform bending or twisting moments at infinity.
Since the crack surface is traction-free the boundary
conditions along the crack surface permitting all of the
free edge conditions for the present problem is given by
the following equations:
The free boundary conditions on the crack surface are
given by,


,0 0,
xy
M
xxL (1)


,0 0,
yy
M
xxL (2)


,0 0,
y
Qx xL (3)
The solution to this problem may be obtained by su-
perposing the simple solution of an uncracked plate un-
der uniform bending moment or twisting moment to that
of a cracked plate with bending or twisting moment ap-
plied to the crack surfaces. That is, the solution may be
obtained by using standard superposition technique and
thus for the purpose of evaluating the crack tip singular
stresses it is sufficient to consider the problem in which
self-equilibrating crack surface loads are the only exter-
nal loads. Thus, it suffices to solve the problem of speci-
fying uniform bending and twisting moment on the crack
segment of the plate. Let the desired system be com-
posed of two parts, one the uniform moment field and the
other a perturbation field due to the crack which dies out
at infinity. While the boundary conditions along the free
edges of the crack require traction free conditions, it is
possible to formulate the problem as one of finding solu-
tions for the perturbation solutions satisfying the field
equations and the boundary conditions
 
*
,0 ,
2
xy
Gx
M
xxL

 (4)

L. CHATTOPADHYAY519
 
*
,0 ,
2
yy
Hx
M
xxL (5)

,0 0
y
Qx

The equilibrium equations are given by,
0
xy y
y
MM
Q
xy


 (6)
0
yx x
x
MMQ
yx


 (7)
0
y
xQ
Q
xy


 (8)
Also, the stress components are the linear combination
of the variable z.
33
12 12 12
σ;σ;σ
xy yy
3
x
x
xy yyxx
Mz Mz
M
z
hh

h
(9)
The strain compatibility equation is given by,
22
2
22
yy xy
xx
x
y yx





  (10)
If we define the moment resultants in terms of the bi-
harmonic function ),( yx

as given by
22 2
22
;;
xyxy
MMM
x
y yx
 
 
 

 (11)
then the governing Equations (6)-(8) are satisfied. From
the compatibility conditions (10), the present problem
reduces to that of solving the bi-harmonic equation in
(, )
x
y

40
  (12)
where,
44
4
422
2
4
4
x
xy y



 

(13)
Let be the Fourier transform of

1(, )G
 y


,
x
y  for
. Then 0y




11
,,ed,
ix
Gy xyxy





0

(14)
Taking Fourier transformation of the bi-harmonic
equation w. r. t the variable x, we get the ordinary differ-
ential equation in as given by

,Gy 

2
2
2
2
d,
dGy y




 0
(15)
whose solutions are given by

 
1
11
,e
y
GyP yQy





0
(16)

 
2
22
,e
y
GyP yQy

  

where is the Fourier transformation of

2
G


,
x
y  for
0y

, and




12 1 2
,,,PPQQ


 are the unknown
functions to be determined. From the moment boundary
conditions we have the following equations,




12
,0,0 0,
yy yy
M
xMx x

 (18)




12
,0,0 0,
xy xy
M
xMx x

 (19)
The bending and twisting moments in terms of
for are given by


1,G


y0y




1
2
1
2
,
1
,e
2π
ix
x
Gy
Mxy y
y




d,0



 (20)




11
2
1
,,e
2π
ix
y
MxyGyy

 


d,0


 (21)




1
1,
,e
2π
ix
xy
Gy
i
Mxy y
y





d,0



 (22)
Similarly we get the bending and twisting moments
for 0y

in terms of


2,Gy

The bending and twisting moments in terms of
for


2,G


y0y

are given by




2
2
2
2
,
1
,e
2π
ix
x
Gy
Mxy y
y


d,0






 (23)





22
2
1
,,e
2π
ix
y
MxyG yy

 


d,0


 (24)




2
2,
,e
2π
ix
xy
Gy
i
Mxy y
y





d,0



 (25)
The displacement components are given by the follow-
ing expressions:
x
w
uz
x

  (26)
y
w
uz
y

  (27)
The displacement boundary conditions are given by


0,
A
xxM (28)


0,Bxx M (29)
where the displacement discontinuities are defined by the
functions A(x), B(x)





12
,0,0 ,
xx
A
xuxuxx
x

L



 (30)
0 (17)





11
,0,0 ,
yy
Bxuxuxx L
x




 (31)

L. CHATTOPADHYAY 520
and the superscripts (1) and (2) denote the components in
the upper half plane and lower half plane 0y0y

respectively.
From the continuity conditions and the moment
boundary conditions we get the four simultaneous equa-
tions for solving




12 1 2
,,,PPQQ



2 1
PP

(32a)
112
QPQ P
2

  (32b)







2 2
112
2
12PPQQA D1



   (32c)
 








2
112
2
13iPPiQQBD1





  
(32d)
Solving the above equations we obtain the un-
knowns as given by,
12 1 2
,,,PPQQ


2
, y

,
M
yG   y (34a)

2
2
,
xx
G
My
y


 (34b)


2
12 2sgn 1
4
i
PP BD





 (33a)

, xy
G
Myi
y


 (34c)


2
1
1sgn 1
4
QA iBD







 (33b) Substituting the values of
 
11
,PQ

 into (21), we
get the bending moment resultants in the upper half plane
, in the transformed co-ordinates as given by the
following equation,
0y


2
2
1sgn 1
4
QA iBD







 (33c)



 

2
11
,sgn1e
8π
ix y
y
D
MxyAy Biyy

 




d,0
(35a)
Performing the inner integral in terms of A(s) and B(s)
we get the bending moment resultants in the upper
half-plane , in terms of the unknown displacement
functions A(s) and B(s) as given by
0y

   
  

22
22
2
1
2
2222
3
1
,d
4π
y
yxsxs y
D
MxyAsys Bsxssy
xs yxs y


 



 
 


 




 

 




d0




(35b)
Substituting the values of
 
22
,PQ

 into (24), we
get the bending moment resultants in the lower half plane
0y

, in the transformed coordinates as given by the
following equation






2
21
,sgn1e
8π
ix y
y
D
MxyAy Biyy

 




d,0
(35c)
Performing the inner integral in terms of A(s) and B(s)
we get the bending moment resultants in the lower
half-plane 0y

, in terms of the unknown displacement
functions A(s) and B(s) as given by



 
  

22
22
2
2
2
2222
3
1
,d
4π
y
yxsxs y
D
MxyAsys Bsxssy
xs yxs y


 



 
 

 
 

 


 
 
 




d0,
 (35d)
Combining the Equations (35b) and (35d) we get the expression for bending moment resultant,


 
  

22
22
2
2
2222
3
1
,d
4π
y
yxsxs y
D
MxyAsys Bsxssy
xs yxs y


 



 
 

 
 

 


 
 
 




d0,
 (36)

L. CHATTOPADHYAY 521
Similarly the expression for the twisting moment


,
xy
M
xy as given by


 
   
22
22
2
22
22
22
3
1
,d
4π
xy
xs yxs y
D
MxyAsxss Bsysy
xs yxs y


 


 
 


 
 


 

  
 



d0,






(37)
where ()
A
sand are the unknown functions to be
determined from the given boundary conditions. The
limiting values as y 0  and y 0  of the bending and
twisting moments along the crack line are given by,
()Bs



2
1
,0 d
4π
y
DBs
M
xs
x
s





 (38a)



2
1
,0 d
4π
xy
D
A
s
M
xs
x
s





 (38b)
By using the conditions (4)-(5) in the above expres-
sions, the interval of integration reduces to L. From the
boundary conditions (4) and the above relations we get
the singular integral equations
  1
d
L
L
As ,
s
GxxL
xs 







(39)
  1
d
L
L
Bs ,
s
HxxL
xs 







(40)
where

2
1
2π
D



, for the determination of un-
known functions A and B on the interval L. Once the
functions A(s) and B(s), are known, the bending
and twisting moments for the crack problem are deter-
mined.
Lx 
3. Single Crack Problem
In order to illustrate the present procedure, we give the
details in the case of a single crack opened by the action
of symmetric bending load applied at the edges of the
plate. In this section, we consider the problem of deter-
mining the distribution of bending stress in the vicinity
of a Griffith crack of length 2c, occupying the interval (-
c, c) on the x-axis in an infinite isotropic elastic plate.
The bending moment resultants and the transverse shear
force components are given by,
222
22
5
x
x
Q wwh
MD
x
xy

 

 




(41)
222
22
5
y
y
Q
wwh
MD y
yx




 

 

(42)

22
22
1
1
x
ww
QD
x
y
xy




 
 




 (43)

22
22
1
1
y
ww
QD
yx
xy




 
 




 (44)
Taking Fourier transform of the above equations w. r. t.
x, we get the displacement component in terms of the
bending moment components in the transformed
co-ordinate system as given by,


2
2
21
x
y
MM
w
wD
y




 



 (45)
The transverse shear force
y
Q are given by,

1
xy
y
MM
Q
yi



 






 (46)
where

is calculated from the equation,
2
10 0
yh






(47)
Taking Fourier Transform of the above Equation (47)
we get

2
22
20
d
ydy





 


(48)
22 22
22 22
12
ee
yy
cc


 
 
 

(49)
where 10
h
 
Since and as we have 0
x
Q0
y
Qy
20c

22
22
1ey
c




 (50)
The constant 0is determined from



,0 0,
1
y
xy
y
Qxxc
MM
Qi
y












(51)
Substituting


,
x
M
y  ,

,
y

M
y  and


,y  in
(46) and using the crack surface boundary condition,


,0 0,
y
Qxx c

L. CHATTOPADHYAY 522
the constant is given by,

2
1
1
2π
D
C
 
B

(52)
From (50), (52) the function

,
x
y  is given by,
 

22
1
,e
2π
c
ixs y
c
Cdd
x
yBs e






s







 (53)
  




22
2
22
1
1
,d
8π
c
xsy
c
Dy
x
yBsKxs




ys






 (54)
  


22
2
2
22
1
2
22
0
0
,1 d
58π5
c
c
y
y
Kxsy
xy D
hh
Bs s
xyx xs y












 


 



 
  

  



 (55)
  

2
2
22
2
2
0
,1
d
58π5
c
c
y
xy DBs
hh
s
Kx
xyx s









 

  (56)
  
2
2
2 2
2
22
0
,1 12
d
00
58π52
c
c
y
xy DBsLt Lt
hh
s
hh
xyx sx
 









 





 



  (57)
  
2
2
2
0
,1 d
058π
c
c
y
x
yD BsLt h
s
h
x
yx







 

 s

(58)
The bending moment

,0
y
M
x along the crack line 0y

, as is given by 0h


  

22
11
,0 dd
4π8π
cc
y
cc
DBs DBs
M
xs
xs xs


 



s (59)
Making use of the boundary condition (4) we get the
singular integral equation for the determination of B(s)
as given by,







2
13d
8π12
c
c
DBsHx
s
xc
xs








 (60)
Solving for B(s), we get the following expression for
B(s),







222
22
114
31π
d
c
c
Bs Das
Hxctx
xs





 



(61)
Substituting the value of B(s) in (38a), the bending
moment for a single crack problem in the limiting case as
is given by, 0h
 







22
22
*
0
sgn 1
,0 d
3
2π
2
c
y
c
Hxc t
x
M
xt
tx
xc
Hx M









 (62)
The bending moment resultant along the crack line
from the above equation is given by,
 




0
22
sgn 1
,0 3
y
xx
M
xM
xc




 (63)
The bending stress

,0
y
x
 along the crack line
0y

, as is given by 0h
 



0
322
12 sgn1
,0 ,
3
yy
Mz xx
x
xc
hxc






 (64)
The bending stress intensity factor KI due to bending
moment at z = h/2 is given by





0
2
1
6
2,03
Iyy
Lim Mc
Kxcx
xc h








(65)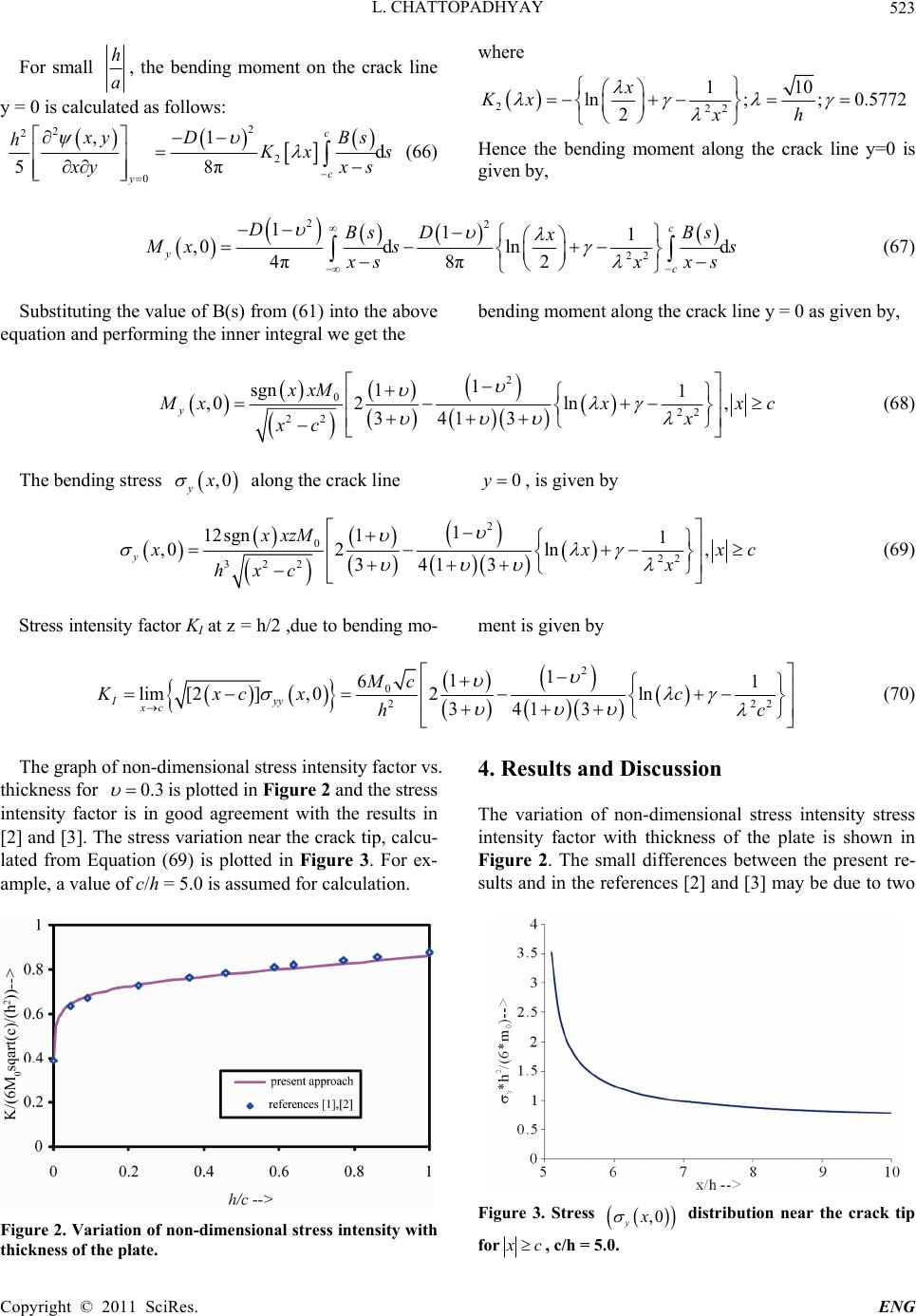

L. CHATTOPADHYAY 523
For small h
a, the bending moment on the crack line
y = 0 is calculated as follows:
 


2
2
2
2
0
,1 d
58π
c
c
y
x
yD Bs
h
K
xs
x
yx








 

 
where

222
110
ln;; 0.5772
2
x
Kx h
x





 




s
(66) Hence the bending moment along the crack line y=0 is
given by,


  
22
22
111
,0d lnd
4π8π2
c
y
c
DBs DBs
x
M
xs s
x
sx
x


 
 








s
(67)
Substituting the value of B(s) from (61) into the above
equation and performing the inner integral we get the
bending moment along the crack line y = 0 as given by,
 







2
0
22
22
1
sgn 11
,0 2ln,
3413
y
xxM
M
xx
x
xc


 




xc









(68)
The bending stress

,0
y
x
 along the crack line 0y

, is given by
 







2
0
22
322
1
12sgn 11
,02ln ,
3413
y
xxzM
x
x
x
hxc



 










xc
  (69)
Stress intensity factor KI at z = h/2 ,due to bending mo- ment is given by








2
0
22
1
1
61
lim[2],02ln
3413
Iyy
xc
Mc
Kxcx c
hc



 
2









 








(70)
The graph of non-dimensional stress intensity factor vs.
thickness for 0.3

is plotted in Figure 2 and the stress
intensity factor is in good agreement with the results in
[2] and [3]. The stress variation near the crack tip, calcu-
lated from Equation (69) is plotted in Figure 3. For ex-
ample, a value of c/h = 5.0 is assumed for calculation.
Figure 2. Variation of non-dimensional stress intensity with
thickness of the plate.
4. Results and Discussion
The variation of non-dimensional stress intensity stress
intensity factor with thickness of the plate is shown in
Figure 2. The small differences between the present re-
sults and in the references [2] and [3] may be due to two
Figure 3. Stress




,0
yx

distribution near the crack tip
for
x
c, c/h = 5.0.

L. CHATTOPADHYAY 524
different approaches being used in [2] and [3]. Hartranft
and Sih [2] used more rigorous method using eigenfunc-
tion expansions for plate bending problem introducing
the effect of plate thickness on crack-tip stress distribu-
tion. The approximate method based partly on finite
element analysis and partly on a continuum analysis us-
ing Irwin’s [11] solution for an infinite plate is used in
[3]. Figure 3 shows the exponential variation of normal
stress component near the crack tip for
x
c, z = h/2. It
decreases away from the crack tip as expected. Future
work in this direction is planned to solve composite plate
problems with delamination.
5. Conclusions
A simple method for determining the analytical expres-
sion for the bending stress distribution, in the vicinity of
a crack in an infinite elastic plate using Reissner plate
theory is explained. The general formulae for the bend-
ing moment and twisting moment in an elastic plate con-
taining cracks located on a single line are derived. The
solution is obtained in a closed form for the case in
which there is a single crack in an infinite plate and the
stress intensity factor is calculated as a function of plate
thickness, when the plate is subjected to symmetric
bending loads. The stress intensity factor is compared
with that obtained in the literature.
10. References
[1] E. Reissner, “The Effect of Transverse Shear Deformation
on the Bending of Elastic Plates,” ASME Journal of Ap-
plied Mechanics, Vol. 12, 1945, pp. A68-A77.
[2] R. J. Hartranft and G. C. Sih, “Effect of Plate Thickness
on the Bending Stress Distribution around Through
Cracks,” Journal of Mathematics and Physics, Vol. 47,
276-291,1968
[3] S. Viswanath, “On the Bending of Plates with through
Cracks from Higher Order Plate Theories,” Ph. D Thesis,
Indian Institute of Science, 1985.
[4] M. L. Williams, “The Bending Stress Distribution at the
Base of a Stationary Crack,” ASME Journal of Applied
Mechanics, Vol. 28, 1961, pp. 78-82.
[5] G. C. Sih, P. C. Paris and F. Erdogan, “Crack-Tip,
Stress-Intensity Factors for Plate Extension and Plate
Bending Problems,” ASME Journal of Applied Mechanics,
Vol. 9, 1962, pp. 306-312.
[6] S. Krenk, “The Stress Distribution in an Infinite Anisot-
ropic Plate with Collinear Cracks,” International Journal
of Solids and Structures, Vol. 11, No. 4, 1975, pp.
449-460.
doi:10.1016/0020-7683(75)90080-3
[7] R. S. Alwar and K. N. Ramachandran, “Influence of
Crack Closure on the Stress Intensity Factor for Plates
Subjected to Bending—A 3-D Finite Element Analysis,”
Engineering Fracture Mechanics, Vol. 17, No. 4, 1983,
pp. 323-333. doi:10.1016/0013-7944(83)90083-8
[8] M. J. Viz, D. O. Potyondy, A. T. Zehnder, C. C. Rankin
and E. Riks, “Computation of Membrane and Bending
Stress Intensity Factors for Thin, Cracked Plates,” Inter-
national Journal of Fracture, Vol. 72, No. 1, 1995, pp.
21-38. doi:10.1007/BF00036927
[9] A. Zucchini, C.-Y. Hui and A. T. Zehnder, “Crack Tip
Stress Fields for Thin Plates in Bending, Shear and
Twisting: A Three Dimensional Finite Element Study,”
International Journal of Fracture, Vol. 104, No. 4, 2000,
pp. 387-407.
[10] A. T. Zehnder and C.-Y. Hui, “Stress Intensity Factors for
Plate Bending and Shearing Problems,” Journal of Ap-
plied Mechanics, Vol. 61, No. 3, 1994, pp. 719-722.
doi:10.1115/1.2901522
[11] G. R. Irwin, “Analysis of Stresses and Strains near the
End of a crack Traversing a Plate,” Journal of applied
Mechanics, 1957, Vol. 24, pp. 361-364.