Journal of Computer and Communications, 2014, 2, 34-40
Published Online November 2014 in SciRes. http://www.scirp.org/journal/jcc
http://dx.doi.org/10.4236/jcc.2014.213005
How to cite this paper: Dung, L.-R., Yang, C.-W. and Wu, Y.-Y. (2014) 3-D EIT Image Reconstruction Using a Block-Based
Compressed Sensing Approach. Journal of Computer and Communications, 2, 34-40.
http://dx.doi.org/10.4236/jcc.2014.213005
3-D EIT Image Reconstruction Using a
Block-Based Compressed Sensing Approach
Lan-Rong Dung1, Chian-Wei Yang1, Yin-Yi Wu2
1Departmentof Electrical and Computer Engineering, National Chiao Tung University, Hsinchu, Chinese Taipei
2Chung-Shan Institute of Science Technology, Taoyuan, Chinese Taipei
Received 16 September 2014
Abstract
Electrical impedance tomography (EIT) is a fast and cost-effective technique that provides a to-
mographic conductivity image of a subject from boundary current-voltage data. This paper pro-
poses a time and memory efficient method for solving a large scale 3D EIT image reconstruction
problem and the ill-posed linear inverse problem. First, we use block-based sampling for a large
number of measured data from many electrodes. This method will reduce the size of Jacobian ma-
trix and can improve accuracy of reconstruction by using more electrodes. And then, a sparse ma-
trix reduction technique is proposed using thresholding to set very small values of the Jacobian
matrix to zero. By adjusting the Jacobian matrix into a sparse format, the element with zeros
would be eliminated, which results in a saving of memory requirement. Finally, we built up the
relationship between compressed sensing and EIT definitely and induce the CS: two-step Iterative
Shrinkage/Thresholding and block-based method into EIT image reconstruction algorithm. The
results show that bloc k-based compressed sensing enables the large scale 3D EIT problem to be
efficient. For a 72-electrodes EIT system, our proposed method could save at least 61% of memory
and reduce time by 72% than compressed sensing method only. The improvements will be ob-
vious by using more electrodes. And this method is not only better at anti-noise, but also faster
and better resolution.
Keywords
EIT, Compressed Sensing, Image Reconstruction
1. Introduction
Electrical Impedance Tomography (EIT) [1] is an imaging technique which calculates the electrical conductivity
distribution within medium using electrical measurements from a series of electrodes on the medium surface. In
this paper, three-dimensional EIT is taken into consideration. Increasing the number of electrodes will increase
the number of independent measurements. This increase will provide more impedance information to the mea-
surement s . For 3D EIT [2], information required extends to multiple layers; a large number of electrodes could
mean better coverage of 3D space. If the number of electrodes increases to 256 electrodes (e.g. 16 planes of 16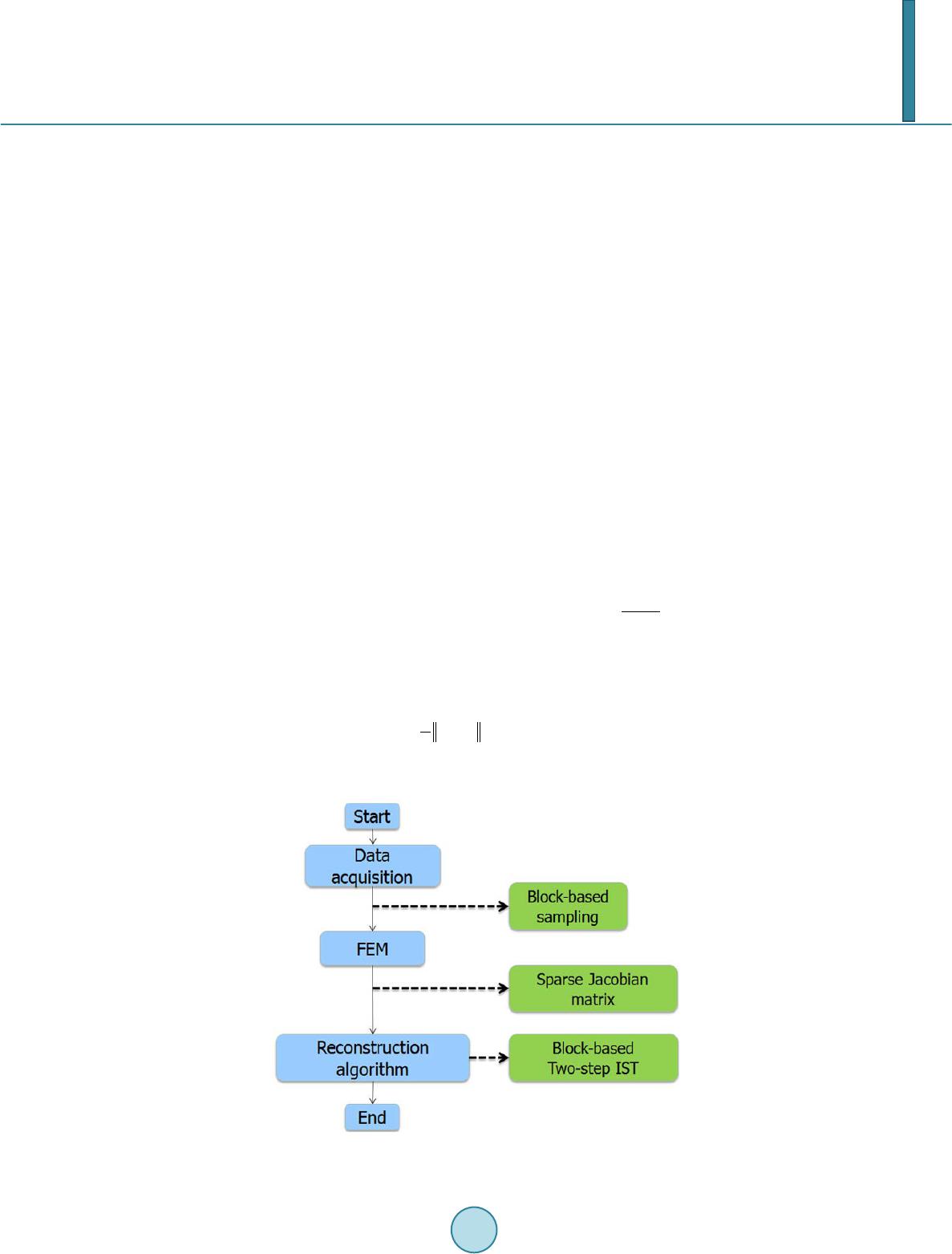

L.-R. Dung et al.
35
electrodes), the number of independent measurement is as high as 64,768. When the problem of a large number
of electrodes and a large number of voxels happens, limitations appearing as large size matrices need to be
stored and large matrix inversion is required.
This paper proposes a time and memory efficient method for solving a large scale 3D EIT image reconstruc-
tion problem and the ill-posed linear inverse problem. We use block-based sampling [3], threshold limits on Ja-
cobian matrix [4] and compressed sensing [5] in 3D EIT reconstruction image. We will introduce this method in
the following section.
In this section, we will present shock filter algorithm in detail. Firstly, the X-ray images need to be noise-free
images. In order to remove noise of X-ray image, we propose an anisotropic diffusion filter, and it’s an adaptive
smoothing technique. Secondly, shock filter algorithm is proposed for the X-ray image segmentation and en-
hancement. Finally, a two-stage shock filter is proposed to optimize the result of shock processing.
2. Block-Based Compressed Sensing in 3-D EIT
In this section, we will illustrate the proposed algorithm in detail. Fig ure 1 is the flow chart of block-based
compressed sensing algorithm with the improved three steps: block-based sampling, sparse Jacobian matrix and
reconstruction algorithm using compressed sensing.
2.1. EIT Image Reconstruction
Most EIT reconstruction methods consider a linear model of the form:
11MMN N
y JXn
× ××
⋅= +
(1)
where
MN
J
×
∈
is the Jacobian or sensitivity matrix and
N
n∈
is the measurement noise, which is assumed
to be uncorrelated white Gaussian. J is calculated from the FEM as
[ ][ ]
[ ]
i
ij j
y
yx
∂
=∂
, and depends on the FEM, the
current injection patterns, the reference conductivity and the electrode models. This system is underdetermined
since
NM
>
. In order to obtain approximation solution; we need to solve the following minimization prob-
lem, which is classical regularization method , called Tikhonov regularization:
2
1
arg min()
2y Jxx
λφ −+
(2)
where
0 λ >
is the regularization parameter and
(x)
φ
denotes penalty function or regularization function.
Figure 1. Flow chart of bloc-based compressed sensing algorithm.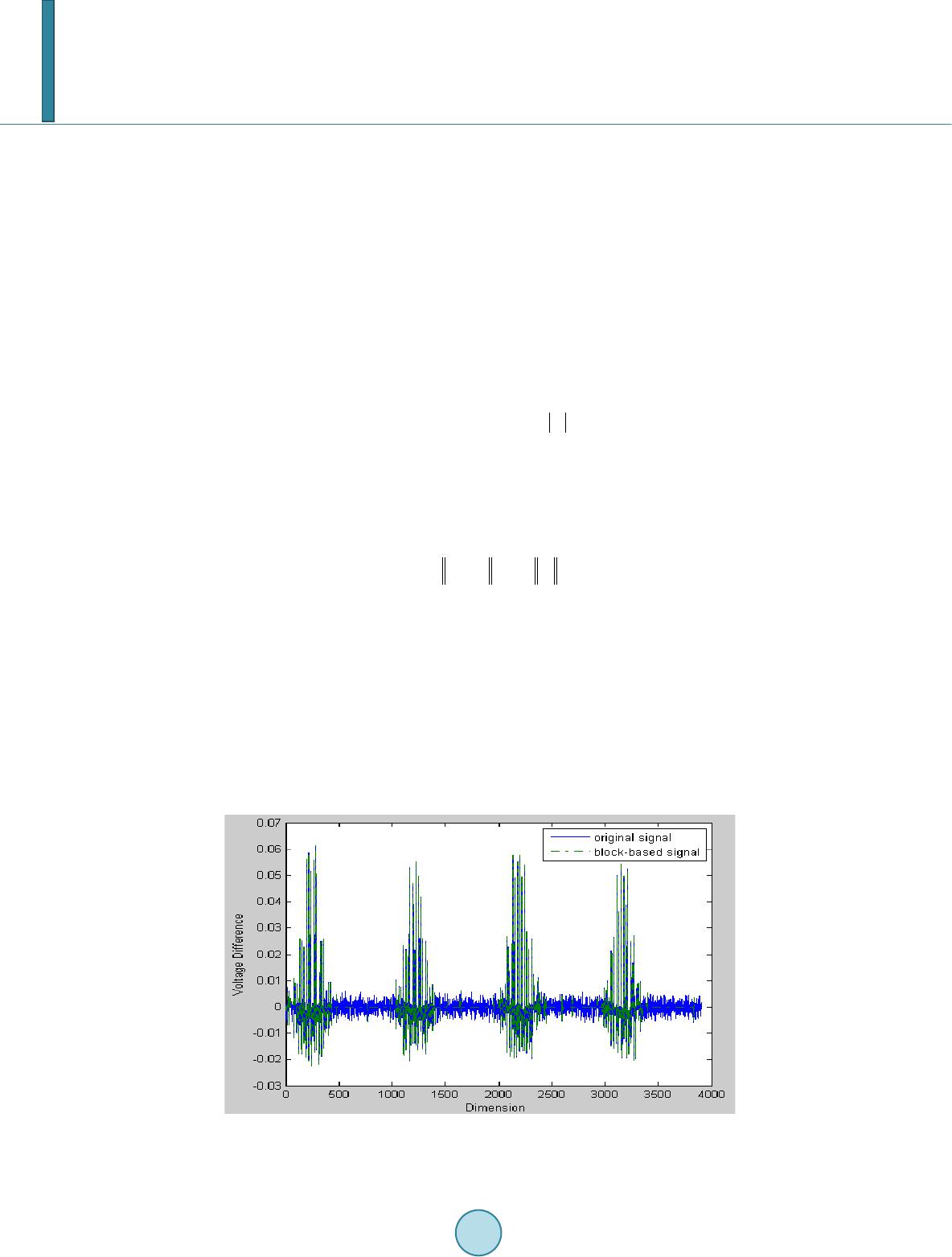

L.-R. Dung et al.
36
2.2. Block-Based Sampling
EIT image is the image of impedance changes. If the measurement data from the specific electrodes has a large
of changes, it represents impedance will have a large of changes near the specific electrodes, vice versa. So we
want to sample the measurement data of huge changes by using block-based sampling. This method will reduce
the size of Jacobian matrix and can improve accuracy of reconstruction by using more electrodes. And then, in
order to retain image quality, the paper use the size of 1/3 original signal as our measurement data, e.g. Figure
2. Consider a class S of signal vectors
JN
x∈
, with J and N integers. This signal can be reshaped into a
JN×
matrix, X and we use both notations interchangeably in the sequel. We will restrict entire columns of to be part
of the support of the signal as a group. That is, signals in a block-spa rse model have entire columns as zeros or
non zeros. The measure of sparsity for X is its number of nonzero columns. More formally, we make the fol-
lowing definition (3).
{ }
1
{[]such that
0 for,1,,,}
JN
KN
n
SXxx R
x nNK
×
==…∈
=∉Ω Ω⊆…Ω=
(3)
We can extend this formulation to ensembles of J, length-N signa ls with common support. Denote this signal
ensemble by
1
ˆ ˆ
{, ,}
J
xx…
, with
N
ˆ,1
j
x jJ∈ ≤≤
. The matrix
ˆ
X
features the same structure as the matrix X
obtained from a block-sparse signal; thus, the matrix
ˆ
X
can be converted into a block-sparse vector
ˆ
x
that
represents the signal ensemble. And then, we use the algorithm
( )
,XK
to obtain the best block-based ap-
proximation of the signal X as follows:
ˆ2,2 2,0
ˆ ˆ
arg min..
S
KX
XXXstXK =−≤
(4)
It is easy to show that to obtain the approximation, it suffices toperform column-wise hard thresholding: let
ρ
be the Kth largest L2-norm among the columns of. Then our approximation algorithmis
( )
,1 ,
, []
ss s
k kkN
XK Xxx= =…
whe re
( )
,1 ,,
,
,where 0,
nn S SSS
K k kNknn
xx
XK Xxxxx
ρ
ρ
≥


==…=

 <


(5)
for each
1n≤≤
. Alternatively, a recursive approximation algorithm can be obtained by sorting the columns of
X by their L2 norms, and then selecting the columns with largest norms.
Figure 2. The measurement data is made up of 3904, and a block-based measurement
data is made up of 1302 for a 64-electrod eEIT s yst em.

L.-R. Dung et al.
37
Accordingly, the measurement data is reduced so that it is made up of only
b
M
entries ratherthan the pre-
vious Mindices. The Jacobian
ij
J
is now determined for each separate sampled measurement i = (d,
b
m
) by
integrating over finite element
Ω
j
from the electrical potential calculated in terms of the measured voltage at
electrode multiplied by the potential induced by injected current
d
I
, i.e.,
,
,:
b
bb
j
dm
bdm jdm
j
V
JJ d
x
φφ
Ω
∂
=== ∇∇Ω
∂∫
(6)
where
,
b
dm
V
represents the sampled measurements resulting from injected current
d
I
. Computing the Jaco-
bian by E q uation (6) yields a reduced matrix of size
b
M
× N.
2.3. Sparse Jacobian and Threshold Limits
Due to the nature of 3D EIT, the sensitivity of the measurements to conductivity changes far from the relevant
electrodes is small. Those values from the sensitivity map would appear to be very small. The zero elements still
remain in the matrix which takes up memory and means they are used in the inverse calculation. The sparse ma-
trix reduction method indicates that values which are very small, typically below a certain threshold, can belo-
cated and transformed to zeros. These zero elements are then eliminated from the Jacobian matrix. This effect
would decrease the total number of non-zero elements of the Jacobian matrix hence reducing the memory sto-
rage. Figure 3 shows an example of the effect after thresholding. The level of sparsity (LOS) is defined as the
number of non-zero elements divided by the total number of elements in the matrix.
The new Jacobian
s
J
after being sparsed is then formed:
max( )
max( )
if %
0 if%
ij ijh
s
ij h
J JtJ
JJt J
≥×

=<×


∑
∑
(7)
whe re the threshold is
%t
of the average value of a sum of h biggest numbers in each row of the Jacobian ma-
trix
max( )h
J
∑
. The Jacobian matrix
s
J
now contains a large amount of zero values.
In order to retain the original image quality, this paper sets the threshold value of 0.5%. And, it can be seen
that LOS is at 50% and approximately 50% of total matrix are transformed to zero and can be eliminated.
2.4. Compressed Sensing: Two-Step Iterative Shrinkage/Thresholding Algorithm (TwIST)
This paper uses Two-step iterative shrinkage/thresholding algorithm [6] which are used in compressed sensing
[7]. TwIST has been proposed to handle a class of convex unconstrained optimization problems for applications
whe re the observation operator is ill-posed or ill-conditioned. Fortunately, TwIST can actually solve the L0 re-
gularized LSP which can be expressed as:
2
0
1
arg min2y Jxx λ −+
(8)
whe re
λ
is the regularization parameter and
0
x
is the L0-norm of the conductivity changes.
The TwIST algorithm has the form
10
()xx
λ
= Γ
(9)
Figure 3. Histogram of the level of sparsity of Jacobian for a
64-electrod eEIT system.
0
100
200
0
0.1
0.5
0.6
1
Level of
sparsity(%)
Threshold value (% of J_max)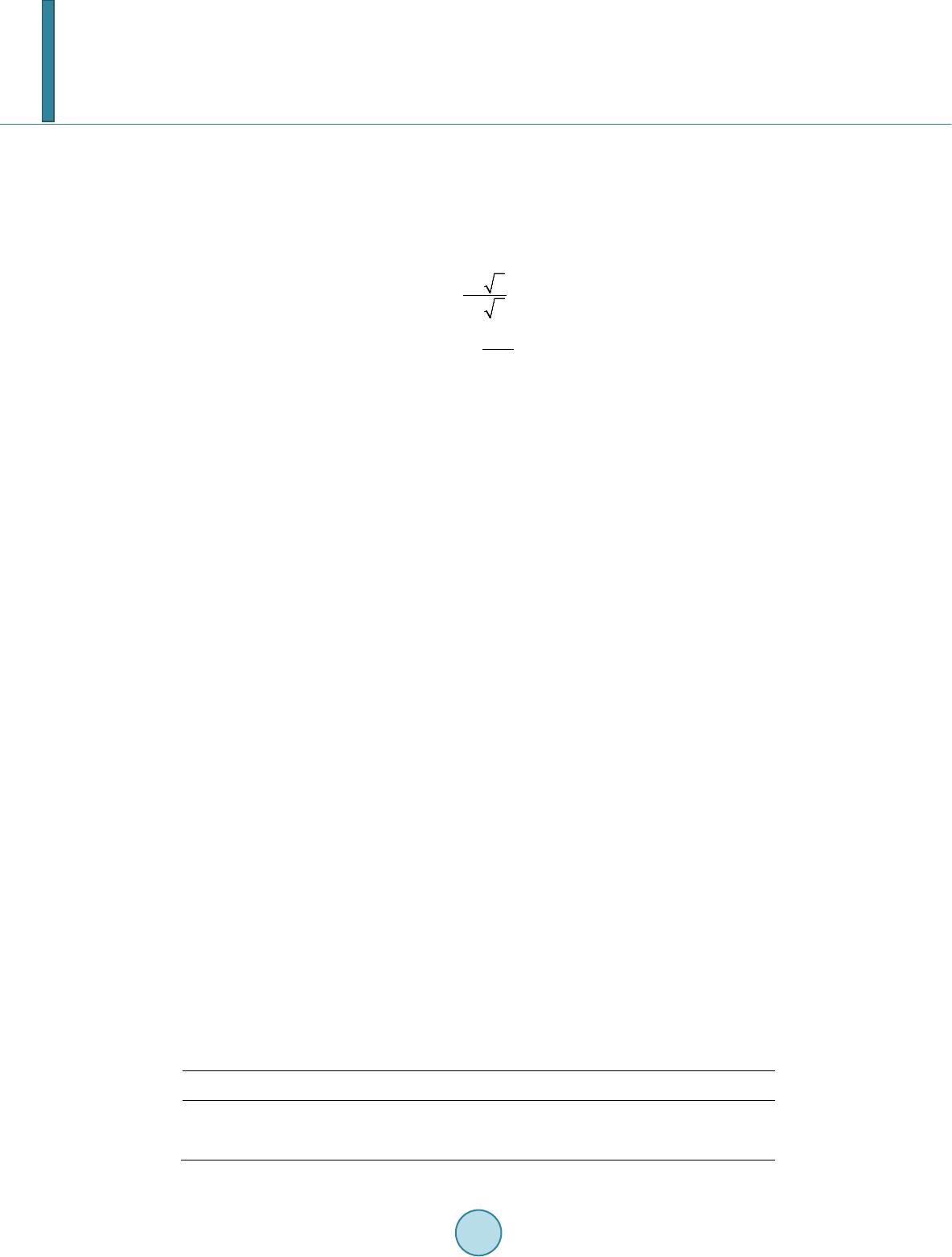

L.-R. Dung et al.
38
( )()
11
1 ()
t ttt
x xxx
λ
α αβ
+−
= −+−+Γ
(10)
for
1 t≥
, where
:
mm
λ
Γ→
is defined as
( )()
( )
T
xxJ yJx
λλ
ψ Γ= + −
(11)
whe re
ψ
λ
is the denoising operator. This paper uses hard threshold function as denoising function. To con-
verge this algorithm, it has the optimal choice of
, αβ
2
1
( )1
1
ξ
αξ
−
= +
+
(12)
2
1
α
βξ =+
(13)
where
ξ
is the real numbers such that
( )( )
min max
01
TT
JJ JJ ξλ λ <≤ ≤=
.
i
(.) λ
is the
th
i
eigenvalue of its
argument .
3. Simulation Results
This paper simulates 3D EIT models by using EIDORS software [8] and modifies EIDORS to use the proposed
algorithm introduced in Section 2. All simulation results are performed on a EIT configuration using adjacent
current stimulation and voltage measurements. We set sparse jacobian threshold value of 0.5%. 10 dB SNR
white Gaussian noise is added in the measurement data.
Figure 4(a) is a 3D EIT model with one circle target. The target is located at (x, y, z) = (0, 0.1, 0.75) and its
radius is 0.2. Figure 4(b) is a 3D EIT model with two circle target. Two targets are located at (x, y, z) = (0.5, 0,
0.75) and (−0.5, 0, 0.75). Their radiuses are 0.2.
3.1. Analysis of Memory and Time
Figure 5 shows comparison of memory storage and reconstruction time for 4 different methods. We use a 3D
EIT model with one circle target at the different number of electrode, and reconstruct them by using 4 different
methods. One-step Gauss Newton and Total variation [9] is conventional EIT reconstruction methods. They
need use more memory usage and calculation time than compressed sensing algorithm. Less than 56-electrode
EIT system, one-step GN is fastest, because there is only the iteration of calculation every computing. For many
electrodes, compressed sensing algorithm will meet significant problems regarding storage space and recon-
struction time. If we use our proposed improved method in large scale 3D EIT, the problems can be solved ef-
fectively. We can use memory efficiently and reduce a lot of reconstruction time.
3.2. Comparisons
The results reconstruct 3D EIT model with one circle target for48-electrodesand 64-electrodes EIT system, as
shown in Figure 4(a). We compare our proposed method with TwIST and use a set of figure of merit to charac-
terize the image qualities based on GREIT [10]. Table 1 and Table 2 show that the average value of AR, POS
and SD is the same at z = 0.55 − 0.95. From the results, 3-D EIT image can retain image quality after using
block-based sampling.
Table 3 and Table 4 show comparison block-based TwIST with one step GN. Block-based TwIST is more
robust to noise and the edges of the objects are more clearly defined. These table also show better spatial resolu-
tion with our propose method. And then, with conventional method the hyper parameter needs to be optimized
with respect to noise level while our method doesn’t need such optimization.
Table 1. Comparison of block-based TwIST with original TwIST for 48-electrodes EIT system.
48-electrodes AR POS (x, y) SD
TwIST 467.5308 0.1113, 0.0026 0.1 048
Block-based TwIST 467.5308 0.1113, 0.0026 0.1048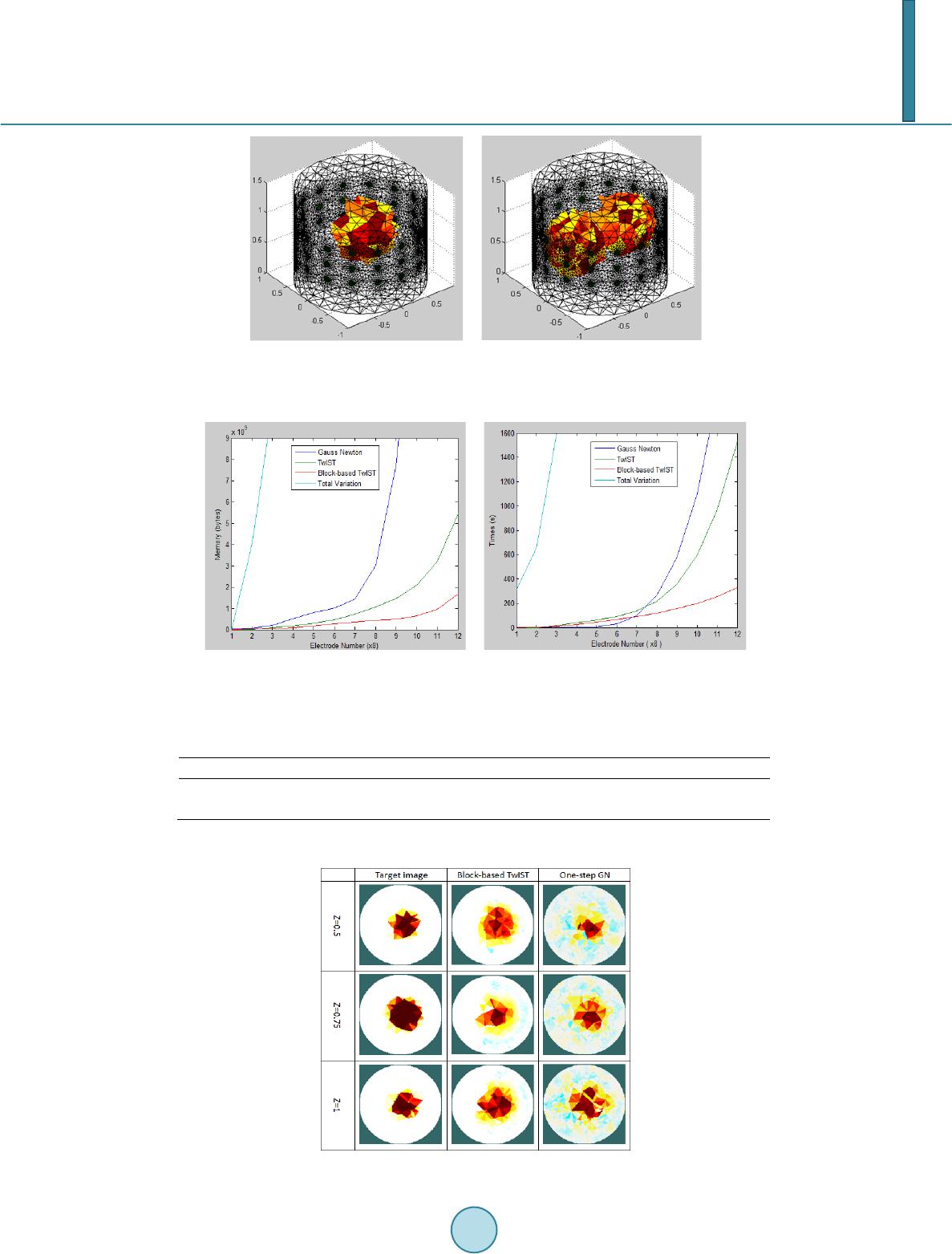

L.-R. Dung et al.
39
(a) (b)
Figure 4. Simulate a 3D EIT model with one and two circle target. (a) One circle target; (b)
Two circle target.
(a) (b)
Figure 5. Analysis of memory and time by using 4 d ifferen t reconstruction image algorithms
in 3D EIT. (a) M e mory; (b) Ti me.
Table 2. Comparison of block-based TwIST with original TwIST for 64-electrodes EIT system.
64-electrodes
AR
POS (x, y)
SD
TwIST 379.5438 0.1086, 0.0016 0.4 431
Block-based TwIST 379.5438 0.1086, 0.0016 0.4431
Table 3. Different reconstruction results with one circus.

L.-R. Dung et al.
40
Table 4. Different reconstruction results with two circuses.
4. Conclusion
In this paper, we presented a time and memory efficient method for solving a large scale 3D EIT image recon-
struction problem and the ill-posed linear inverse problem. For a 72-electrode EIT system, our proposed method
could save at least 61% of memory and reduce time by 72% than compressed sensing method only. The im-
provements will be obvious by using more electrodes. And this method is not only better at anti-noise, but also
faster and better resolution than the conventional method.
References
[1] Ch eney, M., Isaacson, D. and Newell, J.C. (1999) Electrical Impedance Tomography. SIAM Review, 41, 85-101.
http://dx.doi.org/10.1137/S0036144598333613
[2] Vauhkonen, P.J., Vauhkonen, M. and Savo lai, T. (1999) Three Dimensional Electrical Impedance Tomography Based
on the Complete Electrode Model. IEEE Transactions on Biomedical Engineering, 46, 1150-1160.
http://dx.doi.org/10.1109/10.784147
[3] Baran iuk, R.G. , Cevher, V., Duarte, M.F. and Hegde, C. (2010) Model-Based Compressive Sensing. IEEE Transac-
tions on Information Theory, 56, 1982-2001. http://dx.doi.org/10.1109/TIT.2010.2040894
[4] Yang, C.L., Wei , H.Y., Adl e r , A. and Soleimani, M. (2013) Reducing Computational Costs in Large Scale 3D EIT by
Using a Sparse Jacobian Matrix with Block-Wise CGLS Reco nst ructi on. Physiological Measurement, 34, 645-658.
http://dx.doi.org/10.1088/0967-3334/34/6/645
[5] Donoho, D.L. (2006) Compressed Sensing. IEEE Transactions on Information Theory, 52, 1289-1306.
http://dx.doi.org/10.1109/TIT.2006.871582
[6] Bio ucas-Di as, J. and Figueiredo, M. (2007) A New TwIST: Two-Step Iterative Shrinkage/Thresholding Algorithms for
Image Restoration. IEEE Transactions on Image Processing, 16, 2992-3004.
http://dx.doi.org/10.1109/TIP.2007.909319
[7] Tehran i, J.N., Jin , C., McE wan, A. and van Schaik, A. (2010 ) A Comparison between Compressed Sensing Algorithms
in Electrical Impedance Tomography. IEEE Engineering in Medicine & Biology Society, 2010, 3109-3112.
[8] Ad l e r , A. and Lionheart, W.R. B. (2006) Uses and Abuses of EIDORS: An Extensible Software Base for EIT. Ph ysio-
logical Measuremen t, 27, S25-S42 . http://dx.doi.org/10.1088/0967-3334/27/5/S03
[9] Borsic, A., Grah am, B.M., Adler, A. and Lionheart, W.R. B. (2010) In Vivo Impedance Imaging with Total Variation
Regulari zation . IEEE Transactions on Medical Imaging, 29, 44-54. http://dx.doi.org/10.1109/TMI.2009.2022540
[10] Ad l e r , A., Arnold, J.H., Bayford, R., Borsic, A. , Brown, B., Dixon, P., Faes, T.J.C., F rerich s, I., Gagnon, H., Gärber,
Y., Grychtol, B., Hahn , G., Lion heart, W.R. B., Malik, A. , P atterson , R.P., Sto c ks, J., Tizzard, A. , Weil er, N. and Wolf,
G.K. (2009) GREIT: A Unified Approach to 2D Linear EIT Reconstruction of Lung Images. Physiological Measure-
ment, 30 , S35 -S55. http://dx.doi.org/10.1088/0967-3334/30/6/S03