 Journal of Applied Mathematics and Physics, 2014, 2, 1000-1008 Published Online October 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.211114 How to cite this paper: Permana, F.J., Lesmono, D. and Chendra, E. (2014) Valuation of European and American Options under Variance Gamma Process. Journal of Applied Mathematics and Physics, 2, 1000-1008. http://dx.doi.org/10.4236/jamp.2014.211114 Valuation of European and American Options under Variance Gamma Process Ferry Jaya Permana, Dharma Lesmono, Erwinna Chendra Department of Mathematics, Universitas Katolik Parahyangan, Bandung, Indonesia Email: ferryjp@unp a r.a c.id, jdharma@unpar.ac.id, erwinna@unpar.ac.id Received August 2014 Abstract Geometric Brownian Motion (GBM) is widely used to model the asset price dynamics. Option price models such as the Black-Sholes and the binomial tree models rely on the assumption that the underlying asset price dynamics follow the GBM. Modeling the asset price dynamics by using the GBM implies that the log return of assets at particular time is normally distributed. Many studies on real data in the markets showed that the GBM fails to capture the characteristic features of as- set price dynamics that exhibit heavy tails and excess kurtosis. In our study, a class of Levy process, which is called a variance gamma (VG) process, performs much better than GBM model for mod- eling the dynamics of those stock indices. However, valuation of financial instruments, e.g. options, under the VG process has not been well developed. Here, we propose a new approach to the valua- tion of European option. It is based on the conditional distribution of the VG process. We also ap- ply the path simulation model to value American options by assuming the underlying asset log re- turn follow the VG process. Such a model is similar with that proposed by Tiley [1]. Simulation study shows that the proposed method performs well in term of the option price. Keywords Geometric Brownian Motion, European Option, American Option, Variance Gamma Process 1. Introduction Option has become a popular choice as one of instruments for hedging strategy. Nowadays, there are hundreds of traded options in the markets which are tailored to meet the need of market participants. They tailor options depending on the characteristics of underlying assets. The Black-Scholes model which is widely used to value European options and the binomial tree which is well known as the standard model to value American options rely on assumption that the underlying asset price dynamic follows the geometric Brownian motion. It means that the log return of asset is normally distributed. Study on many traded assets showed that distribution of the log return of asset exhibits the excess kurtosis. Its distribution is leptokurtic. Those characteristic features cannot be captured by a normal distribution. Study on some stock indices listed in Indonesia market, i.e. Jakarta Composite Index (JCI), LQ45 and Jakarta Islamic Index (JII), shows that a class of Levy process, i.e. the va- riance Gamma process, can captured those characteristics features [2]. However, modelling of financial instru- ments under the VG process has not been well developed. For valuation of European option, Madan and Seneta  F. J. Permana et al. [3] has proposed a closed form formulae, although it is not easy enough to understand and to apply. Moreover, finding the existing model to value American option under the VG process is still a difficult task. The contribution of this paper is to model the dynamics of Indonesia Stock Indices using VG model and compare the performance to the GBM model according to some performance criteria. We also develop a new approach to value the European plain vanilla options. It is developed by using the conditional distribution of the VG process, that is under the VG process the distribution of the stock indices option, conditionally on the gam- ma time change is log normally distributed. To valuation of American plain vanilla options, we apply the path simulation model which is similar with that apply to American options by Tiley [1] under assumption that the underlying asset price dynamics follow the GBM. To investigate performance of the proposed method applied to European options, we compare the European option prices obtained by the proposed method to those obtained by the Monte Carlo simulation. Performance of the proposed method applied to American options is investi- gated by comparing the obtained American option prices to the European option prices. The rest part of this paper is structured as follows. In Section 2, we describe the stochastic models used in this paper, namely the Variance Gamma (VG process). In this section, we also describe how to value the European and American options under the assumption that the log return of underlying asset price dynamics follows the VG process. In Section 3, we investigate performance of the proposed models. Section 4 is devoted for com- parison between both methods. Conclusions and further research are relegated in the last section. 2. Modeling the Asset Price Dynamics under the VG Process 2.1. The VG Process The VG process with three parameters was introduced by Madan et al. [4] as a development of the two parame- ters VG process proposed in Madan and Seneta [3] and Madan and Milne [5]. The two parameters control the volatility and kurtosis. The third parameter to control skewness is added by generalizing the VG model. Consider a Brownian motion with drift and volatility represented by following stochastic process: where is a standard Brownian motion. The VG process is obtained by evaluating Brownian motion at a random time change given by a gamma process. The Gamma process with mean rate and va- riance rate is the process of independent gamma increments over non-overlapping intervals of time . By using subordinate of Brownian motion process, we define the VG process in terms of Brownian motion and gamma process as follows: ()( ) ( ) ;, ,;1,; ,Xt bGt σνθυ θσ = The three parameters involved in the VG model are: : volatility of Brownian motion which controls volatility : variance rate of the gamma time change which controls kurtosis : the drift in Brownian motion which control skewness. The first four central moments of the VG process are () ( ) ( )( ) ( ) ( ) ( )( ) ( ) ( ) ( )( ) ( ) () () 222 332 2 442224342242 2 , (, (23 , (31263 63. EXt t E XtEXtt E XtEXtt E XtEXttt θ θν σ θ νσθν σνσθνθνσσθν θν = −=+ −=+ −= +++++ Under the risk-neutr al process, the asset price dynamics following the VG process is given by: ()( )() ( ) 0 exp;,,S tSrtX tt συθ ω =++ (1)  F. J. Permana et al. where . Then the asset’s log return can be modeled as follow: ( )( )()()() loglog0; ,,; ,,RtStSrt Xtt ct Xt συθ ωσυθ = −=++=+ where , is the risk-free interest rate and is volatility. Parameters of model can be estimated by applying the moment matching method [6]. Madan and Seneta [3] showed that the VG model used to model the log of S&P500 In de x performed quite well. Other models to determine the index option have been developed by some researchers for indices other than indices in the ISE [7]-[10]. In this paper we will use the VG process to model the log return of the JCI, LQ45 and JII Indices. 2.2. Valuation of European Option Madan and Seneta [3] derived closed form expressions for pricing European plain options under the VG process. The formulae are similar with those derived under the Black-Sholes model, but they are not simple. Instead of the cumulative standard normal distribution functions, the cumulative distribution functions in the formulae in- volve the modified Bessel function of the second kind and the degenerate hypergeometric function of two va- riables. Here, we will proposed a new approach to valuation of the European option. In our proposed model, we will take the advantage of the conditional distribution property of the VG process intro d uced by Luciano and Schoutens [8]. Assuming the asset price process follows Equation (1) then we can obtain the conditional distribution, conditionally on , as follows: is normally distributed with mean: and variance: . It means that is normally distributed with mean: and variance: . In other words, is lognormally distributed with location parameter ()( ) ( ) log 0m xScTx θ = ++ and scale parameter . Then we can calculate the mean of , conditionally on , as follows: ( )( ) ( ) ( ) 2 1 0 exp2 ESTGTxScTxx θσ == ++ . Now, we can calculate the call option price with the strike price by the following integral: ()( ) ( ) ( ) ()()()( ) ( ) 0 exp max,0 exp;,;,dd. YX K crTESTK T rTyKfymxsxgxyx υ ν ∞∞ =−− =−− ∫∫ where is a probability density function of lognormal distribution and is a probability density function of gamma distribution. The last expression can be easily calculated numerically, for example by applying double quadrature integral provided by Matlab. Put option price can be obtained by apply- ing the Put-Call parity as follows: ()( ) ( ) exp pcrTKE ST =−− − , where ( ) ( ) ( )( ) ( ) 0 ;, d X T ESTEST GTxgxx υ ν ∞ == ∫ . 2.3. Valuation of American Option The standard approach to valuation of an American option is to use one factor of the continuous stochastic mod-  F. J. Permana et al. el describing the asset price dynamics, and then to create a lattice, i.e. a binomial tree, to represent the asset price movements. The option price is valued by backward induction on the lattice. Valuation of the American option by using a lattice model is extremely difficult. One approach to valuation of the American option is by applying the simulation model. Many literatures thought that the simulation model, e.g. the Monte Carlo simulation, can- not be used to value the American option efficiently [11]-[13]. Simulation models consume large amounts of computer processing time and also too much execution time. Fortunately, Tiley [1] has developed an algorithm so that the path simulation model can be applied to the American option more efficiently. In the algorithm, Til- ley sampled free-arbitrage underlying asset prices, then the option price is estimated from that sample paths. Here, we will adopt that approach to valuation the American option under the VG process assumption. The algorithm begin by generating a finite sample of underlying asset paths (for example, see [14]). Each path has epochs. It is assumed that the k-th path in the sample is represented by the sequence: ()() ()() 0, ,1, ,2, , ,SSk SkSkN . Reorder the asset price paths by the asset price, then we make partition for the set of paths into distinct bundles of paths each. Let be defined the intrinsic value of the option on path at epoch as: ( )( ) { } ( ) { } max0,, for call option ,,for put option max 0, ST K I ktKST − =− The holding value is defined as the expectation current value option over all paths in the bundle containing the path- . In the same bundles, the holding values are equal. The key of algorithm is to determine the path index as the sharp boundary to make decision to hold or to exercise the option. The exercise-or-hold variable takes 1 for , and takes 0 for The indicator variable is estimated as follows ( )( )() 1, if ,1 and ,0 for all ,0, otherwise yktyksst zkt == < = when the option is exercised, the current option value equals to intrinsic value, and the other hand the current option value equals to holding value when the option is hold. The option price at time 0 can be estimated by backward induction. However, the accuracy of estimation depends on the choosen partition of the paths. 3. Simulation Study To investigate performance of the VG process to model the log return of assets traded in Indonesia market, we will compare performances of the VG process to the GBM model. We collect daily observations of JCI, LQ45 and JII Indices from July 2004 to December 2011. The dynamics of those indices and their log indices is give n in Figure 1. We model those indices’ dynamics by GBM and VG process given by (1). GBM model assumes that the log return of ind ex is normally distributed. However, such assumption is vi- olated for Indonesian Indices data as shown by descriptive statistics and histogram of indices’ log return vs. normal density given by Table 1 and Fi gure 2 below. Descriptive statistics and histogram of log return index of all those indices show that the distribution of log return has positive kurtosis and non-zero skewness. This find- ing gives an indication that the GBM model is not an appropriate model. For modelling the dynamics of Indonesian Indices using variance gamma model, we employ density of VG as given in [3]. Model’s parameters are then estimated by matching the first four moments of log returns to the first four moments of VG process as described in [6]. The parameter estimates of the VG process and GBM are given in Table 2. Note that both GBM and VG models given the same volatility parameter estimates for all three indices. We also compare the performance of the VG model and GBM model by generating 100 paths using Monte Carlo simulation and compare the descriptive statistics of the original data (OG) and the simulated paths based on those two models for all those indices. For simulation gamma process we can refer to [14 ]. The results are tabulated in Table 3 below. The empirical density, the normal density and the VG density for all indices are given in Figure 3. 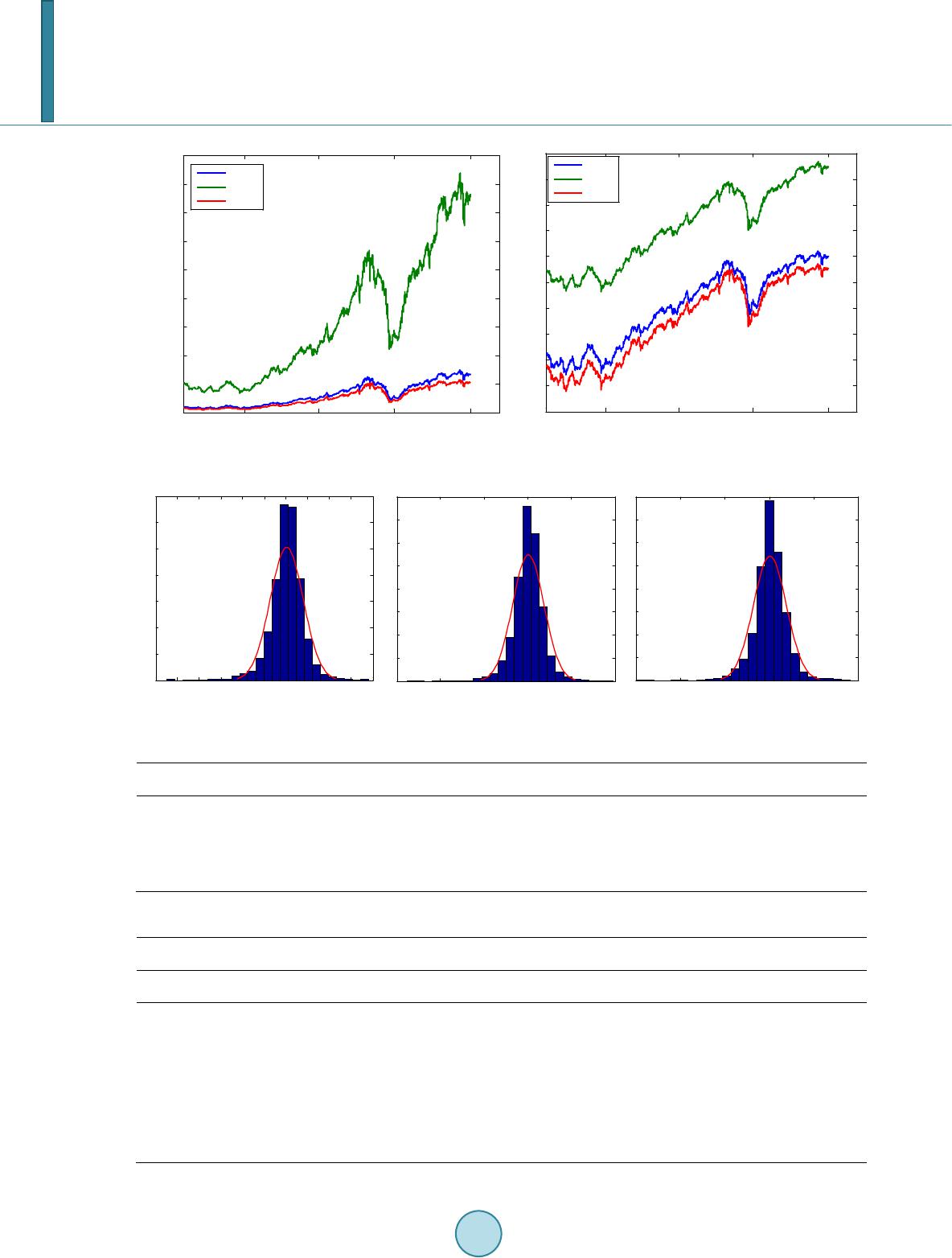 F. J. Permana et al. Figure 1. Dynami cs of indonesian indices (left) and their log indices (right). Figure 2. Histogram of Index log return vs. Normal density, JCI (left), LQ45 (middle) and JII (right). Table 1. Descriptive statistics of log return of indonesia indices. Index Mean Standard Deviation Skewn ess Kurtosis JCI 0.0007 0 .0153 −0 .6909 9 .2000 LQ 45 0.0007 0 .0180 −0 .5968 9 .3325 J II 0 .0007 0 .0185 −0 .5437 8 .8234 Table 2. Parameter estimates of VG process and GBM. JCI LQ4 5 JII VG Pr oc ess VG Pro ces s VG Pr oc es s 0.0024 2.0667 −0.0017 0.0153 0.0024 2.1108 −0.0017 0.018 0.0024 1.9 411 −0.0017 0 .0185 GBM GB M GBM 0.0009 0.0 153 0.0009 0.018 0.0 009 0.0185 Jul00 Jan03Jan06Jan09 Dec11 0 500 1000 1500 2000 2500 3000 3500 4000 4500 time Index Dynamics of Indonesian Indices (July 2000-Dec 2011) : LQ45 : JKSE : JKII Jul00 Jan03Jan06Jan09Dec11 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 time Log index Dynamics of Indonesian log Indices (July 2000-Dec 2011) : LQ45 : JKSE : JKII -0.12 -0.1 -0.08 -0.06 -0.04 -0.02 00.02 0.04 0.06 0.08 0 100 200 300 400 500 600 700 Daily logreturn of JKSE -0.15 -0.1 -0.05 00.05 0.1 0 100 200 300 400 500 600 700 800 Daily logreturn of LQ45 -0.15 -0.1 -0.05 00.05 0.1 0 100 200 300 400 500 600 700 800 Daily logreturn of JKII  F. J. Permana et al. Table 3. Descriptive statistics of original data and simulated paths. Path M ean S ta ndard Deviation Sk ewness Kurtosis JCI OG 0.0007 0.0153 −0 .6909 9 .2000 GBM 0.0007 0.0153 −0.01 27 2.9834 VG 0.0007 0.0156 −0.6488 9.581 LQ45 OG 0.0007 0.0180 −0 .5968 9 .3325 GBM 0.0007 0.0180 0.0001 2.9901 VG 0.0007 0.0181 −0.5509 9.2573 JII OG 0.0007 0.0185 −0 .5437 8 .8234 GBM 0.0007 0.0185 0.0036 2.9897 VG 0.0007 0.0187 −0.5440 8.9276 Fro m Table 3 and Figure 3 it is clear that both VG and GBM model can match the mean and standard deviation of the original log return indices, however the GBM model fails to match the skewness and kurtosis compared to the VG model. Therefore the VG model outperforms the GBM in matching the skewness and kurto si s. To investigate performance of our proposed model, we compare the option prices obtained by our proposed model to those obtained by the Monte Carlo simulation for several assets’ parameters. For the Monte Carlo si- mulation, we generate 10,000 terminal asset prices to get the call option prices, then we repeat it 1000 times. We choose the mean of those option prices as the estimate of call option price. Suppose that the risk-free interest rate is 5% per annum and the time of maturity of option is 1 year and other parameters of the asset price’s dynamics are , , , and the current stock index . The option prices obtained by our proposed method and the Monte Carlo simulation for different strike prices (On The Money, In The Mone y and almost At The Mone y options) are given in Table 4. Standard errors for the Monte Carlo simulation are written in italic. Results tabulated in Table 4 show that the prices obtained by the proposed method (denoted by VG) are very close to those obtained by the Monte Carlo simulation (MC). The relative errors are less than 1%. Note that we calculate the relative error as: ( ) relative error100VGMCMC =∗− . It means that our method performs very well in terms of the option price. It is difficult to find another model to get the American option prices under the VG process. In that reason, to investigate performance of the path-simulation model applied to American options, we compare American op- tion prices obtained by the path-simulation model to European option prices obtained by the VG model and the Monte Carlo simulation. Theoretically, the European option prices is cheaper than the American option prices. Suppose that the basket parameters are given as follow: , per annum, , , , , year. The number of epochs for each path , the number of paths which is divided into 70 bundles . Here, there are 75 paths for each bundle . Simulation results are given in Table 5. Simulation results show that American call option prices obtained by path simulation model are higher than European call option prices obtained by the VG model and the Monte Carlo simulation. The discrepancies are less than 11%. Although we did not compare American option prices obtained by the path simulation model to those obtained by other models, the discrepancies between American and European options prices are shown by Table 5 is suitable with theory given literatures. 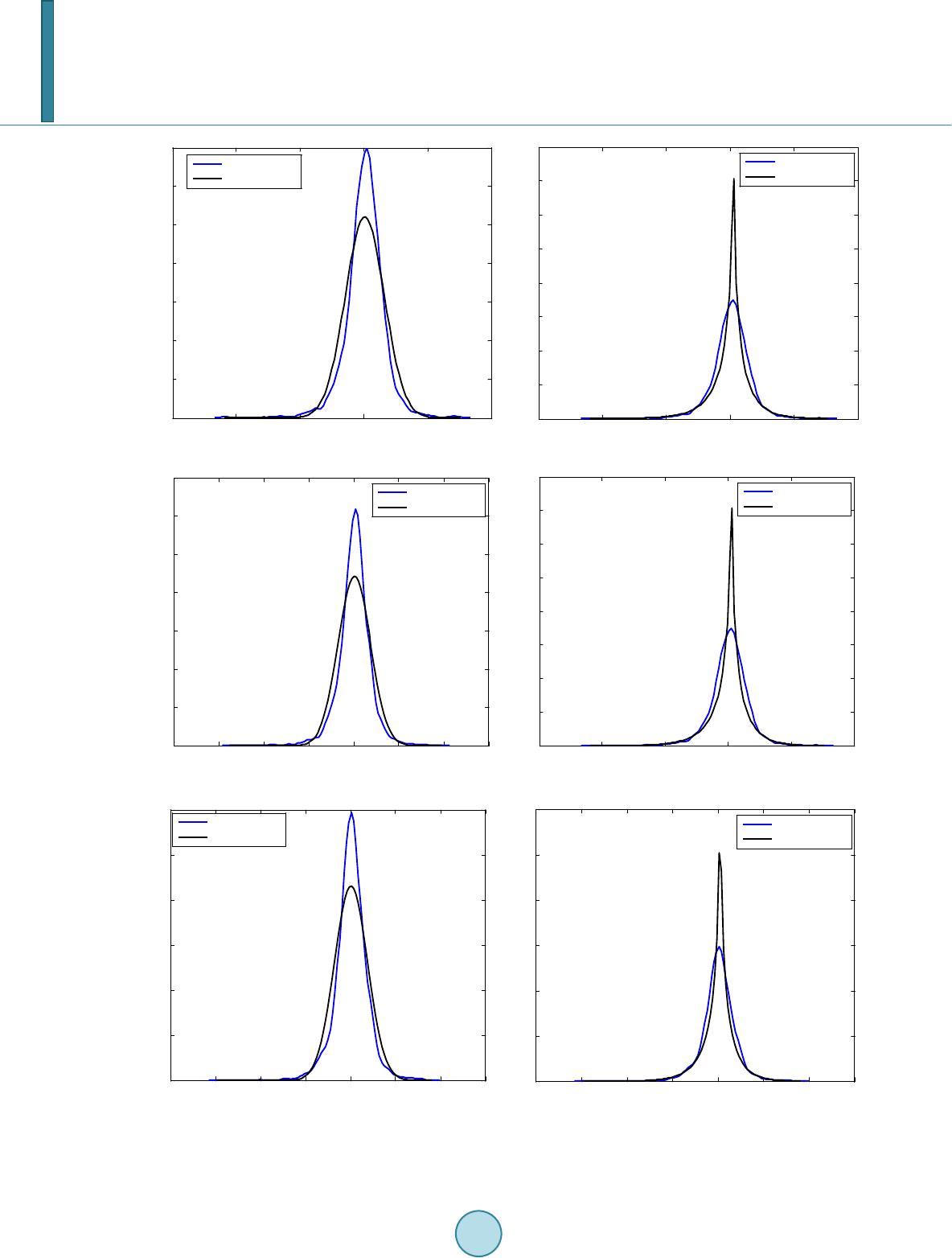 F. J. Permana et al. Figure 3. Empirical vs. Normal density (left) and Empirical vs. VG density (right) of JCI (above), LQ45 (middle) and JII (below). -0.15 -0.1 -0.05 00.05 0.1 0 5 10 15 20 25 30 35 log return density empirical density normal density -0.15 -0.1 -0.05 00.05 0.1 0 10 20 30 40 50 60 70 80 log return density empirical density VG density -0.2 -0.15 -0.1 -0.05 00.05 0.1 0.15 0 5 10 15 20 25 30 35 log return density empirical density normal density -0.15 -0.1 -0.05 00.05 0.1 0 10 20 30 40 50 60 70 80 log return density empirical density VG density -0.2 -0.15 -0.1 -0.05 00.05 0.1 0.15 0 5 10 15 20 25 30 log return density empirical density normal density -0.2 -0.15 -0.1 -0.05 00.05 0.1 0.15 0 10 20 30 40 50 60 log return density empirical density VG density  F. J. Permana et al. Table 4. Put and call option prices obtained by the proposed method vs. by the monte carlo simulation for various strike prices. Strike Price Call Option Price Put Option Price MC VG Rel. Error (%) MC VG Rel. Error (%) 94 16.4577 1 6.453 4 −0.02 61 6.5 034 6.5 090 0.0 861 0.0074 0.0033 99 13.8172 1 3.820 2 0.0 217 8.6345 8.6 319 −0.0301 0.0066 0.0037 104 11. 5179 1 1.520 0 0 .0182 11.0900 1 1.087 9 −0.01 89 0.0063 0.0042 Table 5. European call option prices obtained by the monte carlo simulation and the VG model vs. American Call option prices obtained by path simulation model. Strike Price European Call Option Price American Call Option Price MC Model VG Model Simulation Path Model 94 16.4577 1 6.453 4 16. 7663 99 13.8172 1 3.820 2 15. 2811 104 11. 5179 1 1.520 0 1 1.974 2 4. Conclusions and Further Research Based on our analysis in modeling Indonesia Stock Indices we can conclude that the VG model performs very well compared to the GBM model. The VG model can match the first four moments, including skewnesss and excess kurtosis. We develop a new method to the valuation of the stock indices option based on the conditional distribution of the VG process. Simulation study shows that the proposed method performs very well in term of the stock indices option price. Application the path simulation to value American options by assuming the log return of underlying asset follows the VG process also performs well. The closed form expressions proposed by Madan and Seneta [3] can be more attractive compared to our pro- posed model to valuation of European plain vanilla options, but our proposed model has an advantage. Our model can be extended to valuation of basket options. It is still as our ongoing research. To pursue for further research, we would also like to apply the proposed method for valuing European and American options to the real data in Indonesia market. We want to compare the option prices obtained by the proposed method to those obtained by Black-Scholes. Other directions for further research include comparison the performance of the VG model and the GBM model in VaR calculation. Acknowledgements Funding of this research from the Directorate of Research and Community Services, Indonesian Directorate General of Higher Education (DP2M-DIKTI) under the Research Grant Competition 2014-2016 scheme is highly acknowledged. References [1] Tilley, J. (1993) Valuing American Options in a Path Simulation Model. Transactions of the Society of Actuaries, 45, 83-104. [2] Lesmono, D. and Permana, F.J. (2011) Modelling Dynamics of LQ45 Index using Potential Diffusion. Paper Presented at 7th ICIAM, 18-22 July 2011, Vancouver, British Columbia, Canada [3] Madan, D. and Seneta, E. (1990) The Variance Gamma (V.G.) Model for Share Market Returns. Journal of Business, 63, 511-524. http://dx.doi.org/10.1086/296519  F. J. Permana et al. [4] Madan, D., Carr, P.P. and Chang, E.C. (1998) The Variance Gamma Process and Option Pricing. European Finance Review, 2, 79 -10 5. htt p:// dx. do i.org/ 10 .10 23/ A:1 0097 03 4315 35 [5] Madan, D. and Milne, F. (1991) Option Pricing with VG Martingale Components. Mathematical Finance, 1, 39-55. http://dx.doi.org/10.1111/j.1467-9965.1991.tb00018.x [6] Cont, R. and Tankov, P. (2004) Financial Modelling with Jump Processes. Chapman and Hall/CRC. [7] Bailey, W and Stulz, R.M. (1989) The Pricing of Stock Index Options in a General Equilibrium Model. Journal of Financial and Quantitative Analysis, 24, 1-12. http://dx.doi.org/10.2307/2330744 [8] Luciano, E. and Schoutens, W. (2005) A Multivariate Jump-Driven Financial Asset Model. ICER Applied Mathemat- ics Working Paper No. 6. [9] Miller, M.H., Muthuswamy, J. and Whaley, R.E. (1994) Mean Reversion of Standard & Poor’s 500 Index Basis Changes: Arbitrage-Induced or Statistical Illusion? The Journal of Finance, 49, 4 79-51 3 . http://dx.doi.org/10.1111/j.1540-6261.1994.tb05149.x [10] Nagarajan, T. and Malipeddi, K. (2009) Effects of Market Sentiment in Index Option Pricing: A Study of CNX NIFTY Index Option. MPRA Paper No. 17943. [11] Dyer, L. and Jacob, D. (1991) An Overview of Fixed Income Option Models. The Handbook of Fixed Income Securi- ties, 73, 742. [12] Geske, R. and Shastri, K. (1985) Valuation by Approximation: A Comparison of Alternative Option Valuation Tech- niques. Journal of Financial and Quantitative Analysis, 20, 45-71. http://dx.doi.org/10.2307/2330677 [13] Tilley, J. (1992) An Actuarial Layman’s Guide to Building Stochastic Interest Rate Generators. Transactions of the Society of Actuaries, 44, 509-564 . [14] Avramidis, A.N., L’Ecuyer, P. and Tremblay, P.-A. (2003) Efficient Simulation of Gamma and Variance-Gamma Processes . Proceedings of the 2003 Winter Simulation Conference.
|