Journal of Signal and Information Processing, 2011, 2, 112-116
doi:10.4236/jsip.2011.22015 Published Online May 2011 (http://www.SciRP.org/journal/jsip)
Complex Hilbert Transform Filter*
Juuso T. Olkkonen1, Hannu Olkkonen2
1The VTT Technical Research Centre of Finland, Finland; 2Department of Applied Physics, The University of Eastern Finland, Kuo-
pio, Finland.
Received March 21st, 2011; revised April 25th, 2011; accepted April 28th, 2011.
ABSTRACT
Hilbert transform is a basic tool in constructing analytical signals for a various applications such as amplitude modu-
lation, envelope and instantaneous frequency analysis, quadrature decoding, shift-invariant multi-rate signal process-
ing and Hilbert-Huang decomposition. This work introduces a complex Hilbert transform (CHT) filter, where the real
and imaginary parts are a Hilbert transform pair. The CHT filtered signal is analytic, i.e. its Fourier transform is zero
in negative frequency range. The CHT filter is constructed by half-sample delay operators based on the B-spline trans-
form interpolation and decimation procedure. The CHT filter has an ideal phase response and the magnitude response
is maximally flat in the frequency range 0 ≤ ω ≤ π. The CHT filter has integer coefficients and the implementation in
VLSI requires only summations and register shifts. We demonstrate the feasibility of the CHT filter in reconstruction of
the sign modulated CMOS logic pulses in a fibre optic link.
Keywords: Hilbert Transform, Analytic Signal, Fractional Delay Filters
1. Introduction
Hilbert transform has an essential role in constructing
analytical signals for a variety of signal processing ap-
plications, for example in envelope and instantaneous
frequency analysis and in design of amplitude modula-
tors and digital quadrature encoders. The recent applica-
tions include Hilbert-Huang decomposition [1], the
shift-invariant wavelet transform algorithms [2-5], geo-
physical [6], seismic, ultrasonic radar and biomedical
signal analyses [7-11]. The Hilbert transform theory is
well established, but the computational methods are still
under development. The frequently used methods are
based on the fast Fourier transform (FFT) [7,12]. Also
other methods have been proposed, such as the paramet-
ric modelling approach [13,14] and digital filtering
[12,15].
In this work we describe a complex Hilbert transform
(CHT) filter, where the real and imaginary parts are a
Hilbert transform pair. The CHT yields analytic signals,
whose Fourier transform is zero in negative frequency
range. We construct the CHT filter by half-sample delay
operators based on the B-spline transform. The phase re-
sponse of the CHT filter is ideal and the magnitude re-
sponse is maximally flat in the frequency range 0 ≤ ω ≤ π.
2. Theoretical Considerations
2.1. Hilbert Transformer
Let us denote the frequency response of the z-transform
filter


H
z as


e
njn
nn
nn
Hzhz Hh





 (1)
where ,
n
hn N

is the impulse response of the filter.
Correspondingly, we have the relation


πHz H 

 (2)
Our purpose is to design a Hilbert transform operator
 for the discrete-time signal n
x
, 0,1, 2,n as



  
X
zzXz (3)
where


z denotes the Hilbert transform filter.
The frequency response of the Hilbert transform op-
erator is defined as


sgnj

  (4)
where the sign function is

1, for0
sgn 1, for0







 (5)
*This work was supported by the National Technology Agency of Fin-
land (TEKES).

Complex Hilbert Transform Filter 113
In this work we apply the Hilbert transform operator in
the form
 
π2
esgn
j



 (6)
2.2. Hilbert Transform Filter
We define the half-sample delay filter

Dz by the
infinite impulse response (IIR) structure
 

1/ 2
A
z
Dz zBz

 (7)
where

A
z and

Bzare polynomials in 1 z

. In fre-
quency domain we have
 
/2
ej BA


  (8)
The corresponding quadrature mirror filters are

A
z and

Bz. Due to (2) we have in frequency
domain relation between them



2
πeπ
j
BA



  (9)
Now we may construct the Hilbert transform operator
as
 

2
12π2
πee e
j
j
DD




 
  (10)
In z transform domain we have the Hilbert transform
filter
 
 
1
A
zB z
zDzD zBzAz



 (11)
2.3. Design of the Half-Sample Delay Filter
Our approach is to construct a half-delay filter

1/2
p
Dz z

, which has an exactly linear phase. We
apply the fractional delay (FD) filter design method
based on the B-spline transform interpolation and deci-
mation procedure for implementation of the fractional
delays NM

 (,NM) [16]. The FD filter has
the following representation

  
1
,, N
pp
M
p
DNMzz zFz
z








 (12)
where

pz
 is the p’th order discrete B-spline and

F
z the polynomial

1
11 1
11 1
1
p
p
MMk
pp
ko
z
Fz z
MzM

 




 

  (13)
The half-sample delay operator

1/2
p
Dz z

 is
yielded by inserting 1N and 2
M
 in (12)
 

1, 2,p
p
p
Qz
Dz Dzz

 (14)
where

Qzis a polynomial in 1 z. The phase of the
half-delay operator is exactly linear in the frequency
range ππ


 independently of the B-spline order
p.
Example. For the discrete B-spline order p = 4

12
4
14
6
zz
z 


 (15)
we have

123
4
12323
48
zzz
Qz


 (16)
The phase spectrum of the Hilbert transform filter








44 44
zQzzzQz 

 follows exactly
the definition (4) in the frequency range ππ

 .
The IIR type Hilbert transform filter can be implemented
by the inverse filtering procedure [16].
2.4. Adjustment of the Magnitude Response
The Hilbert transform filter (11) designed by the B-spline
transform has an ideal phase response. However, for
even p the half-sample delay operator

p
Dz has zero
magnitude response at π


due to the zero at 1z

.
Therefore the magnitude response Hilbert transform filter
intensifies at 0


and π. Usually the main demand for
the Hilbert transformer is a maximally flat magnitude
response centered at π2


. However, we may revisit
the design by defining the Hilbert transform filter as




1
1
pp
zDzD z



 (17)
For even p the half delay operator


1p
Dz
 has a
pole at 1z

 (π


). Hence, the

1
1
p
Dz

 opera-
tor has a zero at 1z

(0


).
Example. For the B-spline of the order p = 5

123
5
111 11
24
zzz
z 



 (18)
we obtain

1234
5
1 7623076
384
zzzz
Qz


 
 (19)
The magnitude response of the Hilbert transform filter






45
zDzDz

 has a flat maximum at π2


(Figure 1). The flatness of the magnitude response in-
creases by using the B-spine of the higher order p, e.g.






65
zDzDz

.
2.5. Complex Hilbert Transform Filter
In order to avoid the IIR type implementation of the Hil-
bert transform filter the key idea in this work is to write
(11) as






1pp
pp
DzRz
zDz Sz

  (20)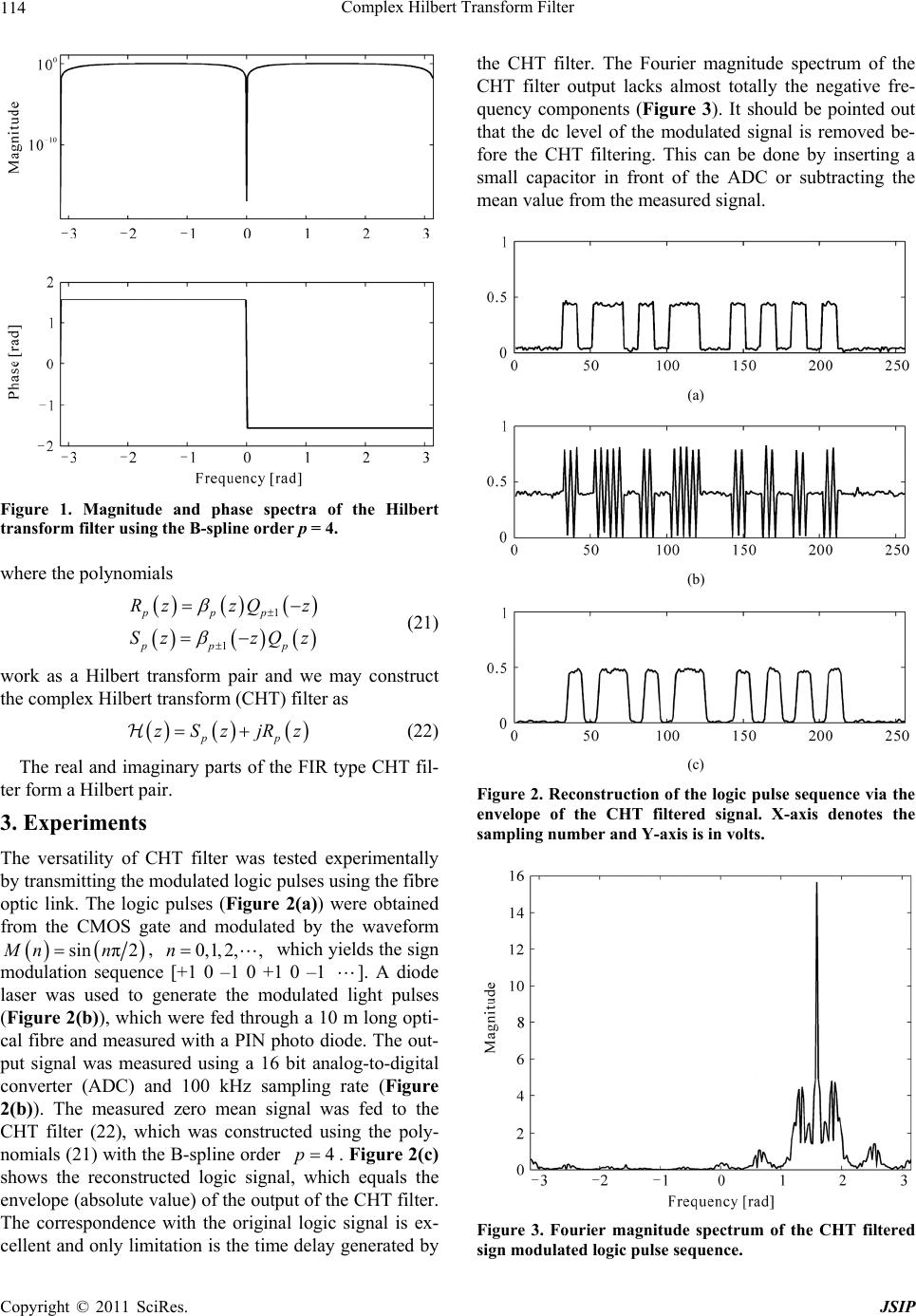

Complex Hilbert Transform Filter 114
Figure 1. Magnitude and phase spectra of the Hilbert
transform filter using the B-spline order p = 4.
where the polynomials
 
 
1
1
ppp
pp p
RzzQz
Sz zQz





 (21)
work as a Hilbert transform pair and we may construct
the complex Hilbert transform (CHT) filter as
 
pp
zSzjRz (22)
The real and imaginary parts of the FIR type CHT fil-
ter form a Hilbert pair.
3. Experiments
The versatility of CHT filter was tested experimentally
by transmitting the modulated logic pulses using the fibre
optic link. The logic pulses (Figure 2(a)) were obtained
from the CMOS gate and modulated by the waveform
 
sin π2Mn n, 0,1, 2,,n which yields the sign
modulation sequence [+1 0 –1 0 +1 0 –1 ]. A diode
laser was used to generate the modulated light pulses
(Figure 2(b)), which were fed through a 10 m long opti-
cal fibre and measured with a PIN photo diode. The out-
put signal was measured using a 16 bit analog-to-digital
converter (ADC) and 100 kHz sampling rate (Figure
2(b)). The measured zero mean signal was fed to the
CHT filter (22), which was constructed using the poly-
nomials (21) with the B-spline order 4p. Figure 2(c)
shows the reconstructed logic signal, which equals the
envelope (absolute value) of the output of the CHT filter.
The correspondence with the original logic signal is ex-
cellent and only limitation is the time delay generated by
the CHT filter. The Fourier magnitude spectrum of the
CHT filter output lacks almost totally the negative fre-
quency components (Figure 3). It should be pointed out
that the dc level of the modulated signal is removed be-
fore the CHT filtering. This can be done by inserting a
small capacitor in front of the ADC or subtracting the
mean value from the measured signal.
(a)
(b)
(c)
Figure 2. Reconstruction of the logic pulse sequence via the
envelope of the CHT filtered signal. X-axis denotes the
sampling number and Y-axis is in volts.
Figure 3. Fourier magnitude spectrum of the CHT filtered
sign modulated logic pulse sequence.

Complex Hilbert Transform Filter 115
4. Discussion
In this work a novel method for designing the Hilbert
transform operator is introduced. The idea is based on the
half-sample delay operator

p
Dz, which is constructed
by the B-spline transform interpolation and decimation
procedure [16]. The method yields a half-sample delay
filter, which has a precisely linear phase. Some compet-
ing fractional delay design methods, such as Taylor se-
ries expansions of

,expDj

  and Thiran
filters produce phase distortion [17-21]. However, the
magnitude response of the Hilbert transform operator (11)
is intensified at DC and at Nyquist frequency, which is
not satisfying for many purposes. We solved the problem
using even and odd order half-delay operators in cascade
(17). The resulting Hilbert transform operator has a
maximally flat frequency response in the range
0π

 (Figure 1). The flatness of the magnitude
response can be increased by using the higher B-spline
order p. It has been shown that the B-spline interpolation
approaches asymptotically the sinc-interpolation with
increasing p [22]. However, in practice a compromise
has to be made between the length of the filter and the
flatness requirements.
One of the advantages of the B-spline transform based
operators is the integer valued filter coefficients. The
CHT filter is feasible to implement in VLSI environment
requiring only register shifts and summations. To avoid
the implementation of the IIR-type filter, we divided the
Hilbert transform filter into a complex FIR-type filter (21,
22). The real and imaginary parts of the resulting com-
plex signal are a Hilbert pair. However, it should be
pointed out that as in classical Hilbert transformers the
real part of the Hilbert transformed signal equals the
original signal, the CHT filter (22) results in a half-sample
delayed version. The perfect reconstruction of the origi-
nal signal requires the inverse filtering by


1
p
Sz
.
However, in many communication systems this is not a
restriction since the relative phase relations of the signals
is of significance.
The CHT has a plenty of applications such as compu-
tation of the envelope and instantaneous frequency and
the construction of the digital quadrature encoders and
amplitude modulators. The FFT-based Hilbert transform
algorithms [5,7] can be directly replaced by the CHT
prefilter in the shift-invariant multi-scale analysis. We
demonstrated the feasibility of the CHT filter in recon-
struction of the sign modulated CMOS logic pulses tra-
verling through a fibre optic link. Compared with the
direct transmission of the light pulses, the sign modula-
tion concentrates the power spectral density of the signal
in the vicinity of the modulation frequency (Figure 3)
and the DC-level variation in the transmitted light pulses
do not interfere the reconstruction. For example in ro-
botics the mechanical vibrations in fibres may originate
errors in direct transmission method.
REFERENCES
[1] N. E. Huang, Z. Shen, S. R. Long, M. C. Wu, E. H. Shih,
Q. Zheng, C. C. Tung and H. H. Liu, “The Empirical
Mode Decomposition and the Hilbert Spectrum for
Nonlinear and Nonstationary Time Series Analysis,” Pro-
ceedings of the Royal Society of London A, Vol. 454, No.
1971, 1998, pp. 903-995.
[2] I. W. Selesnick, “Hilbert Transform Pairs of Wavelet
Bases,” IEEE Signal Processing Letters, Vol. 8, No. 6,
2001, pp. 170-173. doi:10.1109/97.923042
[3] H. Ozkaramanli and R. Yu, “On the Phase Condition and
Its Solution for Hilbert Transform Pairs of Wavelet
Bases,” IEEE Transactions on Signal Processing, Vol. 51,
No. 12, 2003, pp. 3293-3294.
doi:10.1109/TSP.2003.818996
[4] R. Yu and H. Ozkaramanli, “Hilbert Transform Pairs of
Biorthogonal Wavelet Bases,” IEEE Transactions on
Signal Processing, Vol. 54, No. 6, 2006, pp. 2119-2125.
doi:10.1109/TSP.2006.874293
[5] H. Olkkonen, J. T. Olkkonen and P. Pesola, “FFT Based
Computation of Shift Invariant Analytic Wavelet Trans-
form,” IEEE Signal Processing Letters, Vol. 14, No. 3,
2007, pp. 177-180. doi:10.1109/LSP.2006.879983
[6] W. M. Moon, A. Ushah and B. Bruce, “Application of
2-D Hilbert Transform in Geophysical Imaging with Po-
tential Field Data,” IEEE Transactions on Geoscience
and Remote Sensing, Vol. 26, No. 5, 1988, pp. 502-510.
doi:10.1109/36.7674
[7] H. Olkkonen, P. Pesola, J. T. Olkkonen and H. Zhou,
“Hilbert Transform Assisted Complex Wavelet Trans-
form for Neuroelectric Signal Analysis,” Journal of Neu-
roscience Methods, Vol. 151, No. 2, 2006, pp. 106-113.
doi:10.1016/j.jneumeth.2005.06.028
[8] H. Kanai, Y. Koiwa and J. Zhang, “Real-Time Measure-
ments of Local Myocardium Motion and Arterial Wall
Thickening,” IEEE Transaction on Ultrasonics, Ferro-
electrics, and Frequency Control, Vol. 46, No. 5, 1999, pp.
1229-1241. doi:10.1109/58.796128
[9] S. M. Shors, A. V. Sahakian, H. J. Sih and S. Swiryn, “A
Method for Determining High-Resolution Activation
Time Delays in Unipolar Cardiac Mapping,” IEEE Tran-
saction on Biomedical Engineering, Vol. 43, No. 12, 1996,
pp. 1192-1196.
[10] A. K. Barros and N. Ohnishi, “Heart Instantaneous Fre-
quency (HIF): An Alternative Approach to Extract Heart
Rate Variability,” IEEE Transaction on Biomedical En-
gineering, Vol. 48, No. 8, 2001, pp. 850-855.
doi:10.1109/10.936361
[11] O. W. Kwon and T. W. Lee, “Phoneme Recognition Us-
ing ICA-Based Feature Extraction and Transformation,”
Signal Processing, Vol. 84, No. 6, 2004, pp. 1005-1019.
doi:10.1016/j.sigpro.2004.03.004

Complex Hilbert Transform Filter 116
[12] A. V. Oppenheim and R. W. Schafer, “Discrete-Time
Signal Processing,” Prentice-Hall, Englewood Cliffs, NJ,
1989.
[13] A. Rao and R. Kumaresan, “A Parametric Modeling Ap-
proach to Hilbert Transformation,” IEEE Signal Proces-
sing Letters, Vol. 5, No. 1, 1998, pp. 15-17.
doi:10.1109/97.654868
[14] R. Kumaresan, “An Inverse Signal Approach to Compu-
ting the Envelope of a Real Valued Signal,” IEEE Signal
Processing Letters, Vol. 5, No. 10, 1998, pp. 256-259.
doi:10.1109/97.720558
[15] K. L. Peacock, “Kaiser-Bessel Weighting of the Hilbert
Transform High-Cut Filter,” IEEE Transaction on Acous-
tics, Speech, and Signal Analysis, Vol. 33, No. 1, 1985, pp.
329-331. doi:10.1109/TASSP.1985.1164514
[16] J. T. Olkkonen and H. Olkkonen, “Fractional Delay Filter
Based on the B-Spline Transform,” IEEE Signal Proces-
sing Letters, Vol. 14, No. 2, 2007, pp. 97-100.
doi:10.1109/LSP.2006.882103
[17] T. Laakso, V. Valimaki, M. Karjalainen and U. K. Laine,
“Splitting the Unit Delay. Tools for Fractional Delay Fil-
ter Design,” IEEE Signal Processing Magazine, Vol. 13,
No. 1, 1996, pp. 30-60. doi:10.1109/79.482137
[18] S. C. Pei and C. C. Tseng, “An Efficient Design of a Va-
riable Fractional Delay Filter Using a First-Order Diffe-
rentiator,” IEEE Signal Processing Letters, Vol. 10, No.
10, 2003, pp. 307-310. doi:10.1109/LSP.2003.815616
[19] S. C. Pei and P. H. Wang, “Closed-Form Design of
All-Pass Fractional Delay,” IEEE Signal Processing Let-
ters, Vol. 11, No. 10, 2004, pp. 788-791.
doi:10.1109/LSP.2004.835473
[20] H. Johansson and P. Lowenborg, “Reconstruction of
Nonuniformly Sampled Bandlimited Signals by Means of
Digital Fractional Delay Filters,” IEEE Transaction on
Signal Processing, Vol. 50, No. 11, 2002, pp. 2757-2767.
doi:10.1109/TSP.2002.804089
[21] C. C. Tseng, “Digital Integrator Design Using Simpson
Rule and Fractional Delay Filter,” IEE Proceedings of Vi-
sion, Image and Signal Processing, Vol. 153, No. 1, 2006,
pp. 79-85. doi:10.1049/ip-vis:20045208
[22] M. Unser, A. Aldroubi and M. Eden, “Polynomial Spline
Approximations: Filter Design and Asymptotic Equiva-
lence with Shannon’s Sampling Theorem,” IEEE Trans-
actions on Information Theory, Vol. 38, No. 1, 1992, pp.
95-103. doi:10.1109/18.108253