Journal of Signal and Information Processing, 2011, 2, 53-58
doi:10.4236/jsip.2011.22008 Published Online May 2011 (http://www.SciRP.org/journal/jsip)
53
The Color Calibration across Multi-Projector
Display
Shu Liu1,2, Qiuqi Ruan1,2, Xiaoli Li1,2
1Institute of Information Science, Beijing Jiaotong University, Beijing, China; 2Beijing Key Laboratory of Advanced Information
Science and Network Technology, Beijing, China.
Received January 11th, 2011; revised March 15th, 2011; accepted March 18th, 2011.
ABSTRACT
Large plane displays are often achieved by combining tiled imaging elements, which give the appearance of a single,
seamless display. However, this is difficult to realize in practical use, since differences in co lor will make the tiles dis-
tinct even if the geometric calibration is perfect. The paper presents an approach of color calibration using cubic B-
spline. According to the theory of cubic B-spline, we construct the color transfer function of each projector. This ap-
proach reduces the color and photometric non-uniformities to achieve seamless tiled multi-projector display well. Fi-
nally, we propose the difference between blending region and overlapping region which can help to achieve a better
effect of alpha blending.
Keywords: Multi-Projector Display, Color Calibration, Alpha Blend ing, Cubic B-Spline
1. Introduction
With the continuous development of the projection dis-
play technology, the large plane multi-projector displays
technique has been widely used in various fields to meet
people’s increasing demand for high-resolution display.
Large plane multi-projector displays are often created by
combining tiled imaging elements. In practice, even if
the geometric calibration is perfect, it still can not
achieve seamless tiled multi-projector display, because of
the differences in color.
The problems in achieving color and photometric uni-
formity of a multi-projector display can be divided into
two classes [1].
1) Device Dependent
a) Photometric Variation between Different Projectors;
b) Photometric Variation within a Projector’s FOV.
2) Application Dependent
a) Photometric Variation Due to Overlapping P rojectors;
b) Photometric Variation Due to Non-planar or Non-
Lambertian Display Surface.
Taking these causes into account, the work of color
calibration is carried on in three aspects: calibration
within each projector, calibration between the adjacent
projectors, and calibration in the overlapping region of
projectors. At present, the methods of color calibration
mainly fall into two groups . One group is using advanced
measuring instruments, such as spectroradiometer [1],
colorimeter [2,3], etc. to obtain accurate information for
color calibration. The other is extracting information of
color intensity from the camera feedback [4,5]. The ad-
vantage of the former is that the accurate information
obtained by the instruments guarantees the success of
color calibration. But the problem is the professional
instruments are usually too expensive to be afforded. The
latter method greatly reduces the cost, but it brings the
drawback of information imprecise at the same time.
This paper presents an approach of color calibration to
achieve seamless tiled multi-projector display. One cam-
era is used to get the information of each color channel
with different pixel values. Then the projector’s color
transfer function for each channel is constructed using
cubic B-spline.
2. Background
2.1. Color Map
The color reproduction process of a display system can
be described as follow [2]. An RGB triple (r, g, b) in the
graphics frame buffer is converted to either an analog
voltage or digital bits and sent to the projector. The pro-
jector then combines lights of three primary colors pro-
portionally to form the desired color.
The gamut of a display device is the set of all repro-

The Color Calibration across Multi-Projector Display 54
ducible colors. The gamut of a color transfer function F
can be formally defined as
  

,, ,,0,255GF Frgbrgb (1)
If it meets the following equation


 
, ,,0,00, ,00,0,
F
rgbFrFgFb (2)
We call the gamut an additive gamut. The three chan-
nels RGB are independent of each other.
2.2. Cubic B-Spline [6]
The B-spline curve with u and k as its parameter and
power respectively can be denoted as follow:
 
,
0
n
iik
i
PudN u

 (3)
Where ,0,1,,
i
di n are the control points, and

,ik
Nu are the basis function of B-spline. The recur-
sive formula of De Boer-Cox (Cox M.G.) is:

,0
1, if 1
0, else
ii
i
uuu
Nu




 (4)
 
1
,,1 1,1
11
,
0,0,1,,1
iik
ikiki k
ik iiki
uuu u
NuN uNu
uuu u
ki n






  
(5)
Set 0/0 = 0
Given n typical data points

0,1,2, ,1
i
Pi n, we
can construct the cubic B-spline curve which goes
through th e n typical data points as follows: if we set the
control points as

0,1,2, ,1
i
di n, the th r func-
tion of the cubic B-spline curve is:
 
1 32
2
3
13 31
3630
16, ,,13030
1410
r
r
rr
r
d
d
Pt tttd
d



 

 



 






(6)
Where


0,1 ,0,1,2,,2tr n . Set


0
rr
PP

,
then
  
12
16 2316
rr rr
dd dP

,
namely 12
46,0,1,2,,1
rrrr
ddd Prn

,.
01 1
,,,
n
dd d

 are 2n unknown parameters with only
n functions. So we have to add two endpoints premises:
1) For open curve: set 01 1 ,nn ddd d

;
2) For close curve: set 11 0 ,
nn
dddd


.
3. Color Transfer Function
Color matching can be achieved through the color map:

33
0,1, ,2550,1, ,255, before going through the
projector. If the gamut is additive, the color map can be
described as




0,1, ,2550,1, ,255 for each chan-
nel. But after the pixels are sent to the display through
the projector, the color map is no longer what it was.
What we should do is to construct the color transfer
function F for the project system.
To be simplified, we assume the gamut additive, thus
each channel of the color image is treated separately. In
this paper, we only introduce the process of channel R.
The other two channels, G and B, are similar to channel
R. We can construct the color transfer function of chan-
nel R with the following steps.
1) Create 18 images. Set the value of channels G and B
to 0, and sample the value of channel R within [0, 255]
uniformly spaced of 15. So we get the sampled values of
channel


0,15,30, ,255R.
2) Project these 18 images to the display wall in turn,
and capture the images on the display wall.
3) Calculate the average pixel value of these 18 photos
separately. We regard the average as the response of
project for each corresponding pixel value.
4) Calculate the control points using cubic B-spline,
with the 18 original pixel values and their response val-
ues.
5) According to these control points, construct the
color transfer function of the channel R using cubic B-
spline. Now we get the color map of channel R of the
projector.
3.1. Color Look-up-Table
We get the color transfer function of every projector
through the above steps. Now we have to linearize the
color transfer function for each projector, and match the
color of adjacent projectors.
The color transfer function of projector is a non-linear
S-curve [7]. What we should do is to correct this non-
linear S-curve into a power function which is approx-
imately linear. The power of function is the Gamma. Ge-
nerally in order to reflect the true color of the image, we
hope the value of gamma is 1.
We can create the color map through the following
steps:
1) Determine the common range of the color output of
the projectors, and get the desired transfer function.
12
,PP represent the two adjacent projectors. 12 ,
F
F
are the color transfer function of 12 ,PP respectively. In
Figure 1, 11 ,LH are the minimum and maximum re-
sponse respectively when the pixel is sent by projector
1
P, that is,





11
11
min0 255,,
max0 255,
LFxxxN
H
Fxxx N


(7)
22
,LH are the minimum and maximum response re-
spectively when the pixel is sent by projector 2 P, that is,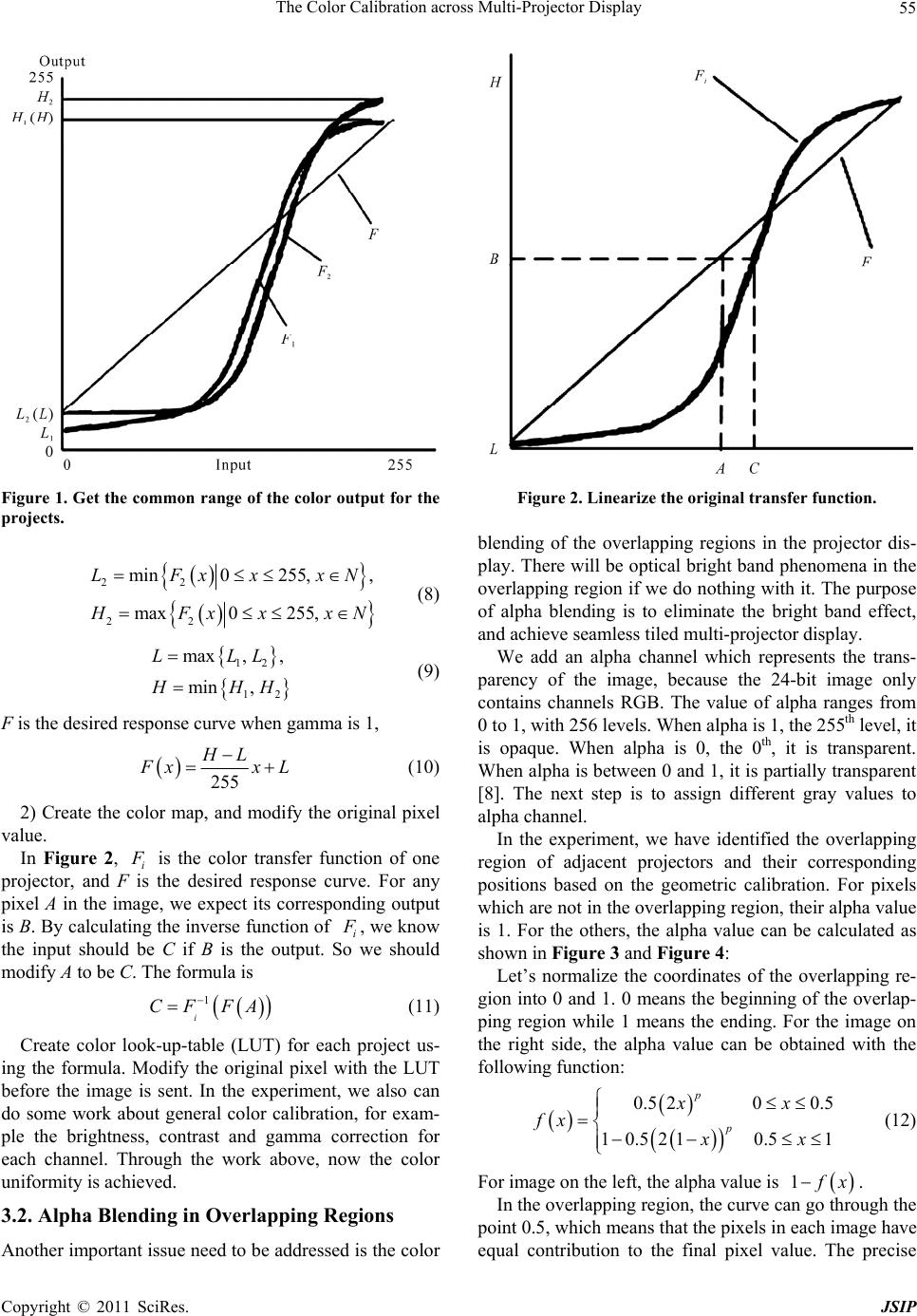

The Color Calibration across Multi-Projector Display 55
Figure 1. Get the common range of the color output for the
projects.




22
22
min0 255,,
max0 255,
LFxxxN
H
Fx xxN


(8)


12
12
max ,,
min ,
LLL
H
HH

 (9)
F is the desired response curve when gamma is 1,

255
HL
F
xxL

 (10)
2) Create the color map, and modify the original pixel
value.
In Figure 2, i
F
is the color transfer function of one
projector, and F is the desired response curve. For any
pixel A in the image, we expect its corresponding output
is B. By calculating the inverse function of i
F
, we know
the input should be C if B is the output. So we should
modify A to be C. The formula is

 
1
i
CF FA

 (11)
Create color look-up-table (LUT) for each project us-
ing the formula. Modify the original pixel with the LUT
before the image is sent. In the experiment, we also can
do some work about general color calibration, for exam-
ple the brightness, contrast and gamma correction for
each channel. Through the work above, now the color
uniformity is achieved.
3.2. Alpha Blending in Overlapping Regions
Another important issue need to be addressed is the color
Figure 2. Linearize the original transfer function.
blending of the overlapping regions in the projector dis-
play. There will be optical bright band phenomena in the
overlapping region if we do nothing with it. The purpose
of alpha blending is to eliminate the bright band effect,
and achieve seamless tiled multi-projector display.
We add an alpha channel which represents the trans-
parency of the image, because the 24-bit image only
contains channels RGB. The value of alpha ranges from
0 to 1, with 256 levels. When alpha is 1, the 255th level, it
is opaque. When alpha is 0, the 0th, it is transparent.
When alpha is between 0 and 1, it is partially transparent
[8]. The next step is to assign different gray values to
alpha channel.
In the experiment, we have identified the overlapping
region of adjacent projectors and their corresponding
positions based on the geometric calibration. For pixels
which are not in the overlapping region, their alpha value
is 1. For the others, the alpha value can be calculated as
shown in Figure 3 and Figure 4:
Let’s normalize the coordinates of the overlapping re-
gion into 0 and 1. 0 means the beginning of the overlap-
ping region while 1 means the ending. For the image on
the right side, the alpha value can be obtained with the
following function:
 
 
0.5 200.5
10.5210.5 1
p
p
xx
fx xx







(12)
For image on the left, the alpha value is


1
f
x.
In the overlapping reg ion , th e curve can go through the
point 0.5, which means that the pixels in each image have
equal contribution to the final pixel value. The precise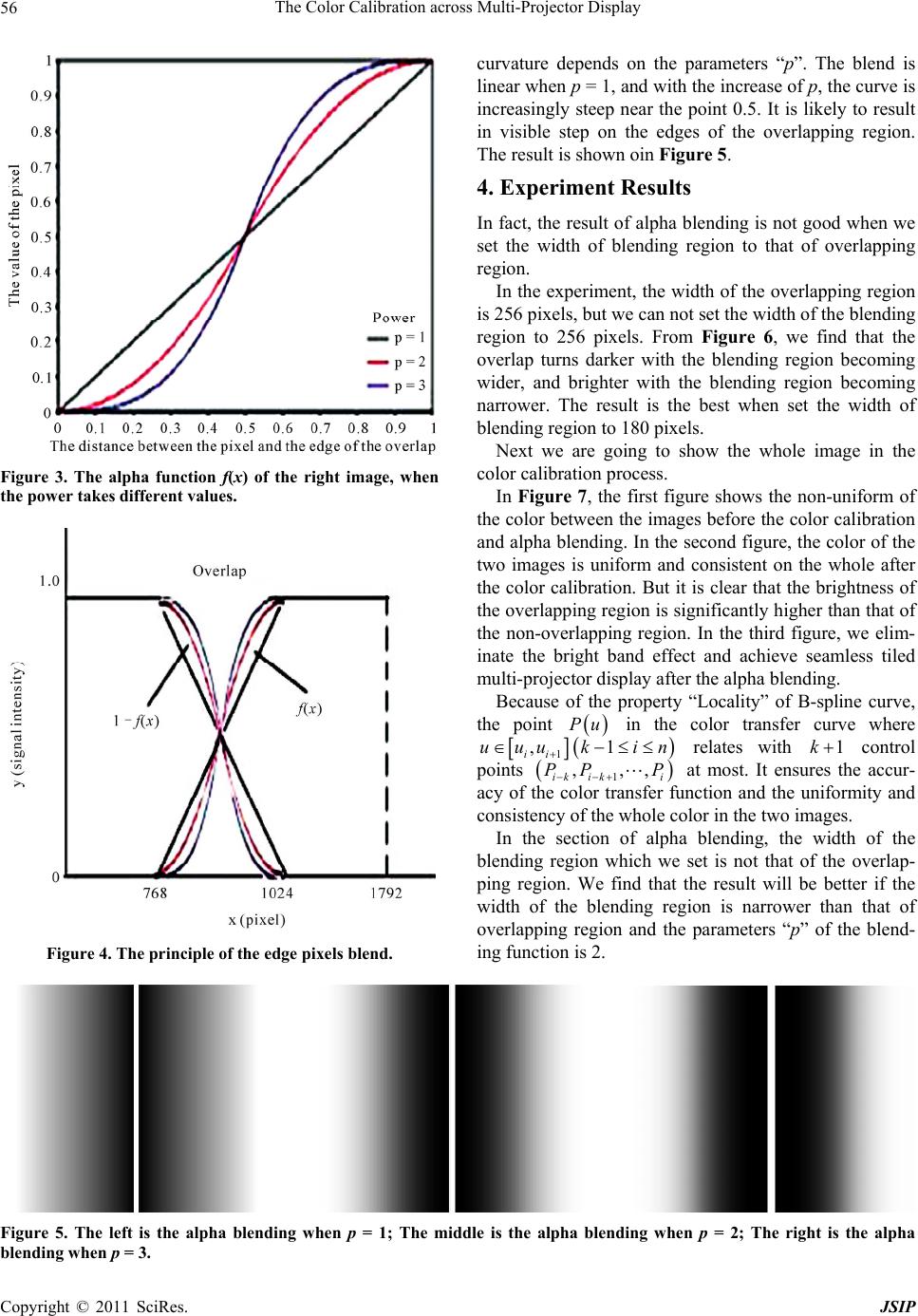

The Color Calibration across Multi-Projector Display 56
Figure 3. The alpha function f(x) of the right image, when
the power takes different values.
Figure 4. The principle of the edge pixels blend.
curvature depends on the parameters “p”. The blend is
linear when p = 1, and with the increase of p, the curve is
increasingly steep near the point 0.5. It is likely to result
in visible step on the edges of the overlapping region.
The result is shown oin Figure 5.
4. Experiment Results
In fact, the result of alpha blending is not good when we
set the width of blending region to that of overlapping
region.
In the experiment, the width of the overlapping region
is 256 pixels, but we can not set the width of the blending
region to 256 pixels. From Figure 6, we find that the
overlap turns darker with the blending region becoming
wider, and brighter with the blending region becoming
narrower. The result is the best when set the width of
blending region to 180 pixels.
Next we are going to show the whole image in the
color calibration process.
In Figure 7, the first figure shows the non-uniform of
the color between the images before the color calibration
and alpha blending. In the second figure, the color of the
two images is uniform and consistent on the whole after
the color calibration. But it is clear that the brightness of
the overlapping region is significantly higher than that of
the non-overlapping region. In the third figure, we elim-
inate the bright band effect and achieve seamless tiled
multi-projector display after the alpha blending.
Because of the property “Locality” of B-spline curve,
the point


Pu in the color transfer curve where




1
,1
ii
uuu kin


 relates with 1k control
points


1
,,,
ik iki
PP P

 at most. It ensures the accur-
acy of the color transfer function and the uniformity and
consistency of the whole color in the two images.
In the section of alpha blending, the width of the
blending region which we set is not that of the overlap-
ping region. We find that the result will be better if the
width of the blending region is narrower than that of
overlapping region and the parameters “p” of the blend-
ing functi on is 2.
Figure 5. The left is the alpha blending when p = 1; The middle is the alpha blending when p = 2; The right is the alpha
blending when p = 3.

The Color Calibration across Multi-Projector Display 57
Figure 6. The width of the blending region is 256 pixels, 200 pixels, 180 pixels, 150 pixels and 128 pixels successively.
Figure 7. The left is the projected image before the color calibration and alpha blending; The right is the projected image
after the color calibration but before alpha blending; The below is the projec ted image after the color calibration and alpha
blending.
5. Conclusions
The color calibration as introduced and studied in this
paper is very important in the large plane multi-projector
displays. The paper presents an approach of color cali-
bration using cubic B-spline. We take channel R as an
example and describe the steps of processing in detail,
and channels G and B are similar to it. Because of the
advantages of B-spline, it has played an imp ortant role in
constructing the color transfer function of projector. Af-
ter this, we also can adjust the brightness, contrast, and
gamma value to make the color calibration well, and the
experiment results show that it works very well. Finally,
we also describe the alpha blending which can eliminate
the bright band effect in the overlapping region, and do
some relevant experiments. It is worth noting that the
blending region is not the overlapping region in the ex-
periment. The width of the blending region is required to
be chosen appropriately to achieve seamless tiled.
6. Acknowledgements
This work is supported by National Natural Science
Foundation (60973060), the Research Fund for the Doc-
toral Program (20080004001), and the Fundamental Re-
search Funds for Central Universities (2009YJS025).
REFERENCES
[1] A. Majumder, Z. He, H. Towles and G. Welch, “Achiev-
ing Color Uniformity across Multi-Projector Displays,”
Proceedings of IEEE Visualization Conference, Salt Lake
City, 8-13 October 2000, pp. 117-124.
[2] G. Wallace, H. Chen and K. Li, “Color Gamut Matching

The Color Calibration across Multi-Projector Display 58
for Tiled Display Walls,” Eurographics Workshop on
Virtual Environments, Zurich, 22-23 May 2003, pp. 293-
302.
[3] M. C. Stone, “Color and Brightness Appearance Issues in
Tiled Displays. Computer Graphics and Applications,”
Computer Graphics and Applications, Vol. 21, No. 5,
2001, pp. 58-66. doi:10.1109/38.946632
[4] A. Majumder, D. Jones, M. McCrory, M. E. Pa pka and R.
Stevens, “Using a Camera to Capture and Correct Spatial
Photometric Variation in Multi-Projector Displays,” Pro-
ceedings of IEEE International Workshop on Projec-
tor-Camera Systems, Nice, France, 12 October 2003, pp.
1-8.
[5] M. Brown, A. Majumder and R. Yang, “Camera-Based
Calibration Techniques for Seamless Multiprojector Dis-
plays,” Visualization and Computer Graphics, Vol. 10,
No. 5, 2005, pp. 193-206. doi:10.1109/TVCG.2005.27
[6] J. P. Li, “Principles of Computer Graphics Tutorial,”
Electronic Science and Technology University Press,
Chengdu, 1998.
[7] G. P. Yang and F. M. Chen, “The Gamma Correction for
Multiple Projectors after Alpha Blending,” Computer Ap-
plications and Software, Vol. 26, No. 1, 2009, pp. 232-
233
[8] S. F. Huang, F. M. Chen and X. C. Chen, “The Applica-
tion of Alpha Blending to Seamless Projection,” Com-
puter Applications and Software, Vol. 24, No. 12, 2007,
pp. 161-162.