Beacon-driven Leader Based Protocol over a GE Channel for MAC Layer Multicast Error Control

doi:10.4236/ijcns.2008.12019

Paper Menu >>

Journal Menu >>

I. J. Communications, Network and System Sciences, 2008, 2, 105-206

Published Online May 2008 in SciRes (http://www.SRPublishing.org/journal/ijcns/).

Beacon-driven Leader Based Protocol over a GE Channel

for MAC Layer Multicast Error Control

Zhao LI1, Thorsten HERFET2

1 Student Member IEEE, USTC CS China & Saarland University, Germany

2 Senior Member IEEE, Saarland University, Germany

E-mail: {li, herfet}@nt.uni-saarland.de

Abstract

In wireless networks current standard MAC layer protocols don’t provide any error correction scheme for

broadcast/multicast. In this paper, we enhance a Leader Based Protocol (LBP) and propose a Beacon-driven

Leader Based Protocol (BLBP) for the MAC layer multicast error control. To guarantee a very low Packet

Loss Ratio (PLR) under strict delay constraints for video multicast over a Gilbert-Elliott (GE) channel, we

analyze BLBP and compare it with LBP and different application layer multicast error control schemes via

simulation experiments. Both the theoretical analysis and simulation results show that BLBP can correct

nearly all the errors for all receivers in the MAC layer and is more efficient than LBP. BLBP is also more

efficient than the application layer Automatic Repeat request (ARQ) scheme and the total multicast delay is

much shorter. BLBP is very good for real-time multicast applications with strict delay constraints.

Keywords: BLBP, Multicast Error Control, Gilbert-elliott Channel

1. Introduction

With the rapid development of wireless networking

technologies, it is becoming possible to supply wireless

terminal users not only with data connections, but also

with real-time communication services. The emerging

real-time multicast applications in wireless networks

include the local distribution of High Definition TV

(HDTV) and Digital Video Broadcasting (DVB) [1],

video-on demand, video conferencing, gaming, local

VoIP, IPTV, Internet-Radio distribution, P2P

broadcasting, etc. Most of these applications require a

very low Packet Loss Ratio (PLR) under strict delay

constraints.

The characteristics of wireless network can be

summarized as a bandwidth variation and terminal

heterogeneity plus a high degree of packet losses. It is

known that the Gilbert-Elliot (GE) channel [2,4] with a

2-state Markov model is a good approximation for the

packet loss model in wireless channels. However, the

current standard MAC layer protocols don’t provide any

error correction scheme for broadcast/multicast. Hence

the multicast error is controlled in the application layer.

The existing application layer multicast error control

schemes include automatic repeat request (ARQ),

forward error correction (FEC) and hybrid error

correction (HEC) [5–10]. Unfortunately the total

multicast delays of the application layer schemes are

always high and sometimes do not satisfy the strict

application delay constraints, or these schemes are not

efficient when the delay constraints are short.

Compared with application layer schemes, MAC

layer multicast error control schemes recover the

multicast loss locally and lead to much shorter delays.

Currently, very few reliable MAC layer multicast

schemes, such as Leader Based Protocol (LBP) [11],

have been proposed for IEEE 802.11 based wireless

networks. LBP elects one of the multicast group

receivers as the leader. On erroneous reception of a data

frame, the leader does not send an acknowledgement

(ACK), prompting a retransmission. On erroneous

reception of the data frame at the non-leader receivers,

LBP allows negative acknowledgements (NACKs) from

these receivers to collide with the ACK from the leader,

thus destroying the ACK and prompting the sender to

retransmit the data frame. We refer to this ACK/NACK

jam as JACK.

However, LBP suffers from two main problems: First,

when the entire data frame is lost, the non-leader

BEACON-DRIVEN LEADER BASED PROTOCOL OVER A GE CHANNEL 145

FOR MAC LAYER MULTICAST ERROR CONTROL

receivers can not reply NACKs because they don’t know

when or how to send them, as the destination is

unknown especially when Request-To-Send (RTS) and

Clear-To-Send (CTS) is not used for small data frames.

As a result, LBP is not reliable for the non-leader

receivers. Second, LBP has poor performance when the

channel error rates are high. The non-leader receivers

send NACKs whenever the received frame is in error,

regardless of whether this erroneous frame has been

received correctly before or not. This is because the

receivers in LBP can not access the data frame sequence

number before the frame is received, as there is no such

field in the structure of RTS/CTS frames for multicast.

So the sender has to retransmit until all receivers receive

the data frame correctly at the same time. There are a lot

of unnecessary transmissions; hence LBP is not efficient

particularly for lossy channels.

In this paper, we enhance LBP and propose a

Beacon-driven Leader Based Protocol (BLBP). The

sender sends a beacon frame before the data frame to

lead the non-leader receivers to set timers and to

announce the sequence number of the following data

frame. BLBP solves the problems of LBP well. Each of

the non-leader receivers can send feedback when the

timer times out. Both the leader receiver and non-leader

receivers can send ACK and NACK respectively based

on sequence check, hence avoids the unnecessary

transmissions in LBP. To guarantee a very low PLR

under strict delay constraints for video multicast over a

GE channel, we analyze BLBP and compare it with LBP

and two application layer multicast error control

schemes via simulation experiments. One is an ARQ

based scheme from [8], called HEC-PR, which combines

a NACK based ARQ scheme with a packet repetition

(PR) technique. The other one is a nearly optimal

application layer multicast error control scheme called

Hybrid ARQ (HARQ) Type I [9,10], which combines

FEC and NACK based ARQ scheme together.

The remainder of this paper is organized as follows.

Section 2 presents the related work. In section 3, we

examine why it is necessary to correct multicast errors in

the MAC layer. We describe BLBP in section 4 and

analyze its performance over a GE channel in section 5.

And in section 6, we evaluate the performance of BLBP

and compare it with LBP, HEC-PR and HARQ Type I

via simulation experiments. We conclude in section 7.

2. Related Work

For the application layer multicast error control, many

authors [5,8] studied the ARQ based schemes and

concluded that when combined with feedback

suppression and other accessorial techniques, ARQ is

effective to repair multicast packet losses for small

groups with low error rates. However, the application

layer ARQ always take a long time and they are not

efficient at high error rates and with large numbers of

receivers due to feedback implosion and the limitation to

scale.

Another technique commonly used to handle losses

for multicast in the application layer is FEC, whereby

redundant information in the data stream enables the

receiver to correct losses without contacting the sender.

Rizzo [6] studied the feasibility of software

encoding/decoding for packet-level FEC. A (n, k) block

erasure code converts k source packets into a group of n

coded packets, such that any k of the encoded packets

can be used to reconstruct the k source packets. Usually,

the first k packets in each group are identical to the

original k data packets; the remaining n-k packets are

referred to as parity packets. The advantage of using

block erasure codes for wireless multicasting is that a

single parity packet can be used to correct independent

single-packet losses among different receivers.

The integrated FEC/ARQ schemes or any other kinds

of combination of more than one error control schemes

are referred to as HEC schemes in this paper. Previous

works [7–10] indicate that HEC schemes are much more

efficient for recovering data packets than the schemes

with either FEC or ARQ alone. We consider the HEC-

PR scheme from [8], which combines a NACK based

ARQ scheme and a packet repetition technique. The

number of feedback/retransmission rounds and the

number of packet repetitions in each round are adapted

to the network condition. HEC-PR is actually an ARQ

based scheme without FEC coding. We also consider

HARQ Type I from [9,10], in which the sender sends a

certain amount of parity packets using FEC following

the original k data transmissions. If the loss rate obtained

after reconstruction at the receiver is still too high, ARQ

is used to retransmit more parity packets. Tan [10]

developed formulas to optimize the performance of

HARQ Type I while guaranteeing the required PLR

under strict delay constraints. HARQ Type I is a nearly

optimal application layer multicast error control scheme.

However, these application layer multicast schemes

always take long multicast delays or they are not

efficient when the delay constraints are short. So we

study MAC layer multicast error control schemes to

support real-time multicast with strict delay constraints.

For the reliable MAC layer multicast, besides LBP [11],

Tourrihes [12] proposed a robust broadcast using a

collision detector to inform the sender whether the

broadcast packet is successful or not. However, this

scheme can not guarantee the reliability of multicast

transmissions because the feedbacks are only from the

detector instead of all receivers themselves. Gupta et al.

[13] proposed a tone-based solution for multicast in both

infrastructure and ad-hoc 802.11 networks. They use

dual busy tones to simulate NACKs or Negative CTS

(NCTS). Although this scheme is good to detect and

correct the multicast errors, it requires an additional

146 Z. LI ET AL.

channel for the tone, which is not always feasible in

practice.

Our BLBP enhances LBP with a beacon frame to lead

the non-leader receivers to set timers and to announce

the sequence number of the following data frame. BLBP

avoids the problems of LBP and is more efficient.

3. Motivation

The emerging real-time multicast applications in

wireless networks (such as wireless HDTV, DVB, game,

video conference) require strict delay constraints. Error

recovery based on application layer ARQ is suboptimal

because the end-to-end application layer feedback and

retransmission take a too long time due to application

layer protocol waiting, MAC layer queuing, hardware

handling, etc. Moreover, the application layer ARQ

based schemes are not efficient when the error rates are

high and the numbers of receivers are large due to

feedback implosion and the limitation to scale. The FEC

coding based application layer schemes can satisfy the

strict delay constraints but they are not efficient when

the delay constraints are very strict particularly for small

multicast groups. And the FEC based ones are not

adaptive to the heterogeneity of receivers because the

code has to be set based on the receiver with the worst

channel condition.

Compared with application layer schemes, MAC

layer multicast error control schemes take a much

shorter time due to the faster feedback and

retransmission. Due to the JACK scheme, BLBP and

LBP even achieve complete feedback suppression. So

the MAC layer multicast error control schemes are very

good for real-time multicast applications. For non-real-

time multicast applications such as file dissemination

and shared whiteboards, reliable MAC layer multicast

saves time as well as both network and end-system

resources.

Moreover, for multi-hop multicast with wired

network and wireless LAN as the last hop, the need for

additional transmissions due to errors in the wireless

LANs puts unnecessary processing burden on the

original remote sender. These additional transmissions

go over the entire wired multicast tree and also the

wireless links, taking a long time, wasting bandwidth

and also leading to processing of unwanted redundant

retransmissions at those receivers which might have

already received the packet. The similar thing also

happens in multi-hop wireless networks such as wireless

mesh networks and wireless ad hoc networks. If the

access points (AP) (or base stations) were to take the

responsibility of supplying retransmissions rather than

the original sender, then the load of supplying

retransmission gets distributed across access points and

takes a shorter time. The total error correction cost will

be much shorter and it is easier to guarantee the final

PLR under strict delay constraints in the application

layer.

4. Main Scheme of BLBP

The MAC layer reliable multicast BLBP requires a slight

modification to the IEEE 802.11 MAC layer protocols.

As mentioned earlier, 802.11 DCF (Distributed

Coordination Function) unicast – assumed RTS/CTS is

switched on to solve the hidden terminal problem – is

more reliable than broadcast/multicast, because unicast

uses RTS/CTS signaling and ACK/retransmission

scheme in the MAC layer and broadcast/multicast does

not.

BLBP enhances LBP with a MAC control frame

called beacon shown in Figure 1. Besides the same fields

in RTS/CTS frames, such as frame control header,

transmission duration, receiver address (RA), transmitter

address (TA) and frame check sequence (FCS), the

beacon frame also includes the sequence number of the

following data frame. The use of the beacon frame is to

lead the non-leader receivers to set timers and to

announce the sequence number of the following data

frame.

Figure 1. The format of the beacon frame

The main scheme of BLBP is shown in Figure 2. A

receiver is selected as the leader for the multicast group.

The AP first sends a RTS frame to all receivers, and

only the leader receiver transmits a CTS frame in reply

to the AP. The AP is then assured that the channel is

granted and starts the transmission of the beacon frame

with the sequence number of the following data frame.

On receipt of the beacon frame, each of the non-leader

receivers sets a timer according to the beacon frame. The

AP then transmits the data frame following the beacon

frame. The leader receiver replies an ACK frame if the

data is correct or it has already got the data based on

sequence check, or does nothing otherwise. When the

timer times out, each non-leader receiver replies a

NACK if the data is error and it has not received it

correctly yet based on sequence check, or does nothing

otherwise. Then if the AP receives an ACK, this

transmission is done. Otherwise, the AP repeats the

whole procedure and retransmits again until the number

of times is beyond the retransmission limit. For example,

in the retransmission phase in Figure 2, although this

time the data frame is lost, the leader receiver still replies

an ACK because it knows this data frame has been

received correctly already in the first transmission,

thanks to the beacon frame.

For the determination of a leader, we use a scheme

BEACON-DRIVEN LEADER BASED PROTOCOL OVER A GE CHANNEL 147

FOR MAC LAYER MULTICAST ERROR CONTROL

from LBP [11]: The first receiver that joins the multicast

group acts as the leader. The group is cancelled if there

is no leader. The other group members can rebuild/rejoin

the multicast group if necessary when time out. Please

note that it is possible to reduce the amount of control

traffic flow for leader election purposes when a higher

layer group management protocol like IGMP (Internet

Group Management Protocol) is running above the link

layer [11]. The leader does not affect the performance

because BLBP supplies fair service for all receivers.

Figure 2. Main scheme of BLBP (Ri denotes receiver i)

BLBP solves the problems of LBP well. All the non-

leader receivers can send feedbacks when the timers

time out. Both the leader receiver and non-leader

receivers send ACK and NACK respectively based on

sequence check thanks to the beacon frame, hence it

avoids the unnecessary transmissions in LBP. Clearly,

BLBP can correct all the errors for all receivers due to

the ACK/NACK feedback and retransmission in the

MAC layer. BLBP is even more efficient than the

application layer ARQ schemes because BLBP

suppresses the multiple feedbacks into just a JACK.

However, the loss of beacon frames will decrease the

performance (reception rate) of the non-leader receivers.

Fortunately, the beacon frames are much more reliable

(nearly error free) than data frames because they are

much smaller and are transmitted using the lowest data

rate, like other control frames in 802.11 (RTS, CTS,

ACK). Moreover, due to RTS/CTS signaling, the beacon

frames also avoid collision loss.

Please also note that BLBP can run without RTS/CTS

exchanges for small data frames just like 802.11 DCF

unicast. Although our discussion is in the context of

802.11 DCF, BLBP is actually applicable to all

ACK/retransmission based MAC protocols, such as

802.11 PCF (Point Coordination Function) etc.

5. Performance Analysis

In this section we first introduce the GE channel model

and then analyze the theoretical performance of BLBP

over the GE channel model with both temporal error

correlation and spatial error correlation.

5.1. GE Channel Model

The GE channel model is a two-state Markov chain

shown in Figure 3. In the Good state (G) errors occur

with (low) probability PG while in the Bad state (B) they

occur with (high) probability PB.

The errors occur in clusters or bursts with relatively

long error-free intervals (gaps) between them. The state

transition is summarized by its transition probability

matrix in formula (1).

Figure 3. GE channel model

αα

−

⎡

⎤

⎢

⎥

−

⎣

⎦ (1)

To reflect most reasonable choices for real scenarios,

it is assumed that PG=0 and PB=1. This model is always

referred to as the simplified GE model. Our analysis and

simulation experiments in the following sections are

based on the simplified GE model.

The occupancy times for state B and G are both

geometrically distributed with respective means 1

(1 )

−

and 1

(1 )

−

−, which are also called as the expected error

burst length and the expected error free length

respectively. The steady state probabilities of being in

states G and B are (1) /(2)

ααβ

=−−− and

(1) /(2)

βαβ

−−−

respectively. So the average

packet loss rate produced by the GE channel model is

(1 )(1)

(11 )

GG BB

pP P

ππ αβ

−+ −

=+=−+− (2)

For the simplified GE channel model, the PLR will be

(1 )

(11 )

−

=−+− (3)

Following [14], the variance of the error symbol (or

packet) X is 22

()(1)EX ppp

−=−

. So we get the

correlation of two consecutive error symbols X1 and X2:

(( )())1

EX pXp

ταβ

−−

=+−

(4)

which is also referred to as the temporal error correlation.

Finally, the two parameters of the simplified model

(

and

) can be expressed in the terms of the more

meaningful quantities p and

by solving formulas (3)

and (4). These yields

148 Z. LI ET AL.

(1 )pp

=+− (5)

(1 )pp

=− + (6)

The transition probability matrix then becomes

1(1)(1)

(1)(1 )1(1)(1 )

Ppp

ττ

−− −

⎡⎤

=⎢⎥

−− −−−

⎣⎦

(7)

And the I-step transition probability matrix is:

1(1 )(1)

(1)(1)1 (1)(1)

Ppp

ττ

⎡⎤

−− −

=⎢⎥

−− −−−

⎣⎦

(8)

Now we compute P[a,b], the probability of a errors

in a sequence of b symbols following [14]. Let PG[a,b]

be the probability of a errors in b transmissions with the

channel ending in state G. Similarly, let PB[a,b] be the

probability of a errors in b transmissions with the

channel ending in state B. Then

[,][,] [,]

abP abP ab=+ (9)

For b =1, 2, 3 … and a=0, 1, 2 …b, assuming the

simplified GE channel, then

[,][,1][, 1](1)

GG B

Pab PabPab

=−+−−

(10)

[,][ 1, 1][ 1, 1](1)

BB G

Pab PabPab

=−−+−−−

(11)

The initial conditions for the recursion are

[0,0](1) /(2)

αβ

=−−− (12)

[0,0](1) /(2)

αβ

=−−− (13)

and [,0][,0]0

Pa Pa==

for 0a

≠

. Note that with these

initial conditions, all numerical values computed will be

steady state results.

5.2. BLBP over the GE Channel Model with

Temporal Error Correlation

Now we analyze BLBP over the GE channel model. As

in most referenced papers, it is assumed that the MAC

layer control frames (RTS/CTS/Beacon/ACK) are error

free from the error model. This also makes sense in

practice because the control frames are very small and

are sent in the lowest data rate, and hence they are more

reliable than data frames. We first consider only the

temporal error correlation. In other words, it is assumed

that the error events at different receivers are

independent. To be clear, we show the used symbols

here.

y P: The original packet error rate for all receivers;

y R: The number of receivers;

y m: The retransmission limit;

y N: The total number of transmissions required to

transmit a multicast packet correctly to all the R

receivers;

y Nr: The number of transmissions required for receiver

r to receive a packet correctly;

y PLRtarget_mac: The PLR target in the MAC layer;

y Dtarget_mac: The Delay target in the MAC layer.

First we consider the final PLR for receiver r, shown

in formula (14).

()[1,1]m

PLRrP mmp

=++= (14)

About the determination of the retransmission limit m,

there are two constraints, the PLR constraints and the

delay constraints which are shown as follows:

arg _

tetmac

pPLR

≤ (15)

arg _

LBPtetmac

mT D≤ (16)

where TBLBP=TCC + TRTS + TCTS + TBEACON + TDATA + TACK

+ DIFS + 4SIFS is the time of one transmission in BLBP.

TCC denotes the channel contention time which can be

calculated theoretically following [15] or by

measurements in practice. TRTS, TCTS, TBEACON, TDATA, and

TACK are the transmission times of frames RTS, CTS,

BEACON, DATA and ACK respectively. DIFS denotes

the Distributed Inter Frame Space while SIFS is the

Short Inter Frame Space. Note that the PLR target and

the delay target may not be satisfied at the same time

sometimes, especially when the delay constraint is too

strict. We will explore this further in simulation

experiments.

Now we consider the expected number of

transmissions for one multicast data packet. The

probabilities that r

≤

, r

Nn= and r

Nn> are shown

in formulas (17), (18) and (19) respectively.

[]1[,]

Nn Pnn

≤

=−

1, 1,2...1

0, 0

pn m

−

⎧

−

=⎨=

⎩

(17)

[][][ 1]

rrr

PN nPN nPN n

=≤−≤−

, 2,3...1

1, 1

ppnm

αα

−−

⎧

−

=⎨−=

⎩

(18)

[][,]

PNn Pnn>= 1, 1,2...

1, 0

pn m

−

⎧=

=⎨=

⎩

(19)

So we get the expected number of transmissions for

one multicast data packet required for receiver r:

()[ ]

ENPN n

∑(1 )

1(1)

−

=+ − (20)

Next the probabilities that Nn≤, Nn= and Nn>

are shown in formulas (21), (22) and (23) respectively.

BEACON-DRIVEN LEADER BASED PROTOCOL OVER A GE CHANNEL 149

FOR MAC LAYER MULTICAST ERROR CONTROL

[][ ]

PN nPNn

≤= ≤

∏

(

)

1, 1,2...1

0, 0

pnm

−

⎧−=+

⎪

=⎨=

⎪

⎩

(21)

[][][ 1]PN nPN nPN n==≤−≤−

()()

()

11, 2,3...1

1, 1

ppnm

αα

−−

⎧−−−=+

⎪

=⎨

⎪−=

⎩

(22)

[]1[]PN nPN n>=−≤

(

)

11, 1,2...

1, 0

pnm

−

⎧−− =

⎪

=⎨=

⎪

⎩

(23)

Finally we get the expected number of transmissions

for one multicast data packet for all receivers, shown in

formula (24).

[][]

ENPN n

∑

()

(

)

111

−

=+− −

∑ (24)

Similarly, we get the expected number of

transmissions for one multicast data packet for all

receivers in LBP, shown in formula (25).

()

[]1 1[1,1]

LBP

EN P

=−−

∑

()

(

)

=−−

∑ (25)

And the redundant information (RI) of BLBP is:

[]1RIEN=− (26)

Similar as in [16], among pure ARQ based multicast

error control schemes, BLBP needs the minimum

number of transmissions (shown in formula (24)) to let

all receivers receive the packet correctly. There are no

unnecessary transmissions due to the sequence check

scheme and the complete feedback suppression based on

the JACK scheme. We will explore this further in

simulation experiments by comparing BLBP with LBP

and an application layer pure ARQ scheme.

5.3. BLBP over the GE Channel Model With

Both Temporal and Spatial Error

Correlation

Now we consider BLBP over a GE channel model with

both the temporal error correlation and the spatial error

correlation. The error events at different receivers are in

a certain correlation. We assume two kinds of error

events, the error event at the sender which leads to the

correlated packet loss among all receivers and the error

events at different receivers which lead to independent

packet losses. Some new symbols are shown as follows.

y Pm: The error rate caused at receivers (called input

error), independent of each other;

y Pout: The error rate caused at the sender (called output

error), which leads to correlated loss covering all

receivers; (1 )

outoutin

ppp p

+− ;

y 1

in in

αα

−

⎡

⎤

⎢

⎥

−

⎣

⎦

: The transition probability matrix

of the input errors at all receivers;

y 1

out out

out

out out

ββ

αα

−

⎡

⎤

⎢

⎥

−

⎣

⎦

: The transition probability

matrix of the output error at the sender;

: The spatial error correlation among different

receivers, out

Combining the output error and the input error, we

can compute the total error model, which is a 4-states

Markov chain, shown as follows.

(1 )(1)(1)(1 )

(1) (1)(1)(1)

(1)(1)(1 )(1 )

(1 )(1)(1 )(1)

out inoutinoutinoutin

outinout inoutinoutin

outinoutinoutinoutin

outinoutinoutinout in

βββββ βββ

βαβαβ αβα

αβαβαβα β

αααα αααα

−− −−

⎡

⎤

⎢

⎥

−−−−

⎢

⎥

⎢

⎥

−−− −

⎢

⎥

−− −−

⎣

⎦

(27)

For the convenience of analyzing, we use a GE

channel model to approximate the total error model. This

is also confirmed by the simulation experiments. The

total GE channel model is

αα

−

⎡

⎤

⎢

⎥

−

⎣

⎦ (28)

where 1(1)(1 )/pp

−− − and out in

ββ

So we get the final PLR for all receivers, shown in

formula (29).

()[1,1]m

PLRrPmmp

=++= (29)

Now we consider the expected number of

transmissions for one multicast data packet for all

receivers. The probability that Nn> is shown as

follows.

[0]1PN>=

(30)

()()

(

)

[1]1 11

out outin

PN ppp>= +−−− (31)

()()

()

[][,]1 11(/)[,]

outout in

PNnPnnpppPnn>≈+− −−

()()

()

(

)

[, ]111(/)[,]

outout in

Pninip pPii

−

+−−−−−

∑

() ()

()

(

)

111

out outoutin

ppp

αα

−−

=+−−−

()( )

()

(

)

(

)

111

ni i

out outoutin

αα α

−−− −

+−−−

∑ (32)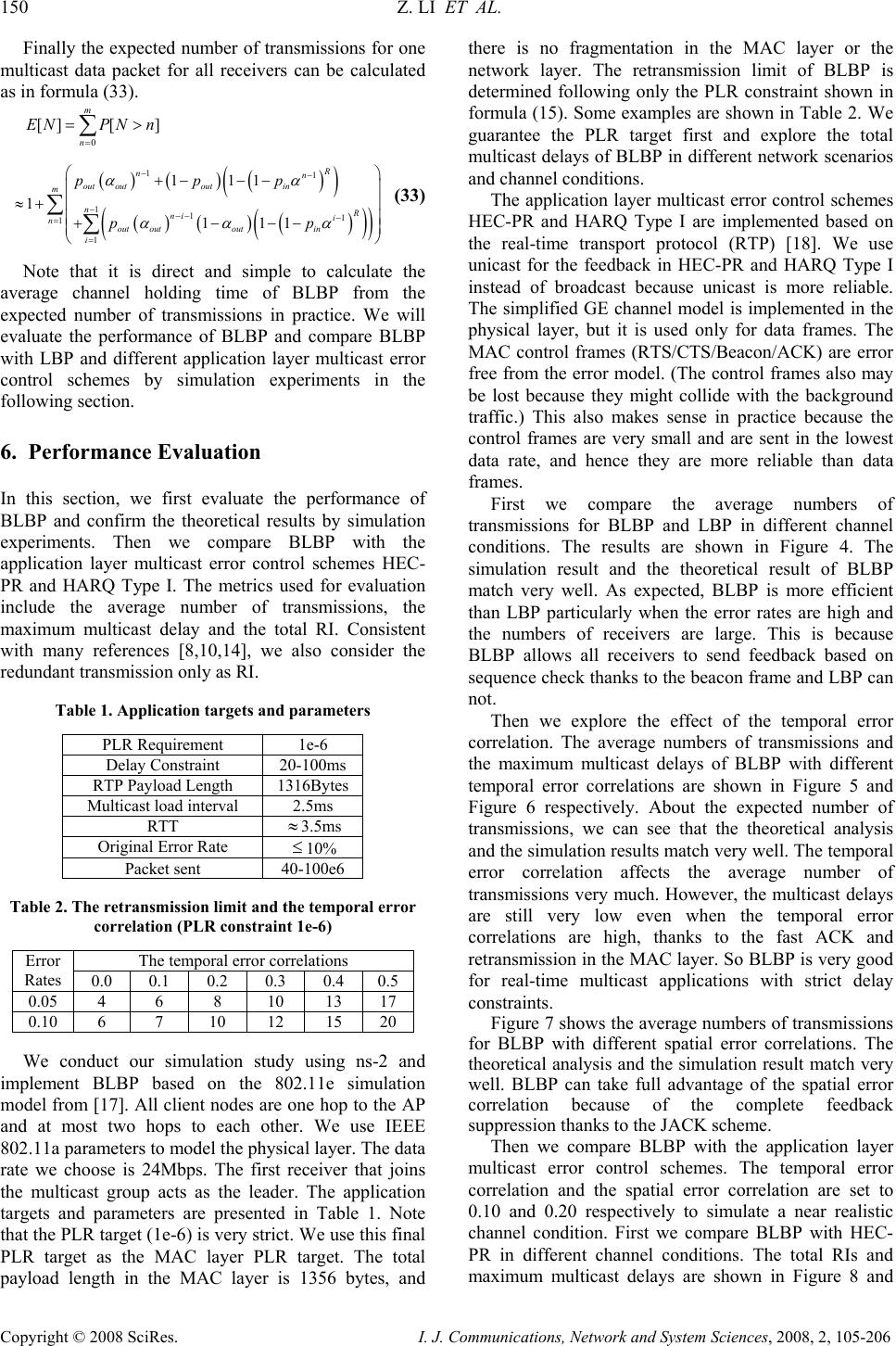

150 Z. LI ET AL.

Finally the expected number of transmissions for one

multicast data packet for all receivers can be calculated

as in formula (33).

[][]

ENPN n

∑

() ()

()

(

)

()( )

()

111

out outoutin

ni i

out outoutin

ppp

αα

αα α

−−

−−− −

⎛⎞

+− −−

⎜⎟

≈+ ⎜⎟

⎜⎟

+−−−

⎜⎟

⎝⎠

∑∑

(33)

Note that it is direct and simple to calculate the

average channel holding time of BLBP from the

expected number of transmissions in practice. We will

evaluate the performance of BLBP and compare BLBP

with LBP and different application layer multicast error

control schemes by simulation experiments in the

following section.

6. Performance Evaluation

In this section, we first evaluate the performance of

BLBP and confirm the theoretical results by simulation

experiments. Then we compare BLBP with the

application layer multicast error control schemes HEC-

PR and HARQ Type I. The metrics used for evaluation

include the average number of transmissions, the

maximum multicast delay and the total RI. Consistent

with many references [8,10,14], we also consider the

redundant transmission only as RI.

Table 1. Application targets and parameters

PLR Requirement 1e-6

Delay Constraint 20-100ms

RTP Payload Length 1316Bytes

Multicast load interval 2.5ms

RTT ≈3.5ms

Original Error Rate ≤10%

Packet sent 40-100e6

Table 2. The retransmission limit and the temporal error

correlation (PLR constraint 1e-6)

The temporal error correlations Error

Rates 0.0 0.1 0.2 0.3 0.4 0.5

0.05 4 6 8 10 13 17

0.10 6 7 10 12 15 20

We conduct our simulation study using ns-2 and

implement BLBP based on the 802.11e simulation

model from [17]. All client nodes are one hop to the AP

and at most two hops to each other. We use IEEE

802.11a parameters to model the physical layer. The data

rate we choose is 24Mbps. The first receiver that joins

the multicast group acts as the leader. The application

targets and parameters are presented in Table 1. Note

that the PLR target (1e-6) is very strict. We use this final

PLR target as the MAC layer PLR target. The total

payload length in the MAC layer is 1356 bytes, and

there is no fragmentation in the MAC layer or the

network layer. The retransmission limit of BLBP is

determined following only the PLR constraint shown in

formula (15). Some examples are shown in Table 2. We

guarantee the PLR target first and explore the total

multicast delays of BLBP in different network scenarios

and channel conditions.

The application layer multicast error control schemes

HEC-PR and HARQ Type I are implemented based on

the real-time transport protocol (RTP) [18]. We use

unicast for the feedback in HEC-PR and HARQ Type I

instead of broadcast because unicast is more reliable.

The simplified GE channel model is implemented in the

physical layer, but it is used only for data frames. The

MAC control frames (RTS/CTS/Beacon/ACK) are error

free from the error model. (The control frames also may

be lost because they might collide with the background

traffic.) This also makes sense in practice because the

control frames are very small and are sent in the lowest

data rate, and hence they are more reliable than data

frames.

First we compare the average numbers of

transmissions for BLBP and LBP in different channel

conditions. The results are shown in Figure 4. The

simulation result and the theoretical result of BLBP

match very well. As expected, BLBP is more efficient

than LBP particularly when the error rates are high and

the numbers of receivers are large. This is because

BLBP allows all receivers to send feedback based on

sequence check thanks to the beacon frame and LBP can

not.

Then we explore the effect of the temporal error

correlation. The average numbers of transmissions and

the maximum multicast delays of BLBP with different

temporal error correlations are shown in Figure 5 and

Figure 6 respectively. About the expected number of

transmissions, we can see that the theoretical analysis

and the simulation results match very well. The temporal

error correlation affects the average number of

transmissions very much. However, the multicast delays

are still very low even when the temporal error

correlations are high, thanks to the fast ACK and

retransmission in the MAC layer. So BLBP is very good

for real-time multicast applications with strict delay

constraints.

Figure 7 shows the average numbers of transmissions

for BLBP with different spatial error correlations. The

theoretical analysis and the simulation result match very

well. BLBP can take full advantage of the spatial error

correlation because of the complete feedback

suppression thanks to the JACK scheme.

Then we compare BLBP with the application layer

multicast error control schemes. The temporal error

correlation and the spatial error correlation are set to

0.10 and 0.20 respectively to simulate a near realistic

channel condition. First we compare BLBP with HEC-

PR in different channel conditions. The total RIs and

maximum multicast delays are shown in Figure 8 and

BEACON-DRIVEN LEADER BASED PROTOCOL OVER A GE CHANNEL 151

FOR MAC LAYER MULTICAST ERROR CONTROL

Figure 9 respectively. When the error rates are high, we

can see BLBP is much more efficient than HEC-PR

which is a pure ARQ based scheme (without FEC

coding). This is because BLBP suppresses the multiple

feedbacks into just a JACK and it is more efficient than

the application layer feedback and retransmission

suppression in HEC-PR. The results also show that the

multicast delays of BLBP are much shorter than the

delays in HEC-PR. This is due to the fast MAC layer

ACK/retransmission in the MAC layer. Moreover,

because of the much longer delays among each

transmission or retransmissions, HEC-PR isn’t much

affected by the temporal error correlation.

Figure 10 shows the total RIs of BLBP, HEC-PR and

HARQ Type I under different delay constraints. As

shown in Figure 9, HEC-PR takes a long time and hence

only satisfies long delay constraints. Both BLBP and

HARQ Type I can satisfy all the delay constraints from

20ms to 100ms. We can see that BLBP is more efficient

than HARQ Type I when the delay constraints are short

and the numbers of receivers are small. This is because

that HARQ Type I has to switch to pure FEC scheme

(no ARQ) when the delay constraint are very short,

hence it is not efficient.

Finally we compare the total RIs of BLBP, HEC-PR

and HARQ Type I with the heterogeneity of receivers.

The error rate for receiver 1 is variable and all the other

receivers have a fixed error rate 0.01. Figure 11 shows

the result. We can see that both BLBP and HEC-PR are

much more efficient than HARQ Type I because HARQ

Type I has to set FEC code and other parameters

according to the receiver with the worst channel

condition but BLBP and HEC-PR are more adaptive.

Moreover, due to the effect of the temporal error

correlation (shown in Figure 5), here BLBP is a little

less efficient than HEC-PR.

7. Conclusions

In this work, we enhance LBP and propose BLBP for

the MAC layer multicast error control in wireless

networks. The use of the beacon frame is to lead the

non-leader receivers to set timers and to announce the

data frame sequence. On erroneous reception of a data

frame that has not been correctly received before, the

leader does not send an ACK, prompting a

retransmission. On erroneous reception (The timer times

out) of the data frame that has not been correctly

received before, the non-leader receivers send NACKs

to collide with the potential ACK from the leader, thus

prompting the AP to retransmit the packet. To guarantee

a very low PLR under strict delay constraints for video

multicast over a GE channel with both the temporal error

correlation and the spatial error correlation, we analyze

BLBP and evaluate its performance via simulation

experiments.

Both the theoretical analysis and simulation results

show that BLBP can correct nearly all the errors for all

receivers in the MAC layer. BLBP needs the minimum

number of redundancy transmissions among all pure

ARQ based schemes. BLBP is more efficient than the

application layer ARQ schemes and the total multicast

delay is much shorter. BLBP is even more efficient than

the best application layer multicast error control scheme

when the delay constraints are short or with the

heterogeneity of receivers. BLBP is very good for the

real-time multicast applications with strict delay

constraints, especially for small groups.

In the future, we plan to extend BLBP with FEC

coding and further improve the QoS of multicast cross

the application layer and MAC layer in wireless

networks.

Figure 4. The expected number of transmissions with

different error rates (

=0 for all receivers)

Figure 5. The expected number of transmissions with

different temporal error correlations (error rate 0.10

for all receivers)

152 Z. LI ET AL.

Figure 6. The maximum multicast delay with different

temporal error correlations (error rate 0.10

=0 for all

receivers)

Figure 7. The expected number of transmissions with

different spatial error correlations (error rate 0.10

=0.10

for all receivers)

Figure 8. The total RI with different error rates (

=0.10

=0.20 for all receivers)

Figure 9. The maximum multicast delay with different

error rates (

=0.10

=0.20 for all receivers)

Figure 10. The total RI with different delay constraints

(error rate 0.10

=0.10

=0.20 for all receivers)

Figure 11. The total RI with a bad receiver 1 (error rate

0.01

=0.10

=0.20 for other receivers, delay constraint

100ms)

BEACON-DRIVEN LEADER BASED PROTOCOL OVER A GE CHANNEL 153

FOR MAC LAYER MULTICAST ERROR CONTROL

8. References

[1] U.H. Reimers, “DVB-The Family of International

standards for Digital Video Broadcasting,” in

Proceedings of IEEE, vol.94, no.1, pp. 173–182, January

2006.

[2] E.N. Gilbert, “Capacity of a burst-noise channel,” Bell

Syst. Tech. J., vol.39, pp. 1253–1265, September 1960.

[3] E.O. Elliott, “Estimates of error rate for codes on burst-

noise channels,” Bell Syst. Tech. J., vol.42, pp. 1977–

1997, September 1963.

[4] M. Mushkin and I. Bar-David, “Capacity and coding for

the Gilbert-Elliott channels,” IEEE Trans. on Inform.

Theory, vol. 35, pp. 1277–1290, November 1989.

[5] J. Nonnenmacher and E.W. Biersack, “Optimal multicast

feedback,” in IEEE Infocom, (San Francisco, California),

pp. 964, March/April 1998.

[6] L. Rizzo, “Effective erasure codes for reliable computer

communication protocols,” ACM Computer

Communication Review, April 1997.

[7] D. Qiao and K.G. Shin, “A two-step adaptive error

recovery scheme for video transmission over wireless

networks,” in Proceedings of IEEE Infocom, 2000,

March 2000.

[8] G.P. Tan and T. Herfet, “The Optimization of an RTP

Level Hybrid Error Correction Scheme for DVB Systems

in Wireless Home Networks under Strict Delay

Constraint,” IEEE Trans. on Broadcasting, November

2006.

[9] G. Carle and E.W. Biersack, “Survey of error recovery

techniques for IP-based audio-visual multicast

applications,” IEEE Network, vol.11, no 6, pp. 24–36,

November –December 1997.

[10] G. Tan and Th. Herfet, “Application Layer Hybrid Error

Correction with Reed-Solomon Code for DVB Services

over Wireless LANs,” the 3rd IEEE International

Conference on Wireless Communications, Networking

and Mobile Computing (WiCOM), Shanghai, China,

September 2007.

[11] J. Kuri, S.K. Kasera. “Reliable multicast in multi-access

wireless LANs,” in Proceedings of Infocom ’99.

[12] J.Tourrilhes, “Robust broadcast: improving the reliability

of broadcast transmission on CSMA/CA,” in Proceedings

of the Ninth IEEE International Symposium on. Personal,

Indoor and Mobile Radio Communications, 1998.

[13] S.K.S. Gupta, V.Shankar, and S. Lalwani, “Reliable

Multicast MAC Protocol for Wireless LANs,” IEEE

International Conference on Communications, vol. 1, pp.

93–97, 2003.

[14] J.R. Yee and E.J. Weldon, Jr., “Evaluation of the

performance of error-correcting codes on a Gilbert

channel”, IEEE Tran. on Communications, vol. 43, no. 8,

August 1995.

[15] G. Bianchi, “Performance analysis of the IEEE 802.11

distributed coordination function,” IEEE Journal on

Selected Areas in Communications, vol. 18, no. 3, March

2000.

[16] D.F. Towsley, J. Kurose, and S. Pingali, “A Comparison

of Sender-Initiated and Receiver-Initiated Reliable

Multicast Protocols,” IEEE Journal on Selected Areas in

Communications, vol. 15, no.3, April 1997.

[17] S. Wiethölter and C. Hoene, An IEEE 802.11e EDCA

and CFB Simulation Model for ns-2, http://www.tkn.tu-

berlin.de/research/802.11e_ns2/.

[18] J. Ott, S. Wenger, N. Sato, C. Burmeister, and J. Rey,

“Extended RTP profile for RTCP-based feedback,” draft-

ietf-avt-rtcp-feedback-11.txt, August 2004.