Paper Menu >>
Journal Menu >>
 I. J. Communications, Network and System Sciences. 2008; 1: 1-103 Published Online February 2008 in SciRes (http://www.SRPublishing.org/journal/ijcns/). Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 PAPR Reduction Scheme with SOCP for MIMO- OFDM Systems Basel RIHAWI, Yves LOUET SUPELEC - IETR Avenue de la Boulaie CS 47601 35576 Cesson Sévigné, France E-mail: {basel.rihawi,yves.louet}@supelec.fr Abstract Combination of multiple-input multiple-output (MIMO) with orthogonal frequency division multiplexing (OFDM) has become a promising candidate for high performance wireless communications. However one major disadvantage of MIMO-OFDM systems lies in a prohibitively large peak-to-average power ratio (PAPR) of the transmitted signal on each antenna. In this paper we extend from SISO to MIMO systems a method based on allocating dedicated subcarriers for PAPR mitigation. These subcarriers are located on unused subcarriers of OFDM spectrum under the assumption they all fall under the power mask. This is originally implemented with a SOCP optimization algorithm applied before space time coding scheme. This jointly mitigates PAPR on each MIMO branch scheme. This approach does not degrade the bit-error-rate (BER) and the data bit rate and no side information (SI) transmission is required. Simulation results are presented in the IEEE 802.16 WiMAX standard contexts: an Alamouti space time code with two transmitted antennas and 256 OFDM subcarriers are considered where 56 of which are unused and allocated for PAPR reduction. PAPR gains up to 7dB are obtained depending on mean power increase limitation. Moreover, with a spectrum mask constraint, this method is standard compliant. Keywords: MIMO-OFDM, PAPR, SOCP 1. Introduction MIMO radio systems have attracted considerable interest and have been studied intensively since Telatar [3] due to its potential of achieving high data rates in multipath channel. It is shown that when multiple transmit and receive antennas are used to form a MIMO system, the system capacity can be improved by a factor given by the minimum between transmitter and receiver antennas number, compared to a single-input single- output (SISO) system with flat Rayleigh fading or narrowband channels [4] For high data rate wireless wideband applications, MIMO combined with orthogonal frequency division multiplexing (OFDM) is being considered in a large number of current technology applications as in IEEE 802.16 WiMAX standard for example. OFDM system has great advantages of having simple equalization and capability of transmitting high data bit rates over frequency selective channels. Nevertheless, its associated signal exhibits high PAPR. To counteract this well known problem, many PAPR reduction techniques have been proposed in the literature [5]. In the same way, OFDM and MIMO association (known as MIMO-OFDM) has faced the similar difficulties. In that case, large peaks can occur in any transmitted branch of the MIMO system. Some recent works have investigated MIMO-OFDM PAPR reduction via selective mapping [6] cross-antenna rotation and inversion [7], unitary rotation [8], polyphase interleaving and inversion [9] or optimal PAPR reduction [10]. All these methods imply SI transmission so as to recover useful data at the receiver which has to be inevitably modified if one of these methods is implemented. To avoid SI transmission, dedicated subcarriers have been generated for PAPR mitigation. In [2], unused subcarriers of OFDM based standards have been allocated and optimized for PAPR reduction under the assumption that they all fall under spectrum mask requirements. The receiver does not take these subcarriers into account and so needs no modification. It has been applied in a single input single output (SISO) context and with a SOCP optimization algorithm, what constitutes a natural extension of the well know Tone Reservation (TR) method [1]. In this paper, we apply SOCP algorithm (discussed in [2] for SISO-OFDM) to MIMO-OFDM systems. The objective is to mitigate the PAPR without any BER and date bit rate degradation and without sending any SI.  30 B. RIHAVI ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 These dedicated subcarriers reveal mean power increase which should be controlled associated with spectrum mask requirements. This paper is organized as follows. Section 2 defines OFDM signal, MIMO-OFDM systems and PAPR for MIMO-OFDM used in this study. Section 3 shows how the problem of PAPR reduction can be formulated as an optimization problem for MIMO-OFDM systems. Section 4 is devoted to simulation results in the IEEE 802.16 WiMAX standard context and exposes the constraints used for SOCP. Finally, Section 5 summarizes and concludes the paper. 2. OFDM Signal and PAPR Definitions for MIMO-OFDM Before proceeding further, let us define the notations used throughout the paper. Time and frequency domain vectors are denoted by small and capital bold case letters respectively. The matrices are denoted by capital italic bold case letters. In OFDM modulation, a block of Ndata symbols )1,...,1,0( −= NkX k, of vector X, will be transmitted in parallel such that each symbol (k X) modulates a subcarrier )1,...,1,0( − = Nkfk. The N subcarriers are orthogonal iffkfk∆= , where Tfk/1=and T is the OFDM symbol period. The resulting analog OFDM base band signal )(tx can be expressed as [] .,0, 1 )( 1 0 2 ∑ − = ∈= N k tfj kTteX N txk π (1) In practice, the frequency complex symbol vector X is transmitted into a discrete-time signal x = [x0,x1,…,xN-1] via an inverse discrete Fourier transform (IDFT) i.e. ).(Xx IDFT= (2) Unfortunately, because of the statistical independence of all subcarriers, time-domain samples are approximately complex Gaussian distributed what results in high amplitude values. This is characterized by PAPR of signal x(t) defined by {} {} , )( )( max )( 2 2 ],0[ txE tx txPAPRTt∈ = (3) where E{.} denotes the expectation operation. To compute easily PAPR, signal x(t) is sampled to get ∑ − =−== 1 0 2,1,...,0, 1N k NL kn j kn LNneX N x π (4) where L is an oversampling factor. It has been proved that L=4 is sufficient for capturing the continuous-time peaks [11]. Then, the resulting temporal signal x is ,Xx L Q = (5) where QL is the IDFT matrix of size NL scaled by L (see Appendix 6.2). Subsequently, PAPR of x is defined as {} {} . x max x2 2 10 E x PAPR k NLk −≤≤ = (6) Figure 1. Structure of the two antennas MIMO-OFDM system In the rest of this paper, all vectors are supposed to be oversampled by factor L. Moreover, we assume a space- time block code (STBC) for the studied MIMO-OFDM system (see Figure 1) that employs Alamouti scheme [12]. In this case, ].......[ * 12 * 2 1 2 * 101 −− −−−−= LNLNLNLN XXXXXXX and ].......[ * 21 * 1 22 * 012 −− − =LNLNLNLN XXXXXXX are the two outputs of Alamouti STBC (see Appendix 6.1). C is the corrective signal added to X in frequency domain in order to reduce PAPR (see Figure 2). ],......[ 12 2 1 2 10 −− − = LNLNLNLNCCCCCCCC1 and C2 are generated by the same STBC. To avoid in and out of band distortions due to non linear power amplification, PAPR of all transmit signals should be simultaneously as small as possible. Since performance is governed by the worst-case PAPR, we define MIMO-OFDM PAPR PAPRMIMO as the maximum of all PAPR related to all NT MIMO paths [14]. Subsequently, {} .max ,....,1 i Ni MIMO PAPRPAPR T x = = (7) PAPR being a random variable, an appropriate description is its complementary cumulative distribution function (CCDF). It gives the probability P0 of exceeding a given threshold PAPR0, i.e., ).( 00 PAPRPAPRP> = Pr (8)  PAPR REDUCTION SCHEME WITH SOCP FOR MIMO-OFDM SYSTEMS 31 Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 The proposed strategy for PAPR reduction is to search an additive corrective signal c in order to verify PAPR(x+c) < PAPR(x). One way to find c is to use an optimization approach, what is detailed in next section. 3. Minimizing PAPR with SOCP Technique 3.1. General Principle of the Propose Method PAPR mitigation principle used through out this paper is to add artificial subcarriers instead of unused ones. The signal addition is achieved in frequency domain as presented in [2] and illustrated in Figure 2. Thus, PAPR of the resulting signal (x+c) is given by Figure 2. Principle of adding corrective subcarriers instead of unused ones for PAPR mitigation {} {} . cx max cx2 2 10 + + =+ −≤≤ E cx PAPR kk NLk (9) Ideal computing would be to mitigate PAPR by minimizing the maximum peak of the combining signal (x+c=x+QLC) while keeping constant its average power. This objective can be formulated as ,maxmin ,C row Lkk k Cqx+ (10) where row Lk q,is the k-th row of QL. Such a minimization problem given by Eq. 10 can be formulated as SOCP much easier than in semi definite program (SDP) or quadratically constrained quadratic program (QCQP) [13]. SOCP is a convex optimization problem class that minimizes a linear function over the intersection of an affine set and the product of second- order (quadratic) cones [13]. 3.2. SOCP Approach Tone reservation (TR) is an efficient technique to reduce the PAPR of a multicarrier signal [1]. This method is based on adding a data-block-dependent time domain signal to the original multicarrier signal to reduce its peaks. This time domain signal can be easily computed at the transmitter and stripped off at the receiver. For this technique, the transmitter optimizes a given subset of subcarriers for PAPR reduction. The objective is to find the time domain signal to be added to the original time domain signal x. If we add a frequency domain vector ],...,,[ 1 10 − =LN CCCC to X, the new time domain signal can be represented as x+c = IDFT(X+C), where c is the time domain signal due to C. The TR technique restricts the data block X and peak reduction vector C to lie in disjoint frequency subspaces, i.e. {} {} ⎩ ⎨ ⎧ ∉= ∈= .,...,,,0 ,...,,,0 21 21 vn vn iiinC iiinX The v nonzero positions in C are called peak reduction carriers. Due to orthogonality, these additional subcarriers cause no distortion on the useful data subcarriers. To find the value of { } vn iiinC ,...,,, 21 ∈ , we must solve a convex optimization problem that can easily be modeled as a linear programming (LP) problem. To reduce the computational complexity of LP, a simple gradient algorithm is proposed in [1]. Nevertheless, TR proposed in [1] allocates subcarriers among those which carry useful information. This results in a data rate loss. In [2] TR has been extended to unused subcarriers of standards with SOCP algorithm. Significant PAPR reduction gains have been obtained, under spectrum mask constraints (all corrective subcarriers must fall under the spectrum mask) and with mean power increase control. 3.3. Application of MIMO-OFDM From Figure 1, signals 1 x and 2 xat the outputs of the OFDM modulators are expressed as ),( 2 * 1 1 ACACx cxx 1 11 •−•+= += L Q (11) ),( 21 *' ACACx cxx 2 22 2 •+•+= += L Q (12) where (.)* denotes complex conjugate, •the element wise (dot) product, ' L Qthe matrix deduced from L Qby pair and odd rows permutations of L Q(see Appendix 6.2), T ]10...1010[ 1=Aand T ]01...1010[ 2=ANL×1 vectors (T denotes the transpose of the vectors). Now PAPR of signals to be transmitted are {} {} , cx max x2 11 2 11 1+ + = E cx PAPR kk k (13)  32 B. RIHAVI ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 {} {} . cx max x2 22 2 22 2+ + = E cx PAPR kk k (14) According to Eq.(7), PAPR of MIMO system is { } { } { } . x,x max21 PAPRPAPRPAPRMIMO= (15) The objective of this method is to reduce MIMO PAPR by jointly reducing { } 1 xPAPR and { } 2 xPAPR . At first, SOCP algorithm does not take into account the mean power increase. So, the problem of PAPR minimization can be formulated as ,)(min minmaxmin 2 2 * 1 2 1 2 11 11 ∞ ∞ •−•+= +=+ ACACx cx 1 C 1 Cc L kk k Q cx (16) .)(min minmaxmin 2 21 *' 2 2 2 22 22 ∞ ∞ •+•+= +=+ ACACx cx 2 C 2 c L C kk k Q cx (17) Eqs.(16) and (17) are convex optimization problems formulated as one with SOCP : )18(.)( )( min 21 *' 2 * 1 β β β ≤•+•+ ≤•−•+ ∞ ∞ ACACx ACACx 2 1 L L Q Qtosubject SOCP algorithm provides optimized solution Copt according to Eq.(18). Nevertheless, the two resulting signals )2,1( =+ iQ optLCxi have larger mean powers compared to x what has to be taken into account for practical applications. Moreover, Copt components must fall under the spectrum mask requirements to make the signal standard compliant. These two points are now discussed. 4. Constraints Statement and Simulation Results 4.1. Mean Power Increase Constraint Figure 3 shows PAPR CCDF of original and optimized signals for randomly generated QPSK symbols. MIMO-OFDM system uses two antennas with N=256 subcarriers per antenna. 56 unused subcarriers are used as the corrective signal. This system is inspired from IEEE 802.16 WiMAX standard. We set the oversampling factor L to a value of 4. As we can see, PAPR is reduced by 7dB for a 10-3 exceed probability level without any mean power constraint. Figure 3. PAPR reduction using SOCP without any constraint in IEEE 802.16 context However, adding a signal c to an original signal x to reduce its PAPR increases the mean transmit power. The relative mean increase power ∆E is defined as [1] . )( )( log10 2 2 10 x cx E E E+ =∆ (19) This parameter must be as small as possible in order to avoid power amplification saturation. Indeed, it is easy to understand that if average power increases indefinitely x+c would obviously have a resulting PAPR of 0dB but the signal cannot be transmitted. Thus, the relative mean power must be upper bounded and can be written as , γ ≤ ∆ dB E (20) what implies )()( 22 xcx EE λ ≤+ , (21) where 10 10 γ λ =.γ is a constant related to the power amplifier characteristics. The above condition can be added as a constraint in the optimization problem. By taking these conditions into account, SOCP algorithm becomes ,)( )22()( )( )( min 221 *' 12 * 1 21 *' 2 * 1 KQ KQ Q Qtosubject L L L L λ λ β β β ≤•+•+ ≤•−•+ ≤•+•+ ≤•−•+ ∞ ∞ ∞ ∞ ACACx ACACx ACACx ACACx 2 1 2 1 where ).2,1(),(. 2== iENLKii x 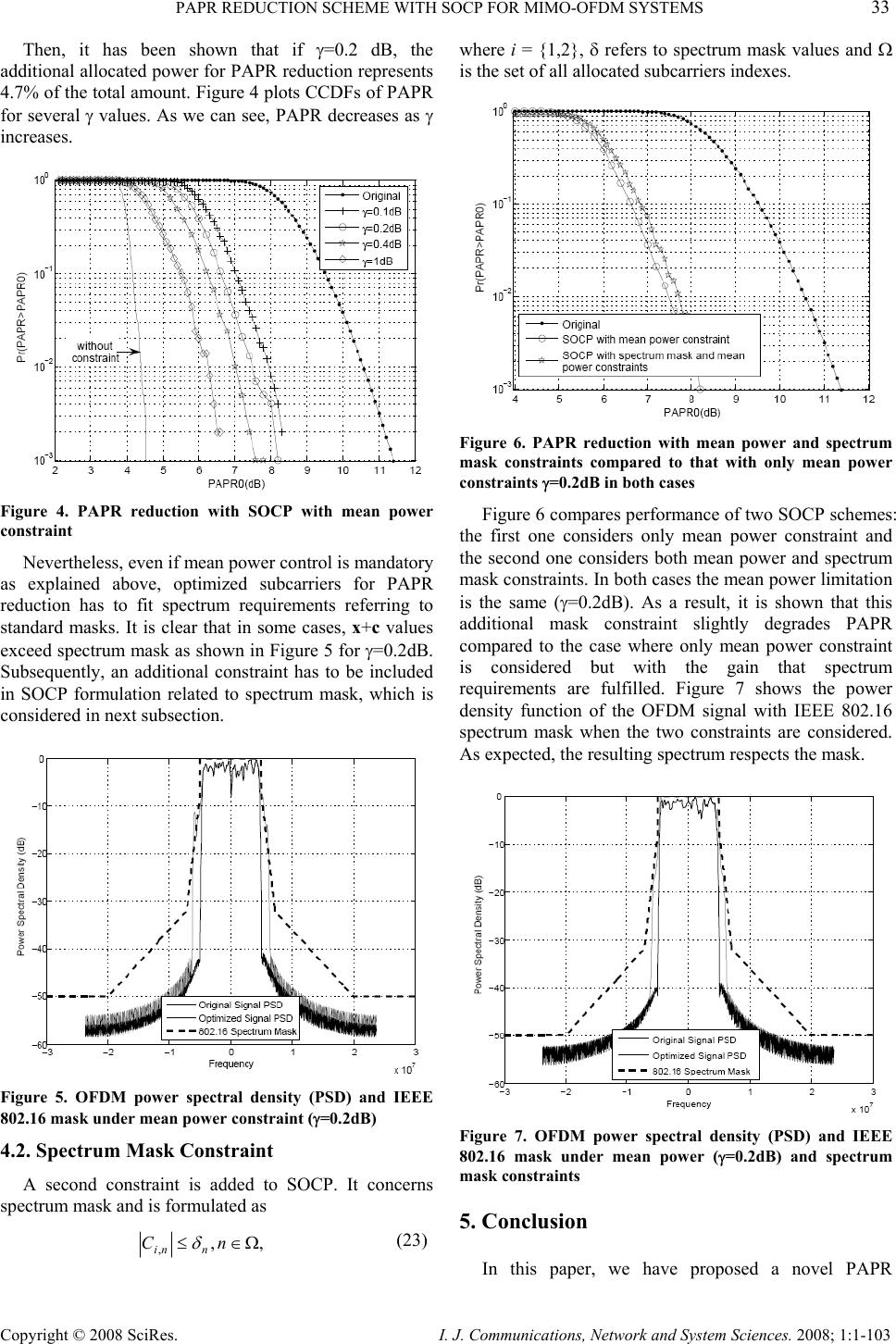 PAPR REDUCTION SCHEME WITH SOCP FOR MIMO-OFDM SYSTEMS 33 Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 Then, it has been shown that if γ=0.2 dB, the additional allocated power for PAPR reduction represents 4.7% of the total amount. Figure 4 plots CCDFs of PAPR for several γ values. As we can see, PAPR decreases as γ increases. Figure 4. PAPR reduction with SOCP with mean power constraint Nevertheless, even if mean power control is mandatory as explained above, optimized subcarriers for PAPR reduction has to fit spectrum requirements referring to standard masks. It is clear that in some cases, x+c values exceed spectrum mask as shown in Figure 5 for γ=0.2dB. Subsequently, an additional constraint has to be included in SOCP formulation related to spectrum mask, which is considered in next subsection. Figure 5. OFDM power spectral density (PSD) and IEEE 802.16 mask under mean power constraint (γ=0.2dB) 4.2. Spectrum Mask Constraint A second constraint is added to SOCP. It concerns spectrum mask and is formulated as ,, ,Ω∈≤ nC nni δ (23) where i = {1,2}, δ refers to spectrum mask values and Ω is the set of all allocated subcarriers indexes. Figure 6. PAPR reduction with mean power and spectrum mask constraints compared to that with only mean power constraints γ=0.2dB in both cases Figure 6 compares performance of two SOCP schemes: the first one considers only mean power constraint and the second one considers both mean power and spectrum mask constraints. In both cases the mean power limitation is the same (γ=0.2dB). As a result, it is shown that this additional mask constraint slightly degrades PAPR compared to the case where only mean power constraint is considered but with the gain that spectrum requirements are fulfilled. Figure 7 shows the power density function of the OFDM signal with IEEE 802.16 spectrum mask when the two constraints are considered. As expected, the resulting spectrum respects the mask. Figure 7. OFDM power spectral density (PSD) and IEEE 802.16 mask under mean power (γ=0.2dB) and spectrum mask constraints 5. Conclusion In this paper, we have proposed a novel PAPR  34 B. RIHAVI ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 reduction approach for MIMO-OFDM. It is based on SOCP and provides significant PAPR reduction gains without transmitting any side information and without degrading BER and data rate at the same time. To do so, we have used the unused subcarriers of standards to generate the corrective signal that jointly mitigates the PAPR of the MIMO-OFDM scheme. We have shown that PAPR can be reduced by 7dB at the 10-3 probability exceed level. To avoid an uncontrolled increase of the relative mean power, we have included a mean power constraint in SOCP algorithm. Finally, to be standard compliant, the allocated subcarriers for PAPR reduction have to fall under the spectrum mask, which has been done in IEEE 802.16 WiMAX standard context. 6. Appendices 6.1. Alamouti STBC Figure 8. Alamouti STBC for 2 antennas 6.2. Fourier matrices QL and Q’L ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = −−− −−− − )1)(1(1).1( 2 )1)(2(1).2( 2 )1.(1 2 1.1 2 1 1 1 111 1 LNLN LN jLN LN j LNLN LN jLN LN j LN LN j LN j L ee ee ee LN Q ππ ππ ππ L L MOMM L L ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = −−− −−− − )1)(2(1).2( 2 )1)(1(1).1( 2 )1.(1 2 1.1 2 ' 1 1 111 1 1 LNLN LN jLN LN j LNLN LN jLN LN j LN LN j LN j L ee ee ee LN Q ππ ππ ππ L L MOMM L L 7. References [1] J. Tellado-Mourelo, “Peak to Average Power Ratio Reduction for multicarrier modulation”, PhD thesis, Stanford University, Sept. 1999. [2] S. Zabre, J. Palicot, Y. Louet, and C. Lereau, “SOCP approach for OFDM peak-to-average power ratio reduction in the signal adding context”, IEEE ISSPIT 06, Vancouver, Canada, Aug. 2006. [3] I. E. Telatar, “Capacity of multi-antenna Gaussian channels”, AT T Bell Labs Internal Tech. Memo., Jun. 1995. [4] G. J. Foschini, and M. J. Gans, “On limits of wireless communications in a fading environment when using multiple antennas”, Wireless Personal Communication, vol.6, Mar. 1998, pp. 314-335. [5] S. H. Han, and J. H. Lee, “An overview of peak- toaverage power ratio reduction techniques for multicarrier transmission”, IEEE Wireless Communication, vol.12, no.2, Apr. 2005, pp.56-65. [6] Y. Lee, Y. You, W. Jeon, J. Paik, and H. Song, “Peak-to-average power ratio in MIMO-OFDM systems using selective mapping”, IEEE Commun. Letters, vol.7, no.12, Dec. 2003, pp. 575-577. [7] M. Tan, Z. Latinovic, and Y. Bar-Ness, “STBC MIMO-OFDM Peak-to-Average Power Ratio Reduction by Cross-Antenna Rotation and Inversion”, IEEE Commun. Letters, vol.9, no.7, Jul. 2005. [8] H.Lee, D. N. Liu, W. Zhu, and M. P. Fitz, “Peak power reduction using a unitary rotation in multiple transmit antennas”, in Proc. IEEE International Conference on Communication, vol.4, Seoul, South Korea, May 2005, pp.2407-2411. [9] Z. Latinovic, and Y. Bar-Ness, “SFBC MIMO- OFDM Peak-to-Average Power Ratio Reduction by Polyphase Interleaving and Inversion”, IEEE Commun. Letters, vol.10, no.4, Apr. 2006. [10] Aggarwal, A. Sauffr, and E.R. Meng T.H, “Optimal Peak-to-Average Power Ratio Reduction in MIMO Systems”, IEEE International Conference on Commnication (ICC 06), vol.7, Istanbul, Turkey, Jun. 2006, pp.3094-3099. [11] G. Wunder, and H. Boche, “Peak value estimation of bandlimited signals from their samples, noise enhancement, and a local characterization in the neighborhood of an extremum”, IEEE Trans. Signal Processing, Mar. 2003, pp.771-780. [12] Siavash M. Alamouti, “A simple Transmit Diversity Technique forWireless communications”, IEEE Journal on Select Areas in Communications, vol.16, no.8, Oct. 1998. [13] M. Lobo, L. Vandenberghe, S. Boyd, and H. Lebret, “Applications of second order cone programming”, Linear Algebra and its Applications, 284:193-228, Special Issue on Linear Algebra in Control, Signals and Image Processing, Nov. 1998.  PAPR REDUCTION SCHEME WITH SOCP FOR MIMO-OFDM SYSTEMS 35 Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 [14] R.F.H. Fischer, and M. Hoch, “Peak-to-Average Power Ratio Reduction in MIMO OFDM”, IEEE International Conference on Communications (ICC 2007), Glasgow, United Kingdom, Jun. 2007. [15] M. Grant, S. Boyd, and Y. Ye, “CVX – Matlab Software for Disciplined Convex Programming”, http://www.stanford.edu/ boyd/cvx/ |

