Technology and Investment
Vol.2 No.2(2011), Article ID:5169,5 pages DOI:10.4236/ti.2011.22012
Instant Diffusion Equation of Price Changing and Time-Space Exchanging Description
School of Civil Engineering and Transportation, South China University of Technology, Guangzhou, China
E-mail: cttqyun@scut.edu.cn
Received March 7, 2011; revised April 16, 2011; accepted April 20, 2011
Keywords: Price, Diffusion of Price Changing, Heat Diffusion Equation, Partial Differential Equation, Order of Commodity, Newton’s Second Law, Time-Space Exchanging.
Abstract
Analogy to heat diffusion equation, an instant diffusion equation of price changing is obtained and explained by “time-space exchange” via Newton’s second law, in which the partial derivative of price respected to time is viewed as a “force”, and the derivative of transportation velocity of price between commodities is viewed as an “acceleration”. It is a partial differential equation of second order. The solution of this equation is found and the definitions of “order of commodities”, “distance between commodities” are given. An important relationship of “time-space exchange” in a stationary process of diffusion of price changing is found. This provides a base for describing the relation of “time-space exchange” quantitatively. Examples for calculating and checking the diffusion of price changing in pork, beef, and mutton based on the data taken on February 5th 2008 are given.
1. Introduction
Control and preventing inflation is a focus goal in the world. It is also an important task of macro-control in China in 2008 and 2011. Now, the price problem is widely concerned in China. However, the solutions of the problem are more on practice monitoring and control (investigation, statistics, monitoring, etc.), rather than on theoretical study. As the theoretical research focuses more on qualitative analysis, or on statistic probability rather than on quantitative analysis, the core of solutions is on policy making, price reform, price system, and price forming. So far, no paper on price diffusion is found in literature. This paper studies diffusion of price changing (rising) quantitatively which is analyzed by a partial differential equation based on analogy of heat diffusion explained by Newton’s second law via “time-space exchange”. It is a creative combination of natural science and social science. In Section 2, certain mathematical model is used basing on the comparability and relativities of commodities. In Section 3, “Time-Space Exchange” description and heat diffusion equation are introduced. In it, the heat diffusion equation is explained via Newton’s second law using “Time-Space Exchange” description. In Section 4, the instant diffusion equation of price changing due to one source is established and the solution is found by the method of departing variables. In Section 5, definitions of order of commodities and distance between commodities are defined. In Section 6, constant of diffusion-inertia and “Time-Space Exchange” are discussed. In Section 7, a typical example of calculation and checking the prices of pork, beef, and mutton from statistical data due to one source of price changing (rising of pork price) via instant diffusion equation is given. Finally, a conclusion on the difference between heat diffusion equation, instant diffusion equation of price changing and the suitable range of solution (3) is reached.
2. Mathematical Model
Similar to author’s work on analysis of the tendency of prices of stocks, futures index [1-12], certain mathematical model is used basing on the predicable of tendency with inertia. Certain mathematical model is also used herein basing on the comparability and relativities of commodities.
When the price of a commodity rises, it is not immediately transmitted (but with a delay time interval) to the prices of its relying products or replacements in general for many reasons such as reserve of goods. The cases of transmission with a delay time interval are more complicated, as the delay time period depends on stocks, economic environment, policy interrupting, and negotiation and gambling on price among commodity owners. Such cases are not discussed herein. The case of immediate transmission of price to the related products or its replacements is the simplest to be discussed. For example the rising price of raw pork is immediately transmitted to the price of beef, or mutton. This is a good case in point.
3. “Time-Space Exchange” Description and Heat Diffusion Equation
The topic of “time and space exchange” is often heard in many areas, such as in sciences, in visco-elasticity; in stock market and in military (Mr. Jiang Jie Shi once mentioned “time and space exchange” in his speech in the period of Anti-Jajanese War) etc. However, why does time and space need to exchange and how do they exchange? What is the standard for the exchange? And what is the relationship between “time-space exchange” and the price change diffusion equation? To answer these questions, let us begin with the history of the birth of calculus.
Two typical examples produce calculus. One is Newton’s explanation of changing rate 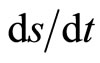 of displacement
of displacement 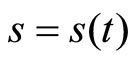 of motion respect to time as “velocity” and
of motion respect to time as “velocity” and 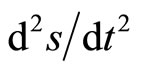 as “acceleration”. The other is Leibniz explanation of changing rate
as “acceleration”. The other is Leibniz explanation of changing rate 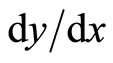 and
and  respect to space
respect to space 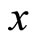 of function
of function 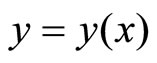 as geometrical meaning “slope” and “curvature” respectively. These two explanations have not been exchanged or even tried to exchange yet since calculus was born.
as geometrical meaning “slope” and “curvature” respectively. These two explanations have not been exchanged or even tried to exchange yet since calculus was born.
Now, let us look at the heat diffusion equation for 1-D (one dimensional) uniform medium [13] shown as follows:
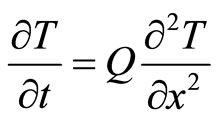 (1)
(1)
where 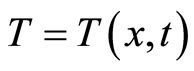 the temperature is the function of time
the temperature is the function of time 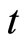 and space
and space .
. 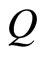 is a constant. The changing rate
is a constant. The changing rate  respect to time
respect to time 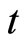 is easily accepted as temperature changing “velocity” by most people via daily life experience. However, what is the meaning of the term
is easily accepted as temperature changing “velocity” by most people via daily life experience. However, what is the meaning of the term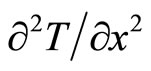 ? The “curvature” is hard to understand by most people. Why not try another way to explain the term which would be easily accepted by people? So exchanging of time and space could be a better way for a clear explanation.
? The “curvature” is hard to understand by most people. Why not try another way to explain the term which would be easily accepted by people? So exchanging of time and space could be a better way for a clear explanation. 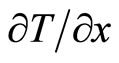 is explained as a “diffusion velocity”, in which the “velocity” is the changing rate respected to time
is explained as a “diffusion velocity”, in which the “velocity” is the changing rate respected to time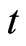 , that means the respected objects are exchanged. Similarly,
, that means the respected objects are exchanged. Similarly, 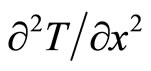 is explained as a “diffusion acceleration”. After the time-space exchange, Equation (1) is viewed as Newton’s second law, where
is explained as a “diffusion acceleration”. After the time-space exchange, Equation (1) is viewed as Newton’s second law, where 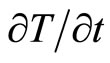 could be an applied “force”,
could be an applied “force”, 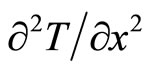 an “acceleration”,
an “acceleration”, 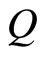 is a constant like inertia of mass.
is a constant like inertia of mass.
4. Instant Diffusion Equation of Price Changing
In a closed relative equilibrium state of commodity system, the price system has a relative fixed ratio among commodities. Once the equilibrium state is bricked by the price changing of a commodity, the price changing will be transmitted to the users’ products, and/or its replacements .For example, the price of raw pork rose rapidly from 2007-09 to 2008-02 in China, then, the users decreased the consumption of raw pork and turned to replacements, such as beef, mutton, eggs, etc. and consequently pushing up their price. Hence the price rising is transmitted to other commodities, due to the requirement of the fixed ratios in equilibrium state.
Now, how do we determine the transmitting (or diffusion) velocity? And what is the base for calculation?
Similar to heat diffusion Equation (1), via Newton’s second law, we set up the following equation:
 (2)
(2)
where 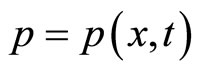 represents the price of commodity
represents the price of commodity 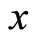 at time
at time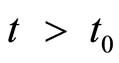 . (
. (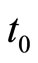 is the beginning time of a non-equilibrium state, i.e.,
is the beginning time of a non-equilibrium state, i.e., 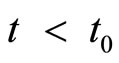 is an equilibrium state. For convenient, let
is an equilibrium state. For convenient, let , at which the price
, at which the price 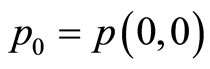 has a changing
has a changing where
where 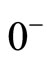 and
and 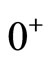 represent the time in equilibrium state and non-equilibrium state respectively.).
represent the time in equilibrium state and non-equilibrium state respectively.). 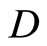 is a constant similar to the inertia of mass.
is a constant similar to the inertia of mass.
The solution of partial differential Equation (2) can be solved by the method of departing variables and is shown in (3).
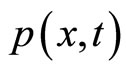 (3)=
(3)= 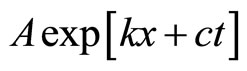
Substituting (3) into (2), we have
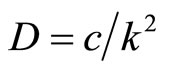 (4)
(4)
By the initial boundary conditions, i.e.
1)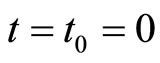 ,
,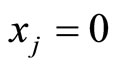 ,
, 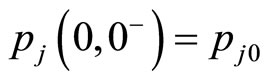 , we have
, we have
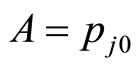 , (5)
, (5)
2) ,
,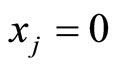 ,
,
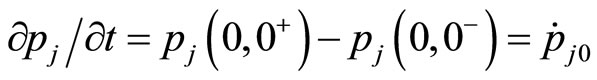 , we have
, we have
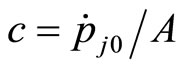 (6)
(6)
3)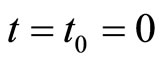 ,
, 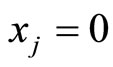 ,
,
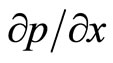 =
=
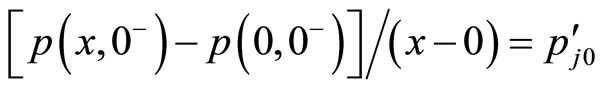 (7)
(7)
By (3) and (7), we have
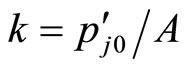 (8)
(8)
Substituting (5), (6), (8) into (3), we have
 =
=
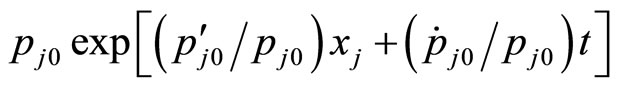 (9)
(9)
Equation (9) is the solution of (2) and describes the price of the commodity with price-changing at the source 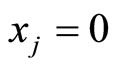 of diffusion.
of diffusion.
5. Definitions of Order of Commodities and Distance between Commodities
Although the instant diffusion Equation (2) has been established and its solution found, however, there are some questions still left: How do we define the order of commodity, and the “distance” between two commodities? Why is it one-dimensional?
Definition:
Let
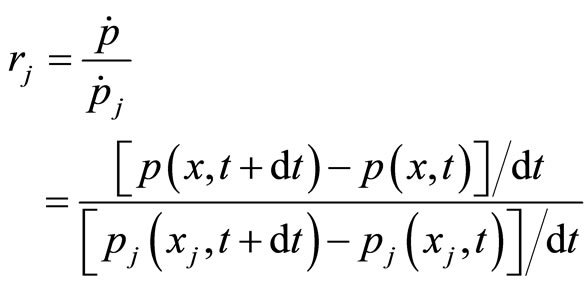 (10)
(10)
be the price relation degree (or dependent degree) of commodity 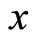 on commodity
on commodity . Note that
. Note that 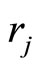 is defined to be determined just by the property of commodity and shown to be fixed in a relative equilibrium state, so that it is independent of time
is defined to be determined just by the property of commodity and shown to be fixed in a relative equilibrium state, so that it is independent of time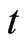 , or it is independent at least in a time interval. For convenience of practical calculation, differential calculation is replaced by difference calculation, so (10) is rewritten as
, or it is independent at least in a time interval. For convenience of practical calculation, differential calculation is replaced by difference calculation, so (10) is rewritten as
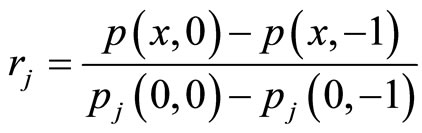 (11)
(11)
where the time 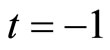 and
and 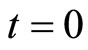 represent the time before and at (or after) the price changing (rising) respectively.
represent the time before and at (or after) the price changing (rising) respectively.
Now, we define the order of commodity 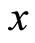 by
by
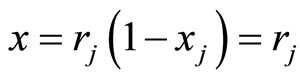 , (12)
, (12)
where there is no lose of generality, let 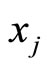 = 0. Since
= 0. Since 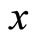 is determined by one parameter
is determined by one parameter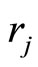 , so
, so 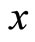 coordinate is one-dimensional.
coordinate is one-dimensional.
We also define the “distance” 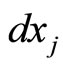 between commodity
between commodity 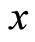 and
and 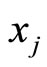 by
by
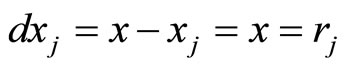 (13)
(13)
i.e., we use the price relation degree to define the distance between two commodities  and
and . Original commodity
. Original commodity 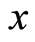 and commodity
and commodity  are a sign of commodity, they have no order. However, once we have introduced the concept of price relation degree to define the order of commodity and set up the distance definition, then we can make use of the calculus for our calculation.
are a sign of commodity, they have no order. However, once we have introduced the concept of price relation degree to define the order of commodity and set up the distance definition, then we can make use of the calculus for our calculation.
6. Constant of Diffusion-Inertia  and “Time-Space Exchange”
and “Time-Space Exchange”
The difference between constant 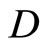 in instant diffusion Equation (2) and constant
in instant diffusion Equation (2) and constant 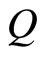 in heat diffusion Equation (1) (or the mass
in heat diffusion Equation (1) (or the mass 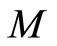 in Newton’s second law) is that
in Newton’s second law) is that 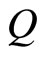 and
and 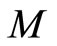 can be measured while
can be measured while  is hard to measured. However,
is hard to measured. However, 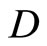 can be determined by substituting (6), (8) into (4), we have
can be determined by substituting (6), (8) into (4), we have
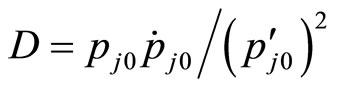 (14)
(14)
where constant 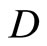 can be calculated by (14).
can be calculated by (14).
Since the data of price for commodities are announced monthly in an average form, that means the price changing rate is averaged or with constant price changing rate for practical use. For such a simple but important case, i.e., 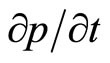 is constant (stationary process), the response at any time
is constant (stationary process), the response at any time 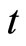 is the same and any
is the same and any 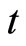 can be chosen as an original, or (14) suits for any time
can be chosen as an original, or (14) suits for any time 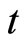 can be rewritten as
can be rewritten as
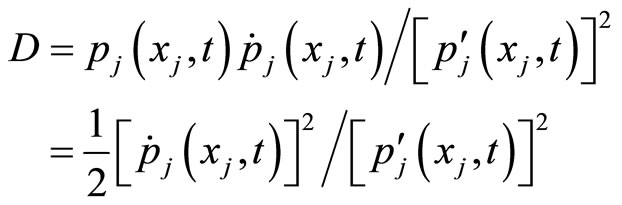 (15)
(15)
or
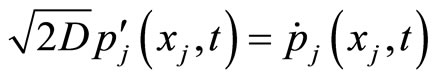 , (16)
, (16)
(16) is called the relation of “time-space exchange” in process of price changing diffusion. It means that a constant velocity of price changing at time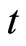 , the
, the 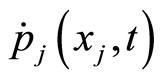 is equal to
is equal to 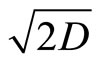 times of the constant transmitted velocity
times of the constant transmitted velocity .
.
7. Examples of Calculation
The typical example of one source of diffusion is the food price rising mainly due to the price rising of pork from 2007-07 to 2008-02 in China. According to www.chinanews.com.cn 2008-02-05 reported data from www.sdpc.gov.cn: The average price of pork is 14.31 (unit 1Yuan/500 g of RMB, same in the following) in 2008-01, with a 4.53% increase in price of 2007-12 (simplifying as a 4.53% increase 2007-12 same in the following); beef 14.85 (2008-01) a 9.51% increase (2007-12); mutton 16.26 (2008-01), a 4.36% increase (2007-12).
The above price rising is mainly caused by pork and transmitted to beef, mutton, etc.
Pork 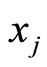
Let 2008-01 be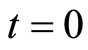 , 2007-12 be
, 2007-12 be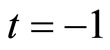 , 2008-02 be
, 2008-02 be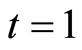 . From the data we have
. From the data we have
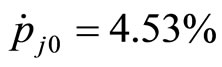 ,
, 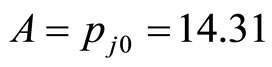 ,
,  ,
,
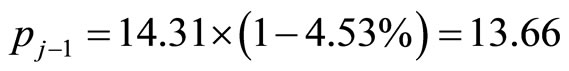
Substituting into (9), we have
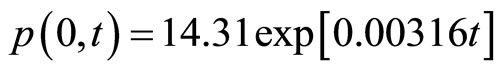 , (17)
, (17)
the prediction of price of pork in 2008-02 shall be (use 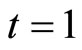 substituting into (17))
substituting into (17))
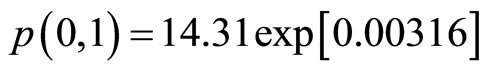 =
= 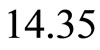 (a little bit increasing).
(a little bit increasing).
Beef (without bone) 
the price of 2007-12 is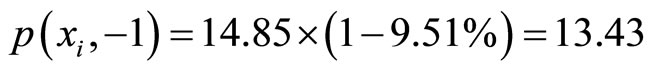 the price ratio of beef and pork is
the price ratio of beef and pork is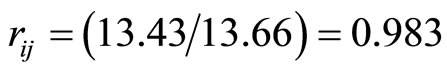 , the coordinate of beef
, the coordinate of beef
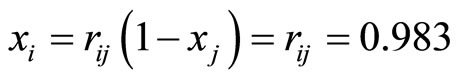 ,
,
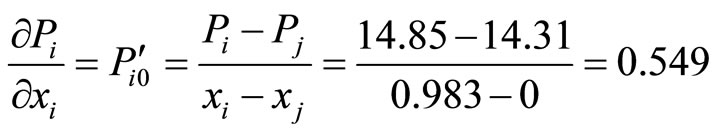
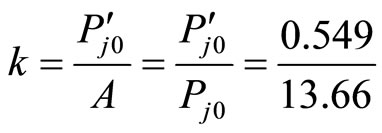 ,
, 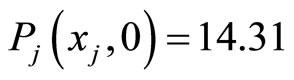
Substituting these data into (9), we get the calculating price of beef of 2008-01 as

=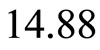 .
.
Comparing with the data 14.85, the error is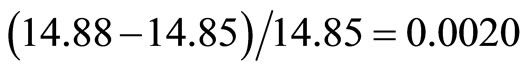 . It shows that the calculation is accurate.
. It shows that the calculation is accurate.
The prediction of price of beef in 2008-02 is (use  substituting into (9)
substituting into (9)
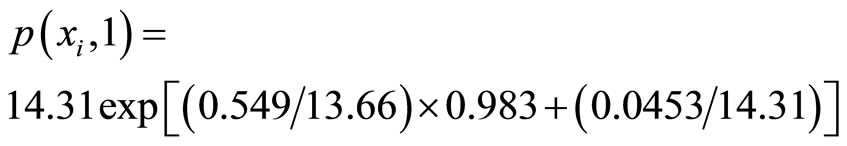
= 15.50.
mutton 
The price of mutton of 2007-12 is 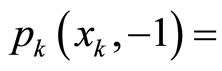
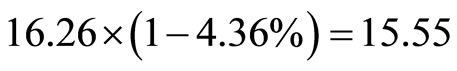 . The price of ratio of pork and mutton is
. The price of ratio of pork and mutton is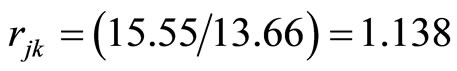 . The coordinate of mutton is
. The coordinate of mutton is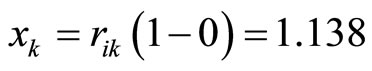 .
.
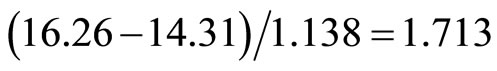
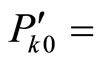 . Substituting into (9), we get the calculating price for mutton in 2008-01 as
. Substituting into (9), we get the calculating price for mutton in 2008-01 as 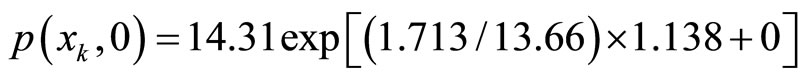 = 16.66 Comparing with the price 16.26 in 2008-01, the error is
= 16.66 Comparing with the price 16.26 in 2008-01, the error is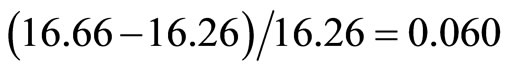 . It also shows that the calculation is accurate. Similar to the above prediction, the predicted price of mutton in 2008-02 is 18.36.
. It also shows that the calculation is accurate. Similar to the above prediction, the predicted price of mutton in 2008-02 is 18.36.
It is regretted that no statistic data of the same form of prices of pork, beef and mutton as shown in 2008-02-05 can be found in Chinese Official Nets. (The statistic data in 2008-03 are differed from that of 2008-02), so the above predictions can not be checked. However, the calculating prices of beef and mutton in 2008-01 are checked to be accurate.
8. Conclusions
Analogy to heat diffusion equation, the price changing diffusion Equation (2) is obtained via the explanation of Newton’s second law. The major difference between our method and heat diffusion equation is that constant 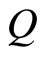 in (1) can be measured and is known as a given constant, while herein the constant
in (1) can be measured and is known as a given constant, while herein the constant 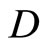 in (2) is hard to be measured and is treated to be an unknown constant to be determined by Equation (14). The solution (3) is not the full solution of all possible solutions of Equation (2) (e.g., the term of
in (2) is hard to be measured and is treated to be an unknown constant to be determined by Equation (14). The solution (3) is not the full solution of all possible solutions of Equation (2) (e.g., the term of 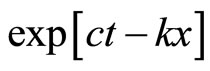 also satisfies (2), but is not included in (3)), but it satisfies all 3 initial boundary conditions for the partial differential Equation (2), so that (3) is simpler and easy to use for practical calculation.
also satisfies (2), but is not included in (3)), but it satisfies all 3 initial boundary conditions for the partial differential Equation (2), so that (3) is simpler and easy to use for practical calculation.
When the price changing decreases, solution (3) is replaced by
 (18)
(18)
Similar initial boundary conditions can be used to determine all constants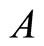 ,
, 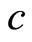 , and
, and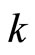 .
.
The above Equation (9) suitable for time  in the interval in which the influent factor is just due to the price changing (rising) of
in the interval in which the influent factor is just due to the price changing (rising) of  at
at  only. (i.e., one source of diffusion).
only. (i.e., one source of diffusion).
The study herein is a primary and rough study on instant diffusion problem. There are many relative diffusion problems worth for further study. For example, the diffusion of price rising; the diffusion of stock price rising; the diffusion of infectious disease; the diffusion of financial crisis; etc.
9. References
[1] T. Q. Yun, “A Basic Integral-Differential Equation of Changing Rate of Stock Price,” Journal of South China University of Technology, in Chinese, Vol. 24, No. 6, 1996, pp. 35-39.
[2] T. Q. Yun, “A Short-Term Prediction of Stock Price for the Normal Case,” Journal of South China University of Technology, in Chinese, Vol. 25, No. 5, 1997, pp. 47-51.
[3] T. Q. Yun, “Basic Equations, Theory and Principles for Computational Stock Market—(I) Basic Equations,” Applied Mathematics and Mechanics, Vol. 20, No. 2, 1999, pp. 154-162. doi:10.1007/BF02481894
[4] T. Q. Yun, “Basic Equations, Theory and Principles for Computational Stock Market—(2) Basic Principles,” Applied Mathematics and Mechanics, Vol. 20, No. 7, 1999, pp. 721-728. doi:10.1007/BF02454893
[5] T. Q. Yun, “Basic Equations, Theory and Principles for Computational Stock Market—(3) Basic Theory,” Applied Mathematics and Mechanics, Vol. 21, No. 8, 2000, pp. 861-868. doi:10.1007/BF02428354
[6] T. Q. Yun, “Analysis of Financial Derivatives by Mechanical Method (1)—Basic Equation of Price of Index Futures,” Applied Mathematics and Mechanics, Vol. 22, No. 1, 2001, pp. 118-125. doi:10.1023/A:1015587319860
[7] T. Q. Yun, “Analysis of Financial Derivatives by Mechanical Method (2)—Basic Equation of Market Price of Options,” Applied Mathematics and Mechanics, Vol. 22. No. 9, 2001, pp. 1004-1011. doi:10.1023/A:1016304107506
[8] T. Q. Yun “The Application of Game Theory to Stock/ Option Trading,” Forecasting, in Chinese, Vol. 20, No. 5, 2001, pp. 36-38.
[9] T. Q. Yun and G. L. Lei, “Simplest Differential Equation of Stock Price, Its Solution and the Relation to Assumptions of Black-Scholes Model,” Applied Mathematics and Mechanics, Vol. 24, No. 6, 2003, pp. 654-658.
[10] T. Q. Yun and J. S. Yu, “Mathematical Analysis for Operators—Gaps, Optimization Pushing up, Tactics of Runaway and Reliability Calculation,” Research on Financial and Economic Issuses (Additional Copy), in Chinese, Vol. 5, 2005, pp. 32-35.
[11] J. S. Yu, T. Q. Yun and Z. M. Guo, “Theory of Computational Securities,” in Chinese, Scientific Publishers, Beijing, 2008.
[12] T. Q. Yun and T. Yun, “Sinple Differential Equations of A & H Stock Prices and Application to Analysis of Equilibrium State,” Technology and Investment, Vol. 1, No. 1, 2010, pp. 111-114.
[13] “Editors of Mathematical Hand Book, Mathematical Hand Book,” in Chinese, High Education Publishers, Beijing, 1979.

