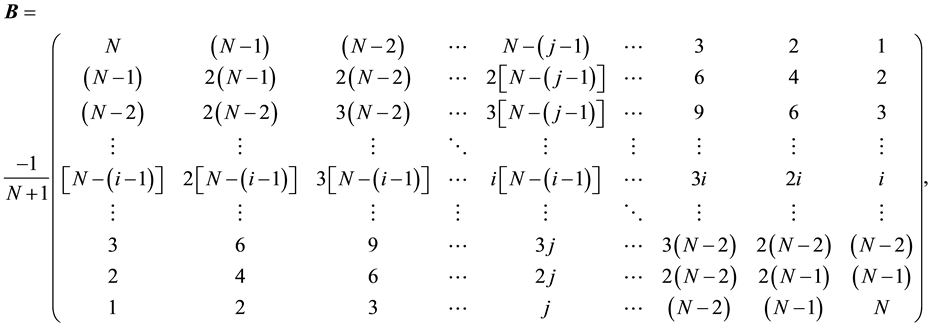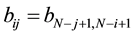Journal of Electromagnetic Analysis and Applications
Vol.06 No.10(2014), Article ID:50041,5 pages
10.4236/jemaa.2014.610030
The Exact Formulation of the Inverse of the Tridiagonal Matrix for Solving the 1D Poisson Equation with the Finite Difference Method
Serigne Bira Gueye
Département de Physique, Faculté des Sciences et Techniques, Université Cheikh Anta Diop, Dakar-Fann, Sénégal
Email: sbiragy@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 June 2014; revised 15 July 2014; accepted 8 August 2014
ABSTRACT
A new method for solving the 1D Poisson equation is presented using the finite difference method. This method is based on the exact formulation of the inverse of the tridiagonal matrix associated with the Laplacian. This is the first time that the inverse of this remarkable matrix is determined directly and exactly. Thus, solving 1D Poisson equation becomes very accurate and extremely fast. This method is a very important tool for physics and engineering where the Poisson equation appears very often in the description of certain phenomena.
Keywords:
1D Poisson Equation, Finite Difference Method, Tridiagonal Matrix Inversion, Thomas Algorithm, Gaussian Elimination, Potential Problem

1. Introduction
The finite difference method is a very useful tool for discretizing and solving numerically a differential equation. It is effectively a classical method of approximation based on Taylor series expansions that has help during the last years theoretical results to gain in accuracy, stability and convergence.
In fact, this method is very useful for solving for example Poisson equation. This elliptic equation appears very often in mathematics, physics, chemistry, biology and engineering. In one dimension, the resolution leads to a tridiagonal matrix in the case of centered difference approximation. This matrix, which is diagonally dominant, can be inverted with methods such as Gauss elimination, Thomas Algorithm Method [1] . These technics are powerful and very efficient.
We proposed here, a new and direct method of inversion of this tridiagonal matrix independently of the right- hand side. For Dirichlet-Dirichlet boundary problems, this innovative method is faster than the Thomas Algorithm. It gives better accuracy and is far more economical in terms of memory occupation.
First, the finite difference method is presented for the 1D Poisson equation. Secondly, the properties of the matrix associated with the Laplacian and its inverse are discussed. Then, the inverse matrix is determined and its properties are analyzed. Thus, verification is done considering an interesting potential problem, and the sensibility of the method is quantified.
2. Finite Difference Method and 1D Poisson Equation
We consider a function 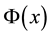 which satisfies the Poisson equation
which satisfies the Poisson equation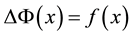 , in the interval
, in the interval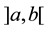 , where
, where  is a specified function.
is a specified function. 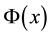 fulfills the Dirichlet-Dirichlet boundary conditions
fulfills the Dirichlet-Dirichlet boundary conditions 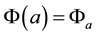 and
and . We consider an one-dimensional mesh with
. We consider an one-dimensional mesh with 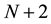 discrete points
discrete points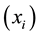 . Each point
. Each point 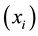 is de-
is de-
fined by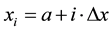 , where
, where 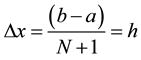 being the step size. We define
being the step size. We define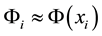 ,
, 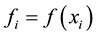 ,
,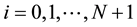 .
.
We have chosen the centered difference approximation , in this work, for the fact that it gives a tridiagonal, diagonally dominant, and symmetric matrix. Considering all the above mentioned criteria, one can rewrite the 1D Poisson equation in a set of algebraic equations:
, in this work, for the fact that it gives a tridiagonal, diagonally dominant, and symmetric matrix. Considering all the above mentioned criteria, one can rewrite the 1D Poisson equation in a set of algebraic equations:
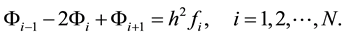
One gets a linear system of 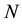

Thus, solving the 1D Poisson equation means to invert the negative definite, and regular 
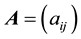
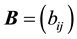

and
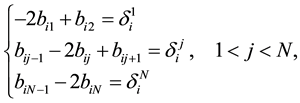
where 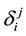
3. The Inverse of Matrix
From (4), we derive successively the following interesting relations:
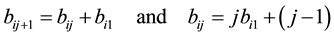
with (5), one sees that the matrix 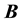
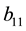
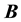
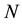
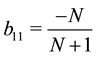
From (5) and (6), we get
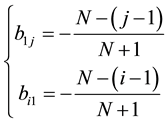
Now, the matrix 

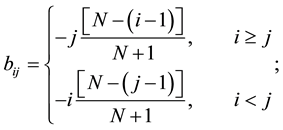
The solution of the 1D Poisson equation is obtained with a simple, extremely fast matrix multiplication: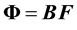
Analysis
A first analysis of the matrix 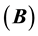
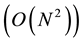


A deeper analysis of the matrix 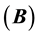
The matrix 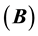
All the information about it, can be found in the upper triangle (in gray color, see Figure 1).
Further, we can even find very interesting relations in this matrix which can help refining the final solution.
That is what we effectively did, and one can see a direct solution for 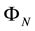
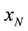
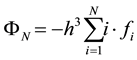
Figure 1. Matrix symmetries.
Also a direct solution for 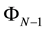
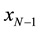
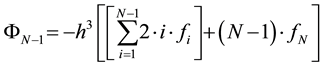
Generally, a very important recurrence relation can be obtained, which gives all solutions:
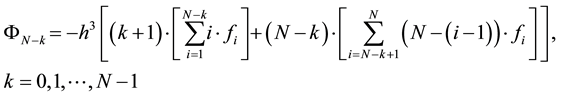
which is equivalent to:
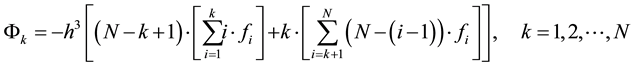
This very innovative Equation (12) gives directly and accurately all the solution that we are looking for. It proves that our method is direct, faster than the one of Thomas’s in this context and gives as well better accuracy. Furthermore, it is far more economical in terms of memory occupation. This is due to the fact that the matrix 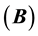
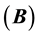
In conclusion to this, we can say that the matrix 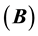
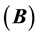
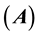
N.B.: One can prove using mathematical induction that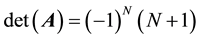
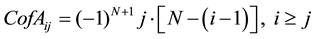
4. Verification with a Potential Problem
We consider a scalar potential
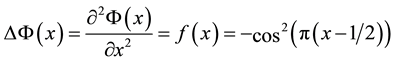


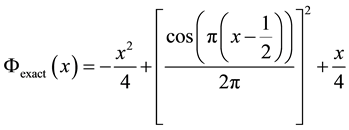
With the finite difference method, we take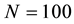
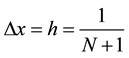
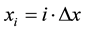
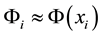
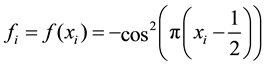
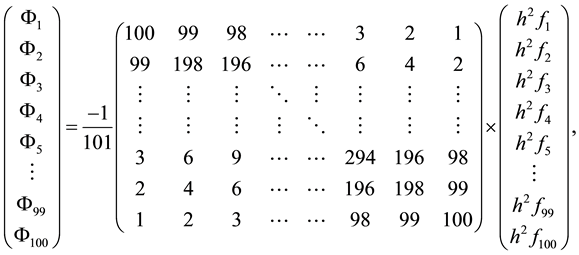
Discussions
We define the variable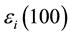
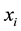

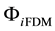
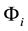
Generally, we have
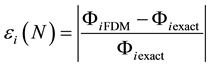
We can also define the average value of the relative error for a given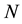
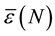
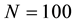
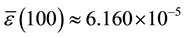
We obtain the following results, presented in Table 1.
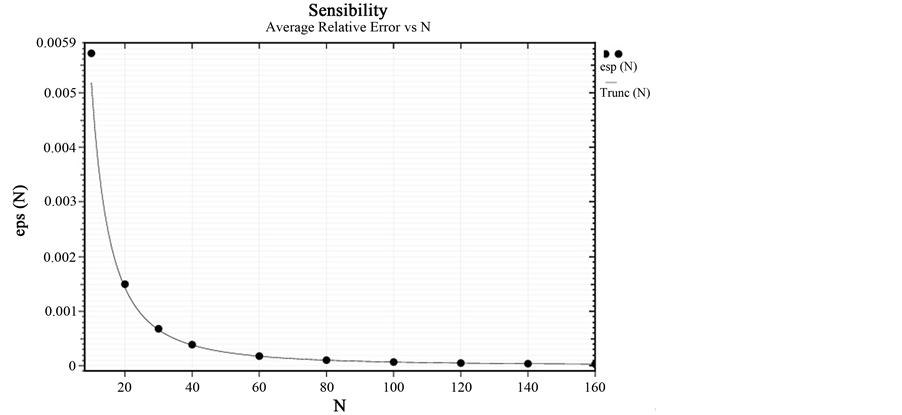
The table shows that the solution is very accurate. Notwithstanding that we have been interested in determining the sensibility of the proposed method. Effectively, we have plotted 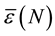
We obtain a hyperbola, which can be predicted as proportional to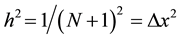
This curve is fitted with a function which can be defined as

where
Table 1. Results and relative error.
Figure 2. Sensibility.
We realize that the average relative error 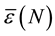
lowing manner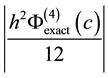
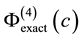
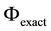
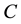
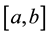
For our given function 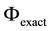

This proves that the method is very accurate, naturally stable, robust, quick and precise.
5. Conclusions
This paper has provided a new improved method for solving the 1D Poisson equation with the finite difference
method. Accurate results have been obtained with a sensibility found to be as the function of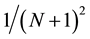
A future work can consider Neumann or mixed boundary conditions.
Acknowledgements
I would like to thank my colleagues Dr. Cheikh Mbow and Dr. Kharouna Talla for benefit discussions and remarks that contribute to improving the quality of this paper.
References
- Conte, S.D. and de Boor, C. (1981) Elementary Numerical Analysis: An Algorithmic Approach. 3rd Edition, McGraw- Hill, New York, 153-157.
- Leveque, R.J.E. (2007) Finite Difference Method for Ordinary and Partial Differential Equations, Steady State and Time Dependent Problems. SIAM, 15-16. http://dx.doi.org/10.1137/1.9780898717839
- Mathews, J.H. and Kurtis, K.F. (2004) Numerical Methods Using Matlab. 4th Edition, Prentice Hall, Upper Saddle River, 323-325, 339-342.