Journal of Electromagnetic Analysis and Applications
Vol.5 No.5(2013), Article ID:31443,6 pages DOI:10.4236/jemaa.2013.55034
Modeling and Analysis of Ladder-Network Transmission Lines with Capacitive and Inductive Lumped Elements
![]()
Associated Plasma Laboratory, National Institute for Space Research (INPE), São José dos Campos, Brazil.
Email: barroso@plasma.inpe.br
Copyright © 2013 Ana Flávia G. Greco et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 2nd, 2013; revised April 5th, 2013; accepted April 17th, 2013
Keywords: Transmission Lines; Right-Handed (RH); Left-Handed (LH); Backward Wave; Metamaterials
ABSTRACT
This paper examines the properties of wave propagation in transmission lines with periodic LC and CL cells, taking into account ohmic losses in resistors connected in series to lumped capacitors and inductors. First order time differential equations are derived for current and charge, thus allowing analysis of transient regimes of the lines being excited by a pulse of arbitrary shape. In particular we examine the propagation characteristics of periodic lines in which identical unit cells are repeated periodically and also discuss the interpretation of positive and negative phase velocities associated with the LC and CL topologies. Loss effects on the propagation bandwidths of both lines are also discussed, and it is shown that in the left-handed transmission line (CL configuration) the phase advance of the crest of the transmitted signal with respect to the source signal is due to the intrinsic dispersive nature of the CL line which, in contrast to the LC line, is highly dispersive at low propagation factors.
1. Introduction
Characterized by negative constitutive parameters (electric permittivity and magnetic permeability) metamaterial [1-3] is an artificially produced material which exhibits properties not found in nature. Such materials are often referred to as LH (left-handed) media to express the fact that they permit propagation of electromagnetic waves with the electric field, the magnetic field and the propagation vector forming a left-handed triad, in contrast to conventional materials in which the triad of these three vectors follows the right-hand rule. However, showing losses and having operation limited to narrow frequency bands, it was soon found that such resonant structures, such as split-ring resonators, become difficult to implement for microwave applications [4,5]. But as early as 2002, there has been proposed [6-9] the use of transmission lines—structures that are not resonant, low-lossy and allows wide frequency range of operation—to implement and put into practice the concept of metamaterials [10-12].
From the above, this paper examines the properties of wave propagation in transmission lines with periodic CL cells (C and L denoting the series capacitance and shunt inductance in each cell). As will be discussed, such a CL line exhibits a characteristic of left-handed (LH) medium in that the phase velocity is negative, namely, with direction opposite to the group velocity. In a comparative study, an analysis is made of its dual line LC (L and C denoting the shunt capacitance and series inductance in each cell). To this end, by assigning the charge in the capacitor and the current flowing in the inductor as state variables, first order time differential equations are derived for a general CL line and its dual configuration LC. The equations so derived allow the transient analysis of the lines being excited by a pulse of arbitrary shape. We also investigate the properties of propagation in the steady state sinusoidal regime and examine the dispersion characteristics of lossy lines by identifying the frequency bands and group delay in the frequency range 100 kHz to 1 MHz.
2. Circuit Equations
2.1. Line LC
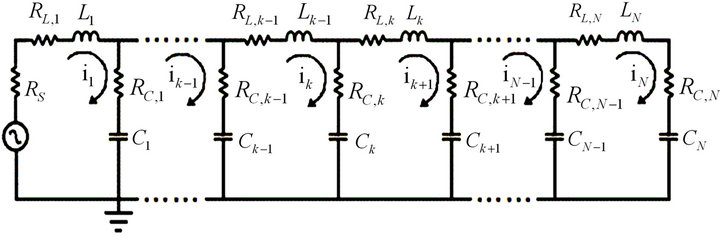
Figure 1(a) shows a generalized LC line, where the assigned state variables are the loop current Ik in a generic section k and the corresponding charge Qk stored in the capacitor. Of importance from the numerical standpoint, these variables were taken so that the line differential equations are all first order. The line is further assumed to be lossy, where each inductor has an associated resistance rL,k, each capacitor has a resistance rC,k and the generator has a resistor rs.
On the basis of Kirchhoff’s laws of voltage and current, we then arrive at a generalized transmission-line equation that applies for any number N of sections k. For the LC line, the circuit equations are written for three categories of sections: starting, intermediate, and ending sections.
Starting section:
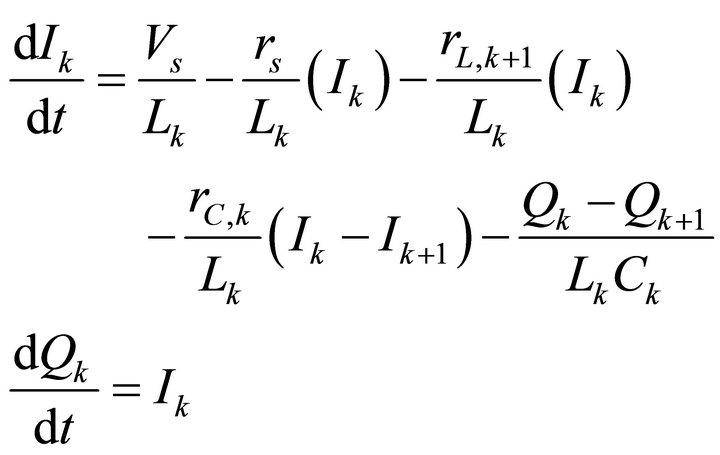 (1)
(1)
where k = 1 and Vs is the input voltage, which may be a sinusoidal signal or a pulse of arbitrary shape (trapezoidal, triangular, etc.).
Intermediate segment:
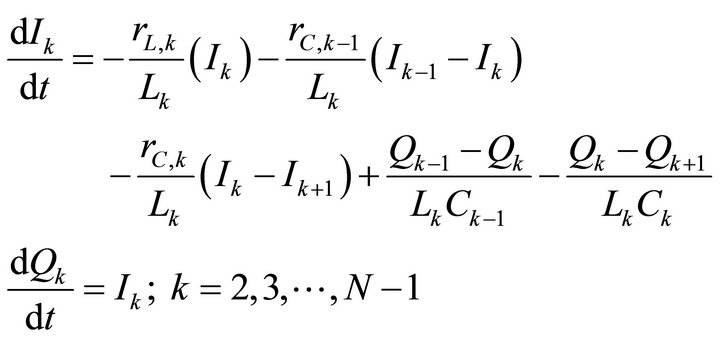 (2)
(2)
Ending segment:
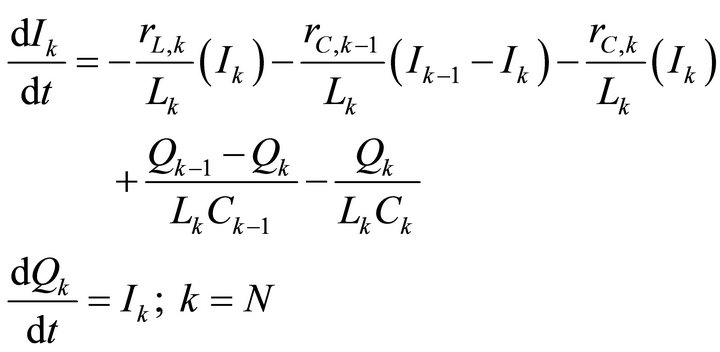 (3)
(3)
2.2. Line CL
Unlike the previous case, in the CL topology (Figure 1(b)) the state-variable current flows in the shunt branch L-rL of each section, so that that the CL line is described by a pair of equations:
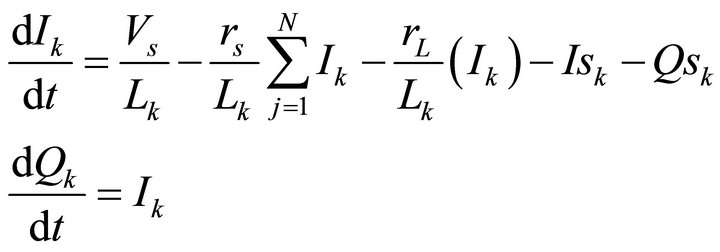 (4)
(4)
where 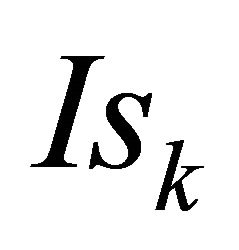 and
and 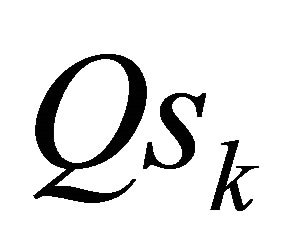 are recursive functions defined as
are recursive functions defined as
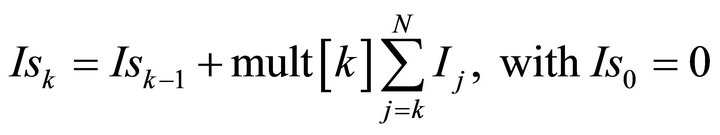 (5)
(5)
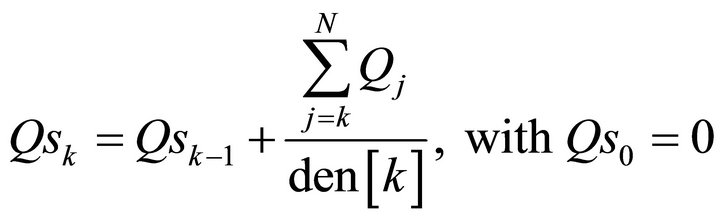
in which 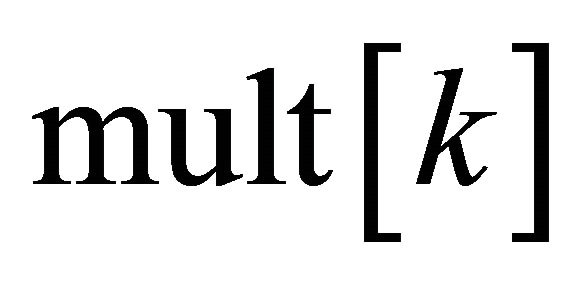 is the k-th element of the array
is the k-th element of the array  and the denominator term
and the denominator term  is the k-th element of
is the k-th element of 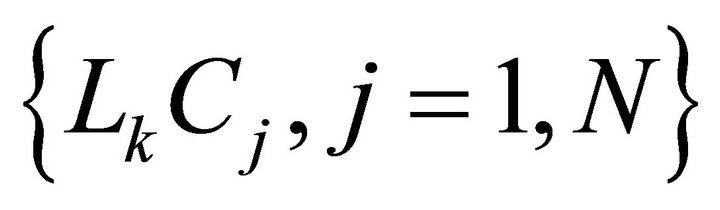 as detailed in the Appendix.
as detailed in the Appendix.
3. Dispersion Relations
3.1. Line LC
To analyze the steady-state sinusoidal regime of a periodic line with elements 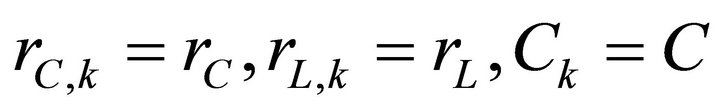 and
and , we consider the spatial and temporal variations in the form
, we consider the spatial and temporal variations in the form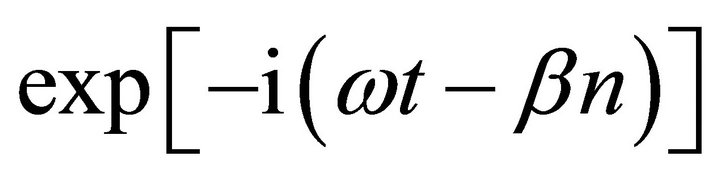 , where
, where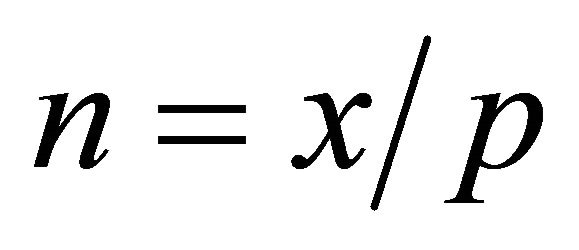 , with x denoting the position of a node with respect to the source at x = 0, p representing the hypothetical length of the unit cell; b is the propagation factor, a complex quantity which quantifies the attenuation and phase shift across each cell. Then the voltage and current equations for the LC line (Figure 1(a)) are
, with x denoting the position of a node with respect to the source at x = 0, p representing the hypothetical length of the unit cell; b is the propagation factor, a complex quantity which quantifies the attenuation and phase shift across each cell. Then the voltage and current equations for the LC line (Figure 1(a)) are
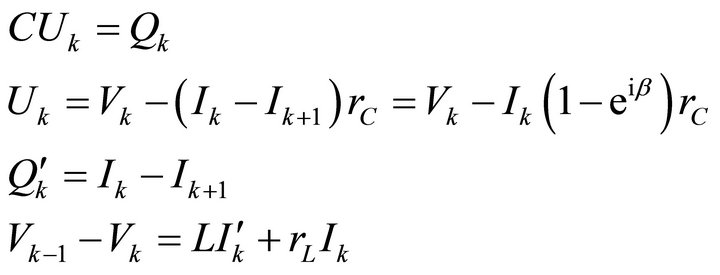 (6)
(6)
where Uk is the voltage across the shunt capacitor of the k-th section. Noting that the time derivate of the currents Ik is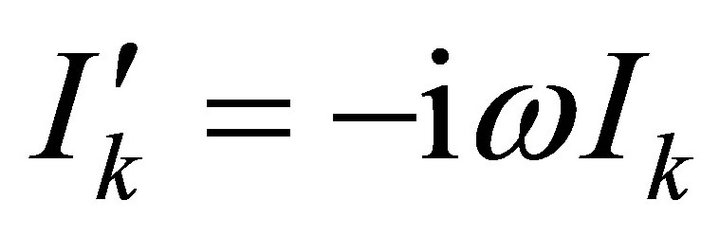 , from the assumption of time-harmonic variation, and
, from the assumption of time-harmonic variation, and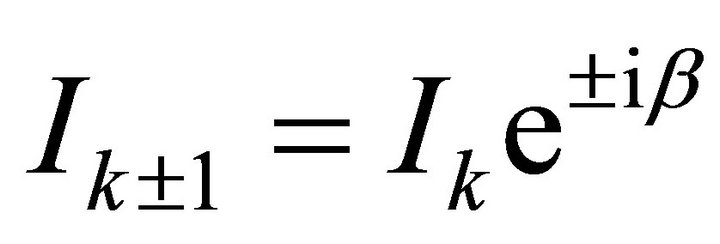 , from the periodic boundary conditions, Equation (6) takes the form
, from the periodic boundary conditions, Equation (6) takes the form
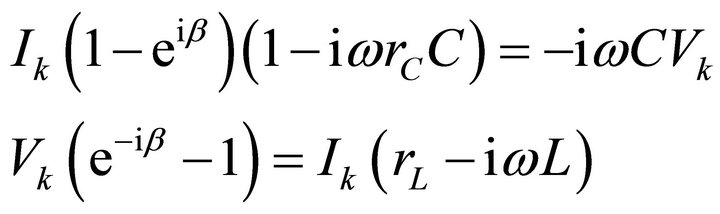 (7)
(7)
 (a)
(a) (b)
(b)
Figure 1. Line topologies (a) LC and (b) CL.
which leads to the dispersion relation
 (8)
(8)
with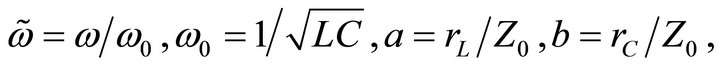 and
and  .
.
For a lossless LC line (a = 0, b = 0), Equation (8) reduces to
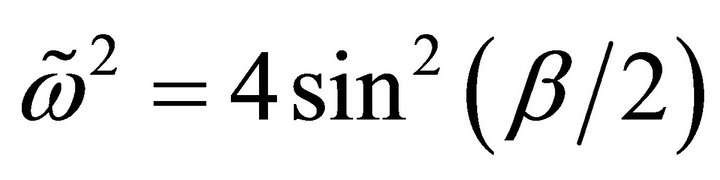 (9)
(9)
where the propagation factor β is real for 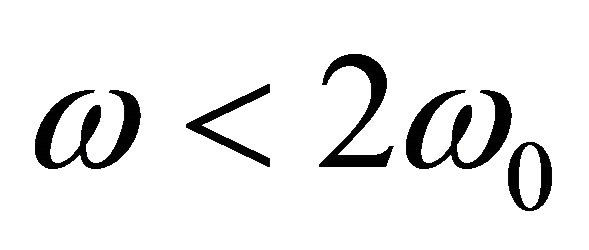 and becomes complex, when
and becomes complex, when 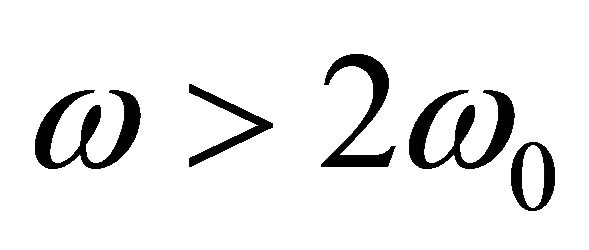 as illustrated by the blue curves in Figure 2. In this plot, both the attenuation and phase shift per section are normalized to π; for example at
as illustrated by the blue curves in Figure 2. In this plot, both the attenuation and phase shift per section are normalized to π; for example at , the phase shift per section is read as 0.331π. Having no cutoff frequency, the RH periodic line exhibits the behavior of a low-pass filter. Propagation starts from zero frequency until the critical frequency
, the phase shift per section is read as 0.331π. Having no cutoff frequency, the RH periodic line exhibits the behavior of a low-pass filter. Propagation starts from zero frequency until the critical frequency  with no attenuation, as demonstrated by vertical branch of the dashed blue line ranging from ω = 0 to ωc. But for lossy lines, attention coexists at all frequencies since the attention curves bend rightwards. In addition for frequencies up to
with no attenuation, as demonstrated by vertical branch of the dashed blue line ranging from ω = 0 to ωc. But for lossy lines, attention coexists at all frequencies since the attention curves bend rightwards. In addition for frequencies up to  the RH line behaves as nondispersive medium, in which the propagation factor
the RH line behaves as nondispersive medium, in which the propagation factor  is a linear function of frequency.
is a linear function of frequency.
3.2. Line CL
Analogously to the previous case, the voltage and current equations for the CL line (Figure 1(b)) are written as
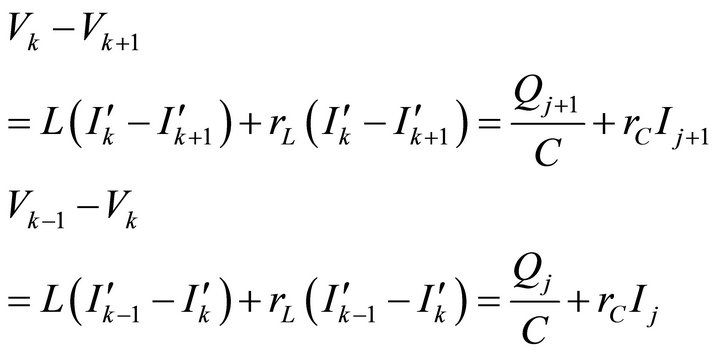 (10)
(10)
to give
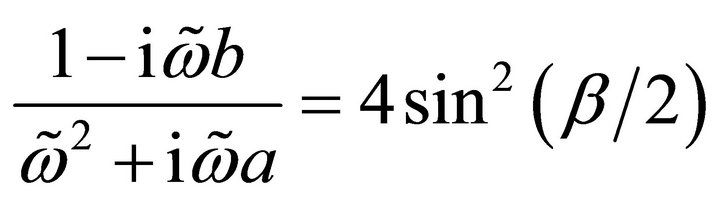 (11)
(11)
which for the lossless case reduces to
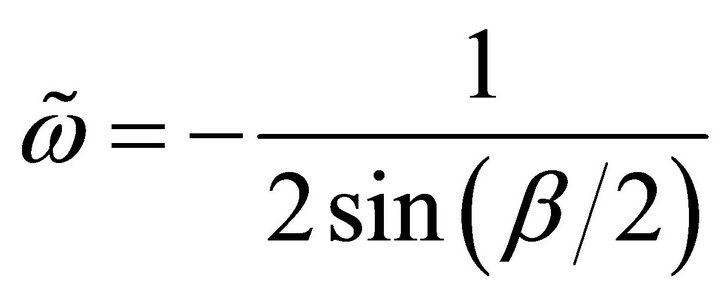 (12)
(12)
The presence of the negative signal (coming from the ambiguity of ± square root sign) is justified by examining Equation (12) in the limit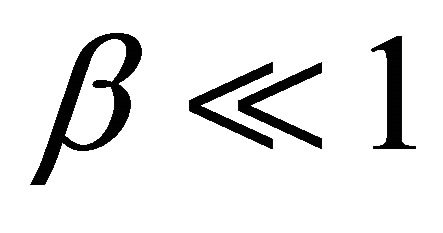 , which leads us to
, which leads us to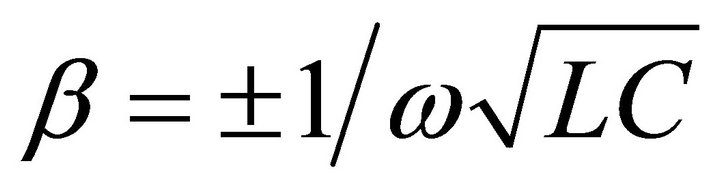 , where
, where 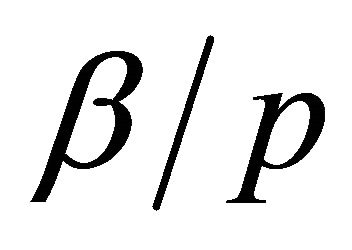 is the propagation constant of this CL line of concentrated elements. But from the theory of transmission lines [13], we know that iβ, relates to the line immittances by
is the propagation constant of this CL line of concentrated elements. But from the theory of transmission lines [13], we know that iβ, relates to the line immittances by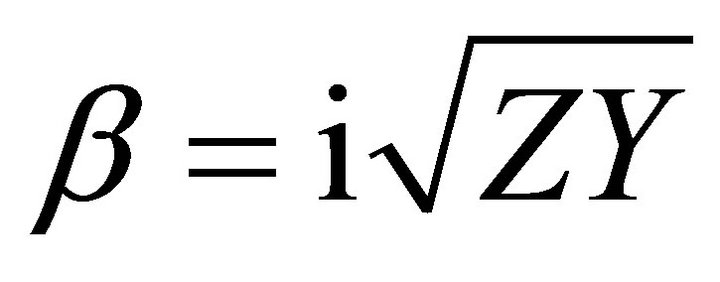 . The present case, in which
. The present case, in which  and
and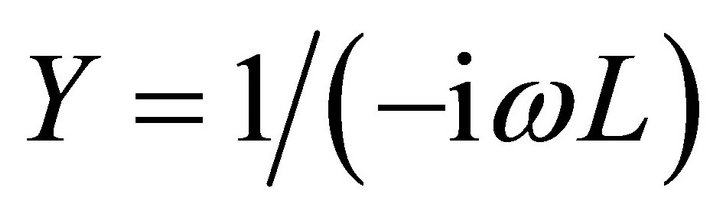 ,
,
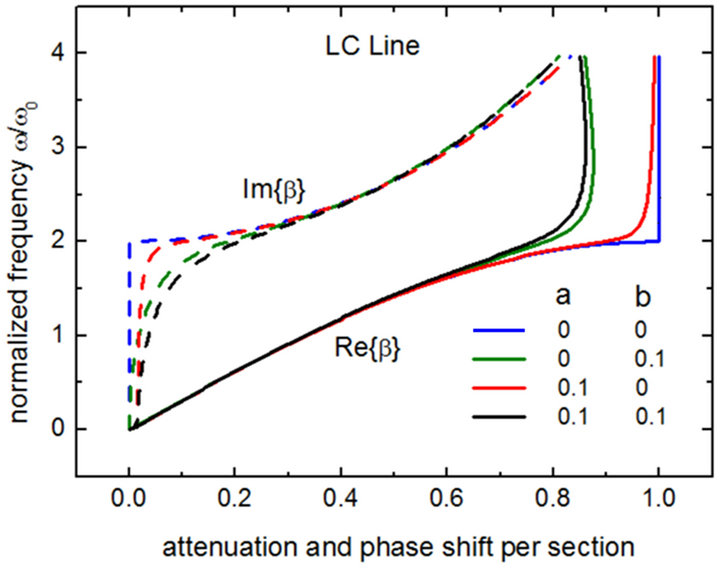
Figure 2. Dispersion/attenuation diagram for the LC line. In lossy lines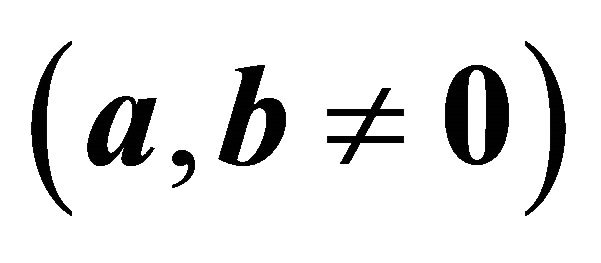 , propagation and attenuation coexist at all frequencies. In the horizontal axis, the attenuation
, propagation and attenuation coexist at all frequencies. In the horizontal axis, the attenuation 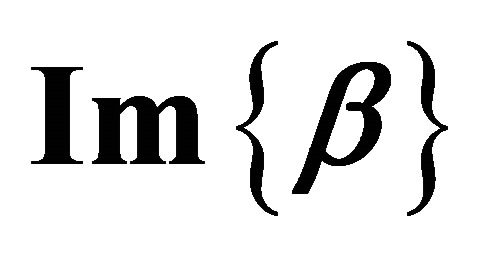 (dashed curves), and phase shift per section
(dashed curves), and phase shift per section 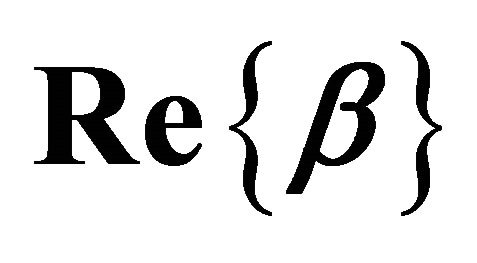 (solid curves) are both normalized to π.
(solid curves) are both normalized to π.
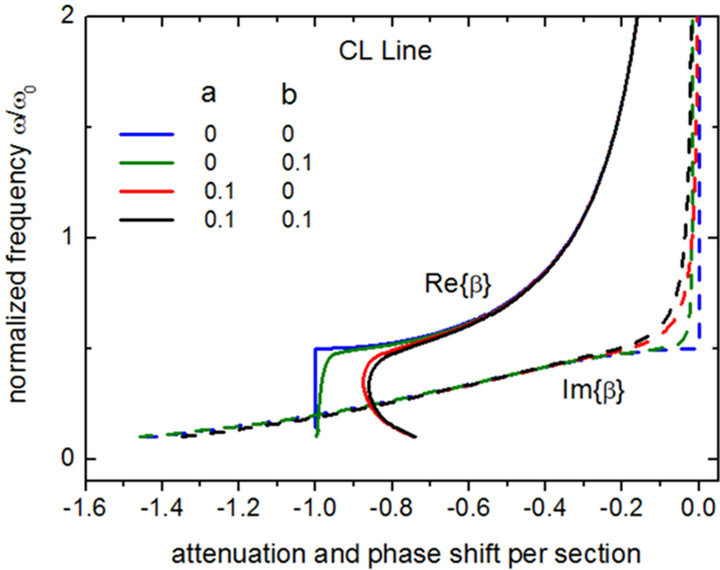
Figure 3. Dispersion/attenuation diagram for the CL line.
gives in the limit
in the limit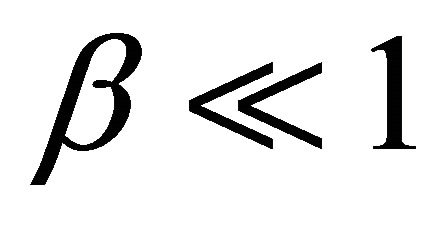 .
.
Thus, the dispersion relation of the CL line satisfies the conditions for excitation of backward wave, whose phase velocity is negative as illustrated in Figure 3. In the frequency range 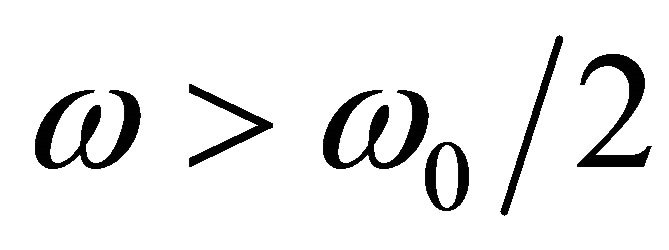 for the lossless line (blue curves), β is purely real, representing propagation without attenuation in the system; when
for the lossless line (blue curves), β is purely real, representing propagation without attenuation in the system; when , β is imaginary, indicating attenuation without energy dissipation. It is interesting to notice that the underlying features of the propagation curve for the CL line, with the lowfrequency branch bending downwards, have been experimentally observed in left-handed transmission lines yielding strong negative refraction index as large as −700 at gigahertz frequencies [14].
, β is imaginary, indicating attenuation without energy dissipation. It is interesting to notice that the underlying features of the propagation curve for the CL line, with the lowfrequency branch bending downwards, have been experimentally observed in left-handed transmission lines yielding strong negative refraction index as large as −700 at gigahertz frequencies [14].
4. Results
The following results refer to signals which propagate in the periodic LC and CL lines driven by a purely sinusoidal signal with 1-V amplitude.
Figure 4 shows the time variation of signals propagating in a low loss 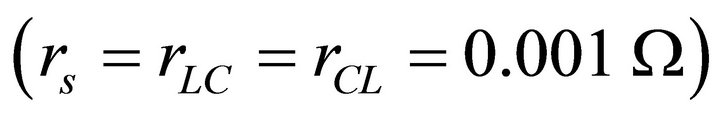 CL line of twenty sections with L = 1 mH, C = 1 mF and being excited by a signal of 250 kHz. Black, red, green and blue curves correspond to the nodes #0, #1, #3 and #5, where the signals are calculated. Note that the blue signal (node #5) reaches the positive peak
CL line of twenty sections with L = 1 mH, C = 1 mF and being excited by a signal of 250 kHz. Black, red, green and blue curves correspond to the nodes #0, #1, #3 and #5, where the signals are calculated. Note that the blue signal (node #5) reaches the positive peak 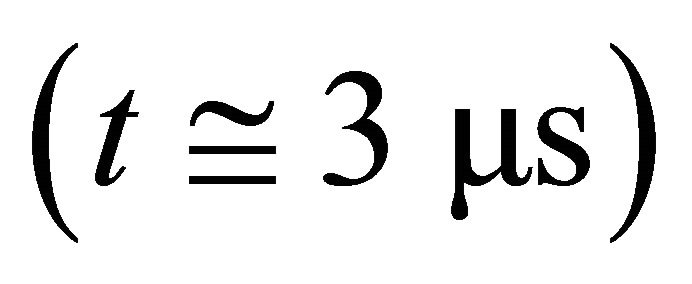 before the other signals at the preceding positions {0, 1 and 3} closer to the exciting source. This is the phenomenon of phase advance in a CL line, and clearly apparent by the peak position at 3 ms in the blue curve, before the other signals, which only reach their respective peaks after 3.5 ms. Similar situation is displayed in Figure 5 showing the time variation of signals propagating in a lossy line CL
before the other signals at the preceding positions {0, 1 and 3} closer to the exciting source. This is the phenomenon of phase advance in a CL line, and clearly apparent by the peak position at 3 ms in the blue curve, before the other signals, which only reach their respective peaks after 3.5 ms. Similar situation is displayed in Figure 5 showing the time variation of signals propagating in a lossy line CL 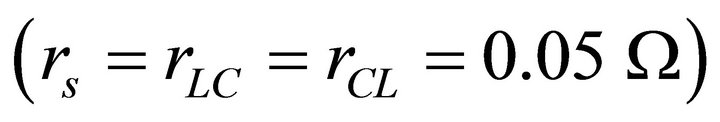 and excited by a signal of 200 kHz. We note that the signals distort themselves early in time (t < 2 ms) so as to occur a pulse sequence of decreasing order {5, 3, 1, 0} at a time later to 8 ms, when all signals turn out to follow sinusoidal variation. In Figure 5, the time difference between the crests of signals #5 and #0, t0 = 11.21 µs and t5 = 7.94 µs, namely, ∆t = −3.27 µs, relates to the phase factor through
and excited by a signal of 200 kHz. We note that the signals distort themselves early in time (t < 2 ms) so as to occur a pulse sequence of decreasing order {5, 3, 1, 0} at a time later to 8 ms, when all signals turn out to follow sinusoidal variation. In Figure 5, the time difference between the crests of signals #5 and #0, t0 = 11.21 µs and t5 = 7.94 µs, namely, ∆t = −3.27 µs, relates to the phase factor through , where n is the number of sections between two given nodes. From Figure 3, at
, where n is the number of sections between two given nodes. From Figure 3, at  one reads
one reads ; then substituting n = 5 and f = 200 kHz (driving signal frequency) into
; then substituting n = 5 and f = 200 kHz (driving signal frequency) into 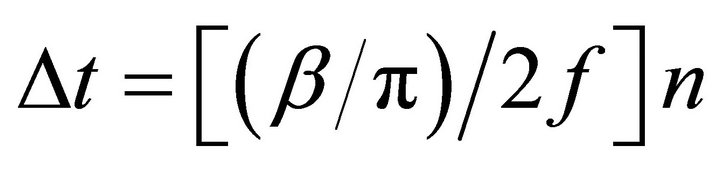 gives 3.25 µs, in excellent agreement with the time difference ∆t = −3.27 µs directly measured from Figure 5.
gives 3.25 µs, in excellent agreement with the time difference ∆t = −3.27 µs directly measured from Figure 5.
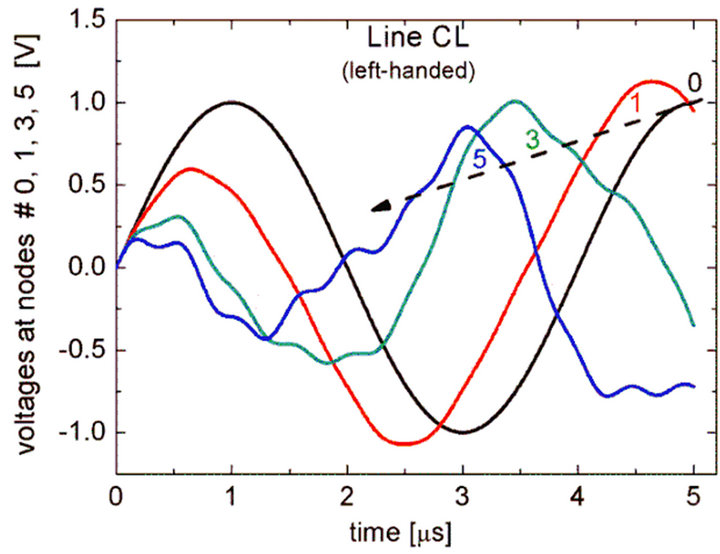
Figure 4. Voltage signals at nodes 0, 1, 3, and 5 in a low-loss, twenty-section CL line (rs = rLC = rCL = 0.001 W, L = 1 mH, C = 1 mF, resonance frequency f0 = 159.0 kHz) driven by a sinusoidal signal of 250 kHz.
Figure 6 shows the time variation of signals propagating in a low-loss 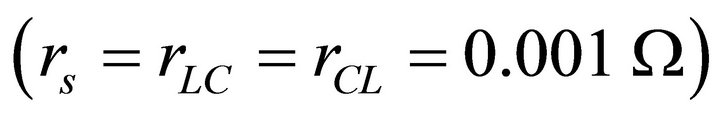 LC line with twenty sections, with immittances L = 1 mH, C = 1 mF and excited by a sinusoidal signal of 50 kHz. Black, red, green and blue curves correspond to the nodes #0, #1, #3 and #5. It appears that the phase velocity is positive, and the phase delay in the low-loss LC line is clearly indicated by the relative position of the peaks, where the blue signal, for example, reaches a peak in the first 10 ms after the signals 0, 1 and 3 have reached their respective peaks. In a lossy LC line
LC line with twenty sections, with immittances L = 1 mH, C = 1 mF and excited by a sinusoidal signal of 50 kHz. Black, red, green and blue curves correspond to the nodes #0, #1, #3 and #5. It appears that the phase velocity is positive, and the phase delay in the low-loss LC line is clearly indicated by the relative position of the peaks, where the blue signal, for example, reaches a peak in the first 10 ms after the signals 0, 1 and 3 have reached their respective peaks. In a lossy LC line 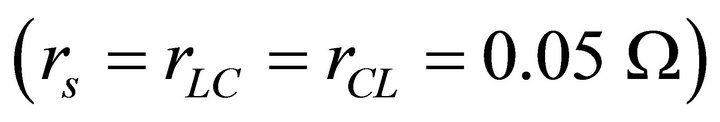 excited by a 20 kHz signal (Figure 7) it is noted that the same blue pulse (node #5) has the smallest amplitude in the sequence of pulses {0, 1, 3, 5}.
excited by a 20 kHz signal (Figure 7) it is noted that the same blue pulse (node #5) has the smallest amplitude in the sequence of pulses {0, 1, 3, 5}.
5. Conclusions
A system of time-varying ordinary differential equations
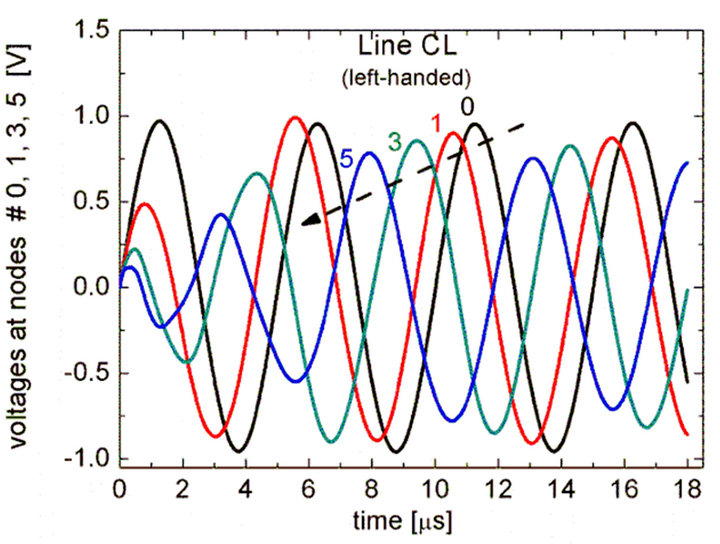
Figure 5. Voltage signals at nodes 0, 1, 3, and 5 in a lossy CL line of twenty sections (rs = rL = rC = 0.05 W, L = 1 mH, C = 1 mF, f0 = 159.0) driven by a 200 kHz sinusoidal signal.
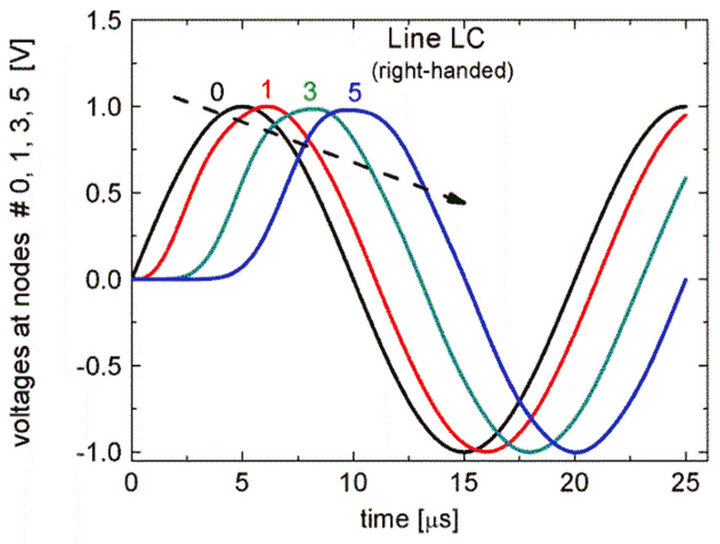
Figure 6. Voltage signals at nodes 0, 1, 3, and 5 in a low-loss LC line excited by a sinusoidal signal of 50 kHz.
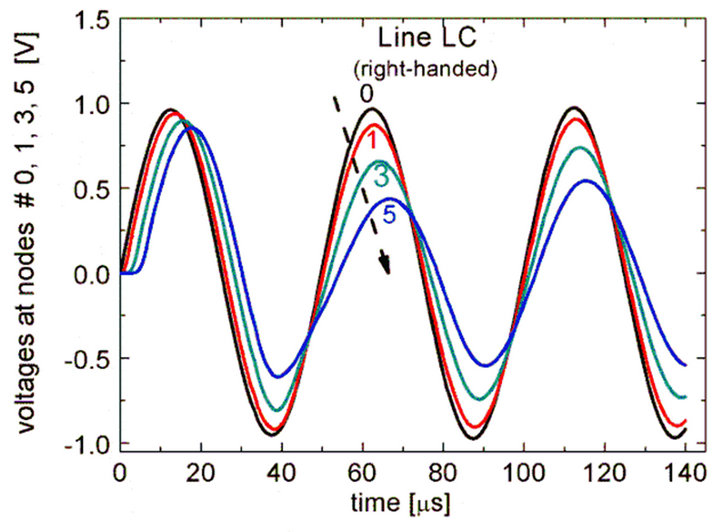
Figure 7. Voltage signals at nodes 0, 1, 3, and 5 in a LC lossy line excited by a sinusoidal signal of 20 kHz.
for lumped-element transmission lines has been derived and solved with given initial conditions for the distributions of charge of the capacitors and the fluxes through the inductors.
We have investigated propagation phenomena in transmission lines consisting of LC and CL cells. By taking the inductor current and the charge stored in the capacitor as state variables, a system of first order equations has been derived for each topology of time (LC and CL) and numerically solved using the Mathematica software [15]. Considering both low-loss and lossy lines, in which identical inductors and capacitors are repeated periodically in each section, we have examined the transient and saturation processes which occur in the signals when excited by a sinusoidal source, thus clearly demonstrating the phase advance of signals that propagate in the CL line.
Arising from the periodicity of the lumped elements, a lossless CL line exhibits a sharp cutoff frequency at  which originates a low-frequency band gap. Loss effects, however, make the gap disappear, such that the propagation curve turns out to be continuous and the bandwidth is enlarged, but at the expenses of high losses. On a complementary way, loss effects on LC lines decrease the passband, as demonstrated by the propagation/attenuation diagram in which energy dissipation starts to become significant for frequencies below the critical frequency
which originates a low-frequency band gap. Loss effects, however, make the gap disappear, such that the propagation curve turns out to be continuous and the bandwidth is enlarged, but at the expenses of high losses. On a complementary way, loss effects on LC lines decrease the passband, as demonstrated by the propagation/attenuation diagram in which energy dissipation starts to become significant for frequencies below the critical frequency  of the lossless LC line.
of the lossless LC line.
Finally we note that certain application of transmission lines demand a large number of cells, such as soliton excitation in nonlinear transmission lines typically requiring 500 cells, which may constitute a cumbersome task the drawing and wiring of 500 LC sections in SPICE-type circuit simulators [16]. On the other hand, a very large number of LC cells and their variant topologies are easily dealt with the mathematical formulation embodied in the system of differential equations.
6. Acknowledgements
Ana Flávia G. Greco thanks the Coordination for the Improvement of Higher Level Personnel (CAPES/Brazil) for financial support.
REFERENCES
- The News and Editorial Staffs, “Breakthrough of the Year: The Runners-Up,” Science, Vol. 302, No. 5653, 2003, pp. 2039-2045. doi:10.1126/science.302.5653.2039
- V. Veselago, “The Electrodynamics of Substances with Simultaneously Negative Values of ε and µ,” Soviet Physics Uspekhi, Vol. 10, No. 4, 1968, pp. 509-514. doi:10.1070/PU1968v010n04ABEH003699
- R. A. Shelby, D. R. Smith and S. Schultz, “Experimental Verification of a Negative Index of Refraction,” Science, Vol. 292, No. 5514, 2001, pp. 77-79. doi:10.1126/science.1058847
- C. R. Simovski, P. A. Belov and H. Sailing, “Backward Wave Region and Negative Material Parameters of a Structure Formed by Lattices of Wires and Split-Ring Resonators,” IEEE Transactions on Antennas and Propagation, Vol. 51, No. 10, 2003, pp. 2582-2591. doi:10.1109/TAP.2003.817554
- E. Ozbay, K. Aydin, E. Cubukcu and M. Bayindir, “Transmission and Reflection Properties of Composite Double Negative Metamaterials in Free Space,” IEEE Transactions on Antennas and Propagation, Vol. 51, No. 10, 2003, pp. 2592-2595. doi:10.1109/TAP.2003.817570
- C. Caloz and T. Itoh, “Transmission Line Approach of Left-Handed (LH) Materials and Microstrip Implementation of an Artificial LH Transmission Line,” IEEE Transactions on Antennas and propagation, Vol. 52, No. 4, 2004, pp. 1159-1166. doi:10.1109/TAP.2004.827249
- C. Caloz and T. Itoh, “Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications,” Wiley, New York, 2004.
- G. V. Eleftheriades, A. K. Iyer and P. C. Kremer, “Planar Negative Refractive Index Media Using Periodically L-C Loaded Transmission Lines,” IEEE Transactions on Microwave Theory and Techniques, Vol. 50, No. 12, 2002, pp. 2702-2712. doi:10.1109/TMTT.2002.805197
- G. V. Eleftheriades and K. G Balmain, “Negative-Refraction Metamaterials,” IEEE Press-Wiley, New York, 2005.
- C. Caloz and T. Itoh, “Lossy Transmission Line Metamaterials,” Microwave and Optical Technology Letters, Vol. 43, No. 2, 2004, pp. 112-114. doi:10.1002/mop.20392
- A. Alù, F. Bilotti and L. Vegni, “Analysis of L-L Transmission Line Metamaterials with Coupled Inductances,” Microwave and Optical Technology Letters, Vol. 49, No. 1, 2007, pp. 94-97. doi:10.1002/mop.22028
- S. Sheng, P. Wang and C. K. Ong, “Compact Tunable Periodically LC Loaded Phase Shifter Using Left-Handed Transmission Line,” Microwave and Optical Technology Letters, Vol. 51, No. 9, 2009, pp. 2127-2129. doi:10.1002/mop.24544
- S. Ramo, J. R. Whinnery and T. Van Duzer, “Fields and Waves in Communication Electronics,” Wiley, New York, 1965, p. 45.
- H. Yoon, K. Y. M. Yeung, V. Umansky and D. Hm, “A Newtonian Approach to Extraordinarily Strong Negative Refraction,” Nature, Vol. 488, No. 7409, 2012, pp. 65-69. doi:10.1038/nature11297
- Wolfram Research, “Mathematica v. 5.0.” http://www.wolfram.com
- Altinum Limited, “Circuit Maker 2000.” http://altinum.com
Appendix
We present in this appendix the equations implemented in the Mathematica software to the solution of differential equations that describe the temporal behavior and propagation of voltage and current signals in the LC (righthanded) and CL (left-handed) periodic lines.
LC line: equation for the starting section

LC line: equation for the intermediate section

LC line: equation for the ending section
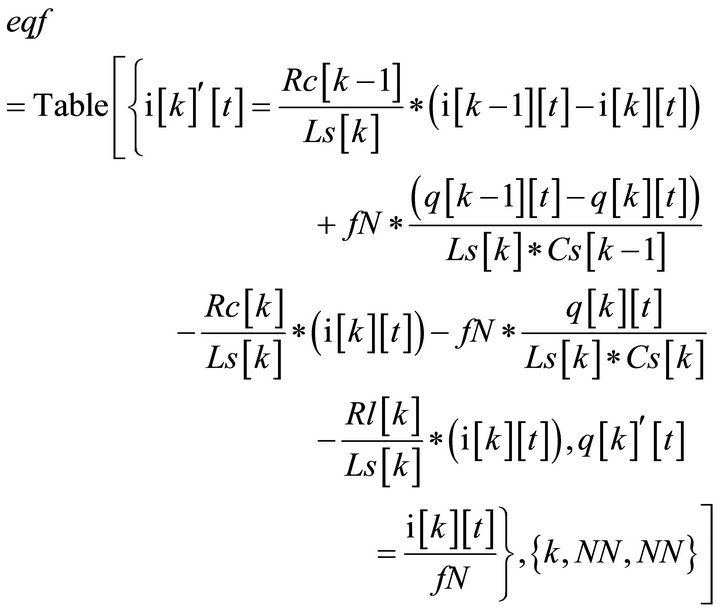
CL line: recursive functions for current and charge
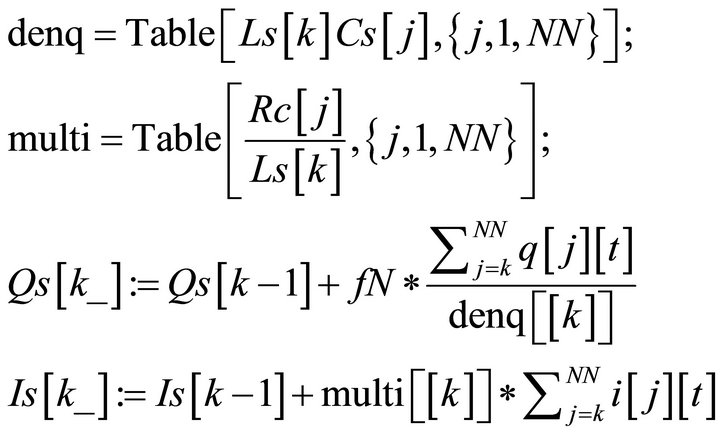
CL line: general equations for currents and charges
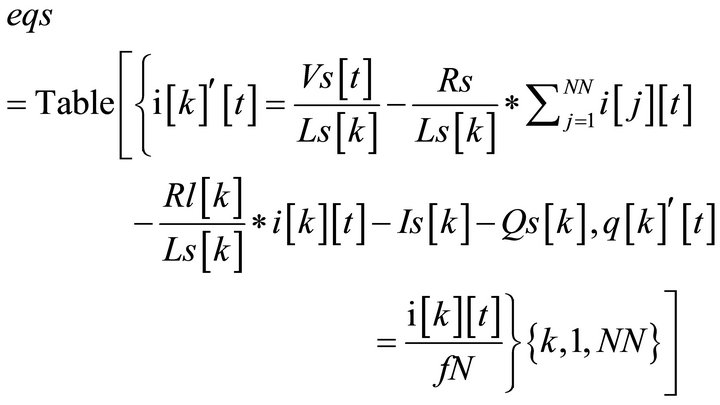
The initial conditions used are 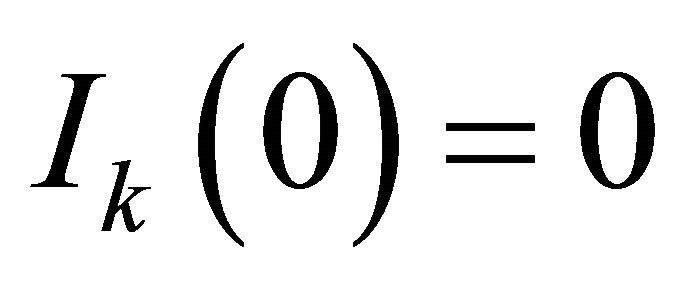 and
and  ; notice that the circuit elements are indexed to any values rL, rC, rs, Lk, Ck in each section k.
; notice that the circuit elements are indexed to any values rL, rC, rs, Lk, Ck in each section k.

