Journal of Electromagnetic Analysis and Applications
Vol.4 No.9(2012), Article ID:22473,4 pages DOI:10.4236/jemaa.2012.49052
The Effects of Rotation and Salt Concentration on Thermal Convection in a Linear Magneto-Fluid Layer Overlying a Porous Layer
![]()
1Mathematics Department, College of Sciences, Taif University, Taif, Saudi Arabia; 2Mathematics Department, College of Applied Sciences, Umm Al-Qura University, Mecca, Saudi Arbia.
Email: *mm.q777@yahoo.com
Received June 29th, 2012; revised July 30th, 2012; accepted August 15th, 2012
Keywords: Navier-Stokes Equation; Darcy-Brinkman Law; Legendre Polynomials; Salt Concentration; Vertical Linear Magnetic Field
ABSTRACT
A linear stability analysis is applied to a system consisting of a linear magneto-fluid layer overlying a porous layer affected by rotation and salt concentration on both layers. The flow in the fluid layer is governed by Navier-Stokes’s equations and while governed by Darcy-Brinkman’s law in the porous medium. Numerical solutions are obtained using Legendre polynomials. These solutions are studied through two modes of instability: stationary instability and overstability when the heat and the salt concentration are effected from above and below.
1. Motivations and Goals
Thermal instability theory has attracted considerable interest and has been recognized as a problem of fundamental importance in many fields of fluid dynamics. The earliest experiments to demonstrate the onset of thermal instability in fluids are those of Bernard’s [1,2]. Benard worked with very thin layers of an incompressible viscous fluid standing on a levelled metallic plate maintained at a constant temperature. The upper surface which was usually free and, being in contact with the air, was at a lower temperature. In his experiments, Benard deduced that a certain critical adverse temperature gradient must be exceeded before instability can set in. The instability of a layer of fluid heated from below and subjected to Coriolis forces has been studied by Chandrasekhar [3,4] for a stationary and overstability case. He showed that the presence of these forces usually has the effect of inhibiting the onset of thermal convection. Nield [5] considered the onset of salt-finger convection in a porous layer. Taunton et al. [6] considered the thermohaline instability and salt-finger in a porous medium and solved the boundary value problem. Sun [7] was the first to consider such a problem, and he used a shooting method to solve the linear stability equations. Sun [7] and Nield [8] used Darcy’s law in formulating the equations of porous layer. In Darcy’s law of motion in porous mediums, the Darcy resistance term took the place of the Navier-stokes viscosity term, while in the modified Darcy’s law (Brinkman model), suggested by Brinkman [9], the Navierstokes viscosity term still exists. Chen & Chen [10] considered the multi-layer problem when the above layer is heated and salted from above, and the solution of the problem is obtained using a shooting method. Lindsay & Ogden [11] worked in the implementation of spectral methods resistant to the generation of spurious eigenvalues. Lamb [12] used expansion of Chebyshev polynomials to investigate an eigenvalue problem arising from a model discussing a finitely conducting inner core of the earth on magnetically driven instability. Bukhari [13] studied the effects of surface-tension in a layer of conducting fluid with an imposed magnetic field and obtained results when the free surface is deformable and non-deformable. He solved that by using Chebyshev spectral method, and thus obtained some different results from that of Chen & Chen [10]. Straughan [14] studied the thermal convection in fluid layer overlying a porous layer and considered the problem of lower layer heated from below and surface tension driven on the free top boundary of upper layer. In [15], he also dealt with the same problem considering the ratio depth of the relative layer and investigated the effect of the variation of relevant fluid and porous material properties. Allehiany [16] studied Benard convection in a horizontal porous layer permeated by a conducting fluid in the presence of magnetic field and coriolis forces. In this work, we studied the effects of rotation and salt concentration on thermal convection in a linear magneto-fluid overlying a porous layer. The numerical solution was presented in different boundary conditions solved by using Legendre polynomials.
2. The Governing Equations
We consider a fluid layer overlying a porous layer so that the top of the porous layer touches the bottom of the fluid layer. The plane interface between the two layers is  the upper boundary of the fluid layer is
the upper boundary of the fluid layer is 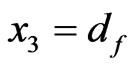 and the lower boundary of the porous medium layer is
and the lower boundary of the porous medium layer is 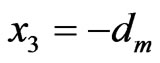 where the subscripts f and m denote the fluid layer and porous medium layer respectively. We suppose that the upper layer is filled with an incompressible thermally and electrically conducting viscous fluid consisting of melted salt which flows in it and governed by Navier-Stokes equations. However, the lower layer is occupied by a porous medium permeated by the fluid flowing in it and governed by Darcy-Brinkman’s law. Both layers subjected to a constant vertical linear magnetic field and affected by a rotation around
where the subscripts f and m denote the fluid layer and porous medium layer respectively. We suppose that the upper layer is filled with an incompressible thermally and electrically conducting viscous fluid consisting of melted salt which flows in it and governed by Navier-Stokes equations. However, the lower layer is occupied by a porous medium permeated by the fluid flowing in it and governed by Darcy-Brinkman’s law. Both layers subjected to a constant vertical linear magnetic field and affected by a rotation around  with a constant angular velocity
with a constant angular velocity . Gravity g acts in the negative direction of
. Gravity g acts in the negative direction of  (see Figure 1).
(see Figure 1).
Convection is driven by the temperature depending on the fluid density and salting, and damped by viscosity. The Oberbeck-Boussineq approximation is used as the density of fluid is constant everywhere except in the body force term where the density is linearly proportional to temperature and salt concentration, i.e.
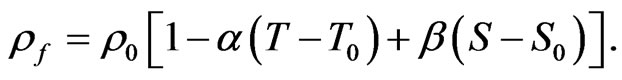 (1)
(1)
where T denotes the Kelvin temperature of the fluid, S is the salt concentration,  is the density of fluid at
is the density of fluid at  and
and ,
,  (constant) is the thermal coefficient of volume expansion of the fluid and
(constant) is the thermal coefficient of volume expansion of the fluid and 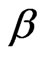 (constant) is the salting coefficient of volume expansion of the fluid. Let
(constant) is the salting coefficient of volume expansion of the fluid. Let  be the solenoidal velocity of the fluid.
be the solenoidal velocity of the fluid.
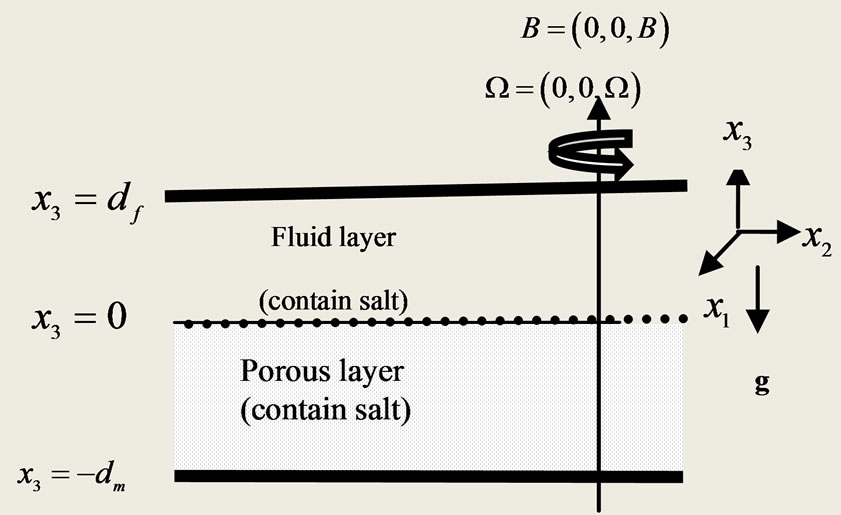
Figure 1. Schematic diagram of the problem.
Let 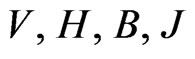 and
and 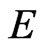 be respectively the solenoiddal velocity of the fluid, the magnetic field, the magnetic induction, the current density and the electric field. Hence
be respectively the solenoiddal velocity of the fluid, the magnetic field, the magnetic induction, the current density and the electric field. Hence
 (2)
(2)
 and
and 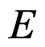 connected by the relations
connected by the relations
 (3)
(3)
where 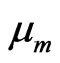 is the magnetic permeability and
is the magnetic permeability and  is the electrical conductivity. And the Maxwell equations
is the electrical conductivity. And the Maxwell equations
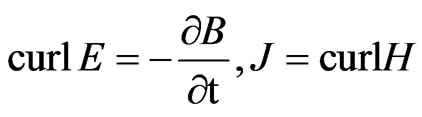 (4)
(4)
where the displacement current has been neglected in the second of these Maxwell equations as is customary in situation when free charge is instantaneously dispersed. By substituting from (3), (4)2 in to (4)1 obtain by
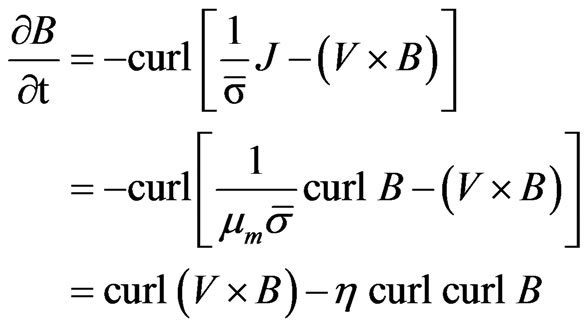 (5)
(5)
where 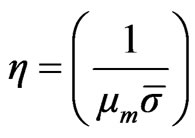 is electrical resistivity. By using
is electrical resistivity. By using
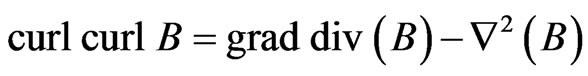
and

then Equation (5) reduce to
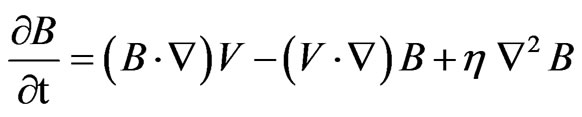 (6)
(6)
The equation of motion is
 (7)
(7)
where  is hydrostatic pressure,
is hydrostatic pressure, 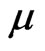 is the dynamic viscosity and
is the dynamic viscosity and  is three-dimensional Laplacian operator. And by subsituting from (3)1, (4)2 in to the Lorentz force
is three-dimensional Laplacian operator. And by subsituting from (3)1, (4)2 in to the Lorentz force  we obtain
we obtain
 (8)
(8)
Hence the equation of motion becomes
 (9)
(9)
and so the governing equations of the fluid layer are
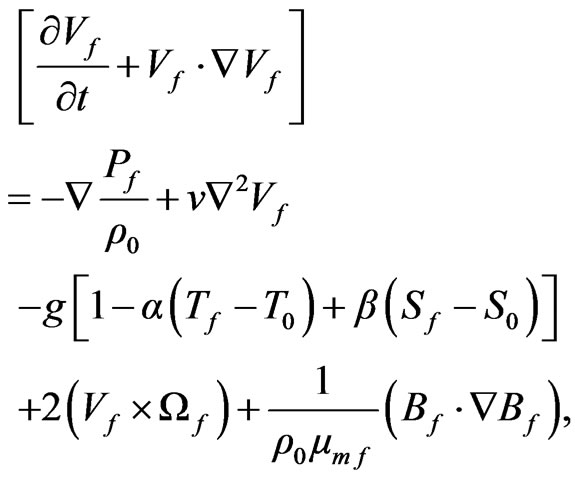 (10)
(10)
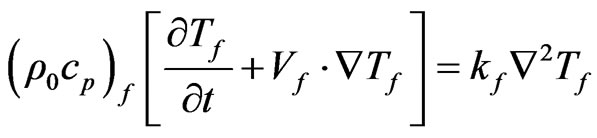 (11)
(11)
 (12)
(12)
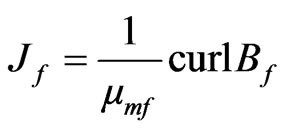 (13)
(13)
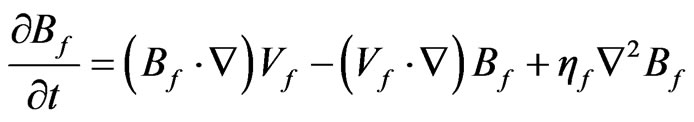 (14)
(14)
and the governing equations of the porous medium layer are
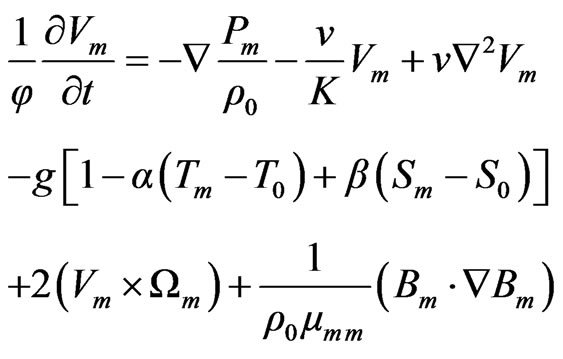 (15)
(15)
 (16)
(16)
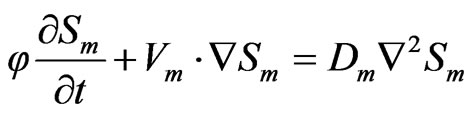 (17)
(17)
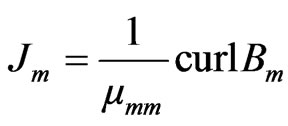 (18)
(18)
 (19)
(19)
where ,
,  are the modified pressure of the fluid and the porous medium layers respectively and
are the modified pressure of the fluid and the porous medium layers respectively and
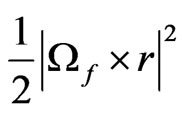 ,
, 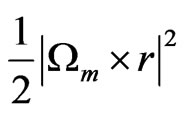 are the centrifugal force of the fluid and porous medium layer respectively,
are the centrifugal force of the fluid and porous medium layer respectively, 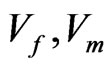 are the solenoidal and seepage velocity respectively,
are the solenoidal and seepage velocity respectively, 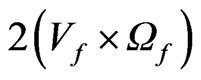 ,
, 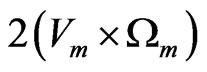 are the coriolis acceleration of the fluid and porous medium layer respectively,
are the coriolis acceleration of the fluid and porous medium layer respectively, 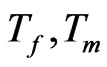 are the Kelvin temperature of the fluid and porous medium layer respectively,
are the Kelvin temperature of the fluid and porous medium layer respectively,  are salt concentration of the fluid and porous medium layer respectively,
are salt concentration of the fluid and porous medium layer respectively,  are the mass diffusivity of the fluid and porous medium layer respectively,
are the mass diffusivity of the fluid and porous medium layer respectively,  are magnetic permeability of fluid and porous layer respectively,
are magnetic permeability of fluid and porous layer respectively,  are the thermal and overall thermal conductivity of fluid and porous layers respectively,
are the thermal and overall thermal conductivity of fluid and porous layers respectively, 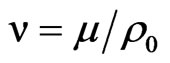 is the kinematic viscosity,
is the kinematic viscosity,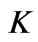 is the permeability,
is the permeability, 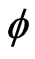 is its porosity and
is its porosity and 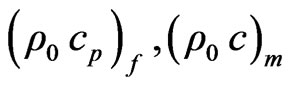 are the heat and overall heat capacity per unit volume of the fluid and porous medium layers at constant pressure. In fact
are the heat and overall heat capacity per unit volume of the fluid and porous medium layers at constant pressure. In fact
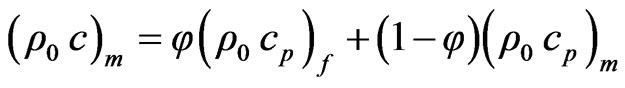
where  is the heat capacity per unit volume of the porous substrate. Suppose that
is the heat capacity per unit volume of the porous substrate. Suppose that 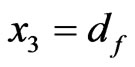 is rigid and maintained at constant temperature
is rigid and maintained at constant temperature  and constant salt concentration
and constant salt concentration , and
, and 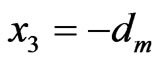 is impenetrable and maintained at constant temperature
is impenetrable and maintained at constant temperature 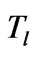 and constant salt concentration
and constant salt concentration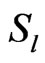 , then the boundary conditions can be written as
, then the boundary conditions can be written as
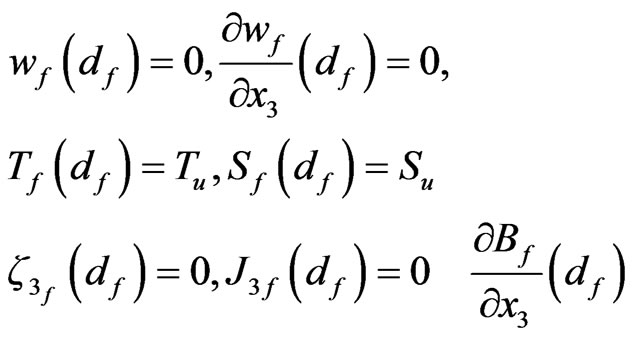 (20)
(20)
on the upper boundary, and
 (21)
(21)
on the lower boundary, where 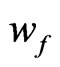 and
and 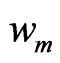 are the normal axial velocity components of the fluid in fluid layer and porous medium layer respectively,
are the normal axial velocity components of the fluid in fluid layer and porous medium layer respectively,  and
and  are the normal axial vortecity components of the fluid in. fluid layer and porous medium layer respectively.
are the normal axial vortecity components of the fluid in. fluid layer and porous medium layer respectively.
The boundary conditions on the interface plane x3 = 0 are based on the assumption that temperature, salt concentration, heat flux, salt flux, normal and tangential fluid velocity, normal stress and tangential stress are continuous so that
 (22)
(22)
Equations (10)-(19) have an equilibrium solution satisfying the boundary conditions (20)-(22) on the form
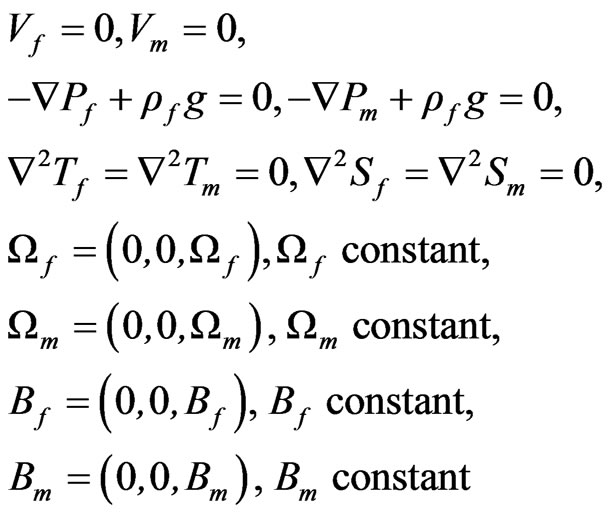 (23)
(23)
and with the boundary conditions
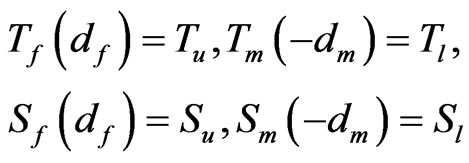 (24)
(24)
and the interface conditions
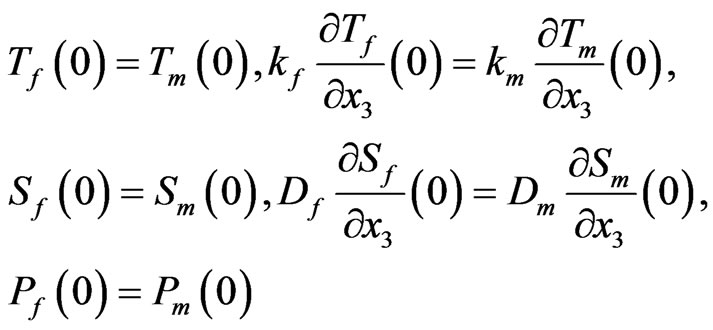 (25)
(25)
the equilibrium temperature field, hydrostatic pressure and salt concentration in the fluid layer and porous medium layer are respectively
 (26)
(26)
where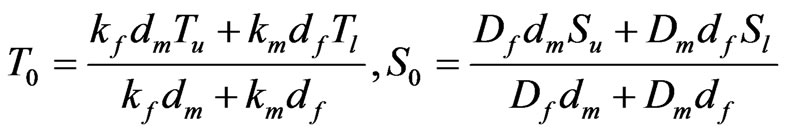 .
.
3. Perturbed Equations
We apply the perturbation by following linear perturbation quantities
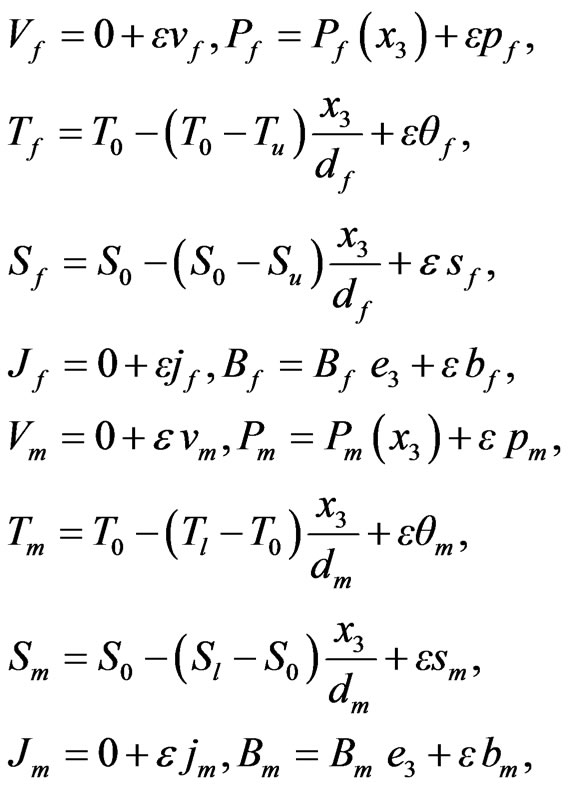 (27)
(27)
to the governing equations in the fluid layer and porous medium layer respectively and to the boundary conditions. After perturbation, the non-dimensionlisation will be apply by using
 (28)
(28)
for the fluid layer, and by using
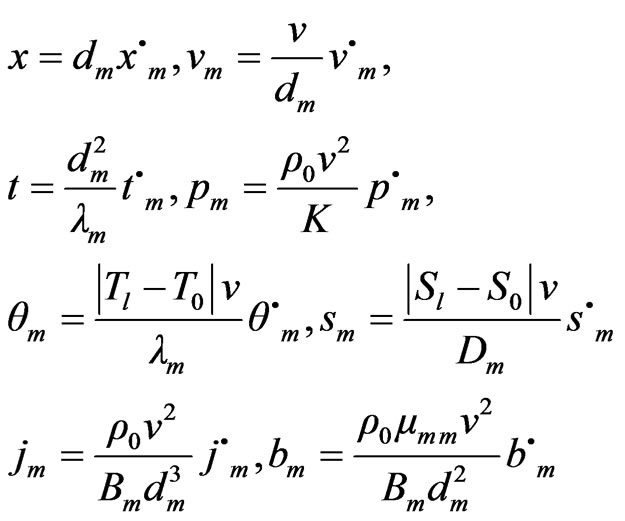 (29)
(29)
for the porous medium layer, here 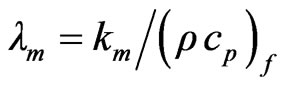 and
and 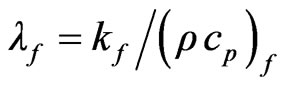 are the thermal diffusivity of the fluid phase and porous medium respectively ,then the Equations (10)-(14) becomes
are the thermal diffusivity of the fluid phase and porous medium respectively ,then the Equations (10)-(14) becomes
 (30)
(30)
 (31)
(31)
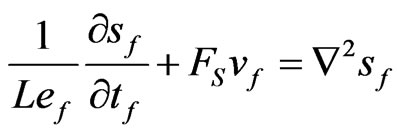 (32)
(32)
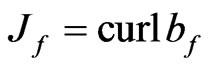 (33)
(33)
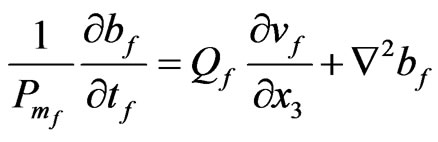 (34)
(34)
where 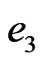 is the unit vector in the
is the unit vector in the  -direction and
-direction and  and
and  are non-dimensional numbers denote the viscous Prandtl number, thermal Rayleigh number, salt Rayleigh number, Taylor number, Chandraskhar number, Lewis number and magnetic Prandtl number of the fluid layer and given by
are non-dimensional numbers denote the viscous Prandtl number, thermal Rayleigh number, salt Rayleigh number, Taylor number, Chandraskhar number, Lewis number and magnetic Prandtl number of the fluid layer and given by

and the Equations (15)-(19) becomes
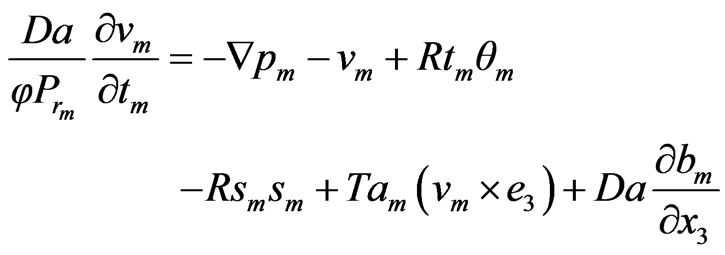 (35)
(35)
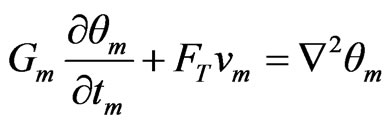 (36)
(36)
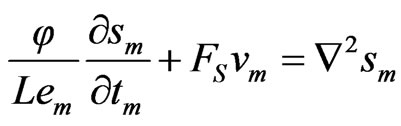 (37)
(37)
 (38)
(38)
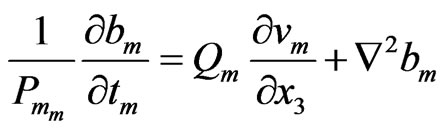 (39)
(39)
where 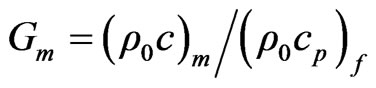 and Da, Prm, Rtm, Rsm, Tam, Qm, Lem and
and Da, Prm, Rtm, Rsm, Tam, Qm, Lem and  are non-dimensional numbers denote the Darcy number, viscous Prandtl number, thermal Rayleigh number, salt Rayleigh number, Taylor number, Chandarsekhar number, Lewis number and magnetic Prandtl number of the porous medium layer and given by
are non-dimensional numbers denote the Darcy number, viscous Prandtl number, thermal Rayleigh number, salt Rayleigh number, Taylor number, Chandarsekhar number, Lewis number and magnetic Prandtl number of the porous medium layer and given by
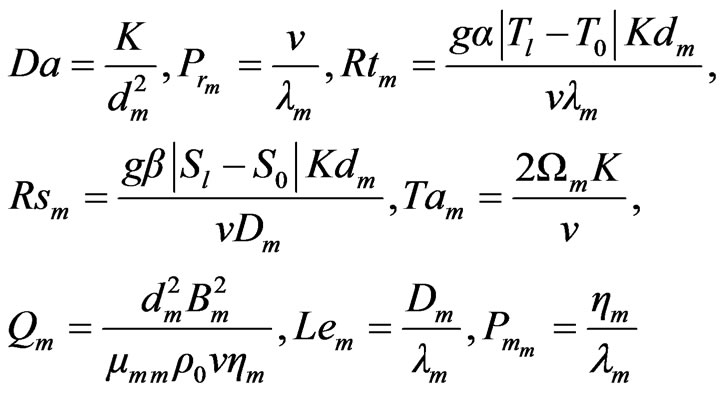
and where
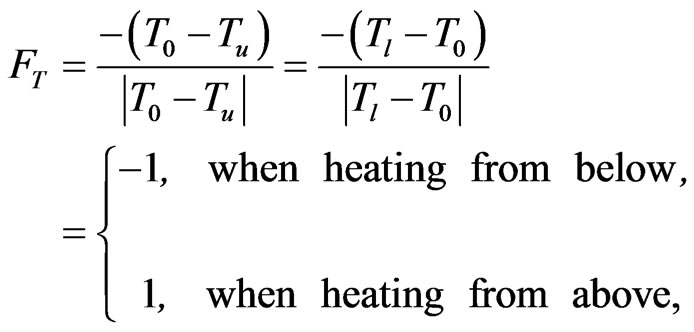

The boundary conditions (20)-(22) becomes
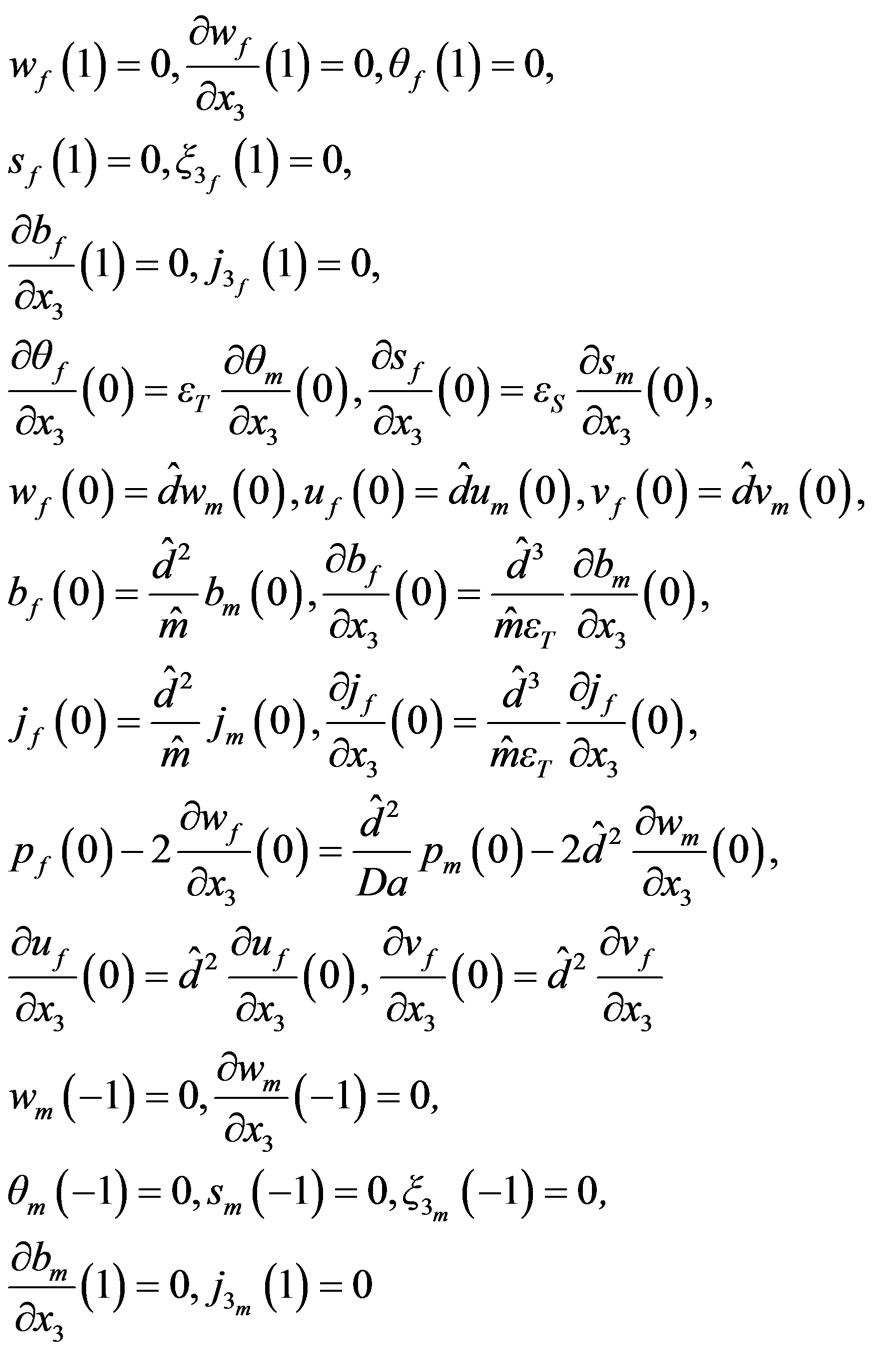 (40)
(40)
where ,
,  and are given by
and are given by
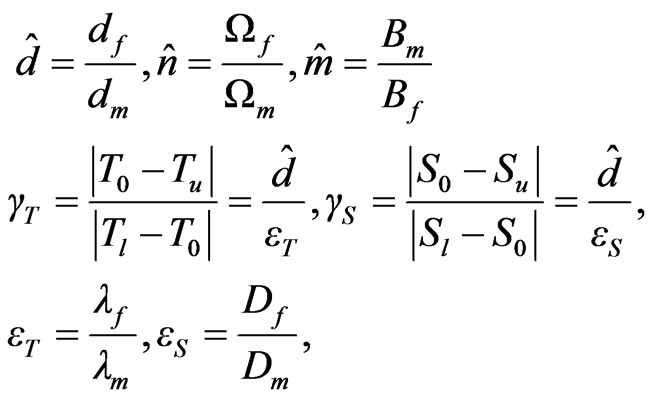
and
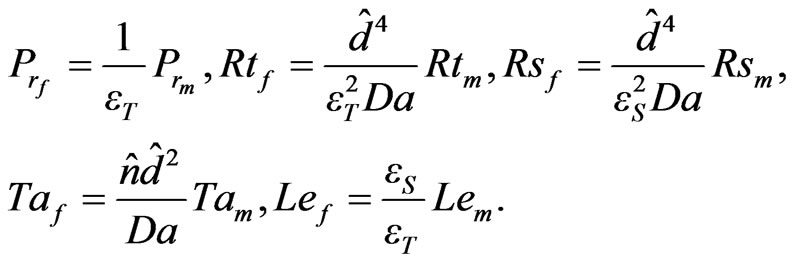
4. The Linearized Equations
Linearization will be done by neglecting all products and powers (higher than the first) of the linear perturbation quantity, and by dropping the (•) superscript, then by taking the curl of the Equations (30) and (35) we obtain
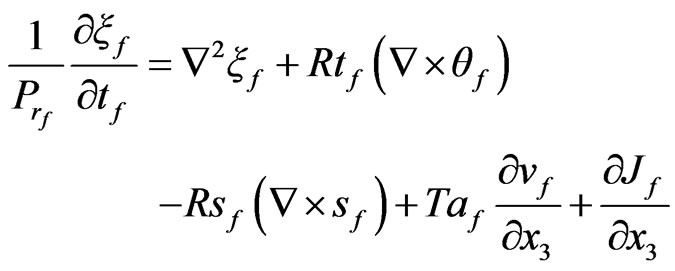 (41)
(41)
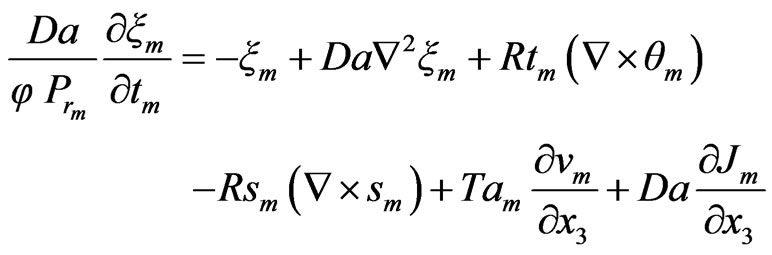 (42)
(42)
if return to the original Equations (30) and (35), but in this case we take the (curl curl). Thus
 (43)
(43)
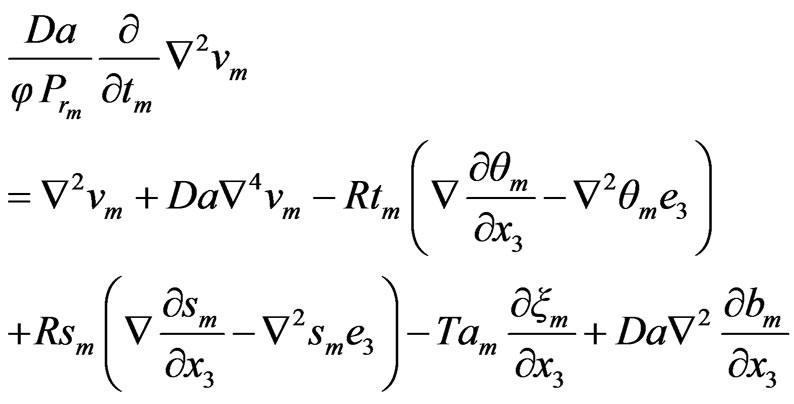 (44)
(44)
and if we use the curl of Equations (34) and (39) with using (33) and (38), we obtain
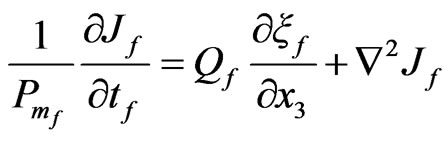 (45)
(45)
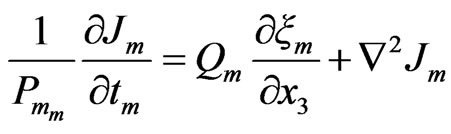 (46)
(46)
Now, the third components of Equations (31), (32), (34), (36), (37), (39) and (41)-(46) are
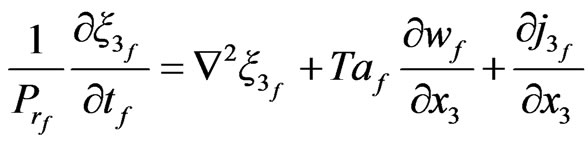 (47)
(47)
 (48)
(48)
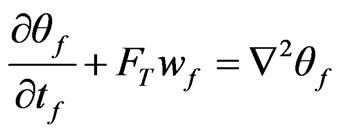 (49)
(49)
 (50)
(50)
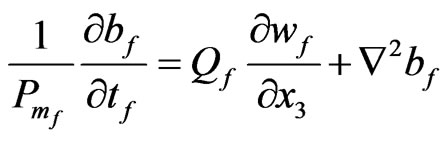 (51)
(51)
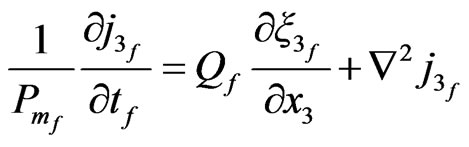 (52)
(52)
 (53)
(53)
 (54)
(54)
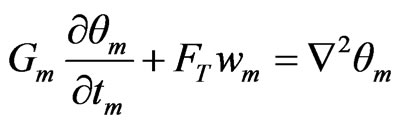 (55)
(55)
 (56)
(56)
 (57)
(57)
 (58)
(58)
where 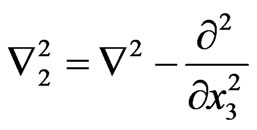 is tow-dimensional Laplacian operator and
is tow-dimensional Laplacian operator and . We apply the normal modes solution in the form
. We apply the normal modes solution in the form

with the functions 
 and
and .Thus the governing equations are
.Thus the governing equations are
 (59)
(59)
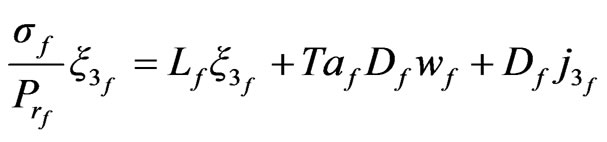 (60)
(60)
 (61)
(61)
 (62)
(62)
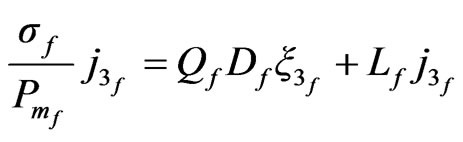 (63)
(63)
 (64)
(64)
 (65)
(65)
 (66)
(66)
 (67)
(67)
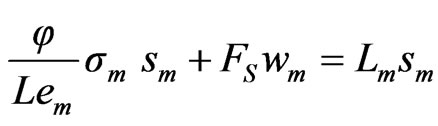 (68)
(68)
 (69)
(69)
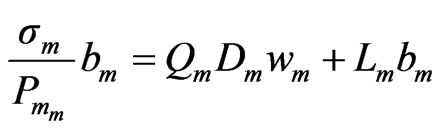 (70)
(70)
where  and
and  are nondimensional wave numbers in the fluid layer and porous medium layer respectively,
are nondimensional wave numbers in the fluid layer and porous medium layer respectively,  is the growth rate and
is the growth rate and
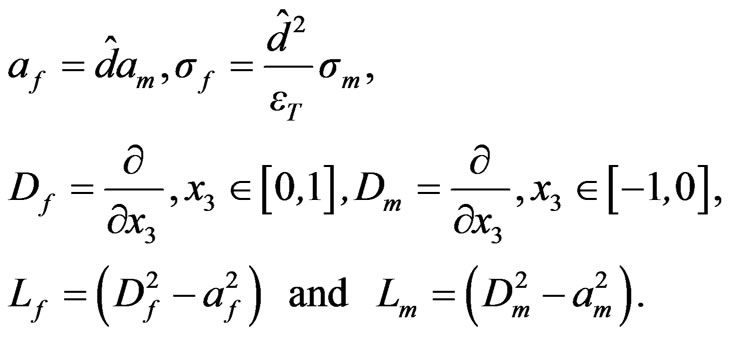
The boundary conditions in the final form are
 (71)
(71)
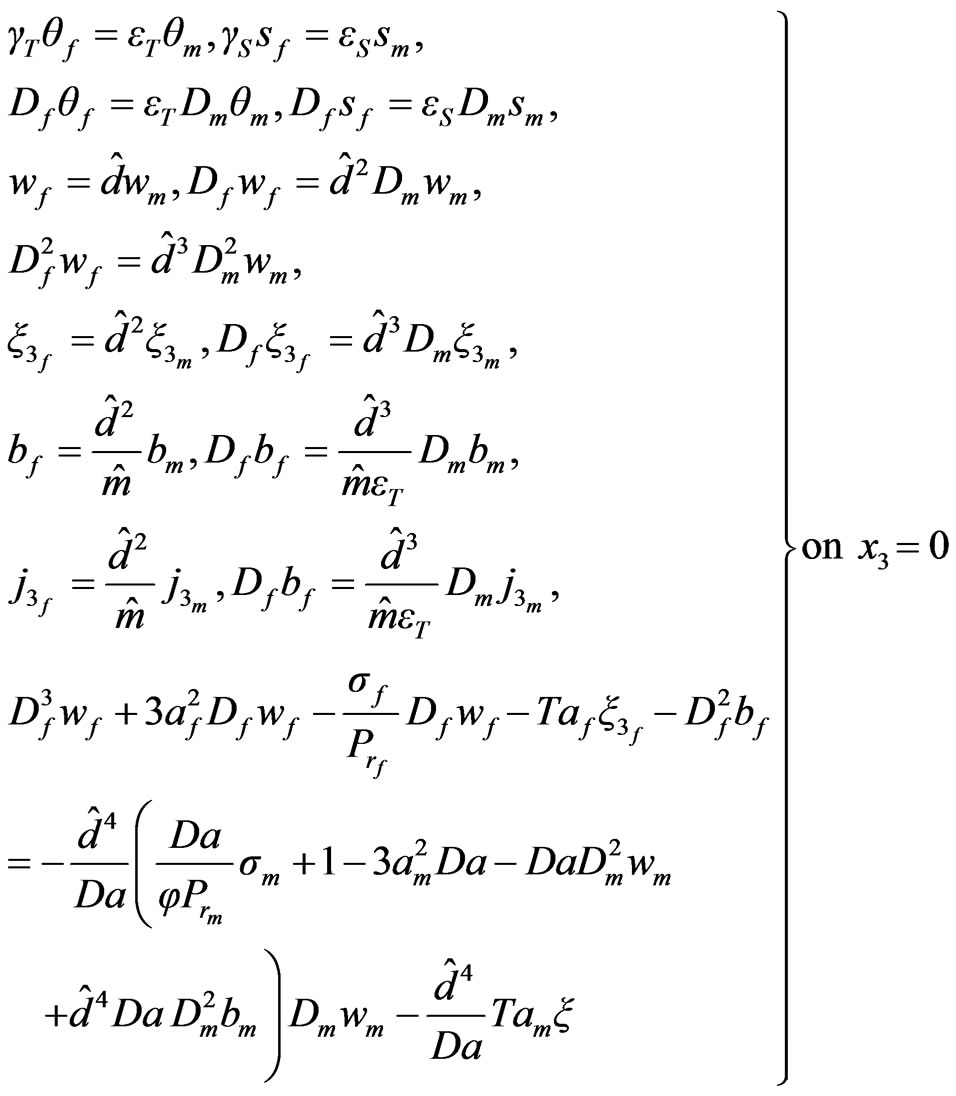
(72)
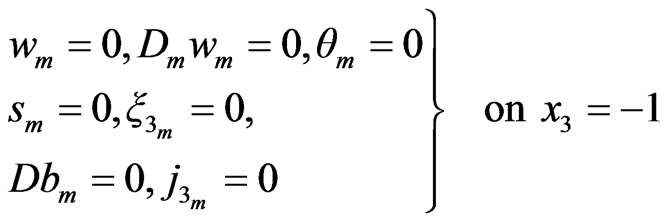 (73)
(73)
5. Numerical Solution
A Legendre polynomials (see Bukhari [5]) is applied to solve the Equations (59)-(70) with the relevant boundary conditions (71)-(73), and we map 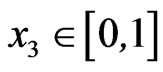 and
and  into
into  by the transformations
by the transformations  and
and 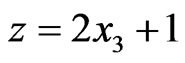 respectively, and get
respectively, and get
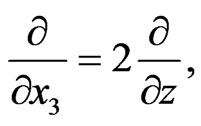 thus
thus 
then, suppose that

let the variables 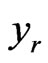 where
where 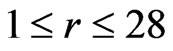 be defined by
be defined by
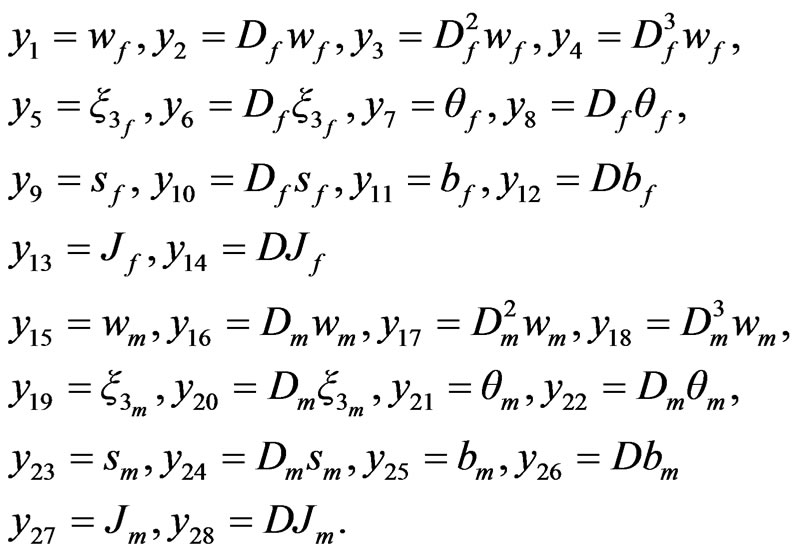
Then the Equations (59)-(70) can be rewritten in a system of twenty ordinary differential equations of first order, since  and if we put
and if we put  then
then
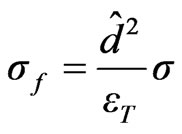 so the eigenvalue problem can be reformulated in the form
so the eigenvalue problem can be reformulated in the form
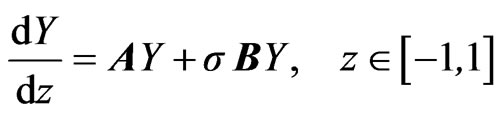
where A and B are real 28 × 28 matrices. The final eigenvalue problem reduces to 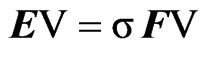 where matrices E and F have the block forms. The boundary conditions replace the 1 Mth, 2 Mth, … 28 Mth rows of E and F.
where matrices E and F have the block forms. The boundary conditions replace the 1 Mth, 2 Mth, … 28 Mth rows of E and F.
6. Results and Remarks
Using Legendre polynomials, the eigenvalue problems (59)-(70) with the boundary conditions (71)-(73) are transformed to a system of fourteen ordinary differential equations of first order in the fluid layer and a system of fourteen ordinary differential equations of first order in the porous layer with twenty eight boundary conditions. In this work, we will discuss the numerical results through two cases—when the heat and salt concentration affected from above and below.
Case (1): the heat and the salt concentration affected from above.
Here, we put FT = 1, FS = 1and the value of the initial salt Rayleigh number of the porous medium Rsm = 5000 to find the thermal Rayleigh number of the porous medium  corresponding to the wave numbers
corresponding to the wave numbers  for the different values of
for the different values of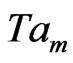 ,
, 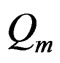 ,
, 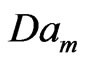 ,
, 
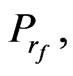
 and
and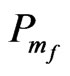 . In this case, the eigenvalues are real, and thus the stationary instability happens, as shown in the following Tables 1-4 and Figures 2-5. Therefore, we concluded that:
. In this case, the eigenvalues are real, and thus the stationary instability happens, as shown in the following Tables 1-4 and Figures 2-5. Therefore, we concluded that:

Table 1. The relation between am and Rtm for different values of Tam when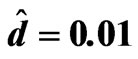 , Dam = 0.0003, Qm = 100,
, Dam = 0.0003, Qm = 100, 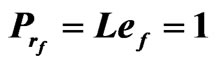 and
and .
.
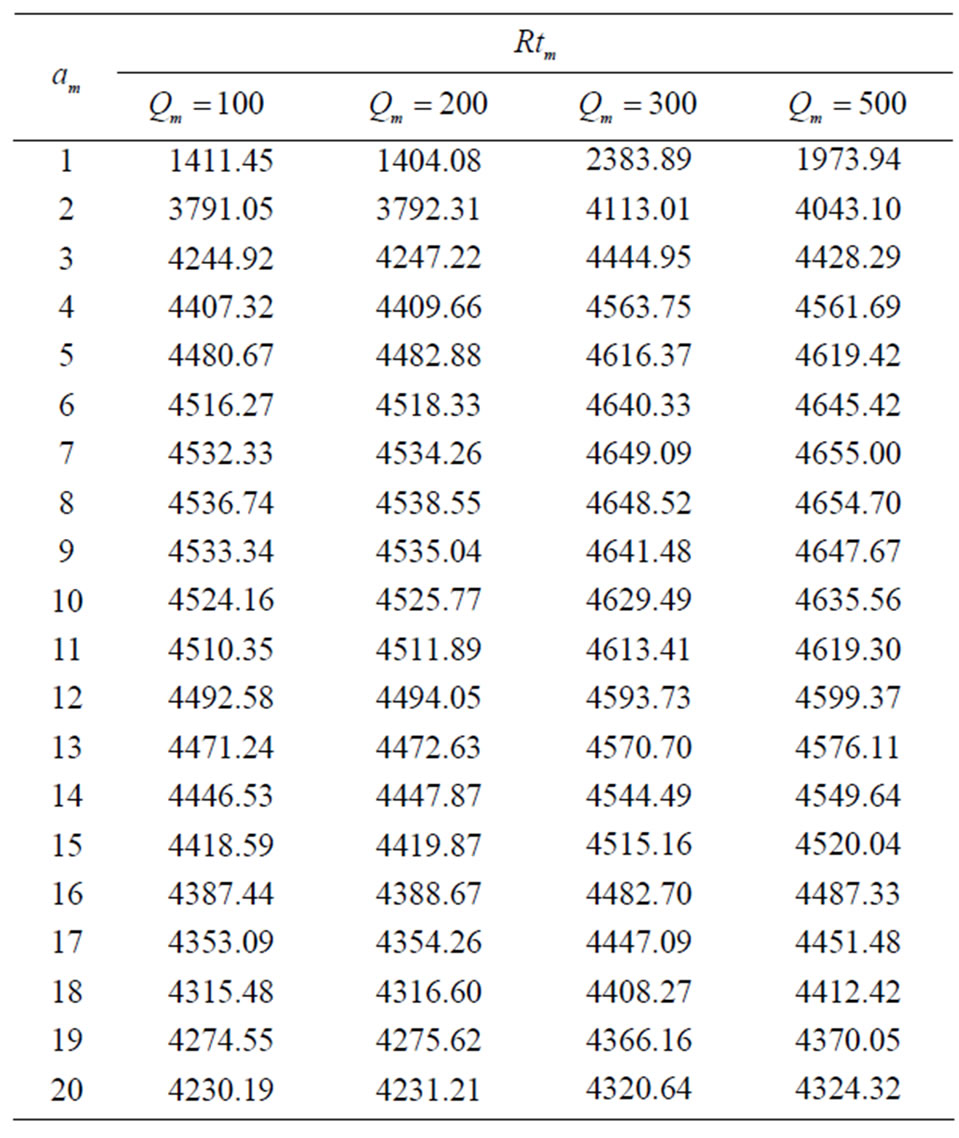
Table 2. The relation between am and Rtm for different values of Qm when Tam = 5,  , Dam = 0.0003,
, Dam = 0.0003,  and
and .
.
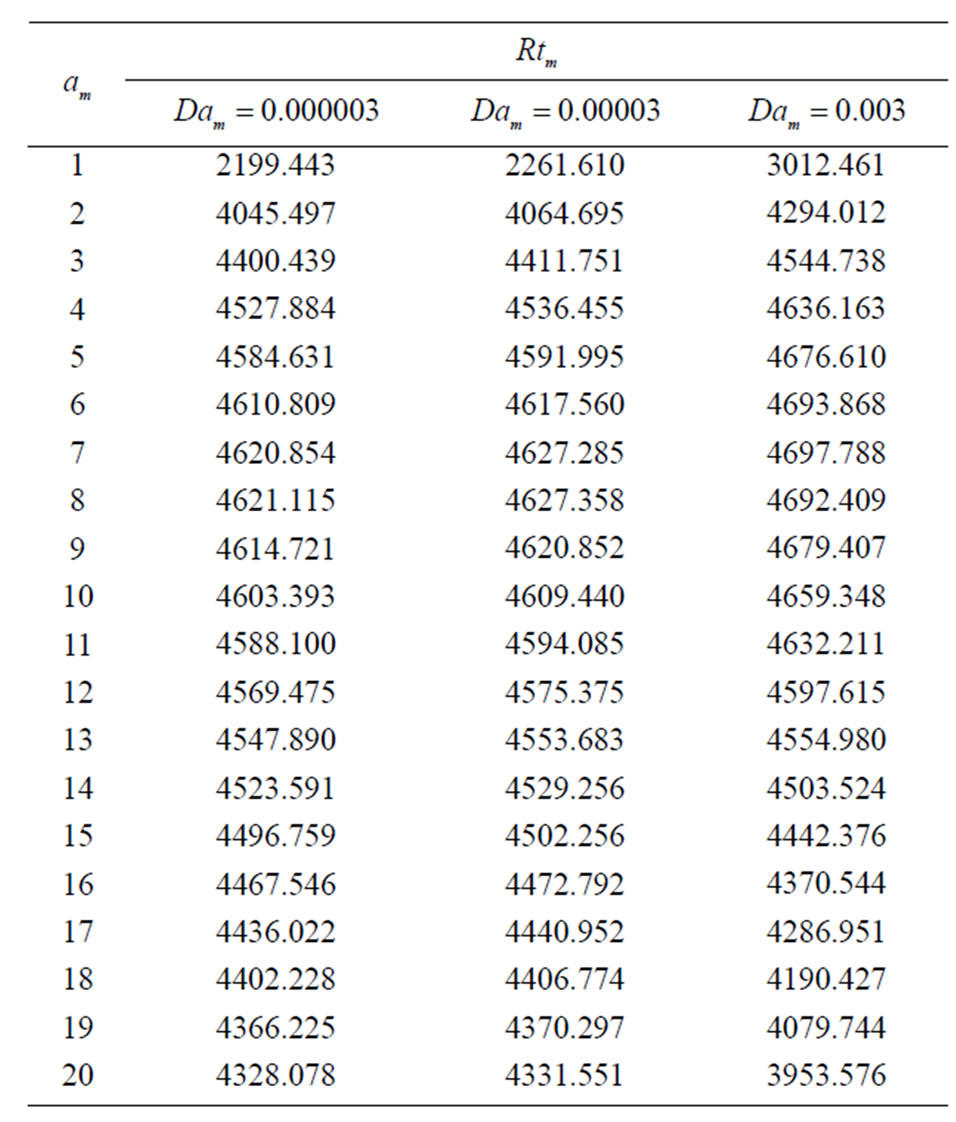
Table 3. The relation between am and Rtm for different values of Dam when Qm = 100, Tam = 5, 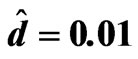 ,
, and
and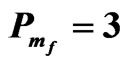 .
.
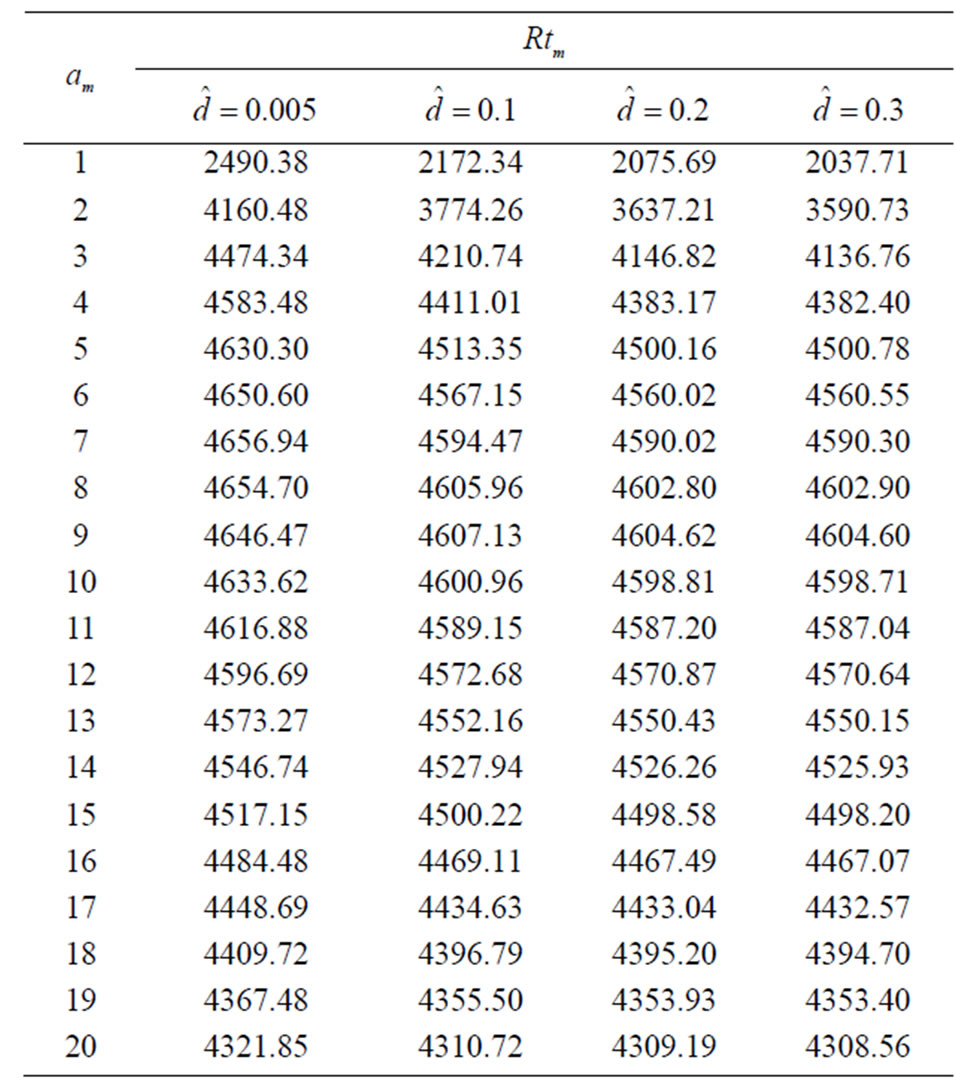
Table 4. The relation between am and Rtm for different values of  when Qm = 100, Dam = 0.0003, Tam = 5,
when Qm = 100, Dam = 0.0003, Tam = 5, 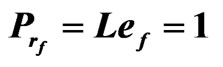 and
and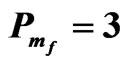 .
.

Figure 2. The relation between am and Rtm for different values of Tam when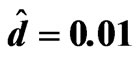 , Dam = 0.0003, Qm = 100,
, Dam = 0.0003, Qm = 100,  and
and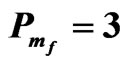 .
.

Figure 3. The relation between am and Rtm for different values of Qm when Tam = 5, 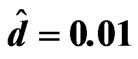 , Dam = 0.0003,
, Dam = 0.0003, 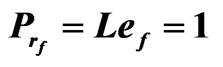 and
and .
.
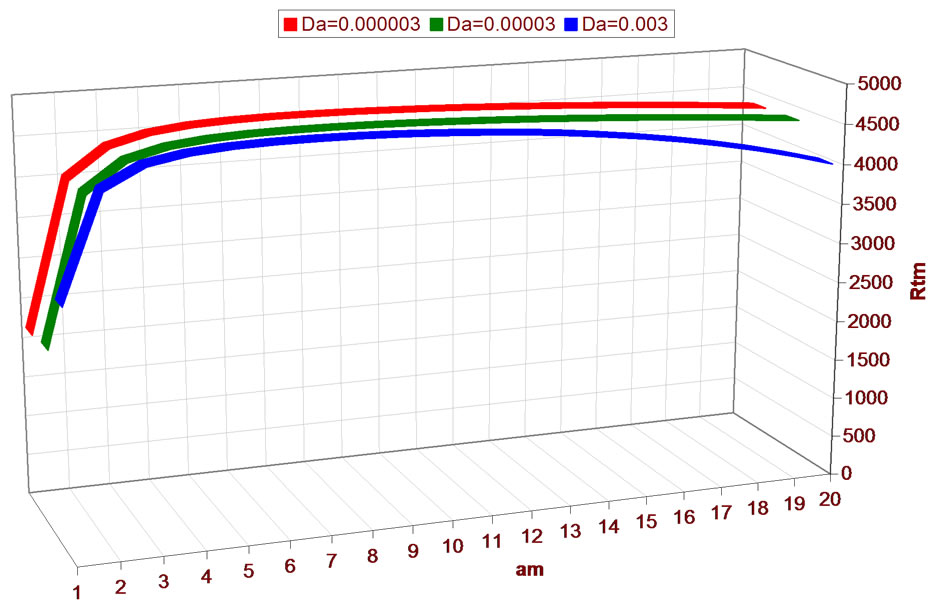
Figure 4. The relation between am and Rtm for different values of Dam when Qm = 100, Tam = 5,  ,
, 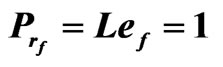 and
and .
.
• As 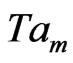 increases
increases 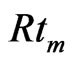 decreases which means that the increase of the rotation causes the increase of the thermal convections, leading to an increase in the instability of the fluid, as shown in Figure 2 and its numerical results in Table 1.
decreases which means that the increase of the rotation causes the increase of the thermal convections, leading to an increase in the instability of the fluid, as shown in Figure 2 and its numerical results in Table 1.

Figure 5. The relation between am and Rtm for different values of 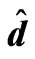 when Qm = 100, Dam = 0.0003, Tam = 5,
when Qm = 100, Dam = 0.0003, Tam = 5, 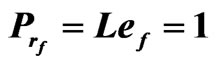 and
and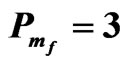 .
.
• The presence of the linear magnetic field helps reduce the currents of the thermal convections, meaning that the stability will increase in the fluid, as shown in Figure 3 and its numerical results in Table 2.
• The fluid becomes unstable when the permeability of the porous medium increases, as shown in Figure 4 and its numerical results in Table 3.
• The increase of depth ratio between the two layers makes the fluid unstable meaning that as 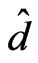 increases Rtm decreases, as shown in Figure 5 and its numerical results in Table 4.
increases Rtm decreases, as shown in Figure 5 and its numerical results in Table 4.
Case (2): the heat and the salt concentration affected from below.
Here, we put  and the value of the initial salt Rayleigh number of a porous medium Rsm = 10000, to find the thermal Rayleigh numbers of a porous medium,
and the value of the initial salt Rayleigh number of a porous medium Rsm = 10000, to find the thermal Rayleigh numbers of a porous medium, 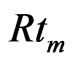 corresponding to wave numbers,
corresponding to wave numbers,  for different values of
for different values of ,
,  ,
, 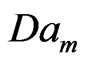 ,
, 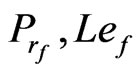
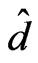 and
and . In this case, the eigenvalues are complex, and thus the overstability happens, as shown in the following Tables 5-8 and Figures 6-9. Therefore, we got the following results:
. In this case, the eigenvalues are complex, and thus the overstability happens, as shown in the following Tables 5-8 and Figures 6-9. Therefore, we got the following results:
• The increase of the rotation helps reduce the currents of the thermal convections meaning that the stability will increase in the fluid, as displayed in Figure 6 and its numerical results in Table 5.
• The presence of the linear magnetic field makes the fluid more stable as displayed in Figure 7 and its numerical results in Table 6.
• As 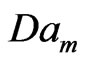 increases
increases  decreases which means that the increase of the permeability causes the increase of the thermal convections, leading to an increase in the instability of the fluid, as shown in Figure 8 and its numerical results in Table 7.
decreases which means that the increase of the permeability causes the increase of the thermal convections, leading to an increase in the instability of the fluid, as shown in Figure 8 and its numerical results in Table 7.
• As 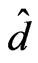 increase
increase 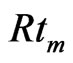 increases meaning that the in-
increases meaning that the in-

Table 5. The relation between am and Rtm for different values of Tam when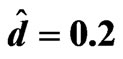 , Qm = 100, Dam = 0.0003,
, Qm = 100, Dam = 0.0003,  and
and .
.
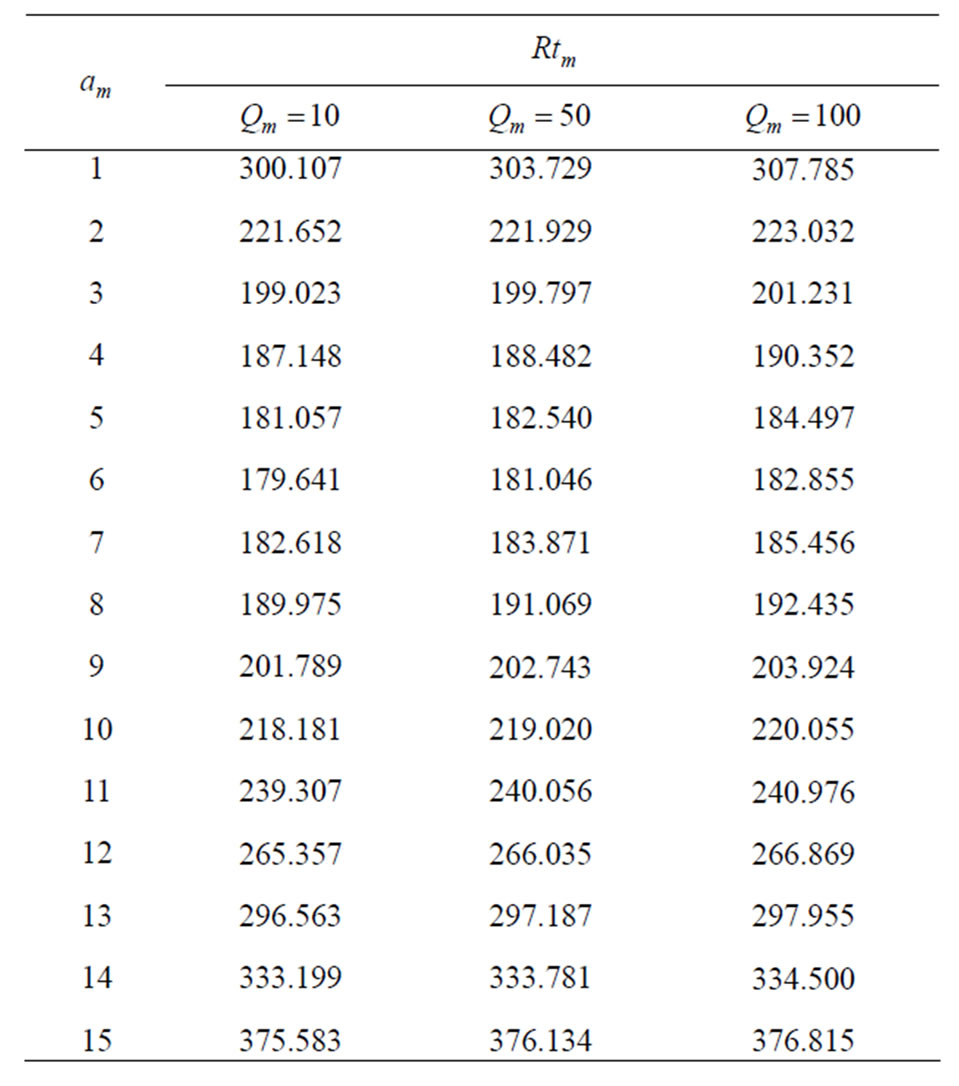
Table 6. The relation between am and Rtm for different values of Qm when Tam = 0.5, 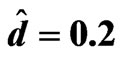 , Dam = 0.001,
, Dam = 0.001,  and
and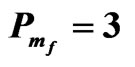 .
.

Table 7. The relation between am and Rtm for different values of Dam when Tam = 0.5, Qm = 50, 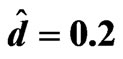 ,
, 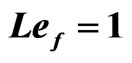
 and
and .
.
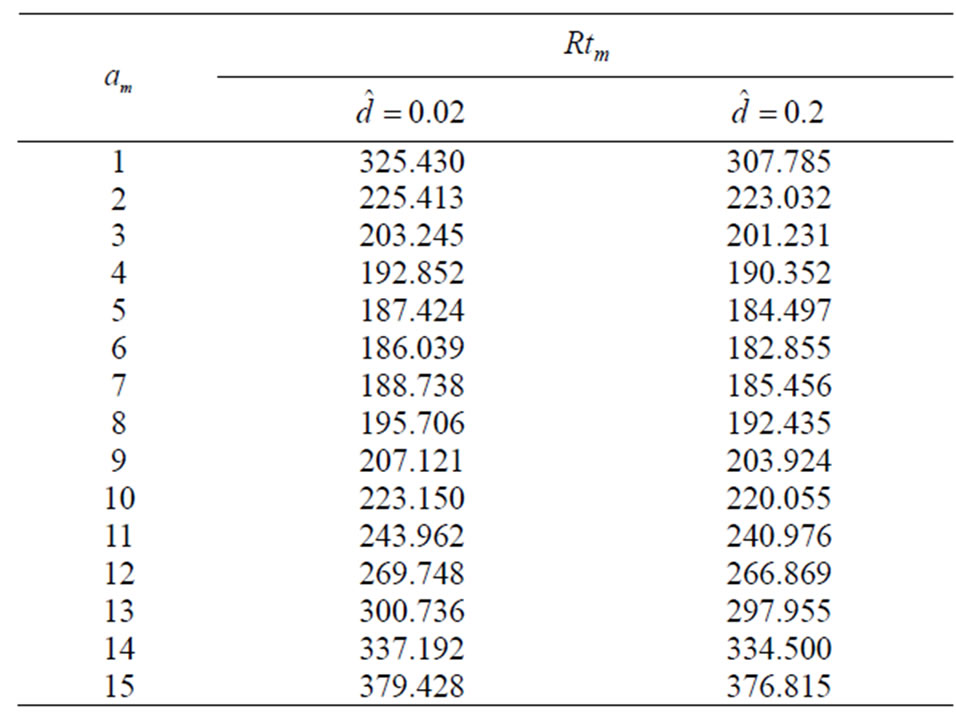
Table 8. The relation between am and Rtm for different values of 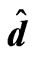 when Tam = 0.5, Dam = 0.001, Qm = 100,
when Tam = 0.5, Dam = 0.001, Qm = 100,  and
and .
.
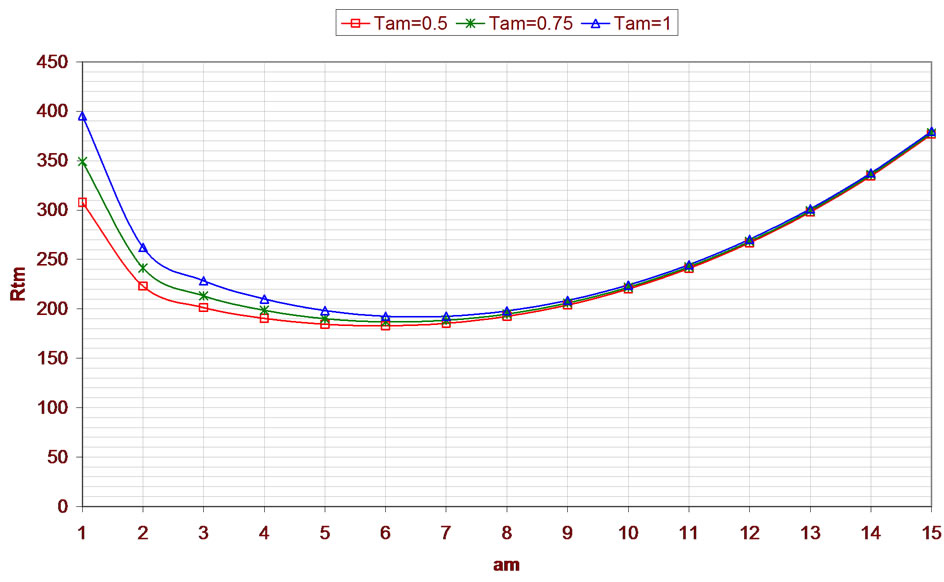
Figure 6. The relation between am and Rtm for different values of Tam when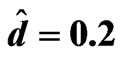 , Qm = 100, Dam = 0.0001,
, Qm = 100, Dam = 0.0001,  and
and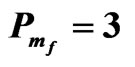 .
.

Figure 7. The relation between am and Rtm for different values of Qm when Tam = 0.5, 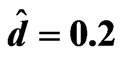 , Dam = 0.001,
, Dam = 0.001,  and
and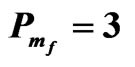 .
.
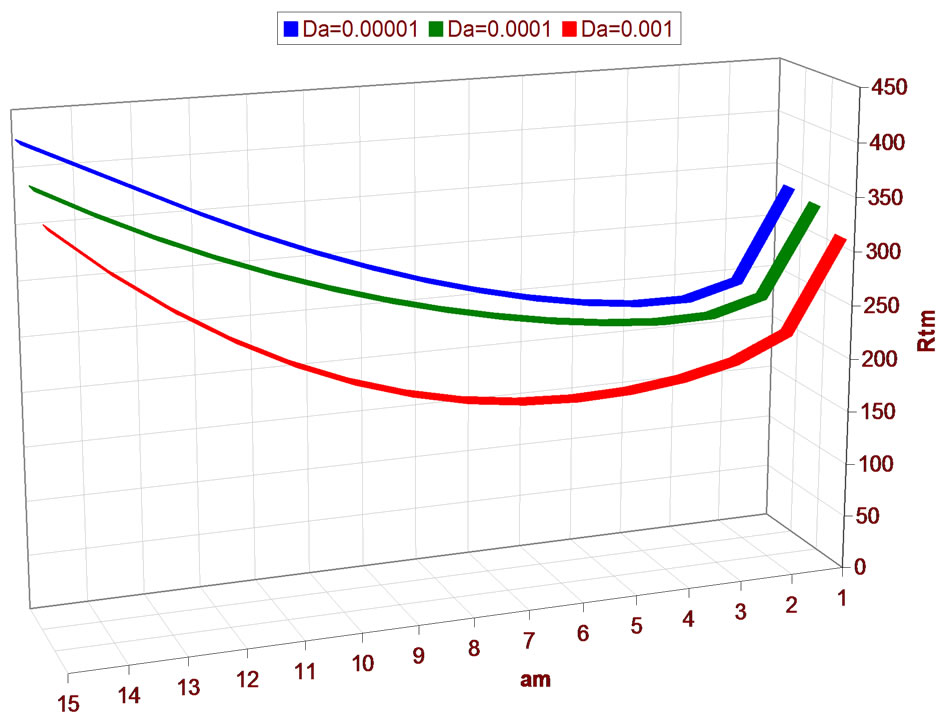
Figure 8. The relation between am and Rtm for different values of Dam when Tam = 0.5, Qm = 50, 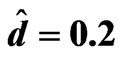 ,
, 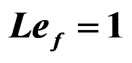
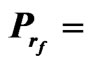 and
and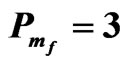 .
.

Figure 9. The relation between am and Rtm for different values of 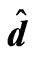 when Tam = 0.5, Dam = 0.001, Qm = 100,
when Tam = 0.5, Dam = 0.001, Qm = 100, 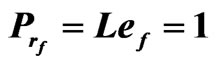 and
and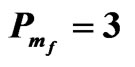 .
.
crease of the depth ratio between the two layers makes the fluid unstable, as displayed in Figure 9 and its numerical results in Table 8.
REFERENCES
- H. Benard, “Les Tourbillons Cellulaires Dans une Nappe Liquide,” Revue Genral des Sciences Pures et Appliquess, Vol. 11, 1900, pp. 1216-1271, 1309-1328.
- H. Benard, “Les Tourbillons Cellulaires Dans une Nappe Liquide Transportant de la Chalaur par Convection en Regime Permanent,” Annales de Chimie et de Physique, Vol. 23, 1901, pp. 62-114.
- S. Chandrasekhar, “The Instability of a Layer of Fluid Heated below and Subject to Coriolis Forces,” Proceedings of the Royal Society A (London), Vol. 217, No. 1130, 1953, pp. 306-327. doi:10.1098/rspa.1953.0065
- S. Chandrasekhar and D. D. Elbert, “The Instability of a Layer of Fluid Heated below and Subject to Coriolis Forces. II,” Proceedings of the Royal Society A (London), Vol. 231, No. 1185, 1955, pp. 198-210.
- D. A. Nield, “Onset of Themohaline Convection in a Porous Medium,” Water Resources Research, Vol. 4, No. 3, 1968, pp. 553-560.
- J. Taunton and E. Lightfoot, “Thermohaline Instability and Salt Fingers in a Porous Medium,” Physics of Fluids, Vol. 15, No. 748, 1972, pp. 784-753.
- W. J. Sun, “Convection Instability in Superposed Porous and Free Layers,” Ph.D. Dissertation, University of Minnesota, Minneapolis, 1973.
- D. A. Nield, “Onset of Convection in a Fluid Layer Overlying a Porous Medium,” Journal of Fluid Mechanics, Vol. 81, No. 3, 1977, pp. 513-522. doi:10.1017/S0022112077002195
- H. C. Brinkman, “A Calculation of the Viscous Force Exerted by a Flowing Fluid on a Dense Swarm of Particles,” Journal of Applied Sciences Research, Vol. Al. 1947, pp. 27-34.
- F. Chen and C. F. Chen, “Onset of Finger Convection in a Horizontal Porous Layer Underlying a Fluid Layer,” Journal of Heat Transfer, Vol. 110, No. 2, 1988, pp. 403-409. doi:10.1115/1.3250499
- K. A. Lindsay and R. R. Ogden, “A Practical Implementation of Spectral Methods Resistant to the Generation of Spurious Eigenvalues Paper No. 92/23,” University of Glasgow, Department of Mathematics Preprint Series, Glasgow, 1992.
- C. J. Lamb, “Hydromagnetic Instability in the Earth’s Core,” Ph.D. Thesis, Department of Mathematics, University of Glasgow, Glasgow, 1994.
- A. F. Bukhari, “A Spectral Eigenvalue Method for MultiLayered Continuua,” Ph.D. Thesis, University of Glasgow, Glasgow, 1996.
- B. Straughan, “Surface-Tension-Driven Convection in a Fluid Overlying a Porous Layer,” Journal of Computational Physics, Vol. 170, No. 1, 2001, pp. 320-337. doi:10.1006/jcph.2001.6739
- B. Straughan, “Effect of Property Variation and Modelling on Convection in a Fluid Overlying a Porous Layer,” International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 26, No. 1, 2002, pp. 75-97. doi:10.1002/nag.193
- F. Allehiany, “Benard Convection in a Horizontal Porous Layer Permeated by a Conducting Fluid in the Presence of Magnetic Field and Coriolis Forces,” M.Sc. Thesis, Umm Al-Qura University, Mecca, 2003.
NOTES
*Corresponding author.

