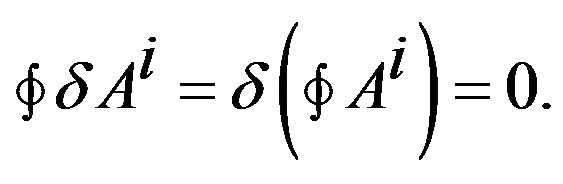Journal of Electromagnetic Analysis and Applications
Vol.4 No.6(2012), Article ID:20338,15 pages DOI:10.4236/jemaa.2012.46035
Electromagnetic Gauges and Maxwell Lagrangians Applied to the Determination of Curvature in the Space-Time and Their Applications
![]()
Department of Research in Mathematics and Engineering, Technological Institute of High Studies of Chalco, Chalco, Mexico.
Email: francisco.bulnes@tesch.edu.mx
Received April 15th, 2012; revised May 13th, 2012; accepted May 24th, 2012
Keywords: Back-Reaction Effects; Electromagnetic Bundles; Form Operator; Electro-Gravitational Detectors; Maxwell’s Lagrangian; Quantum Curvature
ABSTRACT
If we consider the finite actions of electromagnetic fields in Hamiltonian regime and use vector bundles of geodesic in movement of the charges with a shape operator (connection) that measures the curvature of a geometrical space on these geodesic (using the light caused from these points (charges) acting with the infinite null of gravitational field (background)) we can establish a model of the curvature through gauges inside the electromagnetic context. In particular this point of view is useful when it is about to go on in a quantized version from the curvature where the space is distorted by the interactions between particles. This demonstrates that curvature and torsion effect in the space-time are caused in the quantum dimension as back-reaction effects in photon propagation. Also this permits the observational verification and encodes of the gravity through of light fields deformations. The much theoretical information obtained using the observable effects like distortions is used to establish inside this Lagrangian context a classification of useful spaces of electro-dynamic configuration for the description of different interactions of field in the Universe related with gravity. We propose and design one detector of curvature using a cosmic censor of the space-time developed through distortional 3-dimensional sphere. Some technological applications of the used methods are exhibited.
1. Introduction
The curvature perception in the space is associated increasingly with their interpretation as a distortion of the micro-local structure of the space—time due to the interaction of particles of the matter and energy with diverse field manifestations [1,2]. The matter is shaped by hypothetical particles that take as basic the background radiation of the space, which in the last studies due to QFT, SUSY-theory and brane theory, the strings are organized and tacked to form spaces of major dimensions [3,4] represented by diverse particles of the matter as they are gravitons, barions, fermions of three generations, etc., shaping the gravity at quantum level, obtaining representations of the same one for classes of cohomology of the QFT, like for example the FRW-cohomology, which considers diverse symmetries of cylindrical and spherical type for the gravity modeling like a wave of gravitational energy “quasi-locally” [5-8]. Their integrals of action define a energy density (Hamiltonian) given for the gravitational case like [9-13]:
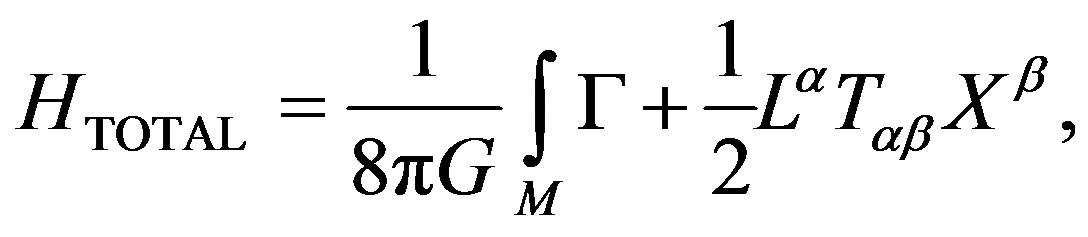 (1)
(1)
where Lα is the Lagrangian, Tαβ, is the corresponding tensor of matter and energy, Γ, is a Hamiltonian density and Xβ, is the corresponding field of displacement of the particles in the space moving for action of Lα influenced by the tensor one of matter and energy Tαβ. it is necessary to indicate that Lα has component that is invariant yet under movements influenced by the tensor Tαβ, which is their electromagnetic component LMAX, (Maxwell Lagrangian (see Table 1 in section 4, and Table 2 in section 6).
In case of the energy and through the neo-relativistic models of strings it was possible to have established that this is only a manifestation of the matter in their deep level, being a product of the interaction with particles as the electro-strong interactions that produce dispersion and cosmic rays in the whole universe, causing backreaction in propagation of photons that can be shaped through hypothetical particles or dilatons [14,15], using a strings of heterotic model [17] on the base of a 10-dimensional space-time defined for
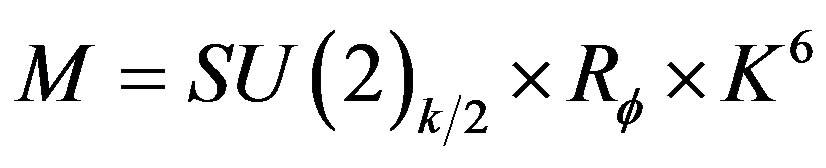 [17]. Then 4-dimensional strings (curved part of the background) can be interwoven to form strings that give birth to the quantum gravity that can be measured by the energy due to the backreaction of the photons with the background through a deviation (distortion) in their Lagrangian, reflected the above mentioned deviation in the action dilaton-gravity that would take in the space—time as an electro-gravitational wave with gravitational norm obtained by quantized electromagnetic fields interacting with the gravity. In this interaction dilatón-gravity, the field action is given theoretically
[17]. Then 4-dimensional strings (curved part of the background) can be interwoven to form strings that give birth to the quantum gravity that can be measured by the energy due to the backreaction of the photons with the background through a deviation (distortion) in their Lagrangian, reflected the above mentioned deviation in the action dilaton-gravity that would take in the space—time as an electro-gravitational wave with gravitational norm obtained by quantized electromagnetic fields interacting with the gravity. In this interaction dilatón-gravity, the field action is given theoretically
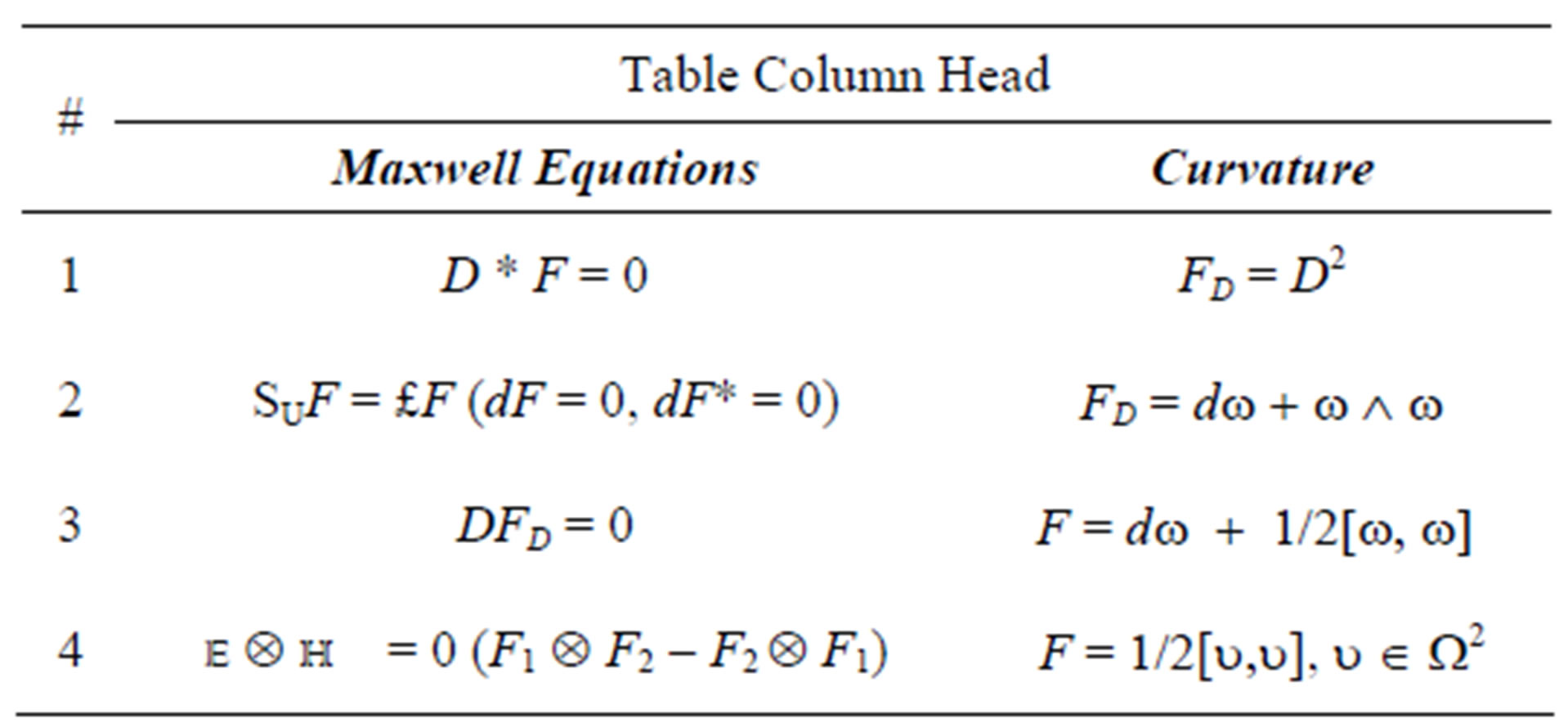
Table 1. Connections by Maxwell tensors [5].

Table 2. Lagrangians to electromagnetic interactions.
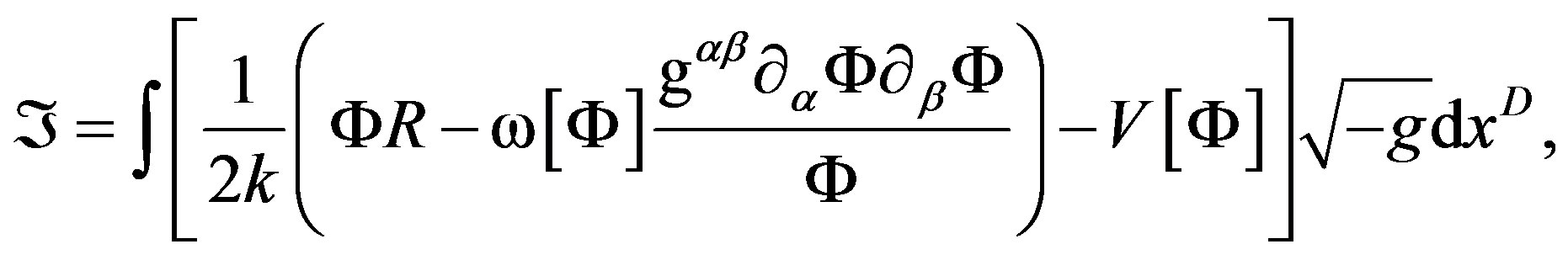 (2)
(2)
where R, is the curvature, 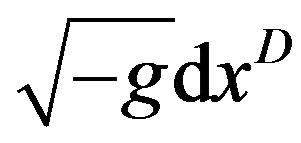 , is the quantized metric of the metric tensor and
, is the quantized metric of the metric tensor and , is the dilaton potential.
, is the dilaton potential.
2. Gauges of Maxwell and Variation Principle
Geometrically, a gauge as a physical concept is a vector bundle with a connection or shape operator between points of the space where the shape operator is an invariant under movements and rotations realized in the space [3].
This determines a quality invariant [2,3] of any of the actions in a field that acts on points among the space, which is useful for the effects measurement or observables of the field such as curvature and torsion [2,3], through an operator so that it could decide by means in other fields using a variation principle [1,5]. In particular we are interested in using finite actions (measurable) of electromagnetic fields with an shape operator determined through Lagrangians of Maxwell to measure observables or effects in other fields, for example, the observable ones of curvature and torsion due to the gravitational fields, or the distortion effects in spaces of energy (quantum curvature [5]) given by strong interactions or quantum fields. Interactions between two photons classes, one created by the matter (fermions), and the photon of the integer spin. Before entering in the quantum context, we consider to behavior particles in the macroscopic case.
Maxwell equations can be obtained like equations of a variation principle: Hamilton principle of a stationary action [2].
In effect, be M, a space of points or particles under movement of the action in a conservative electromagnetic field whose group of actions is SU(2), (group that defines the finite actions through unitary anti-Hermitians matrix of range). Be LMAX, the Maxwell operator on this group of points that establishes the law of conservation of movement in M, and that is produced by the fields of Maxwell F (dF = 0, dF* = 0).
If we consider that Maxwell equations can be obtained also like solution for a variational problem, then due to the actions of the fields F, that they produce the movement of all the particles in the space M, and using the corresponding vector bundle of these electromagnetic fields to define it geometrically we can define the above mentioned action as [4,5]:
 (3)
(3)
with rule of correspondence
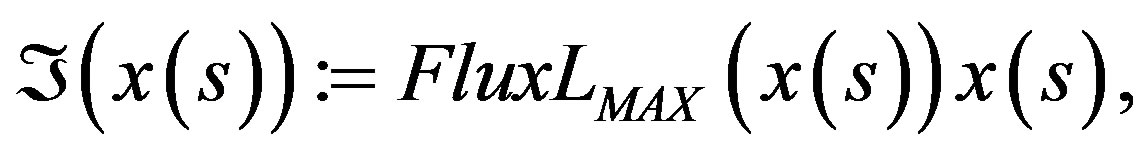 (4)
(4)
and the energy due to LMAX, is
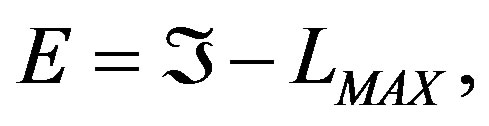 (5)
(5)
If we consider the global evaluation of the operator who acts on the points space x(s), this is given by
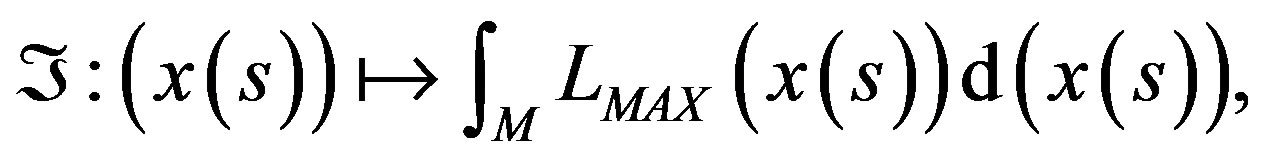 (6)
(6)
The integral Equation (6) represents the action Á(g), in which Hamilton’s principle establishes that the particle will cover that trajectory that minimizes the action. Likewise, the movement equation is predetermined by the minimum of this action Á(g), and pre-established for the variation condition [2]:
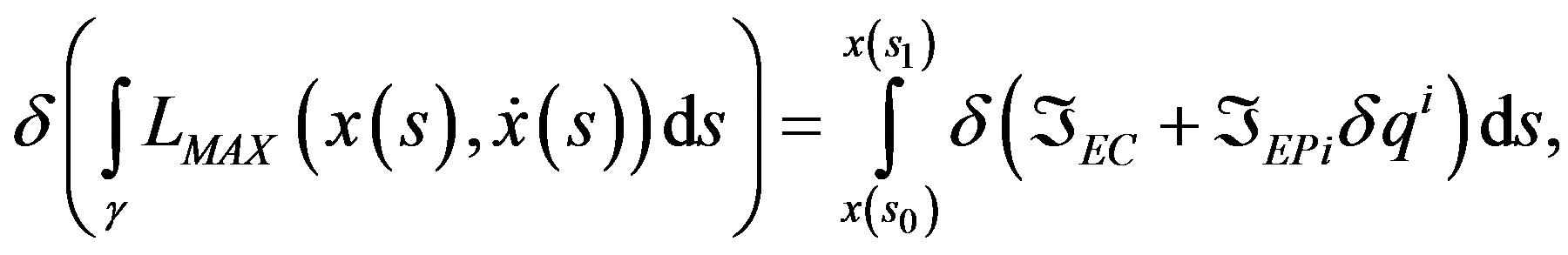 (7)
(7)
Particularly, if we want the evaluation of this Maxwell’s action along a trajectory chosen inside the field of minimal trajectories, as the principle of the minimal action we have the execution of the action of Maxwell’s fields [1,5],
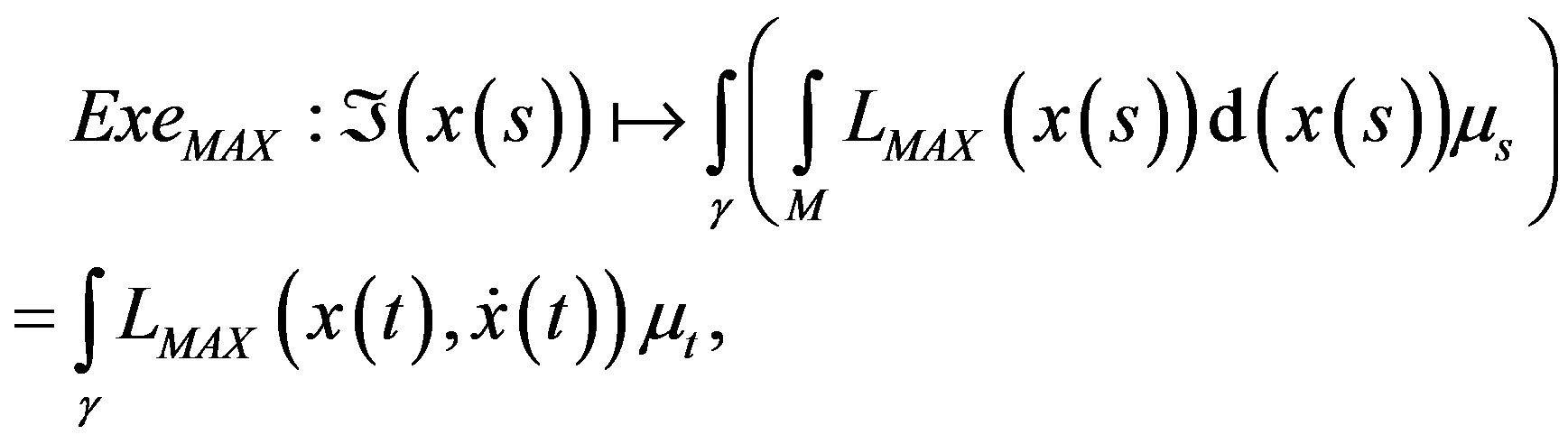 (8)
(8)
where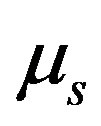 , is the corresponding measure of the trajectory
, is the corresponding measure of the trajectory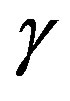 , in M.
, in M.
3. Shape Operators and Curvature in the Lagrangian Context
In particular, the action , of a field that curls the space M, is given by
, of a field that curls the space M, is given by
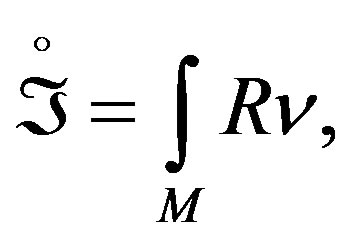 (9)
(9)
with R, a scalar curvature and 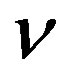 a metric form of volume in a system of invariant generalized coordinates under translations and rotations of coordinates in the space M. Let’s define to
a metric form of volume in a system of invariant generalized coordinates under translations and rotations of coordinates in the space M. Let’s define to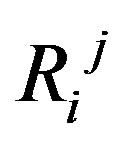 , the 2-form of curvature of the shape operator or corresponding connection D.
, the 2-form of curvature of the shape operator or corresponding connection D.
Then for a region of the space affected by the action , the product
, the product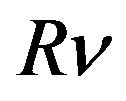 , can be expressed through surface sections
, can be expressed through surface sections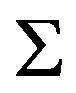 , where establishes the minimal condition of the trajectories followed by particles (mentioned in the section 2) under the action of the field of displacement [2] (remember that the displacement field does not have character of a tensor but it implies the existence of a tensor which is that curvature [2]) in M, that we will establish by means of the Lagrangian, to know
, where establishes the minimal condition of the trajectories followed by particles (mentioned in the section 2) under the action of the field of displacement [2] (remember that the displacement field does not have character of a tensor but it implies the existence of a tensor which is that curvature [2]) in M, that we will establish by means of the Lagrangian, to know
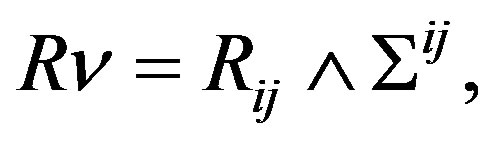 (10)
(10)
But this new expression of the form of curvature is useful to determine the distortion of the space through the value of the integrals along the minimal trajectories considered in surfaces that shape the form of the space, and whose deviations in conserving regime will determine the curvature of a universe.
The variation respect to the shape operator is established by the “free torsion” to us and therefore the equation of the shape operator
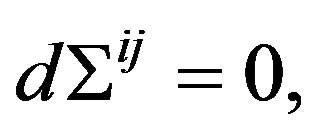 [3](11)
[3](11)
that in the context of the finite actions produced by the fields of distortion in Hamiltonian regime, otherwise the Equation (11) is equivalent to the equation
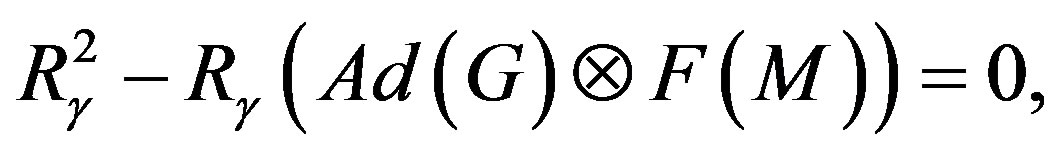 1[5](12)
1[5](12)
which has solutions in all the geometric models of constant curvature in a space M, and their geodesic curvatures are determined by the shape operator evaluated along the geodesic 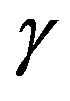 in the corresponding section of the bundle defined by Equation (3).
in the corresponding section of the bundle defined by Equation (3).
The Lagrangian writing through a scalar density of energy h, that produces energy as the determined one by Equation (5) in a pure context of the mechanics, we have that the action , takes the form
, takes the form
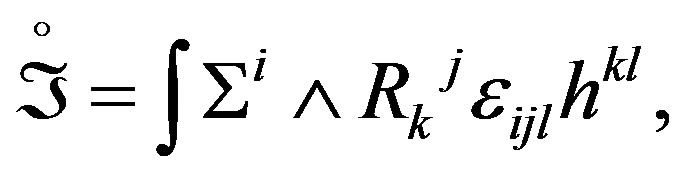 (13)
(13)
where hij, is determined by 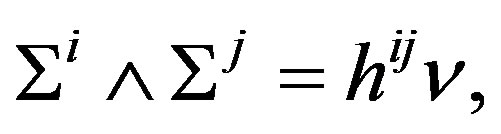 to some form of volume
to some form of volume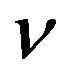 , such that hij, have determinant unity with respect to
, such that hij, have determinant unity with respect to  The action given by
The action given by  is the action of the curvature tensor that preserve the energy densities hij, such that
is the action of the curvature tensor that preserve the energy densities hij, such that
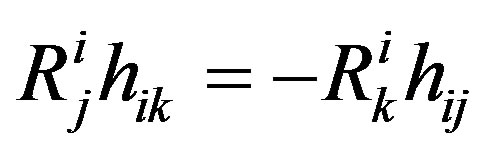 (14)
(14)
The identity from Equation (14), suggests the possibility of using an anti-symmetrical structure similar to the given by the fields of displacement [6], like for example, a structure given by the fields of Maxwell F, in a space of finite actions like the given by the super-canonical algebra [3-5]:
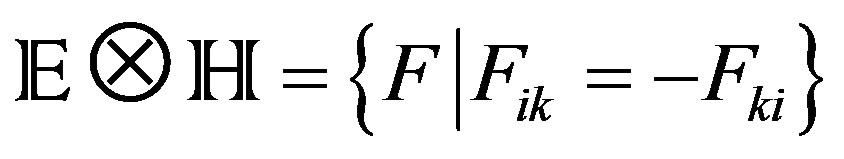 (15)
(15)
In fact in general the elements in the Equation (15) are of the form F1 Ä F2 – F1 Ä F2 – [F1,F2], which proceed of considering to as a bilateral ideal  as a bilateral ideal [5,7]. Here Fik = ÑiAk, with Ak = Ñkf, where f, is a density of electromagnetic field.
as a bilateral ideal [5,7]. Here Fik = ÑiAk, with Ak = Ñkf, where f, is a density of electromagnetic field.
The importance of this one formal structure in electromagnetism is its representation and realization for operators of the quantum mechanics [5,8]. It can be demonstrated under certain restrictions in a co-algebra to the curvature connection in case of a Hamiltonian density of curvature [9]. Other algebra of this co-algebra is the relative one to the curvature of space—time [5], that is what we are interested in.
To reinforce the idea of using an shape operator so that used energy of another field origin (like the of electromagnetic field) and to prepare the use of Lagrangian of Maxwell, for the curvature determination under Hamiltonian regime, let’s consider
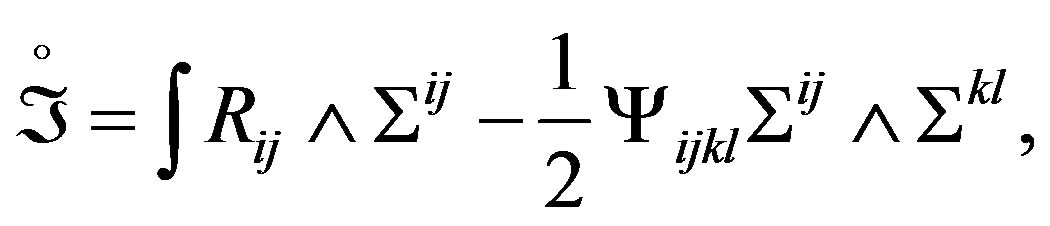 (16)
(16)
where the form of volume in M, remains given for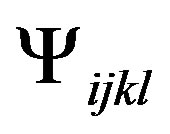 , which is a Lagrange multiplier for the Equation (11) [5]. Then studying the variations happened in the integral of Equation (16) with respect to
, which is a Lagrange multiplier for the Equation (11) [5]. Then studying the variations happened in the integral of Equation (16) with respect to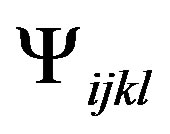 , we obtain a variation condition for the curvature tensor through its shape operator with the new introduced elements, to be known
, we obtain a variation condition for the curvature tensor through its shape operator with the new introduced elements, to be known
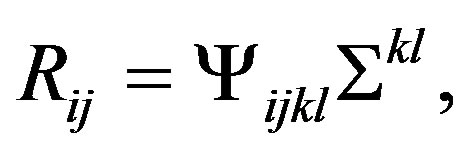 (17)
(17)
This implies that all the terms of the symmetrical tensor of curvature [5] in Rij, are annulled, the Equation (12) being satisfied on the whole  [10].
[10].
4. Electromagnetic Model of Quantum Curvature
We use the generalization of the Maxwell theory given in the section 2, and let’s express the Maxwell-Lagrange operators according to the shape operator or connection and its curvature. Let SG(M)0, be a bundle of vector fields on M, with structural topological group G. Let D, be the shape operator in SG(M)0, defined by the correspondence to a field X
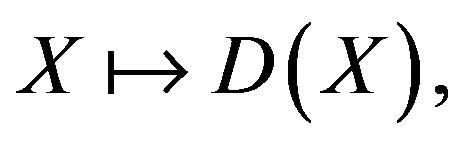 (18)
(18)
and let ÁD, be the action defined by the form of curvature corresponding to the shape operator D, defined in (18). The shape operator this way definite induces a transformation in the bundle vector fields SG(M)0, [5]. This bears to that we could realise gauge transformations on the space M, through generalizing vector fields [5], since it there are the electromagnetic fields of 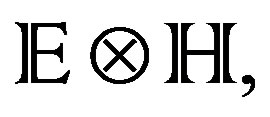 [5], in the structural context given by the topological group of finite actions,
[5], in the structural context given by the topological group of finite actions, 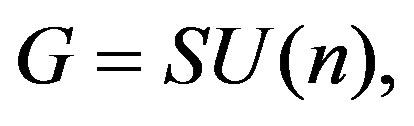 of M, with the Hamiltonian formulation given in the section 2.
of M, with the Hamiltonian formulation given in the section 2.
The Hamiltonian formulation mentioned can be obtained like solution to a variation problem directly of the Maxwell equations [5], namely: Let , be a form on volume in M, and let * be the Hodge operator defined by the metric of M. Then
, be a form on volume in M, and let * be the Hodge operator defined by the metric of M. Then 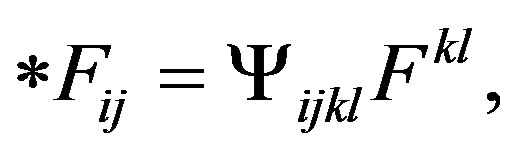 and the Maxwell Lagrangian LMAX, it is possible to express like
and the Maxwell Lagrangian LMAX, it is possible to express like
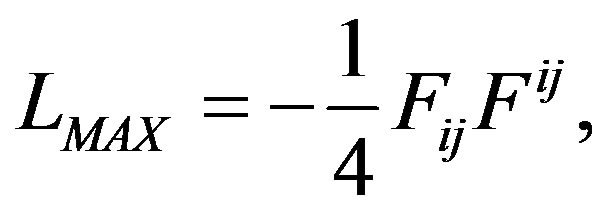 (19)
(19)
This way, Maxwell equations are precisely the EulerLagrange equations of the corresponding variation problem. Their action is given by Equation (6). But we want curvature under the action of these Maxwell fields using the minimal trajectories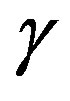 , possible movement of the particles in a microscopic space-time M [5]. Then the finite action originated from the curvature must be the that comes from a finite action of Maxwell fields in Hamiltonian regime as it is defined from Equation (3) to Equation (6), more the action defined by the form of curvature corresponding to the shape operator D, defined in Equation (18) and that is related to Maxwell fields for the form of curvature described in terms of the Maxwell tensor F:
, possible movement of the particles in a microscopic space-time M [5]. Then the finite action originated from the curvature must be the that comes from a finite action of Maxwell fields in Hamiltonian regime as it is defined from Equation (3) to Equation (6), more the action defined by the form of curvature corresponding to the shape operator D, defined in Equation (18) and that is related to Maxwell fields for the form of curvature described in terms of the Maxwell tensor F:
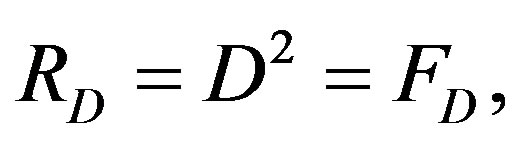 (20)
(20)
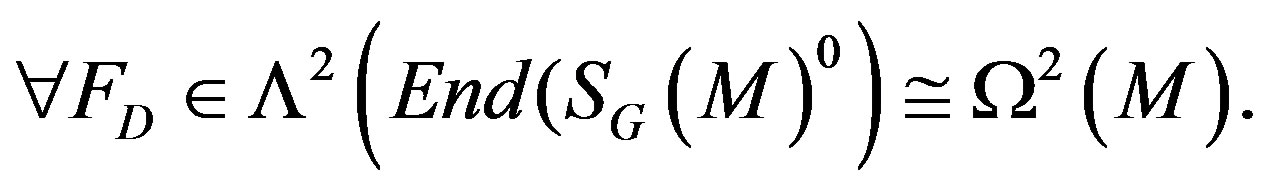
The tensor defined in the Equation (20) is the quantized version of the curvature tensor [5], way that is necessary to be applied to define the curvature according to bundles of light [3,5] (to see Table 1). In fact it is possible to surmise that the reinterpretation of the curvature by electromagnetic fields is established from a quantum or microscopic level using their spinor fields of light [5].
From the Lagrangians described and their gauges (electromagnetic fields), given the following classification of curvature:
5. An Inferior Bound to Localizing Curvature Measured through Energy of Matter
Be considered to be a connection for this phenomenon of quantum curvature the shape operator,
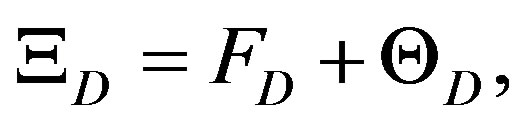 (21)
(21)
where FD, is the linear connection used in the Equation (20), (that is the linear connection of the gauge transformation (quantized electromagnetic fields) and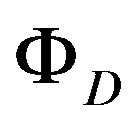 , the connection of movement (translation) of the affine connection describing a small distortion of the space respect to a reference inertial frame, due to this electromagneticgravitational interaction.
, the connection of movement (translation) of the affine connection describing a small distortion of the space respect to a reference inertial frame, due to this electromagneticgravitational interaction.
Then 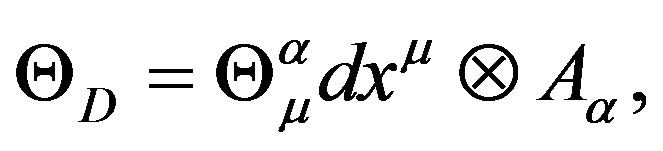 where
where 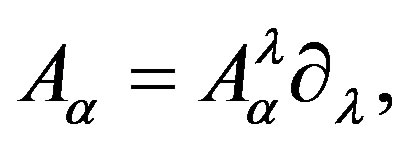 is a nonholonomic frame. Then the connection
is a nonholonomic frame. Then the connection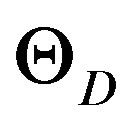 , must be considered to be like the connection of the censoring that contains quantum curvature.
, must be considered to be like the connection of the censoring that contains quantum curvature.
All R4, must be obtained through a micro-local structure of the space-time, whose connection is a generalizetion in a certain sense of the given connection.
Escolium 5.1. The curvature action , on R4, measured by the electromagnetic field through the Lagrangian LMAX, comes given for
, on R4, measured by the electromagnetic field through the Lagrangian LMAX, comes given for
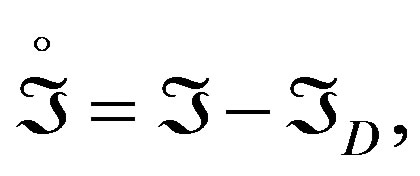 (22)
(22)
where 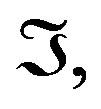 is the action of Maxwell tensor ones as it is defined in the Equation (6) and ÁD, is the action defined by the form of curvature corresponding to the shape operator defined in the Equation (18).
is the action of Maxwell tensor ones as it is defined in the Equation (6) and ÁD, is the action defined by the form of curvature corresponding to the shape operator defined in the Equation (18).
Proof: We consider inequality:
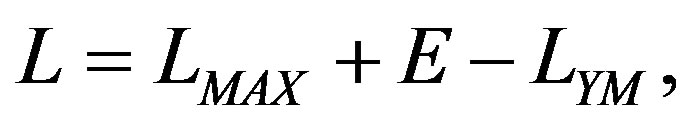 (23)
(23)
and we consider the energy due to the action 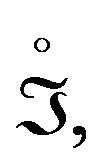 [2], to know:
[2], to know:
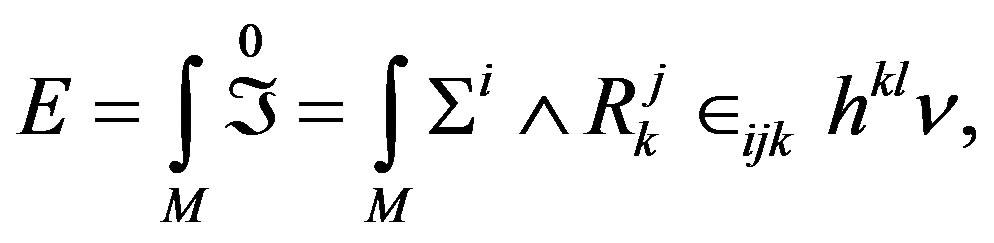 (24)
(24)
from which the curvature Langragian is given by
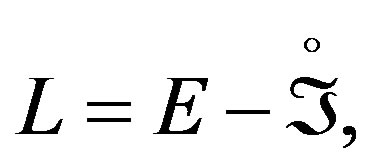 (25)
(25)
Coupling the energy of Maxwell tensor 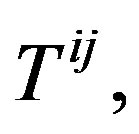 [5] of the structure of the U(1)-bundle
[5] of the structure of the U(1)-bundle 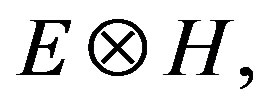 [3], to the equality in the Equation (23) and considering that their compositions
[3], to the equality in the Equation (23) and considering that their compositions 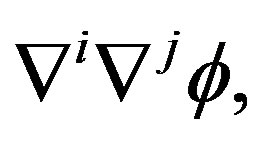 (
(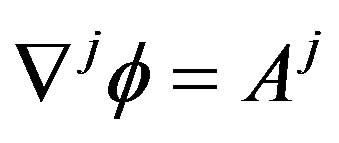 ), are conformably invariants, we have that under the principle of curved translation [11], the endomorphism
), are conformably invariants, we have that under the principle of curved translation [11], the endomorphism 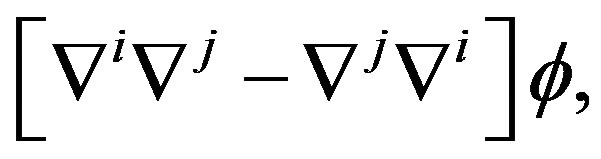 is the curvature of
is the curvature of 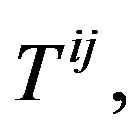 which according to the unified conformably invariant field theory [12], is a good approach to the Bach tensor Bij and their correspondent spinor, the Eastwood-Dighton tensor Eijk [4]. This way we have that the action of curvature through the Lagrangian on
which according to the unified conformably invariant field theory [12], is a good approach to the Bach tensor Bij and their correspondent spinor, the Eastwood-Dighton tensor Eijk [4]. This way we have that the action of curvature through the Lagrangian on 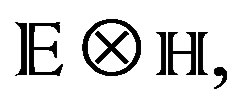 is precisely the contribution of the Bach and Eastwood-Dighton tensors, [12] to know:
is precisely the contribution of the Bach and Eastwood-Dighton tensors, [12] to know:
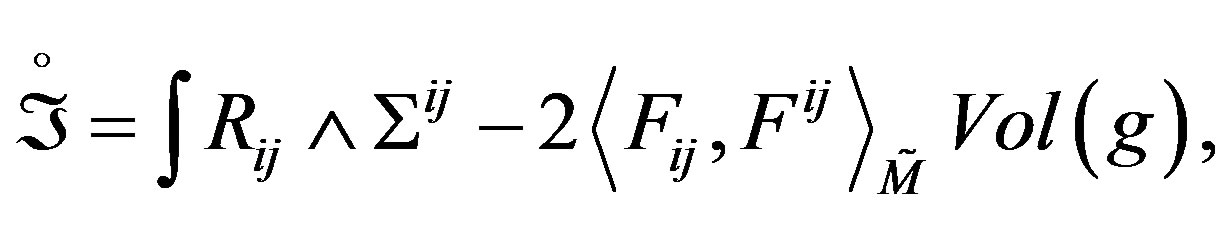 (26)
(26)
where 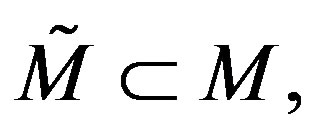 is the compact Riemannian manifold, oriented and of dimension n, of the Riemannian manifold M and g, is the Riemannian metric of M.
is the compact Riemannian manifold, oriented and of dimension n, of the Riemannian manifold M and g, is the Riemannian metric of M.
Corollary. 5.1. Consider the action ÁD, with Lagrangian of Yang-Mills to the Maxwell equations of the variation principle (@ Euler-Lagrange equations)
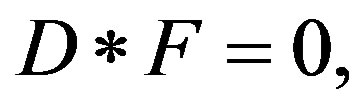 (27)
(27)
Then the curvature on the geodesic one 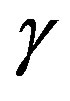 calibrated through the electromagnetism of the Equation (26) using the concept of gravitational norm used in the Equation (21) is given by
calibrated through the electromagnetism of the Equation (26) using the concept of gravitational norm used in the Equation (21) is given by
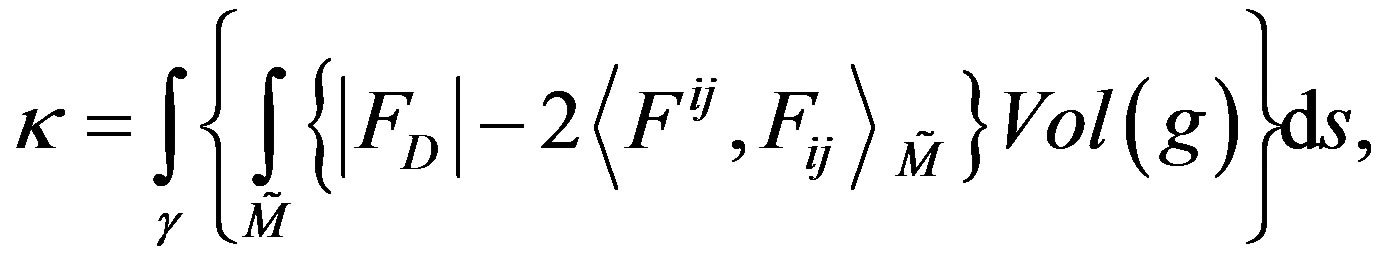 (28)
(28)
with 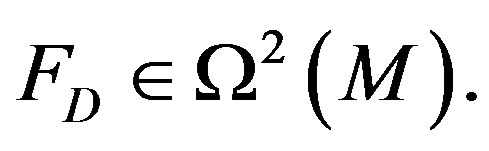 The Equation (28) is the geodesic curvature of light. The bilinear form
The Equation (28) is the geodesic curvature of light. The bilinear form 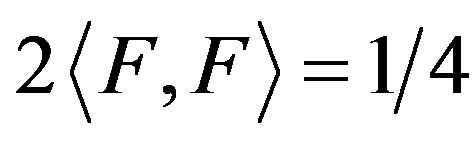
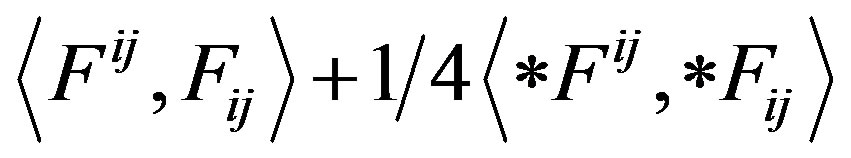 , where * is the Hodge operator.
, where * is the Hodge operator.
Proof: Applying the property of the Hodge operator  due to the metric g of
due to the metric g of 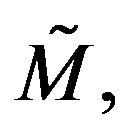 [5,6] jointly with the definition of Yang-Mills functional in the space of shape operators
[5,6] jointly with the definition of Yang-Mills functional in the space of shape operators 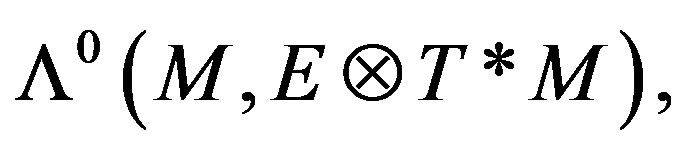 and under the scheme of the energy tensor Tij, (given in the before section through of their Hamiltonian) we have the result wanted [9].
and under the scheme of the energy tensor Tij, (given in the before section through of their Hamiltonian) we have the result wanted [9].
6. Propagation of Photons and Gravity
We consider the photons propagation in a cut of a cone of light with the infinity null of the space-time (that is to say, only the regions of the space-time where photons interaction exists with hypothetical gravity particles) [13] (hypothesis of Kozameh), then we can obtain a curvature expression according to the quantized electromagnetic fields. But the questions arise: how to obtain a formula that includes the effects of distortion of the light for the gravity presence (curvature), using the condition happened in the Equation (16) and that is simultaneously, an electromagnetic representation of curvature? Will it be possible to design an instrument to detect photons radiated by gravity?
Theoretically, the region that can be capable to these electromagnetic measurements must be the shaped one with strings of such theoretical particles like the graviton and the dilaton that magnetic distortions of the photon detect [14].
We want quantum curvature though fields of light that interact with the gravity, but also we want to measure like quantized electromagnetic energy, which comes from the above mentioned distortion.
Then it is necessary to use the Kozameh hypothesis [13], more curvature hypotheses in theory of the geometrical invariants of the space-time that allows us to measure the distortion of the lines of movement in any particle that falls down under the influence of the gravity field at quantum level, using the back-reaction in the background of the space, with certain hypotheses (to see Figures 1-3).

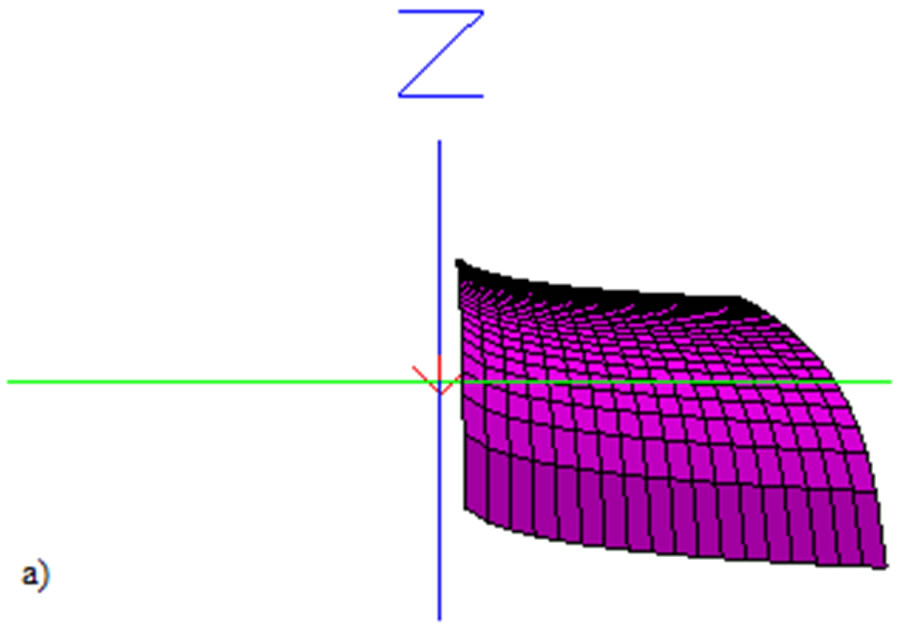
Figure 1. Flat- -Worldsheet of distortion angle obtained for the electromagnetic backreaction with the background radiation (gravity).
-Worldsheet of distortion angle obtained for the electromagnetic backreaction with the background radiation (gravity).
 (a)
(a)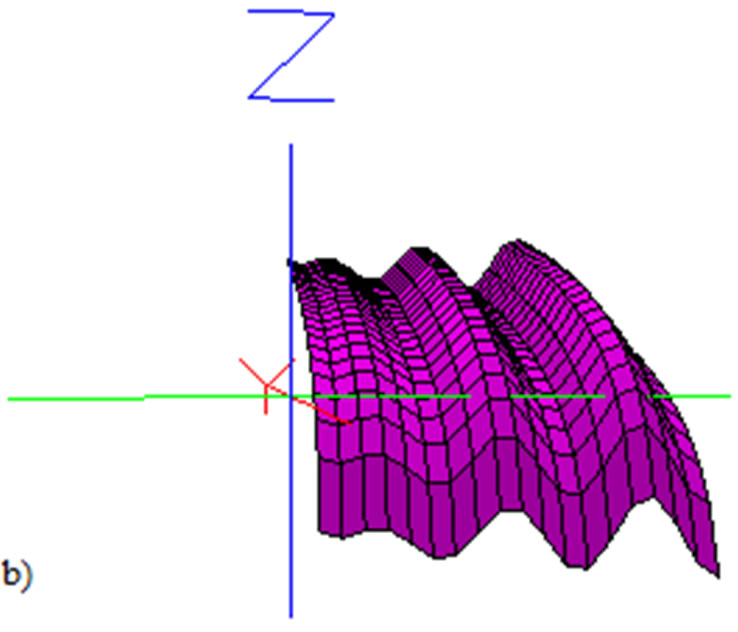 (b)
(b)
Figure 2. Dilaton measuring distortion due to quantum gravity, according to the model computacional magnetic Φ = y/\sqrt(y + 1) – ((1/2)log(x + 1/x + (x – 1/x))cosq) (see Equation (41)). The surface in (a), represents the space-time area before the photons back-reaction with background radiation, their magnetic model is Φ = y/\sqrt(y + 1) – ((1/2)log(x + 1/x + (x – 1/x))). In the surface (b), the distortion is measured by the magnetic oscillations cosq, that is to say, the term of tough deviation q, in the Figure 1.
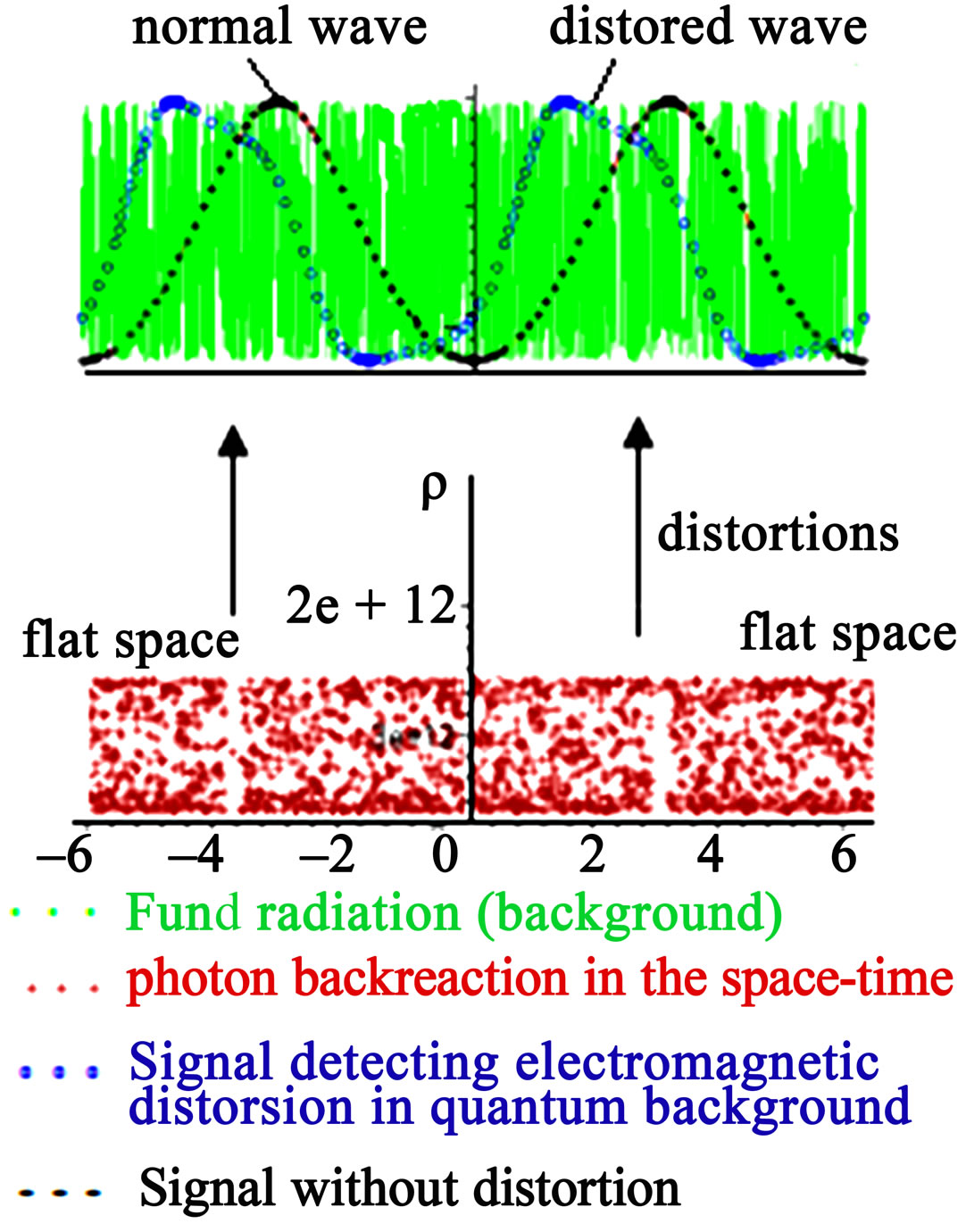
Figure 3. Wave propagation of the background radiation (green), propagation of quantum electromagnetic waves, without background radiation (black) and propagation of quantum electromagnetic waves distorted with background radiation (blue). The stripe in brown represents the flat space with the corresponding distortions that create the angle q. The difference between the two waves come reflected in the corresponding hollows. This figure gives us the microlocal aspect of the space-time in Max Planck dimension.
Conjecture. The quantum curvature can be measureable or detectable across the effects of reaction of the radiation of the electromagnetic fields with the gravitational field that produces the whose curvature, but these can only measure themselves for its Hamiltonians in the kinematics of the curved space in R4, with respect to its micro-local structure.
The previous conjecture establishes that the electromagnetic measurement can be realised, but only in indirect form and with fields without mass of electromagnetic origin (photons) which is not detectable for measuring devices (measuring devices do not exist for these ends).
7. Model of Magnetic Distortion:Magnetic Deformationof Cuadri-Dimensional Part of the Strinf of Background Radiation
We consider SO(3)k/2 ´ , like the 4-dimensional part of the string of background 10-dimensional in which we replace the flat part of
, like the 4-dimensional part of the string of background 10-dimensional in which we replace the flat part of , (that is to say, we are considering the part of
, (that is to say, we are considering the part of , where there is distortion
, where there is distortion ). We consider the corresponding algebra of electromagnetic fields at level k, given by the gauge group to this scale SU(2)k [15], and
). We consider the corresponding algebra of electromagnetic fields at level k, given by the gauge group to this scale SU(2)k [15], and 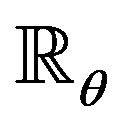 as a real dilaton [14], both appearing in the exact string of background realised by the theory of 2-dimensional superconformal fields. The distortion of such 4-dimensional curved part of the background will be designed in the heteroric superstring theory [12], in the language of the Lagrangian given by
as a real dilaton [14], both appearing in the exact string of background realised by the theory of 2-dimensional superconformal fields. The distortion of such 4-dimensional curved part of the background will be designed in the heteroric superstring theory [12], in the language of the Lagrangian given by
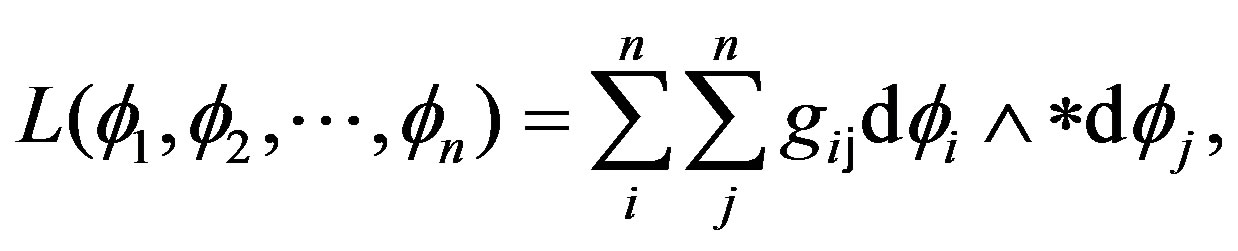 (29)
(29)
The idea is to use the fields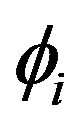 , to establish a map of the basic space (that is a 2-dimensional manifold fitted like string in the space-time) to the real space-time in question, the latter modeling for a Riemanniana manifold [10].
, to establish a map of the basic space (that is a 2-dimensional manifold fitted like string in the space-time) to the real space-time in question, the latter modeling for a Riemanniana manifold [10].
The distortions will correspond the introduction of a constant magnetic field and its gravitational back-reaction on the 4-dimensional part curled of the background.
In theory not deformed and using the notation of Dirac the action of the Lagrangian described for our string in SO(3)k/2 ´ , is [15]:
, is [15]:
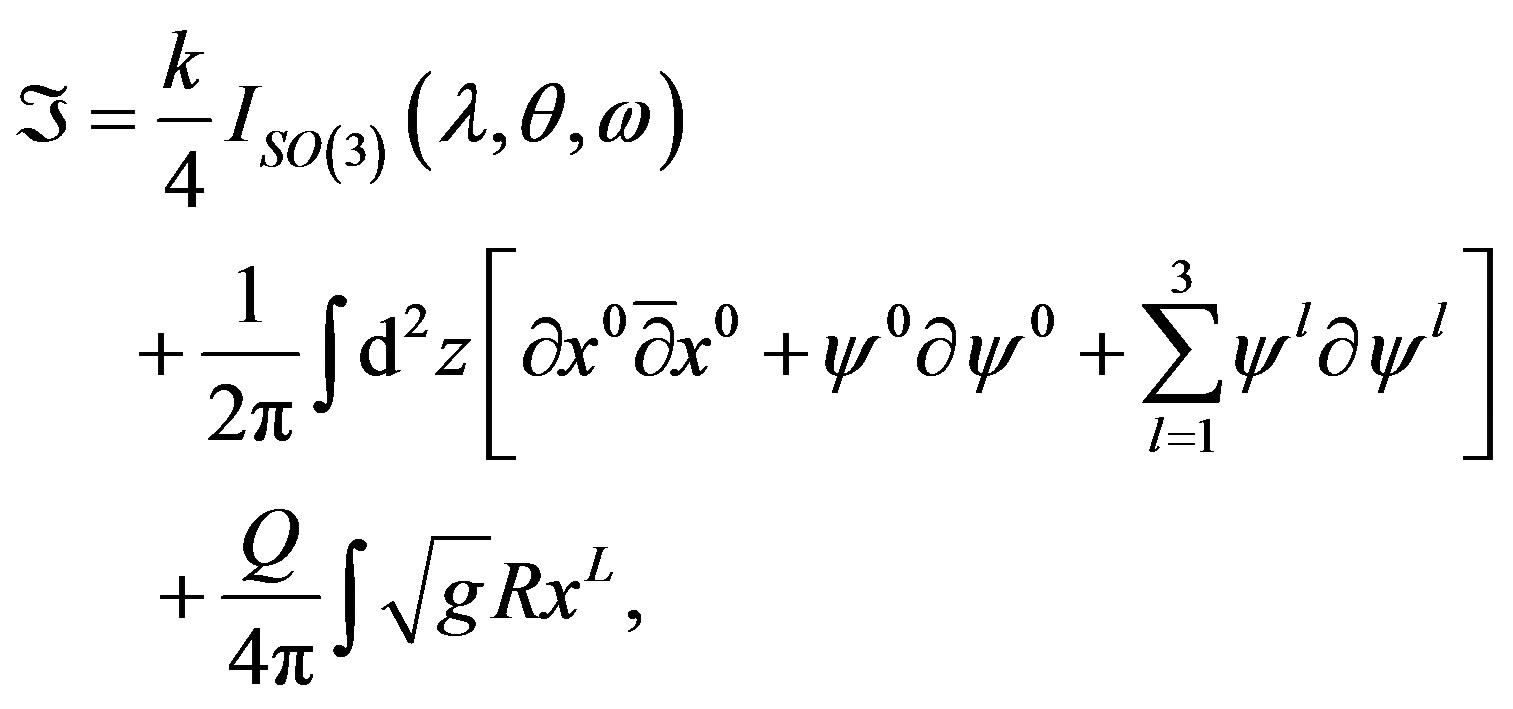 (30)
(30)
where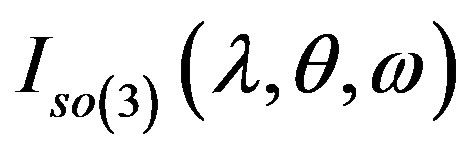 , in Euler angles of SU(2) = S3, is the curvature of the 2-dimensional manifold fitted (embedding inside) as string in the space-time, g, determines the metrics of the target and Q, is the dilaton charge with xL, is the coordinate of
, in Euler angles of SU(2) = S3, is the curvature of the 2-dimensional manifold fitted (embedding inside) as string in the space-time, g, determines the metrics of the target and Q, is the dilaton charge with xL, is the coordinate of . On the other hand, the action of a bosonic Lagrangian is given like (Table 2):
. On the other hand, the action of a bosonic Lagrangian is given like (Table 2):
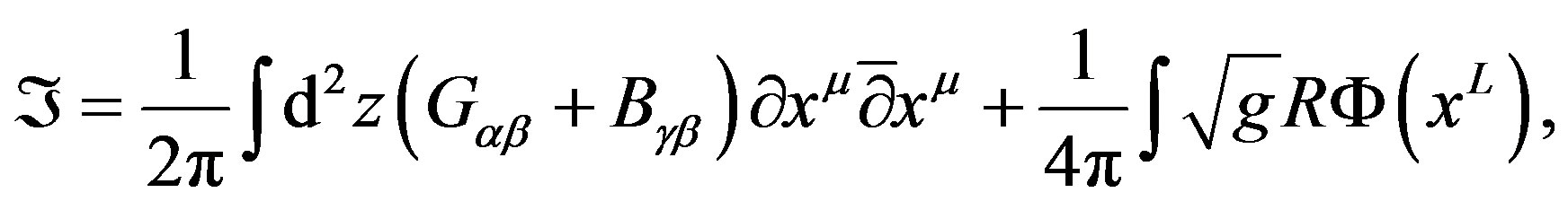 (31)
(31)
Comparing this action with the Equation (6) we obtain the fields of background radiation (since we want to obtain actions dilaton-gravity):
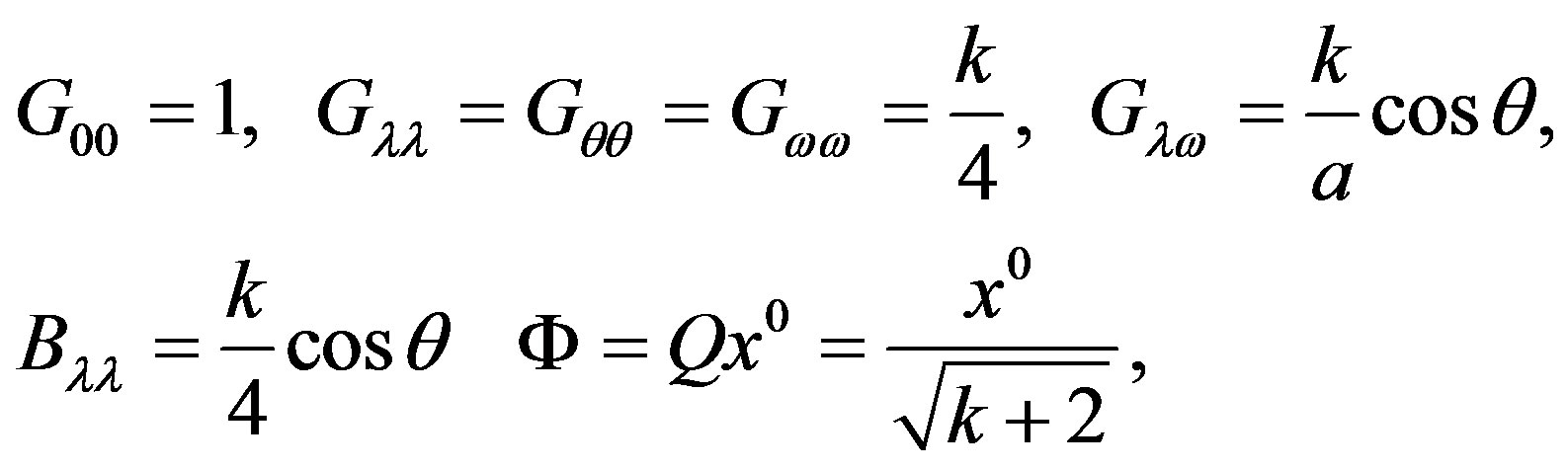 (32)
(32)
Def. 2.1. A dilaton is a hypothetical particle that appears for to do compact strings or quantum dimensions as the theory of Kaluza-Klein. Also is a particle of a scalar field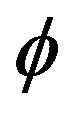 , that always accompanies to the gravity.
, that always accompanies to the gravity.
After introducing the complex fermions combination 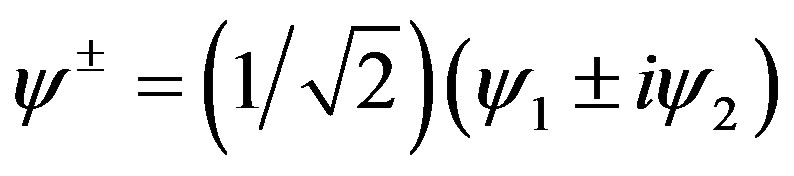 and the corresponding change of the affine bosonic currents J± = J1 ± iJ2, the supersym-metric affine currents read:
and the corresponding change of the affine bosonic currents J± = J1 ± iJ2, the supersym-metric affine currents read:
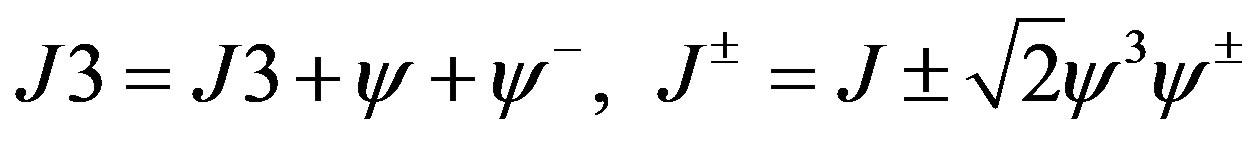 (33)
(33)
Let us redefine the indices in the fermion fields as: + → 1, − → 2, then J3 = J3 + ψ1ψ2. From the Lagrangian point of view, the component of the field of the magnetic field H, of the part 4-dimensional of the radiation background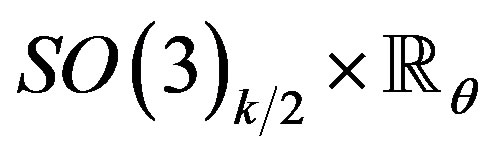 , it is given by the exact marginal operator
, it is given by the exact marginal operator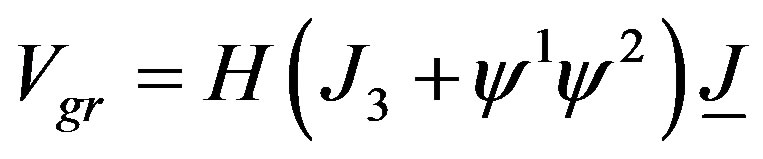 . En forma similar la correspondiente deformación marginal gravitacional viene dada por
. En forma similar la correspondiente deformación marginal gravitacional viene dada por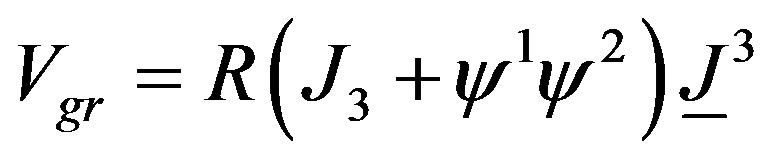 .
.
Similarly, when gravitational marginal deformations as in the operator Vgr = R(J3 + ψ1ψ2)J3, are included, where R, is the curvature parameter of the deformation, one can derive corresponding exact background of string theory via the Lagrangian calculations [16].
Here, following [17], we consider covariantly constant magnetic field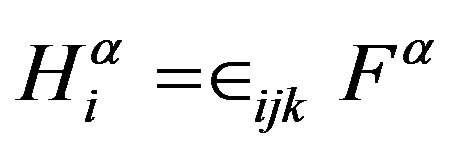 , and constant curvature
, and constant curvature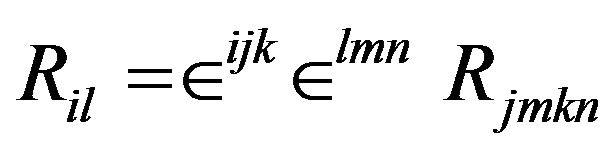 , in the 4-dimensional background as above of closed superstring theory. When this chromomagnetic field is in the μ = 3, direction the following deformation is proportional to
, in the 4-dimensional background as above of closed superstring theory. When this chromomagnetic field is in the μ = 3, direction the following deformation is proportional to 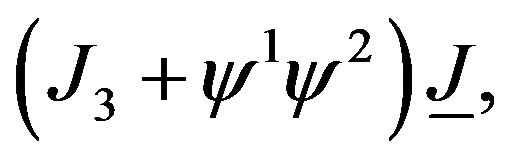 and the right moving current J is normalized as
and the right moving current J is normalized as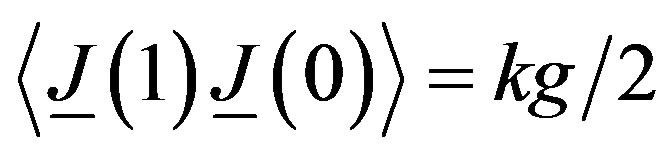 . Rewriting the currents in the Euler angles, i.e.
. Rewriting the currents in the Euler angles, i.e. 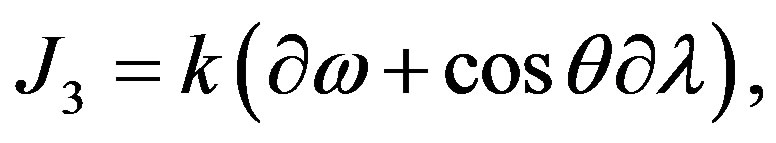
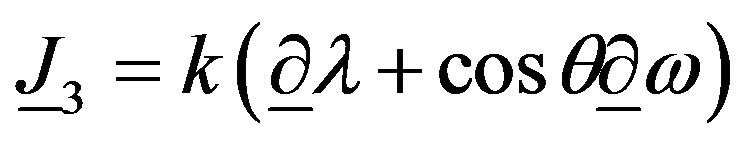 , we obtain for the perturbation of the (heterotic) action in the Equation (28), the following expression:
, we obtain for the perturbation of the (heterotic) action in the Equation (28), the following expression:
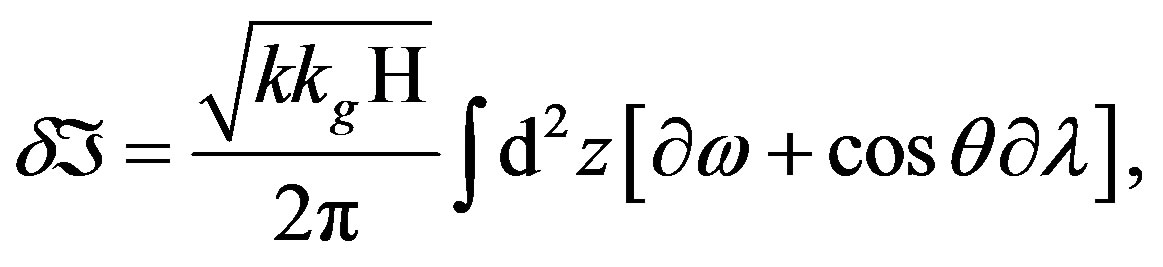 (34)
(34)
The new space with the action Á + dÁ, is conformally invariant. The background radiation corresponding to the perturbation of the Equation (10) is determined by fields of background radiation, that is to say, by gravitons Gαβ, through gauge fields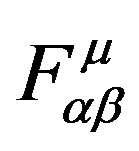 , (electromagnetism), a antisymmetrical field given for
, (electromagnetism), a antisymmetrical field given for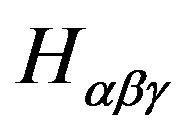 , and a dilaton Φ, which ones are the solutions of the equations of movement [14,15]:
, and a dilaton Φ, which ones are the solutions of the equations of movement [14,15]:
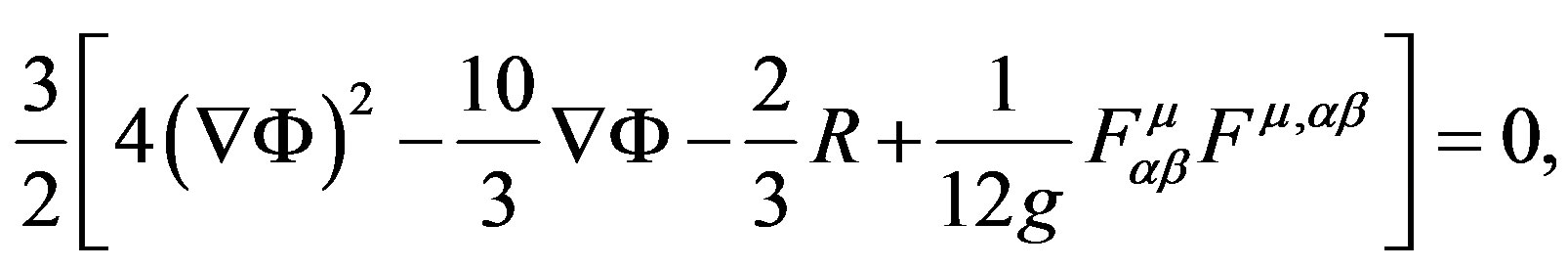 (35)
(35)
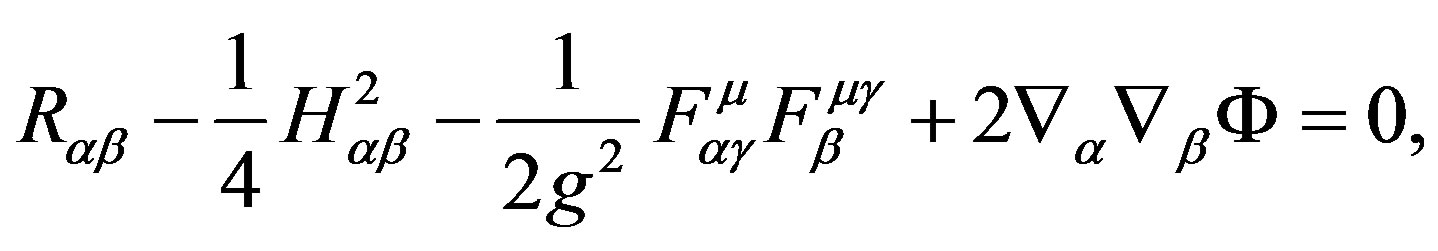 (36)
(36)
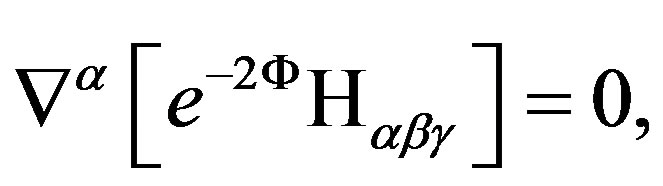 (37)
(37)
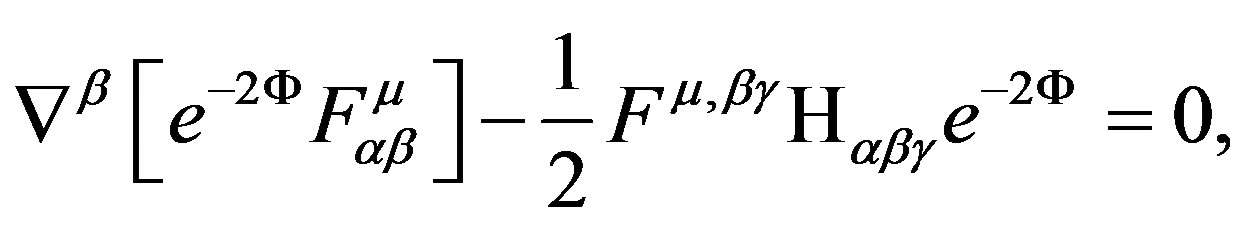 (38)
(38)
These are obtained of the changes of the following action 4-dimensional effective gauge (effective Lagrangian):
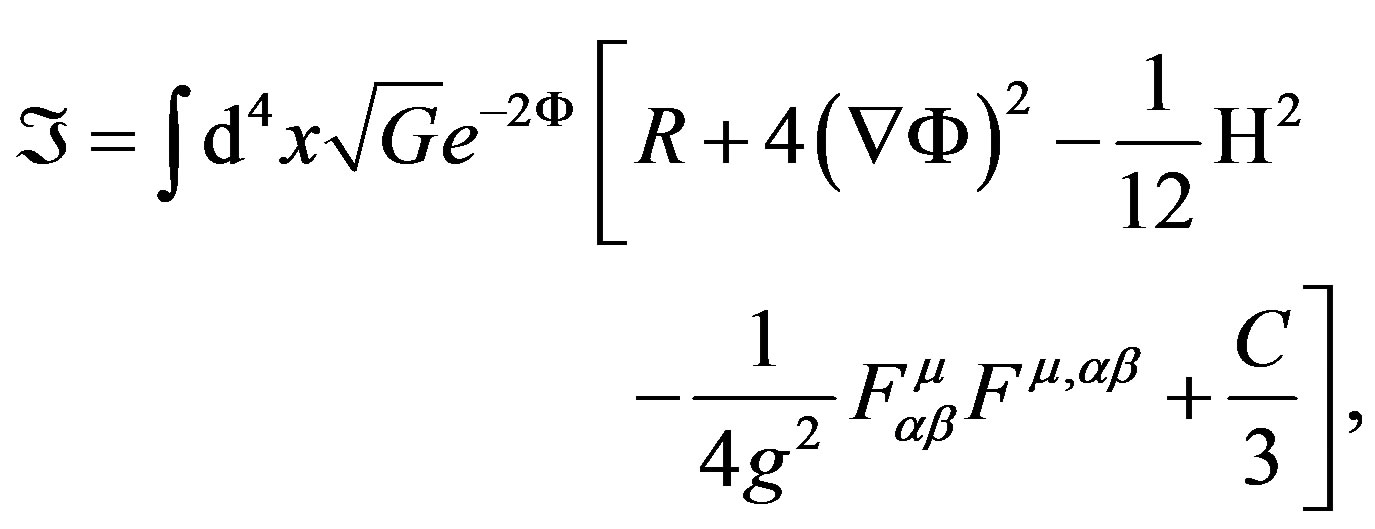 (39)
(39)
where C, is a constant of the Equation (11). Realizing some gauge considerations of the vector potentials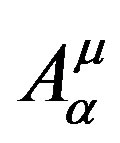 , and the normalization to g, and
, and the normalization to g, and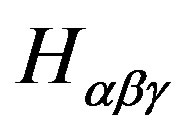 , we have that the background radiation, expiring with the distortions considered in the action of Equation (10) takes the form through their gravity tensor
, we have that the background radiation, expiring with the distortions considered in the action of Equation (10) takes the form through their gravity tensor 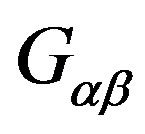
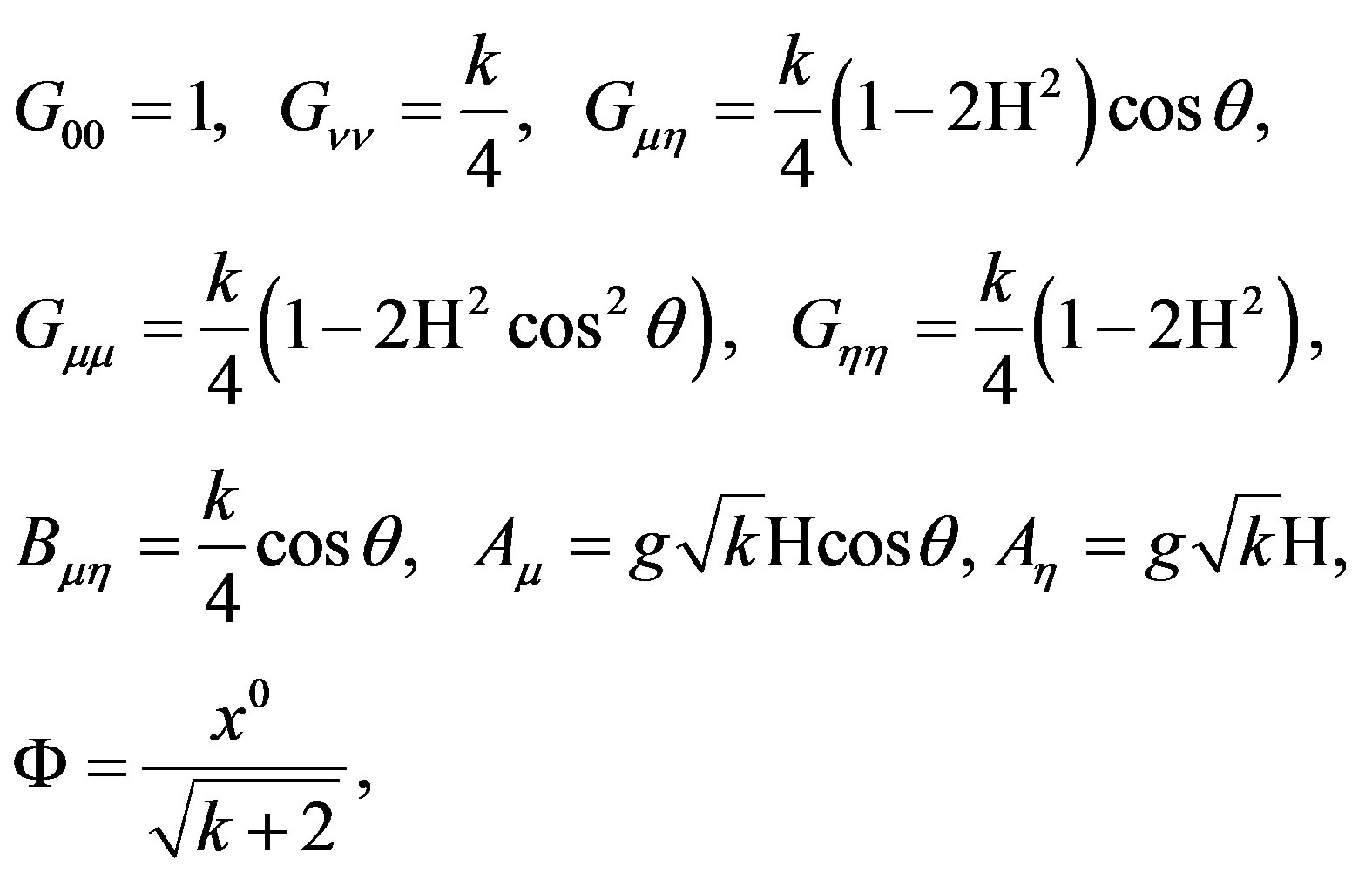 (40)
(40)
where H is the magnetic field as in (34). Similarly, when gravitational marginal deformations as in the vertex Vgr = R(J3 + ψ1ψ2)J3, are included, where R is the curvature parameter of the deformation, one can derive corresponding exact background of string theory via Lagrangian calculations, [17-19]. Again, the fields in this background which solve the effective field theory Equation (10), are [17]:
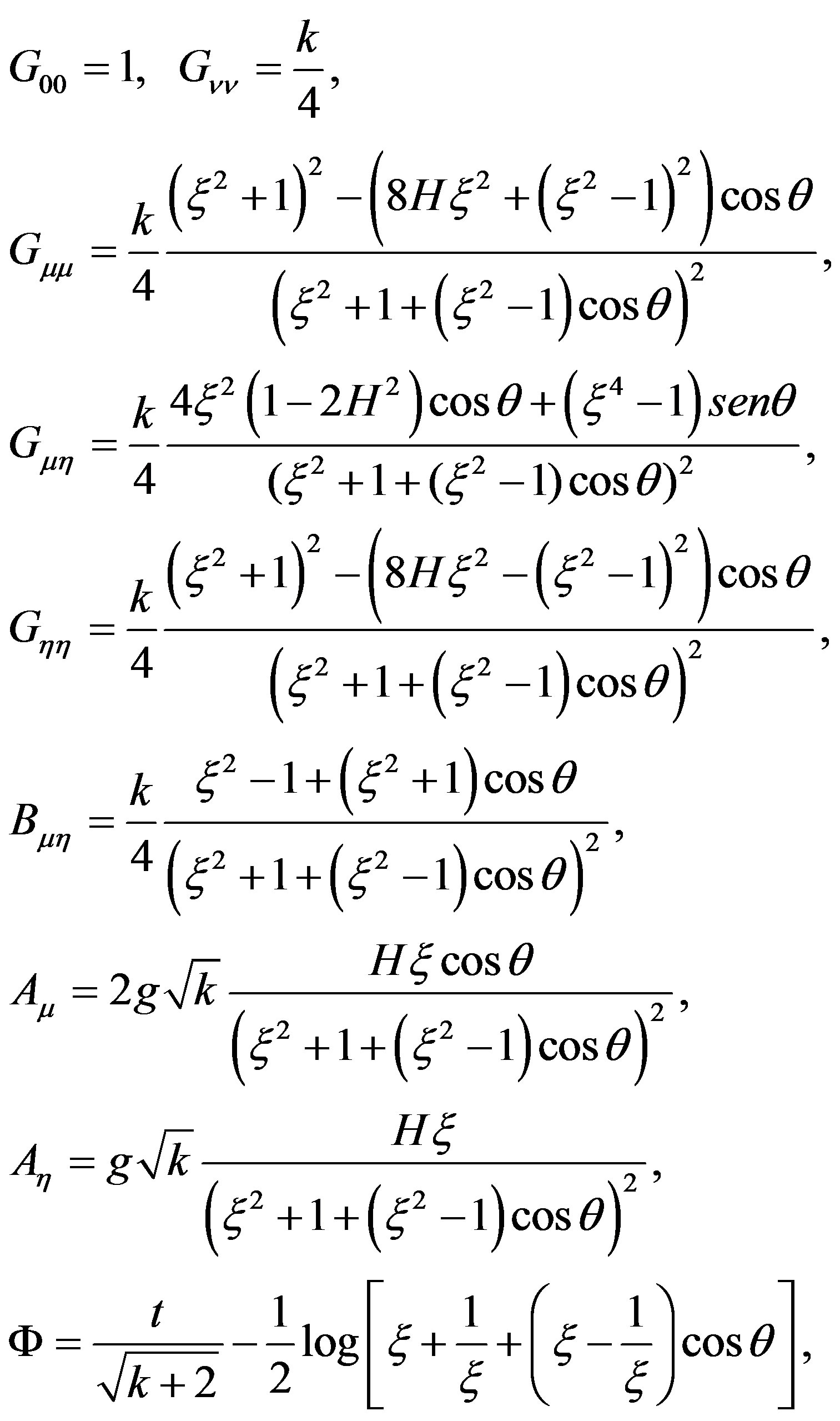 (41)
(41)
The dependence on ξ, shows the existence of gravitational backreaction which was absent in the purely magnetic deformed background (40) (to see Figure 2).
In the following Table 2 we do an inventory of the actions of the used Lagrangians.
8. Electromagnetic Detectors of Curvature: Design of s Cosmic Sensor of Curvature with Penrose Censor
Due there are no instruments for detection and direct measurement of the electromagnetic back-reaction, we can propose the design of an indirect detector based on the concept of cosmic censoring to detect curvature in regions near to a singularity of the space-time.
Nevertheless we can use certain studies of the models of the space of de Sitter, to determine through Hilbert inequality and based on certain bound of cosmic censoring constructed by Penrose [20], the possible integral expression of the total Hamiltonian of electromagnetic energy, establishing a condition of domineering energy [11], where there is curvature (that is to say, if the energy is given by this cosmic censor, there is curvature measured like energy that makes the censoring appear).
The latter condition is in a certain sense similar in the mathematical context to the property of obstruction to the integrability of the field equations but in a practical form (similar physicist) who can serve to us to design a detector and curvature meter at quantum level, using theoretical hypotheses [13].
To realise curvature detection it is necessary to be sure, that the above mentioned property or observable it comes from an intrinsic property of the gravitational field in the space-time, which create the geometric stage of the space.
But the space is influenced by this field on every particle that composes it, that is to say, an intersection between the cone of light of every particle and the infinity null exists of the gravitational field that creates the distortion of the space [21].
In these intersections exist the detectable and measureable part that can be measured through microscopic electromagnetic fields and on the other hand that has the gravitational nature that provokes the curvature, generating enough energy to be bounded by the cosmic censor of Penrose [22].
Relative studies to curvature from quantum distortions (like established in the previous section), confirm the hypotheses of consider the Lagrangian to be able to measure curvature from a quantum level, the above mentioned with the geometric hypotheses on a cinematic model of the predefined space for the geometry for the case of curvature.
We consider the kinematic models given by the spaces that are asymptotically de Sitter and anti-de Sitter [23,24].
Proposition 8.1. Considerating the Cosmic Censorship hypothesis given by Penrose [20], we have that the area A, of a singularity (black hole visualized as a spherically symmetric space) is proportionally minor that the quasilocal mass around of singularity given for 16πM2 [11]. Then in the events of the space like one asymptotically de Sitter space its have:
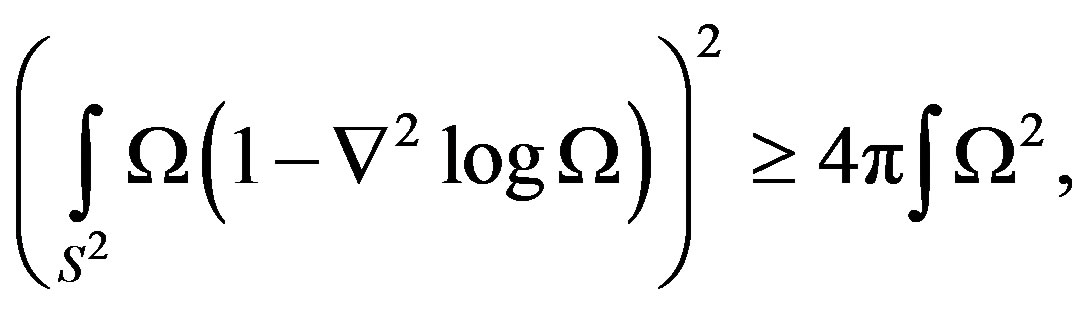 (42)
(42)
which represents the curvature measured like energy doing to appear the censure given in the second member of the inequality and that it goes out to re-shine for the Lagrangian action of gravitational field moving away or approaching the singularity (asymptotically de Sitter and anti-de Sitter spaces).
Proof. [22,25].
The minimum energy (second member of the In-Equation (42)) must be obtained directly in a geometrical condition given by an invariant of curvature. From the exponential of empty expect value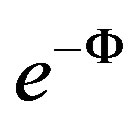 , of the effect action given by the Equation (39), we obtain the coupling constant g, and as by the generalized Gauss-Bonnet theorem we have [7,26].
, of the effect action given by the Equation (39), we obtain the coupling constant g, and as by the generalized Gauss-Bonnet theorem we have [7,26].
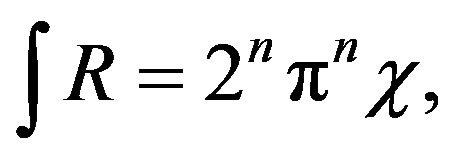 (43)
(43)
then n = 2/2 = 1, since dim M = 2. To compact worldsheets where the Euler characteristic c = 2 - 2g. Pero (43) is the curvature invariant given to the spherical map M ® S2.
For the case of M, see it like a space 4-dimensional, it is necessary to consider the spherical map ¶M ® S3, in this case the electromagnetic fields can be used like gauges remembering that SU(2) @ S3.
Then the cohomological classes of the Cartan forms w1, and w2 are annulled (H1(SU(2), R) = 0, that is the case of the integrals like discussed in the page foot 1,
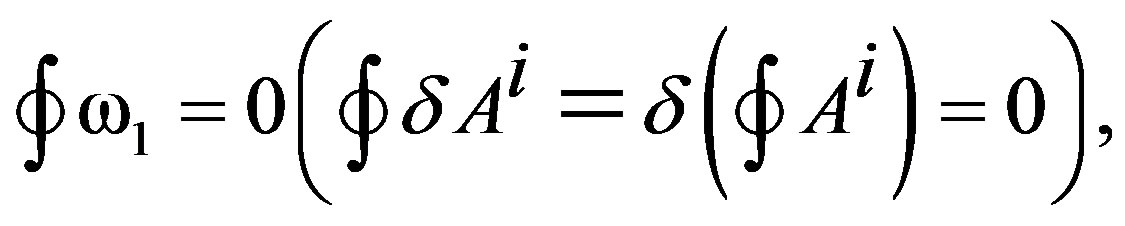
Also it does it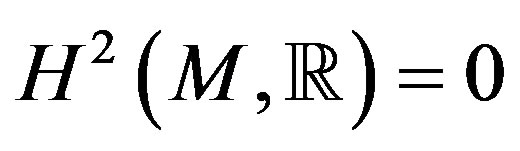 , to
, to 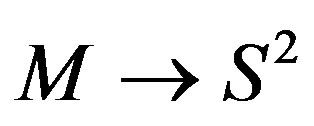 [5], that is to say,
[5], that is to say,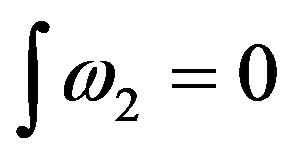 ), remaining only the cohomological group generated by
), remaining only the cohomological group generated by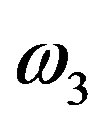 , to know,
, to know, 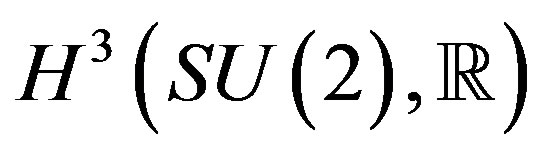 [7, 27]. Then the value of the integral of this group of cohomology is [7,26]:
[7, 27]. Then the value of the integral of this group of cohomology is [7,26]:
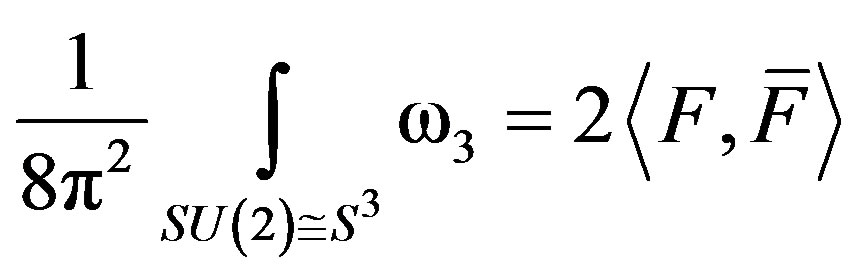 (44)
(44)
But by the background radiation of the Minkowski space M, where the energy of the matter is, it is had that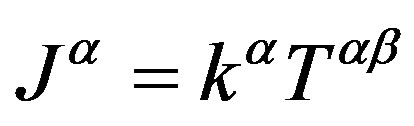 , where
, where 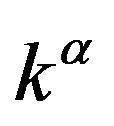 is the density of background radiation which establishes for the curved part of the space (that in this case has spherical symmetry) together with the energy and matter tensor that do not
is the density of background radiation which establishes for the curved part of the space (that in this case has spherical symmetry) together with the energy and matter tensor that do not
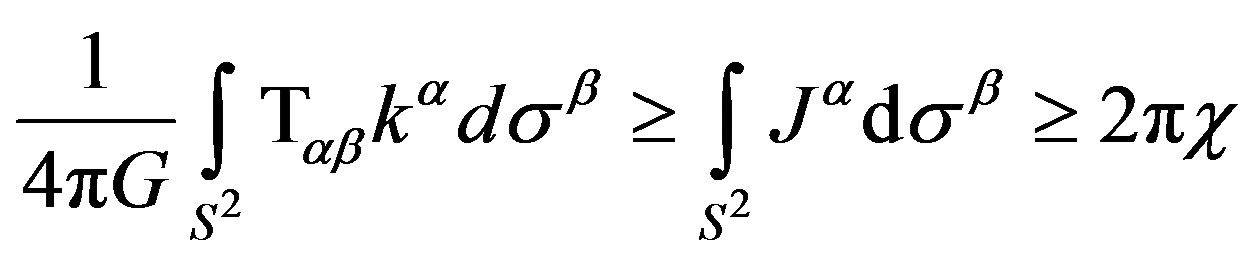 (45)
(45)
But conserved current in whole space is (this include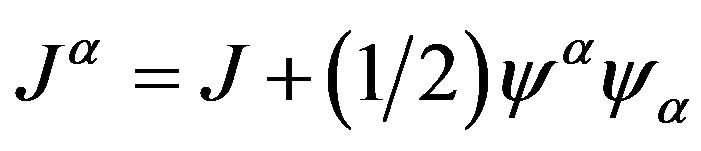 , in our analysis of the section 7),
, in our analysis of the section 7),
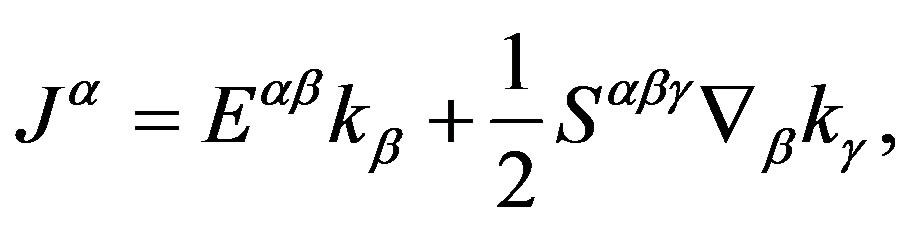 (46)
(46)
Then the energy inside in the sphere satisfies [7,28]
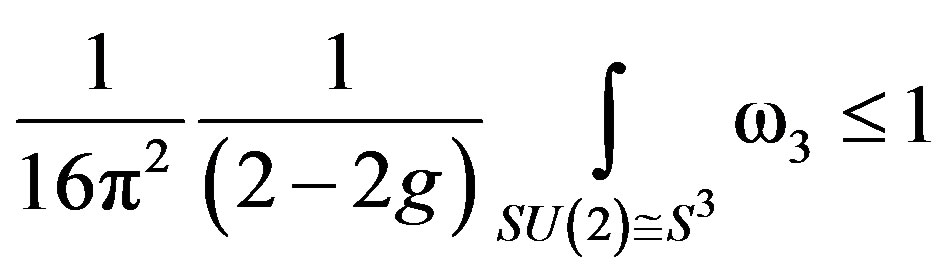 (47)
(47)
since the electromagnetic energy with respect to the energy of background radiation can fulfill that
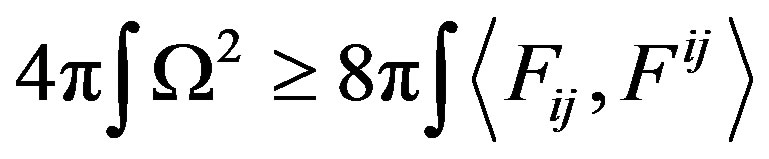 (48)
(48)
Then from (44), (46) y (47), the condition is had
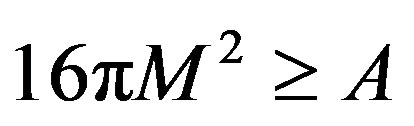 (49)
(49)
which is (42) for a singularity detected of spherical type [25,28] (see Figures 4 and 5).
A table given for manifestations of mass-energy “detected” by this indirect method showing curvature existence [29] is the Table 3.
 (a)
(a)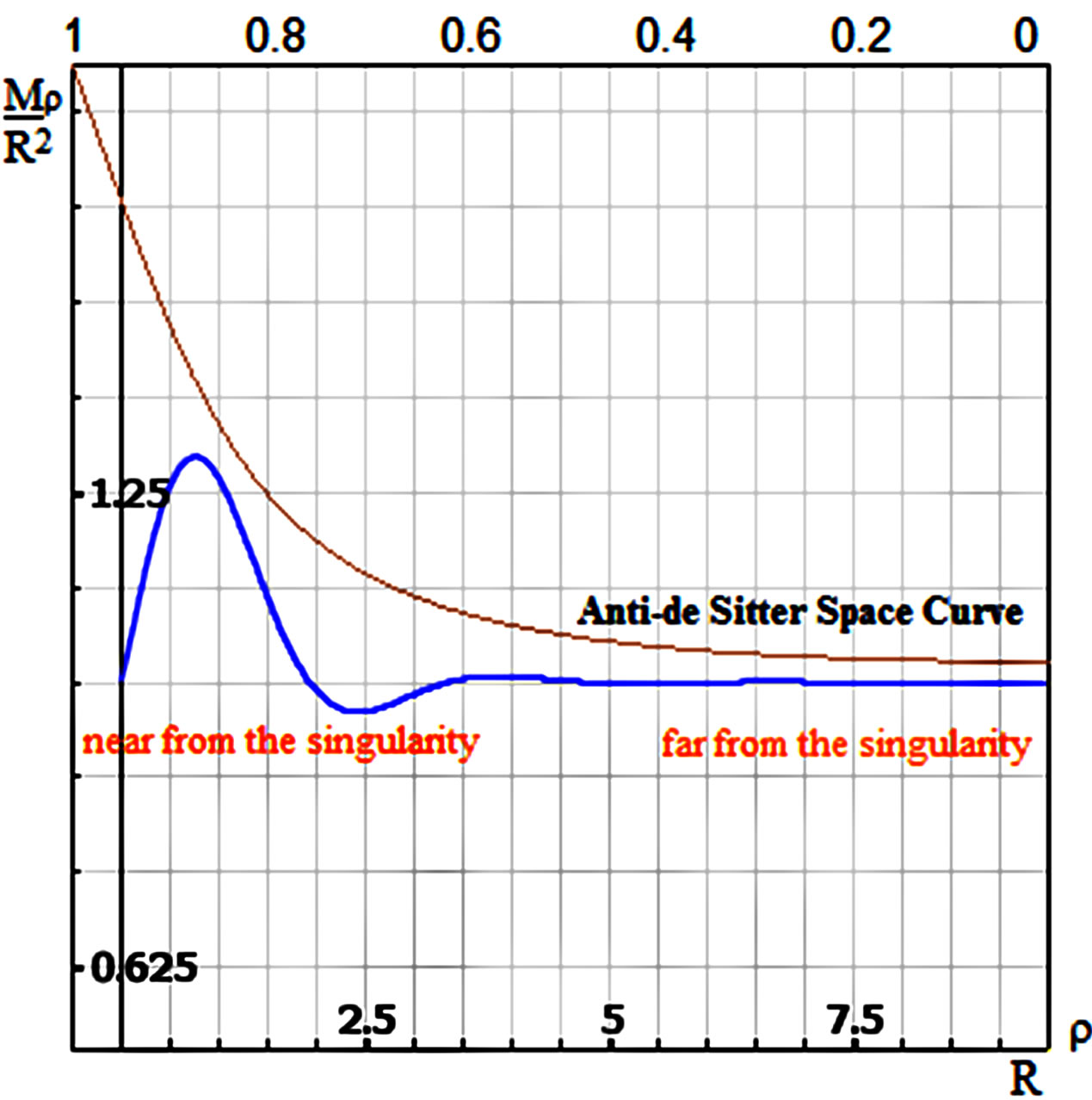 (b)
(b)
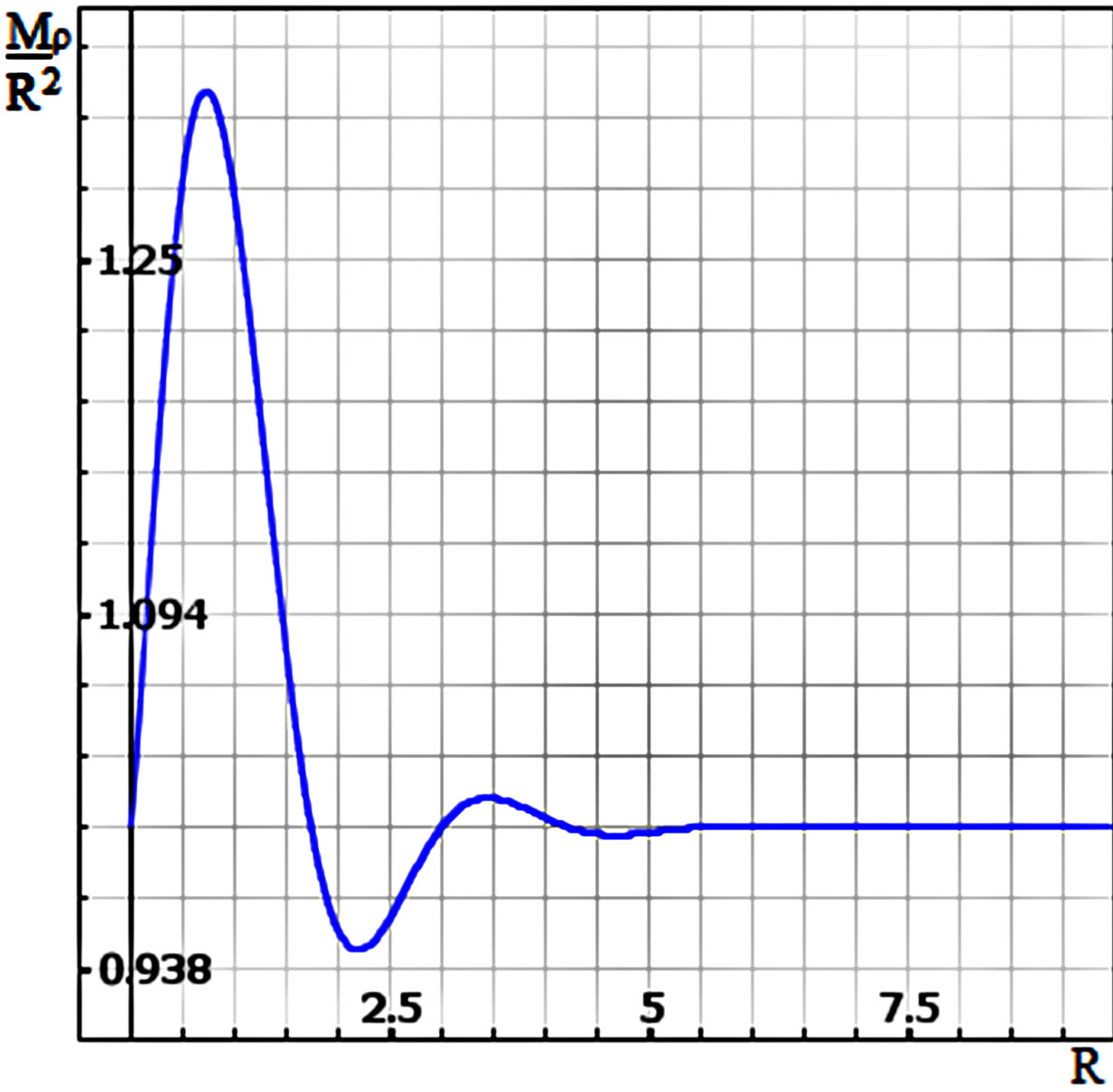
Figure 4. (a) The corresponding wave of “energy-density” in the cosmic sensor of detection of curvature. The waves obtained by the effect of radiation reaction, given by conjecture [13]. (b) The same way as it is moving away from the gravitational field (interaction with the gravitons), these stop producing detectable energy for our cosmic sensor, tending to a flat space in the infinite nullity. This tendency can be observed like the similar hyperbolic of a space of Minkowski or Anti-de Sitter space [24]. In this analysis, cylindrical waves [29], of the form are used Mr(R)/R2 = 1 + exp(-R)(Jn, z(1 - lR, R)), " lÎ(0, 1).
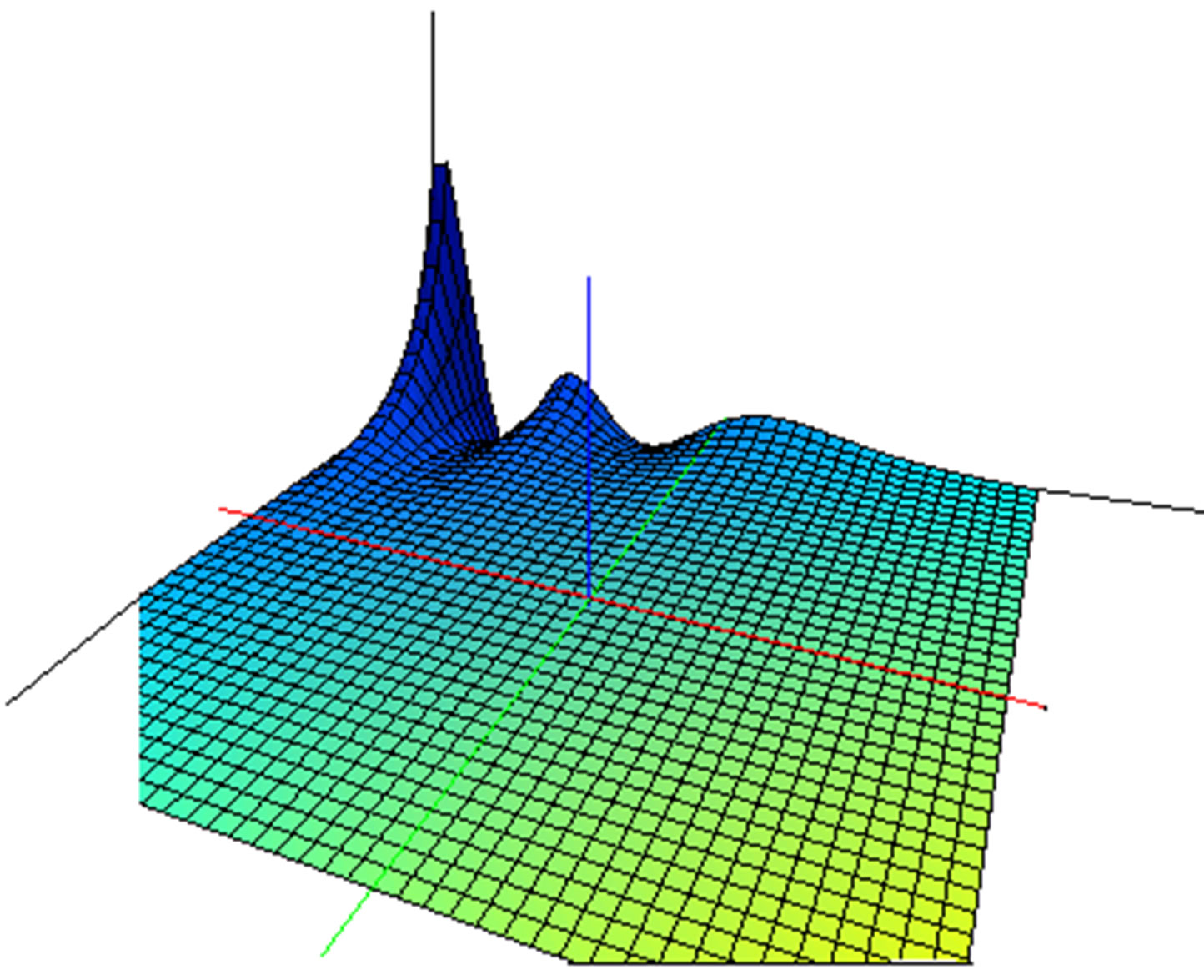
Figure 5. Surface of waves of “energy-density” in the quasilocal mass region of the space-time. This surface include the waves given in the Figure 4.
9. Applications and Technological Development
The equivalence class of the potentials Ai, can be re-interpreted precisely as a connection (operator of form) on a trivial bundle of lines and admitting bundles of not trivial lines with form operator provided with arbitrary fields F (like the curvature of this connection).
The Aharonov-Bohm effect [5], it provides of a physical justification of this formulation. Precisely the resultant physical theory and their generalizations are known like the gauge theory [30].
The following Table 4, establishes the correspondence of operators of form provided with arbitrary fields of Maxwell under the action of the corresponding Lagrangian and their corresponding curvature tensor [31]:
Certain simulations have been realized considering certain restrictive conditions to models of the space-time (to see Figure 6). In particular there have been considered to be models with Lorentzian metrics of negative curvature:
Has been innovated into the design and making of several electromagnetic devices of measurement and detection of curvature (to see Figures 7 and 8), which use signals of light to measure the curvature with the information of the angles of deviation of the incidental signals of light in the surface of the object or body. In case of curvature detection is designed a sensor of curvature based on an integral operator on Gaussian curvature. The patent of these devices is in administrative step.
There are many technological applications that cans be realised by the concept of gravity quantum through their observable that is quantum curvature. For example in nanostructures, we can create through geometrical potentials and light waves the Curvature-induced geometric potential in strain-driven nanostructures [32], and evaluate their curvature in this level [32].
The use of electromagnetic fields to measure observable of other fields like the curvature that is an observable geometric one of the gravitational field in the spacetime they suggest the possibility of a unified theory in a curved similar sense of their vector bundle. The equation 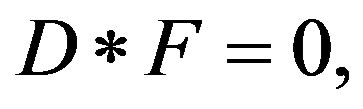 (given in the Equation (20)) is not quite different of the Equation (12), simply is a particular case of this last equation to the case of the actions of a electromagnetic field determined to the 2-forms F, defined in a SU(n)-vector bundle.
(given in the Equation (20)) is not quite different of the Equation (12), simply is a particular case of this last equation to the case of the actions of a electromagnetic field determined to the 2-forms F, defined in a SU(n)-vector bundle.
This way there are obtained fundamental 2-forms of curvature FD, that are integrable in the same sense as the integrals of line given by the Hermitian forms for the Maxwell tensor of the Lagrangian, namely:
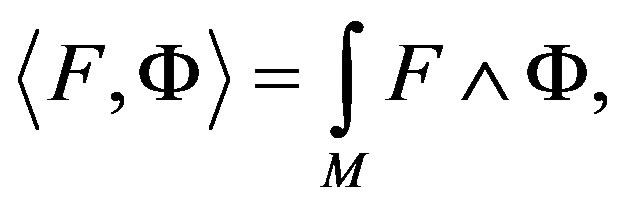 (50)
(50)
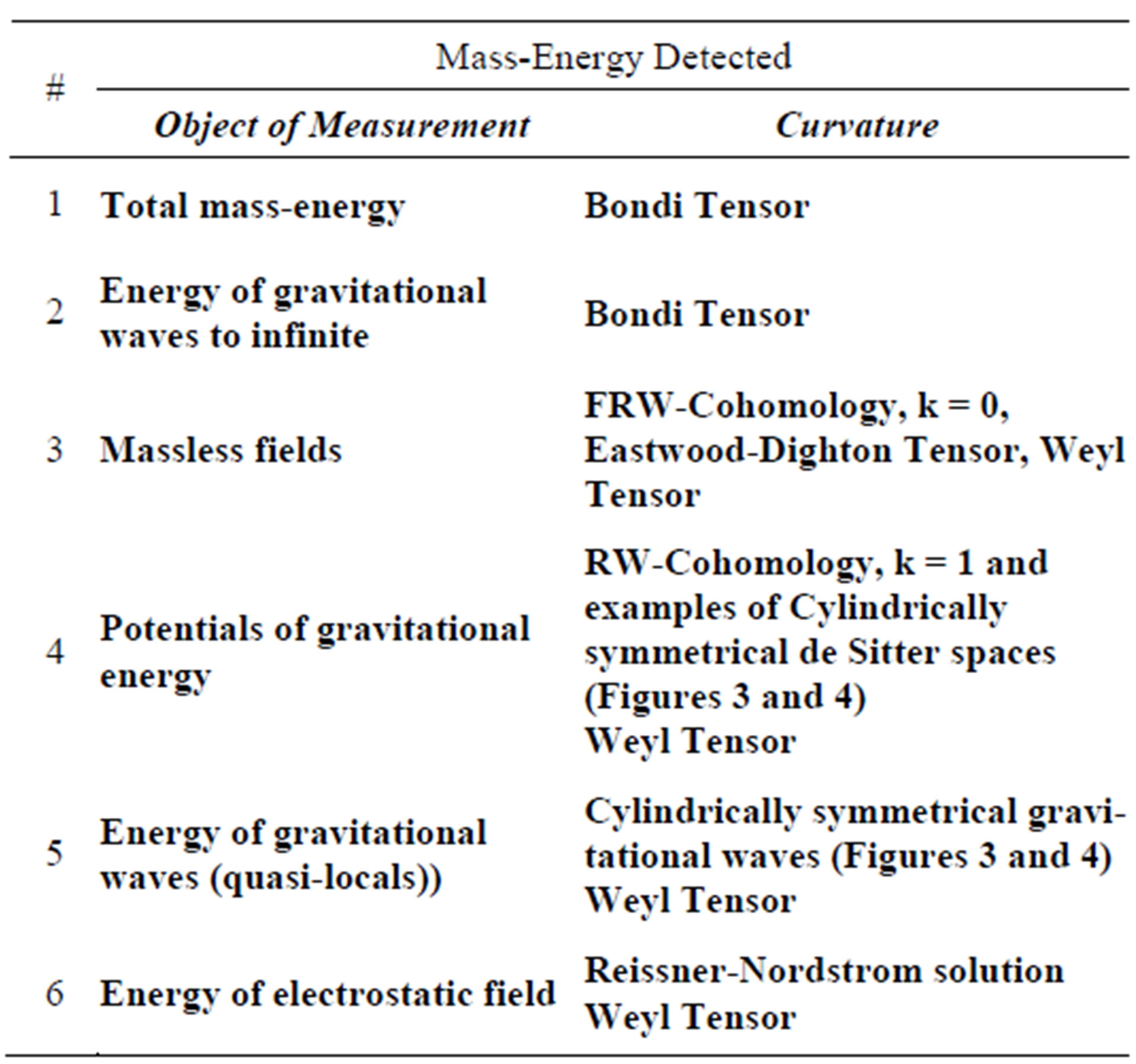
Table 3. Manifestations of mass-energy detected through the method of the cosmic censor of Penrose and their corresponding curvature in a asymptotically flat space—time [23].
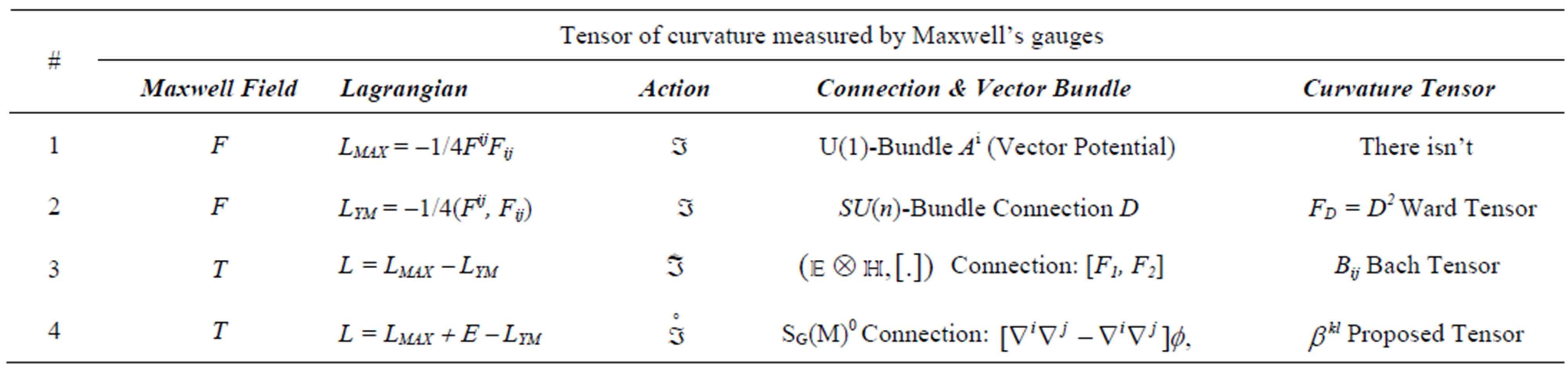
Table 4. [31]. Different tensor of curvature measured by Maxwell’s gauges (vector bundle with shape operator). In the second, third and the fourth lines there is curvature, which could be expressed by Maxwell's fields, through their integral of action and shape operator under the Hamiltonian regime corresponding of the Lagrangian. In the third and the fourth lines we have that the electromagnetic energy tensor is joined to Bach tensor of curvature as in the unified field theory conformably invariant proposed by Merkulov [4]. In the fourth line it is obtained under the application of the scolium. 5.1., a quantized version of the Bach tensor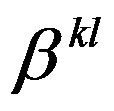 .
.
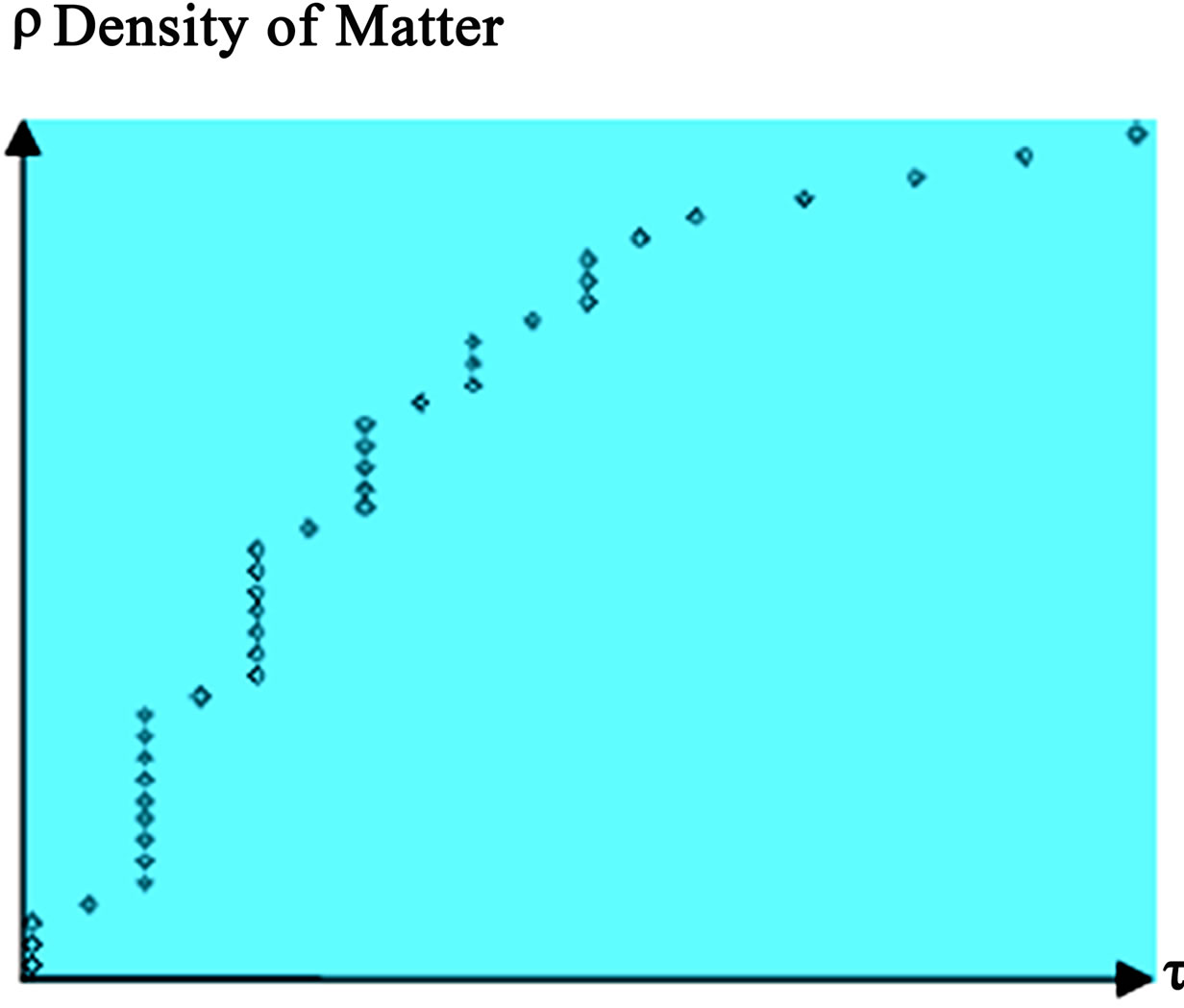
Figure 6. Variable behavior of the density of matter r, in a space-time region with Hubble expansion given for h = 4.71 ´ 10–28 [2,4], considering angles of deviation of the light under F = constant, in points of the space-time to demonstrate the possibility of measuring curvature with electromagnetism [2,3]. The prospective of movement in the elected geodesic determine though the Lagrangian of . The obtained
. The obtained
spectra has curve similar to that of the field G, in Einstein field equations for the case of a space of negative curvature in the 4-dimensional model of the space-time isotropous in three dimensions proposed to the Ricci tensor [3].

Figure 7. Determination of curvature of a sphere using hyperbolic light waves [3]. There are considered to be two directions and main curvatures measure themselves in these directions using a device of measurement of the curvature through light waves, presented in ASME/USA in 2009 [1,5].
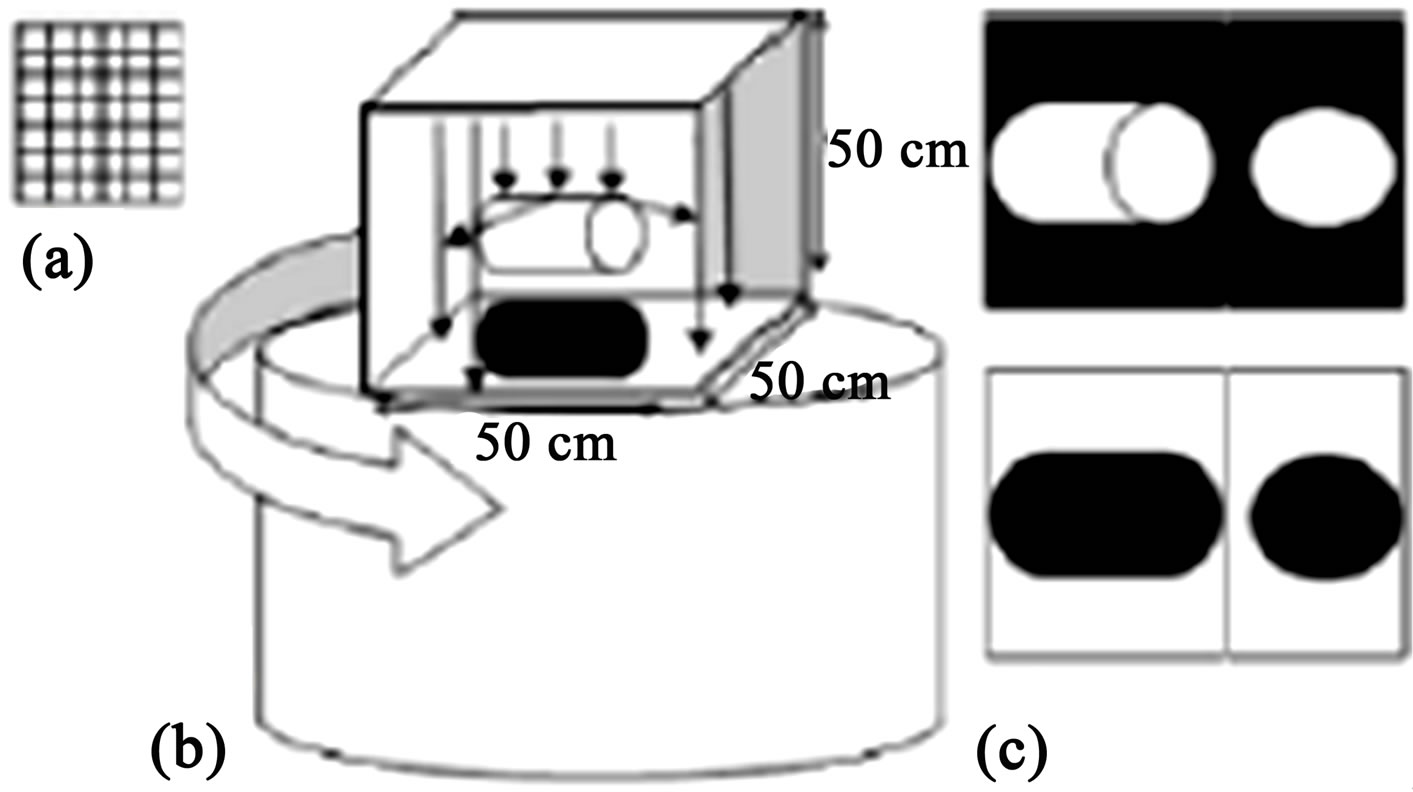
Figure 8. Device of measurement of curvature that uses light waves to measure curvature of 2-dimensional and 3- dimensional objects: (a) Photosensitive grill with complexes phases. The grills are two, which receive the reflexes of the incidental waves of light in the object or body to measure their curvature; (b) Device of rotation and control of wave emission under a constant electromagnetic field; (c) Shades of main directions of emission only for control of position of the body. These get connected to a computer with a program that it transforms the sheen intensities in angles though the phases of the photosensitive grills [1].
on embeddings of 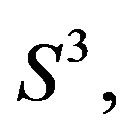 in M. Using the Stokes theorem it is possible to demonstrate that the contours established by the minimal trajectories in Hamiltonian regime on the sphere given for S2, and under the action of Maxwell field to displace particles of M, along the minimal circles, there is obtained a tensor of curvature similar to the tensor of Riemann in the electromagnetic context and their symmetrical part, that is to say, a useful version of the Ricci tensor to calculate Gaussian curvature (to see Figures 7 and 8). The action of Maxwell fields displacing particles of M, along deformable circles is similar to the action continued by the field of displacement defined in mechanics to determine curvature using the deformable contours of field [5].
in M. Using the Stokes theorem it is possible to demonstrate that the contours established by the minimal trajectories in Hamiltonian regime on the sphere given for S2, and under the action of Maxwell field to displace particles of M, along the minimal circles, there is obtained a tensor of curvature similar to the tensor of Riemann in the electromagnetic context and their symmetrical part, that is to say, a useful version of the Ricci tensor to calculate Gaussian curvature (to see Figures 7 and 8). The action of Maxwell fields displacing particles of M, along deformable circles is similar to the action continued by the field of displacement defined in mechanics to determine curvature using the deformable contours of field [5].
A possible progress of this approach of proposed curvature, through bundle of light it is the securing of a field of displacement of the curled (curved) similar one of the similar operator D, according to Maxwell tensor ones considering the similar structure of the space-time. This is precisely what allows to glimpse the Eastwood-Dighton tensor Eijk, in the securing of a model of conformal curvature for Einstein equations in a spinor bundle [12].
Defining the concept of conformal gravity, there is an approach of the tensor of Riemann obtained through the calculation of the Ricci tensor using a conformal factor determined by the anti-symmetrical component of Rij (Weyl tensor Wij), to know
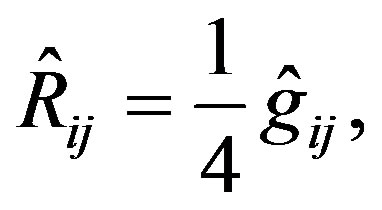 (51)
(51)
where 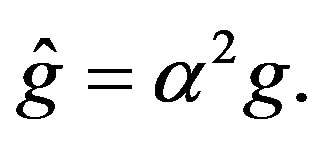 This is other version of the Ricci tensor, considering the space-time of Einstein with solutions to the equations
This is other version of the Ricci tensor, considering the space-time of Einstein with solutions to the equations 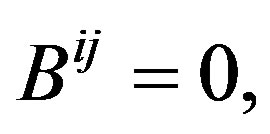
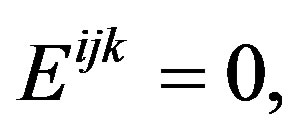 [4], which is comparable to the use of a bundle of lines for any quadric of a Lorentzian manifold. This opens the possibilities mentioned previously of a shape operator defines through rays of light that give shape to the curved image of the space-time, similar to a celestial vault.
[4], which is comparable to the use of a bundle of lines for any quadric of a Lorentzian manifold. This opens the possibilities mentioned previously of a shape operator defines through rays of light that give shape to the curved image of the space-time, similar to a celestial vault.
9.1. Applications to the Coherency, Background and Expansion of the Space-Time
The temperature of the Cosmic Microwave Background (CMB) is nearly isotropic. That is, when you look at different patches of the CMB, their temperatures are the same to within 1 part in 10,000. This implies that when the universe became transparent (about 300,000 years after the Big Bang), it was nearly homogeneous [33]. The homogeneity, or smoothness, of the universe is referred to by cosmologists as the horizon problem (Figures 9 and 10).
9.2. Electrodynamical Configuration
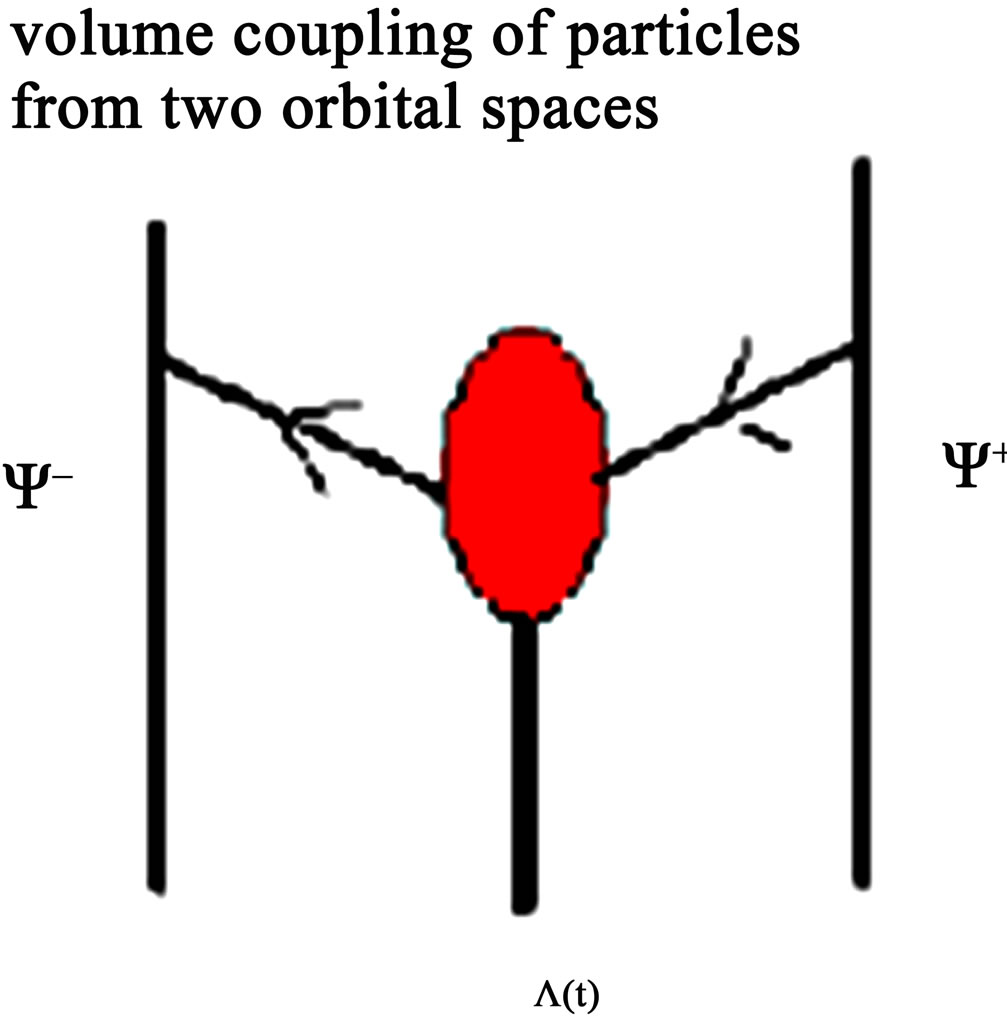
Using the cohomological classes of the integrals in electrodynamics calculated by Lagrangianos module the groups calibrates, U(1), U(2), SO(2), SU(2), SU(2, 2), etc we can establish the following spaces of electrodynamic configuration and their constituent elements (see Table 5). For other side the the Table 5, it serves to us to understand the decomposition of an electrodynamic space in their orbits considering their manifold structure (to see Figure 11). Likewise, considering the backreaction in the space—time, the orbital spaces become more clear (Figure 11).
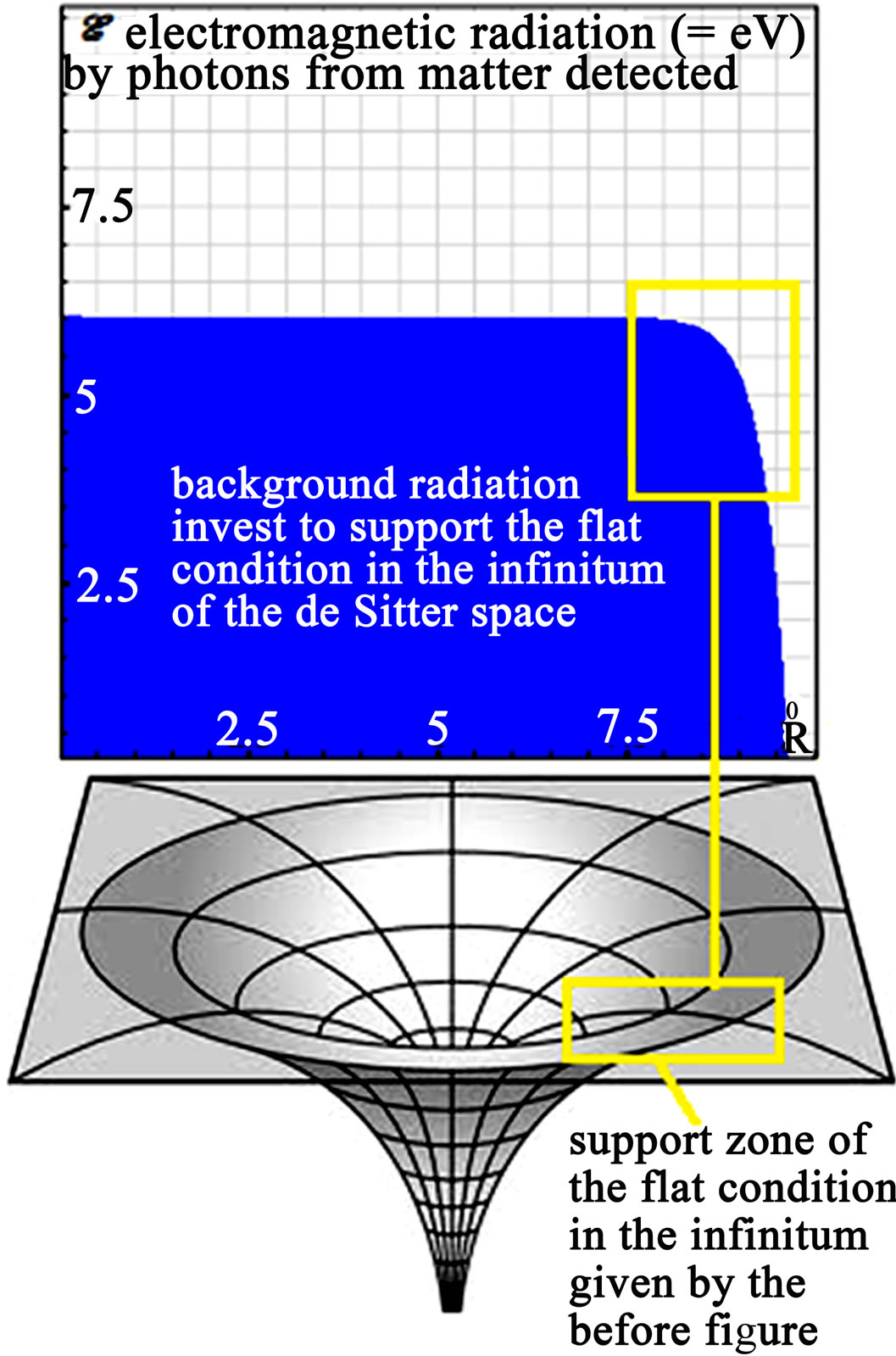
Figure 9. A theoretical study related to the propagation of photons in quantum gravity, shows that the region of spacetime of the mechanical well of a singularity is supported by an energy that decreases asymptotically in the infinite. This hypothetical energy we can construct it with the expression of a Lagrangian like the given in (Table 2) with cylindrical gravitational wave by F = +(1/10000(exp(–4x)Jn,z(3x,1) + exp(–4x)Yn,z(2x,1))) (wave model for energy of gravitational waves (see last line of the table 3)) [13,23].
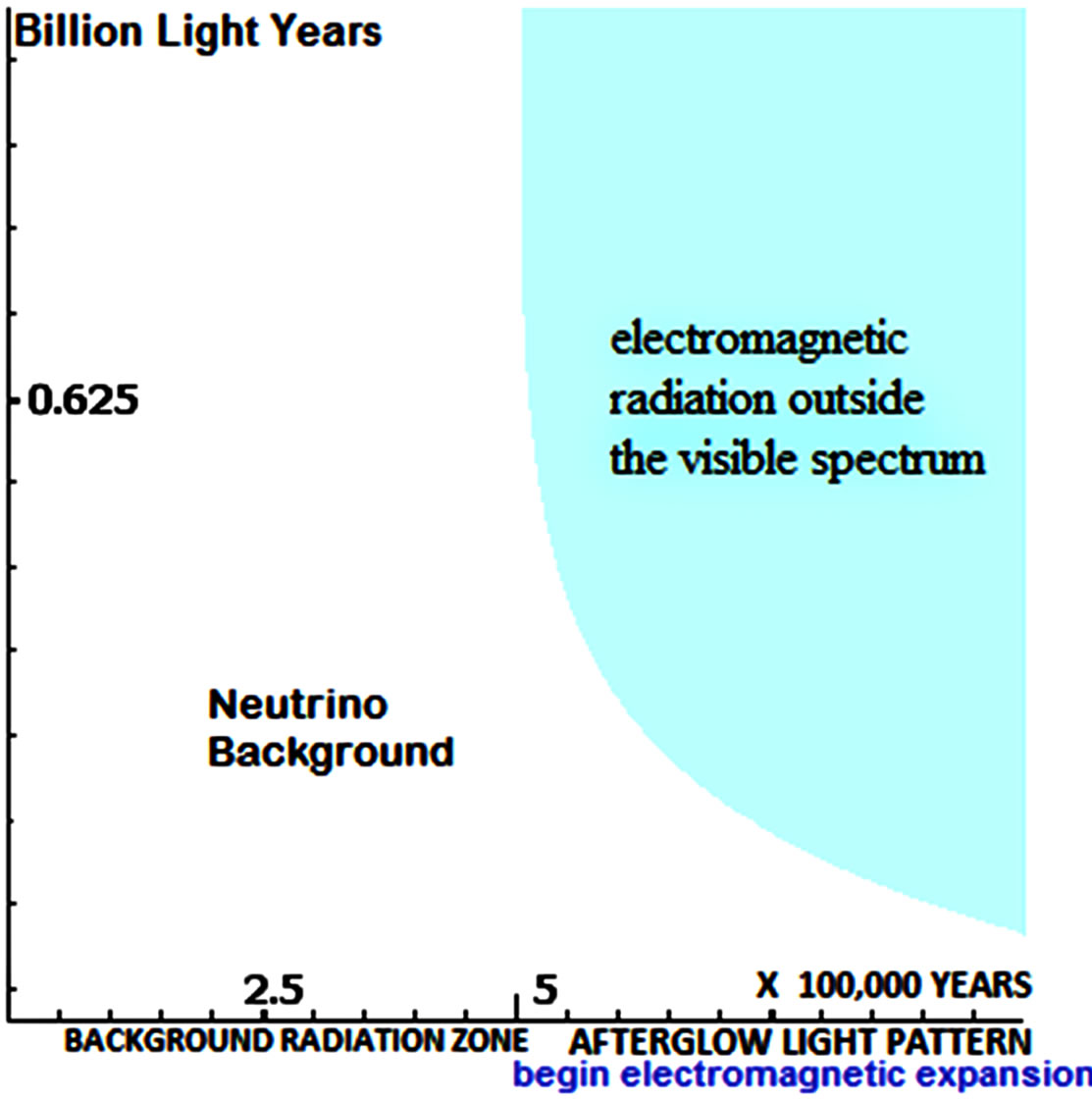
Figure 10. The behavior of the electromagnetic inflation in early step of the universe. The electromagnetic radiation was represented in their totality by the cosmic microwave background and neutrino background. In this model is have used the pure dilaton F = 1/3 – ((1/2)log(z + 1/z + (z – 1/z))) (nether back-reaction) [14].

Table 5. Electromagnetic worldsheets.
 (a)
(a)
Figure 11. The surface w = (2/3) tanh(x/y) = Orbit PM+ Å Orbit PM+. From the quantum level this explains the process of particle coupling (see (a) and (b)). Superposing the two images of light space we obtain the surface of flat hyperbolic space with singularity. Hyperbolic waves in the proof of change of orientation due existence of singularity are given in [13].
9.3. Factible Electro-Gravitational Ultra-Sensor
The Theoretical devices to measure gravity it haves designed from the first serious affirmations on gravitation given by Galileo and Newton. Nevertheless, with the step of the time and due to born of new theories of the universe based in studies inside the field theory from the theory of the relativity, up to the theory M, they have marked the need to design using gauge theories, instruments that could measure at least in indirect form or by means of sophisticated methods of metrology based on dimensional relations gauge field that are constructed by Gaussians units or of another type observables of field as the curvature [34].
An example of such devices there are the electrogravitational devices that try to use electromagnetic waves and electromagnetic field interactions to measure gravity using the concept of background radiation [35] and the traces of particles obtained in the laboratories of the atomic accelerators as the given in the CERN (Organisation européenne pour la recherche nucléaire), measuring the distortion of these waves based on the traces of the particles left in the fog cameras of the accelerators. Other better attempts have been realized by the CMB (Cosmic Microwave Back-ground), radiation spectrums being obtained in the direct measurements by the satellites in the space, for example SMAP.
One important idea inside the study of the microscopic space-time is the group representations of SU(2), where one of which considering the super-symmetry is S3 (sphere of dimension 3) [5,15]. In her the topological invariant of their 2-form ω3, given in the Equation (45) and whose cohomology in not null (see section 8) it shows clearly that the gravity presence can be warned at least on the surface of this sphere, which can be considered to be a mini-twistor in the presence of gravity considering a ambitwistor space of couples (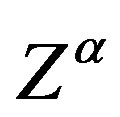 ,
,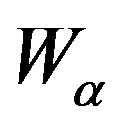 ), to the microscopic space-time, where
), to the microscopic space-time, where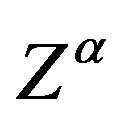 , are the fields of gauge nature (in this case electromagnetic fields) and the fields of particles of the gravity (gravitons), (that in this case is the background).
, are the fields of gauge nature (in this case electromagnetic fields) and the fields of particles of the gravity (gravitons), (that in this case is the background).
Based on it, and considering the value of curvature to be the contour deformation on a surface (initial idea created by relativity to understand curvature in a space-time surface [2]), at the same time that a field distortion created like an undulation in the space time for back-reaction for photon propagation in the presence of gravity (see Figures 2 and 3 (using string theory)), we can extrapolate this idea to the design of a type of accelerometer that can be connected to the devices of navigation of a traveling satellite by the space, where said accelerometer involves in their interior a sensor of ultra-sensitive gravity based on a solid sphere S3, of material similar to a colloid, captured the changes of the weight of a liquid also of colloid type (perhaps of major density that of the ball S3) due to the universal factor G.
10. Conclusions
The methods through Lagrangian actions are useful to obtain expressions of measurable electro-gravitational gauges in a gravitational dynamic system that can be adapted for the detection of observable of the energymatter tensor expressed from the microscopic level in the equations like the given by the system (35,36,37,38) (which one is a gravitational-dilaton version of the Dirac equation) up to the macroscopic dimension of Einstein’s space-time, for tensor saying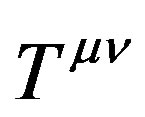 .
.
Then the existence of the observable gravity effects initiate from a field of quantum gravity generating quantum curvature and torsion observables of the space, which can be detected in Einstein’s dimension like cosmic censoring for gravitational waves shaped by electromagnetic waves according to the cosmic censor calculated for Penrose [11,12,20,22]. This cosmic censoring can be detected by a model of ultra-sensor that we design on the ball S3, of certain distortion of the space-time created for back-reaction (Figure 12).
But these methods are based on much in the gauge theory and of the information of the gravity through models of gravitational waves by means of electromagnetic waves where the detection will be realized by means of spiraling created for the back-reaction that will take place through traces of a electro-gravitationally observable type, whose geometry is a 6-dimensional superstring.
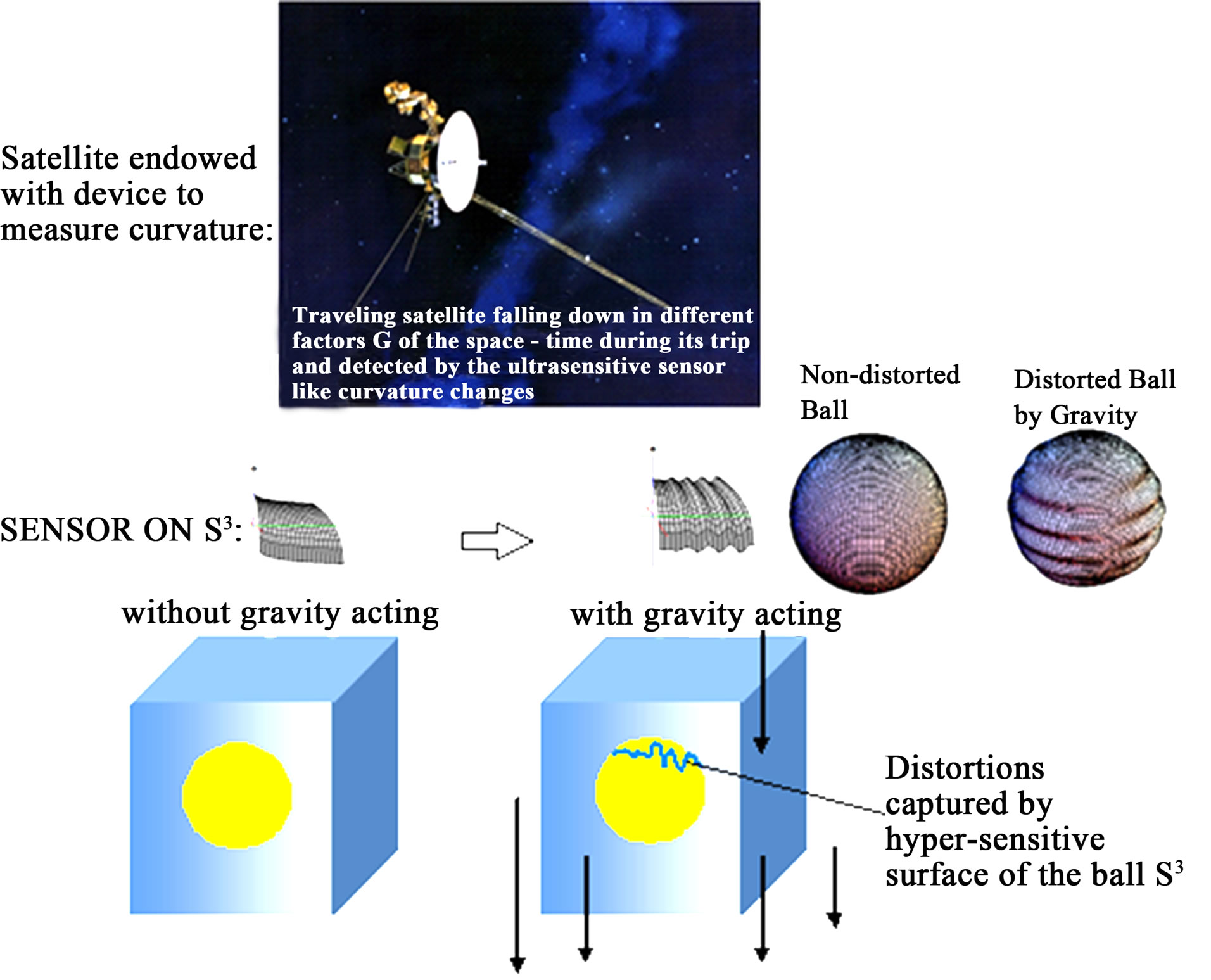
Figure 12. The curvature will be able to express itself like a Gaussian curvature according to spherical harmonics given by Legendre polynomials. The sensor is a sensor of free fall that can register different force factors G. The actions of change can be reprogrammed by the proper device considering these to be a Lagrangian action of the section 8 [10].
The method that we propose in the section 9.3, might adapt itself at quantum level capturing these small interactions and recording in information of quantum gravity codified by field elements already classified under the different types of sub-particles that define at quantum level material forces.
11. Acknowledgements
One is grateful for the support offered by the Institute of Mathematics of the Autonomous National University of Mexico IM-UNAM, by the Department of Research in Mathematics and Engineering of the Technological Institute of High Studies of Chalco (DIMI-TESCHA). Also I am grateful to the teachers of English language, Edgar Milla and Alberto Antonio Sánchez for their review in the quality of the used English language.
REFERENCES
- F. Bulnes, “Design of Measurement and Detection Devices of Curvature through of the Synergic Integral Operators of the Mechanics on Light Waves,” International Mechanical Engineering Congress and Exposition, Lake Buena Vista, 13-19 November 2009, pp. 91-102. doi:10.1115/IMECE2009-10038
- F. Bulnes, “Analytic Dissertations of the Sidereal Hyperspace,” Masterful Conference in UTM, Insurgents University, Mexico City, 1996, pp. 23-98.
- F. Bulnes, “Radon transform and the curvature of One Universe,” Master’s Thesis, National Autonomous University of Mexico, Mexico City, 2001.
- F. Bulnes, “Cohomology of Moduli Spaces in Differential Operators Classification to the Field Theory,” Proceedings of the 8th International Conference on Function Spaces, Differential Operators and Nonlinear Analysis, Thür, 18-24 September 2011, pp. 81101-81119.
- F. Bulnes, “Doctoral course of Mathematical Electrodynamics,” International Proceedings of Appliedmath, Vol. 2, 2006, pp. 398-447.
- S. Kobayashi and K. Nomizu, “Foundations of Differential Geometry, Vol. 1,” John Wiley and Sons, New York, 1963.
- S. Kobayashi, K. Nomizu, “Foundations of Differential Geometry, Vol. 2,” Wiley and Sons, New York, 1969.
- L. K. Landau, E. Lifschitz, “The Classical Theory of Fields,” Addison-Wesley, Cambridge, 1951.
- L. J. Mason, “A Hamiltonian interpretation of Penrose’s Quasi-Local Mass,” Classical and Quantum Gravity, Vol. 6, No. 2, L-7-L13, 1989. doi:10.1088/0264-9381/6/2/001
- L. J. Mason and J. Frauendiener, “Sparling 3-form, Ashtekar variables and Quasi-Local Mass,” Twistor, Twistor in Mathematics and Physics, Cambrindge, 1990.
- R. Penrose, “Quasilocal mass and Angular Momentum in General Relativity,” Proceedings of the Royal Society A, Vol. 381, No. 1780, 1982, pp. 53-63. doi:10.1098/rspa.1982.0058
- G. Giachetta and G. Sardanashvily, “Stress-Energy-Momentum Tensors in Lagrangian Field Theory. Part 2. Gravitational Superpotential,” 1995. http://arxiv.org/abs/gr-qc/9511040v1
- H. Friedrich, “Gravitational Fields Near Space-Like and Null Infinity”, Journal of Geometry and Physics, Vol. 24, No. 2, 1998, pp. 83-163. doi:10.1016/S0393-0440(97)82168-7
- J. D. E. Creighton and R. Mann, “Quasilocal thermodynamics of Dilaton Gravity Coupled to Gauge Fields,” Physical Review D, Vol. 52, No. 8, 1995, pp. 4569-4587. doi:10.1103/PhysRevD.52.4569
- J. Krol, “(Quantum) Gravity Effects via exotic R4,” Annalen der Physik, Vol. 19, No. 3-5, 2010, pp. 355-358. doi:10.1002/andp.201010446
- N. Prezas and K. Sfetsos, “Supersymmetric moduli of the SU(2) × Rφ Linear Dilaton Background and NS5-branes,” 2008. http://iopscience.iop.org/1126-6708/2008/06/080/pdf/1126-6708_2008_06_080.pdf
- E. Kiritsis and C. Kounnas, “Infrared behavior of closed superstrings in Strong Magnetic and gravitational fields,” Nuclear Physics B, Vol. 456, No. 3, 1995, pp. 699-731. doi:10.1016/0550-3213(95)00540-2
- S. Hassan and A. Sen, “Marginal deformations of WZNW and coset models from O(d, d) transformation,” Nuclear Physics B, Vol. 405, No. 1, 1993, pp. 143-165. doi:10.1016/0550-3213(93)90429-S
- J. Król, “Quantum Gravity Insights from smooth 4-geometries on trivial R4,” Quantum Gravity, 2012, pp. 53- 78.
- J. Frauendiener, “On the Penrose inequality,” Physical Review Letters, Vol. 87, No. 100, 2001. doi:10.1103/PhysRevLett.87.101101
- M. F. Parisi, “Propagation of photons in Quantum Gravity,” Ph.D. thesis, National Córdoba University, Córdoba, 2007.
- G. W. Gibbons, “The isoperimetric and Bogomolny inequalities for Black Holes,” in: T. J. Willmore and N. J. Hitchin, eds., Global Riemannian Geometry, Ellis Horwood Halsted Press, Chichester, 1984, pp. 194-202.
- R. Geroch, “Asymptotic structure of Space-Time,” Proceedings of a Symposium on Asymptotic Structure of Space-Time, Cincinnati, 14-18 June 1976, pp. 1-105.
- R. M. Kelly, “Asymptotically Anti-De Sitter Space-Time,” Twistor Newsletter, Vol. 20, 1985, pp. 11-23.
- K. P. Tod, “Penrose’s Quasilocal Mass and Isoperimetric Inequality for Static Black Holes Class,” Classical and Quantum Gravity, Vol. 2, No. 4, 1985, pp. L65-L68. doi:10.1088/0264-9381/2/4/001
- J. Frauendiener and L. B. Szabados, “The kernel of the Edth Operators on Higher-Genus Spacelike 2-Surfaces,” Classical and Quantum Gravity, Vol. 18, No. 6, 2001, pp. 1003-1014. doi:10.1088/0264-9381/18/6/303
- V. Schomerus, “Lectures on branes in curved backgrounds,” Classical and Quantum Gravity, Vol. 19, No. 22, 2002, p. 5781. doi:10.1088/0264-9381/19/22/305
- A. J. Dougan, “Quasi-Local Mass for spheres,” Classical and Quantum Gravity, Vol. 9, No. 11, 1992, pp. 2461- 2475. doi:10.1088/0264-9381/9/11/012
- N. M. J. Woudhouse, “Cylindrical Gravitational Waves Class,” Classical and Quantum Gravity, Vol. 6, No. 6, 1989, pp. 933-943. doi:10.1088/0264-9381/6/6/017
- Y. Aharonov and D. Bohm, “Significance of electromagnetic potentials in Quantum Theory,” Physical Review, Vol. 115, No. 3, 1959, pp. 485-491. doi:10.1103/PhysRev.115.485
- F. Bulnes, “Lagrangian Dynamics and electromagnetic Gauges Applied to the determination of curvature of one Universe,” Proceedings of International 6th Cuban Congress of Mechanical Engineering, Habana, 2010, pp. 242- 248.
- C. Ortix, S. O. G. Kiravittaya, O. G. Schmidt and J. Van den Brink, “Curvature-Induced Geometric Potential in Strain-Driven Nanostructures,” Physical Review B, Vol. 84, No. 4, 2011, Article ID: 045438. doi:10.1103/PhysRevB.84.045438
- G. F. Smoot, “Cosmic Microwave Background Radiation Anisotropies: Their Discovery and Utilization,” Nobel Lecture, Nobel Foundation, 2006. http://nobelprize.org/nobel_prizes/physics/laureates/2006/smoot-lecture.html
- E. Kiritsis and C. Kounnasa, “Curved Four-Dimensional Space-Time as Infrared Regulator in Superstring Theories,” Nuclear Physics B—Proceedings Supplements, Vol. 41, No. 1-3, 1995, pp. 331-340. doi:10.1016/0920-5632(95)00441-B
- Smoot Group, “The Cosmic Microwave Background Radiation,” Lawrence Berkeley National Laboratory, Berkeley, 2008.
Notation
LMAX—Maxwell Lagrangian.
LYM—Yang-Mills Lagrangian.
Á—Action Lagrangian.
 —Minkowsky space.
—Minkowsky space.
M—Space-Time defined as complex Riemannian manifold with Hermitian structure given by J.
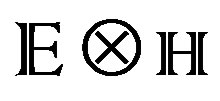 —Supercanonical algebra of fields F. This is the space of connections F2 Ä F1 – F1 Ä F2 – [F1,F2].
—Supercanonical algebra of fields F. This is the space of connections F2 Ä F1 – F1 Ä F2 – [F1,F2].
SU(2)j ´ —4-dimensional curved part of background space.
—4-dimensional curved part of background space.
Φ—Dilaton (field of string).
F—Maxwell tensor (is the 2-form F = Fαβdxαdxβ).
SU(2) —group that defines the finite actions through unitary anti-Hermitians matrix of range.
Rαβ—Curvature Tensor of Riemann.
ω—Cartan form in the exterior calculus.
Tαβ—Tensor of matter and energy (Also acknowledge as stress-energy-momentum tensor).
Abbreviations
CMB—Cosmic Microwave Background.
QFT—Quantum Field Theory.
WMAP—International Deep Exploration Space System from “Soil Moisture Active Passive”. Consist in one cosmological sensor of the electromagnetic type and a network of data.
CERN—European Organization of Nuclear Research (from french: Organisation européenne pour la recherche nucléaire).
FRW—Cohomology Friedman-Robertson-Walker metrics. The cosmological principle (principle of homogeneity and isotropy of the universe to great scale). The cohomology are the relations of similarity in dual spaces.
NOTES
1A particular case of the equation of the shape operator Equation (12) is given by the equation of the metrics established for 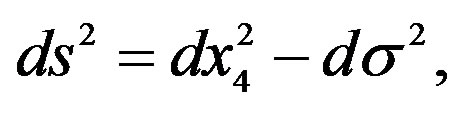 with
with 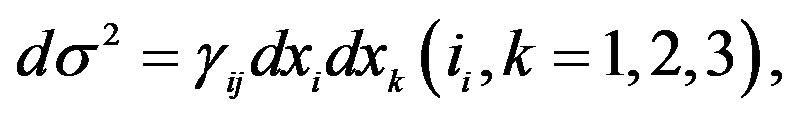 given for [2]
given for [2]
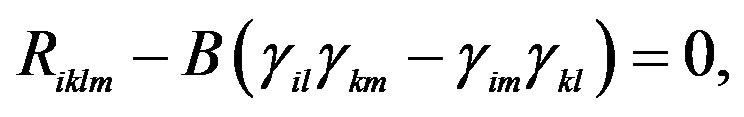
which measures the curvature tensor through displacing the potentials Ai, according to the metrics established along a surface of an infinitesimal 2-dimensional element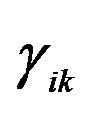 , and calculating their variation in a contour (cycle). In fact, the contours are cycles of a 2-dimensional sphere that is obtained through the spherical map M ( S2, to obtain a Gaussian curvature of M, using the curves or minimal trajectories of the particles in M, submitted under the vector constant electromagnetic potential field Ai. Then the contour variation is established for the displacement produced by the charges in M, for
, and calculating their variation in a contour (cycle). In fact, the contours are cycles of a 2-dimensional sphere that is obtained through the spherical map M ( S2, to obtain a Gaussian curvature of M, using the curves or minimal trajectories of the particles in M, submitted under the vector constant electromagnetic potential field Ai. Then the contour variation is established for the displacement produced by the charges in M, for 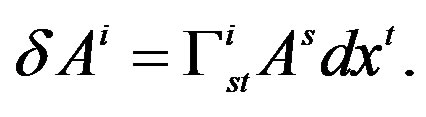 Then for the principle of minimal action all the trajectories or cycles used to determine the curvature, using the vector potential Ai, satisfy in the cycles that
Then for the principle of minimal action all the trajectories or cycles used to determine the curvature, using the vector potential Ai, satisfy in the cycles that