Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 11 (2011) , Article ID: 8338 , 7 pages DOI:10.4236/jemaa.2011.311073
Surface Plasmon Resonance of a Few Particles Linear Arrays
![]()
Universidad de los Andes, Bogotá D.C., Colombia.
Email: ju-aria1@uniandes.edu.co
Received August 17th, 2011; revised September 20th, 2011; accepted October 3rd, 2011.
Keywords: Surface Plasmons, Metallic Nanoparticles, Enhanced Electric Field
ABSTRACT
We present a study of the enhancement of the electric field due to localized surface plasmons in a short chain of metallic nanoparticles with different shapes: spheres, cylinders and spheroids. We calculate numerically the external radiation effect on these chains and analyze besides the shape, also the influence on size, interparticle distances and number of nanoparticles, corroborating that each one plays a definitive role for the enhancement of the electric field. Particularly, we focus on the main features of the electric field in the inter-particle regions, where an enormous increasing is expected due to the longitudinal localized plasmons. The electric field distribution along the chain shows a maximum in the middle of the chain. This fact could be related to a hybridization effect as the gap between particles decreases below 2 nm, we also observe a strong enhancement with the number of nanoparticles. Also regarding the shape we find agreement with reported results on spheroids, moreover we show that lateral coupled cylinders are more flexible to tune the enhancement factor than all other.
1. Introduction
The possible use of visible light to observe directly nanosystems has been opened by means of the mechanism of optical nano-imaging based on the excitation of SPPSurface Plasmon Polariton, which breaks the diffraction limit of light and offers a resolution beyond a value comparable to the wavelength of the applied light [1,2]. Surface plasmons (SPs) are states of polarization that can propagate along metal-dielectric interfaces without radiative losses. Polarization in an SP excitation can be spatially confined on scales that are much smaller than the free-space wavelength. This property proved to be extremely valuable for manipulation of light energy on subwavelength scales and miniaturization of optical elements. SP excitations in ordered one-dimensional arrays of nanoparticles have attracted significant attention in recent years due to numerous potential applications in nanoplasmonics. The interesting behavior of light under the influence of plasmons not only allows superlensing [3,4], in which perfect imaging is possible through a flat thin metal film, plasmonic antennas and lenses can convert optical radiation into intense, engineered, localized field distributions or enable coupling to deep subwavelength guided modes. Thus, wherever subwavelength control over light is desired, nanometallic structures are likely to play an important part [5]. Designing an optical microscope to see life matter in its natural condition and observe electronic transitions in atoms and molecules is the main goal to achieve [6]. However, scaling photonic devices beyond the diffraction limit of light imposes fundamental challenge and is expected to introduce a range of new and enhanced physical effects. Electromagnetic forces acting on linear chains of nanoparticles can produce the effect of optical trapping [7]. Chains of coupled resonant metal particles have been proposed by Quinten et al. and Bronsgerma et al. [8] to allow transport of confined plasmon excitation from particle to particle at nanometer length scale.
It is now well known that the plasmon resonances of illuminated metallic substrates provide the intense optical frequency fields responsible for the electromagnetic contribution to surface-enhanced Raman scattering (SERS) [9- 13]. When metallic nanoparticles are used as SERS substrates, dramatic variations in the degree of enhancement, often by many orders of magnitude, have been observed. This variation has been attributed to the random formation of localized plasmons at the gaps between nanoparticles, giving rise to large enhancements that enable SERS detection at or near single molecule sensitivity [14]. The potential for structural control of the large local fields of junction plasmons has generated much interest in the fabrication, assembly, and properties of structures with nanoscale gaps [15,16]. Correlating the optical response of specific individual nanoparticles with their nanoscale structure permits a more detailed understanding of the optical properties of nanoparticles. SP excitations in ordered one-dimensional arrays of nanoparticles have attracted significant attention in recent years particularly enhancement of the electric field in spherical nanoparticles has been reported emphasizing the possible applications [17]. We present a study of the electric field magnitude at the gaps between metallic particles of several shapes and sizes and make a comparison as function of the inter-particle distance analyzing systematically this parameter-gap-effect as a measure of the coupling between them. In this work we also focus on the enhancement factor as the number of particles increases in linear arrays from two to five. We find enhanced electric fields up to six orders of magnitude, which allows us to propose them as substrates for SERS experiments.
2. The Method
At the resonances, very strong enhancement of the electromagnetic field is achieved, and the field distribution may present a fairly complex structure, which makes that only for those cases in which the electrostatic approximation holds, the computation of the resonances spectrum can be made analytically. Otherwise, it requires the consideration of retardation effects, and hence to solve of the full vector Maxwell equations as it is done in this work. Our numerical method allows the computation of plasmon resonances in a very accurate and quick way.
For the calculation we choose the software COMSOL MULTIPHYSICS [18] because this program offers accuracy and confidence to solve the differential equations of the nanoparticles system with the finite element method, which permits to obtain results in all multipole orders. This is a numerical technique for finding approximate solutions, the PDEs-Partial Differential Equations-can be entered directly or rendering the PDE into an approximating system of ordinary differential equations, which are then numerically integrated using standard techniques such as Euler’s method, Runge-Kutta, etc.
Therefore a cylindrical cut as depicted in Figure 1 is considered. A plane wave generated at the front face of the cylinder is the source of the polarization. The studied system is a gold nanoparticle chain, irradiated by z-polarized electromagnetic wave propagating in x-direction.
The dielectric function depends strongly on the wavelength of the incident electromagnetic wave. This has been explained in a simple way within the Drude-Sommerfeld model [19]. The local response of plasmons chains is expected to be extremely sensitive to frequency of the incident plane wave due to interference effects. For gold, ωp—bulk plasmon frequency—is around 6.3 × 1015 Hz [20]. Instead of trying to calculate the value specifically for our system, we prefer to use the experimental results reports that are valid for the sizes chosen in the present work. To determinate the dielectric constant value, we start from the complex refraction index, and make an interpolation in the data [20,21].
3. Results
The systems used in the simulation are showed in the Figure 2. For all cases the wave moves in the x-axis and its polarization is in the z-axis. The z component of the electric fields is calculated at in the center chain for an even particles number, while for odd particles number we take the value at the nearest gap to the center of the chain.
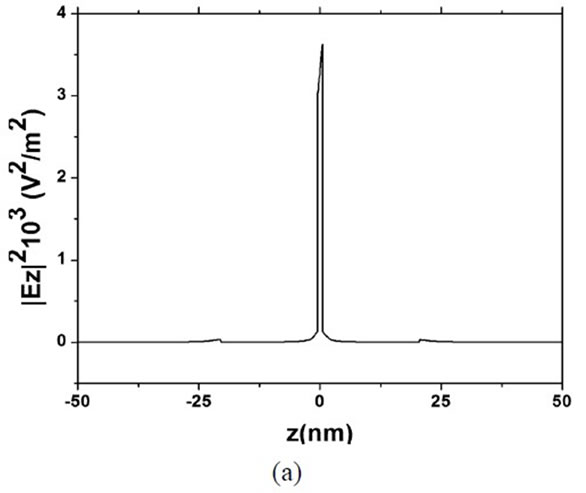
In Figure 3 we present the near field distribution for two to five nanospheres, where we observe the strong variation of the field magnitude in the inter-particle regions when an incident electromagnetic wave of 560 nm polarized along the array axis.
3.1. Two Particle Systems
Nanoparticle dimers are of considerable importance because large electromagnetic field enhancements that can occur at their junctions when the surface plasmons are

Figure 1. Sketch of the setup for the numerical calculation COMSOL can only simulate finite elements with electric field along the chain axis [20].
 (a)
(a)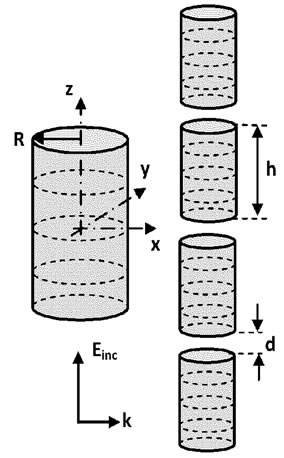 (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 2. Studied systems (a) spheres; (b) vertical coupled cylinders; (c) lateral coupled cylinders; (d) vertical coupled ellipsoids; (e) lateral coupled ellipsoids.
excited [14,22-23]. While nanoparticle dimers may not be the optimal structure for electromagnetic field enhancements, they serve as a simple prototypical model system for the study of the important physical factors underlying the electromagnetic field enhancements. The two major factors are believed to be the interaction of localized plasmons and the interference of the electromagnetic fields generated by these plasmons. The plasmonic properties of nanoparticle dimers have recently been investigated [23]. Our results for two spheres systems agree completely with this reference.
 (a)
(a)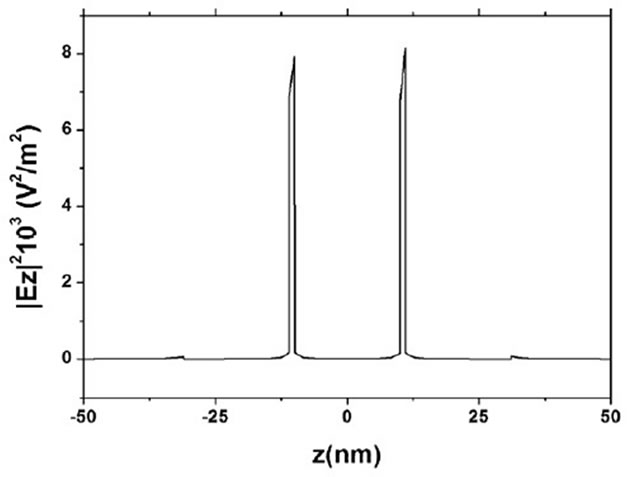 (b)
(b)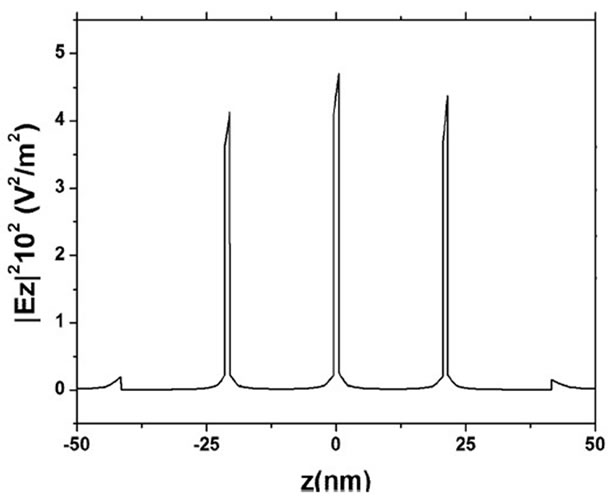 (c)
(c) (d)
(d)
Figure 3. Near field distribution for 2(a) and 3(b) nanospheres with R = 10 nm and d = 1 nm, interacting with a plane wave of 560 nm, that propagates in x-direction. 4(c) and 5(d) nanospheres with R = 10 nm and d = 1 nm, interacting with a plane wave of 500 nm, that propagates in x-direction.
In Table 1 we present for two particle systems of several shapes the corresponding values for the plasmonic resonance wavelength and enhancement factor. We observe that spheres and vertical coupled cylinders show the same resonance wavelength, although their enhancement factor ratio is 34. Lateral coupled cylinders and spheroids present similar values. It is worth to notice that the major enhancement is obtained for vertical coupled spheroids.
In Figure 4 the maximal electric field measured at the middle of the gap is drawn as function of the incident wavelength in whole visible spectrum for interparticles distance varying from 1 to 5 nm. At large separations, the plasmons on the different particles interact only weakly.

Table 1. Plasmon energy peak and enhancement electric field for two nanoparticles separated 1 nm and R = 10 nm for spheres and cylinders and aspect ratio 1:2 for prolate spheroids
 (a)
(a) (b)
(b)
Figure 4. Enhancement electric field spectrum for (a) two spheres R = 10 nm and (b) two lateral coupled cylinders with R = 10 nm and H= 10 nm. In both cases the peak for d = 2 nm is reaches less than one fifth of the corresponding to d = 1 nm.
On the contrary at short distances less than 2 nm the interaction is very strong, the field enhanced five times as d decreases from 2 to 1 nm. This fact can be interpreted as a hybridization of two single particle plasmons. We show separately the energy blue shift of the plasmon resonance as the gap increase for the same system presented in Figure 5, namely two nanospheres and two nanocylinders. In both cases the plasmon peak shifts to higher frequentcies in a similar way.
Size Effect
We compare the enhanced field as the size of the particles increases, thus, as the radius of the nanospheres is doubled the field increases 10 times for the same gap d = 1 nm (see Figure 6). On the other hand, for lateral coupled

Figure 5. Plasmon peak as function of gap for two spheres and two cylinders with R = 10 nm.
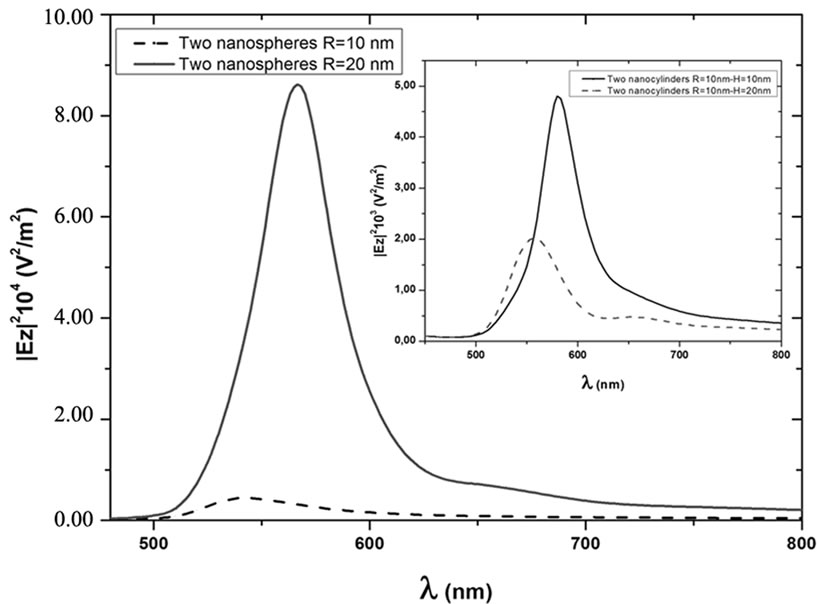
Figure 6. Enhancement factor as function of size for tow nanospheres and two lateral coupled nanocylinders (insert). The enhancement factor for two nanospheres systems is 10 times as the radius doubles, while in lateral coupled cylinders doubling the length means an enhancement is approximately three times.
nanocylinders by doubling the height maintaining the radius, we notice that the field enhancement is approximately three times (see insert Figure 6). This effect can be understood as delocalization of the plasmons along the lateral face. In case of vertical coupled cylinders the enhancement factor is much lower than in lateral coupling due to the fact that the neighboring faces are planes and therefore the charge accumulation lower.
3.2. Systems of More Particles
As the number of nanoparticles increases we observe the same behavior regarding the interparticle distances as for dimers. However, for four particle systems of the same radius we obtain over one order of magnitude enhanced while for four spheres the enhancement is only five times, electric field in case of four lateral coupled cylinders as shown in Figure 7, where can be seen the slopes change as gap varies from 1 to 5 nanometers in steps of 1 nm. In this figure we observed the dramatic enhancement of the field when changing the gap from 2 to 1 nm. This can be understood as a very strong correlation between the single particle plasmons also in case of several particles. It seems that the number of particles increases the plasmon hybridization. As the number increases the coupling between cylinders is stronger than between spheres. For comparison in the inset we show the result for two nanoparticle systems.
To complete our results we present the electric field enhancement for prolate spheroids with aspect ratios 1:2 in Figure 8. The maximum value of the enhancement factor is center symmetric in both gaps for odd number and it is maximal right at the very center in case of even number of nanoparticles. We observe the enhancement
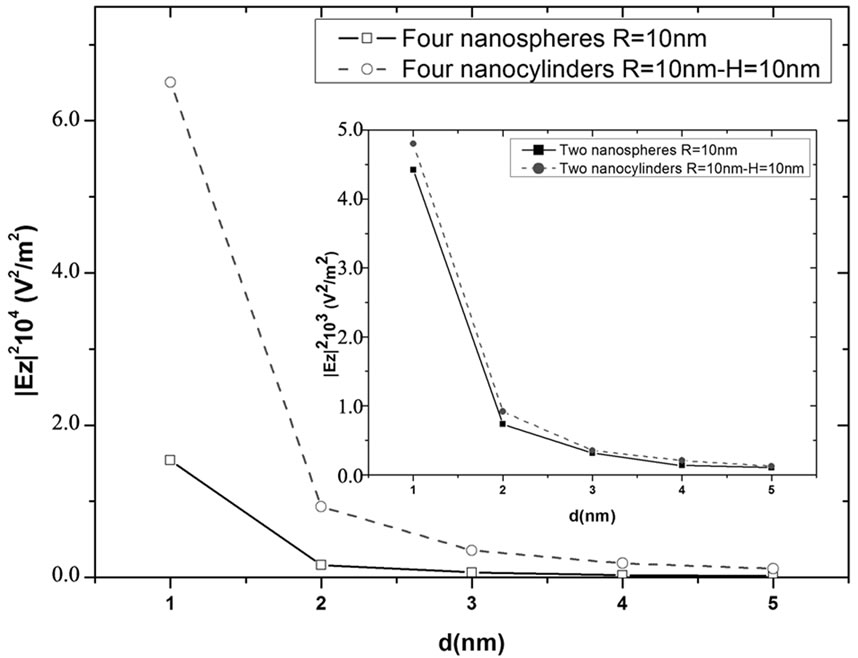
Figure 7. Enhancement factor as function of gap (interparticle distance) for four nanospheres and four nanocylinders of R = 10 nm. In the insert, enhancement factor vs gap for two nanoparticles.

Figure 8. Enhancement factor for three and four lateral coupled spheroids, with aspect radio 1:2, as function of wavelength in the visible region.
factor for two and three nanospheroids, where and enormous increase is obtained compare to the two nanoparticles systems presented in Figure 4.
As the number of nanoparticles increases we obtain a larger enhancement of the electric field, for 5 vertical coupled cylinders the factor reaches 1.3 × 103, while for 6 lateral coupled spheroids this factor grows up to 3.5 × 104 and for 3 vertical coupled ellipsoids the value is 5.8 × 105 times.
The plasmon peak for spheres and lateral coupled cylinders clearly shows a blue-shift as the gap increases for a fixed particle number. Systems of three spheres have the maximum peak value for all gaps changing very little for others numbers. However, as can be seen in Figure 9 the maximum plasmon peak is more sensitive to the number of particles in cylinders than in spheres. Two cylinders show the maximal plasmon peak, although it is lower that for spheres and as the number increases the plasmon peak moves to lower frequencies.
Our results for spheres agree with reference [24] in addition we compared spheres with cylinders and spheroids lateral and vertical coupled.
4. Conclusions
The plasmonic resonance is associated with a very large variation of the field intensity. The plasmonic effect on each nanoparticle plus the incident electric field produces the strong enhancement of the electric field interparticle. We study the evolution of the near field magnitude for systems of few (two to five) gold nanoparticles as function of inter-particle gap, size, shape and number of nanoparticles coupled in a linear array as they are illuminated with visible light polarized along the chain axis.

Figure 9. Plasmon peak as function of gap for two, three, four and five nanoparticles.
This polarization induces a strong field in the middle of the system, contrary, as it has been observed in case of transversal polarization, where the maximal field is at the ends of the chains. This fact relates the field enhancement to the hybridization of few particles. The number of nanoparticles in the one-dimensional configuration of short chains is an important parameter for the enhancement of the electric field. Regarding shape we conclude that lateral coupled spheroids and cylinders show the major enhancement factors, mainly at very short interparticle gaps.
We also report a remarkable difference in the enhancement factor for vertical coupled cylinder chains compared to the lateral coupled chain of the same length. The enhancement is stronger in the last configuration of cylinders and spheroids, where the neighboring side faces present high curvature, due to charge accumulation. On the contrary in vertical coupled cylinders the neighboring side faces are planes and they behave, in the quasistatic limit, more like the plates of a capacitor. Although increasing the size of the nanoparticles means an increase in the enhancement factor, it depends strongly on the coupling as follows, for lateral coupling spheroids and cylinders we obtain enhancement factors of the order of 106, however by doubling its length maintaining the radius, we observe that the plasmon localization decays. This can be explained as a start for propagating plasmons. Finally, lateral coupled cylinders show the best flexibility to tune the plasmon peak and thus the enhancement factor as all others. These results offer valuable basic information about the characteristic enhanced optical fields in metallic nanostructured chains.
5. Acknowledgements
The authors thank the Comite de investigaciones de la Facultad de Ciencias de la Universidad de los Andes for the partial support.
REFERENCES
- E. Abbe, “Beitrge Zur Theorie des Mikroskops und der Mikroskopischen Wahrnehmung,” Archiv für Mikroskopische Anatomie, Vol. 9, 1873, pp. 413-420.
- Y. Inouye and S. Kawata, “Near-Field Scanning Optical Microscope with a Metallic Probe Tip,” Optics Letters, Vol. 19, No. 3, 1994, pp. 159-161. doi:10.1364/OL.19.000159
- J. B. Pendry, “Negative Refraction Makes a Perfect Lens,” Physical Review Letters, Vol. 85, No. 18, 2000, pp. 3966-3969. doi:10.1103/PhysRevLett.85.3966
- D. R. Smith, D. Schurig, M. Rosenbluth and S. Schultz, “Limitations on Subdiffraction Imaging with a Negative Refractive Index Slab,” Applied Physics Letters, Vol. 82, No. 10, 2003, Aiticle ID: 1506.
- J. A. Schuller, E. S. Barnard, W. Cai, Y. C. Jun, J. S. White and M. L. Brongersma, “Plasmonics for Extreme Light Concentration and Manipulation,” Nature Materials, Vol. 9, No. 3, 2010, pp. 193-204. doi:10.1038/nmat2630
- H. W. Ch. Postma, “Rapid Sequencing of Individual DNA Molecules in Graphene Nanogaps,” Nano Letters, Vol. 10, No. 2, 2010, pp. 420-425. doi:10.1021/nl9029237
- M. Guillon, “Field Enhancement in a Chain of Optically Bound Dipoles,” Optics Express, Vol. 14, No. 7, 2006, pp. 3045-3055. doi:10.1364/OE.14.003045
- M. L. Brongersma and P. G. Kik, “Surface Plasmon Nanophotonics,” Springer Series in Optical Sciences, Vol. 131, 2007, pp. 1-9. doi:10.1007/978-1-4020-4333-8
- K. Kneipp, Y. Wang, H. Kneipp, I. Itzkan, R. R. Dassari and M. S. Feld, “Surface-Enhanced Raman Scattering from Individual Au Nanoparticles and Nanoparticle Dimer Substrates,” Physical Review Letters, Vol. 76, 1996, pp. 2444- 2447. doi:10.1103/PhysRevLett.76.2444
- R. C. Maher, L. F. Cohen, P. Etchegoin, H. J. N. Hartigan, R. J. C. Brown and M. J. T. Milton, “Stokes/Anti-Stokes Anomalies under Surface Enhanced Raman Scattering Conditions,” Journal of Chemical Physics, Vol. 120, No. 24, 2004, pp. 11746-11753. doi:10.1063/1.1739398
- A. M. Michaels, J. Jiang and L. Brus, “Ag Nanocrystal Junctions as the Site for Surface-Enhanced Raman Scattering of Single Rhodamine 6 G Molecules,” The Journal of Physical Chemestry B, Vol. 104, No. 50, 2000, pp. 11965-11971. doi:10.1021/jp0025476
- H. Xu, J. Aizpurua, M. Käll and P. Apell, “Electromagnetic Contributions to Single-Molecule Sensitivity in Surface-Enhanced Raman Scattering,” Physical Review E, Vol. 62, No. 3, 2000, pp. 4318-4324. doi:10.1103/PhysRevE.62.4318
- H. Xu, X. H. Wang, M. P. Persson, H. Q. Xu, M. Kall and P. Johansson, “Unified Treatment of Fluorescence and Raman Scattering Processes near Metal Surfaces,” Physical Review Letters, Vol. 93, No. 24, 2004, pp. 243002-243005. doi:10.1103/PhysRevLett.93.243002
- P. Nordlander, C. Oubre, E. Prodan, K. Li and M. Stockman, “Plasmon Hybridization in Nanoparticle Dimers,” Nano Letters, Vol. 4, No. 5, 2004, pp. 899-903. doi:10.1021/nl049681c
- P. J. Schuck, D. P. Fromm, A. Sundaramurthy, G. S. Kino and W. E. Moerner, “Improving the Mismatch between Light and Nanoscale Objects with Gold Bowtie Nanoantennas,” Physical Review Letters, Vol. 94, 2005, pp. 017402-017405. doi:10.1103/PhysRevLett.94.017402
- L. Gunnarson, T. Rindzevicius, J. Prikulis, B. Kasemo, M. Käll, S. Zou and G. C. Schatz, “Confined Plasmons in Nanofabricated Single Silver Particle Pairs: Experimental Observations of Strong Interparticle Interactions,” The Journal of Physical Chemistry B, Vol. 109, No. 3, 2005, pp. 1079-1087. doi:10.1021/jp049084e
- J. V. Hernández, L. D. Noordam and F. Robicheaux, “Asymmetric Response in a Line of Optically Driven Metallic Nanospheres,” The Journal of Physical Chemistry B, Vol. 109, No. 33, 2005, pp. 15808-15811. doi:10.1021/jp0527352
- COMSOLAB, COMSOL, COMSOL MULTIPHYSICS, COMSOL Reaction Engineering Lab and FEMLAB are registered trademarks of COMSOLAB. Other product or brand names are trademarks or registered trademarks of their respective holders. All Rights Reserved. 1998-2010.
- P. Drude, “Zur Elektronentheorie der Metalle,” Annalen der Physik, Vol. 306, No. 3, 1900, pp. 566-613. doi:10.1002/andp.19003060312
- R, Kappeler, “Engineering the Field Enhancement at the Apex of a Structured Noble Metal Tip,” Diploma Thesis, Communication Photonics Group IFH/ifE ETH Zurich and Nano-Optics Group the Institute of Optics, University of Rochester, Rochester, 2006.
- P. B. Johnson and R. W. Christy, “Optical constants of the noble metals,” Physical Review B, Vol. 6, No. 12, 1972, pp. 4370-4379. doi:10.1103/PhysRevB.6.4370
- H. Xu, E. J. Bjerneld, M. Käll and L. Borjesson, “Spectroscopy of Single Hemoglobin Molecules by Surface Enhanced Raman Scattering,” Physical Review Letters, Vol. 83, No. 21, 1999, pp. 4357-4360. doi:10.1103/PhysRevLett.83.4357
- B. Willingham, D. W. Brandl and P. Nordlander, “Plasmon Hybridization in Nanorod Dimers,” Applied Physics B, Vol. 93, No. 1, 2008, pp. 209-216. doi:10.1007/s00340-008-3157-5
- S. A. Maier, P. G. Kik and H. A. Atwater, “Observation of Coupled Plasmon-Polariton Modes in Au Nanoparticle Chain Waveguides of Different Lengths: Estimation of Waveguide Loss,” Applied Physics Letters, Vol. 81, No. 9, 2002, pp. 1714-1716. doi:10.1063/1.1503870

