Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 9 (2011) , Article ID: 7461 , 5 pages DOI:10.4236/jemaa.2011.39059
The Interaction of a Circularly Orbiting Electromagnetic Harmonic Wave with an Electron Having a Constant Time Independent Drift Velocity
![]()
Delft University of Technology, Delft, The Netherlands.
E-mail: mirwaisrashid@hotmail.com
Received June 24th, 2011; revised July 21st, 2011; accepted August 8th, 2011.
Keywords: Interaction, Circularly Orbiting, Electromagnetic Harmonic Wave, Constant Drift Velocity
ABSTRACT
A circularly orbiting electromagnetic harmonic wave may appear when a 1S electron encounters a decelerating stopping positively charged hole inside a semiconductor. The circularly orbiting electromagnetic harmonic wave can have an interaction with a conducting electron which has a constant time independent drift velocity.
1. Introduction
The general theory of relativity has predicted the bending of light [1] which is an electromagnetic wave [2]. The 1S orbital of the electron is said to have a spherical form at the overview of some simple molecules [3] and a sphere may be considered as consisting of circles. Therefore, if an electron is a particle which is one of the particle-wave dual properties of the electron [3] then a 1S electron may have a circular orbit. When an electron encounters a positively charged hole or a positively charged positron then a beam of light emerges of which is also known as the annihilation of electron and positron [4]. If the positively charged hole or the positively charged positron is decelerating and stopping while encountering the negatively charged electron of the 1S orbital, then the law of the conservation of momentum predicts that the K wave vector of light which is proportional to the momentum of the emerging light or the emerging electromagnetic wave should be tangential to a circular orbit [5]. According to Fourier’s theorem every periodic function can be decomposed into its harmonic functions [6]. Therefore, light which is an electromagnetic wave and having a periodic nature can be decomposed into its harmonic functions.
The Hamiltonian function has started in Classical Mechanics as the sum of the kinetic energy and the potential energy [7]. For a system of an electron interacting with an electromagnetic wave the Hamiltonian is given in terms of the A vector potential, the curl of which is the B magnetic field and in terms of the scalar potential the gradient of which is related to the electric field E of an electromagnetic wave [3].
The Einstein relativistic energy relation [7] is already used as a Hamiltonian to derive the Klein-Gordon equation [4]. More recently relativistic Hamiltonians are discussed in the references [8-12].
In this article the interaction Hamiltonian of an electromagnetic field with an electron is derived by the use of the Lorentz force equation [7], the relativistic momentum relation [7] and the Hamilton equation [7].
2. The Representation of a Circularly Orbiting Harmonic Electromagnetic Wave
The parametric representation of a circle [5] with the time parameter is given by
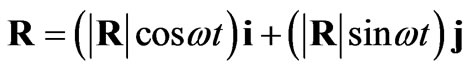 (1)
(1)
The tangential vector K with respect to a circle [5] would have the following parametric representation
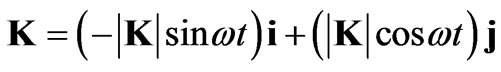 (2)
(2)
One can check that the inner product of R with K is equal to zero meaning that K is perpendicular to R
 (3)
(3)
A circularly orbiting harmonic wave [13] would have an electric field given by
 (4)
(4)
and a magnetic field given by
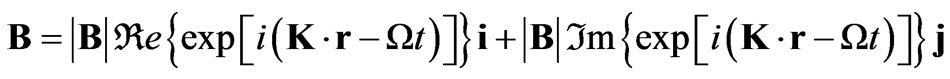 (5)
(5)
where the inner product of the wave vector K with the radius vector r is given by
 (6)
(6)
In quantum physics [3] one often needs the field A such that
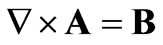 (7)
(7)
where the kinetic part of the Hamiltonian of the interaction of the electron with an electromagnetic field [3] is given by
 (8)
(8)
To find the field A which satisfies Equation (7) and Equation (5) one may write the following equation [14]
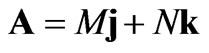 (9)
(9)
Then for the k component of the field A one may write
 (10)
(10)
which results in
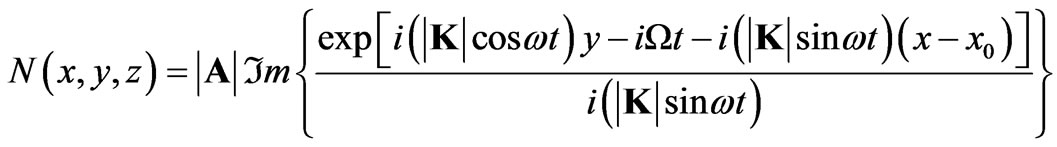
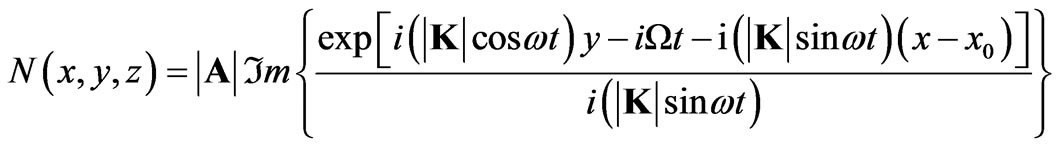 (11)
(11)
and for the j component of the field A one may write
 (12)
(12)
which results in
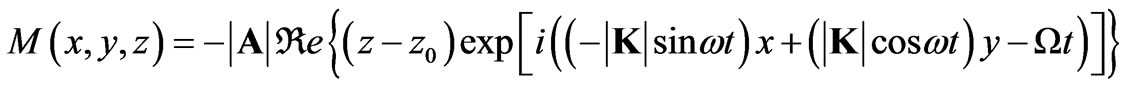 (13)
(13)
3. The Interaction Hamiltonian of the Circularly Orbiting Harmonic Wave with an Electron Having a Constant Time Independent Drift Velocity
When one starts from the following Lorentz force equation [3,7]
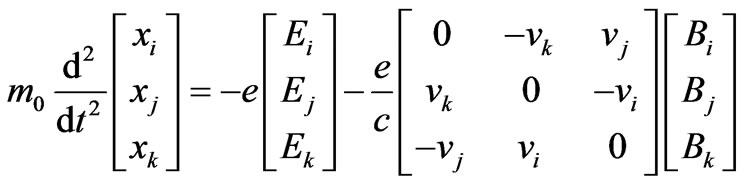 (14)
(14)
and using the following relativistic momentum relation [7]
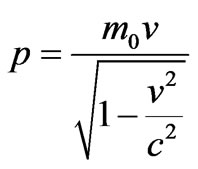 (15)
(15)
From which one can find the following expression for the velocity in terms of the relativistic momentum
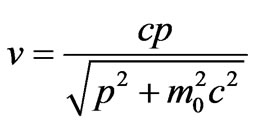 (16)
(16)
Using Equation (16) in Equation (14) and then dividing by 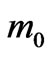 and integrating with respect to time one finds
and integrating with respect to time one finds
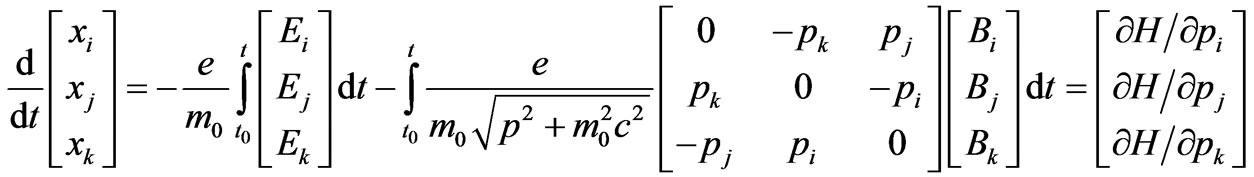 (17)
(17)
where the Hamilton equation [3,7]
 (18)
(18)
is used in Equation (17). Assuming that one may integrate firstly with respect to the components of the momentum then one can find the following relativistic expression for the Hamiltonian
 (19)
(19)
The first term of Equation (19) is a dyadic which involves an integration with respect to time of the electric field. And  is the Levi-Civita pseudotensor [6]. Using the following series expansion for the electric field [7]
is the Levi-Civita pseudotensor [6]. Using the following series expansion for the electric field [7]
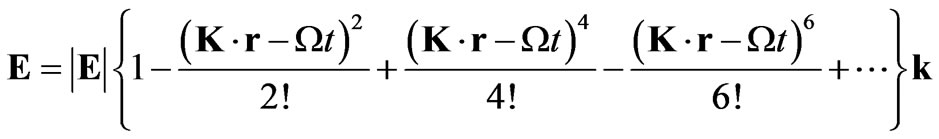 (20)
(20)
and having the following condition
 (21)
(21)
which is equivalent to the following relation for the circularly orbiting electromagnetic wave
 (22)
(22)
Then the electric field can be approximated by the following relation
 (23)
(23)
Taking the relation (6) for 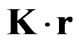 in Equation (23) one obtains
in Equation (23) one obtains

 (24)
(24)
Integrating Equation (24) with respect to time one obtains
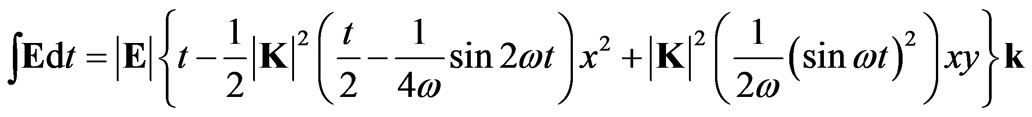
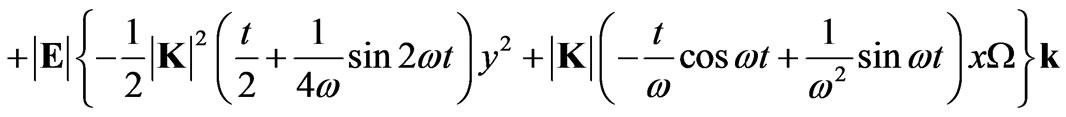
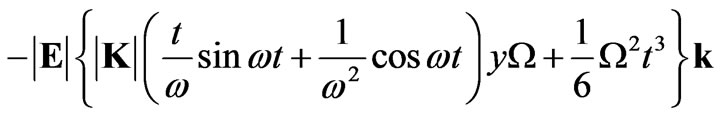 (25)
(25)
To simplify the natural logarithmic term in Equation (19) for the Hamiltonian one may assume that
 (26)
(26)
Then one has
 (27)
(27)
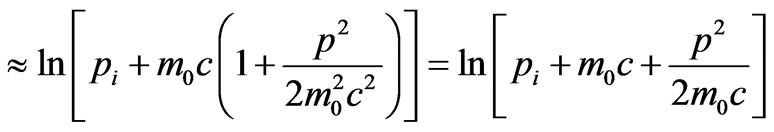 (28)
(28)
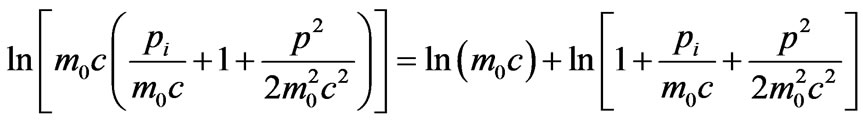 (29)
(29)
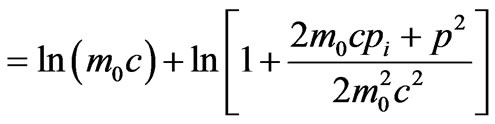 (30)
(30)
Taking the following series expansion for the natural logarithm [7]
 (31)
(31)
And assuming that
 (32)
(32)
Then Equation (27) can become equivalent to the following equation
 (33)
(33)
For an electron with a constant time independent drift velocity or a constant time independent momentum of the following form
 (34)
(34)
The Equation (19) for the Hamiltonian then becomes
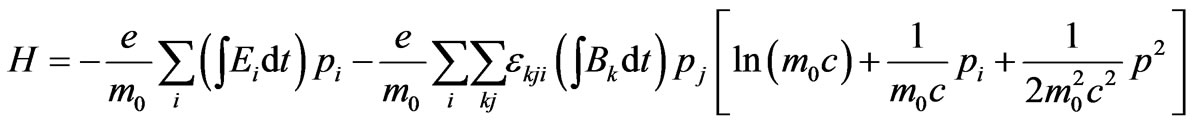 (35)
(35)
Having the condition (21) the magnetic field (5) can be approximated by [7]
 (36)
(36)
And the integral of Equation (36) with respect to time becomes
 (37)
(37)
Considering the particle-wave duality of the electron one may write the following wave equation for a wave function Ψ [3] using the Hamiltonian Equation (35)
 (38)
(38)
Making the replacement  , [15], one obtains the following equation
, [15], one obtains the following equation
 (39)
(39)
4. Conclusions
Starting from the Lorentz force equation and using the Hamilton’s equation of motion and by using the relativistic expression of the momentum a Hamiltonian is found which may describe the interaction of an electromagnetic field (in general) with an electron having a constant time independent drift velocity. The found Hamiltonian has terms involving the integration with respect to time of the electric and magnetic fields. For a circularly orbiting electromagnetic field the approximate expressions of the integrated electric and magnetic fields with respect to time are found in this article.
REFERENCES
- R. d’Inverno, “Introducing Einstein’s Relativity,” Claredon Press, Oxford, 1995.
- H. D. Young and R. A. Freedman, “University Physics,” 9th Edition, Addison-Wesley Publishing Company, Inc., Boston, 1996.
- S. Gasiorowicz, “Quantum Physics,” 2nd Edition, John Wiley & Sons, Inc., Hoboken, 1996.
- W. E. Burcham and M. Jobes, “Nuclear and Particle Physics,” Addison Wesley Longman Ltd., Singapore City, 1997.
- T. M. Apostol, “Calculus,” Vol. I, 2nd Edition, John Wiley & Sons, Singapore City, 1967.
- J. Mathews and R. L. Walker, “Mathematical Methods of Physics,” 2nd Edition, Addison-Wesley Publishing Company, Inc., Boston, 1970.
- J. B. Marion and S. T. Thornton, “Classical Dynamics of Particles and Systems,” 4th Edition, Harcourt Brace & Company, San Diego, 1995.
- G. Sardanashvily, “Geometric Quantization of Relativistic Hamiltonian Mechanics,” International Journal of Theoretical Physics, Vol. 42, No. 4, 2003, pp. 697-704. doi:10.1023/A:1024490011716
- M. Ilias and T. Saue, “An Infinite-Order Two-Component Relativistic Hamiltonian by a Simple One-Step Transformation,” Journal of Chemical Physics, Vol. 126, No. 6, 2007, Article ID: 064102.
- D. Alba, H. W. Crater and L. Lusanna, “Hamiltonian Relativistic Two-Body Problem: Center of Mass and Orbit Reconstruction,” Journal of Physics A: Mathematical and Theoretical, Vol. 40, No. 31, 2007, pp. 9585-9607. doi:10.1088/1751-8113/40/31/029
- C. Tix, “Strict Positivity of a Relativistic Hamiltonian Due to Brown and Ravenhall,” Bulletin of the London Mathematical Society, Vol. 30, No. 3, 1998, pp. 283-290.
- G. González, “Hamiltonian for a Relativistic Particle with Linear Dissipation,” International Journal of Theoretical Physics, Vol. 46, No. 3, 2007, pp. 486-491. doi:10.1007/s10773-006-9099-y
- G. R. Fowles, “Introduction to Modern Optics,” 2nd Edition, Dover Publications, Inc., New York, 1989.
- T. M. Apostol, “Calculus, Vol. II,” 2nd Edition, John Wiley & Sons, Singapore City, 1969.
- W. S. C. Williams, “Nuclear and Particle Physics,” Clarendon Press, Oxford, 1997.

