Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 11 (2010) , Article ID: 3298 , 9 pages DOI:10.4236/jemaa.2010.211084
A Simple Analytic Approximation for the Refracted Field at Gaussian Beam Incidence upon a Boundary of Absorbing Medium
![]()
Research Science Institute of Applied Physical Problems, Belarusian State University, Minsk, Belarus.
Email: serdyukvm@bsu.by
Received September 18th, 2010; revised October 25th, 2010; accepted October 28th, 2010.
Keywords: Gaussian Beam; Refraction; Absorbing Medium; Total internal reflection
ABSTRACT
An approximate analytic model is presented to describe spatial structure of refracted electromagnetic field arising at oblique incidence of a Gaussian beam on a plane boundary of an absorbing homogeneous medium. The analytic solution is obtained by asymptotic approximation of a Fourier field integral under the condition of great beam width in comparison with a wavelength (the geometrical-optics approximation). This model can be used also for approximate simulation of refracted field in the cases of beam incidence near the critical angle on transparent or absorbing (amplifying) refracting medium, if one artificially introduces the additional absorption (amplification), whose value is proportional to the ratio of the wavelength and the effective beam width. It is shown that the analytic model reflects the general features of refracted field at total internal reflection.
1. Introduction
A Gaussian beam is a simple model of coherent laser field that simulates well its basic properties, such as spatial narrowness of transverse structure and diffraction divergence under propagation in homogeneous and inhomogeneous media [1-6]. That is why a lot amount of papers have been devoted to consideration of this model, studying transformation of beam field under various conditions of reflection and refraction on dielectric interfaces (see, for example, [7-21]). It was appeared that the physical picture of these phenomena for a Gaussian beam is other than that for a plane wave. A reflected beam undergoes longitudinal, transverse and angular displacement on the boundary, and the value of such displacement can be sufficiently great, if an incident Gaussian beam is narrow and its angle of incidence is close to the critical value [7-20]. Under these conditions, interesting polarization and amplitude effects also take place [20,21].
However, in the literature, investigation of reflected beams is presented only, but refracted field is not considered (usually, authors do not write actually equations for that). Meanwhile, exactly refracted field determines class of effects connected with the phenomenon of frustrated total internal reflection such as excitation of waveguide modes [22] and of surface polaritons [23], which found wide applications in science and technology. Strictly speaking, the usual analytic representation of a Gaussian beam [4-6] in general is unfit for absorbing media, and determination of solution for beam refraction field in such media at arbitrary angle of incidence remains an urgent problem for theory and practice. So, there is a wide class of problems concerned with refracted field, which have only solutions based on the plane-wave approximation. But this approximation cannot describe effects of spatial inhomogeneity of light beams, which play an important part in some physical and chemical phenomena [24-26]. As it is known for us, only in the paper [27] the field arising under refraction of a Gaussian beam near the critical angle of incidence has been studied more or less in details, but the obtained solution is a too crude approximation. In the given work, we shall consider a new form of solution for refracted field excited under incidence of a Gaussian beam on the plane boundary of an absorbing medium. Our goal is to find the simplest analytic form of such a solution which at the same time should take into account spatial inhomogeneity of incident beam and could be suitable for the field simulation in a large number of applications. That is why we shall ignore polarization effects, considering the scalar approximation for the fields, and shall use the most simple geometrical-optics representation for an incident Gaussian beam. Such an approach is true because in the cases under our study, refracted field propagates not far from the boundary. We shall not also consider the phenomenon of reflected beam displacement and another delicate effect, which display at total internal reflection and have been studied in many works [7-21], because all these effects are out of the geometrical-optics approximation and their values are of the order of the wavelength. They are essential only for very narrow beams, whose effective width is grater then the wavelength not more by several folds.
To ground and clarify our approach, we shall start from the trivial case of the Gaussian beam reflection and refraction on the boundary of two transparent media, when the angle of incidence is much below the critical value. The geometrical-optics solution for this simple case will be used for generalization to the case of absorbing refracting medium. And then, we shall consider possibility of further generalization of the refracted field solution to the Gaussian beam incidence at the critical angle and above that, as for absorbing as for transparent refracting media.
2. Reflection and Refraction of a Gaussian Beam at an Interface between Transparent Media
A beam with the Gaussian profile, or more general, with the Hermite-Gaussian one, is a solution of Maxwell’s equations, obtained under the paraxial approximation, when the phase speed along the direction of its propagation is more greater than the speed of amplitude and phase change in another directions [1-6,11,12]. The most simple representation of a Gaussian beam is realized for the case of its propagation in homogeneous medium within relatively small distance L from the waist plane, when
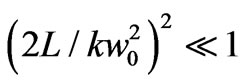 and
and 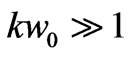 (1)
(1)
where w0 is the effective beam half-width in the cross-section, k = w/c = 2p/l is the wave number (the field temporal dependence is assumed as exp(–iwt)), l is the wavelength. In this case, the scalar beam field function is [4–6,12]
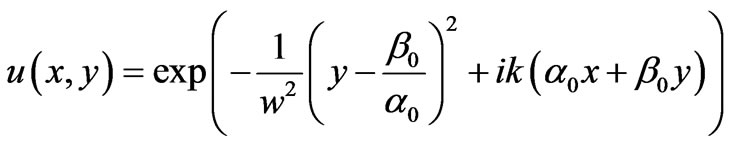 (2)
(2)
where i = Ö-1 is the imaginary unite, w = w0/cosq is the beam half-width in the tangential y-direction, q is the incident angle with respect to the interface normal x (Figure 1), a0 and b0 are the parameters of beam propagation along the xand y-axes (a02 + b02 = e, e is the dielectric permittivity of a medium, such that in a transparent medium a0 = ncosq and b0 = nsinq, where n = e1/2 is the refractive index). The function (2) specifies the field, whose amplitude and phase change in relatively orthogonal spatial directions. It means that the beam (2) maintains its transverse structure in the propagation process, like it appears in geometrical optics [11,13]. That is why the approach based on the conditions (1) can be naturally defined as geometric-optics approximation. By the way of illustration, let us consider numerical evaluation of the field of application for this approach. If the beam has the width 2w0 = 2 mm with the wavelength l = 0.5 mm, these conditions correspond to beam propagation within the distance up to 1 m. For many modern applications, dealing with small volume of optical devices, such an approach is perfectly acceptable.
Let the Gaussian beam (2) incidents from the negative x and y at the angle q on a plane boundary between two homogeneous isotropic media with the dielectric permittivities e and et (Figure 1). Assuming that the first medium, from that a beam incidents, is transparent, i.e. e = n2, where n is the refractive index. At first, we regard that the second medium is also transparent: Imet = 0. On the boundary x = 0, the incident beam field (2) has the form
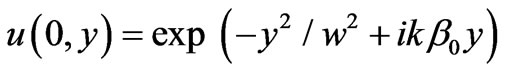 (3)
(3)
To obtain solutions for reflected and refracted fields, we shall use the ordinary technique of incident field expansion in a Fourier integral, and shall consider every
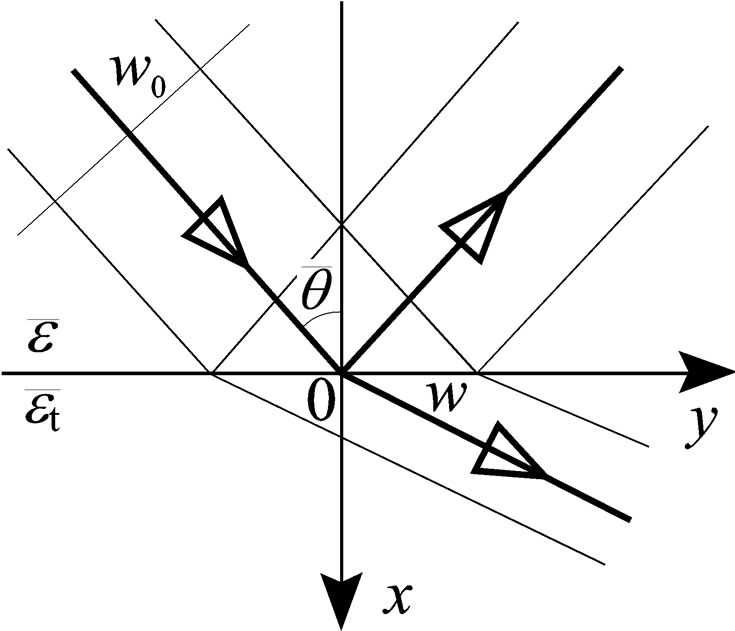
Figure 1. Geometry of the Gaussian beam reflection and refraction at a dielectric interface.
Fourier component as an independent plane wave. Every such a wave generates one reflected plane wave in the first medium and one refracted plane wave in the second medium, whose parameters are determined by the well known laws of reflection and refraction for plane waves [13]. The Fourier spectrum of the incident field (3) is
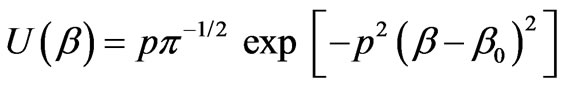 (4)
(4)
where
 (5)
(5)
Then, one can write at once the integral expressions for the fields of reflected and refracted beams
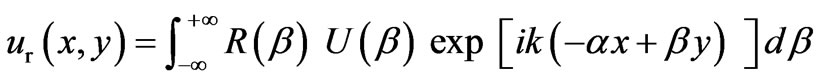 (6)
(6)
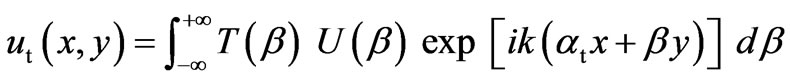 (7)
(7)
where
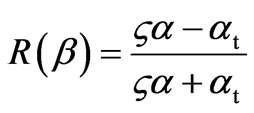
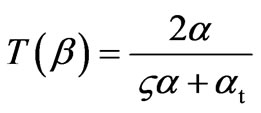 (8)
(8)
are the amplitude reflection and refraction coefficients for every plane-wave component [13], z = 1 for the case of TE polarization of an incident beam, when it is polarized linearly across the plane of incidence xy, and z = et /e for the case of TM polarization, when the electric vector of an incident beam is parallel to this plane,
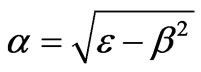
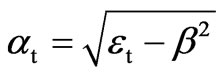 (9)
(9)
The last relationships ensure validity of Maxwell’s equations for the fields (6) and (7). In the integral expressions (6) and (7), the exponents with the values (9) describe propagation of the reflected and refracted fields away from the interface. To provide non-increase of these fields in magnitude under such propagation, one should choose the brunch of roots having the nonnegative imaginary parts.
The geometrical-optics approximation (1) assumes a very great value of the parameter (5). Then, the spectral function (4) appreciably falls off from zero only in a very narrow interval of the frequency variable b, changing near the effective beam propagation parameter b0. That provides opportunity to replace Equation (9) for a and at with their approximate linear expansions in the point b = b0:

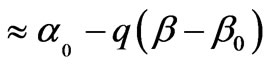 (10)
(10)
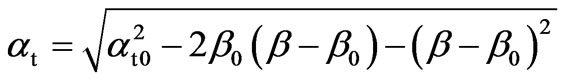
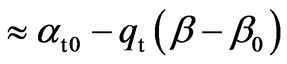 (11)
(11)
where a0 = (n2–b02)1/2 is the effective propagation parameter in the x-axis for the incident beam,
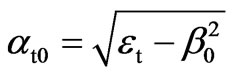 (12)
(12)
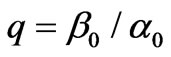
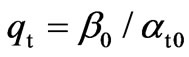 (13)
(13)
The presence of the great real parameter p in integrands of (6) and (7) allows us for calculation these integrals by the asymptotic steepest descent method [5,28,29]. If we shall restrict to a leading asymptotic term, this method yields a simple approximation for integrals in general form, which one can write as
 (14)
(14)
where f(b) and S(b) are the relatively slow and fast changing functions of argument of integration, bs is the pass or saddle point, in which the first derivative of the fast changing function vanishes: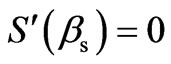 . To apply this method to the integrals (6) and (7), one can set
. To apply this method to the integrals (6) and (7), one can set

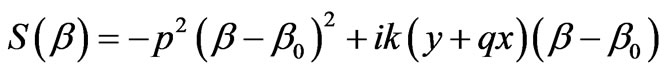
for the first integral and
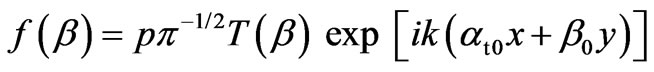
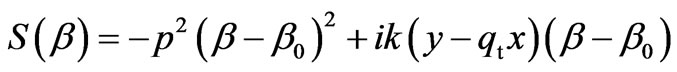 (15)
(15)
for the second integral. The saddle points are respectively as follows:
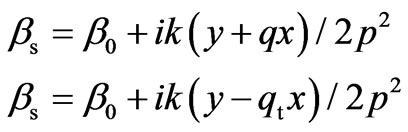 (16)
(16)
Due to a great value of the parameter p (5), one may neglect the small difference between the values bs and b0 for the slowly changing function f(b) (but not for the fast-varying index of an exponent S(b)). Then, the approximate expressions for the integrals (6) and (7) are reduced to the form
 (17)
(17)
 (18)
(18)
These obvious representations for the fields of reflected and refracted beams are in conformity with geometrical optics. The amplitude reflection and refraction coefficients for the beams coincide with the reflection and refraction coefficients for plane waves having the parameters a0, b0 and at0, b0, which characterize effective propagation of the reflected and refracted beams as a whole. These parameters determine also the direction of Gaussian amplitude change in a cross-section, which is determined by the condition y + qx = 0 or y - qtx = 0 and maintains itself under displacement in the beam axis. The half-width of the reflected beam (17) is equal to that of the incident one, and the effective half-width of the refractive beam (18) in the cross-section is
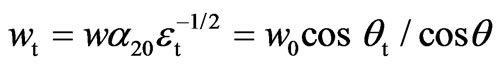
where qt is the angle of refraction. Every such a value is determined as a distance between two points P1 = (x1,y1) and P2 = (x2,y2), for which y1 – x1qt = 0, y2 – x2qt = w and at0x1 + b0y1 = at0x2 + b0y2.
The field of application of the obtained solutions (17) and (18) is determined by two conditions. The first one requires for the values q and qt (13) to be real, as well for the effective parameters of normal propagation a0 and at0, because the effective parameter of tangential propagation b0 is real. The second condition should provide opportunity to use the approximate representations (10), (11) for parameters of normal propagation of Fourier field components. Such linear representations require small magnitudes of the first neglected terms in the corresponding square roots expansions in powers of (b-b0)
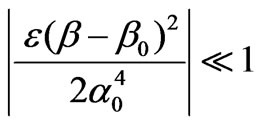
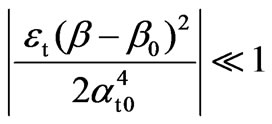
Proceeding from the form of the multiplier (4) of the integral functions (6) and (7), one can regard that the value of |b-b0| does not exceed 2/p. Then, the last inequalities take the form
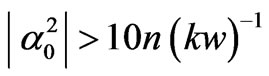
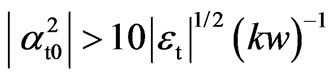 (19)
(19)
If the angle of beam incidence is not too close to the grazing one, i.e. q is smaller than 90° even by one angular minute, the first condition (19) for reflected field can be regarded as true. However, the second condition (19) for refracted field does not always hold true. When the dielectric permittivity et of the second medium in magnitude is smaller than the permittivity e of the first one, from which a beam incidents, the value b02 = (ncosq)2 can be equal to the value et, and the parameter at0 (12) vanishes. Here, we deal with the phenomenon of total internal reflection, at that the second condition (19) is not true and representation of refracted field in the form (18) becomes invalid.
What is more, at et < e the value b02 can exceed et, so that the values at0 (12) and qt (13) at all will be pure imaginary, what will cause unlimited rise of the beam (18) in amplitude under increase of the x-coordinate. The similar problem arises at any values of an incident angle (of the parameter b0) for the case of an absorbing medium, when its dielectric permittivity is complex.
3. The Refracted Field in Absorbing Medium
Let the second medium, into which a beam is refracted, is absorbing with the complex dielectric permittivity et (et = (nt + ikt)2). Then the condition (19) for the refracted field will be presented in the form
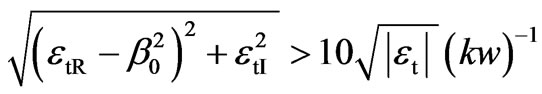 (20)
(20)
where we have used the compact designations etR = Reet and etI = Imet for the real and imaginary parts of the value et. This condition can be satisfied either by sufficiently great value of absorption (the imaginary part of the permittivity etI) or by appreciably great difference between b02 and etR. Assuming validity of the given condition, we suppose as before that the approximate representation (11) can be used for parameters of normal propagation of every plane-wave Fourier component in (7).
Now, the effective parameter at0 (12) of normal beam propagation will be complex, producing complexity of the parameter qt (13) with the negative imaginary part. Its presence exactly can cause false increase of refracted beam amplitude at rise of the x-coordinate. To prevent this effect, let us separate contributions of the real and imaginary parts of the parameter qt in the integral (7), taking into account small value of the imaginary part of et in (12). Namely, providing calculation of this integral by the steepest descent method (the approximation (14)), we shall keep for the fast-changing function S(b) only the component proportional to the real part qtR = Reqt, but the exponent with the imaginary part qtI = Imqt will be related to the slowly-changing function f(b), i.e. instead of (15), let us take
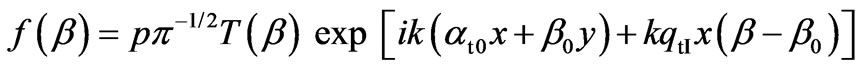
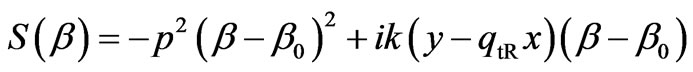
Then, the saddle point (16) of the integral (7) will be determined only by the real part of the value qt, and as a result, one obtains the following asymptotic approximation
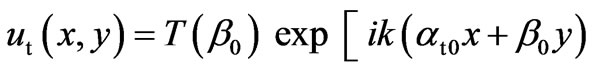
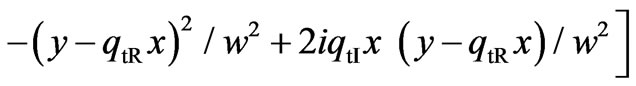 (21)
(21)
It distinguishes from the solution (18) in a transparent medium by the presence of a new imaginary component in the exponent, which describes a nonlinear coordinate dependence of the beam phase in a distance from the interface. Since Equation (21) takes possible complexity of the beam parameters at0 and qt into account, it can be used over a wide range of the incident angle change as below as above the critical angle qC = arcsin(etR1/2/n). The field structure determined by this equation is depended on the value of an incident angle, and this dependence is caused by the dependencies of the beam parameters at0 and qt on this angle. They are shown in Figure 2 for the case of
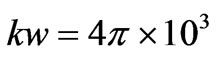
at various values of the index of absorption kt in the me-

Figure 2. The effective parameters at0 and qt of a refracted beam as functions of the deviation of the incident angle from the critical value for the Gaussian beam incidence on the interface between transparent (n = 1.6) and absorbing (nt = 1.4) media at kw = 4p ´ 103. The index of absorption for refracting medium is kt = 10-3(1); 5 ´ 10-3(2); 10-2(3). Solid lines correspond to the real parts of beam parameters, and dashed curves show their imaginary parts.
dium (Dq = q – qC denotes the deviation of the incident angle q from the critical value qC). The case under consideration corresponds to the value of qC = 61°3¢ and to the beam half-width along the interface w = 1 mm at the wavelength of 0.5 mm.
When the incident angle q approaches to qC at small values of the index of absorption, the magnitudes of the real and imaginary parts of the parameter qt appreciably increase (Figure 2). It corresponds to turn of the beam axis to the interface direction and to rise of the phase coordinate nonlinear dependence. But if the incident angle exceeds the critical value, the real part of the parameter qt becomes a decreasing function of q, at the same time the imaginary part of the parameter at0 still remains increasing one. As a result, the beam axis approaches to the normal (the x-axis) with strong amplitude decay away from the interface. Note that under increase of absorption, the pointed effects are smoothed over and cover more wide range of the incident angle change. Such a picture is followed from the ordinary plane-wave model of light beam. However, the imaginary part of qt remains a finite value that determines rather appreciable nonlinear dependence of beam phase on the coordinates. This effect of an inhomogeneous spatial phase distribution near the boundary is not taken into consideration by the ordinary plane-wave representation.
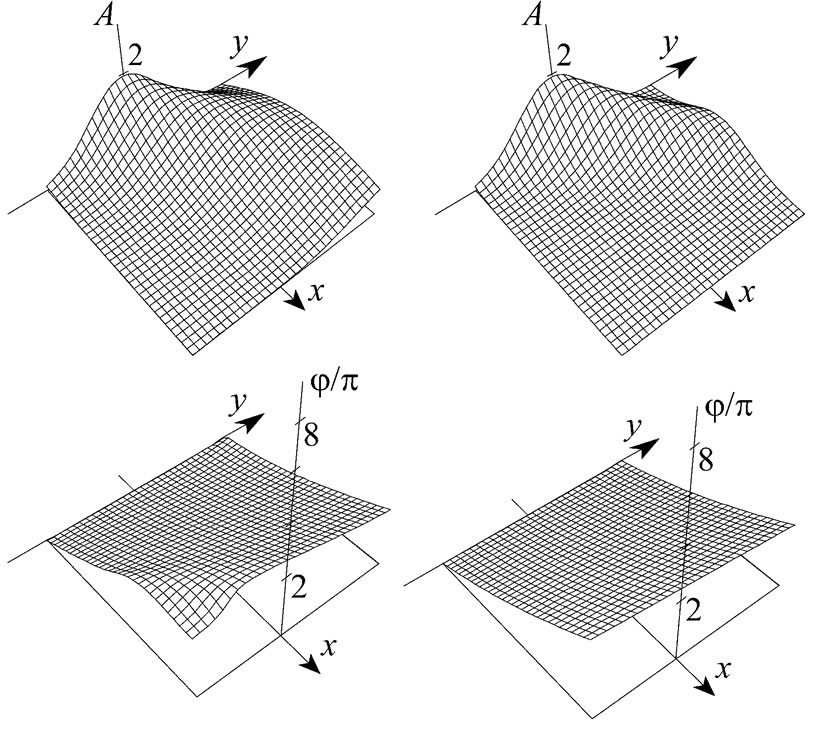
Strictly speaking, one should not regard the presented discussions as correct for the case of small absorption owing to violation of the condition (20) at small deviations from the critical angle. However, they reflect essential features of real spatial structure of refracted field in this range, which is verified by Figure 3 and Figure 4. Here, the exact solutions for the field amplitude and phase is presented, which have been obtained by the method of numerical computation of the Fourier integral (7) for the refracted field in absorbing medium (the phase shift along the interface, proportional to the tangential propagation constant b0, is not taken into account on these figures and everywhere below). For comparison, the spatial field picture determined by the approximate solution (21) is also presented on Figures 3 and Figure 4. For chosen parameters of the problem, the condition (20) is valid for |Dq | ³ 1¢35². We have used more small deviations from the critical angle to show the character of disagreement between the exact and approximate solutions. As it is clear from Figure 3 and Figure 4, this disagreement is not too great. It displays mainly for the phase, and is conspicuous only in the spatial domains of comparatively small value of the beam amplitude.
Figures 2-4 show that in absorbing medium, there is no abrupt transition between field propagation and exponential amplitude decay for incidence below and above the critical angle, as predicted by the model of an isolated plane wave. Amplitude decay presents in both

Figure 3. Spatial distribution of amplitude (A) and phase (j) of refracted field at incidence of the TE-polarized Gaussian beam on the interface between transparent (n = 1.6) and absorbing (nt = 1.4; kt = 10-4) media at kw = 4p ´ 103: the exact solution (left) and the approximate one (right). The scale of x is increased by 150 times in comparison with the scale of y. The angle of beam incidence is smaller than the critical one on 10².

Figure 4. Same as for Figure 3, but here the incident angle is greater than the critical one by 10².
cases, continuously rising under increase of the incident angle. At that, one observes nonlinear character of thephase dependence on spatial coordinates, which displays most largely at the critical angle of incidence.
4. The Refracted Field at Total Internal Reflection of a Gaussiam Beam
In a transparent medium, the abrupt transition between field propagation and exponential decay also does not take place for the refracted beam when the incident angle passes the critical value [27]. Really, in the spectrum of the beam (7), there are plane waves with various directions of propagation, which collect around average direction of propagation of a beam as a whole. Therefore, when the incident angle of a beam is very close to the critical value, for one part of its plane-wave spectrum the incident angle is smaller than that, but for another part of the spectrum it is greater. Summation over all contributions of those and others in the resulting field of the refracted beam (7) should produce averaged picture of continuous transition from beam propagation to amplitude decay, as it takes place in an absorbing medium. From this it follows that the analytic solution (21) obtained for the case of an absorbing medium, can be used for approximate analytic description of a refracted field at total internal reflection in a transparent medium. For that, let us assume the presence of additional absorption, conditioned by spatial narrowness of an incident beam, which arises in a refracting medium at closing to the critical angle. We will also assume that the value of this absorption rapidly decreases under increase of the difference between an incident angle and the critical one. Furthermore, let the value |at2|2 (12), calculated with this additional absorption, is an increasing function of the argument (b0 - nt)2, whose minimum is reached at the critical angle of incidence, when the tangential propagation parameter b0 = nt. These requirements will be satisfied, if the additional absorption in a medium is determined by the following expression
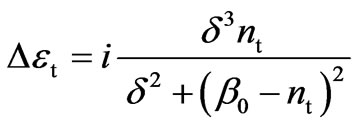 (22)
(22)
where d determines the maximal magnitude of Det at b0 = nt. To ensure satisfaction of the condition (20), that provides linearity of the decomposition (11) and validity of the approximate analytic expression (21), one should regard d = 20/kw. However, numerical computations have shown that the optimal approximation to the exact solution is achieved in the case of
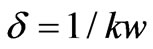 (23)
(23)
So, an approximate simulation of the refracted field in a transparent medium can be carried out by using the analytic expression (21) with (12), (13), where the dielectric permittivity et should be replaced with the sum et+Det. Figure 5 shows that the imaginary addend Det (22), (23) smoothes out sudden steps of the dependencies of beam parameters on incident angle at passing through the critical value. At incidence considerably below this angle, the imaginary addend (22) becomes infinitesimal and the
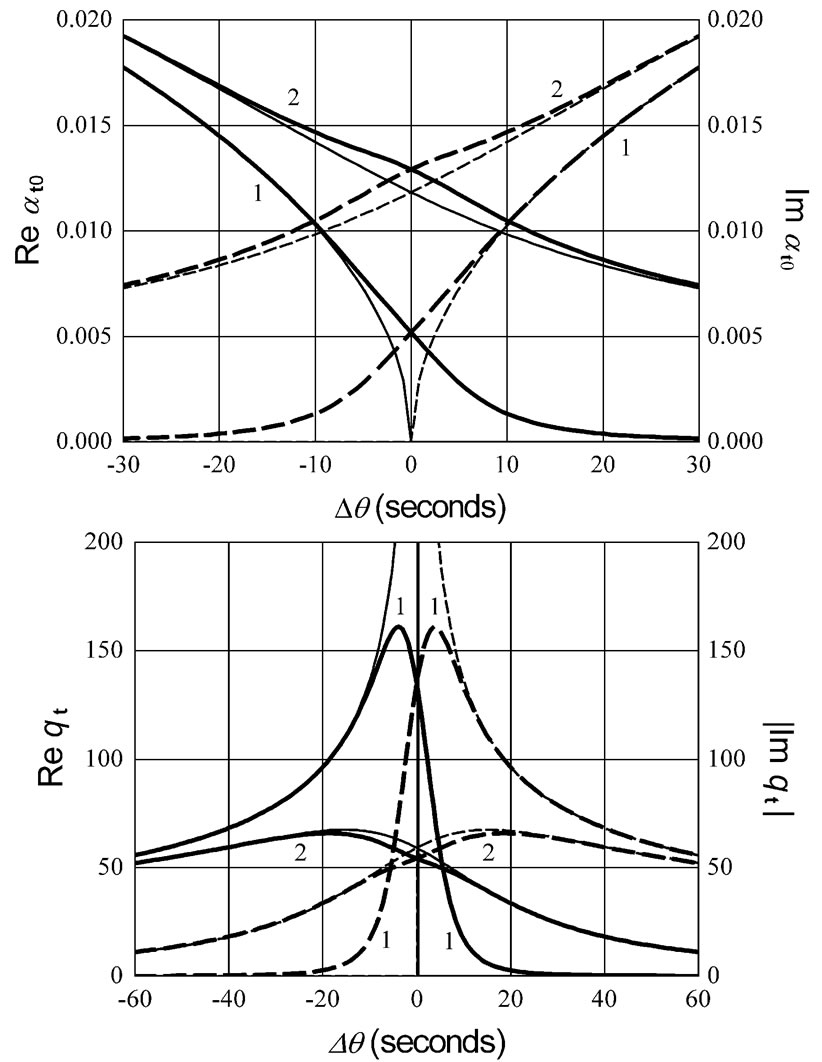
Figure 5. The effective parameters at0 and qt of a refracted beam as functions of the deviation of the incident angle from the critical value for the Gaussian beam incidence on the interface between two media (n = 1.6, nt = 1.4) at kw = 4p´103. The index of absorption for the refracting medium is kt = 0(1); 10-4(2). Solid lines correspond to the real parts of beam parameters, dashed curves show their imaginary parts. Thin lines display the parameters computed according to (12), (13), thick curves show results of their computing with allowance for the imaginary addend (22), (23).
approximate solution (21) turns into the ordinary relation (18). However, when the incident angle magnitude appreciably exceeds the critical one, at0 becomes a pure imaginary value, and this solution takes the form

 (24)
(24)
The first term in the exponent of this equation describes amplitude decay of the field away from the interface, the second and the third ones determine tangential phase shift and the profile of the amplitude distribution along the boundary. One way or another, these effects can be connected with the plane wave simulation of refraction above the critical angle. But the last imaginary summand in the exponent (24), which is proportional to xy, has not analogue in the plane-wave model, because it is due to spatial inhomogeneity of an incident beam. The nonlinear coordinate dependence of the phase described by this summand, will display only at a distance from the interface, but at moving away from that, the beam amplitude decays rapidly, so that the pointed above effect is hardly noticeable. Nevertheless, it should be taken into account under consideration of phase properties of light beam field at total internal reflection.
Figures 6-8 present graphically the computation results for spatial structure of the refracted field in a transparent medium for the Gaussian beam incidence near the critical value. It is seen that the approximate solution (21) with the imaginary addend (22), (23) to dielectric permittivity, differs here from the exact solution. In comparison with the latter, it yields too high value of amplitude decay and more strong dependence of the field phase on coordinates.
In the case of an absorbing medium, the solution (21) can also be used at incidence close to the critical angle, if the imaginary addend (22), (23) is taken into consideration in addition to the complex dielectric permittivity of a medium. It is obvious that discrepancy between approximate and exact solutions will be not so appreciable as for transparent medium, because the medium already has some absorption. And in the medium with strong absorption, the influence of this addend is infinitesimal at all, so that the approximate solution will
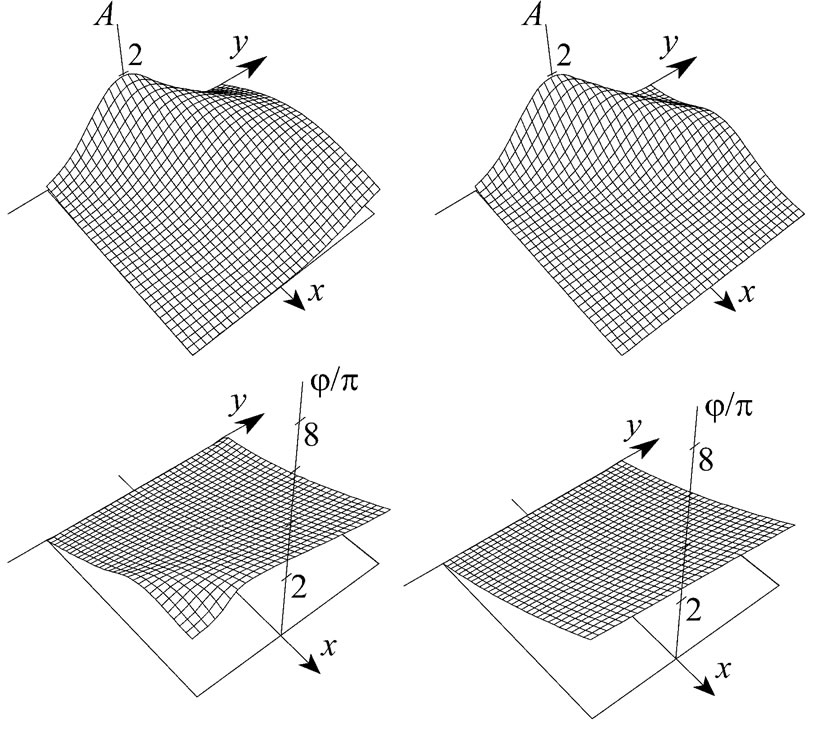
Figure 6. Spatial distribution of amplitude (A) and phase (j) of refracted field at incidence of the TE-polarized Gaussian beam on the interface between two transparent media (n = 1.6 and nt = 1.4) at kw = 4p´103: the exact solution (left) and the approximate one (right). The scale of x is increased by 150 times in comparison with the scale of y. The angle of beam incidence is smaller than the critical one on 5².
be coincide practically with the exact one at any angle of incidence. Note that in the case of an amplifying medium having the negative imaginary part of permittivity, one should take the addend (22) having the negative sign.
5. Conclusions
Our analysis shows that the geometrical-optics approximation of diffraction theory provides opportunity to obtain an analytic expression for the field arising under refraction of the Gaussian beam at a dielectric interface. It is applicable to many kinds of homogeneous refracting media (transparent, absorbing and amplifying) and to any incident angle, excluding, of cause, the case of grazing incidence. The given approximate solution is determined by simple Equation (21) with the parameters (12), (13) and with the imaginary addend (22), (23) to the dielectric permittivity of a refracting medium. We do not assign any physical sense to this artificial addend and consider its introducing only as formal mathematical procedure ensuring an analytic approximation for the integral expression (7) by simple way. The magnitude of such an addend is maximal at the critical angle of incidence, hence the greatest deviations of the approximate solution from the exact integral expression are observed exact here. To demonstrate character of these deviations, we have advisedly choosen for illustration those cases, where the given deviations are maximal. At incidence considerably below or above the critical angle, our solution is in good agreement with exact one, and for a transparent refracting medium it turns into ordinary expression (18) for inclined propagation of a Gaussian beam, when the incident angle is appreciably smaller than the critical one. Overall, one can admit that the obtained approximate solution reflects correctly the main properties of the refracted field spatial structure upon total internal reflection:
1) Continuous character of the transition between beam propagation at incidence much below the critical angle, and exponential amplitude decay much above it;
2) Orientation of the beam axis at inclination to the normal and the presence of amplitude decay at incident angles as below as above the critical value;
3) Nonlinear phase dependence on coordinates at moving away from the interface.
At any case, such a solution describes the refracted field under total internal reflection appreciably better than the model proposed in the paper [27] and the ordinary plane-wave approximation.
6. Acknowledgements
The work was supported by the State Integrated Program of Scientific Research of the Republic of Belarus “Technical Diagnostics”.
REFERENCES
- C. D. Boyd and J. P. Gordon, “Confocal Multimode Resonator for millimeter through optical wavelength maser,” Bell System Technical Journal, vol. 40, no. 2, March 1961, pp. 489-508.
- H. Kogelnik, “Imaging of Optical Modes-Resonators with Internal Lenses,” Bell System Technical Journal, vol. 44, no. 3, March 1965, pp. 455-494.
- H. Kogelnik, “On the Propagation of Gaussian Beams of Light through Lenslike Media Including Those with a Loss or Gain Variation,” Applied Optics, vol. 4, no. 12, December 1965, pp. 1562-1569.
- H. A. Haus, “Waves and Fields in Optoelectronics,” Prentice-Hall, Suffolk, 1983.
- S. Solimeno, B. Crosignani and P. DiPorto, “Guiding, Diffraction and Confinement of Optical Radiation,” Academic Press, New York, 1986.
- D. Marcuse, “Light Transmission Optics,” Van Nostrand Reinhold, New York, 1972.
- T. Tamir, “Nonspecular Phenomena in Beam Fields Reflected by Multilayered Media,” Journal of the Optical Society of America A, vol. 3, no. 4, April 1986, pp. 558-565.
- B. R.Horowitz and T. Tamir, “Lateral Displacement of a Light Beam at a Dielectric Interface,” Journal of the Optical Society of America, vol. 61, no. 5, May 1971, pp. 586-594.
- C. C. Chan and T. Tamir, “Beam Phenomena at and Near Critical Incidence upon a Dielectric Interface,” Journal of the Optical Society of America A, vol. 4, no. 4, April 1987, pp. 655-663.
- J. Alda, “Transverse Angular Shift in the Reflection of Light Beams,” Optics Communications, vol. 182, no. 1-3, August 2000, pp. 1-10.
- W. Szabelak and W. Nasalski, “Transmission of Elegant Laguerre-Gaussian Beams at a Dielectric Interface – numerical simulations,” Bulletin of the Polish Academy of Sciencies, vol. 57, no. 2, 2009, pp. 181-188.
- Y. Zhang and C-F. Li, “On the Representation of an Inclined Gaussian Beam,” European Journal of Physics, vol. 27, no. 4, July 2006, pp. 779-786.
- M. Born and E. Wolf, “Principles of Optics,” Pergamon Press, New York, 1968.
- P. Hillion, “Gaussian Beam at a Dielectric Interface,” Journal of Optics, vol. 25, no. 4, July 1994, pp. 155-164.
- C. W. Hsu and T. Tamir, “Lateral Displacement and Distortion of Beam Incident upon a Transmitting-Layer Configuration,” Journal of the Optical Society of America A, vol. 2, no. 6, June 1985, pp. 978-988.
- P. Berczynski and Y. A. Kravtsov, “Theory for Gaussian beam diffraction in 2D inhomogeneous medium, based on the eiconal form of complex geometrical optics,” Physics Letters A, vol. 331, no. 3-4, October 2004, pp. 265-268.
- M. A. Potenza, D. Brogioli and M. Giglio, “Total internal reflection scattering,” Applied Physics Letters, vol. 85, no. 14, October 2004, pp. 2730-2732.
- K. J. Willis, J. B. Schneider and S. C. Hagness, “Amplified Total Internal Reflection: Theory, Analysis, and Demonstration of Existence via FDTD,” Optics Express, vol. 16, no. 3, February 2008, pp. 1903-1914.
- K. Y. Bliokh, I. V. Shadrivov and Yu. S. Kivshar, “Goos-Hanchen and Imbert-Fedorov Shift of Polarized Vortex Beams,” Optics Letters, vol. 34, no. 3, February 2009, pp. 389-391.
- Y. Wang, Z. Yue, Y. Liu and J. Xu, “Lateral Displacement of a Gaussian Beam Reflected from Absorbing Media,” Optic, vol. 121, no. 4, February 2010, pp. 307-311.
- V. E. Lembessis, D. Babiker and D. L. Andrews, “Surface Optical Vortices,” Physical Review A, vol. 79, no. 1, January 2009, pp. 1-4.
- T. Tamir, “Integrated Optics (Topics in Applied Physics, Vol. 7),” 2nd Edition, Springer, Berlin, 1982.
- V. M. Agranovich and D. L. Mills, Eds., “Surface Polaritons – Electromagnetic Waves at Surfaces and Intersurfaces,” North-Holland, Amsterdam, 1982.
- G. A. Truskey, J. S. Burmeister, E. Grapa and W. M. Reichert, “Total Internal Reflection Fluorescence Microscopy. II Topographical Mapping of Relative Cell/Substratum Separation Distance,” Journal of Cell Science, vol. 103, no. 2, October 1992, pp. 491-499.
- Q. W. Song, Ch.-Yu. Ku, Ch. Zhang, R. B. Gross, R. R. Birge and R. Michalak, “Modified Critical Angle Method for Measuring the Refractive Index of Bio-Optical Materials and Its Application to Bacteriorhodopsin,” Journal of the Optical Society of America B, vol. 12, no. 5, May 1995, pp. 797-803.
- Y. L. Jin, J. L. Chen, L. Xu and P. N. Wang, “Refractive Index Measurement for Biomaterial Samples by Total Internal Reflection,” Physics in Medicine and Biology, vol. 51, no. 20, October 2006, pp. N371-N379.
- P. D. Kukharchik, V. M. Serdyuk and J. A. Titovitsky, “Total internal reflection of a Gaussian light beam,” Technical Physics, vol. 44, no. 4, April 1999, pp. 417-421.
- F. Olver, “Introduction to Asymptotics and Special Functions,” Academic Press, New York, 1974.
- L. B. Felsen and N. Marcuvitz, “Radiation and Scattering of Waves,” Prentice-Hall, New Jersey, 1973.