Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 9 (2010) , Article ID: 2768 , 8 pages DOI:10.4236/jemaa.2010.29071
An Approach to a Universal System of Units
![]()
Department of Mechanical Engineering, CIC, Cairo, Egypt
Email: salama_hady@cic-cairo.com
Received July 9th, 2010; revised August 15th, 2010; accepted August 15th, 2010
Keywords: Dimensions, Units, Potentials, Qualities, Thermodynamics, Electromagnetism
ABSTRACT
According to many scientists, there are some redundancies in the SI system of units. Through an entropy approach that depends on a previous analogy between the electrical, mechanical and thermal fields; it was possible to introduce a system of units that removes such redundancies. According to the second law of thermodynamics, the temperature was defined as a quality of heat. Following a proved analogy, the electrical and magnetic potentials may represent also the qualities of electric and magnetic fluxes. According to published experimental results, the electric and the magnetic potentials generates also electromotive forces, EMF, that were measured by Al-Fe thermocouples. The chemical potential or the concentration gradient generates also an EMF, as in the concentration cells, which is measured here by the same Al-Fe thermocouple. Such measurement-results are introduced to define a unique scale for measuring the potentials or qualities of the thermal, chemical, electric, and magnetic fields. The mentioned qualities are not defined by directly measurable quantities, as length and time, but they are found as functions of dimensionless concentrations of mass or energy fluxes. Hence, the volt, as a unit of the introduced EMF scale for potentials measurement, is postulated as a dimensionless unit. Finally, a universal system of units that is based only on three dimensions; L, T, and E, and four fundamental units; meter, second, Joule and volt is introduced in this paper to delete the SI redundancies. The energy replaces the mass as a fundamental unit in the introduced US as it plays a dominant role in most of the scientific and engineering fields. The ampere is not included as a fundamental unit since the charge is considered as a form of energy that is measured in one of the US fundamental units, Joule. The candela and the mole were also not considered as fundamental units as they can be related to the selected fundamental units by appropriate numbers. The limited number of dimensions in the introduced US simplifies the application of the “π” dimensional theorem to find plausible relations between the main parameters that characterize many physical phenomena and the energy conversions and interactions.
1. Introduction
Many scientists have found the international system of units, SI system, as a historical, independent, and redundant system [1-3]. Using the SI system; the dimensional homogeneity is not satisfied in many physical Equations and constants. In Table 1, we can find examples of such SI conflicts, which are found in literature [1,2], between the units of analogous quantities in the electric and magnetic fields. The ampere is a unit of the electric current, while “ampere/m” is found as a unit of strength or potential of the magnetic fields. According to Maxwell’s wave Equation [4], the unit of the electric field strength, E, should be similar to the unit of the magnetic field strength, H. Both are potentials of the flowing components of the same electromagnetic wave. However, both have conflicting SI units as seen in Table 1. Similarly; the conductivity is analogous to permeability while their SI units are confusing as also seen in Table 1
The system that will be the center of our concern is shown in Figure 1. Such system allows the flow of thermal, electric, magnetic and mechanical energies in addition to mass diffusion to or from the system. According to the second law of thermodynamics; the temperature as a potential of heat flow, is considered as a quality of heat that is defined by hypothetical scales [5]. By analogy [4]; the electric and magnetic potentials are simply postulated as qualities of electric charge and magnetic flux. Such qualities are functions of dimensionless concentrations of charge or energy fluxes similar to the chemical potential that is defined by the dimensionless concentration [6]. So, such potentials may be concluded as dimensionless parameters as they are not defined by directly measurable quantities but they are
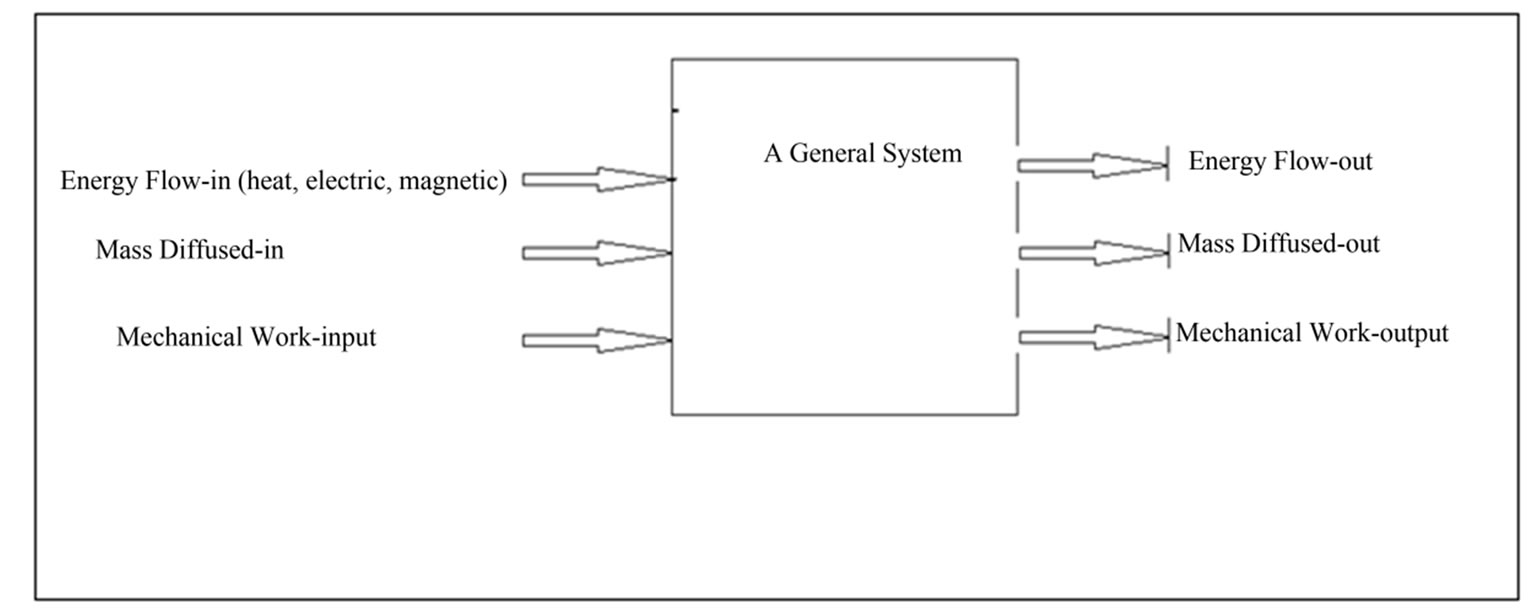
Figure 1. A general system energy-interactions.
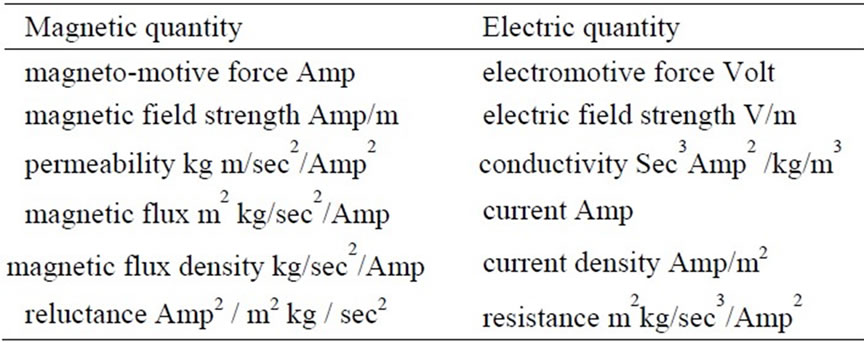
Table 1. Electric/Magnetic analogues in SI System.
defined by hypothetical scales. The examples of such dimensionless scales are the angular scale that cuts the circular angle into 360 dimensionless degrees and as defining the qualities of a viscous fluid flow by dimensionless Reynolds numbers and of a compressible flow by dimensionless Mach numbers [6]. A common tool for measuring such potentials-scale is suggested by the experimental results discussed by Kumar and others [7] and the measurements elaborated in the presented study. The results compared the performance of an Aluminum-iron thermocouple to other thermocouple combinations. Such Al-Fe thermocouple recorded the generation of excess EMF by influence of magnetic and electric fields. Such influences or effects can be introduced to define a unique scale for evaluating potentials or qualities of the thermal, electric and magnetic fields. However; the concentration gradient or chemical potential generates a similar EMF in volt, as in the concentration cell, which is measured in the present study by the use of the same Al-Fe thermocouple. So, the volt will be introduced in the presented approach as a dimensionless fundamental-unit for the measurement of the thermal, chemical, electric and magnetic potentials.
As energy is the core of most scientific and engineering fields; the Joule is considered in the introduced US as a fundamental unit while the unit of mass, kg, is considered as a derived unit. Such selection solves many conflicts found in dealing with properties of vacuum where the mass, involved in the SI system, is meaningless in vacuum. Finally, the introduced universal system is based on four units; meter, second, Joule and volt and three dimensions; Length, Time and Energy. Such system leads to removing the SI redundancies in scientific relations, constants and many physical quantities [2,3]. However, the candela was not considered as a fundamental unit in the introduced approach as such unit is actually defined in terms of the energy intensity of a specified spectrum of energy-radiation; i.e. in Joule. Similarly; the mole was not considered as a fundamental unit as it can be replaced by an appropriate number of molecules, 6.02 x 1023 molecules per mole, which corresponds to a specific mass in kg for each material.
The introduced three dimensional system of units leads also to simple representation of the physical quantities in a three dimensional space, L, T and E. Such system simplifies application of the π theorem to find dimensionally homogenous relations between the parameters that characterize different phenomena and to define different energy interactions.
2. A Universal Thermocouple
During their experimental work to compare the performance of some common thermocouples; Kumar and others [7] found better performances of an Aluminum-Iron thermocouple as compared to other combinations. Aluminum fulfills the requirement of high electrical conductivity while iron is a ferromagnetic material that has a comparatively low thermal conductivity.
Figure 2 shows the variation of the generated EMF due to variable temperature differences by various thermocouples where an EMF of “1.6892” mV was measured at temperature difference of 293˚C when using an Al-Fe thermocouple. However, they also recorded effects of magnetic flux on the performance of such Al-Fe ther
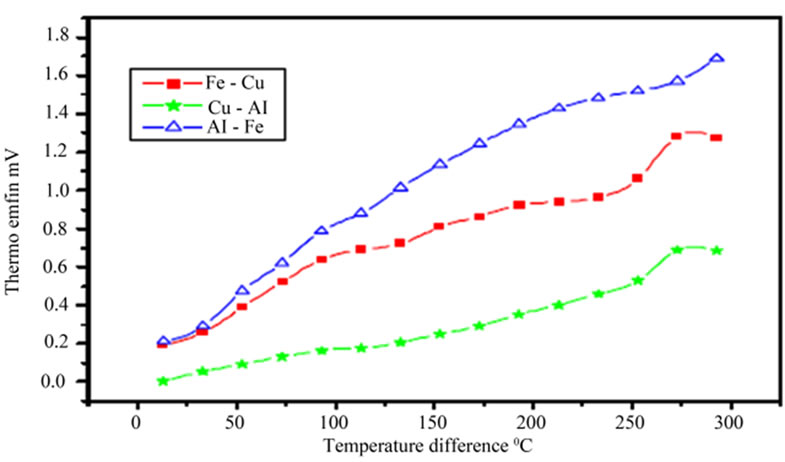
Figure 2. Performance of different thermocouples [7].
mocouple as seen in Figure 3. When a magnetic field of certain magnetic flux intensity was applied on such thermocouple at parallel orientation of the thermocouple, the generated EMF increased to 1.898 mV at the same temperature difference of 293˚C.
By application of an electric field of potential 4 V on such thermocouple at parallel and perpendicular orientation, significant effects on the generated EMF were found according to the results shown in Figure 4.
Such generated EMF by an Al-Fe thermocouple due to application of different fields introduces one unit and a unique instrumentation for measurement of the thermal, electric and magnetic potentials. A voltmeter of a proper scale for each field can be applied to measure directly the potentials of such fields by one unit; Volt. However, such scales may be calculated, as an example, from the found measurement results of Kumar where 1.6983 mV mainly corresponded to 566 K and 0.423 mV corresponded to 300 K. The measured EMF which is generated due to applying a magnetic flux of 120 G was found as (1.898 – 1.698 =) 0.2 mV. Similarly; the EMF found due to applying an electric potential of 4 V was found to be (1.2 – 0.4 =) 1.2 mV.
According to these results; the magnetic and electric fields have specific effects on the involved thermocouple and generate EMF as the EMF generated by the effect of temperature differences. Such results introduce also other

Figure 3. Influence of magnetic field on performance of Al-Fe thermocouple [7].
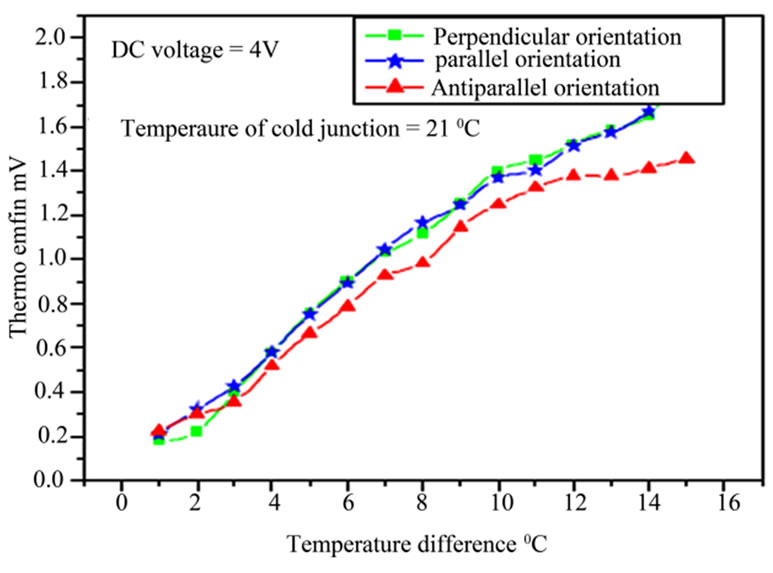
Figure 4. Influence of electric field on performance of Al-Fe thermocouple [7].
newly discovered effects on thermocouples which are similar to the Seebeck effect [5]. Such measured effects of the magnetic and electric fields are sustaining the postulated definitions of magnetic flux and electric char-ges as modified forms of energies or electromagnetic waves that possess specific potentials as the potential possessed by heat [4].
According to literature of physical chemistry [6], the chemical potential or the concentration gradient generates also an electrical potential that can be measured in volt. Such potential have been measured experimentally in this study by using the same Al-Fe thermocouple. The cold junction of the Al-Fe thermocouple was inserted into a water solution of high concentration while the hot junction was inserted into water solutions of less concentration. The difference in concentration generates excess EMF that is measured in volt as seen in Figure 5. So, we may postulate a universal system of units that considers the volt as a unit of the thermal, chemical, electrical, and magnetic potentials.
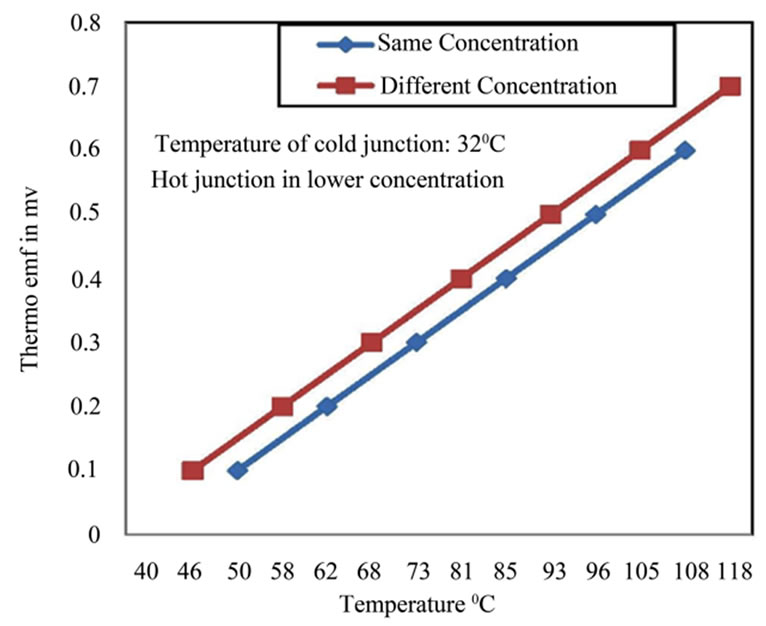
Figure 5. Influence of chemical concentration on performance of Al-Fe thermocouple.
3. Analogy of Thermal, Electric and Magnetic Fields
The Fourier Law of thermal conduction is stated as follows [8]:
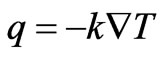 (1)
(1)
Where q is the heat flux density in W / m2. T is the temperature in, as postulated, in volt and is k the thermal conductivity of materials in W/m2 V.
Similarly; Ohms Law of Electric conduction is stated as follows [8, 9]:
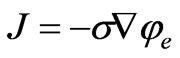 (2)
(2)
Where J is the electric flux density in W/m2. φe is the electrical potential in Volts and σ is electrical resistance in W/m2 V or Ohm.
The commonly used form for the relationship between the magnetic field parameters B and H is [9]:
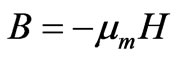 (3)
(3)
B is sometimes called the magnetic flux density or the magnetic induction. The unit of an energyflux density is measured generally in W/m2. Hence, the unit of B should be analogous to the units of the thermal and electrical fluxes in W/m2. μm is the magnetic permeability of a material that is analogous to the thermal and electrical conductivities. By analogy between the electric, magnetic and thermal field [4], Equation (3) that describes the magnetic flux can be expressed by an Equation similar to Equations (1) and (2) of the form [8,9]:
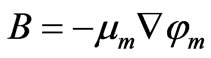 (4)
(4)
Comparing Equations (3) and (4), the magnetic potential φm can be defined in terms of the magnetic field intensity by the following relation:
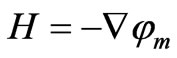 (5)
(5)
According to Equations (1), (2) and (4); the heat, electric and magnetic fluxes are denoted by q, J and B and they are measured in W/m2. Similarly, the thermal, electric and magnetic potentials are denoted by T, φe and φm and they are measured, as postulated, in Volts. Finally, the unit of conductivities k, σ and μm will result, according to the stated Equations, in W/m2 V. Such modified units of the fluxes and potentials may be considered as results of the definition of the electric charge and the magnetic flux as forms of electromagnetic waves [4].
4. An Entropy Approach to a Universal System of Units
In a recently published paper [4], it was introduced a new thermodynamic fundamental Equation of the following (rather modified) form:
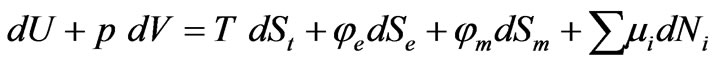 (6)
(6)
Equation (6) represents the electric charge, Q in terms of the electric potential, φe, times a change of entropy dSe and the magnetic flux as magnetic potential, φm , times a change in entropy dSm. Such approach depends on the analogy between the thermal, electric and magnetic fields [4] where heat is expressed in terms of temperature (as the thermal potential or quality), T, times a change in entropy dSt. In Equation (6), the product of the two terms μi and dni is expressing the chemical energy where μ is the chemical energy added to the system per unit increase in the concentration of certain chemical specie by dNi. The term dNi represents the change of relative concentration of a specie “i” by the amount dni/ni where ni is the total number of moles of such specie. As we can discover; the definition of μi as a chemical potential is misleading since it represents the added chemical energy per unit increase in concentration and its driving potential is the concentration of each of the chemical species. In other words, we may consider μi as the entropy increase of the system per unit increase of the relative concentration of the species.
Introducing the definition of the free Gibbs energy:
 (7)
(7)
In this Equation; we may consider the potential T as the sum of the driving potentials of the thermal, electric and magnetic energies.
Taking total differential of G, we have:
 (8)
(8)
Replacing dU in Equation (8) from the fundamental Equation (6); we get:
 , or
, or
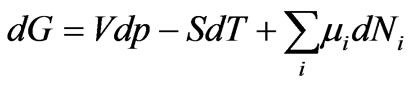 (9)
(9)
Dealing with systems that involve the transfer of different forms of energy as in thermal, electric, magnetic, and chemical energies, Equation (9) can be rewritten as follows:
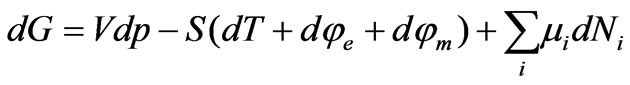 (10)
(10)
The potentials; 
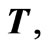 and
and  will be substituted, as previously discussed, in volts and
will be substituted, as previously discussed, in volts and  in Joule/ volt. By comparing the terms of Equation (10); the terms S and
in Joule/ volt. By comparing the terms of Equation (10); the terms S and 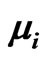 may be considered as the entropy added to the system due to the increase of any of the potentials:
may be considered as the entropy added to the system due to the increase of any of the potentials: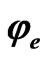
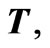 ,
,  and dni/ni. So, the entropy may be considered in general as a specific free energy per unit potential, i.e. it defines the free energy required to increase the potential of a system by one volt.
and dni/ni. So, the entropy may be considered in general as a specific free energy per unit potential, i.e. it defines the free energy required to increase the potential of a system by one volt.
According to the second law of thermodynamics, temperature is considered as a quality of heat [5]. By analogy [4]; the electric and magnetic potentials are considered also as qualities of electric charge and magnetic flux. Such qualities represent, according to Equation (10), the motivating mechanism that releases the entropy from the system into various energy forms. As the chemical potential is determined by the dimensionless concentration gradient of different species [6], different literatures consider also, by analogy, the thermal, electric and magnetic potentials are functions of the concentration of the related fluxes [9-12]. Accordingly, such potentials will be considered dimensionless parameters as they are functions of dimensionless concentrations. This may originate also from the definition of temperature, the quality of heat, by a hypothetical scale similar to a scale that partitions the circle into 360 dimensionless degrees [8].
5. A Three-Dimensional System of Units
Many references [1-3,10-12] found it is undesirable to use SI system of units in the thermo-chemical and electromagnetic fields as it fails to express properly the dimensional homogeneity of the characterizing Equations in such fields. Table 1 shows examples of such redundancies. In addition; the SI system does not find a physical significance of many constants or identical units of the quantities E, D, B, H and µ [9,11,12].
A recently defined system of units that was introduced to modify the SI system depends only on Space and Time, S and T, as basic dimensions and fundamental units [2]. However, such ST system of units did not solve the redundancy that was discussed. Rather, it added many conflicts in its introduced units. As an example, it defines the energy and temperature by the same dimensions T S -1 while energy is physically different than temperature. Similarly, such ST system assigns to the electric charge and the space the same dimension S which contradicts their definitions and physical meanings.
The introduced US of units is relied upon the previously discussed analogy between the thermal, electrical, magnetic and chemical energies. According to Equation (10), the heat, electrical and magnetic fluxes are considered as forms of energy or electromagnetic waves that are measured by the energy dimensions and units. According to the studied measurement-results of the Al-Fe thermocouple, the potentials of these fluxes are defined by a unique scale, the measured EMF, and one dimensionless unit, the volt.
In many scientific and engineering studies, energy plays a dominant role. So, the proposed system of units introduces energy, E, as one of its fundamental dimensions and units. Units of time and space, of the dimensions T and L, are considered also as fundamental units. So, the introduced system is based on three basic dimensions and units: the length in meters, time in seconds, and energy in Joule. The volt is considered as a dimensionless unit that measures, as previously explained, the potentials of the electric, magnetic and thermal fields by a unique EMF scale. The introduced US of units excludes the ampere as a fundamental unit where the charge, as modified electromagnetic waves [4], is measured directly by Joule. The candela is defined as the luminous energy intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 × 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian [8]. Therefore, the candela is defined in terms of energy units and can be skipped as a fundamental unit [8].
Other physical quantities can be derived in terms of the introduced US fundamental dimensions and units according to their physical definitions. Some examples of derived US units are introduced as follows:
Velocity
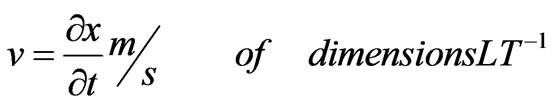 (11)
(11)
Acceleration
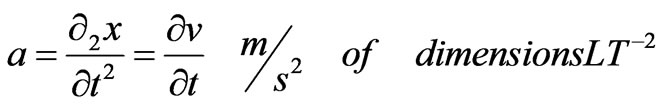 (12)
(12)
Mass From relativity theory:
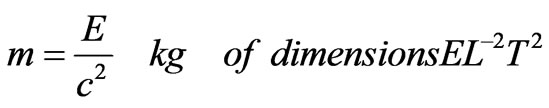 (13)
(13)
Power
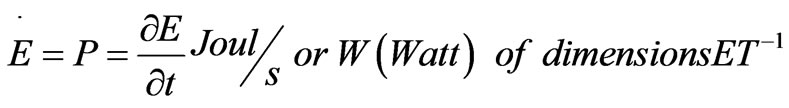 (14)
(14)
Such Power dimensions and units represent also the rate of flow of heat, electric charge and magnetic flux as 
Energy flux
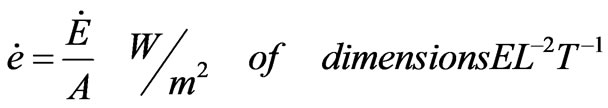 (15)
(15)
Such energy flux represents rate of energy flow per unit area as 
Force
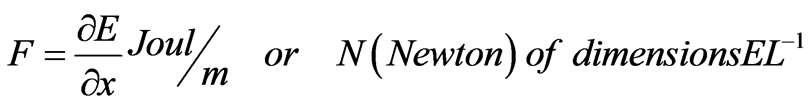 (16)
(16)
Pressure
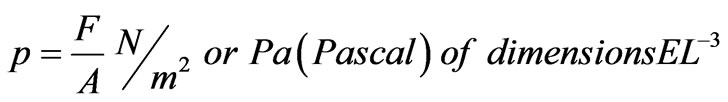 (17)
(17)
Potential gradient:  (as temperature gradient, electric field gradient or magnetic field gradient):
(as temperature gradient, electric field gradient or magnetic field gradient):
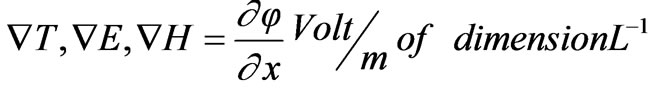 (18)
(18)
Conductivity (as thermal, electric and magnetic conductivity):

 (19)
(19)
Permeability
 (20)
(20)

Permittivity:
 (21)
(21)

Resistivity:
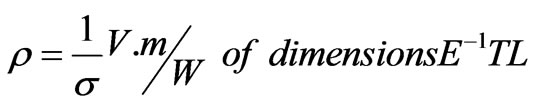 (22)
(22)
Resistance (reluctance):
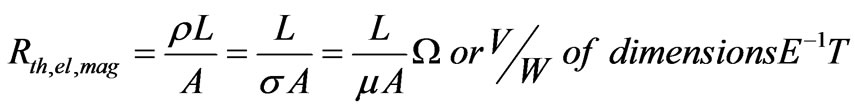 (23)
(23)
Coil Inductance
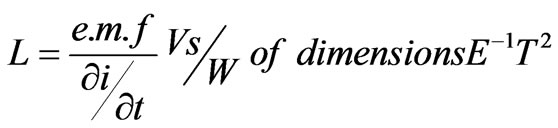 (24)
(24)
Capacitance (Electric and thermal)
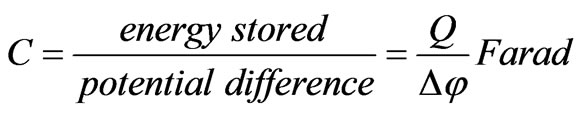 (25)
(25)
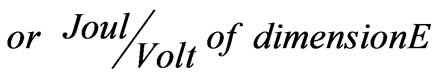
According to the limited number of dimensions of the introduced system, 3 dimensions, it is possible to represent the above mentioned derived units into a threedimensional space which is shown Figure 6. Such representation simplifies the dimensional comparison between different physical quantities and shows directly the analogy between different fields.
6. Discussion of the Introduced US of Units
The introduced US of units assigns unique dimensions for the analogous parameters in the electric and magnetic fields as the energy flux, resistance, conductivities, and resistivity as seen in Table 2 and Figure 5. The conflicts of the SI system of units, discussed in Table 1, are completely deleted as shown Table 2. People with knowledge of the B-field and H-field have argued, as Larson [11], that the SI system is in a mess because physics of such parameters is in a mess. They said that ascribing SI units to the permeability μ is not science but computational legerdemain. The introduced US of units express the permeability and the permittivity by units that are
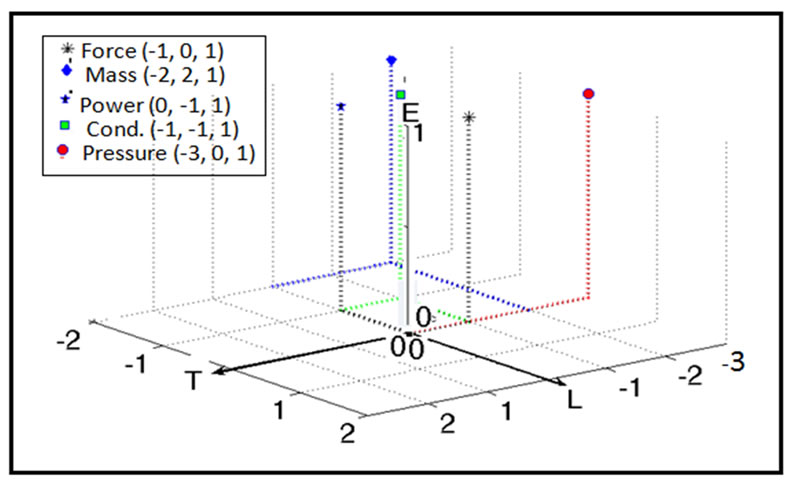
Figure 6. The postulated “TLE” dimensional system.

Table 2. Electric/Magnetic Fields analog in the US system.
analogous to the units of electrical or thermal conductivity. Similarly, the introduced system solves the conflicts of the SI system that measures the free space or vacuum permeability and permittivity by units that involve the mass while mass has no meaning in vacuum. Similarly; vacuum has an impedance SI units of “m2kg/sec3/Amp2”. Such impedance involves the mass in vacuum as one of its units while the mass does not exist in vacuum. As the US excludes the mass as a fundamental unit, it excludes also assigning the mass to vacuum as the unit of such impedance is Volt/watt.
We may look also at the units of the force between two electric charges, Coulomb’s force:
 (26)
(26)
Substituting the introduced dimensions of the charge Q in (E) and of the permittivity ε0 in (E L-1); the force will result directly in force dimensions and units, Newton. Such unit is already derived in Equation (16) as a unit of force in the introduced US of units. Looking at the definition of the fine structure constant; it is found as follows [14]:
 (27)
(27)
According to the introduced system: e is the elementary charge in J, 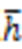 is the reduced Planck constant in J.s,
is the reduced Planck constant in J.s, 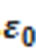 is the permittivity in J/m V and c is the speed of light in m/s. Substituting such units; it also leads to a dimensionless parameter in accordance to its definition.
is the permittivity in J/m V and c is the speed of light in m/s. Substituting such units; it also leads to a dimensionless parameter in accordance to its definition.
According to the SI system of units, the electron-volt is a unit of energy equal to approximately 1.602 × 10−19 J and is described also as a charge of 1.602 × 10−19 [14,15]. By classical definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt. So, it is not known if it is kinetic energy of 1.602 × 10−19 J or as described a charge of the same figure of quantity of 1.602 × 10−19 C. Such redundancy of the SI system that cannot find the plausible explanation of the equality of such figures of the electron’s charge in Coulomb and its kinetic energy in Joule is solved. In the US of units, we consider, as postulated here, the electric charge has the same unit as energy in Joule. In this case the e. V will be defined as the specific charge of the electron or the amount of energy that increases the potential of the electron by 1 volt in analogy to the defined specific heat of a body as the amount of heat that increases the temperature of such body by one degree.
The limited number of dimensions in the introduced system simplifies the application of the π dimensional theorem to express the relation between different physical quantities. As an example; the dimensionlessstructure constant can be found in terms of the permeability, the frequency of the electron charge and the related parameters as follows [16]:
 (28)
(28)
Equating the left sides of Equations (27) & (28) gives an interesting result:
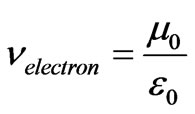 (29)
(29)
As the electron charge is considered, according to the postulated definition [4], a modified electromagnetic wave, it is possible to find the wavelength of an electric charge according to the relation:
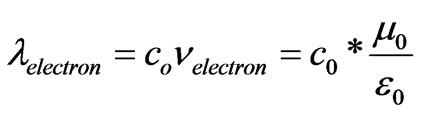 (30)
(30)
Such frequency assures the postulated definition of the charge as an electromagnetic wave of specified frequency [4] which is referred as Bohr’s electron frequency [16].
Applying the π dimensional theorem once more to find an expression for the magnetic attraction force between two parallel conductors of equal length L and carrying electric currents I1 and I2 in terms of the permeability of the surrounding medium (vacuum), speed of electromagnetic waves (or of electric charge) and the spacing between the conductors “d”; it can be found as:
 (31)
(31)
Equation (31) expresses the force is in Newton the force/unit length in N/m; i.e. in accordance to the US derived units.
To remove the mess between the B field and H field [11], the first law of thermodynamics, as a law of conservation of energy, is applied to the case of an electric motor shown in Figure 6. A power source of potential “V” is feeding the motor’s windings, which are connected in parallel, by a total current I as shown in Figure 6.
According to experimental data [16], the magnetic field intensity “H” is found, with sufficient accuracy, proportional to the potential of the feeding current “V”. According to this result, it is possible to prove with sufficient accuracy also that the voltage drop across the armature is equal to the intensity of the magnetic field strength of the shunt coil as both are connected in parallel, according to Figure 6, and both are measured by the same unit, according to the introduced US of units. So;
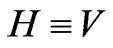 (32)
(32)
Accordingly; the input power to such motor can be determined by the following power relation [8]:
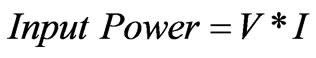 (33)
(33)
I is the sum of currents flowing through the magnet and armature windings. V is the same potential difference across the magnet and coil windings, Figure 7. The output work of such motor is [8]: F * ν or τ * ω; where F is the force acting on the armature-coil and ν is its velocity, τ is the torque acting on the armature-coil and ω is its angular velocity. The efficiency of this process can be written as follows:
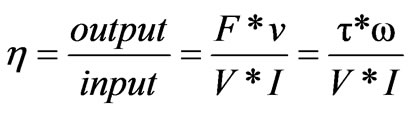 (34)
(34)
Substituting Equation (32) into Equation (33); it is possible to express the input power by a rather new relation:
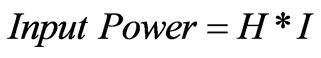 (35)
(35)
Such relation expresses directly the interactions between the intensity of the magnetic field H, that depends on the electrical field potential, V, and the flowing cur
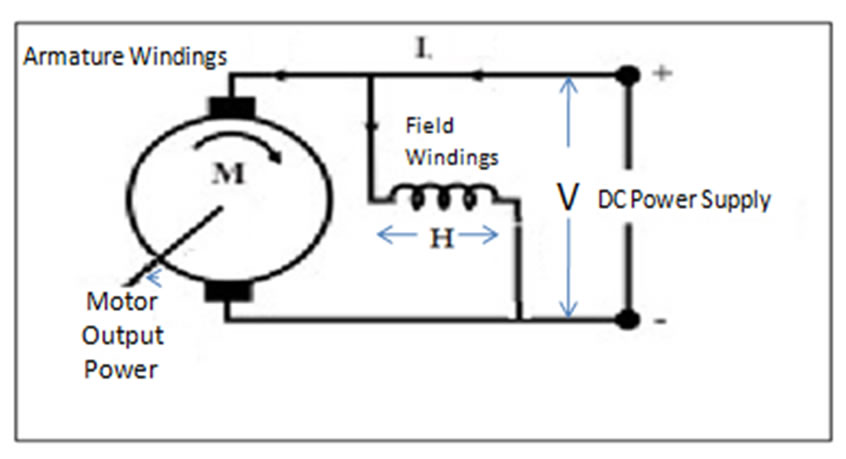
Figure 7. Armature and Field windings in parallel [8].
rent in the motor windings, I. The main effect of the field current is the generation of magnetic field of potential “H” through the magnetic core. Such core does not allow any current to flow but only magnetic flux. Equation (35) may be valid for measuring the power input to motors in general where it expresses interactions between electric and magnetic fields. Substituting Equation (35) into Equation (32), we can define the efficiency of the electric motor by a new relation:
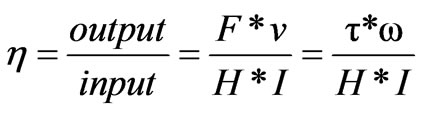 (36)
(36)
Hence, the force acting on a carrying currentconductor that moves in a magnetic field or the torque acting on such conductors can be expressed by dimensionally correct Equations in the US of units of the following form:
 N. (37)
N. (37)
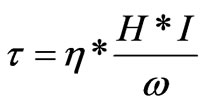 N. m (38)
N. m (38)
Such Equation can be generally validated for motors or generators.
7. Conclusions
This study introduces a system of units that removes the redundancies found in the SI system of units. Such system is called “Universal System” as it can be applied universally to all scientific fields. The introduced system depends on an entropy approach that used analogy between different forms of energy-system interactions and on a unique dimensionless scale that define all energypotentials. The introduced US of units is defined by four fundamental units and three dimensions. The limited number of dimensions in the introduced system simplifies the application of the π dimensional theorem to reformulate the relations between the physical parameters on dimensional basics. It offers also a plausible definition of the electron-volt as a unit for energy or charge. It helps also in expressing electromagnetic relations by dimensionally homogenous relations.
REFERENCES
- M. Abubakr, “On Dimensional Analysis, Redundancy in set of fundamental quantities and Proposal of a New Set,” General Physics, 2007. http://arxiv.org/abs/0710.3483v1
- X. Borg, “Unified Theory Foundations-The ST System of Units,” Blaze Labs Research, 2005. http://www.blazelabs.com/f-u-suconv.asp
- S. Abdelhady, “A Three Dimensional System of Units,” Proceedings of the 14th International Conference on Applied Mechanics and Mechanical Engineering, MTC, Cairo, May 2010, paper MD-4.
- S. Abdelhady, “A Fundamental Equation of Thermodynamics that Embraces Electrical and Magnetic Potentials,” Journal of Electromagnetic Analysis & Applications, Vol. 2, No. 3, 2010, pp. 162-168.
- A. C. Yunus and A. B. Michael, “Thermodynamics: An Engineering Approach,” McGraw-Hill Science Engineering, 2006.
- P. W. Atkins and J. DePaula, “Physical Chemistry,” 8th Edition, Oxford University Press, W.H. Freeman & Co., 2006.
- V. Kumar, J. Singh and S. S. Verma, “Performance Comparison of Some Common Thermocouples for Waste Heat Utilization,” Asian Journal of Chemistry, Vol. 21, No. 10, 2009, pp. 62-65.
- J. Jewett and R. A. Serway, “Physics for Scientists and Engineers with Modern Physics,” 7th Edition, Thomson, Brooks/Cole, 2008.
- G. D. Yarnold, “Notes on Electric and Magnetic Dimensions,” Proceedings of the Physical Society, iopscience. iop.org, 1942, pp. 189-193.
- S. W. Hawking and G. F. R. Ellis, “The Large Scale Structure of Space-Time,” Cambridge University, 1973.
- R. Clarke, “Unit System in Electromagnetism,” 2009. http://info.ee.surrey.ac.uk/Workshop/advice/coils/unit_systems/index.html
- G. M. Trunov, “Correctness of the International System of Units in the Area of Electromagnetism,” Journal of Measurement Techniques, Vol. 26, No. 1, 1983, pp. 9-10.
- A. J. Hewitt, A. Ahfock and S. A. Suslov, “Magnetic Flux Density Distribution in Axial Flux Machine Cores,” Electric Power Applications, IEE Proceedings, 2005, Vol. 152, pp. 292-296.
- F. Stevens and F. Charles, “The Six Core Theories of Modern Physics”, MIT Press. ISBN 0-262-69188-4, 1965.
- J. L. Flowers, N. J. Cleaton, P. W. Josephs and B. W. Betlev, “Progress toward a Precision Measurement of the Helion Magnetic moment in Bohr Magnetons,” Instrumentation and Measurement, IEEE Transactions, Vol. 48, 1999, pp. 209-211.
- R. G. Bartheld and J. A. Kline, “Comparative Efficiency Measurements,” IEEE Proceedings, Vol. 38, No. 2, 1997, pp. 608-614.

