Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 7 (2010) , Article ID: 2334 , 5 pages DOI:10.4236/jemaa.2010.27056
Influence of Magnetic Field Intensity on the Temperature Dependence of Magnetization of Ni2.08Mn0.96Ga0.96 Alloy
![]()
Bulk nanostructures and nanotechnology, Institute for Metals Superplasticity Problems Russian Academy of Sciences, Ufa, Russia.
Email: irekmusabirov@imsp.da.ru
Received April 20th, 2010; revised June 7th, 2010; accepted June 12th, 2010.
Keywords: Shape memory alloy, Magnetization, Ni-Mn-Ga, Martensitic transformation, Heusler alloys
ABSTRACT
Results of investigation of the temperature dependence of magnetization of Ni2.08Mn0.96Ga0.96 alloy in the magnetic fields of various intensities are reported. An abrupt change in magnetization at transformation of low temperature phase to the high temperature one is observed. Magnetization increases during the phase transition in the magnetic field having intensity below 500 kA/m and decreases at higher intensities. The explanation is based on zigzag configuration of domains in twinned structure. In the Curie temperature region the ferromagnetic ↔ paramagnetic phase transition occurs sharply at low field strength, while at higher field strength the transition is smooth. It is concluded that the increase in flatness of the curve σ = f (T) and the increase of ferromagnetic state destruction temperature with increase of the intensity of the magnetic field is indicative of the main role of Mn in magnetization of the alloy.
1. Introduction
Owing to the fact that martensitic phase transition occurs in Ni-Mn-Ga alloys in room temperature region, they exhibit shape memory effect (SME) [1]. It is also known that phases forming in Ni-Mn-Ga system alloys before and after martensitic transformation are ferromagnetic [2]. Such feature of these materials allows controlling the effect of shape memory by means of the external magnetic field [3]. In particular, under the magnetic field there occurs a change in crystal linear dimensions up to 9 % in single crystal Ni48.8Mn29.7Ga21.5 sample [4]. The possibility to control sample dimensions expands practical application of these alloys as functional materials. Observation of similar effect for polycrystalline samples is very promising for applications but this requires a detailed study of physical properties of the material.
In spite of a large number of works considering physical properties of Ni-Mn-Ga system alloys, the mechanisms of changes of some of their properties during the phase transformation are still not fully understood. For example, measurement made in the magnetic field of low intensity has revealed an abrupt increase in magnetization on the temperature dependence of magnetization for Ni2MnGa alloy. Traditionally this increase is attributed to the change in magnetocrystalline anisotropy constant at phase transformation [5-7]. Some authors consider that magnetic moments of Ni and Mn in low temperature phase are antiparallel and after transition to high temperature phase they become parallel [8,9].
In the existing literature, the authors usually do not pay attention to the behavior of the temperature dependence of magnetization in the vicinity of the Curie temperature in spite of the facts, that also in this region the effect of the magnetic field is rather essential. Magnetic field reveals the role of the magnetic moment of Mn atoms in the magnetization of the alloy. Previously its role was confirmed by the neutron diffraction studies [10,11].
In order to obtain additional data on the change of alloys physical properties during the phase transitions we carry out the investigation of temperature dependence of magnetization of polycrystalline Ni2.08Mn0.96 Ga0.96 alloy in magnetic fields of various intensities. An explanation of the obtained results is proposed.
2. Materials and Experimental Procedure
The Ni2.08Mn0.96Ga0.96 alloy was prepared by vacuum arc melting [12]. The sample with 1 mm × 1 mm × 6 mm dimensions was cut from alloy cast ingot by electrospark method. The selection of this alloy was motivated by the absence of intermartensitic transformation and the occurrence of direct transition of the low temperature phase to the high temperature one. Therefore during measuring the temperature dependence of magnetization in low intensity magnetic field only one abrupt changing of magnetization in phase transition region was observed.
The data of temperature dependence of magnetization have been recorded by means of a vibrating-coil magnetometer using a sample cut from the ingot processed for former studies of thermal expansion [13]. In measurements, magnetic field of intensity not greater than 1 MA/m was applied along the long side of the sample. To simplify the task, heating curves for all values of intensity are shown in Figure 2, and heating and cooling curves for two values of field intensity in Figure 3. Measurements were made within the temperature range 225-425 K at a rate of 5 K/min.
The sample surface was polished at 340 K for the purpose to expose of microrelief of the low-temperature phase. At this temperature the alloy is in the height temperature phase. Martensitic transformation that takes place on cooling of the sample results in the appearance of microrelief on its surface visible by optical microscope. Investigation of microstructure was carried out by optical metallographic microscope AXIOVERT-100A with especial attachment for cooling the sample down to 230 K.
3. Results and Discussion
Figure 1 shows a fragment of the low temperature phase microstructure of the sample processed at 260 K. Evidently the polycrystalline sample has sufficiently coarse grains (grain size ~ 360 μm) and each is divided into many twin plates with a width varying from 1 to 30 μm. Since the sample is polycrystalline the distribution of twins is chaotic. After repeated heating and cooling the distribution of twin structure does not change. The essential influence of magnetic field with intensity below 916 kA/m on twin plate dimensions and theirs distribution in low temperature phase formed during martensitic transformation without applying of magnetic field has not been revealed. Figure 2 shows the temperature dependence of magnetization (σ/σS (T), where σS is saturation magnetization measured at 223 K) for the selected alloy, the measurement being made in the magnetic field of different intensity. From figure 2 one can conclude that the influence of magnetic field on the σ/σS (T) dependence is most apparent in phase transition regions. In particular, in the region of martensite transformation it causes an abrupt changing of magnetization while in the region of magnetic phase transition it increases the transition temperature of ferromagnetic to paramagnetic state. From curve 1 in Figure 2 (H = 24 kA/m) it is seen that magnetization of low temperature phase remains equal to 0.10 × σS until 271 K. Then with increasing temperature a value of magnetization increases abruptly and reaches 0.46 × σS at 315 K. This abrupt increase is obviously due to the transition to high temperature phase. On further heating magnetization of high temperature phase starts to decrease slowly at first and then rapidly drops to zero at 375 K.
The character of curve 2 (Н = 80 kA/m) is almost similar to curve 1.The difference is in the value of magnetization which is higher by 16%. The transition of the alloy to the paramagnetic state begins at 380 K and also has an abrupt character.
The character of curve 3 (Н = 409 kA/m) slightly differs from that of curve 2. The increase in magnetization is not so abrupt and is about 4%. Moreover, the declineation of σ/σS (T) dependence curve to zero is smoother. In this case ferromagnetic state is destroyed at 391 K.

Figure 1. Optical micrograph of low temperature phase Ni2.08Mn0.96Ga0.96 alloy

Figure 2. Curves of temperature dependence of magnetization Ni2.08Mn0.96Ga0.96 alloy, recorded during the heating in magnetic field follow intensity: 1) Н = 24 kA/m, 2) Н = 80 kA/m, 3) Н = 409 kA/m, 4) Н = 916 kA/m
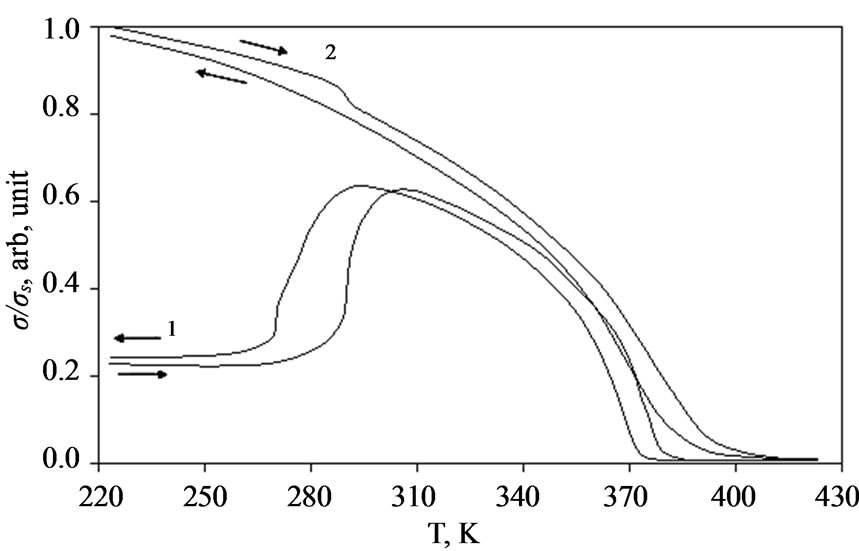
Figure 3. Curves of temperature dependence of magnetization Ni2.08Mn0.96Ga0.96 alloy, recorded during the heating and cooling in magnetic field follow intensity: 1) Н = 80 kA/m, 2) Н = 916 kA/m
The character of curve 4 (Н = 916 kA/m) is absolutely different. Unlike the previous cases, characterized by the abrupt increase in magnetization, a decrease in magnetization by 3.5% is observed here. In the region of paramagnetic transition the σ/σS (T) curve is flatter and it drops to zero at 396 K. The measurements σ = f (H) have shown that in this magnetic field magnetization almost reaches saturation.
We think that the most interesting result is an abrupt increase in magnetization in the field of low intensity. The known explanation of this phenomenon [5-9] requires a deeper analysis. The present work proposes a different explanation of the observed effect presented in what follows.
It is known that in ferromagnetic crystals magnetic moments of domains are aligned with defined direction relative to crystallographic axes, named easy magnetic axes. Easy magnetic axis is tilted by 45° relative to the plane of twinning [14,15]. In the absence of the magnetic field 180°- domains of similar width are formed in twins. It is typical for uniaxial ferromagnets. Such distribution of domains in twinning structure of low temperature phase is shown in figure 4(a). Consequently at transition from one twin to another MS vectors will form a zigzag type line. In the case of the magnetic field of low intensity the domains orientated favorably to the field direction start to expand while adjacent ones shrink. Then magnetization of the sample in this field is the sum of projections of differences ΔMS of wide and narrow domains on the direction of external magnetic field. Obviously, due to the zigzag type orientation of domains, the vector sum ΔMS is less than the algebraic sum. This results in a smaller value of magnetization in low temperature phase as compared to its value in high temperature phase. This explanation is similar to the one proposed in 1996 by Vasil’ev A.N. et al. [16]. However, it has not become widespread.
Below it has been shown that with the increase of magnetic field intensity up to 80 kA/m the curve σ/σS (T) increases only slightly (by 16%) and it practically does not change. So one can conclude that in the field with such intensity the orientation of vectors are controlled by magnetic crystalline anisotropy while the increase in σ is due to the change in the width of the domains orientated favorably to the applied field. The distribution of domains in this case is shown in figure 4(b). The significant increase in σ and a decrease in magnetization jump in the case of H = 409 kA/m testify that the effect of the external field is commensurable with that of crystalline anisotropy. Under such conditions the magnetization of the sample occurs not only due to the shift of domain boundaries but also due to the rotation of MS toward the direction of the external field (Figure 4(c)). A small increase in σ indicates that there remains the influence of anisotropy.
The essential growth of magnetization in the field of saturation (curve 4, Figure 2) testifies that under the effect of such a field MS of domains in all twins are aligned along the magnetic field irrespective of their previous orientation, as in figure 4(d). Some decrease in a value of saturation magnetization at phase transformation is evidently attributed to the occurring distortion of crystal lattice symmetry.
Before explaining the character of the curves σ/σS (T) in the region of magnetic phase transformation (ferromagnetic ↔ paramagnetic), one should note a significant influence of magnetic field intensity on both the transition temperature in paramagnetic state and the gradient of its drop to zero. One can expect the effect of magnetic field on these characteristics because Mn atom has a great magnetic moment. In high temperature phase of Ni2MnGa
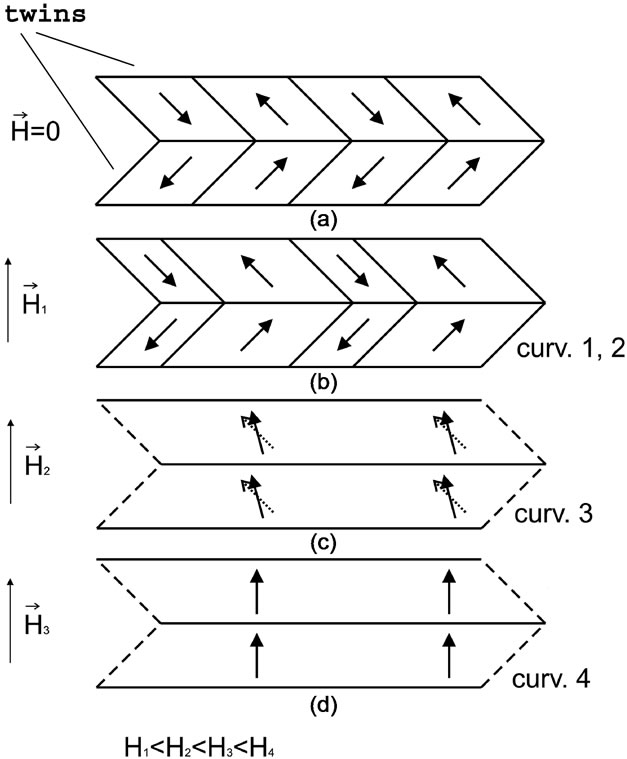
Figure 4. Scheme of domain structure in twins with magnetic fields various intensities
magnetic moment of Mn (2.3 μB) is larger than that of Ni (0.22 μB) by a factor of 10 [11]. Therefore atoms of Mn play the major role in forming the alloy magnetization.
The value of magnetization of ferromagnetic in the magnetic field at each temperature is a result of competition between the exchange energy (Wex.en.) and interaction energy of magnetic moments of atoms with magnetic field (Wmagn. int.) on one hand and thermal energy on the other hand.
The exchange interaction and the interaction of atom magnetic moments with external field tend to keep the ferromagnetic order in the sample whereas the thermal fluctuations tend to disorder the arrangement of atom magnetic moments. In ferromagnetic, where the magnetization is created by relatively small magnetic moments, the relation Wmagn. int. << Wex.en. should be fulfilled. For this reason, the intensity of the applied field in this case does not noticeably affect the character of the curve σ/σS (T) in the region of magnetic transformation. When magnitude of magnetic moments is large, the values Wmagn. int. and Wex.en. are comparable and their joint action should maintain the ferromagnetic order at higher temperatures. As a result, the σ/σS (T) curve in the region of the Curie temperature should be flatter and the ferromagnetic state should be destroyed at higher temperature.
The σ/σS (T) dependencies obtained on heating and on cooling of the sample in the magnetic field with the intensities 80 kA/m and 916 kA/m are shown in Figure 3. The heating curves have been described above. As for the cooling curves, one can say the following.
Apparently the curves σ/σS (T) obtained on heating and on cooling in the magnetic field of 80 kA/m intensity are similar. The difference is that cooling curve is shifted to the low temperature region. The shift is 19 K in the structure transition region, and 7 K in the magnetic transformation region. Such difference in temperature hysteresis evidently testifies to the fact that magnetic transformation (second order phase transition) occurs easier, while structural transition (first-order phase transformation) occurs with more difficulties, since it requires more essential overcooling. Magnetization of the low temperature phase after cooling down to 223 K remains slightly higher its initial value. Most likely, this is related to the fact that ferromagnetic undergoes stronger magnetization when cooling takes place in magnetic field.
From the cooling curve in the magnetic field of 916 kA/m intensity it is seen that temperature hysteresis in the magnetic transition region is 9 K. In the region of structure transformation the temperature hysteresis is not observed and after cooling magnetization of low temperature phase remains lower than its initial value.
4. Conclusions
In can be concluded that in the region of structural phase transformation the curves σ/σS (T) is affected by the magnetic field of low intensity, while in the region of magnetic phase transformation it is affected by the magnetic field of high intensity. The abrupt decrease in magnetization at the transition from the high temperature phase to the low temperature one in magnetic fields of low intensity is attributed to a zigzag change of vector MS in the domains of twin structure. The increase in the intensity of the magnetizing field leads to a noticeable increase of the ferromagnetic ↔ paramagnetic transition temperature.
5. Acknowledgements
The authors would like to thank Professor V. Shavrov and V. Koledov for providing us with the alloy for the present study.
REFERENCES
- K. Ullakko, J. K. Huang, C. Kantner, R. C. O’Handley and V. V. Kokorin, “Large Magnetic-Field-Induced Strains in Ni2MnGa Single Crystals,” Applied Physics Letters, Vol. 69, No. 13, 1996, pp. 1966-1968.
- A. N. Vasil’ev, V. D. Buchel’nikov, T. Takagi, V. V. Khovailo and E. I. Estrin, “Shape Memory Ferromagnets,” Physics-Uspekhi, Vol. 46, No. 6, 2003, pp. 559-588.
- A. A. Cherechukin, I. E. Dikshtein, D. I. Ermakova, A. V. Glebov, V. V. Koledov, D. A. Kosolapov, V. G. Shavrov, A. A. Tulaikova, E. P. Krasnoperov and T. Takagi, “Shape Memory Effect due to Magnetic Field-Induced Thermoelastic Martensitic Transformation in Polycrystalline Ni– Mn–Fe–Ga Alloy,” Physics Letters A, Vol. 291, No. 2-3, 2001, pp. 175-183.
- A. Sozinov, A. A. Likhachev, N. Lanska and K. Ullakko, “Giant Magnetic-Field-Induced Strain in NiMnGa SevenLayered Martensitic Phase,” Applied Physics Letters, Vol. 80, No. 10, 2002, pp. 1746-1748.
- P. Lazpita, J. M. Barandiaran, J. Gutierrez, M. Richard, S. M. Allen and R. C. O’Handley, “Magnetic and Structural Properties of Non-Stoichiometric Ni-Mn-Ga Ferromagnetic Shape Memory Alloys,” European Physical Journal: Special Topics, Vol. 158, No. 1, 2008, pp. 149-154.
- D. Kikuchi, T. Kanomata, Y. Yamaguchi, H. Nishihara, K. Koyama and K. Watanabe, “Magnetic Properties of Ferromagnetic Shape Memory Alloys Ni2Mn1−xFexGa,” Journal of Alloys and Compounds, Vol. 383, No. 1-2, 2004, pp. 184-188.
- J.-H. Kim, F. Inaba, T. Fukuda and T. Kakeshita, “Effect of Magnetic Field on Martensitic Transformation Temperature in Ni–Mn–Ga Ferromagnetic Shape Memory Alloys,” Acta Materialia, Vol. 54, No. 2, 2006, pp. 493-499.
- V. D. Buchelnikov, M. A. Zagrebin, S. V. Taskaev, V. G. Shavrov, V. V. Koledov and V. V. Khovaylo, “New Heusler Alloys with a Metamagnetostructural Phase Transition,” Bulletin of the Russian Academy of Sciences: Physics, Vol. 72, No. 4, 2008, pp. 564-568.
- V. D. Buchel’nikov, S. V. Taskaev, M. A. Zagrebin and P. Entel, “Phase Diagrams of Heusler Alloys with Inversion of the Exchange Interaction,” Letters to Journal of Experimental and Theoretical Physics, Vol. 85, No. 11, 2007, pp. 560-564.
- A. Ayuela, J. Enkovaara, K. Ullakko and R. M. Nieminen, “Structural Properties of Magnetic Heusler Alloys,” Journal of Physics: Condensed Matter, Vol. 11, No. 8, 1999, pp. 2017-2026.
- P. J. Brown, A. Y. Bargawi, J. Crangle, K.-U. Neumann and K. R. A. Ziebeck, “Direct Observation of a Band Jahn–Teller Effect in the Martensitic Phase Transition of Ni2MnGa,” Journal of Physics: Condensed Matter, Vol. 11, No. 24, 1999, pp. 4715-4722.
- A. A. Cherechukin, I. E. Dikshtein, D. T. Ermakov, A. V. Glebov, V. V. Koledov, D. A. Kosolapov, V. G. Shavrov, A. A. Tulaikova, E. P. Krasnoperov and T. Takagi, “Shape Memory Effect due to Magnetic Field-Induced Thermoelastic Martensitic Transformation in Polycrystalline Ni–Mn–Fe–Ga Alloy,” Physics Letters A, Vol. 291, No. 2-3, 2001, pp. 175-183.
- K. Y. Mulyukov and I. I. Musabirov, “Effect of a Magnetic Field on the Thermal Expansion of Ni2.08Mn0.96Ga0.96 Alloys,” Technical Physics, Vol. 53, No. 6, 2008, 802- 803.
- Y. Ge, O. Heczko, O. Soderberg and V. K. Lindroos, “Various Magnetic Domain Structures in a Ni–Mn–Ga Martensite Exhibiting Magnetic Shape Memory Effect,” Journal of Applied Physics, Vol. 96, No. 4, 2004, pp. 2159-2163.
- O. Heczko, “Magnetic Shape Memory Effect and Magnetization Reversal,” Journal of Magnetism and Magnetic Materials, Vol. 290-291, 2005, pp. 787-794.
- A. N. Vasil’ev, S. A. Klestov, R. Z. Levitin and V. V. Snegirev, “Magnetoelastic Interaction in the Martensitic Transformation in an Ni2MnGa Single Crystal,” Journal of Experimental and Theoretical Physics, Vol. 82, No. 3, 1996, pp. 524-526.

