Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 5 (2010) , Article ID: 1918 , 7 pages DOI:10.4236/jemaa.2010.25040
Finite Element Based Analysis of Magnetic Forces between Planar Spiral Coils
![]()
1Department of Electrical Engineering, Iran University of Science and Technology, Tehran, Iran; 2Mapna Generator Engineering & Manufacturing Company (PARS), Tehran, Iran.
Email: abbas_shiri@iust.ac.ir
Received January 23rd, 2010; revised March 21st, 2010; accepted March 25th, 2010.
Keywords: Magnetic Force, Finite Element Method, Concentric Rings Method, Planar Spiral Coils
ABSTRACT
This paper elaborates on the magnetic forces between current carrying planar spiral coils. Direct and concentric rings methods are employed in order to calculate the magnetic force between these coils. The results obtained by two calculation methods show the efficiency of the replaced rings method in both simplicity and calculation time. Simulations using the Finite Element Method (FEM) are carried out to analyze the distribution of the magnetic flux density around the coils. Also, coils with precise size have been constructed and tested. The experimental results as well as the results obtained by FEM are used to validate the accuracy of the calculations.
1. Introduction
Regarding the extensive application of planar spiral coils in communication and robotics, determination of magnetic fields around them and forces between these coils are interesting for engineers. In these systems, to have a high inductance and flat configuration, spiral windings are employed [1-3]. Besides, these coils have an extensive application in power electronics and DC/DC converters due to their flatness and special configuration; so, they are better replacement for the ordinary inductances in order to reduce the volume of the converter [4-7]
In recent decades, spiral coils are employed in casting industries to form the thin metal sheets. In [8] the finite difference method is employed to calculate the force between them; furthermore, in this reference to calculate the magnetic force, spiral coils are replaced by concentric rings, but there is no study and discussion on the precision of the method. In [3] these forces are obtained just by test. In [9, 10] the force between circular coaxial coils has been investigated. Recently, the mesh-matrix method has been employed in order to calculate the force between spiral coils [11]. In this paper, using concentric rings instead of spiral coils, an effective and simple procedure is proposed to calculate the magnetic force between these coils. Using the results obtained from the numerical solution of the direct calculation method, the precision of the proposed method is investigated and finally compared with experimental results.
2. Calculation of Magnetic Force between Planar Spiral Coils Using Direct Method
Suppose a system of two spiral coils as shown in Figure 1. To calculate the magnetic force between them, we should first calculate the vector magnetic potential resulting from one of the coils in any given point like P (see Figure 2).
Vector magnetic potential of spiral coil 1 in any given point P is obtained by the following equation [12]:
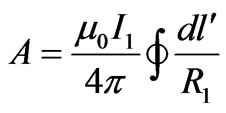 (1)
(1)
where ![]() is the current of the coil,
is the current of the coil, 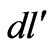 is the longitudinal differential component, and
is the longitudinal differential component, and 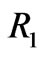 is the distance between this differential component and point P.
is the distance between this differential component and point P.
The coordinates marked by prime are related to the source. With suitable substitutions for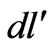 , the following equation for vector magnetic potential is obtained:
, the following equation for vector magnetic potential is obtained:
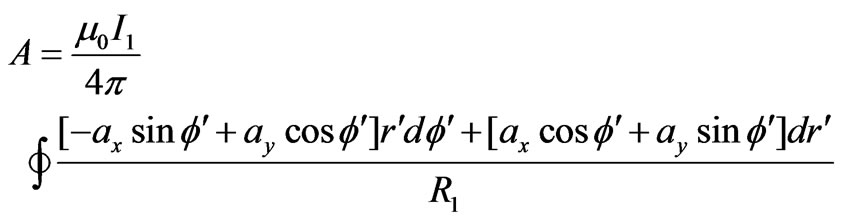 (2)
(2)
To calculate the integral in (2), one of the integral variables must be replaced by another one according to the
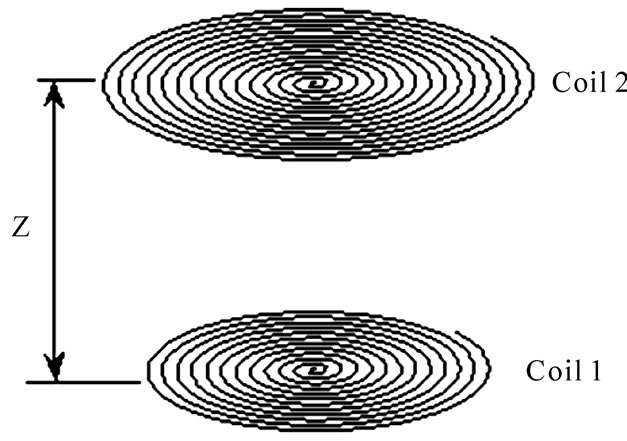
Figure 1. The two spiral coils in z distance of each other

Figure 2. Calculation of the vector magnetic potential of spiral coils in any given point like P
relations between them. The variables  and
and 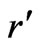 have a linear relation; consequently, we can write [13,14]:
have a linear relation; consequently, we can write [13,14]:
 (3)
(3)
where 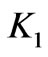 is a constant coefficient that is called “compression factor” of coil 1 in this paper. This factor depends on the diameter of the wire used and the structure of the coil and determines its compression. Having the vector magnetic potential, magnetic field is calculated using the following equation [12]:
is a constant coefficient that is called “compression factor” of coil 1 in this paper. This factor depends on the diameter of the wire used and the structure of the coil and determines its compression. Having the vector magnetic potential, magnetic field is calculated using the following equation [12]:
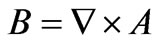 (4)
(4)
The force acted on the coil 2 is [12]:
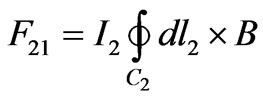 (5)
(5)
In the above equation,  is longitudinal differential component on coil 2. Substituting proper expression for
is longitudinal differential component on coil 2. Substituting proper expression for 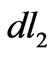 and employing (4) in (5) and doing some mathematical calculations, we get:
and employing (4) in (5) and doing some mathematical calculations, we get:
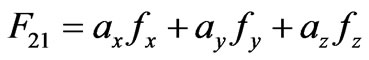 (6)
(6)
where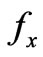 ,
,  and
and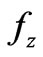 are the components of the force in directions x, y and z, respectively, and equal to (7)-(9) at the bottom of the page.
are the components of the force in directions x, y and z, respectively, and equal to (7)-(9) at the bottom of the page.
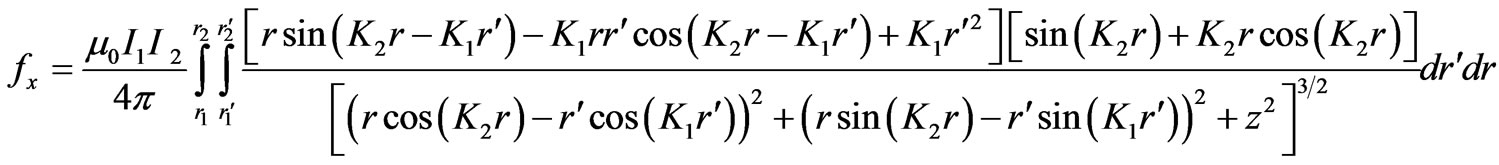 (7)
(7)
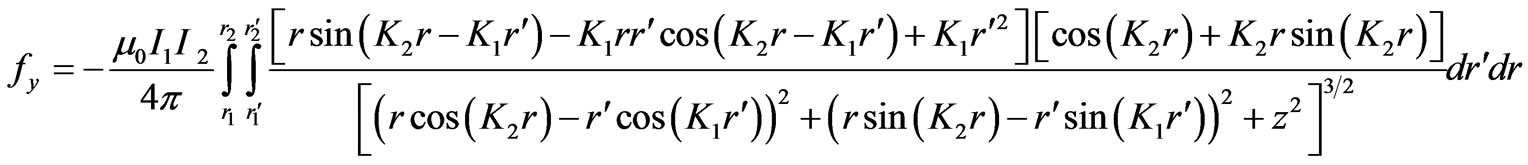 (8)
(8)
 (9)
(9)
In (7)-(9), the parameters 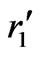 and
and 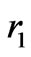 are the inner radii of coil 1 and 2, respectively, and
are the inner radii of coil 1 and 2, respectively, and 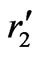 and
and ![]() are the outer radii of coil 1 and 2, respectively. Also, the following equation has been used [14]:
are the outer radii of coil 1 and 2, respectively. Also, the following equation has been used [14]:
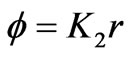 (10)
(10)
where 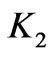 is compression factor of coil 2 determined with regard to the compression of the coil and the diameter of the wire used in it.
is compression factor of coil 2 determined with regard to the compression of the coil and the diameter of the wire used in it.
3. Concentric Rings Method
In calculation of the magnetic force between spiral coils, as Equations (7)-(8) show, using the analytical method is slightly complex and time-consuming. Furthermore, the obtained integrands are not smooth functions, and we have some difficulties in calculation of their integrals. To overcome this problem, we can replace the spiral coils with concentric rings and then calculate the forces between them [13,15]. To do this, the force between two concentric current carrying rings should be determined. Suppose rings 1 and 2 with radiuses ![]() and
and  while carrying currents
while carrying currents ![]() and
and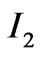 , respectively (see Figure 3). The force between the two rings is given by (11)
, respectively (see Figure 3). The force between the two rings is given by (11)
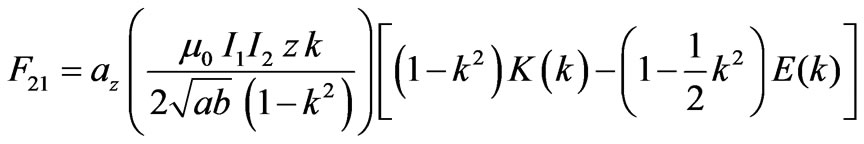 (11)
(11)
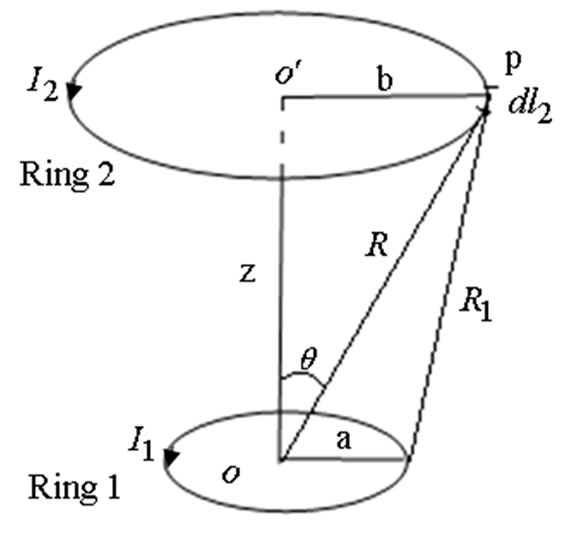
Figure 3. Two concentric current carrying rings
In the above equation, 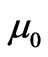 is the permeability of vacuum and k is a constant parameter which is equal to:
is the permeability of vacuum and k is a constant parameter which is equal to:
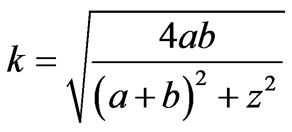 (12)
(12)
and 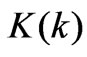 and
and  are the first and the second order elliptic integrals, respectively, and are equal to:
are the first and the second order elliptic integrals, respectively, and are equal to:
 (13)
(13)
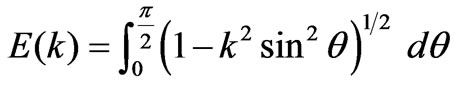 (14)
(14)
Now, having the force between the two rings, we can calculate the force between the two spiral coils with replacing them by concentric rings (Figure 4). The magnetic force between the two coils (the force exerted on coil 2 from coil 1 in Figure 4) will be as follows:
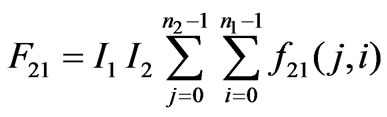 (15)
(15)
where 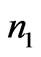 and
and  are the number of turns of coil 1 and 2, respectively, and
are the number of turns of coil 1 and 2, respectively, and  is equal to:
is equal to:
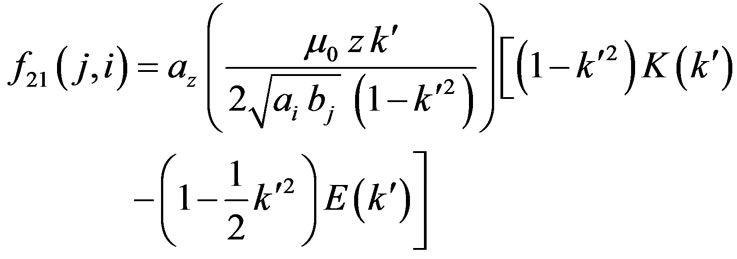 (16)
(16)
In the above equation, z is the distance between the two coils, and the parameters ,
, 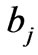 and
and 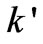 are defined as:
are defined as:
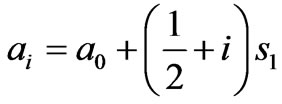 (17)
(17)
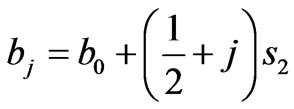 (18)
(18)
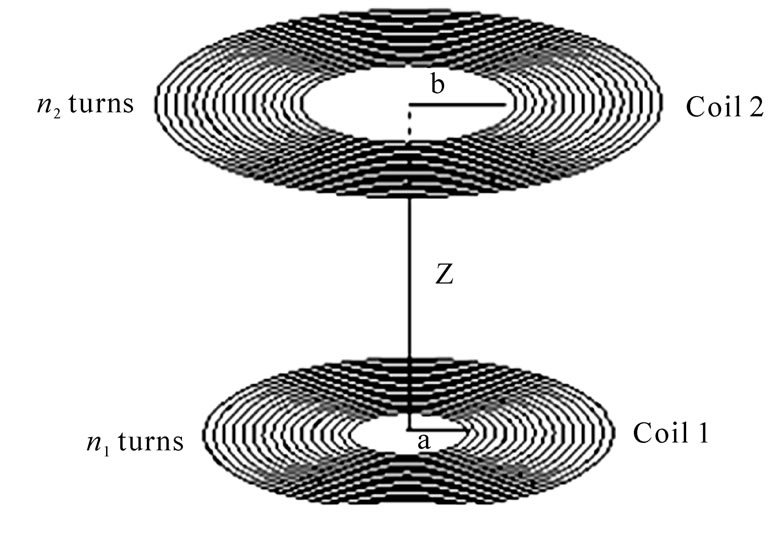
Figure 4. Two coils with concentric rings
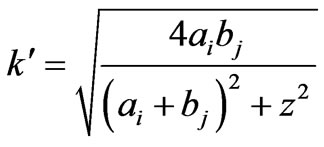 (19)
(19)
where 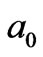 and
and 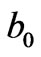 are the inner radius of coils 1 and 2 and
are the inner radius of coils 1 and 2 and ![]() and
and 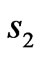 are the distance between two neighboring turns in coils 1 and 2, respectively. If the coils are wound compressively, then
are the distance between two neighboring turns in coils 1 and 2, respectively. If the coils are wound compressively, then ![]() and
and 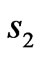 must be replaced by diameter of the wires used in coils 1 and 2, respectively.
must be replaced by diameter of the wires used in coils 1 and 2, respectively.
4. Calculation Results
In Section 2, the force between two spiral coils was analytically obtained (6). Suppose that the compression factors of the coils are high. In this case, the force values in x and y directions are almost zero, and the component of the force in z direction is non-zero [13,15] which is given by (9). The force in this relation is the force exerted on coil 2 from coil 1 as it is shown in Figure 1.
Although we use precise analytical relations to obtain the force in (9), its integral has no analytical solution, and numerical integration techniques must be used to solve it. The integrand of (9) has some “semi-poles” which depend on the value of the compression factors  and
and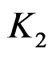 . In [11] it was shown that integration of (9) is much more difficult because in order to obtain higher precisions, one needs to increase the number of iterations of numerical integration intensively which, in turn, requires much longer computational time to solve such a problem.
. In [11] it was shown that integration of (9) is much more difficult because in order to obtain higher precisions, one needs to increase the number of iterations of numerical integration intensively which, in turn, requires much longer computational time to solve such a problem.
Now, we compare the results of direct calculation of the force using (9) with that of replaced concentric rings method. To calculate the integral in (9), we used recursive adaptive Simpson Quadrature method. In the replaced concentric rings method, the radius of each ring is assumed to be the average of the inner and the outer radii of each turn of spiral coils. In Tables 1 and 2 the results of calculation of the force using two methods for different values of turn number and different center to center
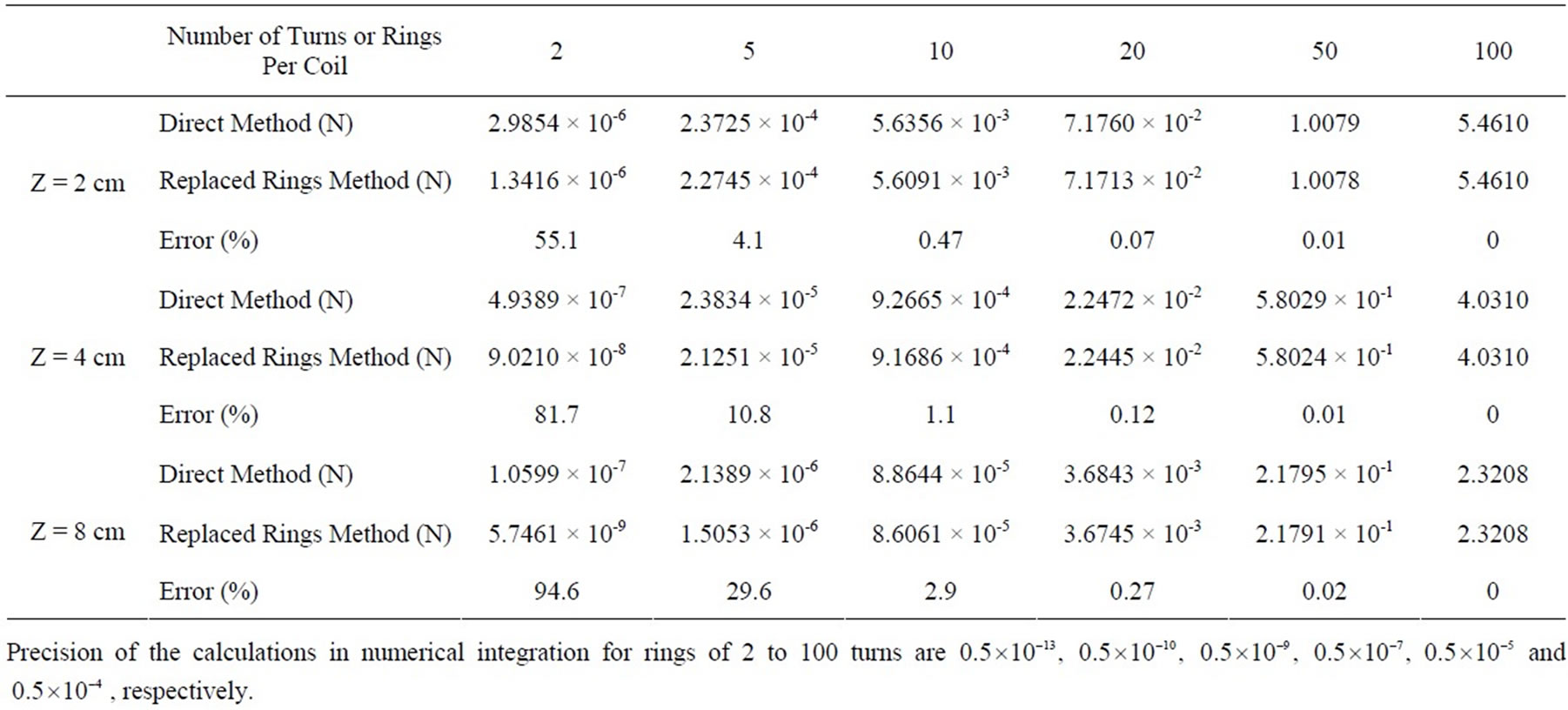
Table 1. Comparison of the force calculation methods between two spiral coils (inner radii and compression factor of the coils are 0 and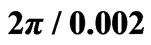 , respectively)
, respectively)
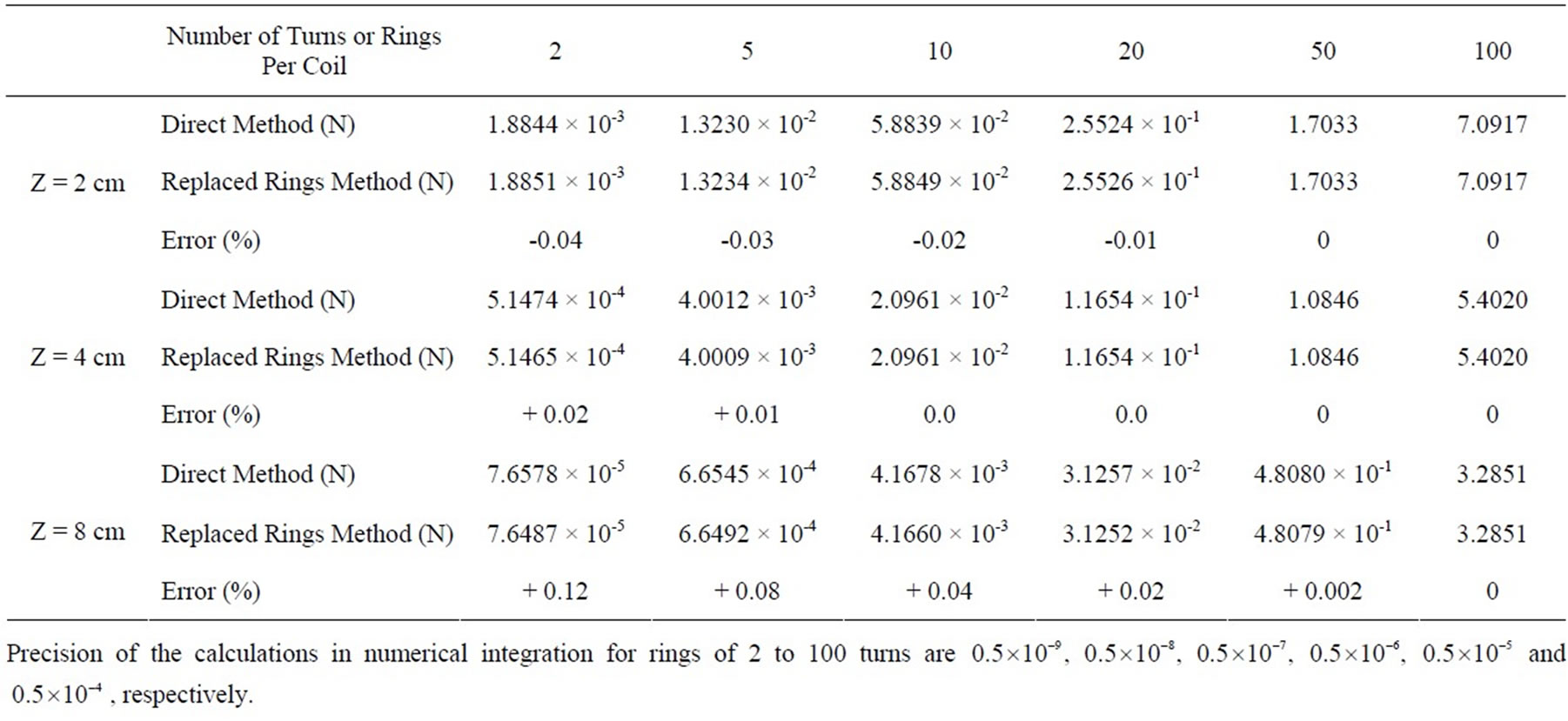
Table 2. Comparison of the force calculation methods between two spiral coils (inner radii and compression factor of the coils are 2.5 cm and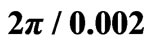 , respectively)
, respectively)
distance of coils are compared. In these tables, the current in both coils is 20 Amperes, the diameter of the wires is 2 mm, and the compression factor for both coils is assumed to be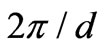 , where d is the diameter of the wires in both coils. In Table 1, it is assumed that the coils start to grow from point (0, 0). Comparing the results of the two methods in this table, it is seen that for the fewer number of turns the error is high, but by increasing the number of turns, the error gradually decreases, and when the turn number approaches to 100, the error becomes zero. In Tables 1 and 2 the precision of the calculations is adjusted according to the numerical value of the results. For instance, for the first column of Table 1 the calculated numbers are in the range of
, where d is the diameter of the wires in both coils. In Table 1, it is assumed that the coils start to grow from point (0, 0). Comparing the results of the two methods in this table, it is seen that for the fewer number of turns the error is high, but by increasing the number of turns, the error gradually decreases, and when the turn number approaches to 100, the error becomes zero. In Tables 1 and 2 the precision of the calculations is adjusted according to the numerical value of the results. For instance, for the first column of Table 1 the calculated numbers are in the range of 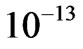 (their minimum value). To compare the calculation time in two approaches, it suffices to mention that the required calculation time using the adaptive Simpson method for 100 turns in Table 1 for precision of
(their minimum value). To compare the calculation time in two approaches, it suffices to mention that the required calculation time using the adaptive Simpson method for 100 turns in Table 1 for precision of 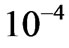 is 28000 times more than that of using replaced concentric rings method. As seen in the table, the results precisely coincide with each other. Another interesting point about Table 1 is that by increasing the distance between the two coils, the calculation error increases showing that in large distances, the replaced concentric rings method does not present a proper approximation of the force.
is 28000 times more than that of using replaced concentric rings method. As seen in the table, the results precisely coincide with each other. Another interesting point about Table 1 is that by increasing the distance between the two coils, the calculation error increases showing that in large distances, the replaced concentric rings method does not present a proper approximation of the force.
In Table 2, the comparison between two methods is made for the case in which the inner radius of two coils are equal to 2.5cm; in other words, the coils start to wind from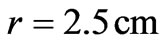 . As seen from the results of the table, the errors in this case are less than the corresponding errors in Table 1. For example, the force error for 2 turn coils in distance of 8 cm reduced from 94.6% in Table 1 to 0.12% in Table 2. These fewer errors for lower turn numbers decrease expeditiously to zero by increasing the turn numbers.
. As seen from the results of the table, the errors in this case are less than the corresponding errors in Table 1. For example, the force error for 2 turn coils in distance of 8 cm reduced from 94.6% in Table 1 to 0.12% in Table 2. These fewer errors for lower turn numbers decrease expeditiously to zero by increasing the turn numbers.
According to the results of Tables 1 and 2, generally for turn numbers higher than 10 turns in each coil, using the replaced concentric rings presents good approximations while having much simpler and faster calculations compared with that of direct method and using (9).
Also the calculation have been done for the case in which there is smaller compression factor for the coils compared with previous cases, i.e. for each turn of coils or for change of  Radians in the value of variable
Radians in the value of variable 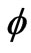 in cylindrical coordinate, the change in the value of variable r is more than the diameter of the wires used in the coils. At first, it seemed that by decreasing the compression factor the calculation error increases, but this assumption is not true because by decreasing the compression factor, the relative error of calculations with replaced rings method decreases [11].
in cylindrical coordinate, the change in the value of variable r is more than the diameter of the wires used in the coils. At first, it seemed that by decreasing the compression factor the calculation error increases, but this assumption is not true because by decreasing the compression factor, the relative error of calculations with replaced rings method decreases [11].
5. Analysis of the Magnetic Force between Planar Spiral Coils Using FEM
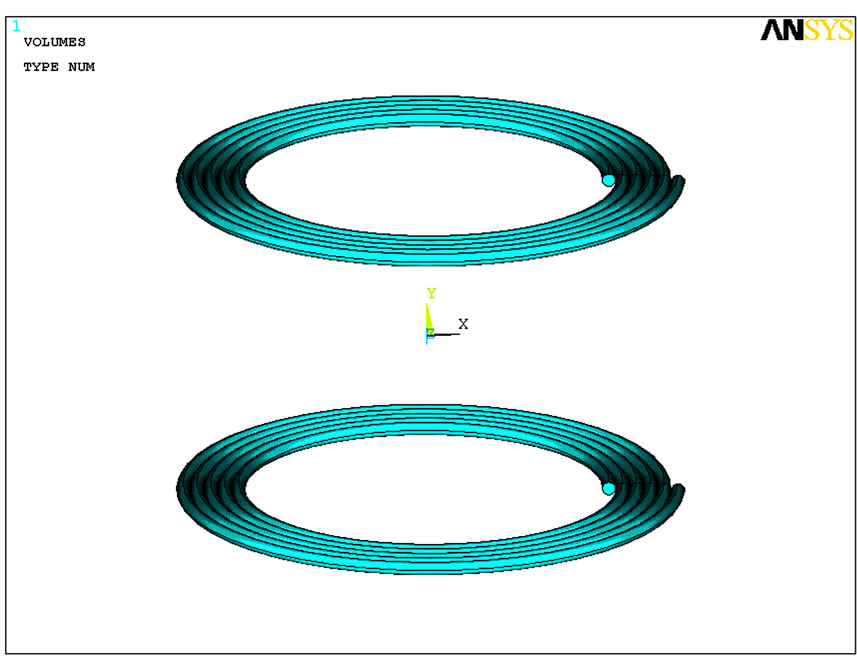
To demonstrate the effectiveness of the concentric rings method, in this section the spiral and replaced concentric coils are simulated using 3-D finite element method. Figure 5 shows the configuration of the two coils in two methods. The distribution of the flux density for spiral coils and replaced concentric rings with the same current and turn number are illustrated in Figures 6 and 7, respectively. It is clear from these figures that the magnetic flux distribution of the spiral coil is similar to that of the replaced concentric rings with the same turn number. The calculations of the force between two coils have been done using concentric rings method and compared with FEM results. Also, the coils have been constructed in laboratory and the force between them has been measured. The characteristics of the constructed coils are given in Table 3. The calculation, FEM, and experimental results for the mentioned coils at different distances are compared in Table 4. As seen in this table, the results of the force measurement and the results obtained using FEM are in good agreement with the results of the calculations. It is noted that in calculating the force between two coils using FEM, given in Table 4, the number of meshes were doubled; however, it did not have impact on the accuracy of the force. This indicates that the number of selected meshes is enough for the calculations.
 (a)
(a)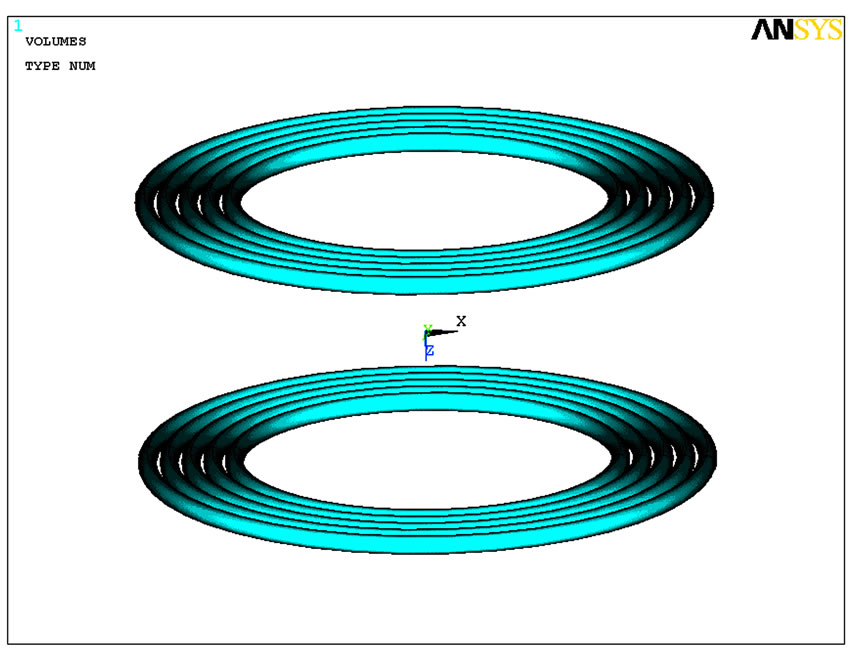 (b)
(b)
Figure 5. Configuration of the two coils in two methods. (a) Spiral coils; (b) Concentric rings

Table 3. Characteristics of the constructed spiral coils
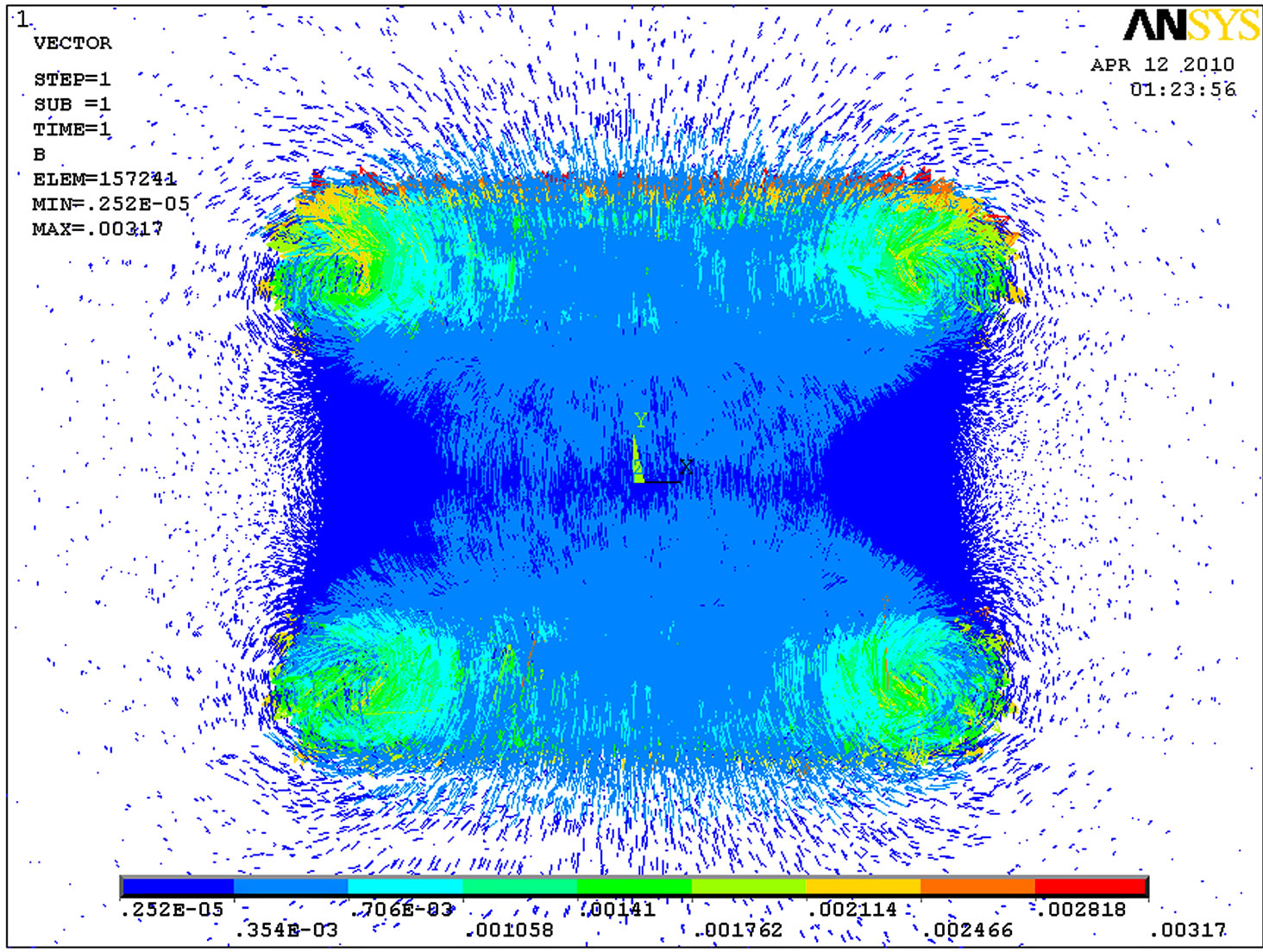
Figure 6. Flux density distribution for spiral coils
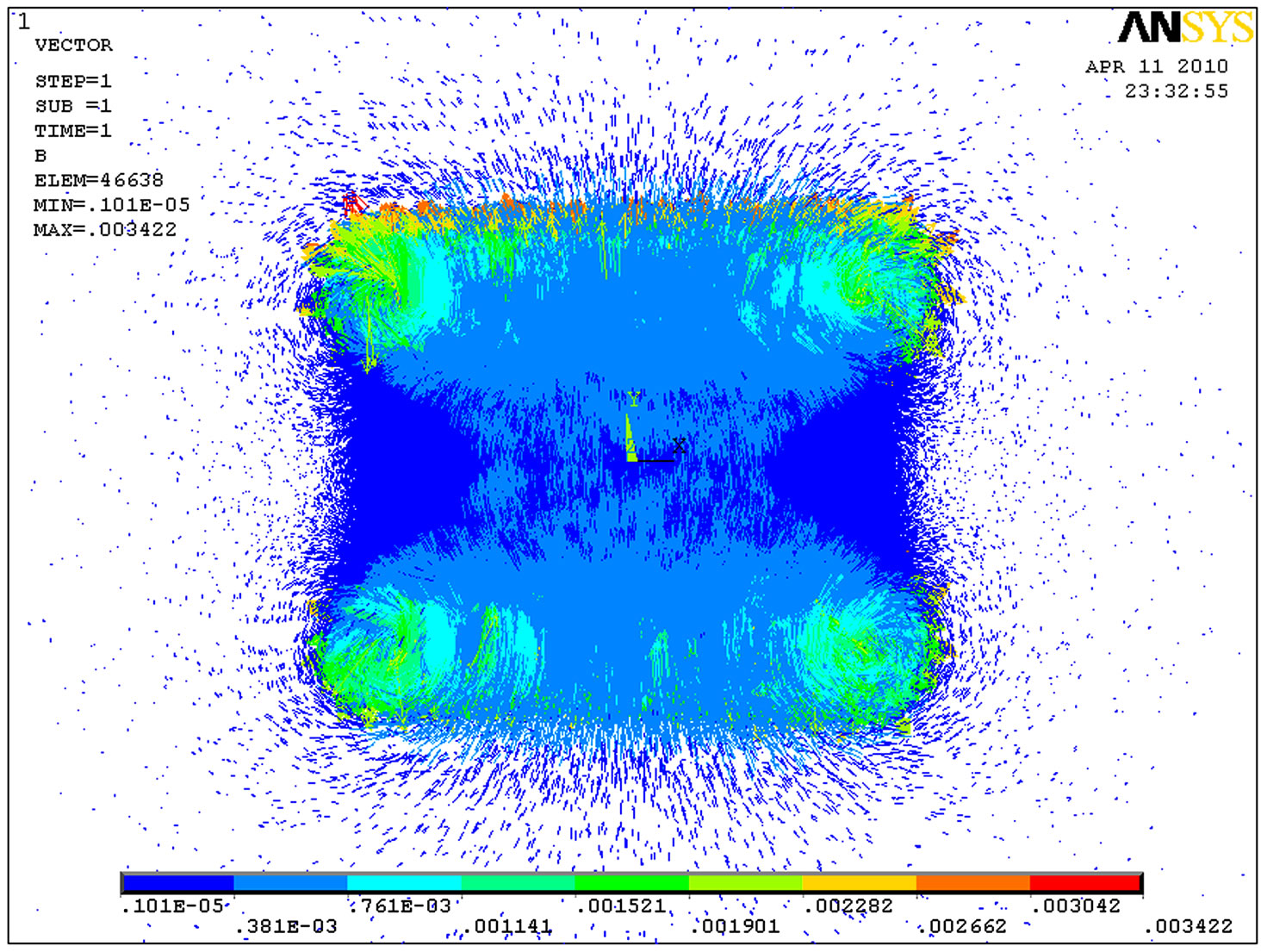
Figure 7. Flux density distribution for replaced concentric rings
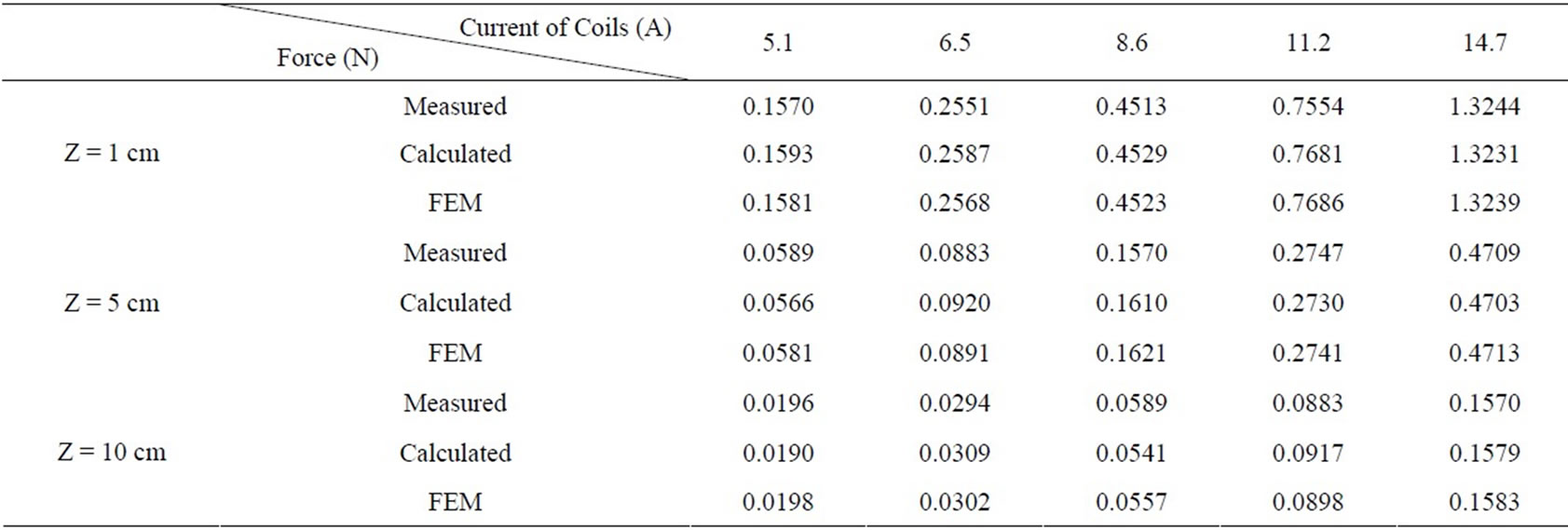
Table 4. The experimental and FEM results and their comparison with calculation results of the replaced rings method
6. Conclusions
The force between planar spiral coils is analyzed using finite element and concentric rings methods. The results of 3-D FEM simulations show that the magnetic flux density distribution for concentric rings is similar to that of the spiral coils. Further investigations on the calculation of the magnetic force between spiral coils confirm the effectiveness of the replaced concentric rings method when compared with the direct calculation method. Therefore, the former method simplifies the calculation procedure and decreases the computation time. According to the obtained results, the accuracy of the replaced rings method for the number of turns more than 10, which is the case of many practical applications, is acceptable; hence, the method is applicable for variety of spiral coils. Also, the calculation results are in good agreement with the experimental and FEM results, validating the precision of the replaced rings method.
REFERENCES
- X. Ding, K. Kuribayashi and T. Hashida, “Development of a New Type Tactile Sensor Using Micro Electromagnetic Coil for Human Robot,” IEEE International Symposium on Micromechatronics and Human Science, Nagoya Congress Center, 2000, pp. 181-187.
- S. Atluri and M. Ghovanloo, “A Wideband Power-Efficient Inductive Wireless Link for Implantable Microelectronic Devices Using Multiple Carriers,” IEEE International Symposium On Circuits and Systems, Island of KAS, 2006, pp. 1131-1134.
- K. Kawabe, H. Koyama and K. Shirae, “Planar Inductor,” IEEE Transactions on Magnetics, Vol. 20, No. 20, 1984, pp. 1804-1811.
- T. Sato, M. Hasegawa, T. Mizogochi and M. Sahashi, “Study of High Power Planar Inductor,” IEEE Transactions on Magnetics, Vol. 27, No. 6, 1991, pp. 5277-5279.
- Y. Fukuda, T. Inoue, T. Mizoguchi, S. Yatabe and Y. Tachi, “Planar Inductor with Ferrite Layers for DC-DC Converter,” IEEE Transactions on Magnetics, Vol. 39, No. 4, 2003, pp. 2057-2061.
- I. Sasada, T. Yamaguchi, K. Harada and Y. Notohara, “Planar Inductors Using NiZn Ferrite Thin Plates and the Application to High-Frequency DC-DC Converters,” IEEE Transactions on Magnetics, Vol. 29, No. 6, 1993, pp. 3231-3233.
- I. Kawase, T. Sato, K. Yamasawa and Y. Miura, “A Planar Inductor Using Mn-Zn Ferrite/Polyimide Composite Thick Film for Low-Voltage and Large-Current DC-DC Converter,” IEEE Transactions on Magnetics, Vol. 41, No. 10, 2005, pp. 3991-3993.
- A. Meriched, M. Feliachi and H. Mohellebi, “Electromagnetic Forming of Thin Metal Sheets,” IEEE Transactions on Magnetics, Vol. 36, No. 4, 2000, pp. 1808-1811.
- A. Shiri , M. R. A. Pahlavani and A. Shoulaie, “A New and Fast Procedure for Calculation of the Magnetic Forces between Cylindrical Coils,” International Review of Electrical Engineering, Vol. 4, No. 5, 2009, pp. 1053- 1060.
- A. Shiri and A. Shoulaie, “New Results in Calculation of Magnetic Forces between Cylindrical Coils,” 23nd International Power System Conference, Tehran, 2008.
- A. Shiri and A. Shoulaie, “A New Methodology for Magnetic Force Calculations between Planar Spiral Coils,” Progress in Electromagnetics Research, Vol. 95, 2009, pp. 39-57.
- D. K. Cheng, “Field and Wave Electromagnetics,” 2nd Edition, Addison Wesley, 1989.
- A. Shiri, “Calculation of magnetic forces between current carrying coils in two plates,” Master of Science Thesis, Iran University of Science & Technology, 2006.
- M. R. Spiegel, “Schaum’s Outline Series: Mathematical Handbook of Formulas and Tables,” McGraw-Hill, 1968.
- A. Shiri and A. Shoulaie, “Calculation of Magnetic Forces between Planar Spiral Coils,” 15th Iranian Conference on Electrical Engineering, Tehran, 2007, pp. 547- 554.

