International Journal of Communications, Network and System Sciences
Vol.07 No.10(2014), Article ID:50871,9 pages
10.4236/ijcns.2014.710046
Performance Enhancement of Grouped MCCDMA-MIMO System through Power Control Using Water Filling Game Theory under Imperfect Channel State Condition
Sundhar Arumugam1, Dananjayan Perumal2
1Department of Electronics and Communication Engineering, Perunthalaivar Kamarajar Institute of Engineering and Technology, Karaikal, India
2Department of Electronics and Communication Engineering, Pondicherry Engineering College, Pondicherry, India
Email: aisundhar@rediffmail.com, pdananjayan@pec.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 June 2014; revised 10 July 2014; accepted 6 August 2014
ABSTRACT
Continuous increase in demand of wireless services such as voice, data and multimedia is fueling the need of spectrally efficient techniques in communication networks. The MCCDMA-MIMO, a system of Multi Carrier Code Division Multiple Access (MCCDMA) technique with multiple antennas at both the transmitter and receiver gets benefits of ability to adopt multiple access capability from MCCDMA technique, achieves high data rate from MIMO concepts and becomes a very attractive multiple access technique for the future wireless communication systems. But, the wireless channels in MCCDMA-MIMO networks are known to display significant variations across active users’ subcarriers as well as among subcarriers of the same user due to simultaneous spectrum utilization. This leads to the undesirable Multiple-Access Interference (MAI) and Inters Carrier Interference (ICI), accordingly degrades the performance of the system. So, the interference mitigation methodology in the MCDMA-MIMO system has received a lot of attention in next generation mobile environment. The power control and sub carrier grouping methods have been long standing open solutions for capacity enhancement. The strategic choice of assigning the transmission power to each individual subcarrier in the MCCDMA-MIMO system is subjected to the knowledge of Channel State Information (CSI), which usually becomes imperfect due to the time varying nature of the channels. The goal of this paper is to allocate proper power to sub-carriers of MCCDMA- MIMO system by playing water filling game theory against the CSI errors to improve the performance of the system.
Keywords:
CSI, IWFA, MCCDMA-MIMO, MAI, QoS

1. Introduction
The Multi Carrier Code Division Multiple Access (MCCDMA) is becoming a very attractive multiple access technique for high-rate data transmission in the future wireless communication because of its multiple access capability, robustness against fading, and ISI mitigations [1] . Due to the simultaneous transmissions; sub-car- riers interfere with each other and limit the wireless network performances. To achieve robustness and spectral efficiency in MCCDMA system over multipath fading channels, the technology is ruled by two main functions; power allocation [2] over the sub carriers and sub carrier group assignment [3] . Power allocation is the scheme by which users share the power available at the serving base station. Group assignment depicts selection of appropriate subcarriers to support information bit streams of individual users. So, the distributions of users across subcarrier groups as well as their transmission power distribution has a significant effect on QoS enhancement like mean capacity of the system and BER. The Multiple Input and Multiple Output (MIMO) system is another promising technique to increase the transmission rate without expanding the signal bandwidth. So, the interconnection of MCCDMA technology with MIMO system is highly regarded as a possible candidate for implementation of physical layer in the fourth generation.
In this paper, the MCCDMA-MIMO system subdivides subcarriers into a set of non-overlapping subcarrier groups. A user in the system is assigned to the subcarrier group that holds the best CSI and transmits the whole data of the user through the selected group of sub-carriers or varying the number of sub-carriers according to user’s requirement. The power control and group assignment methods processed with the knowledge of CSI as an objective function that is received from receiver. Power control and group assignment in MCCDMA give optimal solution only if the CSI is actual and valid. However, such performance gain comes at the expense of significant signaling overhead due to the sharing of CSI and transmission data. So, the CSI is subjected to the errors because of the imperfect channel estimation/measurement due to the time varying nature of the channels and does not provide the optimal solution for the mutual-information maximization problem. This paper considered the Signal Interference/Noise Ratio (SINR) of the given user assigned on the subcarrier group as an objective function to distribute power along the sub carrier groups to restrict the interference noise.
The game theory is an effective tool used to allocate power for each user with the independent knowledge of actual channel realization and gives solution for overall capacity maximization problem [4] . In the power control game, each user seeks to choose its transmitting power over each carrier to maximize its capacity. The water-filling rule in game theoretic perspective is used to allocate proper power for every user in order to improve system capacity performance with global constraint (total available power at base station) and imperfect CSI [5] [6] . In this paper, the interference based sub carrier group assignment strategy with dynamic power allocation using Iterative Water Filling Game theoretic Algorithm (IWGA) is implemented for MCCDMA-MIMO [8] [9] system and an attempt has been made by adopting the Iterative Water Filling Game theoretic Algorithm (IWGA) to enhance the performance of the MCCDMA-MIMO system like capacity, BER. While playing the game for power allocation and sub carrier grouping, The CSI impairment due to the channel variation during the unavoidable delay, the noisy channel estimation and the limited feedback is thoroughly considered to determine the variance of the CSI error [7] . To keep the separability of subcarriers while allocating power, the correlation of channel coefficients of subcarriers is not taken into account. The IWFA algorithm was implemented based on the erroneous CSI and performance degradation due to imperfectness is also analyzed.
The organization of this paper is as follows. Section 2 deals with the system architecture of MCCDMA- MIMO system considered in this paper, formation of game model and strategy of the game for power control algorithm in MCCDMA-MIMO system. Section 3 describes solution for the problem and to maximize the pay- off using water filling game theory. The results are depicted in section 4 and the conclusions are given in Section 5.
2. System Architecture and Game Model
2.1. System Architecture
A multi cellular MCCDMA network constituted of 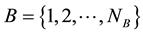 base stations is considered. The system
base stations is considered. The system
bandwidth “W” is subdivided into “NC” subcarriers. Bandwidth of subcarriers is selected such that they approx-
imately exhibit flat fading channel characteristics (i.e., 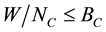 , where “BC” is the coherence band-
, where “BC” is the coherence band-
width). Each “G” subcarriers constitute a group over which individual streams will be spread. As a result of subcarrier grouping, system bandwidth could be described in terms of a set of subcarrier groups,
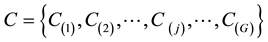 , where
, where  is the number of subcarrier groups. Each base station, b
is the number of subcarrier groups. Each base station, b
Î B, is effectively supporting “U” active data users. Each base station operates under the constraint that it has at its disposal a maximum amount of power to share among all active sessions [8] [9] . The symbol of user “u” in the base station “b” of an MCDMA system is presented as
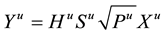 (1)
(1)
where
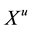 is the active user’s symbol.
is the active user’s symbol.
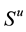 is the code matrix.
is the code matrix.
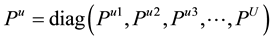 is each user’s transmit power.
is each user’s transmit power.
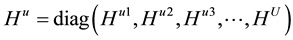 is each user’s channel fading.
is each user’s channel fading.
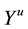 is MCCDMA symbol vector.
is MCCDMA symbol vector.
The time domain data stream for each user is divided into multiple parallel streams and each stream is spread using a spreading sequence as shown in Figure 1. The sequences are then spread with sub carrier group domain using IFFT and power allocation to each user is followed by IWFA. The sub carrier group assignment is processed by CSI. The IWFA allocate power to each user with the help of SINR value as an objective function. The MCCDMA symbols are then transmitted through MIMO structure of “Nt” transmit antennas and “Nr” receive antennas and is illustrated in Figure 1 and Figure 2 [10] .
2.2. Game Model
The game model in the MCCDMA transmitter plays against the behavior of a wireless channel and assigns power level to the respective sub carriers. The game model also considered that the CSI errors are uncorrelated across subcarriers. The strategies of this game are the possible power level which can be assigned on the sub carriers subject to the constraint of total power at the transmitter and total sub carriers. The objective function in the strategy of the game is the SINR value received from the receiver [11] [12] . A mobile user “u” of interest served by base station “b” has the SINR value given below.
 (2)
(2)
where
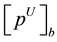 is power of user “u” in base station “b”.
is power of user “u” in base station “b”.
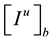 is the interference to the user “u” due to other users in the base station “b”.
is the interference to the user “u” due to other users in the base station “b”.
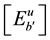 is inter cell interference.
is inter cell interference.
This SINR value is considered as an objective function for the power control game to allocate the optimal power to each user. The channel capacity of the individual user “u” in the base station “b” is considered as utility function of the game and expressed as
 (3)
(3)
The total system capacity of the base station “b” that constitutes “U” active users [13] is given as
 (4)
(4)
Figure 1. MCCDMA-MIMO transmitter.
Figure 2. MCCDMA-MIMO receiver.
Then the MCCDMA symbols are transmitted through MIMO system of Nt, Nr antenna with channel matrix H(t, t) [14] [15] as shown in Figure 1 and system capacity or the utility function is modified as

3. Water Filling Game Theoretic Solution under Imperfect CSI
The water filling game theory concept is modeled with selfish users and each user is interested in maximizing their own normalized effective capacity, or achievable throughput (rate), subject to an average power constraint [16] [17] . The capacity maximization of users in the MCCDMA-MIMO system with power constraint under Gaussian interference channel is optimized by sub carrier group forming and power distribution algorithm using water filling game theory. In order to maximize the capacity of the system, the power control game must calculate all utilities and expected payoffs for each one of his possible strategies. To maximize the overall link capacity, users need to be grouped optimally under the interference and QoS requirements constraint, the optimization problem with respect to sub carrier and power constraint is formulated as

where 


The water filling (WF) algorithm results in optimal solution only if the CSI is actual and valid. This, however, is not usually the case in realistic systems and environments due to the CSI estimation error. Due to the channel variation during the unavoidable delay, the noisy channel estimation and the limited feedback, perfect channel knowledge is not reachable by the transmitter in practice. The Clark’s correlation function of the fading process is defined as

where αm is defined by the Bessel function of 0th order J0(2πfDmT), and fD is the Doppler frequency.
are the channel gain of the lth and (l + m)th frame of the nth carrier.
3.1. Time Varying Channel
After the lth frame arrives the receiver, power and rate allocation can be effectively performed for the (l + m)th frame at the transmitter, where the delay “m” is caused by the distance between the transmitter and the receiver. With the correlation function (7), the channel coefficient of the nth subcarrier in frequency domain for the (l + m)th frame can be written

where Vn,k is complex Gaussian distributed with zero mean and variance given by

3.2. Noisy Channel Estimation
If the transmitted data is known or correctly decided by the receiver, the estimated channel coefficient of the nth subcarrier in frequency domain hn,k can be derived with the least squares channel estimation, shown as

The channel estimation error En,k is a zero-mean complex Gaussian random variable with variance

3.3. Limited CSI Feedback
The additive channel noise has almost identical characteristics over time. Thus, the reliability of the channel prediction can be available at the transmitter, and the receiver only needs to feed the estimated channel coefficients back. Before that, they must be quantized, i.e., represented by a limited number of bits, denoted by “B”. The quantized channel estimate of an arbitrary subcarrier “n” is referred to as

The quantization error can be generally expressed as a complex Gaussian distributed random variable with zero mean and variance

From the previous analysis, the channel estimation error En,k, the quantization error Zn,k and the channel time-variation Vn,k can be treated as stochastically independent. Therefore, the integrated CSI error ηn,k is complex Gaussian distributed with zero mean and variance

With these imperfect CSI, the capacity maximization of overall MCCDMA-MIMO system is given by

which includes the CSI imperfection due to the channel variation during the feedback delay, the limited feedback.
4. Results and Analysis
To show the advantage of the sub carrier grouping with power distribution using IWFA algorithms under imperfect CSI, computer simulations are performed in multi-path propagation. The uncertainty of the CSI is
achieved through error variance in noise 
and 150 Hz). The performance improvements of mean capacity of the system and BER reduction are analyzed with the numerical conditions shown Table 1.
The group assignment strategy to maximize the overall mean capacity and minimize the BER using IWFA is followed by the algorithm mentioned in section 3. The capacity improvement of MCCDMA in SISO using IWFA is compared with power allocation without water filling algorithm. The Further capacity enhancement of MCCDMA through MIMO multiplexing (2 × 2, 4 × 4) is also analyzed with and without IWFA. Figure 3, Figure 4 and Figure 5 show the capacity improvement of MCCDMA-MIMO (SISO, 2 × 2, 4 × 4) using IWFA with interference based sub carrier grouping under the Doppler frequency of fD = 50, fD = 100 and fD = 150 respectively. The power control and sub carrier group assignment strategy in the MCCDMA system improves the BER performance by eliminating transmission on poor subcarrier. Since majority of bit errors occur on severely de-graded subcarriers. The BER performances of the MCCDMA-MIMO system are shown in Figure 6, Figure 7 & Figure 8 for fD = 50, fD = 100 and fD = 150 respectively.
The MCCDMA-MIMO system with water filling has a greater performance enhancement as compared to the system without water filling even under the imperfect CSI. The capacity enhancement of the system is due to the proper power allocation to all users by IWFA with sub carrier group assignment strategy. The algorithm limits the interference noise among all users by avoiding excess power to any particular user and assigns the favorable
Table 1. Simulation parameters.
Figure 3. Capacity improvements of MCCDMA-MIMO with fD = 50 Hz.
Figure 4. Capacity improvements of MCCDMA-MIMO with fD = 100 Hz.
Figure 5. Capacity improvements of MCCDMA-MIMO with fD = 150 Hz.
Figure 6. BER performance of MCCDMA-MIMO with fD = 50 Hz.
Figure 7. BER performance of MCCDMA-MIMO with fD = 100 Hz.
Figure 8. BER performance of MCCDMA-MIMO with fD = 150 Hz.
sub carrier group according to data rate demands. The signal transmission of the system through MIMO gives an additional improvement of the system capacity.
5. Conclusion
The effect of CSI impairment caused by the channel variation during the unavoidable delay, the noisy channel estimation and the limited feedback in MCCDMA-MIMO system is considered in this paper. With this uncertainty conditions, the capacity enhancement and BER reduction in MCDMA-MIMO are achieved by IWFA based power control and sub carrier group assignment method. The power distribution to each user using IWFA is modeled based on the SINR value as an objective function which is received from receiver in the presence of imperfect CSI. The distribution of users across subcarrier groups as well as their transmission powers by IWFA method has a significant effect on how users and power are accordingly distributed elsewhere in the network to maximize the capacity and minimize the BER of the system.
References
- Le Nours, S., Nouvel, F. and Helard, J.-F. (2004) Design and Implementation of MC-CDMA Systems for Future Wireless Networks. EURASIP Journal on Applied Signal Processing, 2004, 1604-1615. http://asp.eurasipjournals.com/content/2004/10/371603 http://dx.doi.org/10.1155/S1110865704402066
- Lee, Y.H. and Bar-Ness, Y. (2007) Transmission Power Adaptations in MC-CDMA Communications over Rayleigh Fading Channels. IEEE Transactions on Vehicular Technology, 56, 3486-3494. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4357018
- El Shabrawy, T. and Le-Ngoc, T. (2007) Subcarrier Group Assignment for MC-CDMA Wireless Networks. EURASIP Journal on Wireless Communications and Networking, 2007, Article ID: 037091. http://jwcn.eurasipjournals.com/content/2007/1/037091 http://dx.doi.org/10.1155/2007/37091
- Meshkati, F., Chiang, M., Poor, H.V. and Schwartz, S.C. (2006) A Game-Theoretic Approach to Energy-Efficient Power Control in Multicarrier CDMA Systems. IEEE Journal on Selected Areas in Communications, 24, 1115-1129. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1637718
- Palomar, D.P. and Fonollosa, J.R. (2005) Practical Algorithm for a Family of Water-Filling Solutions. IEEE transactions on Signal Processing, 53, 686-695. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1381759
- Sundhar, A. and Dananjayan, P. (2012) Capacity Enhancement in MCCDMA-MIMO System Using Iterative Water Filling Approach Based Power Distribution Method. Proceedings of IEEE International Conference on Computing Communication and Networking Technologies, Coimbatore, 26-28 July 2012, 1-5. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6396081
- Kim, D.K. and Sung, D.K. (2000) Capacity Estimation for an SIR-Based Power-Controlled CDMA System Supporting ON-OFF Traffic. IEEE Transactions on Vehicular Technology, 49, 1094-1101. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=875216 http://dx.doi.org/10.1109/25.875216
- Catreux, S., Driessen, P.F. and Greenstein, L.J. (2001) Attainable throughput of an Interference―Limited Multiple- Input Multiple-Output (MIMO) Cellular System. IEEE Transactions on Communications, 49, 1307-1311. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=939839 http://dx.doi.org/10.1109/26.939839
- Rong, Y. and Hua, Y. (2008) Optimal Power Schedule for Distributed MIMO Links. IEEE Transactions on Wireless Communications, 7, 2896-2900. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4600200.
- Wang, Y.-C., Zhang, P., Liu, Y.-A. and Li, N. (2008) Suboptimal Resource Allocation with MMSE Detector for Grouped MC-CDMA Systems. The Journal of China Universities of Posts and Telecommunications, 15, 30-36. http://www.sciencedirect.com/science/article/pii/S100588850860103X
- Sundhar, A. and Dananjayam, P. (2012) Interference Based Sub Carrier Group Assignment and Power Distribution For MCCDMA-MIMO System Using Iterative Water Filling Game Theory. Proceedings of IASTED International Conference on Engineering and Applied Science, Sri Lanka, December 2012. http://www.actapress.com/PaperInfo.aspx?paperId=454879
- Adachi, K., Adachi, F. and Nakagawa, M. (2008) A Study on Channel Capacities of MC-CDMAMIMO and OFDMMIMO. Proceedings of IEEE International Conference on Communication Systems, Guangzhou, 19-21 November 2008, 1384-1388. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4737410
- Lo, E.S., et al. (2007) Adaptive Resource Allocation and Capacity Comparison of Downlink Multiuser MIMO-MC- CDMA and MIMO-OFDMA. IEEE Transactions on Wireless Communications, 6, 1083-1093. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4133895
- Li, L.F. and Goldsmith, A.J. (2001) Capacity and Optimal Resource Allocation for Fading Broadcast Channels―Part II: Outage Capacity, IEEE Transactions on Information Theory, 47, 1083-1102. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=915665
- Kumaratharan, N., Jayapriya, S. and Dananjayan, P. (2010) Performance Enhancement of MC-CDMA System through STBC based STTC Site Diversity. International Journal of Computer and Electrical Engineering, 2, Article ID: 1973- 8163. http://www.ijcee.org/papers/105.pdf
- Xie, J.L., Li, C.R. and Li, C.S. (2007) Analysis of multicarrier CDMA System with Adaptive Subcarrier and Power Allocation. IEEE Proceedings of Signal Design and Its Applications in Communication, Chengdu, 23-27 September 2007, 279-282. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4408377
- Fu, P.-W. and Chen, K.-C. (2012) Rate, Sub-Carrier, and Power Allocations for Multi-Carrier CDMA with LMMSE Multiuser Detections. IEEE Transactions on Wireless Communications, 6, 1574-1580. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4202156











