Int'l J. of Communications, Network and System Sciences
Vol.7 No.1(2014), Article ID:42176,6 pages DOI:10.4236/ijcns.2014.71005
A Simplified Improvement on the Design of QO-STBC Based on Hadamard Matrices
1Mobile and Satellite Communications Research Centre, University of Bradford, Bradford, UK
2An-Najah National University, Nablus, Palestine
Email: o.o.anoh@student.bradford.ac.uk, yasdama@najah.edu
Copyright © 2014 K. O. O. Anoh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property K. O. O. Anoh et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 9, 2013; revised December 9, 2013; accepted December 16, 2013
KEYWORDS
Hadamard Matrix; QO-STBC; Full Diversity; Multi-Antenna Systems
ABSTRACT
In this paper, a simplified approach for implementing QO-STBC is proposed and evaluated with improved performance. It is based on the Hadamard matrix, in which the scheme exploits the Hadamard matrix property to attain full diversity. Hadamard matrix has the characteristic that diagonalizes a quasi-cyclic matrix and consequently, a decoding matrix so that a diagonal matrix which permits linear decoding is achieved. Using quasicyclic matrices in designing QO-STBC systems requires that the codes should be rotated to reasonably separate one code from another such that error floor in the design can be minimized. It will be shown that, orthogonalizing the secondary codes and then imposing the Hadamard criteria of the scheme can be well diagonalized. The results of this simplified approach demonstrate full diversity and better performance than the interference-free QO-STBC. Results show about 4 dB gain with respect to the interference-free QO-STBC scheme and it performs alike with the earlier Hadamard based QO-STBC designed with rotation. These results achieve the consequent mathematical proposition of the Hadamard matrix and its property is also shown in this study.
1. Introduction
One of the ways of achieving dependable broadband network in wireless communications systems is by the use of multiple input multiple output (MIMO) technology. MIMO technology is a transmission scheme that is used to transfer high data rate depending on the number of transmission branches (diversities). The commonest of all is the space-time block codes (STBC) for two transmitter diversities discussed in [1]. This technique exploits full transmission power for orthogonal codes so long as the transmitter diversity order is no more than two [2,3]. In transmissions involving more than two antennas, the full rate power is not attainable [1]. Beyond the two transmitter diversity transmissions for full rate, the codes are rather formed in a special orthogonal way. The new codes are usually described as the quasi-orthogonal STBC (QOSTBC). Besides performing transmissions of more than two antennas, the QO-STBC also improves the channel capacity and also improves bit error ratio (BER) statistics for MIMO technology [3].
TheQO-STBC scheme [2,4,5] has been discussed to achieve full transmission rate but not full diversity [6]. The BER curves suggest that the codes outperform the codes of orthogonal design only at low signal-to-noise ratios (SNRs), but worsen at increased SNRs. This is due to the fact that the slope of the performance curve depends on the diversity order gain, i.e. whether full of partial diversity gain. One of the major problems that limit the BER performance of the QO-STBC system is from interference incurred in the decoding process. These interference terms are off-diagonal terms that violate the possibility of simple linear decoding such that full diversity is not achievable. It is has been shown that these interfering terms are removable by some methods [3,7].
Examples of common methods of eliminating these interfering terms to improve the QO-STBC codes performance towards full diversity have been discussed in [3, 6-9]. For instance, the minimum distance between different codewords may reduce the likelihood of correctly decoding the right code. Hence, it is discussed that by properly choosing the constellations such that the minimum distance between the STBC codewords is increased, then the QO-STBC performance can be improved towards full diversity [6,7,10]. Some other common methods by which full diversity can be attained by interference reduction have been shown in [3,8,9]. Most of these techniques have been presented for three and four transmitter antennas QO-STBC designs.
The Hadamard matrix has the ability to diagonalize quasi-cyclic matrices [11,12] and matrices are readily invertible if they are complex [10,13]. These properties have been exploited in discussing QO-STBC systems based on Hadamard matrices in [8,10]. In this work, the Hadamard based QO-STBC is extended. The base quasicyclic codes are rather formulated according to the space-time block codes design criteria earlier discussed in [1]. This design is shown for frequency flat fading channel using a QPSK mapping scheme. The Hadamard based QO-STBC studied is for three and four transmitter diversities. Using the Hadamard matrix, it will be shown that the Hadamard based STBC maintains the orthogonality criteria with no interference. The resulting decoding matrix shows the perfect diagonal matrix with no offdiagonal terms and results obtained agree with the ones earlier presented in [10] with optimal rotation. This optimal rotation is not used in this study.
In Section 2, the system model is described and then in Section 3, the Hadamard based STBC is presented. The numerical simulation results are compared with that of interference-free QO-STBC and the traditional orthogonal QO-STBC in Section 4 and ended with summarized conclusions.
2. System Model
In this section, the applied system model is discussed. Assume that there are NT transmit antennas and NR receive antennas. In addition, QO-STBC that encodes a vector of input symbols 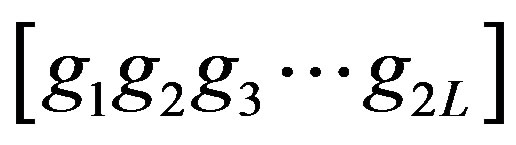 into G where
into G where 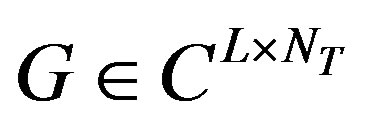 is considered, such that
is considered, such that 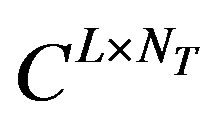 is a complex matrix of L × NT dimension, whereL is the block size. Let the channel impulse response be correlated such that multipath with
is a complex matrix of L × NT dimension, whereL is the block size. Let the channel impulse response be correlated such that multipath with 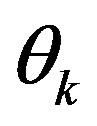 phase that influences signal of
phase that influences signal of 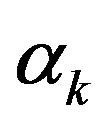 amplitude exist. If the transmission channel is flat, then
amplitude exist. If the transmission channel is flat, then  will be uniform for all paths, K, where K is the number of all resolvable paths traversed by the signal. Consequently, the channel impulse response will be summarized as
will be uniform for all paths, K, where K is the number of all resolvable paths traversed by the signal. Consequently, the channel impulse response will be summarized as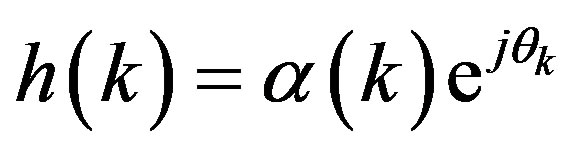 . For more than one transmit antenna such as
. For more than one transmit antenna such as  whose output is received by each j-antenna (j is equivalently 1 in this study), then;
whose output is received by each j-antenna (j is equivalently 1 in this study), then;
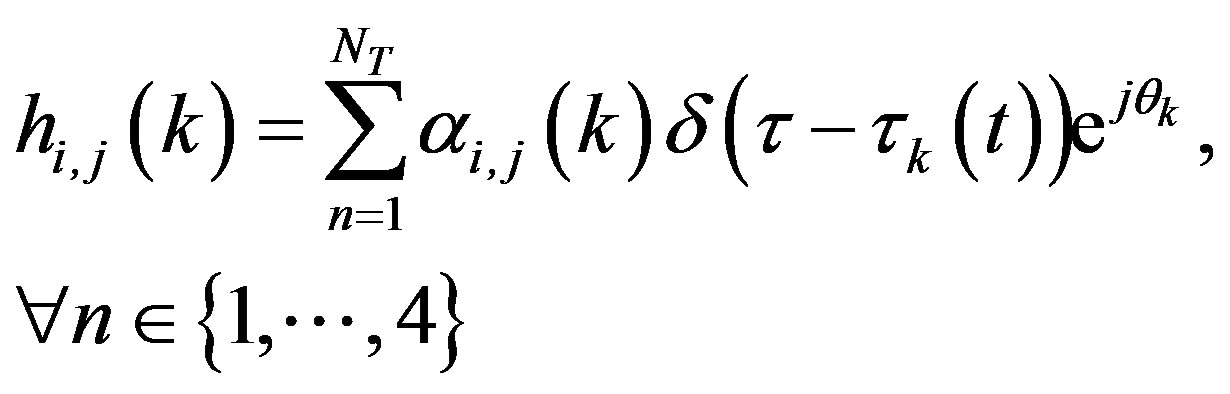 (2)
(2)
The frequency response of Equation (2) becomes:
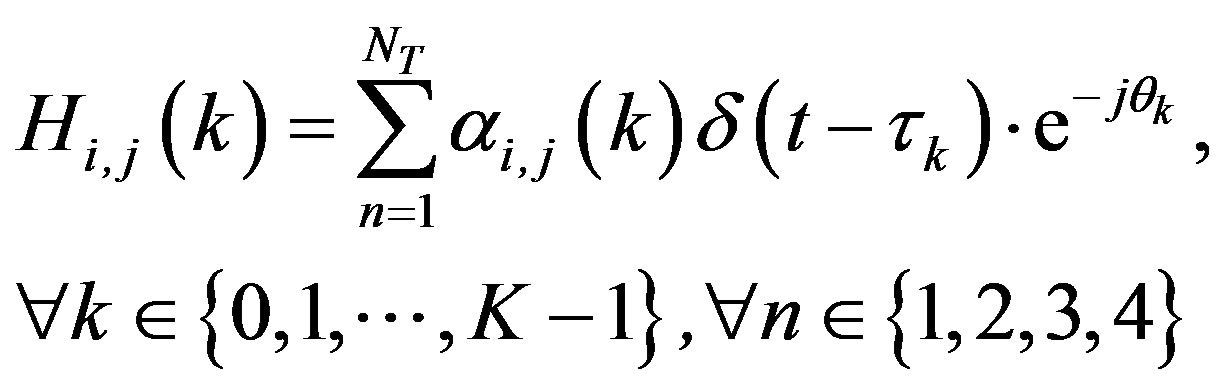 (3)
(3)
If H describes the channel matrix, the transmit signal is G, then the received symbol will be [14];
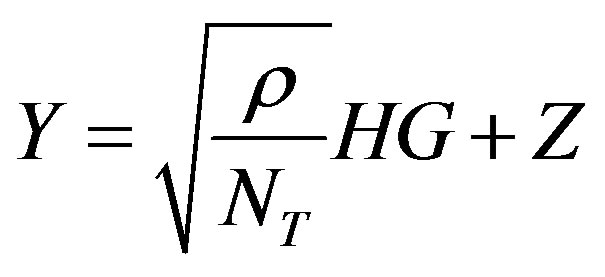 (4)
(4)
where Z is the Gaussian noise term similar to the additive white Gaussian noise (AWGN) and G is the QO-STBC codeword matrix formed according to the approaches in [2,5] also discussed in [8,10] as;
 (5a)
(5a)
where NT is the maximum number of transmit antenna and L is the length of the input symbols. Notice that  matrix from code-word in Equation (5a). Also, notice that G is formed from the Alamouti space time block coding method [1] as:
matrix from code-word in Equation (5a). Also, notice that G is formed from the Alamouti space time block coding method [1] as:
 (5b)
(5b)
Such that in QO-STBC scheme,

It is possible to decompose G into two such as G1 and G2 to permit maximum-likelihood decoding. This can be expressed in the following way [7]:
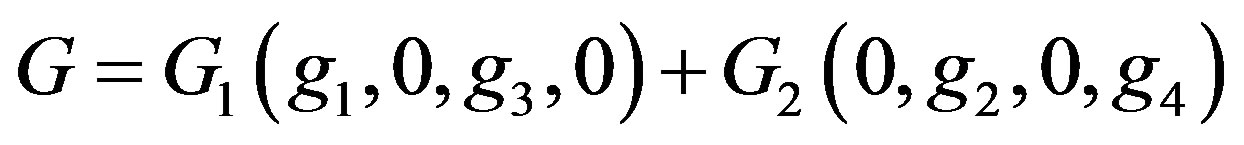
This is because,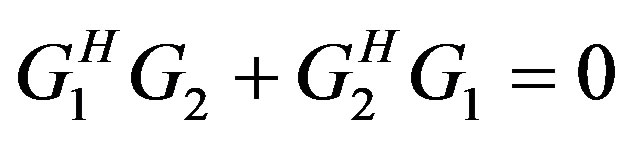 .
.
The equivalent channel matrix of the above QO-STBC code (G) can be represented as:
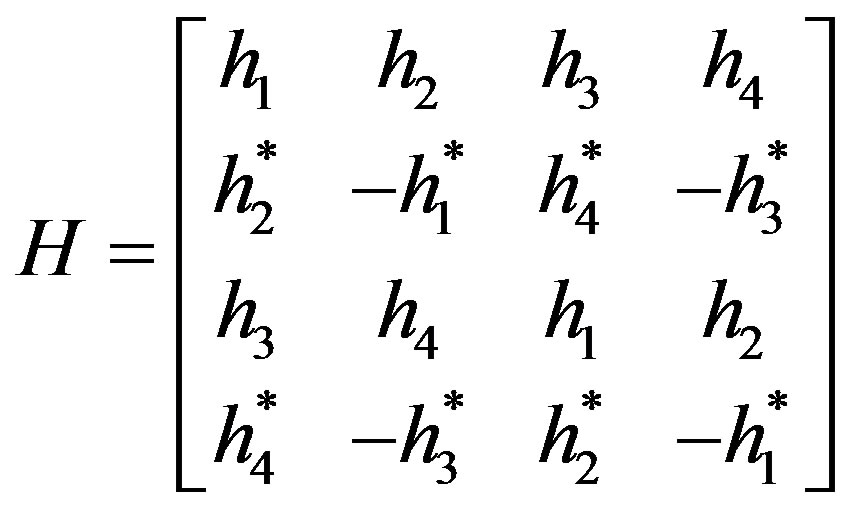 (6)
(6)
It is can be noted that the above description is performed for four transmit antennas diversity order. The detection matrix can be formed as:
 (7)
(7)
where λ is the diagonal of the (4 × 4) I4 matrix which is the sum of the channel power (or the path gains) and represented as . Also, the other terms in the detection matrix, β, represent the interfering terms that deplete the full diversity performance expected of QO-STBC of the 4-transmit antenna elements and is computed as:
. Also, the other terms in the detection matrix, β, represent the interfering terms that deplete the full diversity performance expected of QO-STBC of the 4-transmit antenna elements and is computed as: . Thus, β will degrade the BER (the pairwise error probability) performance of the system so long as the following decoding approach is followed and the full diversity will not be attained.
. Thus, β will degrade the BER (the pairwise error probability) performance of the system so long as the following decoding approach is followed and the full diversity will not be attained.
3. Hadamard Based QO-STBC
In this section, the traditional Hadamard based QOSTBC system is reviewed, then with the simplified Hadamard based QO-STBC approach following. The Hadamard matrices are described as matrices of 1’s and −1’s entries whose columns are orthogonal. It has the property that [13];
 (8)
(8)
where In is an identity matrix for an n × n order which belongs to the channel gain. Equation (8) has the property that the channel gain is amplified n-times. Since the Hadamard matrix is defined for rem (n, 4) = 0, then in our case where n = 4, the channel gain is amplified four times.
Let the Hadamard matrix be thought of as being formed from the traditional orthogonal STBC codes. Then, recall the orthogonal codes of the channel matrix for a two transmitter system discussed in [15] as;
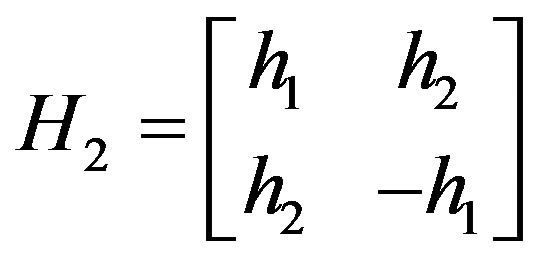 (9)
(9)
From Equation (9), the eigenvectors of the matrix can be given as;
 (10)
(10)
By Equation (10) tradition, we further define eigenvectors for a 4 transmit element (with one receiver) system as in [16] following Equation (10) as follows:
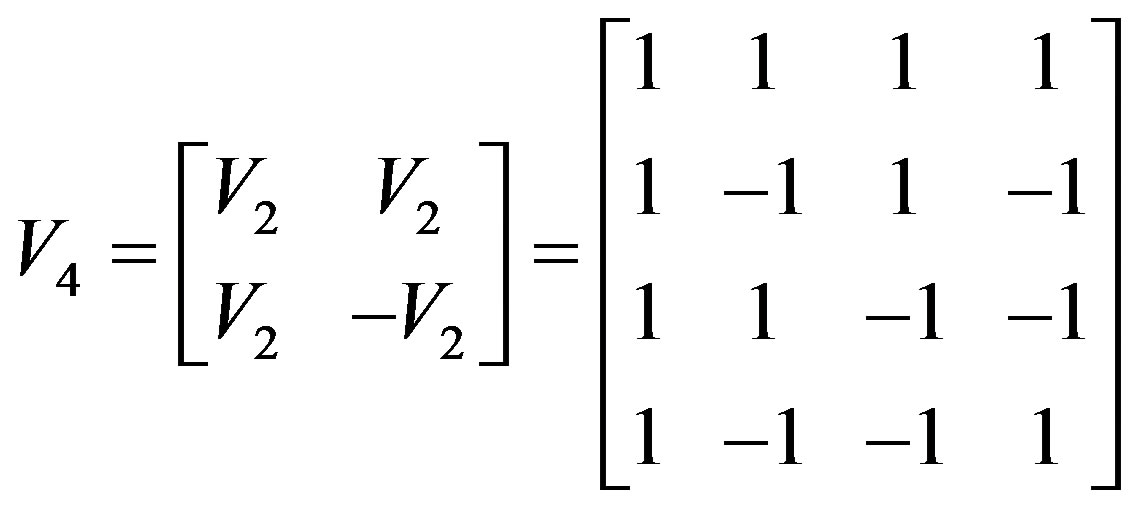 (11a)
(11a)
It is well-known that the codes that construct QO-STBC are not orthogonal, instead quasi-orthogonal. However, only the codes that construct the orthogonal STBC are orthogonal. We shall henceforth refer to Equation (11a) as:
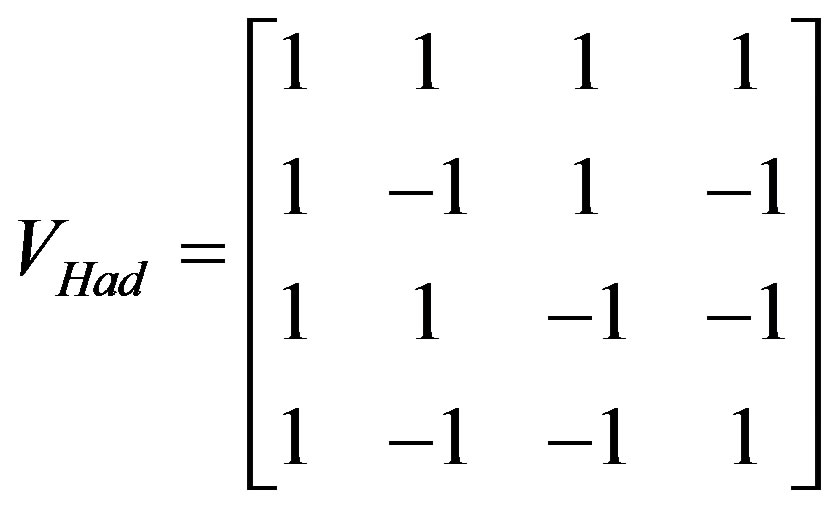 (11b)
(11b)
Meanwhile, the columns of the QO-STBC system hold orthogonal characteristics. Then by constructing an encoding matrix according to the Hadamard matrix yields QO-STBC systems whose decoding matrix is a diagonal matrix provided a proper quasi-cyclic Hadamard design is maintained. This explicitly eliminates any interfering terms (by default) so that exact full diversity will be achieved.
3.1. Traditional Hadamard Based QO-STBC
The earlier design of QO-STBC based on Hadamard matrix like in [8] stemmed from the quasi-cyclic matrix discussed in [11,12]. Recently, [8] has described the QOSTBC for the quasi-cyclic Hadamard matrix as:
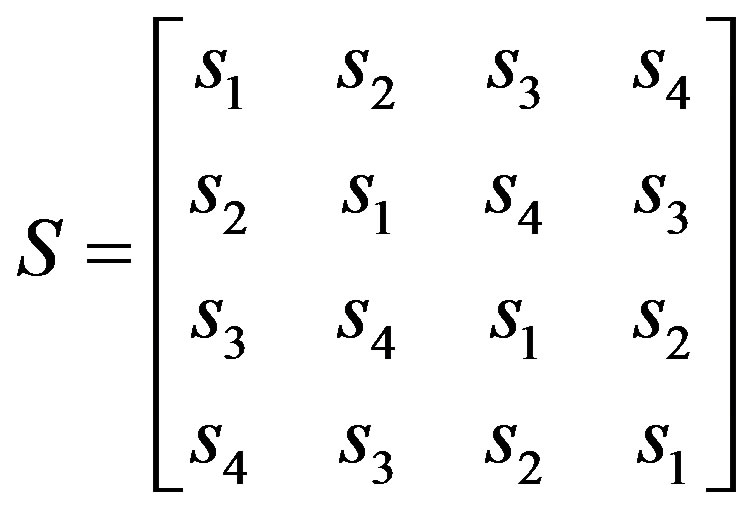 (12)
(12)
Equation (12) can be decomposed into two to permit maximum likelihood decoding according to [7] as follows:
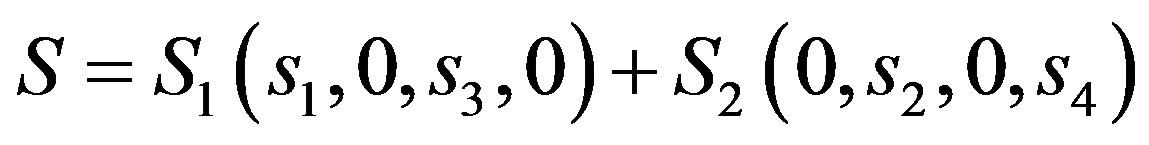
This is because, 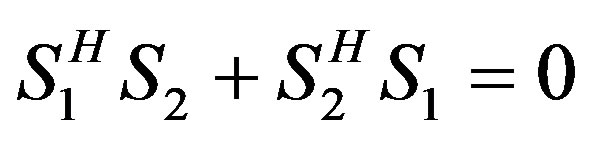 provided the orthogonal space-time block coding criteria discussed in [1] is satisfied. In the case of a Hadamard based QO-STBC, the codewords belong to [10];
provided the orthogonal space-time block coding criteria discussed in [1] is satisfied. In the case of a Hadamard based QO-STBC, the codewords belong to [10];
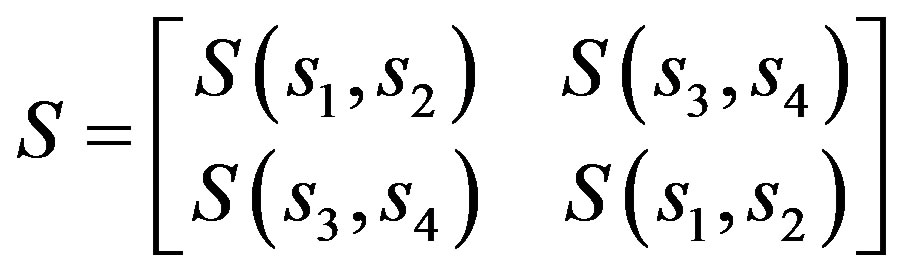 (13)
(13)
Where,
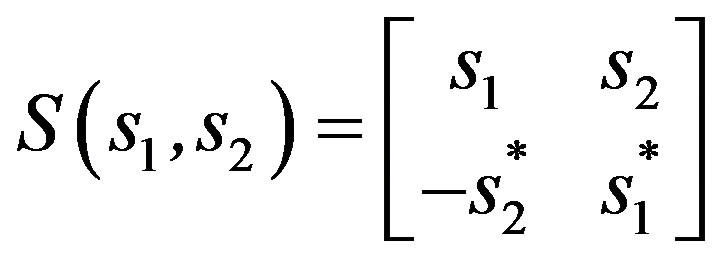
Sometimes, the constellation  are rotated (see [10] and then [7]). This rotation is to increase the minimum separation between different received codewords which minimizes the error floor of received symbols and improves the BER performance statistics of the QO-STBC code. The channel matrix of Equation (12) is constructed similarly to the encoding matrix of Equation (12) except for changing symbols si to hi
are rotated (see [10] and then [7]). This rotation is to increase the minimum separation between different received codewords which minimizes the error floor of received symbols and improves the BER performance statistics of the QO-STBC code. The channel matrix of Equation (12) is constructed similarly to the encoding matrix of Equation (12) except for changing symbols si to hi  in that case.
in that case.
In this work, we describe a Hadamard-based formulation of QO-STBC system whose decoding matrix is a diagonal matrix which would lead to linear decoding and has the form:
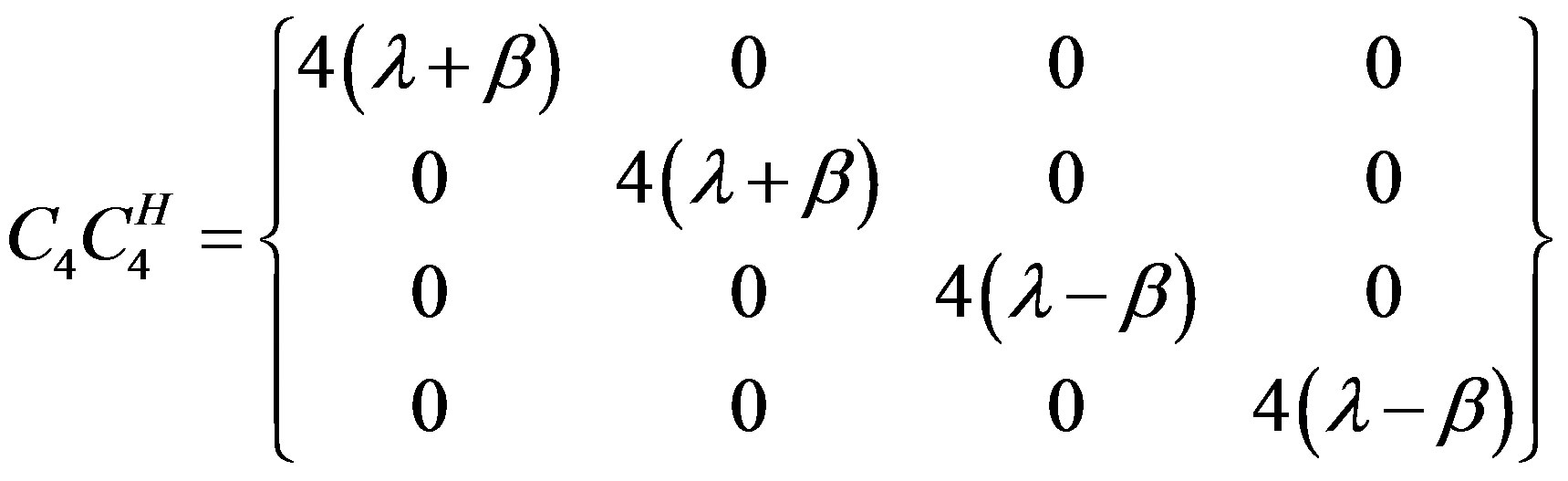 (14)
(14)
Equation (14) is the decoding matrix. If properly formulated, the encoding matrix which is usually complex and invertible must satisfy the condition
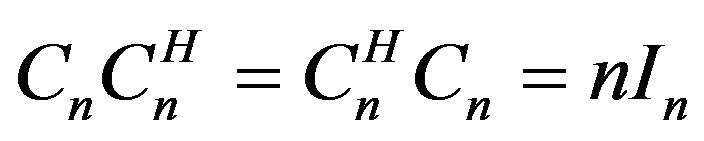 nIn where In is the identity of n × n matrix and the superscript, (.)H is the Hermitian transpose operator. Notice that n = 4 in this study. It is possible to extend these conditions for QO-STBC code constructions that satisfy the Hadamard matrix criteria.
nIn where In is the identity of n × n matrix and the superscript, (.)H is the Hermitian transpose operator. Notice that n = 4 in this study. It is possible to extend these conditions for QO-STBC code constructions that satisfy the Hadamard matrix criteria.
3.2. Simplified Hadamard Based QO-STBC
Now, let the formulation of the quasi-cyclic Hadamard codes for the channel matrix proceed in the following way:
 (15a)
(15a)
and,
 (15b)
(15b)
Instead of the combination that yielded Equation (12), let the orthogonal space time block coding reported in [1] be invoked such that:
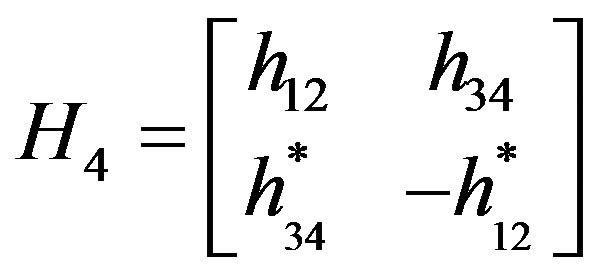 (16)
(16)
Then, by multiplying the resulting codes of Equation (16) according to the Hadamard matrix to form the new channel matrix, we obtain that:
 (17a)
(17a)
This is equivalent to: (see Equation (17b)).
This is the case of a 4 × 1 MISO antenna configuration. By applying Equation (8) in the formulation of Equation (17) during the decoding process, it can be found that (remembering that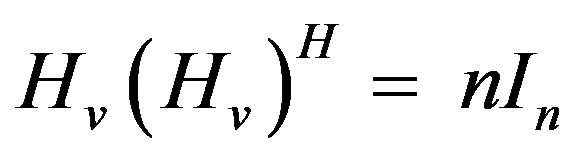 ):
):
 (18)
(18)
where  and
and
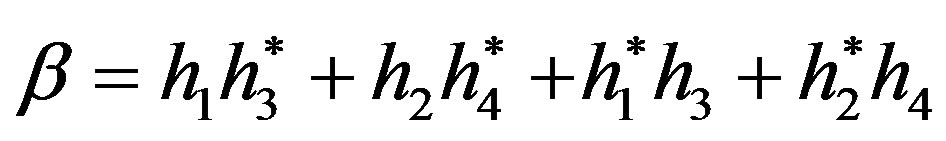
Notice that Equation (18) yields full diversity and is 4- times louder in amplitude compared to the interferencefree QO-STBC which is a diagonal matrix. Notice also that the Hadamard property of Equation (8) defined as 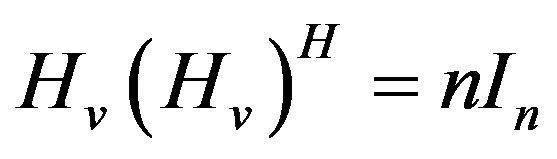 is well satisfied. The equivalent encoding matrix can as well be easily formed as: (see Equation (19)).
is well satisfied. The equivalent encoding matrix can as well be easily formed as: (see Equation (19)).
The converse of Equation (17) is also true, for instance;

In that case, the decoding property satisfies the following: 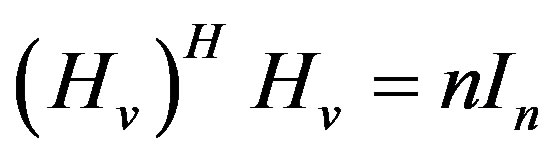 instead of
instead of .
.
By nulling the fourth antenna element, a three-antenna scheme can be shown as:
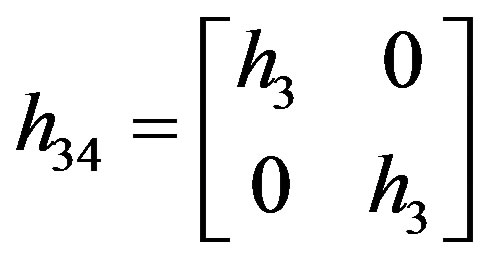 (20)
(20)
Now, substituting Equation (20) into Equation (17):
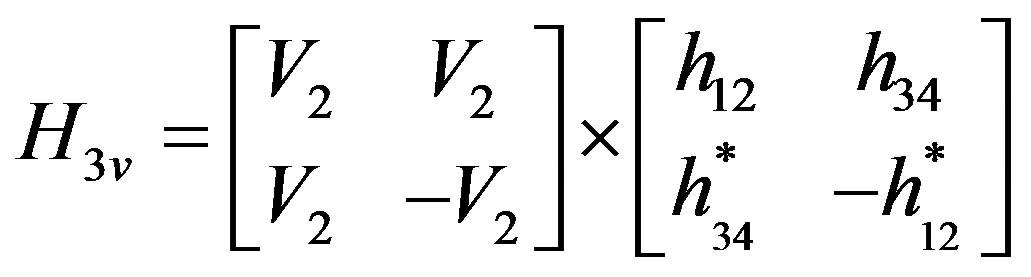 (21)
(21)
Expanding Equation (21), it can be seen that:
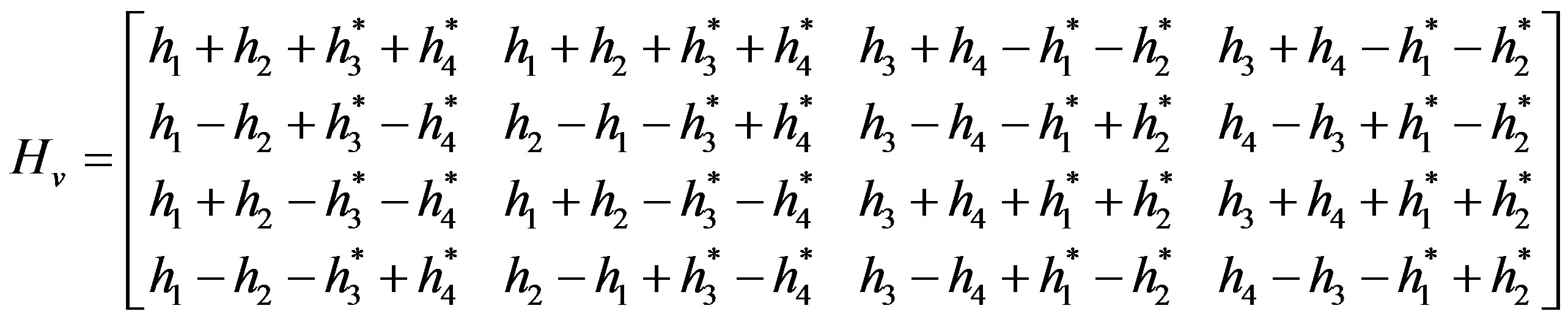 (17b)
(17b)
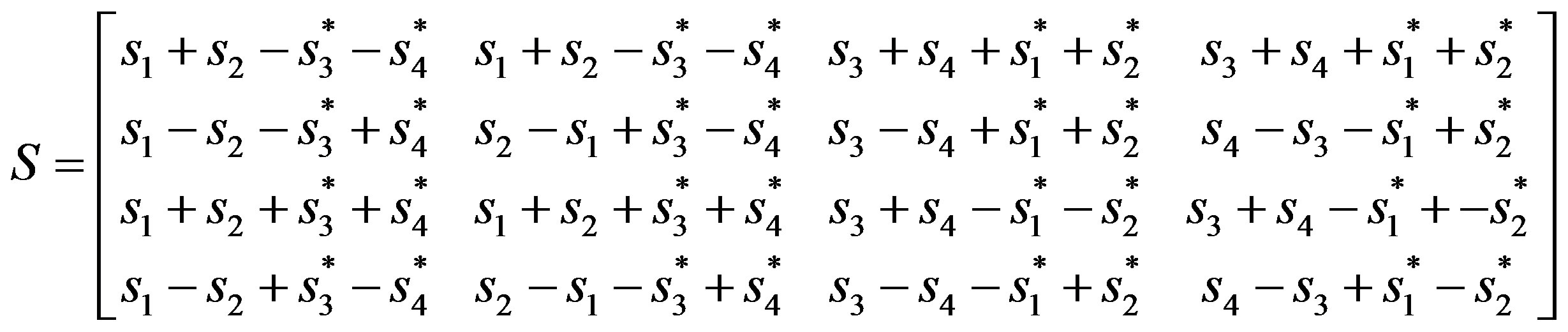 (19)
(19)

The equivalent encoding matrix of Equation (21) is easy to be formed by the elimination of a column in Equation (19) in a similar method to [9] and in the following:
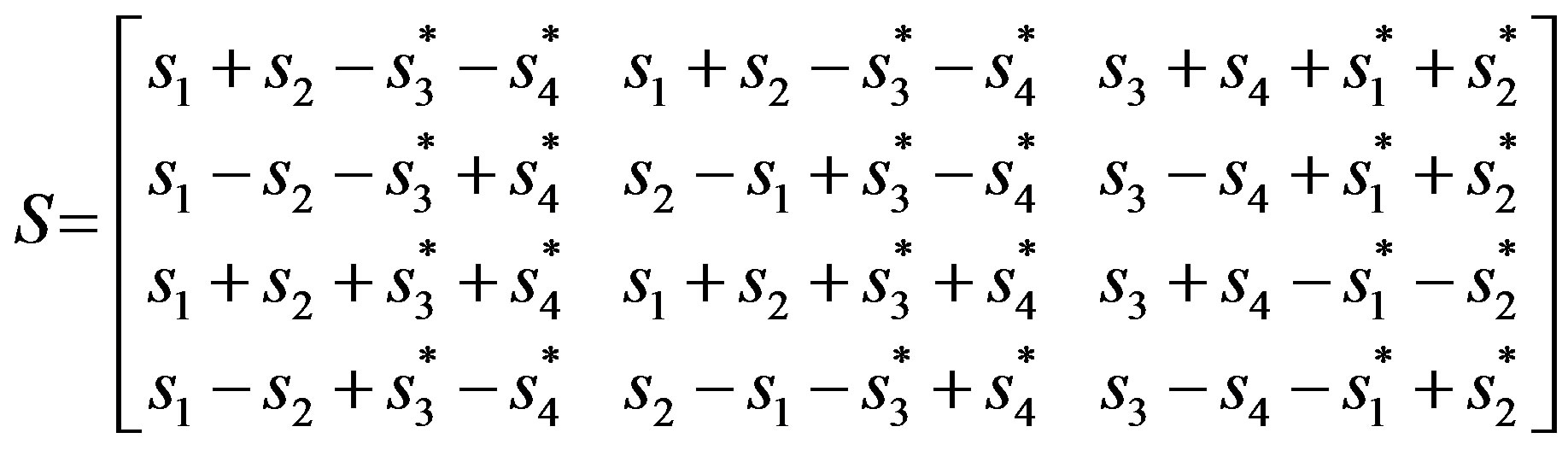 (22)
(22)
It is easy to verify via simulation that, the received symbol can be expressed as:
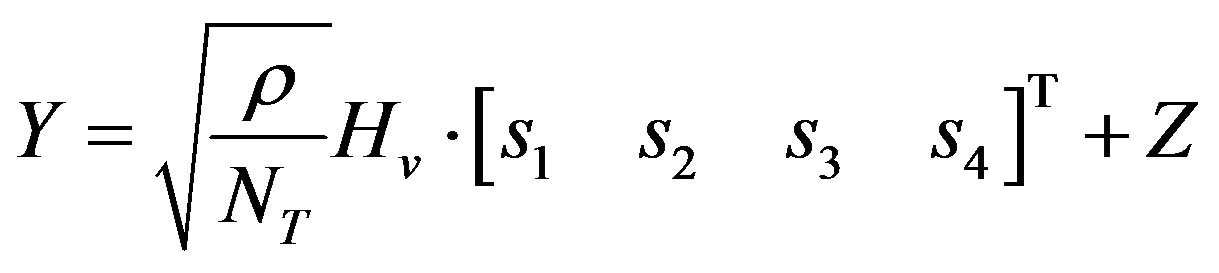 (23)
(23)
where 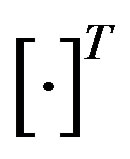 is a transpose operation. Notice that Equation (23) can easily be processed by computing
is a transpose operation. Notice that Equation (23) can easily be processed by computing 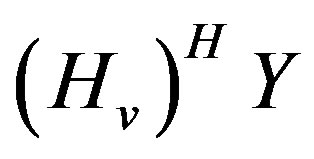 which leads to recovering the input symbols with the amplitudes of
which leads to recovering the input symbols with the amplitudes of  influenced by the resulting coding gain.
influenced by the resulting coding gain.
4. Numerical Simulation Results and Discussion
Using the Rayleigh fading channel model for a frequency non-selective fading, we evaluate the performance of the proposed method with respected to the traditional QOSTBC along with the interference-free QO-STBC.
This performance comparison is carried out for a QPSK system. In the study, it is assumed that the signal total transmit power for the respective three-transmit antenna and four transmit antenna systems were shared uniformly over the respective transmission branches for each case. During the transmission process, it is also assumed that, for three-transmit antennas that the scheme was quasi-static for three time slots and for four-transmit antennas, it was supposed that the system was constant for four-time slots.
In Figure 1, the results are shown in terms of bit error ratio (BER) for different signal-to-noise powers. The results obtained for the interference-free method and traditional QO-STBC are consistent with the earlier referred work. However, it is seen from the simulation results that the proposed method agrees with the mathematical proposition consequent on the Hadamard matrix property exploited and is four-time louder than the interferencefree QO-STBC. Also, the results are similar to the ones reported in [10]. This scheme provides the advantage of improved performance in comparison to interference reduction approach and reduced computation when compared to the rotation method discussed in [10].
As in Figure 1, Figure 2 shows a comparison of the proposed QO-STBC scheme with earlier methods such as the traditional QO-STBC and the interference QO-STBC for a MISO systems (3 × 1). The result is approximately 4dB times better than the interference approach.
5. Conclusion
A simplified method for implementing quasi-orthogonal space-time block codes has been presented with improved performance. Earlier QO-STBC based on Hadamard matrix used the quasi-cyclic codes. In this work, it was shown mathematically that, by computer simulation,
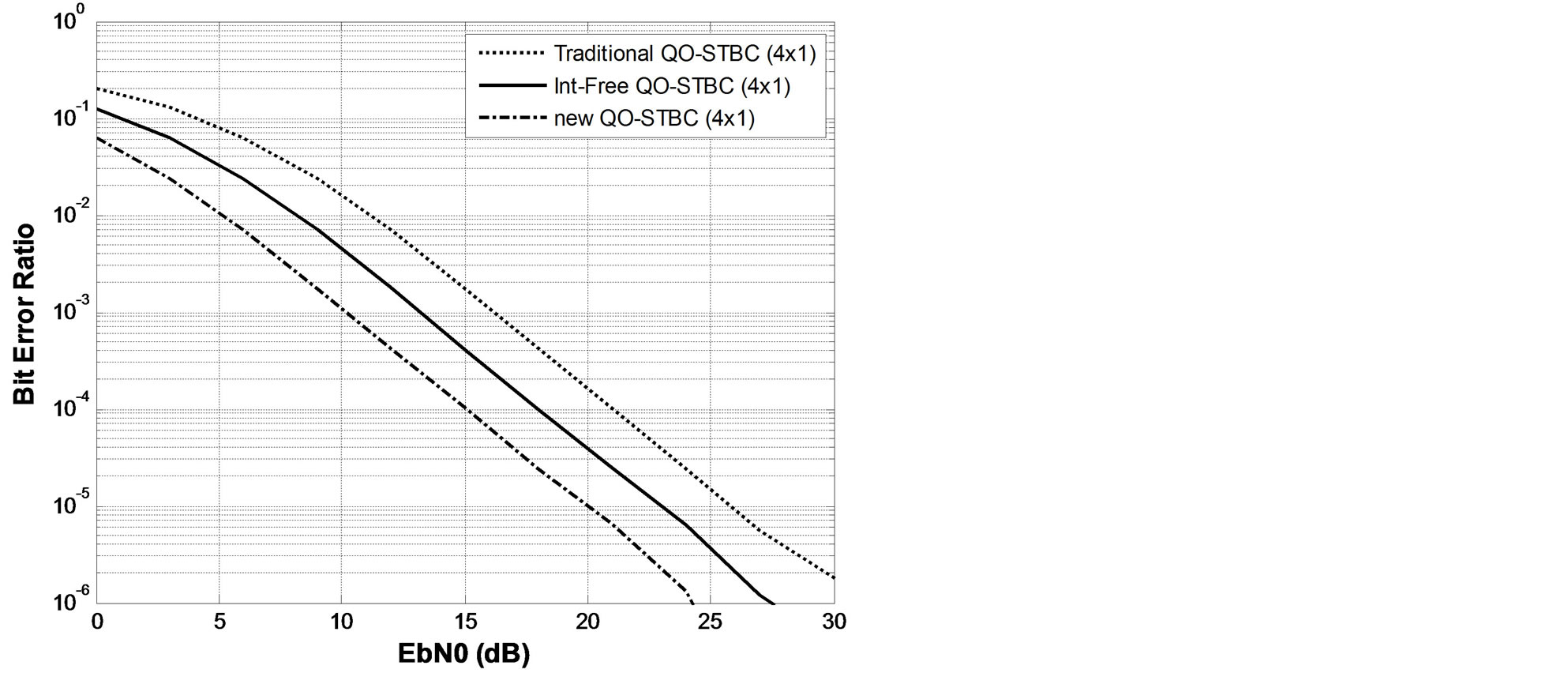
Figure 1. Comparison of new QO-STBC with traditional QO-STBC and interference-free QO-STBC (4 × 1).
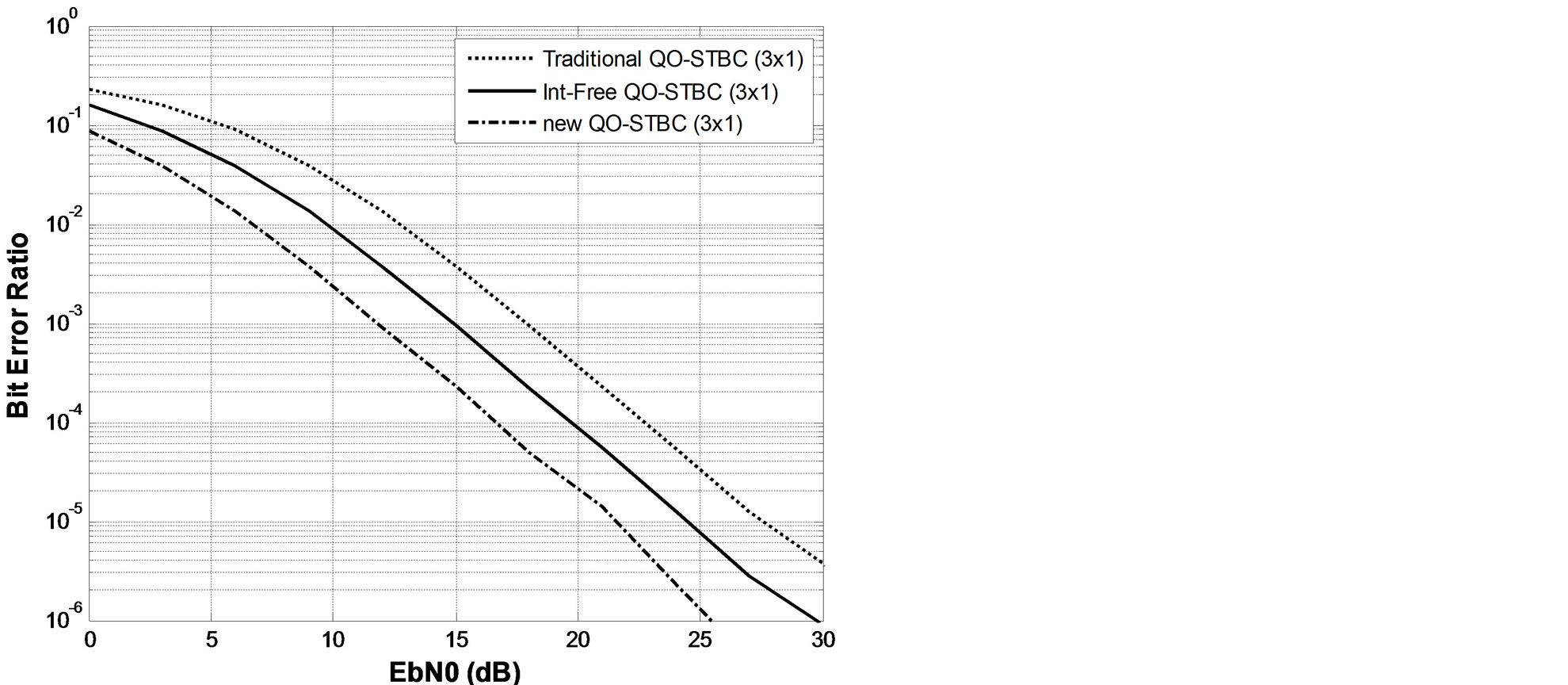
Figure 2. Comparison of new QO-STBC with traditional QO-STBC and interference-free QO-STBC (3 × 1).
these code constructions do not completely exploit the Hadamard advantage and also, do not attain full diversity. These were addressed by adopting a different approach to this code construction. It was shown that Hadamard matrix diagonalizes the QO-STBC codes which permits linear decoding. This property paves the way for achieving full diversity with reduced computational complexity. The results obtained are consistent with the mathematical property and fully exploit full diversity advantage of the QO-STBC scheme based on the Hadamard criteria. Consequently, the design of a QO-STBC system using the Hadamard matrix provides useful design advantage for improved multi-antenna design.
REFERENCES
- S. M. Alamouti, “A Simple Transmit Diversity Technique for Wireless Communications,” IEEE Journal on Selected Areas in Communications, Vol. 16, No. 8, 1998, pp. 1451- 1458. http://dx.doi.org/10.1109/49.730453
- H. Jafarkhani, “A Quasi-Orthogonal Space-Time Block Code,” IEEE Transactions on Communications, Vol. 49, No. 1, 2001, pp. 1-4. http://dx.doi.org/10.1109/26.898239
- Y. A. S. Dama, R. A. Abd-Alhameed, S. M. R. Jones, H. S. O. Migdadi and P. S. Excell, “A New Approach to Quasi-Orthogonal Space-Time Block Coding Applied to Quadruple Mimo Transmit Antennas,” 4th International Conference on Internet Technologies & Applications, September 2011.
- C. B. Papadias and G. J. Foschini, “Capacity-Approaching Space-Time Codes for Systems Employing Four Transmitter Antennas,” IEEE Transactions on Information Theory, Vol. 49, No. 3, 2003, pp. 726-732. http://dx.doi.org/10.1109/TIT.2002.808119
- O. Tirkkonen, A. Boariu and A. Hottinen, “Minimal NonOrthogonality Rate 1 Space-Time Block Code for 3+ Tx Antennas,” IEEE 6th International Symposium on Spread Spectrum Techniques and Applications, 2000, pp. 429- 432.
- W. Su and X.-G. Xia, “Signal Constellations for Quasiorthogonal Space-Time Block Codes with Full Diversity,” IEEE Transactions on Information Theory, Vol. 50, No. 10, 2004, pp. 2331-2347. http://dx.doi.org/10.1109/TIT.2004.834740
- N. Sharma and C. B. Papadias, “Improved Quasi-Orthogonal Codes through Constellation Rotation,” IEEE Transactions on Communications, Vol. 51, No. 3, 2003, pp. 332-335. http://dx.doi.org/10.1109/TCOMM.2003.809753
- Y. Dama, R. Abd-Alhameed, T. Ghazaany and S. Zhu, “A New Approach for OSTBC and QOSTBC,” International Journal of Computer Applications, Vol. 67, No. 6, 2013, pp. 45-48.
- U. Park, S. Kim, K. Lim and J. Li, “A Novel QO-STBC Scheme with Linear Decoding for Three and Four Transmit Antennas,” IEEE Communications Letters, Vol. 12, No. 12, 2008, pp. 868-870. http://dx.doi.org/10.1109/LCOMM.2008.081323
- F. Fazel and H. Jafarkhani, “Quasi-Orthogonal Space-Frequency and Space-Time-Frequency Block Codes for MIMO OFDM Channels,” IEEE Transactions on Wireless Communications, Vol. 7, No. 1, 2008, pp. 184-192. http://dx.doi.org/10.1109/TWC.2008.060420
- J.-W. Jang, J.-S. No and H. Chung, “Quasi-Cyclic Generalized Hadamard Matrices,” http://ita.ucsd.edu/workshop/06/papers/283.pdf
- J.-W. Jang, J.-D. Yang, J.-S. No and H. Chung, “New Construction of Balanced Quasi-Cyclic Generalized Hadamard Matrices,” IEEE International Symposium on Information Theory, 2006, pp. 307-310.
- F. Szöllősi, “Construction, Classification and Parametrization of Complex Hadamard Matrices,” 2011. arXiv preprint arXiv:1110.5590
- W. Su, Z. Safar, M. Olfat and K. R. Liu, “Obtaining FullDiversity Space-Frequency Codes from Space-Time Codes via Mapping,” IEEE Transactions on Signal Processing, Vol. 51, 2003, pp. 2905-2916. http://dx.doi.org/10.1109/TSP.2003.818200
- J. Proakis and M. Salehi, “Digital Communications,” 5th Edtion, McGraw-Hill, Asia, 2008.
- K. J. Horadam, “Hadamard Matrices and Their Applications,” Princeton University Press, Princeton, 2007.

