Int'l J. of Communications, Network and System Sciences
Vol. 6 No. 6 (2013) , Article ID: 33230 , 8 pages DOI:10.4236/ijcns.2013.66034
Adaptive Switching between Space-Time and Space-Frequency Block Coded OFDM Systems in Rayleigh Fading Channel
Laboratoire d’Electronique et de Communications (LEC), Ecole Mohammedia d’ingénieurs (EMI), Université Mohammed V Agdal (UM5A), Rabat, Morocco
Email: ab.youssefi@gmail.com, nawal.bounouader@gmail.com, j.elabbadi@gmail.com, zouhair@emi.ac.ma
Copyright © 2013 My Abdelkader Youssefi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 25, 2013; revised March 25, 2013; accepted April 25, 2013
Keywords: OFDM; MIMO; Rayleigh Fading Channel; STBC; SFBC
ABSTRACT
This work explores the performances of Space-Time and Space Frequency Coded Orthogonal Frequency Division Multiplexing (OFDM) with simple two branches transmit diversity scheme. The combination of multiple-antenna and orthogonal frequency division multiplexing (OFDM) provides reliable communications over frequency selective fading channels. We focus on the application of space-time block codes (STBC) and space-frequency block codes (SFBC) in OFDM systems over time-varying and frequency-selective channels. SFBC transmitter shows superior performance in fast varying channels while STBC shows better performance in frequency selective channels. A switching technique is presented that selects an appropriate transmission scheme between the STBC and SFBC assuming Rayleigh fading model.
1. Introduction
Future Wireless communication systems have to be designed to integrate high data rates and high quality of service and multimedia wireless communications. This increasing demand has led to the demand for higher network capacity and performance. Multiple antenna architecture on the transmitter and receiver sides, which is called multiple input multiple output (MIMO) is a suitable technique to improve the channel capacity [1].
Two MIMO schemes can be exploited, Space diversity and Spatial Multiplexing. In Space Diversity scheme, Space-Time Block Coding (STBC) and Maximal Ratio Combining (MRC) can be used to exploit the maximum spatial diversity available in the channel [1].
Space diversity is employed to counter fight fading and it is widely used in wireless systems. The basic idea behind this approach is to transmit more copies of a signal which permits to be more resistant to deep fading: if the receiver is supplied with more than one replica of the signal, transmitted over independent fading channels, the probability that all the copies are in deep fade is greatly reduced. The MIMO diversity gain can be obtained exploiting every domain of the wireless transmission. Typical examples are time diversity and frequency diversity where signals are repeated over time or over different frequencies [2]. For multiple antennas, an effective way of providing diversity is through STBC; usually multiple transmissions are done over the two dimensions of space (antennas) and time (successive time slots), STBC system assume that the channel is constant over time for the whole duration of the STBC block, as the performance is degraded if the channel is varying over successive time slots.
The simplest STBC is the Alamouti code. In its basic version, it employs two antennas at the base station and one antenna at the mobile terminal. The scheme transmits two symbols from two antennas in two successive time slots, thus a total of four symbols per Alamouti-block are transmitted [3]. Alamouti has been widely adopted because it is simple and requires a low signal processing load at the receiver (i.e. a portable device, being mobile and energy-limited). A simple receiver, with a linear combiner and a single antenna, can extract an order of diversity equal to 2 if the assumption of constant channel over two time slots is met. Alamouti code with two transmitting antennas and a single receiving antenna provides a diversity gain of two; if two receiving antennas are used, the diversity gain will be four [3]. No spatial gain is achieved with STBC. Over the recent years, the combination of Multiple Input Multiple Output (MIMO) with Orthogonal Frequency Division Multiplexing (OFDM) has gained significant interest and is considered as one of the most promising techniques for present and future wireless communication systems [4]. MIMO-OFDM system is used in many applications like WiMax, WiFi, WLANs. Block Coding is also possible over the two domains of antenna and frequency with Space-Frequency Block Coding (SFBC) in a Multi Carrier system, such as OFDM. This means that the SFBC coded blocks are transmitted during the same symbol time but from different antennas and over various sub carriers [5].
This paper is focused on the analysis of the performances of Space-Time and Space Frequency Coded MIMOOFDM with simple two branches transmit diversity scheme over time frequency selective channels. The assumption of constant channel response during the transmission becomes critical in STBC-OFDM over time varying channels. Similarly, the channel gain can not be constant for neighboring subcarriers in SFBC-OFDM over frequency selective channels. Adaptive switching between STBC and SFBC has been proposed in [6]. It has been found that the adaptive system switching between STBC and SFBC provides remarkable performance improvement. However, the proposed criteria in [6] can not be implemented at the transmitter side without perfect channel state information, channel correlation matrix is needed. Otherwise, this adaptive switching might cause some problems such as feedback delay, sensibility to channel estimation errors, etc.
In this paper, we propose a switching criterion based on normalized maximum Doppler frequency and normalized delay spread. Different from [6], the system needs only to estimate the channel delay spread and the Doppler frequency. Therefore, assumptions can be made at the transmitter side.
This paper is organized as follows. Section 2 presents Space-Time and Space Frequency Coded MIMO-OFDM system model. Section 3 describes time frequency selective channel. The proposed adaptive switching system is introduced in Section 4. The system simulation results are presented in Section 5.
2. MIMO-OFDM System Description
2.1. MIMO Alamouti Space Time Block Coding
Alamouti coding is defined by using two transmit antennas using an orthogonal space time coding which is presented in Figure 1.
It means that the first antenna transmit s0 and 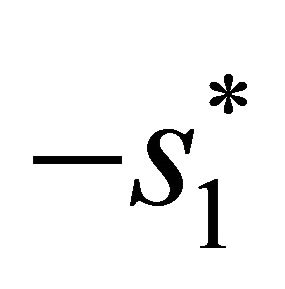 respectively, simultaneously the second antenna transmit s1 and
respectively, simultaneously the second antenna transmit s1 and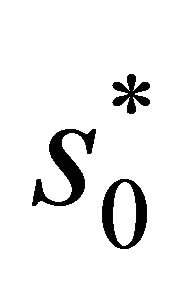 .
.

Figure 1. Space Time Alamouti coding [3].
If we assume that the channel is invariant between the first and second time of transmission, it results that the received signal can be expressed as:
 (1)
(1)
 (2)
(2)
Equations (1) and (2) show the output r of the receiver at time t and t + T, w0 and w1 are complex random variables representing receiver noise. H0 and H1 are the channel coefficients.
The main advantage using this coding is that we can recover the signal using a simple linear operation without amplifying the noise [3]:
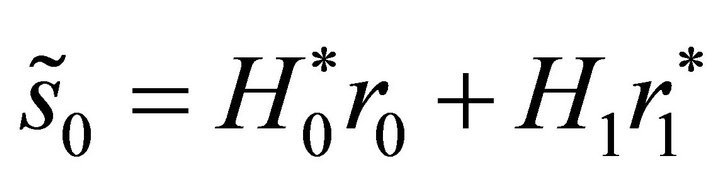 (3)
(3)
 (4)
(4)
Equations (3) and (4) give the symbol’s estimation by the Alamouti combining scheme. The combiner is shown in Figure 1 and the two combined signals  and
and ![]() are sented to the maximum likelihood detector.
are sented to the maximum likelihood detector.
2.2. Combining MIMO with OFDM
As well as known, the OFDM is a promising technology, which transforms a frequency selective channel into flat fading sub channels. In this paragraph we will present how the OFDM is used with MIMO systems.
2.2.1. Alamouti STBC-OFDM Scheme
Let us consider that we have a transmission sequence . In normal transmission, we will be sending s1 in the first time slot, s2 in the second time slot, s3 and so on. However, Alamouti suggested that we group the symbols into groups of two. In the first time slot, we send s1 and s2 from the first and second antenna. In second time slot we send
. In normal transmission, we will be sending s1 in the first time slot, s2 in the second time slot, s3 and so on. However, Alamouti suggested that we group the symbols into groups of two. In the first time slot, we send s1 and s2 from the first and second antenna. In second time slot we send 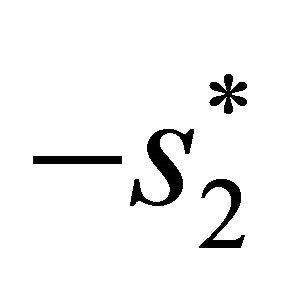 and
and 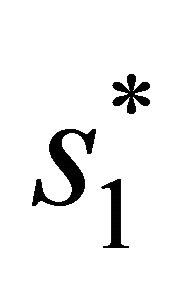 from the first and second antenna. In the third time slot send s3 and s4 from the first and second antenna and so on.
from the first and second antenna. In the third time slot send s3 and s4 from the first and second antenna and so on.
According to Alamouti Space time code applied for the OFDM system, we have the signals transmitted at times t and t + T from antennas 1 and 2 respectively given by:
Antenna 1: 
Antenna 2: 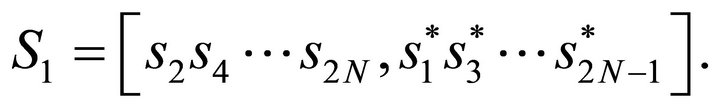
Where S0 and S1 are the outputs for pathways 1 and 2 respectively of the space time encoder, 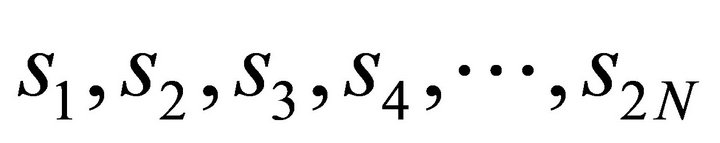 are the signal symbols, 2N is representing the total symbol number and N is equal to the number of subcarriers.
are the signal symbols, 2N is representing the total symbol number and N is equal to the number of subcarriers.
The encoded data are passed through a serial to parallel block where data are regrouped according to the subcarrier and time as shown in Table 1.
The MIMO-OFDM system model based on STBC is shown in Figure 2 [7].
We suppose that the channel is invariant, by assuming  the received signal can be expressed as:
the received signal can be expressed as:
 (5)
(5)
where

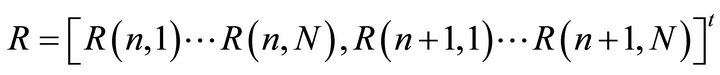
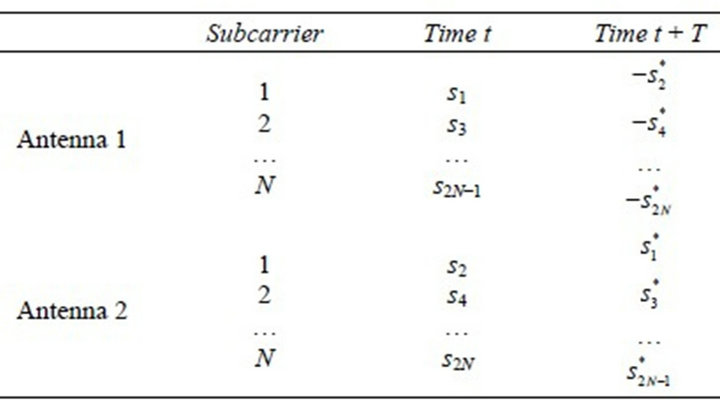
Table 1. STBC-OFDM scheme for two antennas.
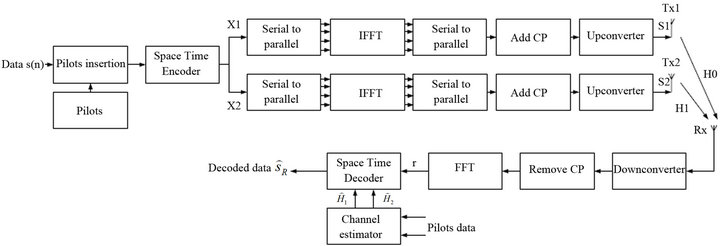
Figure 2. Block diagram of a two transmit and one receive antennas MIMO-OFDM system In Space Time Alamouti coding.
R(n, k) is the received symbols in subcarrier k. S0 and S1 are the transmitted symbols, W the Gaussian noise, n refers to the n-th OFDM block.
According to (3) and (4) the combined signals ![]() and
and 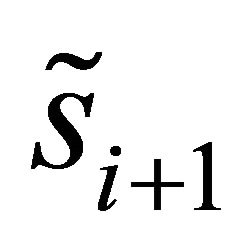 sent to the maximum likelihood detector are given by:
sent to the maximum likelihood detector are given by:
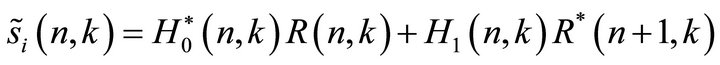 (6)
(6)
 (7)
(7)
where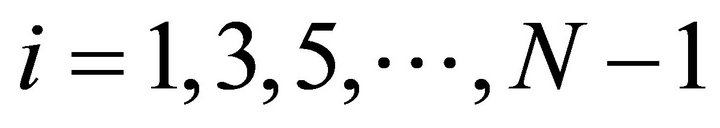 , represent the symbol number and k refers to the kth subcarrier,
, represent the symbol number and k refers to the kth subcarrier, .
.
The receiver need to estimate the channel H0 and H1 in order to use the Maximum Likelihood Decision Rule to produce ![]() and
and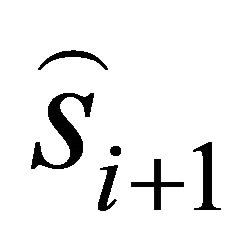 .
.
2.2.2. Alamouti SFBC-OFDM Scheme
The main idea behind the use of SFBC in OFDM is that the channel frequency response of adjacent subcarriers remains almost constant in such a system. The space-time block code STBC has been applied to frequency selective channels by using OFDM, which transforms a frequency selective channel into flat fading sub channels. The use of OFDM offers the opportunity for coding in the frequency domain in the form of space-frequency block codes SFBC [8].
The use of frequency diversity SFBC has an impact on spectral efficiency but this problem can be overcome by an increase of modulation order.
For 2 transmitter antennas, for each OFDM symbol, adjacent subcarriers k and k + 1  are used in space-frequency code. The nth OFDM symbol vector,
are used in space-frequency code. The nth OFDM symbol vector,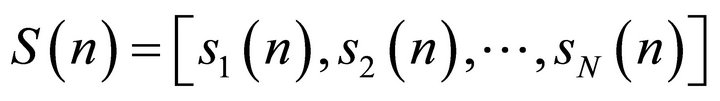 , is coded into two vectors
, is coded into two vectors  and
and  by space-frequency block encoder. S1(n) is transmitted from the first antenna while S2(n) is transmitted simultaneously from the second antenna. The symbol assignment of the 1st OFDM symbol vector is shown in Figure 3.
by space-frequency block encoder. S1(n) is transmitted from the first antenna while S2(n) is transmitted simultaneously from the second antenna. The symbol assignment of the 1st OFDM symbol vector is shown in Figure 3.
According to the symbol assignment given in Figure 3, the receiver output for subcarriers k and k + 1 for adjacent subcarriers can be written as
 (8)
(8)
 (9)
(9)
By assuming that adjacent subchannels in the OFDM spectrum have the same channel transfer functions [7], we have  and
and , in this case Equations (8) and (9) are similar to (1) and (2) and maximum diversity is achieved [3].
, in this case Equations (8) and (9) are similar to (1) and (2) and maximum diversity is achieved [3].
 (10)
(10)
 (11)
(11)
3. Time Frequency Selective Channel
In the design and implementation of a transmitter/receiver for wireless communications, it is very important to understand the wireless radio channel. The channel is characterized by two important parameters: the delay spread τmax and the maximum Doppler frequency fdmax. Channels with long delay spread τmax and high Doppler frequency fd, exhibit a lower coherence bandwidth and a lower coherence time, corresponding to time-frequency selective channel as it is indicated in Figure 4. In other words, the frequency selectivity of the channel depends on the delay spread τmax, and time selectivity depends on the Doppler frequency [8].
3.1. Channel Model
In the analogue domain, the multipath channel is described by the following complex-valued impulse response [9]:
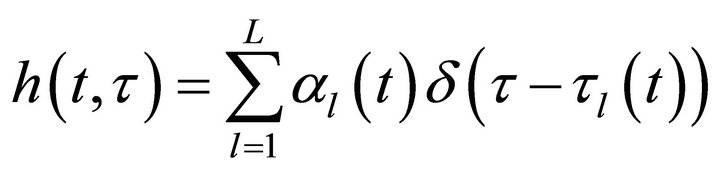
where αl is the complex gain of the lth path, τl is the propagation delay for the lth path. In digital transmission systems, symbols are often transmitted in regular time interval Ts, called the sampling period. This period is often small in comparison with the maximum delay time τmax.
The discrete multipath model is regarded as a reference for most of the contemporary wideband terrestrial wireless systems under a reasonable approximation of constant

Figure 3. Symbol assignment for subcarriers in SFBC.
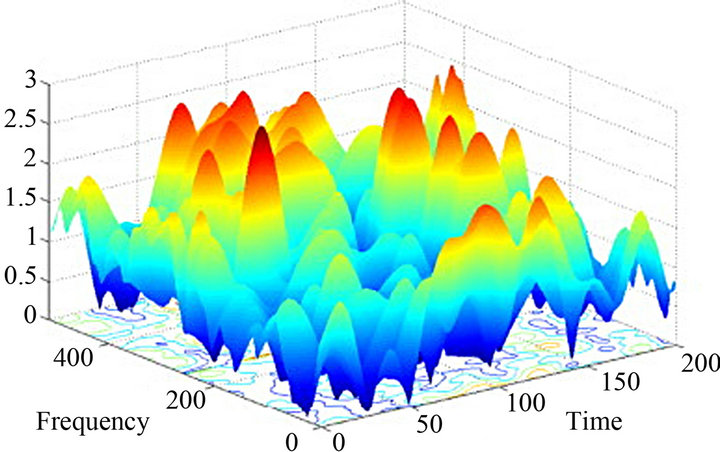
Figure 4. Time frequency selective channel.
number of multipath components L and slow variation of the delay values τl(t). The multipath channel is then modeled as

αl(t) depends on Doppler frequency fd which is caused by the velocity vm of the receiver.
 ,
,  is the azimuth of arrival of the radio wave, f is the carrier frequency, and c is the speed of the impacting radio wave.
is the azimuth of arrival of the radio wave, f is the carrier frequency, and c is the speed of the impacting radio wave.
3.2. Time Selectivity in Mobile Radio Channel
The channel time selectivity is due to the movement of the transmitter and/or the receiver. The frequency changes due to the Doppler effect depends on the relative motion between the source and receiver and on the speed of propagation of the wave.
The Doppler effect is characterized by two parameters:
The coherence duration Tc and the Doppler spread Bd.
• Coherence time Tc is a statistical measure of the time duration over which the channel impulse response is essentially invariant.
• The Doppler spread Bd given by 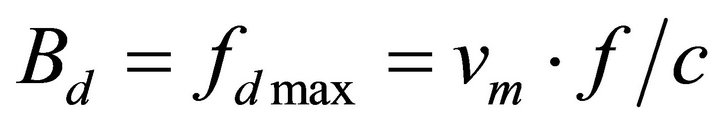
The Doppler spread Bd, and the coherence time Tc, are reciprocally related (within a multiplicative constant) [8].

A channel is referred to as fast fading channel if
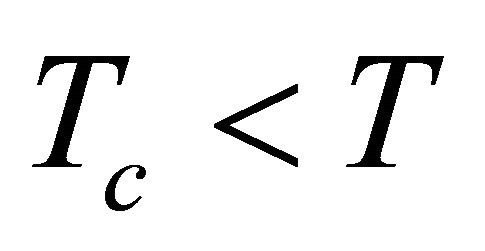
where T is the time duration of an OFDM symbol.
The below Figure (Figure 5) shows simulation results obtained with Rayleigh fading model for different Dop-
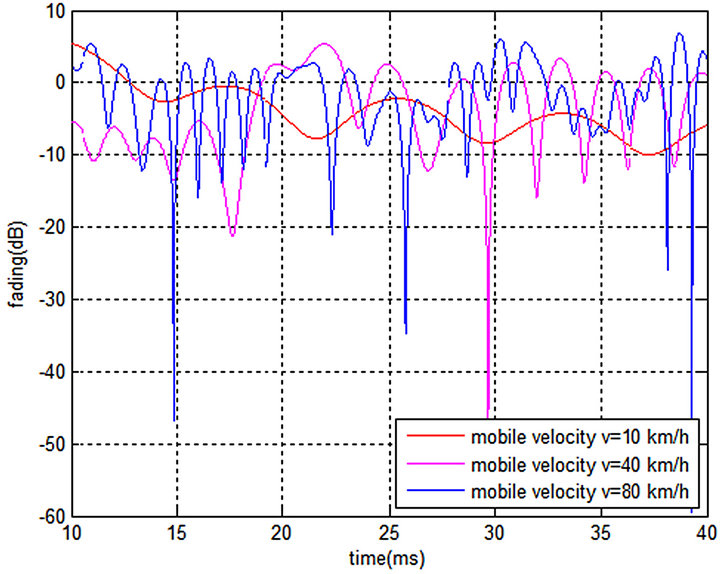
Figure 5. Rayleigh fading channel for varying mobile velocities.
pler frequency at varying mobile velocity ranging 80, 40 and 10 km/hour.
It can be observed from Figure 5 that the mobile velocity affect channel time selectivity.
3.3. Frequency Selectivity in Mobile Radio Channel
New applications such as wireless local area networks (LANs) require very high data rate transmissions. These applications are usually used in indoor environments. The result of radio signal multipath propagation in real environment is signal spread in time and it leads to the frequency selectivity of the channel.
Indoor fading channels are usually frequency selective for data rates over several Mbps.
Coherence bandwidth Bc is a statistical measure of the range of frequencies over which the channel can be considered “flat”.
We define severely frequency selective channel when coherence bandwidth is smaller than a pair of sub-carrier bandwidth, Δf < Bc < 2Δf, where Bc denote the coherence bandwidth and Δf the sub-carrier spacing in the OFDM spectrum.
In relation to severely frequency-selective channel, we define moderately frequency-selective channel when Bc > 2Δf, and in that case we can easily say that neighboring sub-carriers have identical channel frequency response.
For the Rayleigh fading model, the relation between the coherence bandwidth and delay spread was stated [8]
- 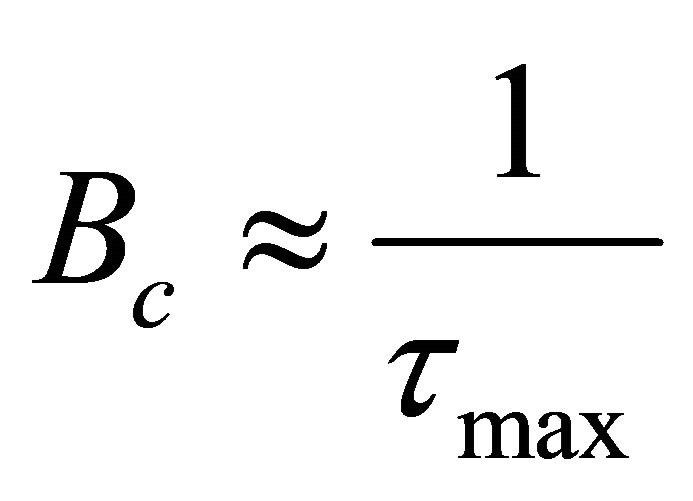
- A channel is said to exhibit frequency nonselective or flat fading if B < Bc, this inequality can be expressed as Ts > τmax, where B is the signal bandwidth (B = 1/Ts), Ts is the sampling time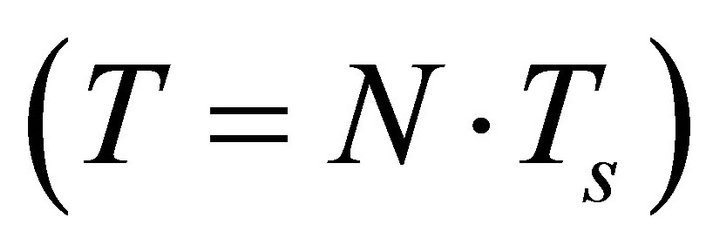 . In this case, all the received multipath components of a symbol arrive within the symbol time duration.
. In this case, all the received multipath components of a symbol arrive within the symbol time duration.
- A channel is said to exhibit frequency selective fading if B > Bc, this inequality can be expressed as Ts < τmax.
This condition occurs when the received multipath components of a symbol extend beyond the symbol’s time duration.
4. Proposed Adaptive Switching Technique
4.1. The Time-Frequency Correlation
The basic idea of adaptive switching is to choose the appropriate transmission mode at the given channel condition. In [6], the correlation for the same subcarrier between adjacent blocks,  , and the correlation between adjacent subcarriers for the same block,
, and the correlation between adjacent subcarriers for the same block, 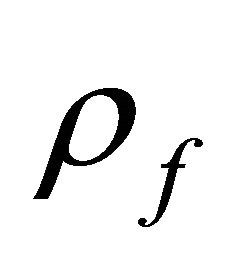 , are compared to choose an appropriate transmission mode. In [10], the theoretical value of
, are compared to choose an appropriate transmission mode. In [10], the theoretical value of 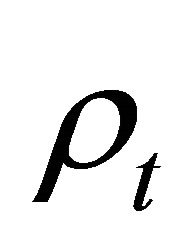 and
and  over Rayleigh fading channels are represented as
over Rayleigh fading channels are represented as
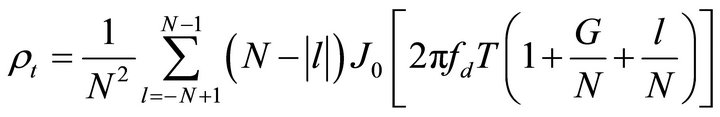
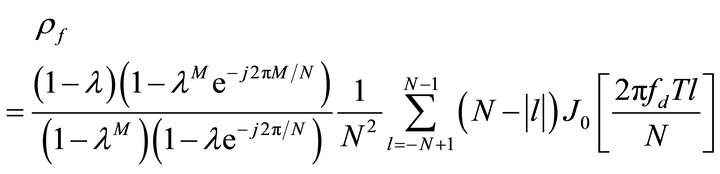
where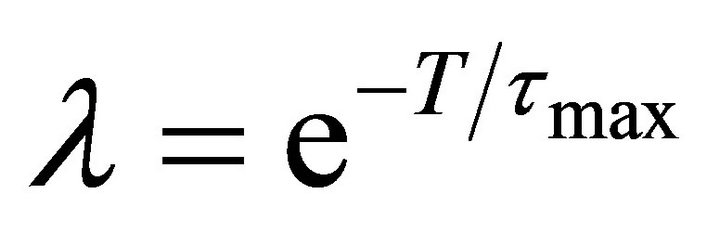 , G is the number of guard samples, N number of OFDM subcarriers and T is the duration of an OFDM block. J0[ ] is Bessel function of order zero.
, G is the number of guard samples, N number of OFDM subcarriers and T is the duration of an OFDM block. J0[ ] is Bessel function of order zero.
The correlation coefficients  and
and  between subcarriers along time and frequency respectively is needed to decide the switching mode (STBC or SFBC).
between subcarriers along time and frequency respectively is needed to decide the switching mode (STBC or SFBC).
4.2. Dynamic Allocation of STBC and SFBC in an OFDM System
The proposed adaptive switching system is illustrated in Figure 6.
The transmitter or receiver calculates  and
and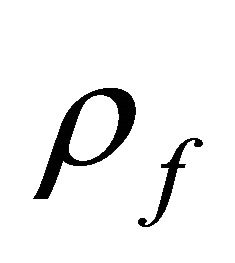 . Then it decides where the correlation is higher. The system needs only to estimate the channel delay spread and the Doppler frequency. Therefore, assumption can be made in the transmitter side.
. Then it decides where the correlation is higher. The system needs only to estimate the channel delay spread and the Doppler frequency. Therefore, assumption can be made in the transmitter side.
Notice that, for a Rayleigh fading channel,  depends only on
depends only on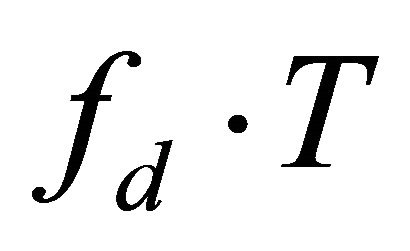 .
. 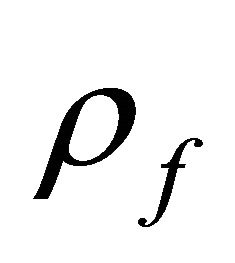 depends on
depends on 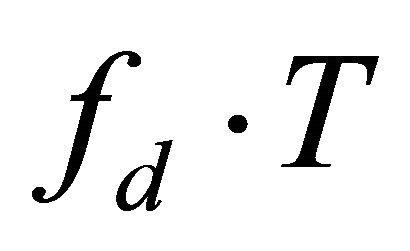 and
and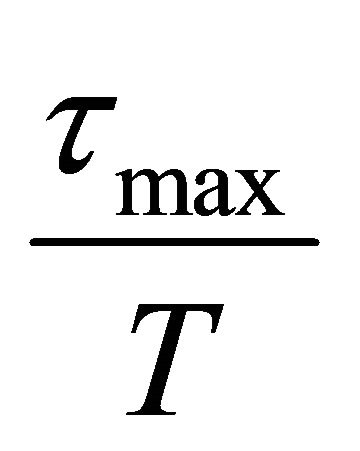 .
.
5. Simulation Results
In this section, we verify the theory by simulation and we test the performance of the proposed adaptive switching technique. The channel model is Rayleigh with parameters shown in Table 2.

Figure 6. Adaptive switching system.

Table 2. Simulation parameters.
We assume a perfect channel estimation since the aim of our simulation is to study the performance under different channel conditions by varying channel delay spread and Doppler frequency.
5.1. The Comparison between STBC-OFDM and SFBC-OFDM
The performance of OFDM STBC and SFBC schemes are evaluated depending on the BER versus the signalto-noise ratio (SNR) in Eb/N0.
Two types of channels slow fading and fast fading channel are examined. The performance comparison between STBC and SFBC in OFDM system over slow fading channel (fd = 20 Hz) is shown in Figure 7, the performance of the two systems STBC and SFBC-OFDM in fast fading channel (fd = 100 Hz) are shown in Figure 8, and the performance of STBC and SFBC-OFDM in slow fading (fd = 20 Hz) over frequency selective channel is shown in Figure 9.
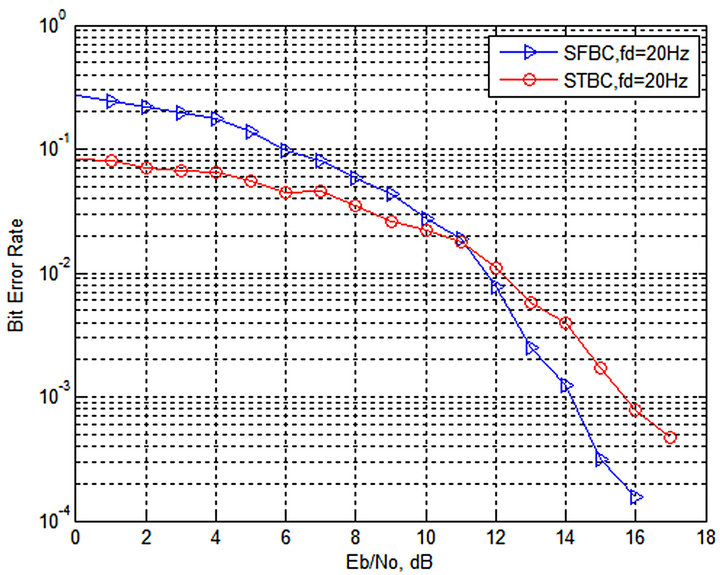
Figure 7. Performance of STBC and SFBC-OFDM for (fd = 20 Hz).

Figure 8. Performance of STBC and SFBC-OFDM for (fd = 100 Hz).

Figure 9. Performance of STBC and SFBC-OFDM over severely frequency selective channel.
In Figure 7, it can be observed, that SFBC OFDM achieves similar performance as STBC-OFDM in slow fading channel. It can be observed that SFBC-OFDM performs better in fast varying channel (Figure 8).
In Figure 9 it is seen that in the frequency selective channel the performance of SFBC is lost. The raison is that in this case the condition Bc > 2Δf is not fulfilled as well as the past.
5.2. The Adaptive Switching under Rayleigh Fading Channel
Comparing the values  and
and  from Figure 10, we note that the correlation coefficient can be lower in the time or frequency domain, depending on the terminal velocity and delay spread.
from Figure 10, we note that the correlation coefficient can be lower in the time or frequency domain, depending on the terminal velocity and delay spread.
Figure 10 shows the correlation  and
and 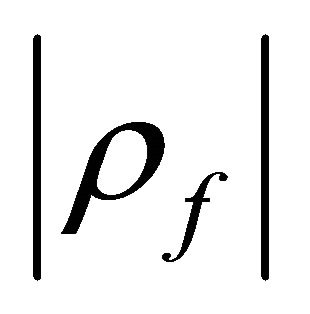 in terms of
in terms of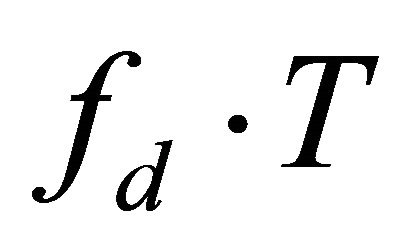 . We notice that the time correlation is strong (
. We notice that the time correlation is strong (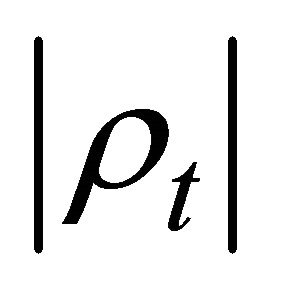 >
> ) under slow time varying channels such as
) under slow time varying channels such as 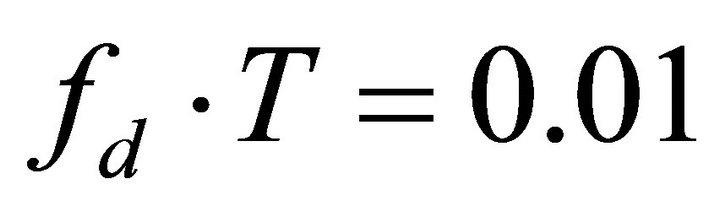 and
and 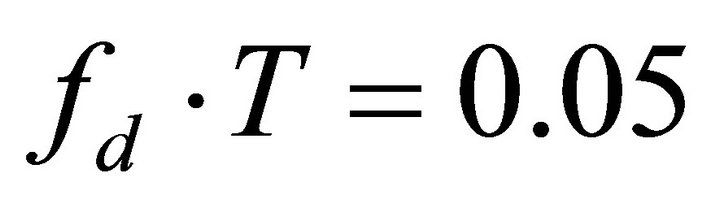
 . Under these conditions STBC performs better than SFBC.
. Under these conditions STBC performs better than SFBC.
In rapid time varying channels such as 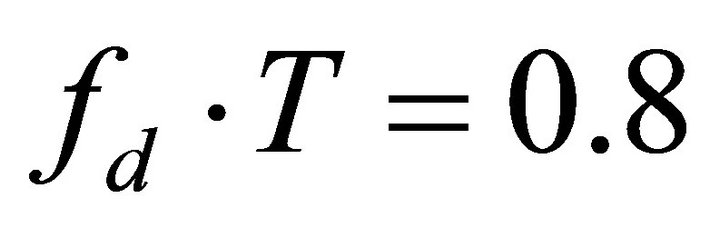 and
and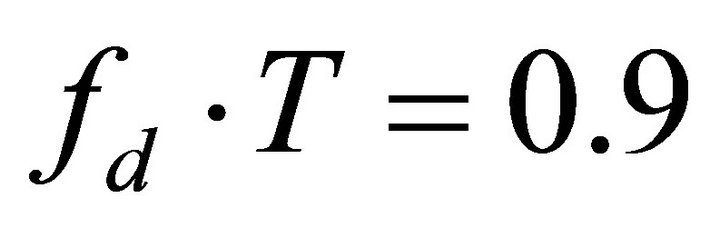 , the frequency correlation can be higher. However, frequency correlation,
, the frequency correlation can be higher. However, frequency correlation,  , is governed by the two parameters:
, is governed by the two parameters:  and
and .
.
Therefore, the performance of STBC-OFDM is only related to the channel time selectivity. Indeed, the performance of SFBC-OFDM is governed by both channel time and frequency selectivity.
The performance of the proposed adaptive switching system is illustrated in Figure 11. We note that the bit error rate of the adaptive scheme remains below the STBC-OFDM and SFBC-OFDM, as expected. Figure 11 shows that adaptive switching scheme performs better than STBC and SFBC over time frequency selective
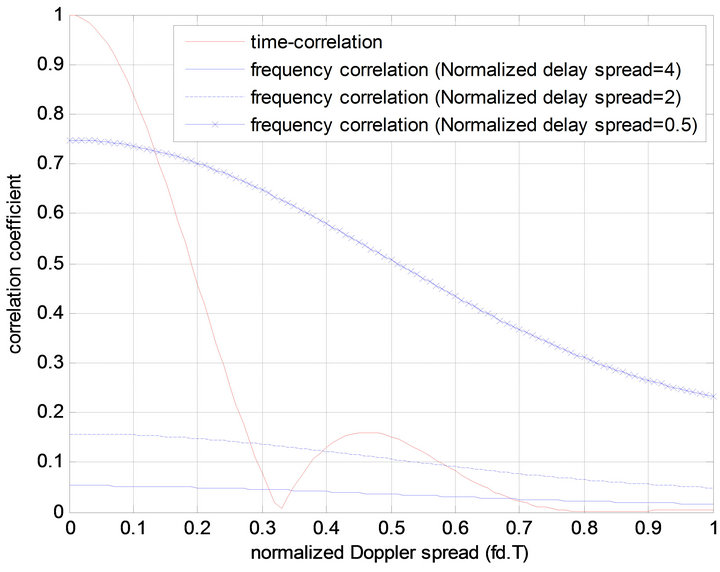
Figure 10. Time and Frequency correlation in terms of fd∙T.
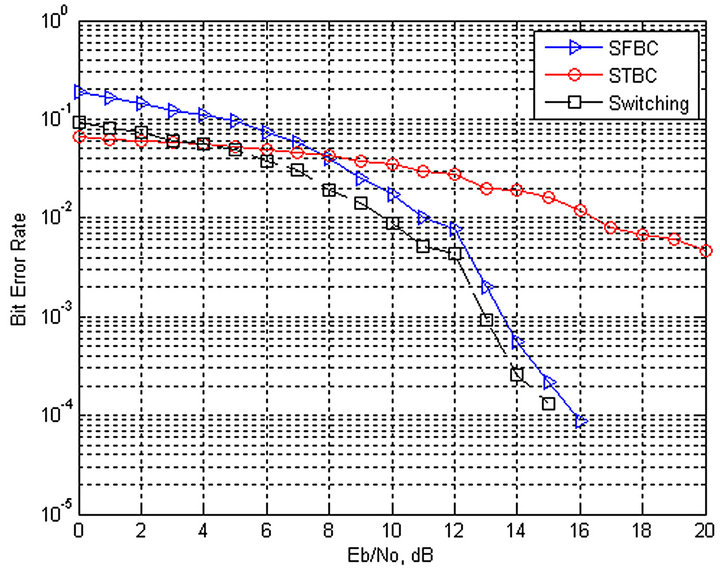
Figure 11. Performance of adaptive switching over time varying channel.
channels.
6. Conclusions
A combination of STBC in MIMO system with OFDM over time frequency selective channels has been presented. STBC-OFDM system is very tolerant to slow time varying environments where the channel time variation is slow but when the channel variation is increased due to the mobility of users, the system performs poorly. In this paper, it is found that SFBC has the same performance as STBC in slow fading channels, thus, SFBC improve the system performance better than STBC over high mobility environments. However, SFBC performs poorly in severely frequency selective channels.
Based on the proposed adaptive switching technique, we showed that adaptive switching between STBC and SFBC provides performance improvement over time frequency selective channels.
REFERENCES
- Y. S. Cho, J. Kim, W. Y. Yang and C. G. Kang, “MIMOOFDM Wireless Communications with MATLAB,” Wiley, 2010, 263 Pages.
- F. Meucci, “Multiple Input Multiple Output: From Signal Processing to Protocol Gain,” Ph.D. Thesis, University of Florence, Florence, 2009.
- S. M. Alamouti, “A Simple Transmit Diversity Technique for Wireless Communications,” IEEE Journal on Select Areas in Communications, Vol. 16, No. 8, 1998, pp. 1451-1458.
- Z. S. Wu, “MIMO-OFDM Communication Systems: Channel Estimation and Wireless Location,” Louisiana State University, Ph.D. Thesis, Louisiana State University, Baton Rouge, 2006.
- S. Kaiser, “Space Frequency Block Codes and Code Division Multiplexing in OFDM Systems,” Global Telecommunications Conference, San Francisco, 1-5 December 2003.
- K. Lee, Y. Kim and J. Kang, “Adaptive Switching between Space-Time and Space-Frequency Block Coded OFDM Systems,” Military Communications Conference, Milcom, 2008, pp. 1-5.
- L. Hanzo, J. Akhtman, M. Jiang and L. Wang, “MIMOOFDM for LTE, WIFI and WIMAX,” Wiely IEEE Press, 2010, 591 Pages.
- B. Sklar, “Rayleigh Fading Channels in Mobile Digital Communication Systems Part I: Characterization,” IEEE Communications Magazine, Vol. 35, No. 9, 1997, pp. 90- 100.
- D. Tse and P. Viswanath, “Fundamentals of Wireless Communication,” Cambrige University Press, Cambrige, 2005. doi:10.1017/CBO9780511807213
- D. B. Lin, P. H. Chiang and H. J. Li, “Performance Analysis of Two-Branch Transmit Diversity Block Coded OFDM Systems in Time-Varying Multipath Rayleigh Fading Channels,” IEEE Transactions on Vehicular Technology, Vol. 54, No. 1, 2005, pp. 136-148. doi:10.1109/TVT.2004.838826

