Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 8 (2012) , Article ID: 21932 , 9 pages DOI:10.4236/ijcns.2012.58058
Cognitive Congestion Control for Data Portals with Variable Link Capacity
Department of Electrical & Computer Engineering, University of Nevada, Las Vegas, USA
Email: Sharifah@unlv.nevada.edu, Shahram.Latifi@unlv.edu
Received May 31, 2012; revised June 28, 2012; accepted July 5, 2012
Keywords: Available Bandwidth; Cognitive System; Data Portal; Network Congestion; Queue Length; Variable Link Capacity
ABSTRACT
Network congestion, one of the challenging tasks in communication networks, leads to queuing delays, packet loss, or the blocking of new connections. In this study, a data portal is considered as an application-based network, and a cognitive method is proposed to deal with congestion in this kind of network. Unlike previous methods for congestion control, the proposed method is an effective approach for congestion control when the link capacity and information inquiries are unknown or variable. Using sufficient training samples and the current value of the network parameters, available bandwidth is adjusted to distribute the bandwidth among the active flows. The proposed cognitive method was tested under such situations as unexpected variations in link capacity and oscillatory behavior of the bandwidth. Based on simulation results, the proposed method is capable of adjusting the available bandwidth by tuning the queue length, and provides a stable queue in the network.
1. Introduction
A data portal provides information from diverse sources in a unified way. It enables instant, reliable and secure exchange of information over the web; in particular, a data portal focuses on providing centralized, robust access to specific data and supported manipulations. The concept of a portal functions to offer a single web page that aggregates content from various servers.
There are different types of data portals, for instance, academic portals, including those for scientific data; commercial portals; and enterprise portals. A data portal can be considered as an application-based network that consists of databases, different servers, web-based application software, communication links, and computing clusters.
With regard to a data portal, congestion can happen when a link or node carries so much data that a loss of quality of service for the portal results. As an early effort to control the network congestion, the Jacobson’s algorithm [1] was embedded into the Transmission Control Protocol (TCP) [2]. Although this protocol controls endto-end congestion conveniently, it also deteriorates network performance due to unstable throughput, increased queuing delay, and restricted fairness. Furthermore, longer delays will lead to weak link utilization, significant packet losses, and poor adaptation to changing link loads.
Conventional congestion control methods often cannot achieve both fairness and appropriate bandwidth utilization due to packet loss. To deal with the problem, various TCP parameters have been utilized for the estimation of the available link capacity and the Round-Trip Time (RTT) in order to predict congestion [3-7].
When a delay-bandwidth product grows, the TCPbased networks exhibit an oscillatory behavior under some congestion-control algorithms. Reference [8] explains that when the delay or capacity increases, Random Early Marking (REM) [9], Random Early Discard (RED) [10], proportional integral controller [11], and virtual queue [12] show oscillatory behavior. Whereas the bandwidth-delay product relating to a flow during high bandwidth links could contain many packets, TCP could waste a lot of RTTs ramping until full utilization, following a congestion burst.
The main obstacle in TCP is related to its reliance on scarce events that provide poor resolution information.
To improve adaptation to network conditions, achieve high utilization, attain stable throughput, and decrease standing queues in the network, some approaches have been proposed in the literature [13-20]. Explicit Congestion Control (XCC), one of the famous congestion control approaches, is able to inform sources concerned with the network status and control the bit rate in network. The XCC uses a header to carry the throughput information and Round-Trip Time (RTT) of the flow to which the packet belongs. When the throughput is used for the adjustment of bandwidth distribution, the RTT enables sources to control the speed of adaptation to network conditions. In XCC, routers play an important role in informing sources concerned with the network status and in helping sources to control their bit rate by accurate feedback. In fact, to determine the feedback for sources, a router should calculate the current spare bandwidth for outgoing links and compute the link capacity.
Some congestion control methods need explicit and precise feedback. As congestion is not a binary variable, congestion signaling should provide the congestion degree. By means of precise congestion signaling, it is possible to determine when the network tells the sender the congestion state and how to react to it. In fact, the senders can decrease their sending windows quickly when the bottleneck is extremely congested. However, these methods—based on a control loop with feedback delay—become unstable for long feedback delay. To deal with this effect, the system should slow down while the feedback delay increases. In other words, when delay increases, the sources should change their transmission rates more slowly [8,21-23].
As one of crucial issues related to network congestion, robustness of the method should be independent of unknown and quickly changing parameters (e.g., the number of flows). Also, for such methods as XCC, convenient bandwidth sharing is difficult when the information inquiries and capacity of links are variable. In other words, the unpredictability of the network creates a problem for XCC. This study focuses on a cognitive method to control congestion; it also can perform well when the link capacity and information inquiries are unknown or variable.
1.1. Cognitive Concept
A cognitive system is a complex system that has the ability for emergent behavior [24]. It processes data over the course of time by performing the following steps: 1) perceive defined situations; 2) learn from defined situations and adapt to their statistical variations; 3) build a predictive model on prescribed properties; and 4) control the situations and do all of these procedures in real time for the purpose of executing prescribed tasks.
To optimally adapt the network parameters and to provide efficient communication services using a cognitive approach, learning the relationships between parameters of network is crucial. In learning phase, it is possible to utilize the Bayesian Network (BN) model. A BN is a probabilistic graphical model that represents conditional independence relations between random variables by means of a Directed Acyclic Graph (DAG) [25]. The DAG is constructed with a set of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at vertex i and follow a sequence of edges that eventually loops back to i [26-28].
The BN model can be used to provide a representation of the dependence relationships among network parameters and adjust cognitive parameters to improve the network’s efficiency. It is utilized to deal with congestion, one of the challenging tasks in the TCP; there is no efficient mechanism to determine when congestion occurs in the network.
1.2. Variable Link Capacity
As mentioned earlier, to efficiently control the network congestion, and preserve stable throughput, low queuing delay, the critical parameters in network can be defined and adjusted based on pre-defined criteria and statistical variations of the network.
The available bandwidth,  , which is distributed among different flows during a certain time period T, is defined as follows:
, which is distributed among different flows during a certain time period T, is defined as follows:
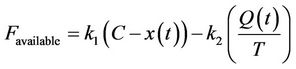 (1)
(1)
where coefficients 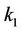 and
and 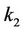 are constant, x(t) is the bandwidth utilized for the last period T, C is the estimated capacity of the data transmission link, and Q(t) is the minimum queue length that happened during the last T seconds.
are constant, x(t) is the bandwidth utilized for the last period T, C is the estimated capacity of the data transmission link, and Q(t) is the minimum queue length that happened during the last T seconds.
The parameter T can be written as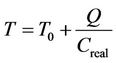 , in which
, in which  is the system base delay, or the delay excluding queuing delay; and
is the system base delay, or the delay excluding queuing delay; and 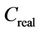 is the actual capacity of the data transmission link.
is the actual capacity of the data transmission link.
The capacity C is a function of various factors, such as the data rate of every link, the number of active links, failed transmissions, the number of collisions, and handshake procedures. The estimation error of link capacity is defined as . The given error should be compensated up to a certain limit. To define the limit, the parameter C in (1) is replaced by
. The given error should be compensated up to a certain limit. To define the limit, the parameter C in (1) is replaced by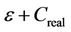 . When the capacity of the data transmission link is fully utilized, i.e.,
. When the capacity of the data transmission link is fully utilized, i.e., 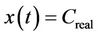 , it is expected that the available bandwidth is zero or close to zero, due to error. Therefore, the limit of the estimation error is defined as the following:
, it is expected that the available bandwidth is zero or close to zero, due to error. Therefore, the limit of the estimation error is defined as the following:
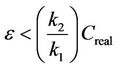 (2)
(2)
The value of  depends on the available bandwidth and the standing queue in the router. In fact, if the link capacity changes, the Favailable can be adjusted to distribute the bandwidth among the active flows.
depends on the available bandwidth and the standing queue in the router. In fact, if the link capacity changes, the Favailable can be adjusted to distribute the bandwidth among the active flows.
The proposed method computes the Favailable with no knowledge of exact channel capacity. It also can adjust the Favailable according to bandwidth variations.
2. Proposed Method
2.1. Adjustment of Available Bandwidth
Typically, a router controls each of its output queues; therefore, available bandwidth is computed for each of them. With the proposed method, in order to compute available bandwidth, it is not required for the router to be configured with certain medium capacity. In addition, the proposed method can adapt to changing bandwidth conditions over time.
First, the effect of queue speed on available bandwidth Favailable is considered. The queue speed can be defined as the difference between the capacity of the transmission channel and utilized bandwidth during the time period T. Equation (3) is written as follows:
 (3)
(3)
where 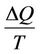 is the queue speed. Due to queue variationsthe queue length should be adjusted for Favailable, so parameter α is defined. It is possible to conveniently tune Favailable using the parameter α during extreme queue variations. The parameter α is adjusted by the cognitive algorithm. In fact, the parameter α controls the target queue length in which the network stabilizes.
is the queue speed. Due to queue variationsthe queue length should be adjusted for Favailable, so parameter α is defined. It is possible to conveniently tune Favailable using the parameter α during extreme queue variations. The parameter α is adjusted by the cognitive algorithm. In fact, the parameter α controls the target queue length in which the network stabilizes.
2.2. Cognitive Congestion Control
The schematic of the cognitive congestion control is illustrated in Figure 1. Each network parameter is periodically sampled and collected in the input matrix. The cognitive process is decomposed into four steps: 1) observation, 2) learning, 3) decision, and 4) action.
During the observation step, required information from network is collected. Then, the cognitive algorithm learns the relations between the parameters and their conditional independences as well as the effect of controllable parameters on observable parameters.
During the decision step, the values to be assigned to controllable parameters are calculated to meet pre-defined requirements. In other words, the values of the

Figure 1. Schematic of cognitive congestion control.
network parameters of interest are predicted based on the observations. This prediction is done by inference, using the Bayesian network.
In the action step, the controllable parameters are tuned, and the appropriate actions are taken in the network.
2.3. Cognitive Process
2.3.1. Observation
During the observation step, seven network parameters are examined. These parameters are:
1) The Round Trip Time (RTT), that is, time period for which a signal to be sent plus the time period for which an acknowledgment of that signal to be received;
2) The queue length;
3) The queue speed;
4) The throughput, that is, total amount of successful delivered data over a link;
5) The contention window size;
6) The congestion window size, that is, the total amount of unacknowledged data;
7) The congestion window status.
The congestion window status is considered as 0 if the congestion window size at time t becomes 25% less than the congestion window size at time t − 1; otherwise the status is 1. The status equals to zero is of interest, as the congestion is being decreased.
Here, observed network parameters are considered as random variables (x1, ···, x7). It is assumed the given variables have unknown dependence relations. The independent samples from every variable have been gathered into the input matrix (size of n × 7). The construction of input matrix is performed during the observation step.
2.3.2. Learning
The learning step is a key step in the cognitive algorithm. During this step, the BN is built to provide a structure representing conditional independence relations between parameters of interest in a DAG. To form the BN and demonstrate the relations in a DAG, learning from the qualitative relations between the variables and their conditional independences is considered.
A node in the DAG represents a random variable, while an arrow that joins two nodes represents a direct probabilistic relation between the two corresponding variables. For , if there is a direct arrow from j to i, node j will be a parent of node i. (
, if there is a direct arrow from j to i, node j will be a parent of node i. ( describes the set of parents of node i). A complete DAG with all nodes connected with each other directly can represent all possible probabilistic relations among the nodes.
describes the set of parents of node i). A complete DAG with all nodes connected with each other directly can represent all possible probabilistic relations among the nodes.
During the learning phase, based on the input matrix (Im), the dependency is exploited among the variables represented as nodes in a DAG. To build the DAG representing the probabilistic relation between the variables, the selection of DAGs and the selection of parameters are utilized.
2.3.2.1. Selection of DAGs For the selection of DAGs, the scoring approach and the constraint approach can be utilized [29,30].
In the constraint approach, a set of conditional independence statements is defined by a priori knowledge. Then, the given set of statements is utilized to build the DAG, following the rules of d-separation [29].
The scoring approach generally is utilized when a set of given conditional independence statements is not available [31,32]. The scoring approach is capable of inferring a sub-optimal DAG from a sufficiently large data set (i.e., Im). The scoring approach consists of two phases: 1) Searching to select the DAGs to be scored within the set of all possible DAGs and 2) scoring each DAG according to how accurately it defines the probabilistic relations between the variables based on the Im.
1) Searching process
The searching process to select the DAGs (i.e., the first phase of the scoring approach) is required because it is not computationally efficient to score all the possible DAGs, since the scoring procedure generally takes a great deal of time. For instance, to find the DAG with the highest score for a set of m variables, the following formula is expressed [33]:
 (4)
(4)
where 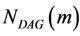 is the total number of possible DAGs. When m increases, the
is the total number of possible DAGs. When m increases, the 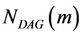 increases significantly, and the scoring procedure takes more time. Therefore, a searching process is required to choose a small, and possibly representative, subset of the space of all DAGs.
increases significantly, and the scoring procedure takes more time. Therefore, a searching process is required to choose a small, and possibly representative, subset of the space of all DAGs.
Most of searching processes in scoring approaches are based on heuristics that find local maxima almost appropriately. However, the heuristics do not generally guarantee that global maxima is obtained [30].
There are two classical searching procedures in literature [34]: 1) Hill Climbing and 2) Markov Chain Monte Carlo.
Hill Climbing is an iterative algorithm by which an arbitrary solution is initially defined for a problem. Then, the hill climbing algorithm searches a better solution by incrementally changing a single element of the solution. If the change generates a better solution, an incremental change is made to the new solution; this is repeated until no further improvements can be reached [34,35].
Markov Chain Monte Carlo (MCMC) is a category of algorithms for sampling from probability distributions based on constructing a Markov chain that has the distribution of interest as its equilibrium distribution. After specific procedure, the state of the chain is utilized as a sample of the distribution of interest [36,37].
The searching process results in some DAGs.
2) Scoring
The Bayesian information criterion is selected for scoring, and is based on the maximum likelihood criterion. The Bayesian information criterion is expressed as follows [32]:
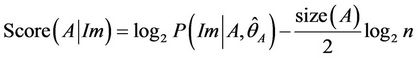 (5)
(5)
where Im is the dataset (i.e. input matrix), A is the DAG to be scored,  is the maximum likelihood estimation of the parameters of A, and n is the number of observations for every variable in the dataset.
is the maximum likelihood estimation of the parameters of A, and n is the number of observations for every variable in the dataset.
When all random variables are multinomial, the Bayesian information criterion is formulated as follows [30- 33,38]:
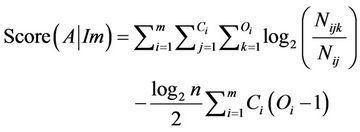 (6)
(6)
where 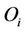 is a finite set of outcomes for every variable
is a finite set of outcomes for every variable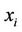 ;
; 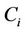 is the number of different combinations of outcomes for the parents of
is the number of different combinations of outcomes for the parents of ;
; 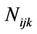 is the number of cases in the input matrix in which the variable
is the number of cases in the input matrix in which the variable 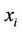 took its kth value (k = 1, 2, ···, Oi), and its parent was instantiated as its jth value (j = 1, 2, ···, Ci); and
took its kth value (k = 1, 2, ···, Oi), and its parent was instantiated as its jth value (j = 1, 2, ···, Ci); and 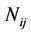 is the total observations related to variable
is the total observations related to variable  in the input matrix
in the input matrix
(Im) with parent configuration j (i.e.,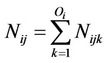 ).
).
Therefore, based on Equation (6), the scoring approach is computationally tractable. More details about Bayesian information criterion are presented in [38].
Now, the DAG with highest score can be selected.
2.3.2.2. Selection of Parameters During the selection of parameters, the best set of the controllable parameters are chosen and estimated, based on the observed parameters and their independence relations.
Based on the Bayesian network definition, every variable is directly calculated by its parents; thus, the estimation of the parameters for every variable xi is performed according to the set of its parents in the DAG selected during structure learning. The Maximum Likelihood Estimation (MLE) technique is used to build a predictive model and to estimate the appropriate set of parameters describing the conditional dependencies among the variables. The MLE technique is expressed as follows:
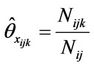 (7)
(7)
For , the parents of node i are in the configuration of type j, and the variable
, the parents of node i are in the configuration of type j, and the variable  takes its kth value (i.e.
takes its kth value (i.e.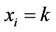 ).
).
The estimated value 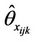 provides an approximation of the posterior distribution of
provides an approximation of the posterior distribution of 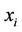 given the evidence j (i.e., parents of node i in the configuration of type j). Therefore, Equation (7) can be re-written as follows [30]:
given the evidence j (i.e., parents of node i in the configuration of type j). Therefore, Equation (7) can be re-written as follows [30]:
 (8)
(8)
2.3.3. Decision
The Bayesian network is completed after selection of DAGs and parameters in the learning step. The completed BN provides the probabilistic relations among selected parameters from the selected DAG.
In this step, the future values of the queue length and queue speed—that is, the unobserved parameters—are predicted based on selected observed parameters. The estimated value of unobserved parameter 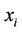 is defined as the expectation of the given parameter, using probability function represented in Equation (8). Therefore, the expected value of
is defined as the expectation of the given parameter, using probability function represented in Equation (8). Therefore, the expected value of 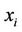 at time t,
at time t, 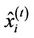 , is calculated as follows:
, is calculated as follows:
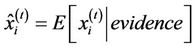 (9)
(9)
where 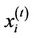 is the actual value of the unobserved parameter
is the actual value of the unobserved parameter 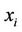 at time t, and evidence is the set of selected observed parameters.
at time t, and evidence is the set of selected observed parameters.
2.3.4. Action
To calculate α in Equation (3), the predicted values of the unobserved parameters (i.e., queue length and queue speed) are considered. In fact, the fluctuation of predicted values for the queue length and queue speed are utilized to set the parameter α; then, parameter α adjusts the available bandwidth, Favailable.
As mentioned earlier, α represents the target queue length in which the network stabilizes. When there is no queue constructed (underutilization), α explains how much bandwidth is distributed in every control interval. During full utilization or overutilization, α will control how much queuing delay is introduced.
During the time of underutilization, the bandwidth is maximally distributed; if a link is saturated, the queuing delay is significantly decreased. Generally, α is high during underutilization, and is low during full utilization.
3. Result
The base scenario used in the simulation includes a dumbbell network topology, which provides a number of nodes connected to a single router. The router is connected to another router over a serial link. A group of nodes are connected to that router, creating the dumbbell topology.
The network traffic consists of flows between the client and server nodes in both directions. It is assumed that the flows traversing the network from server nodes to client nodes are downloads, while flows in the opposite direction are considered uploads.
The simulations were performed using the ns-3 network simulator [39]. During the simulation, parameters of interest were sampled for each flow at certain sampling periods (i.e., every 30 ms and 60 ms). The queue length was set to 50 packets while the bottlenecks happened. The size of the data packets was 1200 bytes, and the size of acknowledgment packets was 50 bytes.
3.1. Variable Capacity
In this part of the procedure, the response of the proposed method to unexpected variations of link capacity was emphasized. During this simulation, the data rate changed. At first, the simulation was performed by the data rate of 56 Mbps. The variable capacity was simulated by changing the data rate, as shown in Figure 2. The data rate changed each 20 seconds, that is, 56 Mbps at t = 0, 21 Mbps at t = 20, 5 Mbps at t = 40, 21 Mbps at t = 60, and 56 Mbps at t = 80.
Due to sudden bandwidth reduction, there are queue spikes in the Figure 2. When queue length significantly increases, the parameter α increases. Thus, based on Equation (3), the difference between the queue length and α will not significantly change. Therefore, these spikes were compensated by the method, and available bandwidth was conveniently utilized.
3.2. Dynamics of Parameter α
To demonstrate the responsiveness of the proposed method to arrival and departure flows, a 40-sec simulation was performed, and the RTT was set to 60 ms. The average queue length as well as the parameter α throughout the time are illustrated in Figure 3. It was observed that the proposed method responded conveniently to the queue fluctuation. In fact, the dynamic of parameter α was assessed by observing the queue fluctuation.
When the queue is reduced, that is a sign of underutilization, and α is increased. During the increase of α, more bandwidth is distributed among servers to quickly provide full utilization.
To match the variation of the queue, the queue length was increased, while parameter α was decreased. Generally, there was a low latency caused by queue buildup.
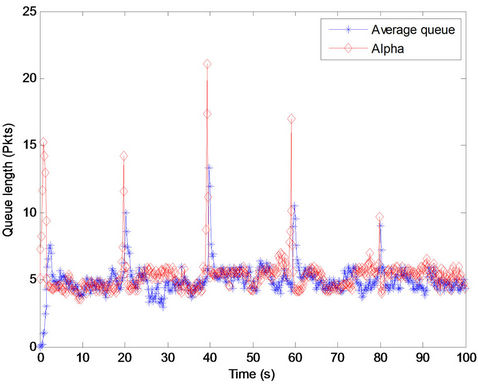
Figure 2. The fluctuation of average queue length and parameter α throughout time during variable capacity.
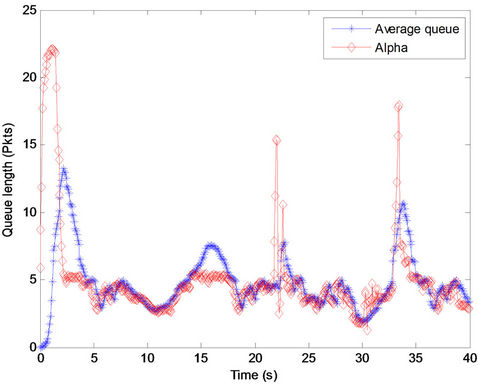
Figure 3. The fluctuation of average queue length and parameter α throughout time.
To prevent high queue spike, the maximum value of α should be less than the maximum value for queue length (i.e., channel capacity). Parameter α can tune the variation of bandwidth as it affects the queue.
3.3. Different Data Rates
In this part of the procedure, the response of the method was assessed while different data rates are used in network. It is considered that a part of the network has a data rate of 10 Mbps and the rest of the network has the data rate of 56 Mbps. In other words, new flows enter the network with data rate of 10 Mbps; other flows with data rate of 56 Mbps leave the network, or vice versa. It causes an oscillatory behavior for the bandwidth. The proposed method provides a stable queue under the given situation (Figure 4).
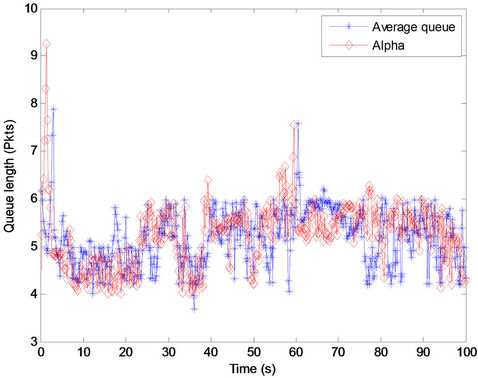
Figure 4. Fluctuation of average queue length and parameter α throughout time, while different data rates used in the network.
3.4. Efficiency
Now, the efficiency of the method is evaluated as network utilization. It is demonstrated that the increase of the bandwidth-delay product of network negatively affects the efficiency of the TCP; however, it has trivial influence on the efficiency of the proposed method.
To simulate a traffic pattern, two kinds of flows are considered: 1) flows with exponentially distributed duration, with certain minimum value (1 s) and mean value (10 s); and 2) other flows that are active during the simulation.
Each wired path between the end-system and router was configured with a specific latency; latencies of wired paths were between 20 ms and 120 ms. The growth of the bandwidth-delay product of network was simulated by increasing the path delay.
The result of simulation is shown in Figure 5. As shown in the figure, the efficiency scales change based on the increase of the link capacity.
It can be demonstrated that the TCP was not able to scale with the bandwidth-delay product of network because of its fixed dynamics. Based on the traffic pattern and the number of flows, the TCP was not able to fully utilize network resources for a specific bandwidth threshold.
Overall, the proposed method was able to maintain convenient utilization at all times.
3.5. Accuracy of Learning Process
To predict the status of congestion in future (i.e., t + k) at time t, the current value of all parameters of interest was considered. It is possible to predict when the congestion happens, and try to act before it affects the network.
To analyze the accuracy of the learning process for predicting congestion at time t, the value of Status (t + k)—that is, the presence or absence of congestion at time t + k, with k ≥ 1—was considered.
The performance of the learning process is assessed as a function of the size (i.e., number of samples) of the training set utilized to learn the relations between the desired parameters. The parameters are stored during the training, and the stored values become the input for the inference phase.
In Figures 6 and 7 the training set size changes. The vertical axis of the figures represent the average error for the inference, i.e. the expected value of 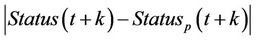 , for which
, for which 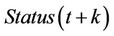 is the actual value of congestion status at time t + k and
is the actual value of congestion status at time t + k and
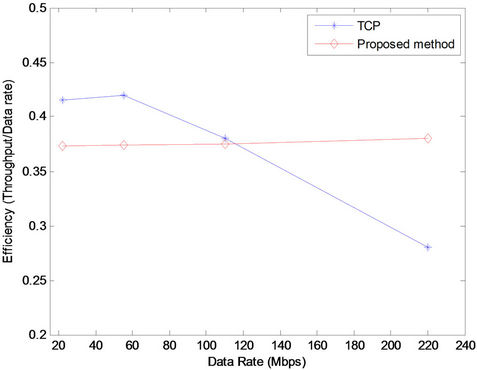
Figure 5. Efficiency versus capacity. Unlike the proposed method, the growth of the bandwidth-delay product of the network leads to TCP utilization decreases. In contrast, the proposed method is able to maintain utilization.
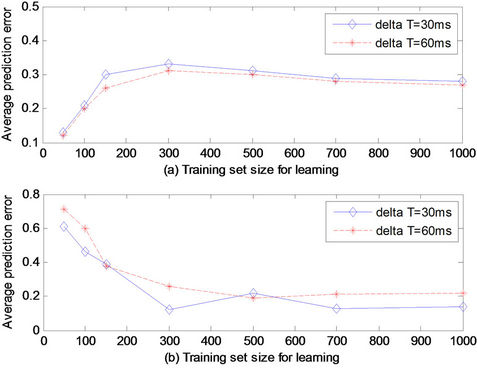
Figure 6. Average prediction error for status (t + 1) which depends on the training set size: (a) when the congestion status is predicted as Status (t + 1) = 0, i.e., congestion is present; and (b) when the congestion status is predicted as Status (t + 1) = 1.

Figure 7. Average prediction error for Status (t + 1) as a function of the training set size for different values of the sampling period ∆T: (a) when the congestion status is predicted as Status (t + 1) = 0, i.e., congestion is present; and (b) when the congestion status is predicted as Status (t + 1) = 1.
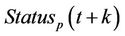 is the predicted value of congestion status at time t + k. When congestion is present, the variable of Status is zero, otherwise it is one. This variable can be illustrated as the frequency of an error in the process of prediction. In Figures 6 and 7, two cases are separately assessed. In other words, the results are shown for
is the predicted value of congestion status at time t + k. When congestion is present, the variable of Status is zero, otherwise it is one. This variable can be illustrated as the frequency of an error in the process of prediction. In Figures 6 and 7, two cases are separately assessed. In other words, the results are shown for 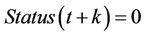 and
and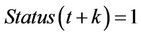 .
.
In Figure 6, under a different training set size from RTT and queue length, the average prediction error is not the same. As shown in the figure, if more information about RTT and queue length is available, the average prediction error decreases. Therefore, the number of collected samples from each parameter of interest should be more than 300.
In Figure 7, the average prediction error changes, based on the training set size for different values of the sampling period . If enough data (i.e., input samples) is available, the learning phase is conveniently preformed, and the prediction will be more accurate.
. If enough data (i.e., input samples) is available, the learning phase is conveniently preformed, and the prediction will be more accurate.
4. Conclusions
In this paper, a cognitive method is proposed to improve bandwidth sharing and deal with congestion in a data portal. For example, when the data portal is about climate change data, congestion control is more emphasized because the scientific climate data is voluminous; there is high traffic to/from the data portal by the scientific community, research groups, and general readers. In fact, this study was performed to improve congestion control in such data portals as the climate change portal.
Here, the data portal is considered as an applicationbased network. The proposed method was able to adjust the available bandwidth in the network when the link capacity and information inquiries were unknown or variable. In fact, it was possible to conveniently adjust available bandwidth, using the cognitive method, during extreme queue variations.
The variation of link capacity has an influence on the queue. In fact, α dynamically changes over the time, and helps the queue to have a smoother behavior while guaranteeing that the set is based on pre-defined operating conditions.
The learning phase is a key step in the cognitive method. During this step, the collected information in the observation phase is used by the Bayesian network model to build a probabilistic structure to predict variations of queue length.
The efficiency of proposed method was tested by a network simulator. Based on results, available bandwidth during extreme queue variations can be conveniently adjusted by the proposed method. Unlike TCP, in which the growth of the bandwidth-delay product of network affects negatively TCP’s efficiency, the proposed method is able to maintain convenient utilization at all times.
5. Acknowledgements
This work was conducted as a part of an Innovation Working Group supported by the Nevada EPSCoR Programs, and funded by NSF Grant # NSFEPS-0814372.
REFERENCES
- V. Jacobson, “Congestion Avoidance and Control,” ACM SIGCOMM Computer Communication Review, Vol. 18, No. 4, 1988, pp. 314-329.
- J. Postel, “Transmission Control Protocol,” IETF RFC 793, 1981.
- L. Xu, K. Harfoush and I. Rhee, “Binary Increase Congestion Control (BIC) for Fast Long-Distance Networks,” INFOCOM 23rd Annual Joint Conference of the IEEE Computer and Communications Societies, Hong Kong, 7-11 March 2004, pp. 2514-2524.
- S. Ha, I. Rhee and L. Xu, “CUBIC: A New TCP-Friendly High-Speed TCP Variant,” ACM SIGOPS Operating Systems Review, Vol. 42, No. 5, 2008, pp. 64-74. doi:10.1145/1400097.1400105
- S. Floyd, “High Speed TCP for Large Congestion Windows,” RFC3649, ICSI, Berkeley, 2003.
- S. Ekelin, M. Nilsson, E. Hartikainen, A. Johnsson, J. E. Mangs, B. Melander and M. Bjorkman, “Real-Time Measurement of End-to-End Available Bandwidth Using Kalman Filtering,” Proceedings of the 10th IEEE/IFIP Network Operations and Management Symposium, Vancouver, 3-7 April 2006, pp. 73-84.
- J.-C. Bolot, “Characterizing End-to-End Packet Delay and Loss in the Internet,” Journal of High Speed Networks, Vol. 2, No. 3, 1993, pp. 305-323.
- S. H. Low, F. Paganini, J. Wang, S. Adlakha and J. C. Doyle, “Dynamics of TCP/AQM and a Scalable Control,” Proceedings of IEEE INFOCOM, New York, 23-27 June 2002, pp. 1-10.
- S. Athuraliya, S. H. Low, V. H. Li and Q. Yin, “REM: Active Queue Management,” IEEE Network, Vol. 15, No. 3, 2001, pp. 48-53. doi:10.1109/65.923940
- S. Floyd and V. Jacobson, “Random Early Detection Gateways for Congestion Avoidance,” IEEE/ACM Transactions on Networking, Vol. 1, No. 4, 1993, pp. 397-413. doi:10.1109/90.251892
- C. V. Hollot, V. Misra, D. Towsley and W.-B. Gong, “On Designing Improved Controllers for AQM Routers Supporting TCP Flows,” Proceedings of IEEE INFOCOM, Anchorage, 22-26 April 2001, pp. 1726-1734.
- R. J. Gibbens and F. P. Kelly, “Distributed Connection Acceptance Control for a Connectionless Network,” Proceedings of the 16th International Teletraffic Congress, Edinburgh, 7-11 June 1999, pp. 941-952.
- F. Abrantes and M. Ricardo, “XCP for Shared-Access Multi-Rate Media,” ACM SIGCOMM Computer Communication Review, Vol. 36, No. 3, 2006, pp. 27-38. doi:10.1145/1140086.1140091
- N. Dukkipati, M. Kobayashi, R. Zhang-Shen and N. McKeown, “Processor Sharing Flows in the Internet,” In: H. de Meer and N. Bhatti, Eds., IEEE International Workshop Quality of Service, IFIP International Federation for Information Processing, 2005, pp. 267-281.
- A. Afanasyev, N. Tilley, P. Reiher and L. Kleinrock, “Host-to-Host Congestion Control for TCP,” IEEE Communications Surveys & Tutorials, Vol. 12, No. 3, 2010, pp. 304-342. doi:10.1109/SURV.2010.042710.00114
- L. Chen, T. Ho, M. Chiang, S. H. Low and J. C. Doyle, “Congestion Control for Multicast Flows with Network Coding,” IEEE Transactions on Information Theory, No. 99, 2012.
- B. Wydrowski and M. Zukerman, “MaxNet: A Congestion Control Architecture,” IEEE Communications Letters, Vol. 6, No. 11, 2002, pp. 512-514. doi:10.1109/LCOMM.2002.805519
- B. Wydrowski, L. L. H. Andrew and M. Zukerman, “MaxNet: A Congestion Control Architecture for Scalable Networks,” IEEE Communications Letters, Vol. 7, No. 10, 2003, pp. 511-513. doi:10.1109/LCOMM.2003.818888
- Y. Zhang and T. Henderson, “An Implementation and Experimental Study of the Explicit Control Protocol (XCP),” Proceedings of the IEEE AVFUCUM, 13-17 March 2005, pp. 1037-1048.
- Y. Xia, L. Subramanian, I. Stoica and S. Kalyanaraman, “One More Bit Is Enough,” IEEE/ACM Transactions on Networking, Vol. 16, No. 6, 2008, pp. 1281-1294. doi:10.1109/TNET.2007.912037
- V. Misra, W.-B. Gong and D. Towsley, “Fluid-Based Analysis of a Network of AQM Routers Supporting TCP Flows with an Application to RED,” Proceedings of the Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication, New York, 28 August-1 September 2000, pp. 151-160.
- G. Montenegro, S. Dawkins, M. Kojo, V. Magret and N. Vaidya, “Long Thin Networks,” RFC 2757, Texas A & M University, College Station,, 2000.
- F. Paganini, J. C. Doyle and S. H. Low, “Scalable Laws for Stable Network Congestion Control,” Proceedings of 40th IEEE Conference on Decision and Control, Orlando, 4-7 December 2001, pp. 185-190.
- R. G. M. Morris, L. Tarassenko and M. Kenward, “Cognitive Systems: Information Processing Meets Brain Science,” Academic Press, Cambridge, 2005.
- R. E. Neapolitan, “Learning Bayesian Networks,” Prentice Hall, Upper Saddle River, 2004.
- N. Christofides, “Graph theory: An Algorithmic Approach,” Academic Press, Cambridge, 1975.
- K. Thulasiraman and M. N. S. Swamy, “Graphs: Theory and Algorithms,” John Wiley & Son, Hoboken, 1992.
- J. Bang-Jensen and G. Gutin, “Digraphs: Theory, Algorithms and Applications,” 2nd Edition, Springer-Verlag, London, 2008.
- C. M. Bishop, “Pattern Recognition and Machine Learning,” Springer, Madison, 2006.
- D. Koller and N. Friedman, “Probabilistic Graphical Models: Principles and Techniques,” The MIT Press, Cambridge, 2009.
- F. V. Jensen and T. D. Nielsen, “Bayesian Networks and Decision Graphs,” 2nd Edition, Springer Science and Business Media, New York, 2007. doi:10.1007/978-0-387-68282-2
- G. Schwarz, “Estimating the Dimension of a Model,” Annals of Statistics, Vol. 6, No. 2, 1978, pp. 461-464. doi:10.1214/aos/1176344136
- G. Quer, H. Meenakshisundaram, B. R. Tamma, B. S. Manoj, R. Rao and M. Zorzi, “Using Bayesian Networks for Cognitive Control of Multi-Hop Wireless Networks,” IEEE Military Communications Conference, San Jose, 31 October-3 November 2010, pp. 201-206.
- S. J. Russell and P. Norvig, “Artificial Intelligence: A Modern Approach,” 2nd Edition, Prentice Hall, Upper Saddle River, 2003.
- T. Ellman, J. Keane and M. Schwabacher, “Intelligent Model Selection for Hill Climbing Search in ComputerAided Design,” Proceedings of the 11th National Conference on Artificial Intelligence, Washington, 11-15 July 1993, pp. 594-599.
- C. Andrieu, N. de Freitas, A. Doucet and M. I. Jordan, “An Introduction to MCMC for Machine Learning,” Machine Learning, Vol. 50, No. 1, 2003, pp. 5-43. doi:10.1023/A:1020281327116
- P. Diaconis, “The Markov Chain Monte Carlo Revolution,” Bulletin of the American Mathematical Society, Vol. 46, No. 2, 2009, pp. 179-205. doi:10.1090/S0273-0979-08-01238-X
- S. Yang and K.-C. Chang, “Comparison of Score Metrics for Bayesian Network Learning,” IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, Vol. 32, No. 3, 2002, pp. 419-428. doi:10.1109/TSMCA.2002.803772
- http://www.nsnam.org/

