Journal of Intelligent Learning Systems and Applications
Vol. 5 No. 1 (2013) , Article ID: 27939 , 9 pages DOI:10.4236/jilsa.2013.51005
Hybrid Intelligent Modeling for Optimizing Welding Process Parameters for Reduced Activation Ferritic-Martensitic (RAFM) Steel
![]()
1Metallurgy and Materials Group, Indira Gandhi Centre for Atomic Research, Kalpakkam, India; 2Nuclear Engineering Academy, PM Dimensions, Hyderabad, India.
Email: *dev@igcar.gov.in
Received May 14th, 2012; revised August 10th, 2012; accepted August 17th, 2012
Keywords: ANFIS; Genetic Algorithm; RAFM Steel; A-TIG Welding
ABSTRACT
Reduced-activated ferritic-martensitic steels are being considered for use in fusion energy reactor and subsequent fusion power reactor applications. Typically, those reduced activated steels can loose their radioactivity in approximately 100 years, compared to thousands of years for the non-reduced-activated steels. The commonly used welding process for fabricating this steel are electron-beam welding, and tungsten inert gas (TIG) welding. Therefore, Activated-flux tungsten inert gas (A-TIG) welding, a variant of TIG welding has been developed in-house to increase the depth of penetration in single pass welding. In structural materials produced by A-TIG welding process, weld bead width, depth of penetration and heat affected zone (HAZ) width play an important role in determining in mechanical properties and also the performance of the weld joints during service. To obtain the desired weld bead geometry, HAZ width and make a good weld joint, it becomes important to set up the welding process parameters. The current work attempts to develop independent models correlating the welding process parameters like current, voltage and torch speed with weld bead shape will bead shape parameters like depth of penetration, bead width, HAZ width using ANFIS. These models will be used to evaluate the objective function in the genetic algorithm. Then genetic algorithm is employed to determine the optimum A-TIG welding process parameters to obtain the desired weld bead shape parameters and HAZ width.
1. Introduction
Reduced-activation steels were developed to enhance safety and reduce adverse environmental effects of future fusion power plants. Ferritic and Martensitic steels were developed during the 1985-1990 timeframe, and the feasibility of their use for fusion was investigated in an international collaboration from 1994 to present. Work continues to improve the steels and understand the effect of neutron irradiation on them [1]. Low activation materials were defined as materials that during irradiation would either not activate or any induced radioactivity caused by transmutation of elements in the material by interaction with high-energy neutrons from the deuterium-tritium fusion reaction would decay rapidly to allow safe operation and hands-on reactor maintenance [2]. True low-activation structural materials were not feasible, and “reduced-activation” steels were proposed that would not contain elements that would result in longlived, transmutation produced, radioactive elements. This would allow for safer and more economical disposal of radioactive reactor components after service exposure. Radioactivity from reduced-activation steels should decay to low levels in approximately 100 years, compared to thousands of years for some non-reduced-activation steels.
The tungsten inert gas (TIG) welding process was developed in 1938 and its usage is widespread in modern industry, such as aerospace, nuclear, petroleum and chemical industries, for its quality. It seems to be well adapted to weld this kind of materials, needing a great precision. Unfortunately, the principle disadvantages of TIG welding process ascribe to its limited penetration ability in a single pass, poor tolerance to some material composition and the low production [3,4]. Activated flux TIG welding (A-TIG) process first developed by the E. O. Paton Electric welding Institute in the 1960s, at Kiev (Ukraine) [5]. In A-TIG welding process, a very thin coating of activatedflux is applied to the surface of the material before welding. Thanks to this flux, there is a great increase of the penetration depth (up to 300%), under the same welding conditions [6-8]. The A-TIG welding can greatly increase welding productivity and reduce the welding cost as well as welding distortion simultaneously huge amount of cost saving and its sensibility to the chemical composition of the base metal reduced [9, 10].
The weld bead shape parameters such as depth of penetration (DOP), weld bead width (BW) and heat affected zone (HAZ) width in RAFM steels produced by A-TIG welding plays an important role in determining the weld quality and the mechanical properties such as creep, low cycle fatigue and the toughness. The weld bead shape parameters and the HAZ width are decided according to the current, voltage and torch speed. Experimental optimization of the process parameters required to achieve the desired depth of penetration and HAZ width in the above structural materials may require many experiments and is indeed time consuming. Therefore, it is necessary to develop a computational model for determining the optimum A-TIG welding process parameters to achieve the target depth of penetration and HAZ width.
Soft computing is a natural option for solving nonlinear and complex problems in welding [11,12]. Fundamental areas of soft computing are artificial neural networks (ANNs), fuzzy logic and genetic algorithms (GA) etc. The application of these techniques offers new opportunities in solving complex problems. Artificial neural networks are parallel-distributed processing systems comprising nonlinear process elements that perform in a similar manner to biological neurons. Artificial Neural Networks posses the ability to learn from experience and generalize new data from previous data sets. They are particularly useful for problems in which a lack of complete understanding exists of relationships among the variables. Fuzzy logic predicts the complex characteristics of the problems based on the concept of relative importance of precision of solutions. Fuzzy logic offers a powerful frame of reasoning as how human reasoning works. These systems employ a rule-based approach and interpolative reasoning as well as perform nonlinear mapping of inputs. In fuzzy logic, expert’s knowledge also can be added to bring out the results accurately. Genetic algorithms are nondeterministic stochastic optimization methods to use theories of evolution and natural selection to solve a problem within a complex solution space [13]. GAs possesses a population of solutions that evolve according to the rules of selection and other operators such as recombination and mutation. GA represents an efficient global method of optimizing nonlinear problems.
Nowadays, Hybrid techniques such as a combination of ANN and GA or Fuzzy Logic and GA are emerging as innovating solutions to non-linear problems [14]. These systems bring out the advantages of both techniques. Datta et al. [15] have worked on a similar hybrid system consisting of ANN and Multi-Objective GA for designing high strength multi-phase steels. S. Dey et al. [16] have modeled the mechanical properties of TRIP assisted steels using Fuzzy Inference System.
Adaptive Neuro Fuzzy Inference System (ANFIS), a modified Fuzzy Inference System (FIS) works similar to that of Neural Networks. With the help of ANFIS, tuning of membership function parameters can be done by either using a back propagation algorithm or in combination with the least square type of method. This allows the FIS to learn from the data that are to be modeled. Several attempts were made to model complex problems using this advanced tool. Hancheng et al. [17] modeled material properties using fuzzy neural networks. Chen and Linkens [18] have predicted impact toughness for alloy steels. Hybrid computing techniques are hence used for modeling non-linear and complex problems involving welding process parameters and welding bead shape parameters. Edwin and Kumanan [19] have predicted weld bead width in Submerged Arc Welding using ANFIS. Kovacevic and Zhang [20] have experimentally modeled weld pool geometry using Neurofuzzy. Vasudevan et al. [21-23] have used hybrid techniques along with GA to optimize process parameters for GTAW of austenitic Stainless steels. De and Bag [24] have coupled GA with heat transfer model to predict process variables in GTA spot welding. Since it is very appropriate to apply GA to nonlinear welding problems, Genetic Algorithms are being increasingly applied in the field of welding in recent times.
Combining ANFIS with GA or ANN with GA are emerging methodologies for solving the non-linear problems such as optimization of welding processes. The reason for choosing them over regression models is that these tools are very efficient in learning and become very accurate predictive tools after training. Accurate models using ANFIS or ANN can be developed for predicting weld bead shape parameters as a function of welding process variables. These models then find application during the evaluation of objective function in genetic algorithm.
In the present work, welding process parameters like current, voltage and torch speed are correlated, using ANFIS, which incorporates effective learning from given data, to weld bead shape parameters like depth of penetration, bead width and HAZ width. Then these ANFIS models are employed in GA to evaluate the objective function and to arrive at the optimal solutions for obtaining target Weld bead geometry and HAZ width during A-TIG welding of Reduced-Activated Ferritic-Martensitic steels.
2. Data Generation
Bead-on welding was carried out on Reduced-Activated Ferritic-Martensitic steel plates of 6mm thickness. Several experiments were conducted to generate 56 data sets by altering the process parameters. Current was adjusted between a minimum value of 75 amps and a maximum value of 250 amps in steps of 25 amps (say 75, 100, 125 - 250). Torch speed was set in the range of 1.33 mm/s - 3.33 mm/s and arc voltage in the range of 10.1v to 16.9v. A thoriated tungsten electrode of 3 mm diameter was used in which the tip is inclined at 45˚ to the vertical plane. Arc gap was fixed as 1mm. Argon at a flow rate of 10 Liter/minute was used for shielding. Multi component specific activated flux was utilized to reduce the production time. The samples cut from the bead-on plate welds were polished and etched to see the cross section for making measurements on depth of penetration, weld bead width and HAZ width. Machinist’s microscope was used for making the measurements. Figure 1 describes the various weld bead shape parameters and HAZ width in a typical weld joint.
3. Methodology
The methodology applied for optimizing weld bead geometry using GA based models involves two important steps. Initially, three different models were created using ANFIS correlating welding process parameters like current, torch speed and arc voltage with depth of penetration, bead width and HAZ width respectively. The flow chart giving the steps involved in the methodology is shown in Figure 2. Then these models were incorporated in GA to evaluate the objective function and hence the GA code was developed to optimize the welding process parameters to achieve target weld bead geometry and HAZ width.
4. Results and Discussions
4.1. Development of Adaptive Neuro Fuzzy Inference System Models
Adaptive Neuro Fuzzy Inference System embeds the

Figure 1. Schematic figure depicting weld bead shape parameters. A: Bead width; B: Depth of penetration; C: HAZ width; D: Weld metal; E: Base metal.
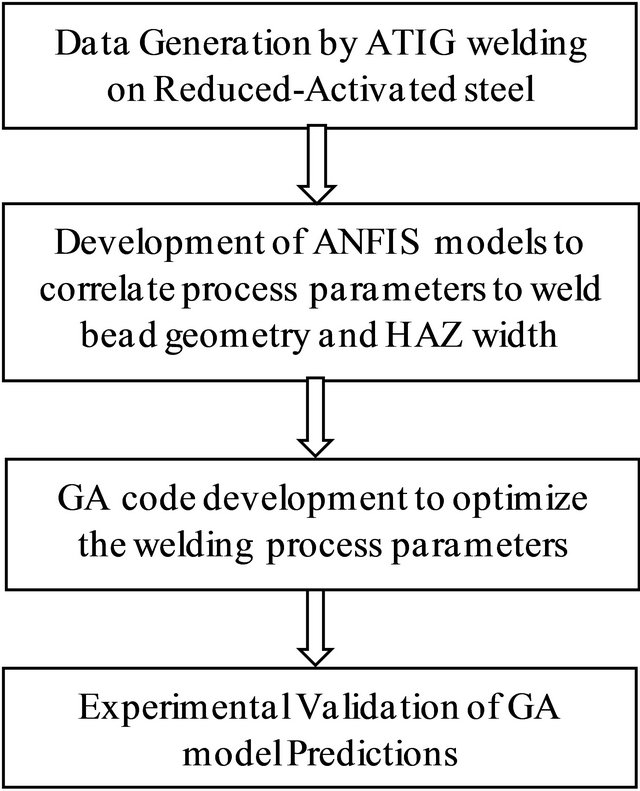
Figure 2. Flowchart representing methodology involved.
Fuzzy Inference System into the framework of the adaptive networks. It serves as a basis for constructing a set of fuzzy if-then rules with appropriate membership functions to attain the stipulated input-output data pairs. It models or remodels the entire fuzzy inference system whose membership function parameters are tuned by using either back propagation algorithm or in combination with the least square method. It learns and hence trains the fuzzy inference system based on the given input data sets. This fuzzy system has mainly three components: 1) A rule base that has a collection of rules; 2) A database with the help of which the membership functions can be decided and its parameters are to be tuned and; 3) A decision making mechanism which carries out inference procedure to map the inputs and the rules [19]. The schematic network like structure that is used in ANFIS is shown in Figure 3 indicating the essential input and the output parameters.
In this current work, out of the 56 data sets, 47 were used for training, 9 for checking and 9 for testing the FIS. Three independent ANFIS models were developed separately for predicting the weld bead width, depth of penetration and HAZ width. The Sugeno model represents the FIS compactly with high computational efficiency. It works well in non-linear problems and with optimization and adaptive techniques. The triangular function, that maps this non-linear problem with high efficiency, is utilized for each welding process parameter and the number of membership functions is fixed as three representing the linguistic variables like Low, Medium and High. Then, the new FIS is generated implementing grid partitioning technique which clusters all the data sets and creates the rules accordingly. The membership function parameters are initially assigned by ANFIS and are changed on training of the FIS. The combination of back propagation and the least square technique (Hybrid Optimization Method) is used for the training process at the

Figure 3. Schematic sketch of ANFIS network.
least error value for about 250 - 300 iterations. The parameters of the FIS developed are the following:

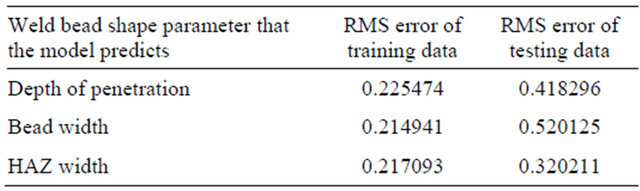
Then the rules that do not contribute to the output value are deleted. Ultimately, the numbers of rules are found to be 2, 15 and 26 in models predicting the depth of penetration, bead width and HAZ width respectively. The Root Mean Square (RMS) Error values were obtained in these ANFIS models using tri membership function for the training and testing data sets are given in Table 1.
The Figure 4 clearly shows that there is a good agreement between the actual values and the predicted values of weld bead shape parameters in the models developed by ANFIS. The values of RMS error mention in Table 1 show that there is an excellent correlation between the actual and the predicted values. Thus, the weld bead geometry and HAZ width predicted by the models created by ANFIS are found to be quite good.
4.2. Development of Genetic Algorithm Code
The Genetic Algorithm code was developed in Matlab for optimizing the welding process parameters like current, torch speed and arc voltage of Reduced-Activated Ferritic-Martensitic steels. The flowchart that represents the steps [13] involved in the code development by GA is given in Figure 5.
Table 1. RMS error in predicting weld bead shape parameters by ANFIS models using trimf.
4.3. Multi-Objective Function
To attain the target values of the weld bead shape parameters like depth of penetration, bead width and heat affected zone width, the GA code should be made to converge for solutions. To facilitate the objective function, to converge at the solutions with less iteration, the least square error minimization is used as the objective function. In this present work, the sum of the least square error values of the weld bead shape parameters multiplied by weights, which are assigned based on their relative importance, is chosen as the objective function as in Equation (1). Thus, the weighted sum converts the multiobjective optimization problem into a scalar one [25].
 (1)
(1)
where ObjV is the objective function, DOPT, HAZWT are target values of depth of penetration, HAZ width respectively, DOP, HAZW are the depth of penetration, HAZ width values respectively of the ith individual. Although the objective function is mainly for minimizing the error values, GA always strives to maximize the solutions.
Thus, the solutions are ranked based on the fitness index, which is defined as the inverse of the objective
 (a)
(a)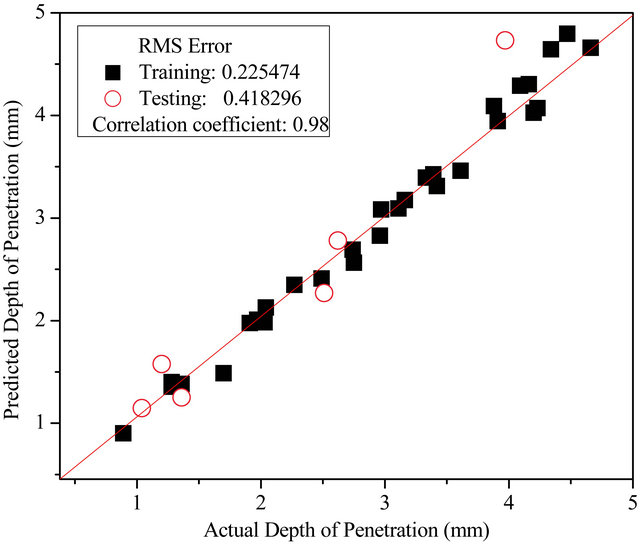 (b)
(b) (c)
(c)
Figure 4. Plots depicting the comparison between Actual values and predicted values by the ANFIS model with trimf for (a) Bead width; (b) Depth of penetration; and (c) HAZ width.

Figure 5. Flowchart describing various steps in GA.
function value, such that the solution with the low objective function value has a high fitness index value. The solutions with the higher fitness values are selected for the next generation.
4.4. Selection of Genetic Algorithm Parameters
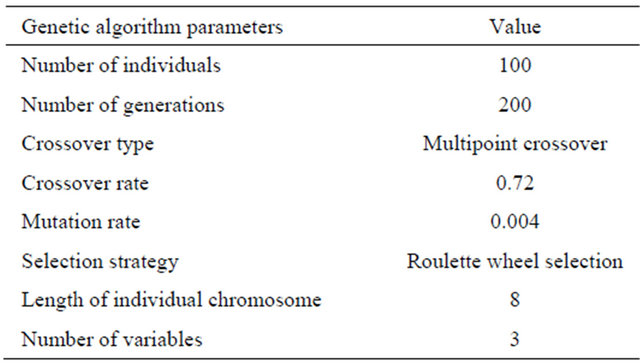
There are several parameters in Genetic Algorithm like number of individuals, number of generations, crossover type, crossover rate and mutation rate that control the speed of convergence. Deb [26] neatly explains the different terminologies that are used in GA. These parameters are varied in the range as listed below before arriving at the optimum values:

The best set of parameters that lead to a fast convergence was selected based on the trial-and-error method and the influence of the parameters on the convergence of the solutions is studied. The parameters that produced exact convergence at a faster rate were chosen and are listed in Table 2.
The maximum and the minimum values (the range) for each welding process parameter like current, torch speed and arc voltage were also specified. The initial population, in a binary form, is randomly selected within the specified values for the iteration process. Each individual in the initial population represents each welding process parameter. In the present case, the maximum value among all independent parameters was 250 (i.e. the value of current), therefore the length of each individual gene in the chromosome is chosen as eight (28 = 256). Since there are three parameters controlling the target process variables, the total length of the chromosome is 24 (8 × 3). Standard gray coding is employed for decoding the binary representation of the strings along with logarithmic scaling.
Then the binary strings that are converted to real values are evaluated for their fitness using the objective function. The weights are selected in such a way that their sum accounts to one and are assigned according to their influence on the target process parameters. Based on the fitness index values that are calculated as the inverse of the objective function value, these chromosomes are ranked.
For selection of the best chromosomes from this population, roulette wheel selection is used. In this method, the parents are selected based on their fitness index values. The better the chromosomes are, the more chances to be selected they have. A virtual roulette wheel (pie chart) is created in which each individual is assigned a portion proportional to the normalized fitness value. An unbiased spinning of the roulette pointer is simulated through a random number generator, and the individual corresponding to the region where it points is picked up for further processing often with an assigned probability [26]. The chromosomes with higher fitness values are selected more times since they occupy more space on the pie [13]. This algorithm works similarly until it has generated the entire population for the next generation.
Then multi-point crossover was carried out on these selected chromosomes. The basic idea behind this multipoint crossover is that the parts of the chromosome representation that contribute to the most to the performance of a particular individual may not necessarily be contained in adjacent substrings. This method takes two parent strings from the mating pool and performs the exchange at some positions between them to form a new string (children). The crossover proceeds in three steps.
Table 2. Genetic algorithm parameters selected for optimizing welding process parameters.
First, the two parent strings are selected randomly. Secondly, a number of positions (as crossover sites) are chosen randomly in both the strings. Finally, the portions of the strings at the crossover sites are exchanged between both the parents to form the offspring’s. This crossover is limited only to certain parents, which is determined by the crossover rate. Based on the error values in the predicted weld bead parameters, the crossover rate was fixed as 0.72 implying that crossover was carried out only on 72 chromosomes among the 100 chromosomes and the remaining chromosomes were carried over to the next generation without any alteration [25].
After the crossover, mutation was carried out on the offspring’s in which one allele of the gene is randomly replaced by another to produce a new genetic structure. The mutation probability is kept low at a rate of 0.004 to avoid any possible perturbations. The offspring’s are then decoded into real values. Then the objective function is evaluated for this new set of chromosomes and they are ranked based on their fitness index values. From this mix of parents and offspring’s, 100 best chromosomes are selected based on their fitness ranking. Then these newly selected chromosomes were reinserted for the next iterations. Similar iterations continue until there are no further changes in the value of the optimized process parameters or any of the terminating conditions like attaining a fixed number of generations, getting a solution with the highest fitness ranking, lapsing the fixed computational time is achieved. In this case, arriving at the fixed number of generations was used as a terminating condition.
4.5. Validation of the GA Model
In order to obtain the best results, the GA program was run ten times, giving the most of the time ten different results, which are nearly close. Then only the best parameters were chosen, which give the better results, depending on the targets. Those chosen parameters are given in the Table 3.
The comparison between the actual and the target values of DOP and HAZ width are given in Table 4. The comparison plots between the target and the actual weld bead shape parameters are presented in Figure 6.
A close agreement was achieved between the target and the actual values of depth of penetration, HAZ width. Thus, the present work shows that Genetic Algorithm has the capability to optimize and produce a multiple set of welding process parameters that can lead to the desired weld bead profile and HAZ width accurately in RAFM steel.
5. Conclusion
Genetic algorithm in combination with ANFIS models has been used for optimizing the A-TIG welding process parameters to achieve the target weld bead geometry and HAZ width in RAFM steel. The methodology is implemented in two steps. First, independents ANFIS models were developed correlating the welding process parame
Table 3. Multiple welding process parameters for achieving the same target weld bead shape parameters.
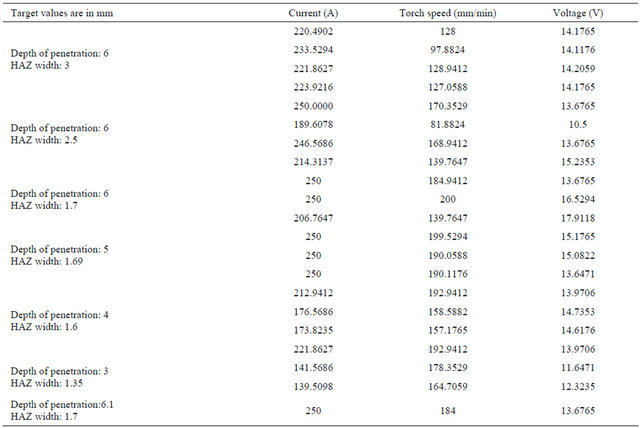
Table 4. Comparison of the target and the actual depth of penetration and HAZ width.

 (a)
(a)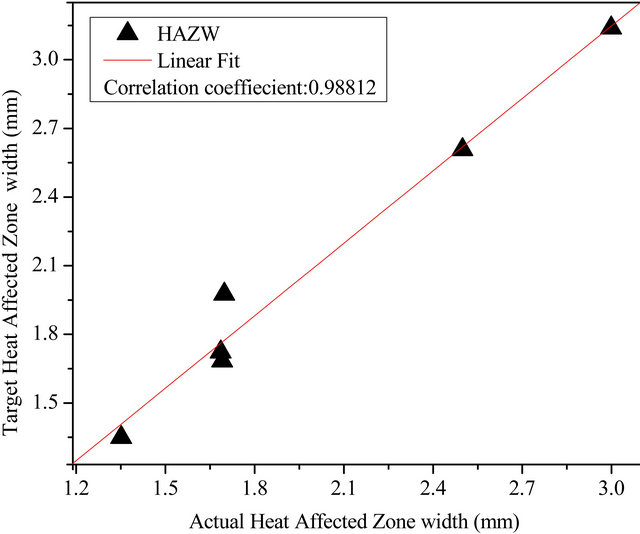 (b)
(b)
Figure 6. Comparison between actual and target values of (a) Depth of penetration and (b) HAZ width.
ters like current, torch speed and arc voltage with weld bead parameters like depth of penetration, bead width and HAZ width. Second, a GA code was developed to optimize the process variables to achieve the desired target depth of penetration and HAZ width. The ANFIS models were used to evaluate the objective function in the GA code. A close agreement was achieved between the target and the actual values of depth of penetration and HAZ width. Thus, the present work shows that the GA has the capability to optimize and produce multiple sets of welding process parameters that can lead to the desired weld bead profile and HAZ width accurately in RAFM steel.
REFERENCES
- R. L. Klueh,“Reduced-Activation Bainitic and Martensitic Steels for Nuclear Fusion Applications,” Current Opinion in Solid State and Materials Science, Vol. 8, No. 3-4, 2004, pp. 239-250. doi:10.1016/j.cossms.2004.09.004
- R. W. Conn, E. E. Bloom, J. W. Davis, R. E. Gold, R. Little, K. R. Schultz, D. L. Smith and F. W. Wiffen, “Report on Low Activation Materials for Fusion Applications,” Nuclear Technology/Fusion, Vol. 5, 1984, pp. 291-310.
- P. J. Modenesi, E. R. Apolinario and I. M. Pereira, “TIG Welding with Single-Component Fluxes,” Journal of Materials Processing Technology, Vol. 99, No. 1-3, 2000, pp. 260-265. doi:10.1016/S0924-0136(99)00435-5
- K. A. Yushchenko, D. V. Kovalenko and I. V. Kovalenko, “Peculiarities of A-TIG Welding of Stainless Steel,” Proceedings of the 7th International Conference on Trends in Welding Research, Callaway Gardens Resort, Pine Mountain, 16-20 May 2005.
- L. N. Lie, D. H. Cai and Z. D. Zhang, “Gas Tungsten Arc Welding of Magnesium Alloy Using Activated Flux Coated Wire,” Scripta Materialia, Vol. 57, No. 8, 2007, pp. 695- 698. doi:10.1016/j.scriptamat.2007.06.040
- Z. D. Zhang, L. M. Liu, Y. Shen and L. Wang, “Mechanical Properties and Microstructure of Magnesium Alloy Gas Tungsten Arc Welded with a Cadmium Chloride Flux,” Materials Characterization, Vol. 59, No. 1, 2008, pp. 40-46. doi:10.1016/j.matchar.2006.10.012
- Z. D. Zhang, L. M. Liu, Y. Shen and L. Wang, “Welding of Magnesium Alloys with Activating Flux,” Science and Technology of Welding & Joining, Vol. 10, No. 6, 2005, pp. 737-743. doi:10.1179/174329305X70702
- T. Paskell, C. Lundin and H. Castner, “GTAW Flux Increases Weld Joint Penetration,” Welding Journal, Vol. 76, No. 4, 1997, pp. 57-62.
- M. Vasudevan, “Computational and Experimental Studies on Arc Welded Austenitic Stainless Steels,” Ph.D. Thesis, Indian Institute of Technology, Madras, 2007.
- P. C. J. Anderson and R. Wiktorowicz, “Improving Productivity with A-TIG Welding,” Welding and Metal Fabrication, Vol. 64, No. 3, 1996, pp. 108-109.
- M. Vasudevan and B. Raj, “Soft Computing in Materials Science and Engineering,” IIM Metal News, Vol. 12, No. 1, 2009, pp. 15-21.
- M. Vasudevan, “Soft Computing Techniques in Stainless Steel Welding,” Materials and Manufacturing Processes, Vol. 24, No. 2, 2009, pp. 209-218. doi:10.1080/10426910802612338
- N. Chakraborti, “Genetic Algorithm in Materials Design and Processing,” International Material Reviews, Vol. 49, No. 3-4, 2004, pp. 246-260. doi:10.1179/095066004225021909
- A. Abraham and B. Nath, “Hybrid Intelligent System Design—A Review of a Decade of Research,” IEEE Transactions on Systems, Man and Cybernetics (Part C), Vol. 3, No. 1, 2000, pp. 1-37.
- S. Datta, F. Pettersson, S. Ganguly, H. Saxen and N. Chakraborti, “Designing High Strength Multi-Phase Steel for Improved Strength-Ductility Balance Using Neutral Networks and Multi-Objective Genetic Algorithm,” ISIJ International, Vol. 47, No. 8, 2007, pp. 1195-1203. doi:10.2355/isijinternational.47.1195
- S. Dey, S. Datta, P. P. Chattopadhyay and J. Sil, “Modeling the Properties of TRIP Steel Using AFIS: A Distributed Approach,” Computational Materials Science, Vol. 43, No. 3, 2008, pp. 501-511. doi:10.1016/j.commatsci.2007.12.009
- H. C. Qian, B. C. Xia, S. Z. Li and F. G. Wang, “Fuzzy Neural Network Modeling of Material Properties,” Journal of Materials Processing Technology, Vol. 122, No. 2-3, 2002, pp. 196-200. doi:10.1016/S0924-0136(02)00019-5
- M.-Y. Chen and D. A. Linkens, “Impact Toughness Prediction for TMCP Steels Using Knowledge-Based Neural-fuzzy Modeling,” ISIJ International, Vol. 46, No. 4, 2006, pp. 586-590. doi:10.2355/isijinternational.46.586
- J. E. R. Dhas and S. Kumanan, “ANFIS for Predicted of Weld Bead Width in a Submerged Arc Welding Process,” Journal of Scientific and Industrial Research, Vol. 66, No. 5, 2007, pp. 335-338.
- Radovan Kovacevic and Yu.M.Zhang, “Neurofuzzy Model-Based weld Fusion State Estimation, IEEE control Systems,” Vol. 17(2), 1997, pp.30-42.
- M. Vasudevan, M. V. Kuppuswamy and A. K. Bhaduri, “Optimizing Process Parameters for Gas Tungsten Arc Welding of an Austenitic Stainless Steel Using Genetic Algorithm,” Transactions of the Indian Institute of Metals, Vol. 63, No. 3, 2010, pp. 1-10. doi:10.1007/s12666-010-0001-5
- M. Vasudevan, K. N. Gowtham and T. Jayakumar, “Predicting Depth of Penetration, Weld Bead Width and HAZ Width in mod. 9Cr-1Mo Steel Welds Using Adaptive Neuro Fuzzy Inference System (ANFIS) Based Models,” International Journal of computational Materials Science and Surface Engineering, Vol. 4, No. 3, 2011, pp. 205- 218.
- K. N. Gowtham, M. Vasudevan, V. Maduraimuthu and T. Jayakumar, “Intelligent Modeling Combining ANFIS and Genetic Algorithm for Optimizing Welding Process Parameters,” Metallurgical and Materials Transactions B, Vol. 42, No. 2, 2011, pp. 385-392.
- S. Bag and A. De, “Development of Efficient Numerical Heat Transfer Model Coupled with Genetic Algorithm Based Optimization for Prediction of Process Variables in GTA Spot Welding,” Science and Technology of Welding and Joining, Vol. 14, No. 4, 2009, pp. 633-645. doi:10.1179/136217108X356791
- M. Vasudevan, V. ArunKumar, N. Chandrasekhar and V. Maduraimuthu, “Genetic Algorithm for Optimization of A-TIG Welding Process for Modified 9Cr-1Mo Steel,” Science and Technology of Welding and Joining, Vol. 15, No. 2, 2010, pp. 117-123. doi:10.1179/136217109X12577814486773
- K. Deb, “An Introduction to Genetic Algorithms,” Sadhana, Vol. 24, No. 4-5, 1999, pp. 239-315. doi:10.1007/BF02823145
NOTES
*Corresponding author.

