Journal of Intelligent Learning Systems and Applications
Vol.4 No.1(2012), Article ID:17554,6 pages DOI:10.4236/jilsa.2012.41005
Design of Fuzzy Controller for Robot Manipulators Using Bacterial Foraging Optimization Algorithm
![]()
1Department of Electrical & Computer Engineering, Semnan University, Semnan, Iran; 2Department of Electrical & Robotic Engineering, Shahrood University of Technology, Shahrood, Iran.
Email: m_aghajarian@semnan.ac.ir, kourosh.kiani@aut.ac.ir, mmfateh@shahroodut.ac.ir
Received March 12th, 2011; revised April 26th, 2011; accepted May 10th, 2011
Keywords: BFO Algorithm; PSO Algorithm; Fuzzy Control; Robot Manipulator; Tracking Control
ABSTRACT
Trial and error method can be used to find a suitable design of a fuzzy controller. However, there are many options including fuzzy rules, Membership Functions (MFs) and scaling factors to achieve a desired performance. An optimization algorithm facilitates this process and finds an optimal design to provide a desired performance. This paper presents a novel application of the Bacterial Foraging Optimization algorithm (BFO) to design a fuzzy controller for tracking control of a robot manipulator driven by permanent magnet DC motors. We use efficiently the BFO algorithm to form the rule base and MFs. The BFO algorithm is compared with a Particle Swarm Optimization algorithm (PSO). Performance of the controller in the joint space and in the Cartesian space is evaluated. Simulation results show superiority of the BFO algorithm to the PSO algorithm.
1. Introduction
A wide variety of control strategies were proposed to control robot manipulators. PID controls are certainly the most widely adopted control strategy in industry because of its simple structure and robust performance in a wide range of operating conditions. Although PID control offers the simplest and yet most efficient solution to many real world control problems [1], optimally tuning gain is quite difficult [2]. Alternatively, fuzzy control as a modelfree approach is simply designed to control complicated systems [3]. To form fuzzy rules, an exact knowledge of model is not required. Fuzzy controller is an intelligent controller using linguistic fuzzy rules to include information from experts. Consequently, fuzzy control of robot manipulators has attracted a great deal of researches to overcome uncertainty, nonlinearity and coupling by providing a model free control [4]. To design a Fuzzy Logic Controller (FLC), a major task is to determine fuzzy rules, Membership Functions (MFs) and scaling factors. Therefore, the controller is tuned until a desired performance is achieved. The evolutionary algorithms such as Bacterial Foraging Optimization (BFO), Particle Swarm Optimization (PSO), Genetic algorithm (GA), and Simulated Annealing (SA) are getting popular because of their abilities to find the global minima in both continuous and non-continuous domains.
Since a foraging organism takes a necessary action to maximize the energy per unit time under considering all the constraints such as sensing and cognitive capabilities, natural foraging strategy can be applied to real-world optimization problems. Based on such evolutionary idea, Passino proposed BFO as an optimization algorithm [5]. BFO algorithm is a new evolutionary computation technique, which also includes powerful optimization techniques like PSO [6] and ant colony optimization [7]. To improve BFO search performance, several researchers have extended the basic BFO to deal with multi-modal and high dimensional functions [8-10]. BFO algorithm has also been combined with other evolutionary algorithms [11] in order to reduce the convergence time and enhance the accuracy. Over certain real-world optimization problems, BFO has been reported to outperform many powerful optimization algorithms like GA [12] and PSO algorithms [13].
The PSO algorithm proposed by Kennedy and Eberhart [6], has proved to be very effective for solving complex optimization problems. The underlying motivation for the development of PSO algorithm was social behavior of animals such as bird flocking and fish schooling. Generally, PSO is characterized as a simple concept, easy to implement, and computationally efficient. Unlike the other heuristic techniques, PSO has a flexible and well-balanced mechanism to enhance the global and local exploration abilities [14].
Trial and error method is a major task to find a suitable design of a fuzzy controller. We may use an optimization algorithm to achieve an optimal design. This paper presents a BFO algorithm to design a fuzzy PID controller for trajectory tracking control of a robot manipulator driven by permanent magnet DC motors. Performance of the BFO algorithm is compared with a PSO algorithm in terms of Integral Time Absolute Error (ITAE) in the joint space and Integral Square Error (ISE) in the Cartesian space. This paper is organized as follows: Section 2 introduces dynamics of the robotic system. Section 3 designs a fuzzy PD + I controller. Section 4 applies the BFO and PSO algorithms for tuning the fuzzy PD + I controller. Section 5 presents simulation results and Finally Section 6 concludes the paper.
2. Manipulator Dynamics
Robust control of robot manipulators is difficult because of complexity robot dynamics. The dynamics of an n-link robotic manipulator driven by permanent magnet dc motors is characterized by a set of highly nonlinear and strongly coupled second order differential equation [15] as
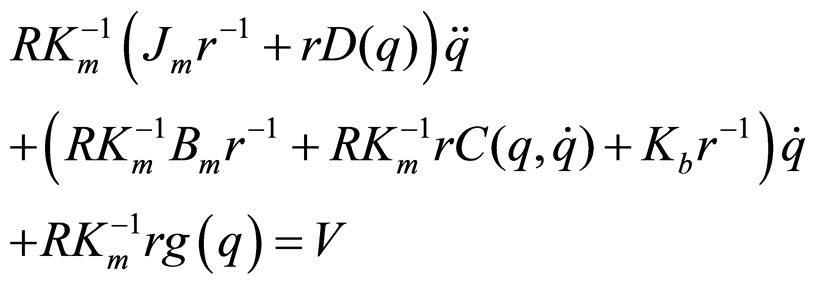 (1)
(1)
where 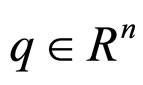 is a vector of generalized joint positions,
is a vector of generalized joint positions, 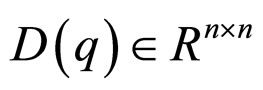 is the inertia matrix,
is the inertia matrix, 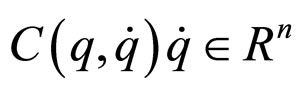 is a vector of centripetal and Coriolis generalized forces,
is a vector of centripetal and Coriolis generalized forces, 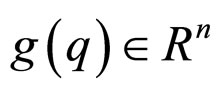 is a vector of generalized gravitational forces,
is a vector of generalized gravitational forces, 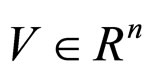 is a vector of motor voltages,
is a vector of motor voltages, 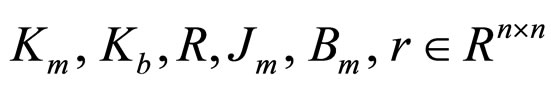 are constant diagonal matrices of torque constant, back emf constant, resistance, inertia, damping and reduction gear ratio of motors, respectively.
are constant diagonal matrices of torque constant, back emf constant, resistance, inertia, damping and reduction gear ratio of motors, respectively.
3. Fuzzy PD + I Controller
Fuzzy PID controller is implemented as fuzzy PD + I controller as shown in Figure 1. Each fuzzy set consists of a number of MFs to describe the heuristic variables in a mathematical manner. The motor voltage is the output of fuzzy controller while the joint position error and its derivative are its inputs. MFs for the inputs and output of the controller are five fuzzy sets namely NB (Negative Big), NM (Negative Medium), Z (Zero), PM (Positive Medium) and PB (Positive Big).
The following assumptions are given to design the FLC:
• MFs are triangular specified with three points.
• The physical range of inputs are scaled between [–1, 1].
• Axes of the first and the last MF are at –1 and 1, respectively.
• Number of fuzzy sets is an odd integer greater than one.
• MFs are arranged such that the second point of each MF is coincident with the third point of the left one and the first point of the right one.
Then, number and position of second point of MFs are selected as two design parameters.
Position of the MF is specified by spacing parameter where one indicates an even spacing, while any value larger than unity indicates that the MFs are close together in the center of the range and more spaced out at the extremes as shown in Figure 2. This method of designing the MFs is introduced in [16].
The rule-base also is designed based on the ideas pre-
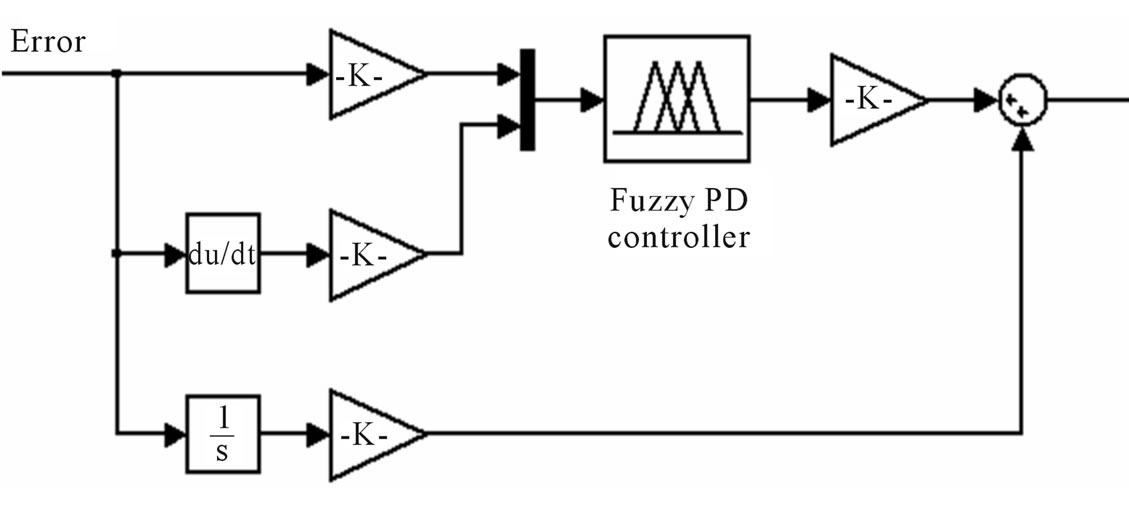
Figure 1. Fuzzy PD + I controller.
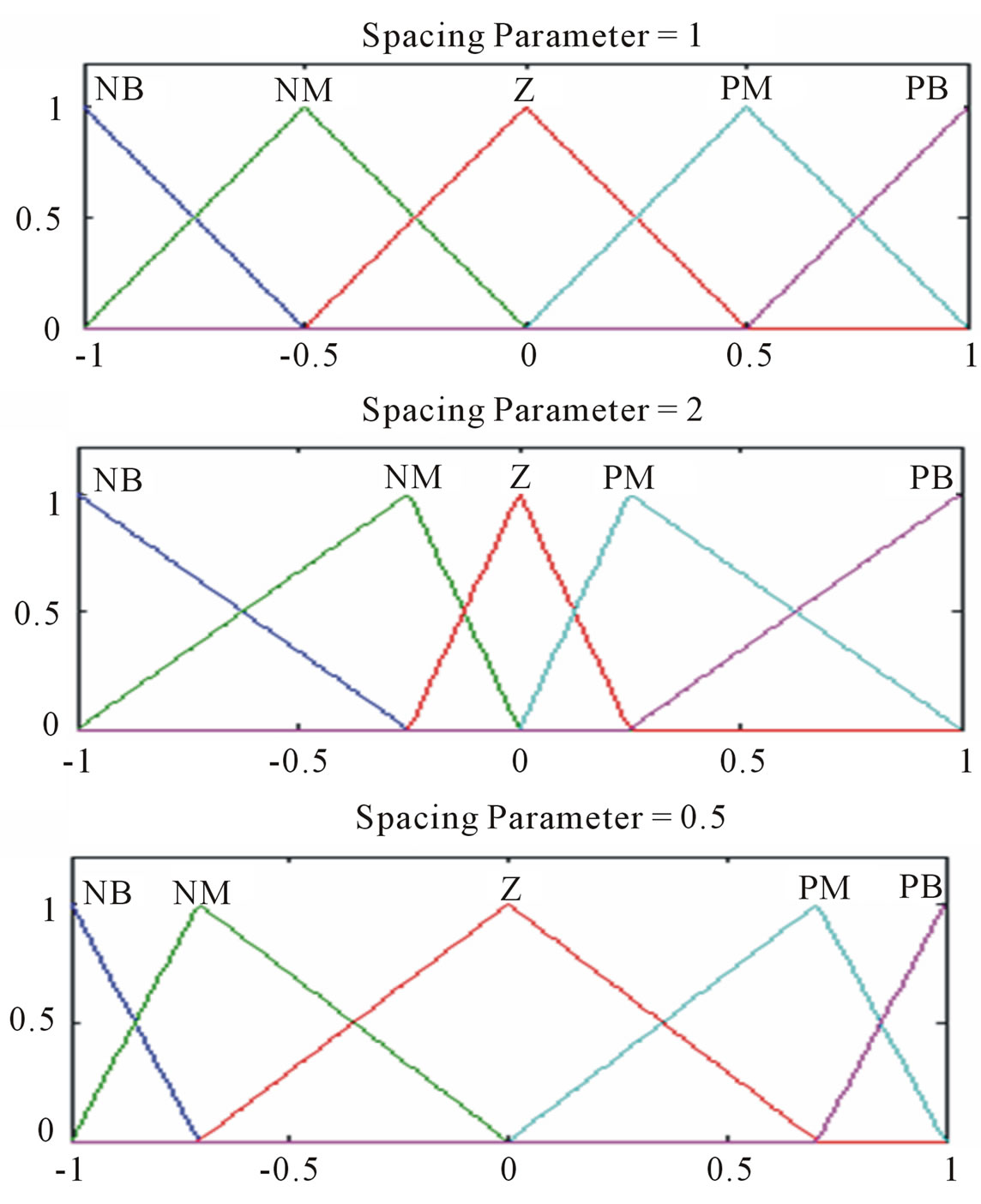
Figure 2. Effect of spacing parameter on MFs.
sented in [16]. In specifying a rule base, characteristic spacing parameter for each variable and characteristic angle for each input variable are used to construct the rules. The characteristic spacing parameters and the characteristic angle determine how the space is partitioned. The angle determines the slope of a line through the origin on which seed points are placed. The positioning of the seed points is determined by a similar spacing method as was used to determine the centers of the MFs as illustrated in Figure 3 where seed points are blue circles and grid-points are red circles. The lines on the graph delineate the different regions corresponding to different consequents. The parameters for this example are 1 for both input spacing, 0.85 for the output spacing and 40˚ for the angle. Table 1 shows the derived fuzzy rules.
4. Bacterial Foraging Optimization Algorithm
The BFO algorithm can be explained by four processes namely, chemotaxis, swarming, reproduction, and elimination-dispersal [6]. Below we briefly describe each of these processes.
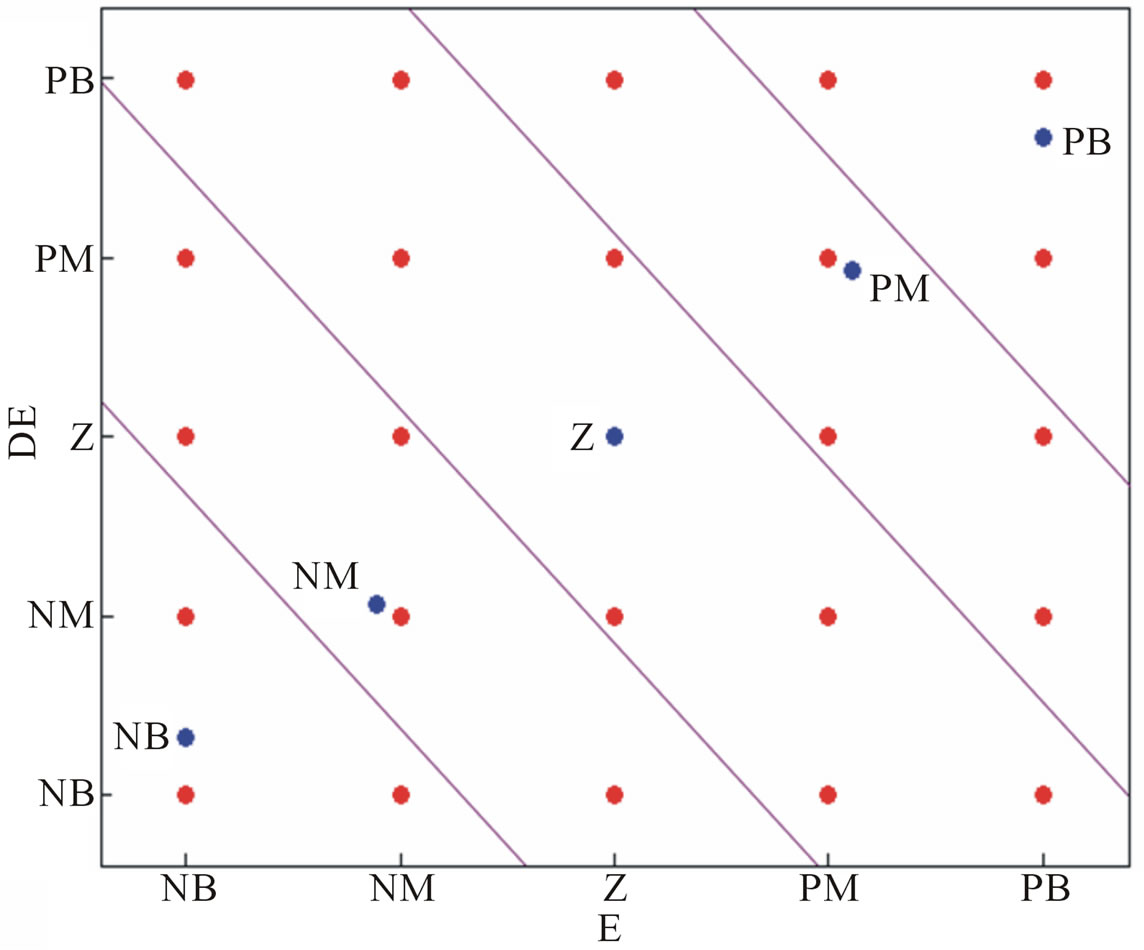
Figure 3. Sample decision plane.
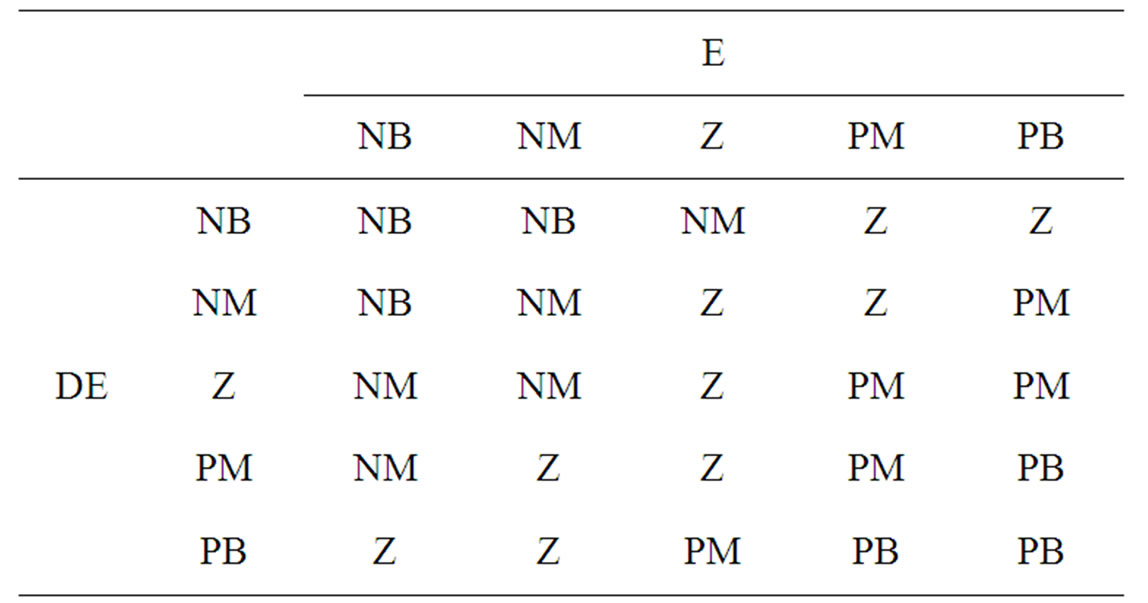
Table 1. Fuzzy rules.
Chemotaxis: This process simulates the swimming and tumbling movements of an E. coli cell by a set of rigid flagella. An E. coli bacterium can move in two different ways. It can swim for a period of time in the same direction or it may tumble, and alternate between these two modes of operation for the entire lifetime. This alternation between the two modes enables the bacterium to move in random directions and search for nutrients. Suppose 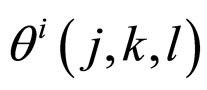 represents i-th bacterium at j-th chemotactic, k-th reproductive and l-th elimination-dispersal step. C(i) is the run length which is a constant in basic BFO algorithm. In computational chemotaxis, the movement of the bacterium is represented as
represents i-th bacterium at j-th chemotactic, k-th reproductive and l-th elimination-dispersal step. C(i) is the run length which is a constant in basic BFO algorithm. In computational chemotaxis, the movement of the bacterium is represented as
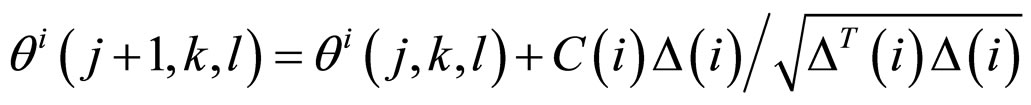 (2)
(2)
where  indicates a vector in the random direction whose elements lie in [–1, 1].
indicates a vector in the random direction whose elements lie in [–1, 1].
Swarming: It is always desired that when any one of the bacteria reaches the better location, try to attract other bacteria so that they reach the desired place more rapidly. The effect of swarming is to make the bacteria congregate into groups and move as concentric patterns with high bacterial density. Mathematically, swarming can be represented by
 (3)
(3)
where Jcc(h,P(j,k,l)) represents the objective function value to be added to the actual objective function (to be minimized) to present a time varying objective function, S is the total number of bacteria, p is the number of variables to be optimized, which are present in each bacterium and 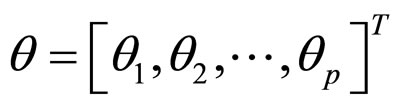 is a point in the p-dimensional search domain. dattractant, wattractant, hrepellant, wrepellant are different coefficients that should be chosen properly.
is a point in the p-dimensional search domain. dattractant, wattractant, hrepellant, wrepellant are different coefficients that should be chosen properly.
Reproduction: The least healthy bacteria eventually die while each of the healthier bacteria (each with the lower cost function) asexually split into two bacteria, which are then placed in the same location. Thus, the population size after reproduction is maintained constant.
Elimination and dispersal: A gradual or sudden changes in the location where a bacterium population lives may occur due to noxious substance, the temperature rises abruptly in the area or some other influence. Events can kill or disperse all the bacteria in a region. This reduces the chances of convergence at local optima location. To simulate this phenomenon in BFO algorithm, some bacteria are chosen, according to apreset probability Ped, to be dispersed and moved to another position within the environment.
The BFO algorithm parameters are denoted as p, S, Nc, Ns, Nre, Ned, Ped, where p is dimension of the search space, S is the total number of bacteria in the population, Nc is number of chemotactic steps, Ns is swimming length, Nre is number of reproduction steps, Ned is number of elimination-dispersal events, Ped is elimination-dispersal probability. The parameters selected for the proposed BFO algorithm are shown in Table 2.
It is certainly impossible to explore all the potential uses of BFO in this single article, but we briefly point to the some of them. It should seem at least plausible that there are applications of the methods to optimization, optimal control, adaptive estimation and control, and model predictive control.
4.1. Particle Swarm Optimization
PSO is a population-based optimization method inspired by the social behavior of animals such as bird flocking and fish schooling. Like evolutionary algorithms, PSO algorithm conducts search using a population of particles, corresponding to individuals. Each particle has a velocity vector vi and a position vector xi to represent a possible solution to the optimization problem. The first positions and velocities of a PSO algorithm are randomly initialized within a population. At the next iteration, position and velocity of each particle are updated by the two values. The first value, pbest, is the personal best position of particle that it has achieved so far. The other, gbest, is obtained by choosing the overall best value from all particles. The new velocity for each particle is updated by the following equation
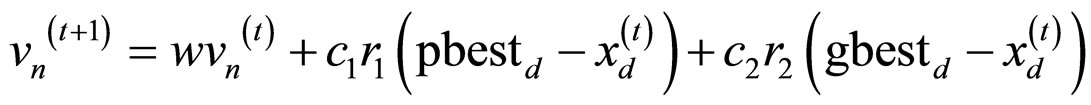 (4)
(4)
where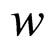 ,
, 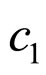 and
and 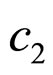 are called the coefficient of inertia, cognitive and society study, respectively. The
are called the coefficient of inertia, cognitive and society study, respectively. The 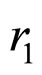 and
and 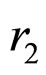 is uniformly distributed random numbers in [0, 1].
is uniformly distributed random numbers in [0, 1].
Changing velocity enables every particle to search around its individual best position and global best position. Based on the updated velocities, each particle changes its position as following
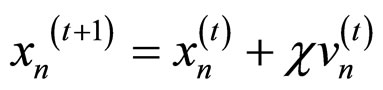 (5)
(5)
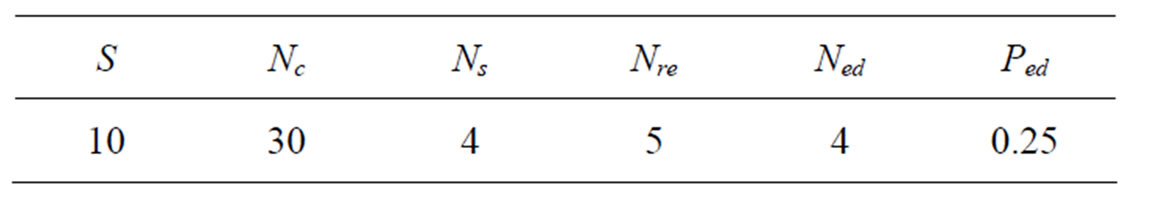
Table 2. Parameters of BFO algorithm.
4.2. Optimization of FLC Using BFO Algorithm
In this paper, spacing parameter for MFs of input/output variables, spacing parameters and angle parameters for rule base and input/output scaling factors of FLCs are determined with BFO algorithm. Figure 4 illustrates the block structure of the FLC optimizing process using BFO algorithm. All parameters of the FLC are updated at every final time (tf). The method of tuning PID parameters is based upon minimizing the ITAE of joints. If qd(k) is desired trajectory and q(k) is output trajectory then error e(k) is
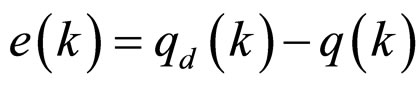 (6)
(6)
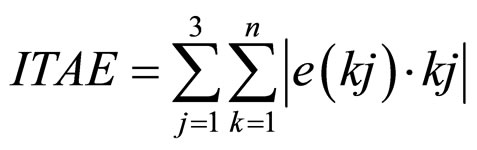 (7)
(7)
where e(kj) is the system error at k-th sampling instant for j-th joint. Tuning process of FLC parameters with PSO is similar to BFO algorithm.
5. Simulation Results
The objective of this section is to verify the performances of the Fuzzy-BFO based controller and the Fuzzy-PSO based controller. Results of the tuning methods are tested in terms of ITAE in joint space and ISE in Cartesian space. The desired Cartesian space trajectory is a spiral path. Integral Square Errors ISEX, ISEY and ISEZ are calculated to compare controller performance stated as follows
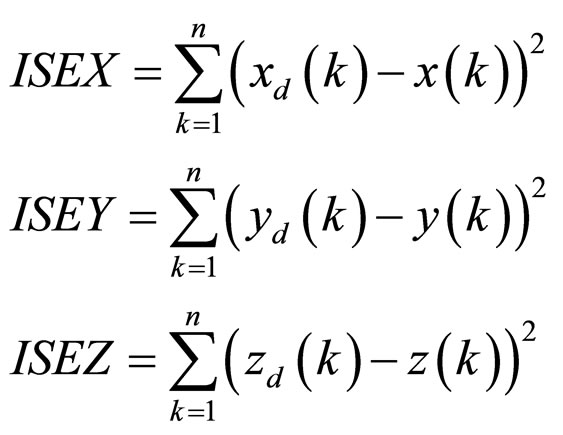 (8)
(8)
where 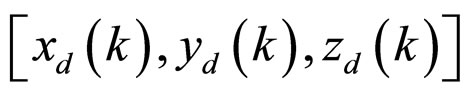 and
and 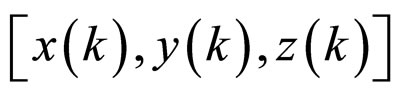 are desired and output Cartesian space points at k-th sampling instant. The ability of control system for rejecting disturbances is simulated. For checking the robustness of controller a disturbance torque D is applied as an example in the form of
are desired and output Cartesian space points at k-th sampling instant. The ability of control system for rejecting disturbances is simulated. For checking the robustness of controller a disturbance torque D is applied as an example in the form of
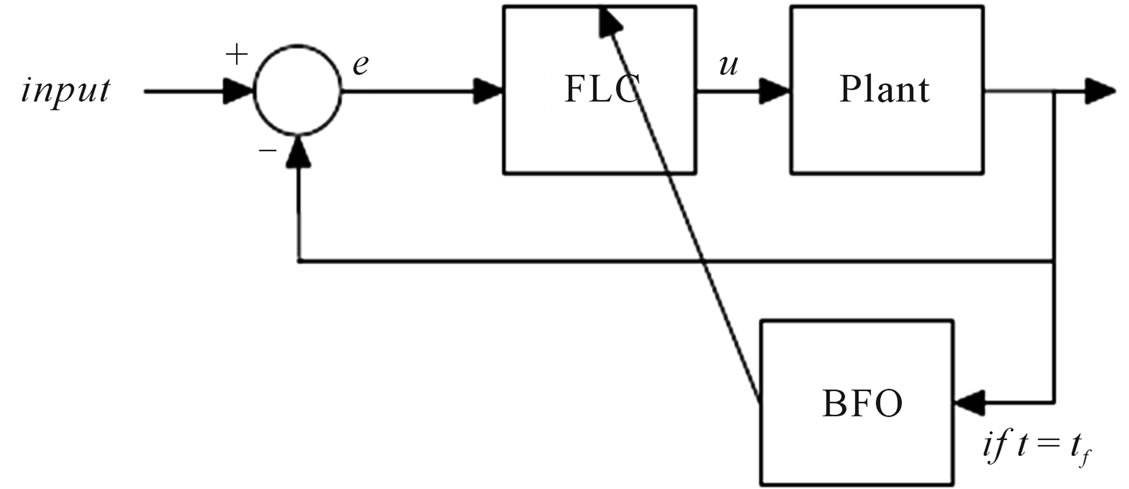
Figure 4. Tuning of FLC parameters by BFO algorithm.
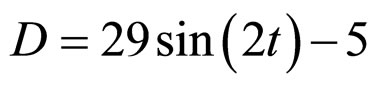 (9)
(9)
Initial angles of all three joints are set to zero, however spiral trajectory is starting from a non-zero value in Figure 6. Fitness function curve of PSO tuning is shown in Figure 5. Performance of the second joint for tracking spiral trajectory and corresponding error are shown in Figures 6 and 7, respectively. We can see a good tracking, where the tracking error of the joint is very small. Tables 3 and 4 give the values of the two cost functions, ISE and ITAE, with and without disturbance for the controllers. As can be seen, the Fuzzy-BFO based controller
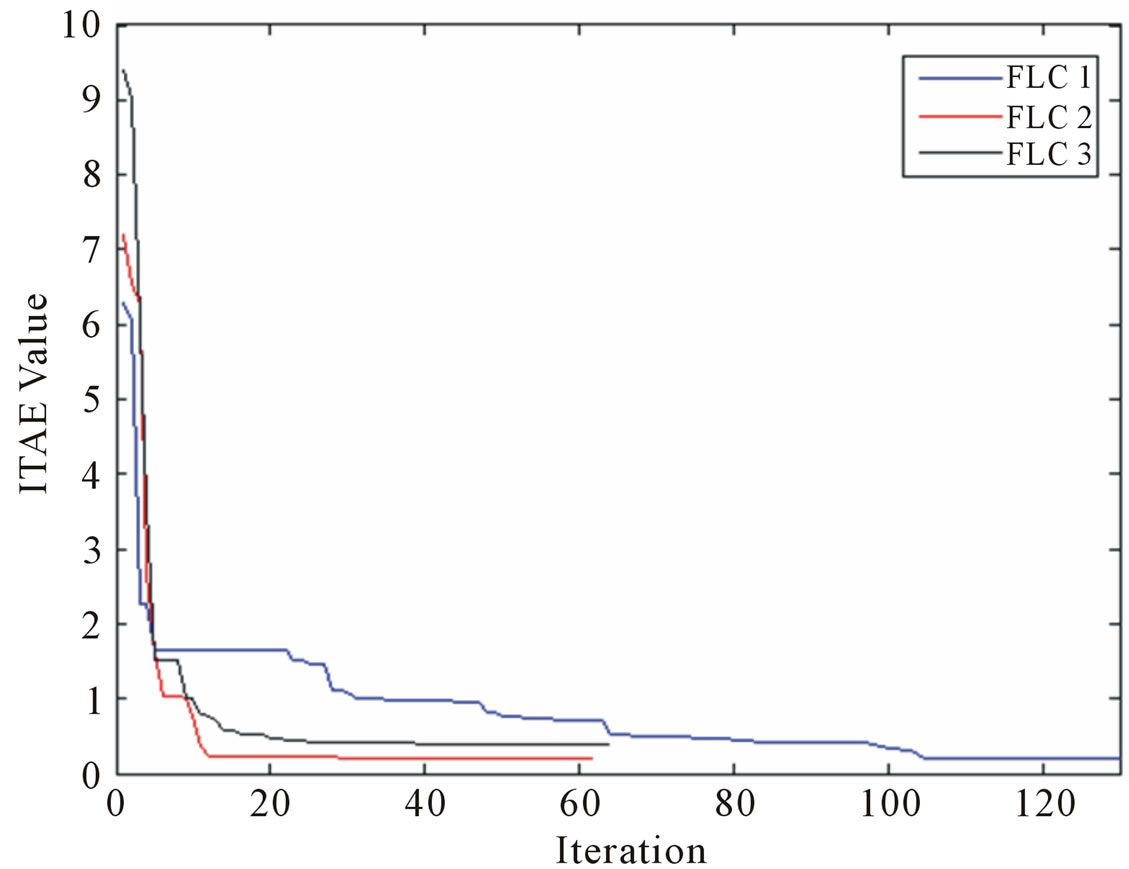
Figure 5. Fitness function in PSO algorithm.
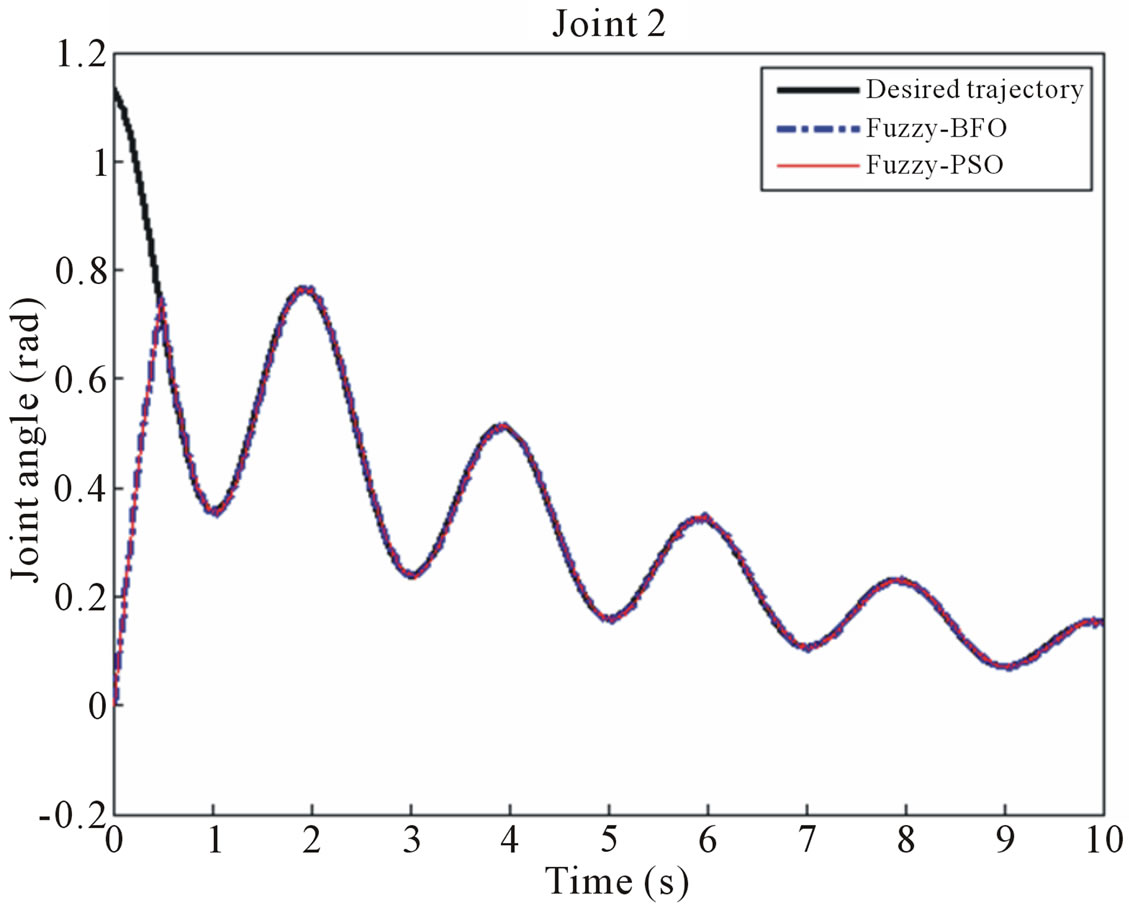
Figure 6. Performance of second joint angle.
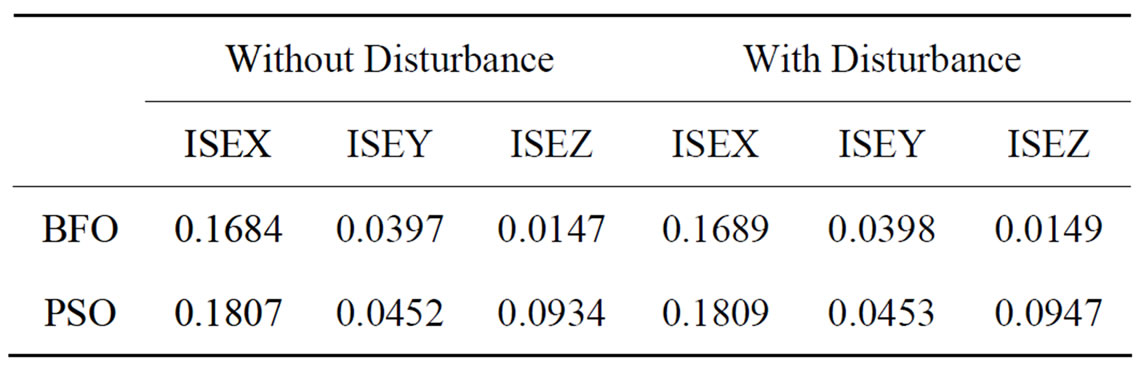
Table 3. Fitness function (ISE) in Cartesian space.
is better than the Fuzzy-PSO based controller. Considering the results confirm a powerful ability of rejecting disturbances. Figures 8 and 9 show desired and tracked trajectory for tuned controllers. With comparing performances in simulations, it can be concluded that the BFO algorithm is superior to the PSO algorithm in term of accuracy of response.
6. Conclusion
In this paper, we have presented a comparison study of using BFO and PSO algorithms for a design of a fuzzy PID controller to tracking control. Performances of controllers in the cases of with and without disturbances are

Table 4. Fitness function (ITAE) in joint space.
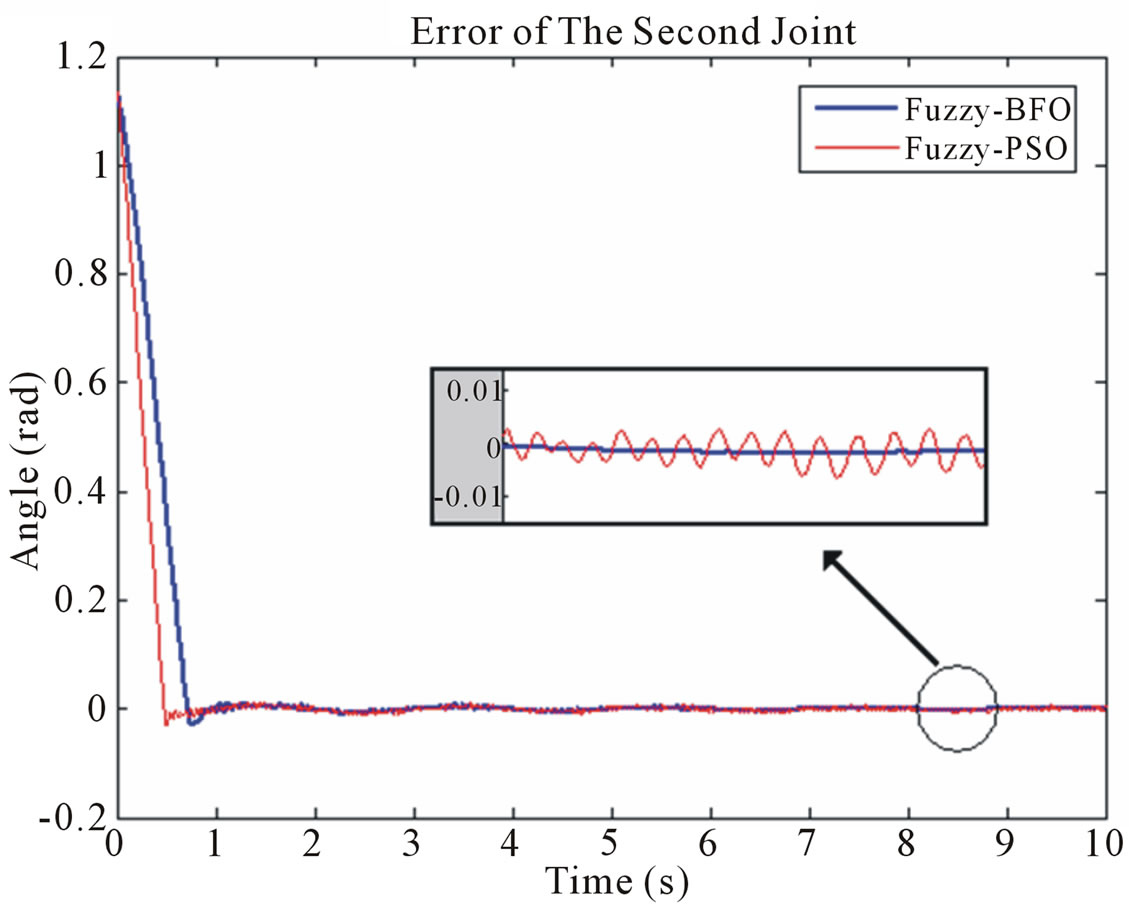
Figure 7. Joint space error of second joint.
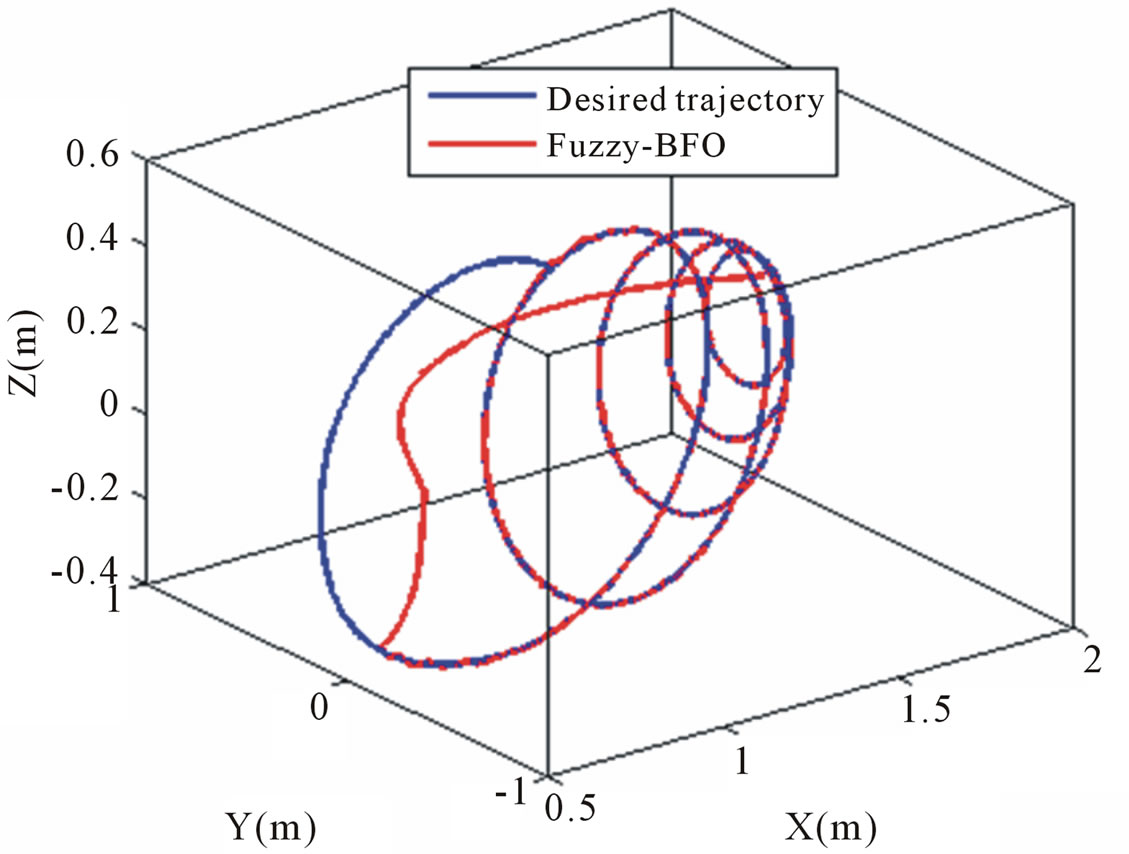
Figure 8. Performance of FLC using BFO algorithm.
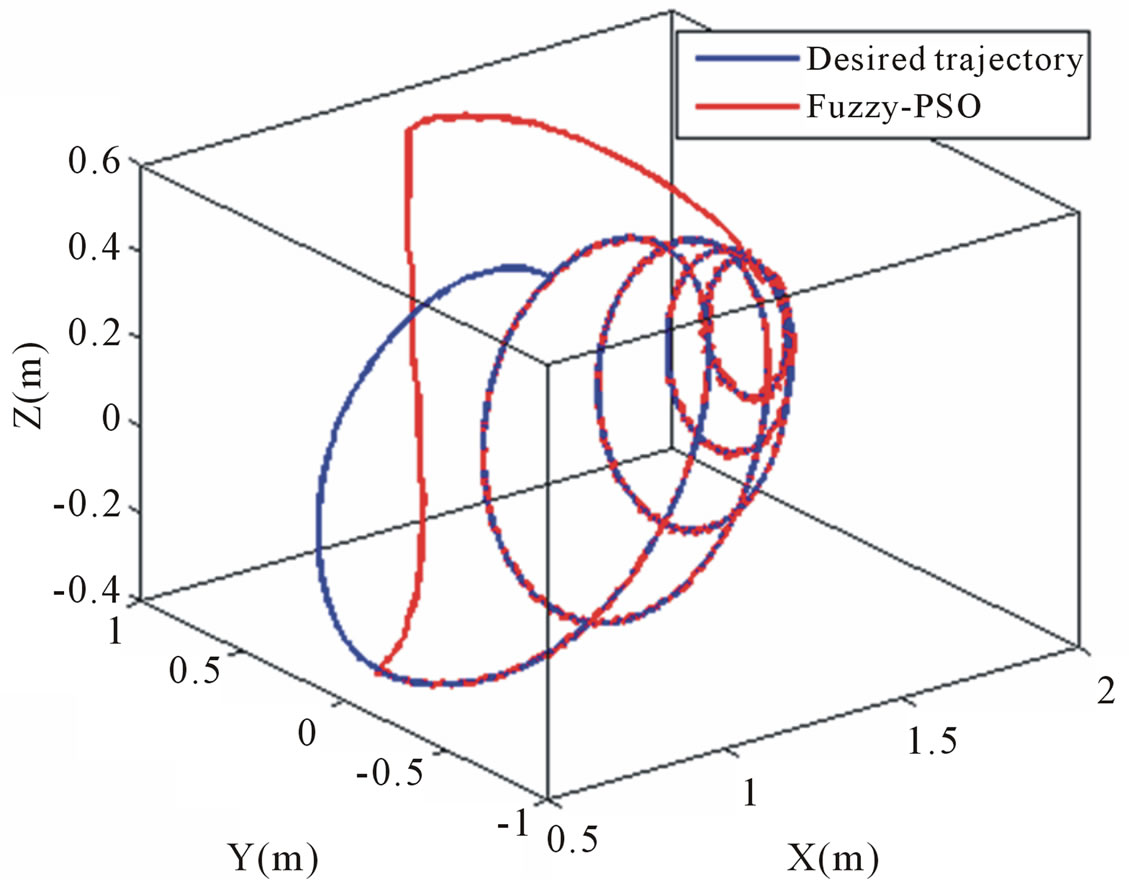
Figure 9. Performance of FLC using PSO algorithm.
compared for the above approaches in joint space, as well as in Cartesian space. The simulation results show that BFO algorithm is superior to PSO algorithm in term of accuracy of response. An improvement of this work can be made by designing an online adaptive controller based on BFO algorithm.
REFERENCES
- K. H. Ang, G. Chong and Y. Li, “PID Control System Analysis, Design, and Technology,” IEEE Transactions on Control Systems Technology, Singapore, Vol. 13, No. 4, 2005, pp. 559-576. doi:10.1109/TCST.2005.847331
- T. H. Kim, I. Maruta and T. Sugie, “Robust PID Controller Tuning Based on the Constrained Particle Swarm Optimization,” Automatica, Vol. 44, No. 4, 2008, pp. 1104- 1110. doi:10.1016/j.automatica.2007.08.017
- L. X. Wang, “A Course in Fuzzy Systems and Control,” Prentice Hall, New York, 1996.
- M. M. Fateh, “Robust Fuzzy Control of Electrical Manipulators,” Journal of Intelligent and Robotic Systems, Vol. 60, No. 3-4, 2010, pp. 415-434. doi:10.1007/s10846-010-9430-y
- K. M. Passino, “Biomimicry of Bacterial Foraging for Distributed Optimization and Control,” IEEE Control Systems Magazine, Columbus, Vol. 22, No. 3, 2002, pp. 52-67. doi:10.1109/MCS.2002.1004010
- J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” IEEE International Conference on Neural Networks, Vol. 4, Perth, 27 November-1 December 1995, pp. 1942-1948. doi:10.1109/ICNN.1995.488968
- M. Dorigo and T. Stutzle, “Ant Colony Optimization,” MIT Press, Cambridge, 2004. doi:10.1007/b99492
- M. Tripathy and S. Mishra, “Bacteria Foraging-Based to Optimize Both Real Power Loss and Voltage Stability Limit,” IEEE Transactions on Power Systems, Vol. 22, No. 1, 2007, pp. 240-248. doi:10.1109/TPWRS.2006.887968
- M. A. Munoz, J. A. Lopez and E. Caicedo, “Bacteria Swarm Foraging Optimization for Dynamical Resource Allocation in A Multizone Temperature Experimentation Platform,” Analysis and Design of Intelligent Systems using Soft Computing Techniques, Advances in Intelligent and Soft Computing, Vol. 41, 2007, pp. 427-435.
- H. Shen, Y. Zhu, X. Zhou, H. Guo and C. Chang, “Bacterial Foraging Optimization Algorithm with Particle Swarm Optimization Strategy for Global Numerical Optimization,” Proceedings of the First ACM/SIGEVO Summit on Genetic and Evolutionary Computation, Shanghai, June 2009, pp. 497-504.
- D. H. Kim, A. Abraham and J. H. Cho, “A Hybrid Genetic Algorithm and Bacterial Foraging Approach for Global Optimization,” Information Sciences, Vol. 177, No. 18, 2007, pp. 3918-3937. doi:10.1016/j.ins.2007.04.002
- T. J. Su, G. Y. Chen, J. C. Cheng and C. J. Yu, “Fuzzy PID Controller Design Using Synchronous Bacterial Foraging Optimization,” 3rd International Conference on Information Sciences and Interaction Sciences, Kaohsiung, June 2010, pp. 639-642.
- A. Biswas, S. Dasgupta, S. Das and A. Abraham, “Synergy of PSO and Bacterial Foraging Optimization: A Comparative Study on Numerical Benchmarks,” Innovations in Hybrid Intelligent Systems, Advances in Intelligent and Soft Computing, Vol. 44, 2007, pp. 255-263. doi:10.1007/978-3-540-74972-1_34
- M. Clerc and J. Kennedy, “The Particle Swarm-Explosion, Stability and Convergence in A Multidimensional Complex Space,” IEEE Transactions on Evolutionary Computation, Vol. 6, No. 1, 2002, pp. 58-73. doi:10.1109/4235.985692
- M. M. Fateh, “Proper Uncertainty Bound Parameter to Robust Control of Electrical Manipulators Using Nominal Model,” Nonlinear Dynamics, Vol. 61, No. 4, 2010, pp. 655-666. doi:10.1007/s11071-010-9677-7
- Y. J. Park, H. S. Cho and D. H. Cha, “Genetic AlgorithmBased Optimization of Fuzzy Logic Controller Using Characteristic Parameters,” IEEE International Conference on Evolutionary Computation, Taejon, Vol. 2, 1995, pp. 831-836.

