Received 10 May 2016; accepted 20 June 2016; published 24 June 2016

ABSTRACT

In the present study, an analytical solution is presented to solve the problem of combined seepage, under a sheet piling cofferdam, applied to dewatering systems. Existence of the sheet pile creates a confined seepage followed by an unconfined seepage in the same field, which presents a combined seepage problem. Two equations were developed to analyze the combined seepage underneath a sheet piling wall. Using such equations, both the maximum height of the free surface just behind the sheet piling cofferdam (H_o) and the quantity of seepage discharge to be pumped out from the construction site (q) can be determined. The main parameters affecting the combined seepage characteristics underneath a sheet piling wall are: The depth of permeable foundation layer (T), the horizontal distance behind the sheet pile (X), the depth of excavation in the construction site (D), the embedded depth of sheet pile (S), the retained water head (H₁), the accumulated seepage water depth (H₂), and the side slope factor of excavation line (M). Study showed that, the above parameters have a great effect on the combined seepage, but with different extents.

Keywords:

Confined Seepage, Unconfined Seepage, Combined Seepage, Sheet Piling Cofferdam, Seepage Discharge, Phreatic Surface

1. Introduction

Excavation and preparation of the construction sites for both hydraulic and marine structures are accompanied by some problems concerned with seepage of groundwater towards the excavated area. Site drainage is conducted by lowering the groundwater table, to be below the foundation surface, using different techniques called dewatering systems. Seepage in zones of hydraulic structures may either be confined or unconfined. Practically confined or unconfined seepage often occurs with an individual form. Combination of both types may also take place in the same field beneath hydraulic structures. Seepage flow underneath a sheet piling cofferdam, surrounding an excavated area prepared for constructing a hydraulic structure, is a typical example for the combined seepage flow.

In the present study a sheet piling wall is used as a cofferdam not only to retain water head but also utilizing its penetration depth to lower the seepage line below the foundation level in the construction site. In this case, the sheet piling wall divides the flow pattern into two zones: (I) and (II). Zone (I) is equipped with confined seepage while in zone (II) unconfined seepage takes place. Existence of such two types of seepage in the same field under the same head presents a combined seepage problem, as shown in Figure 1.

Pavlovsky (1933) [1] presented a mathematical solution for some idealized problems of confined seepage beneath gravity hydraulic structures using the stream and potential functions. Khosla (1954) [2] derived formula to calculate both the uplift pressure along the subsurface contour of the floor and the exit gradient at the downstream bed. Harr (1962) [3] explained the use of transformations and mapping to transfer the geometry of a seepage problem from one complex plane to another. Chawla and Garg (1969) [4] derived an exact solution to calculate the uplift pressures and the exit gradients for a hydraulic structure founded on an infinite pervious stratum with finite and infinite pervious reaches on the upstream and downstream sides. Chawla (1972) [5] resolved the same problem for the case when the structure is founded on finite pervious stratum. Kimura and Ohne (1983) [6] studied the three dimensional seepage around the abutment foundation of a dam with a cut off wall using both model tests and numerical computations by finite element method. Elganainy (1985) [7] studied the seepage beneath a horizontal flat floor, without cutoff, based on pervious foundation bounded by an impermeable layer. He

presented formulae to calculate the uplift pressure distribution along the floor, the exit gradient along the downstream bed and the seepage discharge per unit width. Hathoot (1986) [8] studied the problem of confined seepage beneath a concrete dam with flat horizontal floor and a downstream filter, based on a homogeneous isotropic soil. He investigated the optimum length of the filter so that the most of seepage quantity can be drained. Later, Hathoot et al. (1992) [9] used the same procedure, but for a floor with an end sheet pile. They recommended that, the length of filter is in the range of 2.24 to 2.52 of the permeable foundation soil depth. Nasr (1992) [10] developed an analytical solution using the conformal mapping technique for the problem of seepage beneath a hydraulic structure having two unequal cutoffs founded on two pervious strata. The lower stratum has higher permeability than the upper one. El-Fitiany and Nasr (1992) [11] presented a numerical model using the finite element model to study the effect of the flow domain dimensions on the seepage characteristics beneath a floor having upstream or downstream sheet pile. They concluded that, the inlet and exit surfaces have 1.5 to 2.0 times the floor length is sufficient to keep the resulting deviations within 3%. Sherif (2004) [12] applied the finite element method to develop the numerical solution for case of unconfined seepage between two parallel and unequal water level open streams. The analysis indicated that, increase each of the pervious layer thickness, the lower stream side slopes, and the water head difference cause an increase in the quantity of seepage. Albehbah (2006) [13] studied the combined seepage flow underneath a sheet piling coffer dam using the finite element method, considering only one specific value for the excavation depth to be one third the depth of foundation layer. Results of such solution cannot be used for other values of the excavation depth. Therefore, the analytical solution, developed in the present study, may be applied for different values of the relative excavation depth.

The objective of this research is to propose an analytical solution to solve the problem of combined seepage under a sheet piling cofferdam. Two equations including the factors influenced the combined seepage are developed to determine the maximum height of the free surface just behind the sheet piling cofferdam and the quantity of seepage discharge.

2. Analytical Study

The analytical solution aims at predicting theoretical equations including the main parameters involving in the current problem. These equations may give estimation for the quantity of seepage water to be drained outside the construction site as well as the maximum depth and shape of the free surface. The combined seepage presents a combination of the two basic types of seepage; confined and unconfined. Therefore, the analytical solution for both types will be individually discussed; hence a combination of the two solutions is then developed.

2.1. Confined Seepage Flow

Confined seepage problem is characterized in that all boundaries of the flow domain are initially known and completely defined. As given by Harr (1962) [3] , the case of a confined seepage under impervious structure with sheet pile based on layer of finite depth was studied by Pavlovsky (1956) [14] and Muskat (1936) [15] , as shown in Figure 2, using the Schwarz-Christoffel transformation. As a result, the seepage discharge due to confined seepage per unit width can be determined as follows:

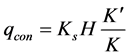(1)

where K_s is the hydraulic conductivity coefficient for the pervious foundation soil, H is the total effective head on the structure, and K', K are the constants of complete elliptic integral of the first kind with respect to modulus (m), which may be found as follows:

(2)

where S is the depth of sheet pile, T is the depth of pervious foundation soil, and b is length of the left and right parts of the structure base width with respect to sheet pile (b₁ = b₂ = b).

It should be noticed that, the values of the constants k, k' can be determined from specific tables according to the value of the modulus (m), as given by Milton, et al. (1970) [16] .

2.2. Unconfined Seepage Flow

The unconfined seepage problem is characterized by one boundary of the flow domain, free surface. Considering

a two dimensional flow on a horizontal impervious boundary, the Dupuit’s formula for the unconfined seepage discharge per unit width is:

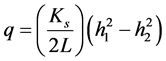(3)

where h₁ and h₂ are the elevation of the two points on the free surface, with distance (L) in between.

2.3. Combined Seepage Flow

Considering the confined seepage problem shown in Figure 2 and eliminating the width of structure, the problem is transformed to a seepage flow beneath a single sheet pile. This case is typically found in zone (I) concerning confined seepage. Therefore, the seepage discharge due to confined seepage in zone (I) may be found using Equation (1).

Substituting for the effective head (H), where H = T + H₁ ? H_o, the confined seepage discharge equation per unit width may be written as follows:

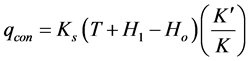(4)

where H₁ is the depth of retained water by the sheet pile, and H_o is the maximum height of free surface just behind sheet piling cofferdam.

Considering the base width (b) = 0 in Equation (2), the modulus (m) becomes:

(5)

Substituting for h₁ = H_o and h₂ = T ? D +H₂ in Equation (3), the unconfined seepage discharge equation per unit width is given as follows:

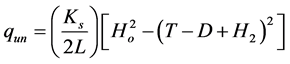(6)

where D is the depth of excavation in the site, H₂ is the depth of seepage water above the foundation layer, and L is the horizontal projection of the free surface length.

For the steady flow condition, the discharge of both confined and unconfined seepage should be the same. Then, equating Equations (4) and (6), one can obtain the following equation:

(7)

Adding the term 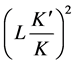to each side of the above equation and rearranging, the maximum relative height of free surface 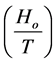may be given as follows:

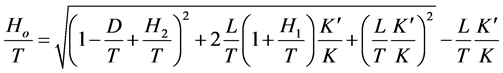(8)

The relative horizontal projection of the free surface length can be determined as follows:

(9)

where X is the horizontal distance between the sheet piling cofferdam and the excavated area, M is the side slope factor (M = cotθ), and θ is the inclination angle of excavation slope.

Once the maximum height of free surface (H_o) is found from Equation (8), quantity of the relative seepage

discharge is then calculated, using Equation (4),by:

(10)

3. Analysis and Discussion

The depth of foundation layer (T) is kept constant as a reference parameter to which the other parameters are related. Using the dimensional analysis technique, the maximum relative height of the free surface (H_o/T) and the relative quantity of seepage discharge (q/(K_sT)) could be written in the following forms:

,and (11)

(12)

The following analysis deals with the effect of specific values of the considered parameters on the values of (H_o/T) and (q/(K_sT)).

3.1. Effect of the Seepage Water Depth (H₂)

Considering specific values of the relative parameters (H₁/T) = 0.0, 0.2, (X/T) = 0.0, 0.5, 1.0, (D/T) = 0.2, 0.6, 1.0, M = 1.0, and (S/T) = 0.2, 0.4, 0.6, 0.8, values of (H_o/T) are plotted against (H₂/T) values. Figure 3 is an example to illustrate the effect of variation of (H₂/T) values on (H_o/T) values for specific values of (H₁/T) = 0.0, (X/T) = 0.0, M = 1.0, (D/T) = 0.6, and (S/T) = 0.2, 0.4, 0.6, 0.8. It is found that, values of (H_o/T) increase with increasing values of (H₂/T) for values of (D/T) = 0.2 to about 0.8. For values of (D/T) > 0.8, values of (H_o/T) slightly decrease with increasing values of (H₂/T), as shown in Figure 4.

Also, values of (q/(K_sT)) corresponding to values of (H_o/T) are plotted against (H₂/T) values. Figure 5 illustrates the effect of variation of (H₂/T) values on (q/(K_sT)) values for specific values of (H₁/T) = 0.2, (X/T) = 0.0, M = 1.0, (D/T) = 0.2, and (S/T) = 0.2, 0.4, 0.6, 0.8. It is seen that, values of (q/(K_sT)) linearly decrease with increasing values of (H₂/T). Such decrease in (q/(K_sT)) values gradually disappears with increasing values of (D/T), as shown in Figure 6.

From results of the analysis in this case, it is noticed that, when value of (H₂/T) = (D/T) = 0.2, and (H₁/T) = 0.0, the value of (H_o/T) = 1.0 and in turn value of (q/(K_sT)) = 0.0. For all values of (H_o/T) > 1.0, the corresponding values of (q/(K_sT)) are deleted since combined seepage is only existed for values of (H_o/T) < 1.0.

3.2. Effect of the Retained Head (H₁)

Considering specific values of the relative parameters (H₂/T) = 0.0, 0.2, (X/T) = 0.0, 0.5, 1.0, (D/T) = 0.2, 0.6, 1.0, M = 1.0, and (S/T) = 0.2, 0.4, 0.6, 0.8, the effect of the relative retained water head (H₁/T) on values of (H_o/T) and (q/(K_sT)) is analyzed. Figure 7 shows the relation between (H_o/T) and (H₁/T) for specific values of (X/T) = 0.5, (H₂/T) = 0.0, M = 1.0, (D/T) = 0.2, and (S/T) = 0.2, 0.4, 0.6, 0.8. It is shown that, (H_o/T) linearly increases as (H₁/T) increases for all values of (D/T). Also, it is shown that, when (H₂/T) = (D/T) = 0.20, and (H₁/T) = 0.05, 0.10, 0.15, 0.20, the values of (H_o/T) > 1.0. In this case, the theory of combined seepage is not valid and the seepage flow becomes confined seepage.

Figure 8 illustrates the effect of variation of (H₁/T) values on (q/(K_sT)) values for specific values of (H₂/T) = 0.0, (D/T) = 0.2, M = 1.0, and (S/T) = 0.2, 0.4, 0.6, 0.8. It is obvious that, (q/(K_sT)) increases as (H₁/T) increases. Also, it is noticed that, when value of (H₂/T) = (D/T) = 0.2, the values of (q/(K_sT)) = 0.0 for any value of (H₁/T).

3.3. Effect of the Sheet Pile Depth (S)

Applying specific values of the relative parameters (H₁/T) = (H₂/T) = 0.0, 0.2, (D/T) = 0.2, 0.6, 1.0, M = 1.0, and (X/T) = 0.0, 0.5, 1.0, the effect of variation of (S/T) values on both (H_o/T) and (q/(K_sT)) values is checked as

illustrated in Figure 9 and Figure 10. Figure 9 shows the effect of variation of (S/T) values on (H_o/T) values for specific values of (H₁/T) = (H₂/T) = 0.0, M = 1.0, (D/T) = 0.6, and (X/T) = 0.0, 0.5, 1.0. It is clear that, values of (H_o/T) strongly decrease as values of (S/T) increase up to (S/T) = 0.20, after which a slight decrease is obtained. Also, it is seen that, when (H₂/T) = (D/T) = 0.20, (X/T) = 0.0, 0.5, 1.0, values of (H_o/T) ≥ 1.0.

On the other hand, Figure 10 illustrates the effect of variation of (S/T) values on (q/(K_sT)) values for specific values of (H₁/T) = (H₂/T) = 0.0, M = 1.0, (D/T) = 0.6, and (X/T) = 0.0, 1.0. It is found that, values of (q/(K_sT)) have the same trend as values of (H_o/T), where decrease as (S/T) values increase. Also, it is shown that, for values of (H₂/T) = (D/T) = 0.2, (H₁/T) = 0.0, the obtained values of (q/(K_sT)) = 0.0 for values of (X/T) = 0.0, 1.0 at which (H_o/T) ≥ 1.0.

3.4. Effect of the Sheet Pile Location (X)

Using specific values of the relative parameters (H₁/T) = 0.0, 0.2, (H₂/T) = 0.0, 0.2, (D/T) = 0.2, 0.6, 1.0, M = 1.0,

and (S/T) = 0.2, 0.4, 0.6, 0.8, the effect of variation of (X/T) values on values of (H_o/T) and (q/(K_sT)) is investigated. Figure 11 shows the effect of variation of (X/T) values on (H_o/T) values for specific values of (H₁/T) = 0.2, (H₂/T) = 0.0, M = 1.0, (D/T) = 0.6, and (S/T) = 0.2, 0.4, 0.6, 0.8. It is clear that, values of (H_o/T) increase with increasing of (X/T) values. Also, it is seen that, for values of (H₂/T) = (D/T) = 0.2, values of (H_o/T) ≥ 1.0.

Figure 12 shows the effect of variation of (X/T) values on (q/(K_sT)) values for the same specific values of parameters as shown in Figure 11. It is found that, values of (q/(K_sT)) decrease when values of (X/T) increase. Also, it is noticed that, for values of (H₂/T) = (D/T) = 0.2, values of (q/(K_sT)) = 0.0 at which (H_o/T) ≥ 1.0.

3.5. Effect of the Excavation Depth (D)

Applying specific values of the relative parameters (H₁/T) = 0.0, 0.2, (H₂/T) = 0.0, 0.2, (X/T) = 0.0, 0.5, 1.0, M = 1.0, and (S/T) = 0.2, 0.6, 0.8, the effect due to variation of (D/T) values on values of (H_o/T) and (q/(K_sT)) is

analyzed. Figure 13 shows the effect of variation of (D/T) values on (H_o/T) values for specific values of (H₁/T) = (H₂/T) = 0.0, M = 1.0, (X/T) = 0.5, and (S/T) = 0.2, 0.6, 0.8. It is seen that, values of (H_o/T) decrease as values of (D/T) increase reaching to its minimum value, nearly, at (D/T) = 0.7 after which it slightly increases again. This may be referred to that the flow cross section area at the entrance to the excavation area being more contracted when (D/T) = 0.7. Such contraction causes backing effect to the flow which slightly raises the free surface and then increases value of (H_o/T) again. For values of (D/T) > 0.8, the values of (H_o/T) increase because the flow has no way to enter the excavation through its bed surface. Hence, the sloped face of excavation becomes the only possible path for seepage flow to the excavated area.

Values of (q/(K_sT)) are also affected by variation of (D/T) values, as shown in Figure 14 for specific values of

(H₁/T) = 0.2, (H₂/T) = 0.0, M = 1.0, (X/T) = 0.5, and (S/T) = 0.2, 0.6, 0.8. It is noticed that, values of (q/(K_sT)) slightly increase as (D/T) values increase reaching to its maximum value, nearly, at (D/T) = 0.7, then a slight decrease occurred. This may be due to the reverse relation between H_o and q where value of q increases when value of H_o decreases and vice-versa.

3.6. Effect of Side Slope Factor (M)

To investigate the effect of the side slope factor (M) on values of (H_o/T) and (q/(K_sT)), some specific values of the relative parameters are tested such as; (H₁/T) = (H₂/T) = 0.0, 0.2, (X/T) = 0.0, 0.5, 1.0, (D/T) = 0.2, 0.6, 1.0, and (S/T) = 0.2, 0.8. Thus, various values of the side slope factor are used where M = 0.5, 0.67, 1.0, 1.5, 2.0. The effect of M values on values of (H_o/T) and (q/(K_sT)) is presented as shown in Figure 15 and Figure 16.

Figure 15 illustrates the effect of variation of M values on (H_o/T) values for specific values of (X/T) = 0.0, (S/T) = 0.2, (D/T) = 0.6, and (H₁/T) = (H₂/T) = 0.0, 0.2. It is clear that, increasing the side slope factor (M) leads to a slight increase in values of (H_o/T) for (D/T) = 0.2. Such increase is being noticeable when (D/T) increases as shown in Figure 15 where (D/T) = 0.6.

Figure 16 illustrates the effect of variation of M values on (q/(K_sT)) values for the same specific values of the relative parameters used in Figure 15. It is seen that, increasing the side slope factor (M) leads to a slight decrease in values of (q/(K_sT)) for (D/T) = 0.2. Such decrease of (q/(K_sT)) values increases when (D/T) increases as shown in Figure 16 where (D/T) = 0.6.

4. Conclusions

In the present work, an analytical solution is developed for the problem of combined seepage under a sheet piling cofferdam when used in dewatering systems. Two analytical equations including the parameters affecting the characteristics of combined seepage are obtained. The first equation is used to determine the maximum height of the phreatic surface (H_o) while the second is used to determine the quantity of seepage discharge (q) to be pumped out from the construction site. Thus, the capacity and number of pumping units are then determined.

As a result of the analysis, concerned with the effect of the main parameters on both H_o and q, the main conclusions of the present study are arranged as follows:

1) The main parameters have an obvious effect on characteristics of the combined seepage but with different extents. Such seepage characteristics are greatly affected by variation of H₂, S, X, and D, and with lower extent by variation of H₁.The seepage characteristics are slightly affected by variation of M.

2) Value of H_o increases due to increasing values of H₁, H₂, X, and M, while it decreases with increasing values of S and D.

3) The minimum and maximum values of (H_o/T) are 0.614 and 1.0, respectively, within the range of the tested parameters.

4) Value of q decreases due to increasing values of H₂, S, X, and M while it increases with increasing values of H₁ and D.

5) The minimum and maximum values of (q/(K_sT))are 0.0 and 0.442, respectively, within the range of the tested parameters.

6) The side slope factor of excavation (M) has a slight effect on both q and H_o.

Acknowledgements

The author acknowledges, with gratitude, the support provided by Prof. Dr. M. A. Abourohim of Irrigation Engineering and Hydraulics Department, Faculty of Engineering, Alexandria University, Egypt.

Cite this paper

Magdy M. Aboelela, (2016) Theory of Combined Seepage Applied to Dewatering Systems. Journal of Water Resource and Protection,08,743-755. doi: 10.4236/jwarp.2016.87060

References