Journal of Water Resource and Protection
Vol.08 No.02(2016), Article ID:63378,15 pages
10.4236/jwarp.2016.82014
Rain Variability and Population Growth to Explain Historical Levels of the Patzcuaro Lake in Mexico
Isabel Quintas1, María Antonieta Gómez-Balandra2, Willem Vervoort3
1Humanities and Social Sciences Division, Metropolitan Autonomous University, Mexico City, Mexico
2Hydrobiology and Environmental Assessment, Mexican Institute of Water Technology, Morelos, Mexico
3Faculty of Agriculture and Environment, The University of Sydney, Sydney, Australia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 December 2015; accepted 2 February 2016; published 5 February 2016
ABSTRACT
The height variability of Lake Patzcuaro, in central Mexico, remained constant for several decades, and during that period, the lake maintained its functionality and environmental services. However, in the last twenty years, there has been a significant decrease in the variability range. In order to estimate the water balance, in this work, an approach was developed to understand how water moves in time and space, and to determine possible inherent thresholds to lake variability. The historical Lake Patzcuaro height above 2035 masl was correlated with several climatic variables. The correlation with monthly rainfall shows that there is a delay of three months, indicating that the lake volume depends on three factors: precipitation, surface runoff and underground contribution, of which precipitation over the lake surface is the least significant. In the long term, using annual data, there is a remarkable memory of precipitation extending beyond five years, seen as a correlation with the accumulated precipitation anomaly (r2 = 0.76). This behavior should be explained by understanding relationship between the lake and its aquifer. Also important is the population growth, which affects the lake level in two ways: water extraction and water discharge. The models pointed out a nonlinear relationship between water level and the aforementioned variables, and suggest that the carrying capacity of the basin is around 90 thousand people, under current patterns of water consumption. It also indicates that, in order to allow lake recovery or to maintain system resilience, the anomaly of precipitation accumulated during several years should exceed 1000 mm. Although a correlation with land use was attempted, historical data do not reflect a trend that could be associated with water balance.
Keywords:
Lake Modeling, Patzcuaro, Population, Resilience, Rain Variability

1. Introduction
Lake Patzcuaro is a tropical, high-altitude, endorheic and fresh water body located on the Mexican plateau at 2036 meters above sea level (masl). Its origin is due to tectonic-volcanic processes associated with the Mexican Neovolcanic Axis [1] . It is considered a climatically-sensitive, with amplified effects on a closed basin lake that is affected by the magnitude of seasonal changes and inter-annual variability [2] [3] . Its maximum depth (12 m) occurs in the northern part of the lake, whereas shallow areas are located in the south [4] [5] .
In general, variations in water levels of lakes are due to several factors that can be classified into: (1) evolutionary processes, (2) climate natural variability, (3) extreme natural events and (4) events that are associated to human activities in the catchment area. Aside from rainfall patterns, volume variability in lakes shows that historical fluctuation trends are generally explained by variations in catchment land use and extractions [6] [7] . According to paleo-historical studies of the Patzcuaro Lake, water level variations have been related to paleo- historical climatic conditions and induced erosion [8] , during three major periods. During the last period, after AD 1200, a destructive and irreversible process occurred, mainly due to the increasing population.
Imagery and remote sensing techniques have been used to estimate the Patzcuaro Lake’s surface. According to aerial photographs taken in 1974, it was estimated to be 116.48 km2 [9] . In other studies, the lake surface has been estimated to lie between 88 and 130 km2 [4] [10] -[13] . Overall, the Patzcuaro Lake drains a catchment of 927 km2.
The annual water balance has been calculated by integrating surface and underground water, over several years. Surface water includes estimates of the natural runoff, direct discharge to the lake by sub-basins. Underground water accounts for infiltrated water, springs and wells. For 2004, the inputs and outputs were estimated at 138.3 and 119.3 Mm3 respectively, leading to lake variations of approximately 18.7 Mm3. For this balance, the interaction with groundwater was identified as output rather than input [14] . In years 2005 and 2006, the main inputs to the lake were identified as: rain, runoff and groundwater. This last one was estimated to be approximately 20 Mm3 each year, resulting in a negative variation of the water volume of the lake in 2005 of −10.26 Mm3 and an increase of 14.31 Mm3 in 2006.
The Equation (1) shows the most extensive monthly water balance of the lake (Mm3/month) [14] and has been written as:
∆V = (Vll + Re + B + Vman) − (ET + In + Inter + Ab + Uc + f) (1)
where,
∆V = Change in water storage
Vll = Rain volume in the basin = P A (P = precipitation in A = basin area)
Re = Water returns from agricultural fields
B = Extractions and water pumping
Vman = Creeks volume
ET = Evapotranspiration
In = Rain infiltration
Inter = Rain intercepted by vegetation
Ab = Volume downstream
Uc = water consumption (superficial and underground)
f = Losses in public networks
Based on data from the seven sub-basins, it has been estimated that only 10% of rainfall is infiltrated and just 6% reaches the lake. However, the lake response to fluctuations in precipitation (P) and evaporation (E) depends on the relative contribution of groundwater inflow and outflow [14] . Changing the level of the lakes is not very large in closed basins that have no surface or groundwater discharge, and there is no delay in climate forcing [15]
Some closed basin lakes show an immediate response to an increase in rainfall, but it may exhibit a delayed response to a reduction in rainfall, as was observed in Lake Rukwa. In general lake levels fall when evaporation exceeds the total input from precipitation plus inflow, which has been the case in Lake Patzcuaro for several years. On the other hand, Lake Tanganyika shows a close relationship between rainfall variability and lake levels. Correlations were high (0.80) between lake-levels and mean rainfall for the previous five years, with lagged effects from 2 to 5 years [6] . For some lakes, regional-scale climate change, which pre-dates instrumental records, have also been recorded [16] .
After the Limnological research station was established in Lake Patzcuaro (1939), Yamashita measured the silica concentrations in water and suggested that an underground spring is discharging in the lake [17] . The water balance for the Lake Patzcuaro suggests that hydrologic inputs from the watershed have been reduced as a result of watershed deterioration and land use changes [5] . The use of a reference condition, or of a natural variability threshold, is important to assess the relative health of ecosystems, and it is commonly applied [7] .
An analysis of the relationship between environmental and social transformations in the Patzcuaro Lake during the Pre-Columbian Tarascan (Purepecha) empire, results in a challenge to common conceptions regarding the impact of agriculture, urbanism and state collapse on ancient landscapes [18] .
Indeed, the data gathered on the lake level over 500 years [19] indicate a long and relatively slow decline, followed by fluctuations between low states and recovery (Figure 1). Therefore, at present it is unknown whether the current low level has resulted in unrepairable degradation of the ecosystem or whether it is one more of the lake’s historical variations, and that the lake is still resilient enough.
2. Objectives
The main objectives of this paper are: 1) to use statistical models to find the physical and anthropogenic factors that best describe the annual cyclic and long-term behavior of Lake Patzcuaro’s level; 2) to identify variables that negatively affect the water balance and resilience of the system; and 3) to identify steps to mitigate the damage and to enhance conservation of the lake.
3. Study Area
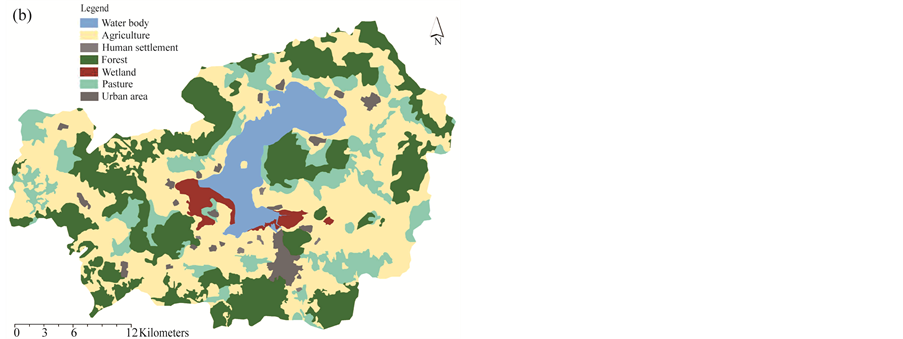
Lake Patzcuaro Basin is located between 19˚27' and 19˚44' North latitude and longitude 101˚26' and 101˚53' West (Figure 2), at 2036 masl. The basin is bounded by a series of volcanic cones up to 3400 meters high. It is a closed basin stretching no more than 40 km from East to West line. The hydrographic basin is formed by short duration intermittent streams from the hills. Only one creek carries water throughout the year and serves as drainage of the agricultural area.
Of the watershed area, 37% of the land has slopes less than two percent and 29% has slopes of less than six percent, this being the only land suitable for agriculture. More than 12% has slopes greater than 12%, with little resistance to erosion especially if deforested.
At the arrival of the Spaniards, the study area was occupied by a Tarascan estimated population of 60,000 inhabitants, who had been exploiting natural resources for several centuries. It became an important colonial settlement whose center was the town of Patzcuaro. Nowadays, the population of the study area is mainly composed of indigenous people originally dedicated to farming, fishing and timber harvesting. More recently handcrafts and tourism have become very important. Today Patzcuaro is a cultural tourism site that receives more than 200,000 visitors annually.
Figure 1. Historical Lake Patzcuaro level fluctuations over the last five centuries.
Figure 2. Study area.
4. Methods
Three data sets were analyzed in this study: (1) Historical lake levels, (2) Local and regional climate data, 3) Population and land use data.
The historical lake level data were recorded by the Michoacán Government Fisheries Commission. Almost daily data are available since January 1950. In addition, from 2003 to 2010 a more detailed data set was generated in a specific study made by the Mexican Institute of Water Technology (IMTA for its acronym in Spanish). In this study, the 2035 masl was set as the inferior reference limit, and we have used this value here.
The main source of climatological data is the Maya database which contains daily values of rain, maximum and minimum temperature data, from January 1961 to December 2010, on a 0.2 × 0.2 degrees grid over the whole Mexican soil. Maya is an interpolated climate data base that uses all existing daily data, interpolated using inverse square distance criteria [20] . The rain data before year 2000 were filtered using the homogeneity algorithm tests of Alexandersson and Buishand [21] .
The monthly average maximum temperature was taken from the National Meteorological Service (SMN in Spanish) database for station 16087 located at 16˚32', 101˚37' and 2043 masl, in the Patzcuaro town.
In order to validate the historical data, short term data were collected by IMTA, during the 2003-2010 period, over a dense grid of 10 automatic stations across the basin. These stations were equipped with a rain gauge, temperature and evaporation sensors and a wind gauge.
Because evaporation and evapotranspiration data from the national database had many gaps, the monthly maximum average temperature was used instead as proxy value for evaporation. The coefficient of correlation found between these variables over several periods is above 0.8.
Population and land use were obtained from the INEGI (National Institute of Geography and Statistics, México) database. Population was estimated from a decadal INEGI census, which takes into account the number of inhabitants of the four municipalities included in the Patzcuaro watershed. The annual and monthly data were interpolated linearly. To determine urban and rural population it was assumed that all villages with more than two thousand people where urban. The information on land use is mainly concentrated in recent years, although some authors prior to 1980 give rough estimates. The information is not homogeneous but shows no significant changes in the distribution of forest area (30%), agriculture (7%), grasslands (20%), mixed or degraded forest (28%), and the area occupied by the lake, which is around 10%.
The methodology consisted of the following steps:
1) Obtaining data and apply quality control measures
2) Calculate annual and monthly data for precipitation, average maximum temperature, and lake level above 2035 masl, population and urban population and derived variables such as moving averages
3) Explore data qualitatively through plotting
4) Calculate auto correlations and cross correlations between data
5) Construct statistical models to predict and explain changes in the lake level
Cross correlations were calculated to identify relationships between variables, but mainly to explain lake level. The rainfall anomaly was calculated by removing the annual average over the period 1961 to 2010, which was 938.2 mm, Equation (2):
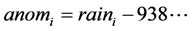 (2)
(2)
Because the lake acts as a reservoir, the 5 year rainfall moving average was calculated. Also a series of cumulative rainfall anomaly was created, adding the rainfall anomaly year by year, Equation (3):
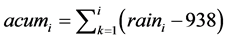 (3)
(3)
Furthermore, because the rain regime of the area results in the majority of precipitation falling between June and October, the monthly rainfall anomaly was calculated by subtracting the average rainfall for each particular month, and the series of the monthly cumulative rainfall anomaly was calculated adding the monthly anomalies, Equation (4).
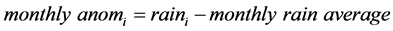 (4)
(4)
Two statistical models were developed using Generalized Additive Models, in the mgcv package [22] in R (www.r-project.org). The first one used the monthly data to analyze the seasonal behavior; the second one used the annual data to visualize trends and factors that might be controlled to manage the lake level decline and the subsequent degradation, thus improving the resilience of the lake.
5. Results
5.1. Temporal Fluctuations
The strong decrease observed in the lake levels during the decade of the 1980’s frightened both the population and the government, because it appeared that the lake was going to disappear. However the historical data (Figure 1) shows that the lake attained similar levels at the beginning of the 1950’s. This happened after a long dry period which occurred in the 1940’s in central Mexico. However, after several years of positive rainfall anomalies, especially during 1967 and 1968, the lake level increased by almost 2 m (Figure 3). In 1979 rainfall decreased again and, in the next decade, the rainfall was above average only three years. As a consequence, the lake level fell 2.5 m, the surface area shrunk and it did not recover. During the 2000 decade, precipitation was less than average for most of the years: only two years had rainfalls over 1000 mm, whereas it would take at least 6 - 8 years of above 1100 mm rainfall, or three years above 1250 mm for the lake to recover 1 meter. Rainfall of about 1000 mm over the entire basin is needed to compensate for the 1400 mm average annual evaporation of the lake.
During the 1960’s and 1970’s, the five-year moving average rainfall was well above the average, which is 950 mm (Figure 4(b)). Over the next three decades, the moving average rainfall tended to be lower, and indicated a decreasing trend. The peak during the sixties was followed by a low level period from 1979 to 1984 with average precipitation close to 935 mm per year. Yet, during this period, the lake level was maintained. Over the following five years (1985-1990) both the annual precipitation and the five year moving average rainfall decreased, and the lake reached its lowest level ever.
Figure 3. (a) Lake level 1950 to 2011 (above 2035 masl); (b) Annual rainfall estimated (Maya database).
Figure 4. (a) Lake level; (b) Five-year moving average rain; (c) Cumulative rainfall anomaly.
Over the next 5 years the annual rainfall returned to 950 mm but this was not sufficient to raise the lake level. Between 1996 and 1997 rain was scarce and the lake lost more water. The lake level (Figure 4(a)) and the five year moving average rainfall (Figure 4(b)) yield visually similar curves, but the lake level lags 5 years behind the moving average.
Because the lake is a dynamic storage system it has memory, therefore the cumulative rainfall anomalies has to take into account what happened in the years before. The time series (Figure 4(c)), visually resembles the lake level (Figure 4(a)), except that in the beginning: the former starts at zero because there are no data before 1961.
Although the average precipitation during the 1961-2010 fifty years period was 938 mm, a high variability was observed. During the 1961-1985 interval it was 985 mm, 50 mm above average; while for the 1986-2010 period, it was only 891 mm, about 100 mm less than average, with a significant downward trend of −3.5 mm/year.
In order to investigate the lake seasonal behavior, the following variables were used: lake level, rainfall, the rainfall anomaly, rainfall five year moving average, cumulative rainfall anomaly and the average maximum temperature. Aside from the temperature, all available data cover the January 1961 to December 2010 period. There are a few missing values in the lake level data in 1992 and 1993. Seasonal cycles are observable in precipitation, lake level and maximum temperature (Figure 5).
After removing the annual seasonal cycles, the lake level fluctuations appear to follow the cumulative rainfall anomaly better than the five year moving average. It is interesting to point out the differences in the data cycles: the level, rainfall and temperature are out of phase. The lake level has its minimum from May to July, when the rain season begins, and it generally reaches a maximum between November and December.
In Figure 6, the monthly lake level, and maximum temperature data for the 1974-1984 eleven years have been represented against the rainfall in order to show the phase difference between the main variables. The annual maximum temperatures occur just before the onset of the rainy season. The lake reaches its minimum level one month after the rainy season starts, while the maximum level occurs two months after it ends. The annual lake level variation is about 0.5 m.
Figure 5. (a) Rain, (b) lake level, (c) cumulative rainfall anomaly, (d) maximum temperature.
Evaporation also follows an annual cycle that is out of phase with the annual rainfall cycle (Figure 7), and which also peaks just before the rainy season. The potential evaporation is lowest in June, due to a decrease in both temperature and insolation. The average annual evaporation is 1400 mm while the average annual rainfall generally does not exceed 940 mm.
On the other hand, the population in the basin has been rising at a rate of almost 2% each year. From 1960 to 2010 the number of people in the area changed from 60 to almost 140 thousand. The urban population (i.e., towns with more than two thousand inhabitants) grew at even higher rates, from 15 to 106 thousand in 50 years, mainly in the Patzcuaro and the Quiroga cities and their surroundings. In Figure 8, the population data were linearly interpolated from the decadal census.
Figure 6. (a) Rain and lake level; (b) Rain and maximum temperature.

Figure 7. Monthly rainfall and potential evaporation.
Figure 8. Population growth.
In spite of counting with some data related to changes in land use, these do not reflect important changes or a trend that can be correlated with patterns of rain or runoff in the basin. Therefore, data are included in order to let know the dynamic of registered change in the area but at 1:250000 scale. Updated land uses are related to the precision of tools to measure areas in images. Table 1 and Figure 9(a), Figure 9(b). Nevertheless, accelerated deforestation occurred for more than forty years, as well as important afforestation activities took place.
5.2. Variables Correlations
Because the climatic seasonal cycles are out of phase, investigating cross-correlations with different lags can be important. Figure 10 shows that the lake level correlates significantly with the 3 - 6 months lagged rainfall, and of course also with the same month one year before. This is clearly a result of the annual rainfall cycle. The cumulative rainfall anomaly is highly correlated with the lake level for lags of more than 24 months, which suggests a several years’ memory of the lake.
The population and the lake level also appear to be highly inversely correlated: when the population increases, the lake level decreases. Similarly, the correlation with maximum temperature is negative and the maximum correlation occurs with a 2 - 3 months lag, which also indicates the expected seasonal cyclical behavior.
5.3. Monthly Data Model
The regression model that yields the best fit (Table 2) for the seasonal behavior of the lake level and the long
Table 1. Historical land use data (INEGI―National Institute of Statistics, Geography and Informatics).
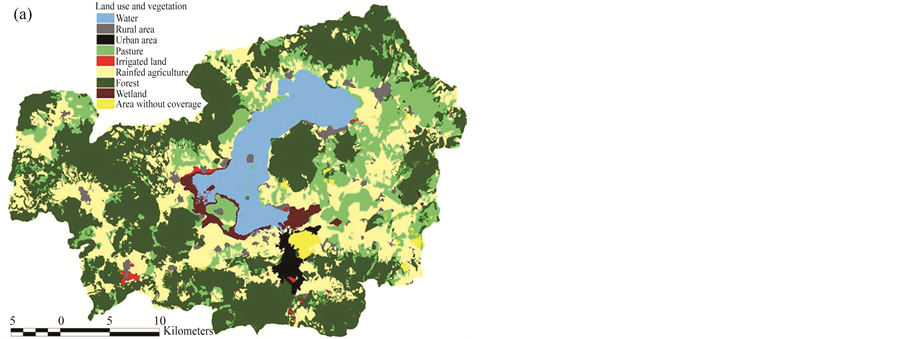
Figure 9. (a) Land use (Series III―2005); (b) Land use (Series V―2013).
Figure 10. Cross correlation for (a) rainfall, (b) cumulative rainfall anomaly, (c) population and (d) maximum temperature against lake level.
Table 2. Monthly model.
term fluctuation explains more than 90% of the variability of the lake level. The following predictor variables were used: rainfall, rainfall anomaly, cumulative rainfall anomaly, population in the basin and average maximum temperature. Actually, the absolute rainfall and the rainfall anomaly are linearly correlated, indicating that only one of them is necessary.
The general additive model shows that the lake level is mainly determined by the value of the cumulative rainfall anomaly: if the cumulative anomaly exceeds 900 mm, the level of the lake will rise, but if the cumulative anomaly decreases below 400 mm the lake will lose water (Figure 11(b)). The other important factor is population. The trend function for this variable clearly indicates that, beyond 90,000 people, the effect on the lake level is definitely negative: the lake level will decline if the population in the basin exceeds 90 thousand people, independently of the rainfall effect (Figure 11(c)). Thus, this number can be seen as the estimated maximum population load for the basin under the current climate and practices of land and water use.
The climatological factors: monthly rainfall and maximum monthly temperature have less influence. The rainfall shows an almost inverse linear relationship with the lake level, which corresponds to the cyclic behavior observed in the cross correlation (Figure 10(a)): one or two months after the end of rainy season, the lake reaches its maximum level for the cycle. The maximum temperature also has a negative influence because of its link with potential evaporation, which increases mainly for Tmax > 26 Celsius degrees.
The final monthly model takes into account all the smoothed terms (Figure 11) that are significant (p < 2 e-16). It is given by the following equation:
This model is able to reproduce the observed monthly variations in the lake level.
5.4. Annual Model Regressions
In order to explore the long term Lake level trend, the annual variation of the variable using the annual average values during the last half century were analyzed. The following variables were considered: rainfall, five-year moving average rainfall (Figure 4), cumulative rainfall anomaly (anomaly from the 938 mm average in the fifty years), population in the basin, urban population and annual average maximum temperature. Only some of the variables are significant in the final model. Because of the small number of available data points, n = 50, it is not possible to introduce all the variables at the same time in a model. Since the total population and the urban population are linearly correlated, the model includes only the total population. The cross correlations obtained with the annual data yield results that are to those obtained from the monthly data.
Our best annual model uses four predictor variables: population, cumulative rainfall anomaly, annual rainfall and the average annual maximum temperature (Table 3).
The obtained model explains almost 99% of the variability (Table 2). The model is:

Figure 11. Smoothed terms of the model: (a) monthly rainfall, (b) accumulated rainfall anomaly, (c) population and (d) tmax.
As in the case of the monthly model, the annual model (Figure 12) clearly shows that the lake level declines abruptly when the population grows above 90,000 inhabitants. The similarity between the monthly and annual model for this variable might be due, in part, to the fact that the population data have been interpolated linearly using the available values reported only every ten years. The basin reached 90,000 inhabitants in 1980. The functions s1 and s4 (Figure 12(a), Figure 12(d)) indicate the impact of annual rainfall and of maximum temperature. Their trend values are close to zero across the full range, indicating that their effect on the lake level is very small.
In contrast, a major predictor is the cumulative rainfall anomaly, which presents a positive slope: the greater
Table 3. Annual model.
Figure 12. Smoothed terms of the annual model: (a) rainfall, (b) population, (c) accumulated rainfall anomaly and (d) max temperature.
the anomaly, the higher the lake level. The zero point on the trend line corresponds to a cumulative anomaly of about 1000 mm: below this point, the lake level declines. In 2010 the cumulative anomaly was around 290 mm, which means that a six or seven year-long wet period with at least a 1000 mm of rainfall would be needed to allow some recovery of the lake level.
The five-year moving average rain does not appear in the model; because it does not correlate as well as the cumulative rainfall anomaly.
6. Conclusions
This is the first work to explain the behavior of Lake Patzcuaro using data from an extended period of 50 years. Daily data from the Maya database have undergone certain quality controls; the lake height comes from the Michoacán Government Fisheries Commission with monitoring of the National Water Commission since the early 50’s. Population data were taken from the institute responsible from the national decadal censuses.
The correlation analysis and the statistical models obtained using monthly and annual data, point out that climate variables such as: rain, evaporation and temperature are responsible for a natural annual variation of the lake level of about 0.5 m, with certain time lags. The maximum level occurs between October and November, just after the rainy season, and the lowest level occurs in May-June.
The two models suggest that the main causes that explain the long term behavior of the lake are both natural and anthropogenic. Anthropogenic effects are measured by the size of the population, which in turn can be seen as a proxy for water consumption per person for both individual use and for different economic activities. An important question that needs to be addressed is why the lake degradation is so much related to population, given that the population is becoming more urban, while agriculture is decreasing in the region.
The next most important component is the variable derived from precipitation. It is implicit in the history of this phenomenon, which we find is best determined as the accumulation of the precipitation anomaly. This result coincides with the correlation coefficients obtained for different lags. The interpolation functions obtained from the models show that, in the case of the monthly data model, the lake is in a stable condition as long as the accumulated precipitation anomaly remains between 400 mm and 1000 mm. above this range, the lake increases its volume, while it decreases rapidly below 400 mm. In the model with annual data, a cumulative anomaly of 1000 mm allows the lake to maintain its level, but below this value, the level decays rapidly.
The memory of almost five years can be best explained by coupling the lake to its aquifers. This interaction occurs at different depths and by path of different lengths as proposed by [23] for the groundwater flow in small drainage basins. Moreover, it is not possible to disregard the possible effect of water pumping in the surroundings, where vast areas of intense agriculture are found.
It is needed to know the lake-aquifer interactions in order to understand how the rainfall, infiltration, runoff, lake and aquifer processes influence the lake behavior. The memory of at least five years cannot be explained by rain runoff only. Groundwater monitoring wells would be needed to determine the water depth and flow directions at different times throughout the year. Existing data are sporadic, and for only few wells, and do not cover extended periods.
The population has grown from 62,000 to almost 140,000 inhabitants during this period. In addition the floating population almost doubles these numbers: it is especially concentrated at certain dates with massive tourism. On the other hand, agriculture, which used to be the largest water user as well as the main economic generator, now covers only 45% of the surface, while the main activity is related to crafts made and tourist services. Because there is not enough data, it was not possible to employ land use as a predictor for lake level changes.
The Patzcuaro Lake has lost almost 4 m in depth between 1982 and 2010. This is translated into approximately 25% of the water volume, with a surface area estimated between 130 to 90 km2 at different times. The reasons for this variability have to do with both natural causes and human activities.
The average annual rainfall during last 50 years is about 938 mm, but with a considerable variation between 670 mm to 1300 mm, and decreasing at a trend of −3.5 mm/year, with dry periods lasting for four to five consecutive years after 1985 (Figure 3).
Lake level statistical models suggest that the main causes are natural and anthropogenic effects, which are mostly non-linear. In particular the results indicate that beyond a level of 90,000 inhabitants the lake level loses its resilience.
Because it is a closed basin, the most important contribution indicated by the model is that the lake acts as a reservoir with a long memory that takes into account the rainfall of the previous years. The cumulative rainfall anomaly shows best correlation, with the monthly level of lake.
Cite this paper
IsabelQuintas,María AntonietaGómez-Balandra,WillemVervoort, (2016) Rain Variability and Population Growth to Explain Historical Levels of the Patzcuaro Lake in Mexico. Journal of Water Resource and Protection,08,168-182. doi: 10.4236/jwarp.2016.82014
References
- 1. Alcocer, J. and Escobar, E. (2006) Limnological Regionalization of Mexico. Lakes & Reservoirs: Research and Management, 2, 55-69.
- 2. Street-Perrott, F.A. and Harrison, S.P. (1985) Lake Levels and Climate Reconstruction. In: Hecht, A.D., Ed., Paleoclimate Analysis and Modeling, John Willey & Sons, New York, 291-331.
- 3. Qin, B. and Huang, Q. (1998) Evaluation of the Climatic Change Impacts on the Inland Lake—A Case Study of Lake Qinghai, China. Climatic Change, 39, 695-714.
http://dx.doi.org/10.1023/A:1005319616456 - 4. Chacon Torres, A., Ross, L.G. and Beveridge, M.C.M. (1989) Lake Patzcuaro, Mexico: Results of a New Morphometric Study and Its Implications for Productivity Assessments. Hydrobiologia, 184, 125-132.
http://dx.doi.org/10.1007/BF00014307 - 5. Chacón Torres, A. (1993) Lake Patzcuaro, Mexico: Watershed and Water Quality Deterioration in a Tropical High-Altitude Latin American Lake. Lake and Reservoir Management, 8, 37-47.
http://dx.doi.org/10.1080/07438149309354457 - 6. Nicholson, S. (1999) Historical and Modern Fluctuations of Lakes Tanganyika and Rukwa and Their Relationship to Rainfall Variability. Climatic Change, 41, 53-71.
http://dx.doi.org/10.1023/A:1005424619718 - 7. Reid, M.A. and Ogden, R.W. (2006) Trend, Variability or Extreme Event? The Importance of Long-Term Perspectives in River Ecology. River Research and Applications, 22, 167-177.
http://dx.doi.org/10.1002/rra.903 - 8. O’Hara, S.L. (1993) Historical Evidence of Fluctuations in the Level of Lake Pátzcuaro, Michoacán, México over the Last 600 Years. The Geographical Journal, 159, 51-62.
http://dx.doi.org/10.2307/3451489 - 9. Gomez-Tagle Chavez, A., Bernal-Brooks, F.W. and Alcocer, J. (2001) Sensitivity of Mexican Water Bodies to Regional Climatic Change: Three Study Alternatives Applied to Remote Sensed Data of Lake Patzcuaro. Hydrobiologia, 467, 169-176.
- 10. De Buen, F. (1944) Los lagos michoacanos II. Pátzcuaro. Sociedad Mexicana de Historia Natural, Mexico.
- 11. Tellez, R. and Motte, O. (1980) Estudio planctonológico preliminar del Lago de Pátzcuaro, Michoacán, México. In: Proceedings of the Second Latin American Symposium on Aquaculture, Ministry of Fisheries, Mexico, 1797-1836.
- 12. Herrera, E. (1979) Características y manejo del Lago de Pátzcuaro, Michoacán. National University of Mexico (UNAM), Mexico.
- 13. Velasco, A. (1982) Evaluación de la calidad del agua con base en algunos aspectos de la comunidad planctónica del Lago de Pátzcuaro, Michoacán. National University of Mexico (UNAM), Mexico.
- 14. Lafragua, J. and Gutiérrez, L.A. (2005) Balance Hídrico en la Cuenca del Lago de Pátzcuaro. Instituto Mexicano de Tecnología del Agua (FGRA-IMTA), Jiutepec.
- 15. Fritz, S.C., Cumming, B.F., Gasse, F. and Laird, K.R. (1999) Diatoms as Indicators of Hydrologic and Climatic Change in Saline Lakes. In: Smol, J.P. and Stoermer, E.F., Eds., The Diatoms: Applications for the Environmental and Earth Sciences, Cambridge University Press, Cambridge, 41-72.
http://dx.doi.org/10.1017/cbo9780511613005.004 - 16. Jones, P.D. (2001) The Evolution of Climate over the Last Millennium. Science, 292, 662-667.
http://dx.doi.org/10.1126/science.1059126 - 17. Bradbury, J.P. (2000) Limnologic History of Lago de Pátzcuaro, Michoacán, Mexico for the Past 48,000 Years: Impacts of Climate and Man. Palaeogeography, Palaeoclimatology, Palaeoecology, 163, 69-95.
http://dx.doi.org/10.1016/S0031-0182(00)00146-2 - 18. Fisher, C.T. (2005) Demographic and Landscape Change in the Lake Pátzcuaro Basin, Mexico: Abandoning the Garden. American Anthropologist, 107, 87-95.
http://dx.doi.org/10.1525/aa.2005.107.1.087 - 19. Bernal-Brooks, F.W., Gomez-Tagle Rojas, A. and Alcocer, J. (2002) Lake Patzcuaro (Mexico): A Controversy about the Ecosystem Water Regime Approached by Field References, Climatic Variables, and GIS. Hydrobiologia, 467, 187-197.
http://dx.doi.org/10.1023/A:1014919032228 - 20. Quintas, I. (2004) Explotación de la base de Datos Climatológica Nacional del siglo XX: Base de datos Maya. Informe OMM-PROMMA No. 199, WMO.
- 21. OMM/PREMIA (2007) Indicadores de Confiabilidad de la Información Registrada en la Base de Datos Climatológica de México Análisis de Consistencia Temporal para las variables: Precipitación, Temperatura Máxima y Tem-peratura Mínima.
- 22. Wood, S.N. (2008) Fast Stable Direct Fitting and Smoothness Selection for Generalized Additive Models. Journal of the Royal Statistical Society. Series B: Statistical Methodology, 70, 495-518.
http://dx.doi.org/10.1111/j.1467-9868.2007.00646.x - 23. Tóth, J. (1963) A Theoretical Analysis of Groundwater Flow in Small Drainage Basins. Journal of Geophysical Research, 68, 4795-4812.
http://dx.doi.org/10.1029/JZ068i016p04795