Journal of Water Resource and Protection
Vol.06 No.07(2014), Article ID:46227,13 pages
10.4236/jwarp.2014.67067
Tracing Water Flow and Colloidal Particles Transfer in an Unsaturated Soil
Dieuseul Prédélus1, Laurent Lassabatere1, Artur Paiva Coutinho2, Cédric Louis3, Thomas Brichart2, Erij Ben Slimène1, Thierry Winiarski1, Rafael Angulo-Jaramillo1
1Université de Lyon, CNRS, UMR 5023 LEHNA, ENTPE, Vaulx-en-Velin, France
2Universidade Federal de Pernambuco, Recife, Brazil
3Nano-H S.A.S., 38070, Saint Quentin Fallavier, France
Email: angulo@entpe.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2014; revised 8 March 2014; accepted 7 April 2014
ABSTRACT
In recent years, many studies have been carried out on colloidal particle transfer in the unsatu- rated zone because they can be a risk to the environment either directly or as a vector of pollut- ants. A study was conducted on the influence of porous media structure in unsaturated conditions on colloidal particle transport. Three granular materials were set up in columns to replicate a flu- vio-glacial soil from the unsaturated zone in the Lyon area (France). It is a sand, a bimodal mixture in equal proportion by weight of sand and gravel, and a fraction of bimodal mixture. Nanoparticles of silica (SiO2-Au-FluoNPs), having a hydrodynamic diameter between 50 and 60 nm, labeled by organic fluorescent molecules were used to simulate the transport of colloidal particles. A non- reactive tracer, bromide ion (Br−) at a concentration of C0,s = 10−2 M was used to determine the hy- drodispersive properties of porous media. The tests were carried out first, with a solution of nano- particles (C0,p = 0.2 g/L) and secondly, with a solution of nanoparticles and bromine. The transfer model based on fractionation of water into two phases, mobile and immobile, MIM, correctly fits the elution curves. The retention of colloidal particles is greater in the two media of bimodal par- ticle size than that in the sand, which clearly demonstrates the role of textural heterogeneity in the retention mechanism. The increase in ionic strength produced by alimenting the columns with col- loidal particle suspension in the presence of bromide, increases retention up to 25% in the sand. The total concentration profile of nanoparticles collected at the end of the experiment shows that the colloidal particles are retained primarily at the entrance of the columns. Hydrodispersive cal- culated parameters indicate that flow is more heterogeneous in bimodal media compared to sand.
Keywords:
Colloidal Particle Transport, Microstructure, Modeling, Unsaturated Soil

1. Introduction
Nanoparticles will inevitably proliferate in soil due to the development of nanotechnologies for consumer products, as well as their eventual landfill or incineration. All compartments are then impacted: surface water, soil, groundwater [1] . These mobile colloidal particles can be a risk to the environment either directly or as a vector for pollutants [2] . The function of the unsaturated zone occupying a central position between the atmosphere and subterranean water is to filter groundwater recharge and protect its quality. In depth knowledge of transfer mechanisms in this area is still quite scarce. It is important to understand better colloidal particle transfer in the unsaturated zone in order to protect water resources. The transport of colloidal particles in soil is due to convection, diffusion and dispersion. The heterogeneity of flow velocities in soil creates the phenomenon of mechanical dispersion. This phenomenon of mixing is due to velocity distribution within pore space, the range of pore size and the tortuosity of the medium [3] . These parameters are related to soil structure; however the medium structure itself also plays an important role in colloidal particle transfer. In addition, during transfer, interactions can occur between the colloidal particles themselves and between colloidal particles and the porous medium. These interactions can cause retention of colloidal particles. The main mechanisms of colloidal particle retention in soil are: adsorption, attachment at the air-water interface and “straining” (i.e. pore network constriction). Adsorption (physicochemical interactions with porous medium) occurs when colloidal particles approach the surface of soil particles. Interactions on the surface of colloidal particles lead to temporary or permanent attachment to the solid phase of porous medium. The attachment of colloidal particles at the air-water interface depends on pH, ionic strength and surface properties of colloidal particles [4] [5] . Constriction (where pores have diameters inferior to colloidal particles) provides sites for depositing, including areas where local water flow is not zero [6] . This type of deposit called “straining” mainly concerns larger colloidal particles. Furthermore, the straining effect is greater in unsaturated medium because water flow is towards the smallest pores and drives colloidal particles to where they are blocked.
Research on synthetic colloidal particle transport in soil reveals that colloidal particles size increases up to several hundred microns, when the particles are suspended and injected into columns of sand [7] . The aggregation mechanisms of synthetic colloidal particles indicate that deposition in porous medium depends on interactions between the medium and colloidal particles but also between the colloidal particles themselves [8] . The chemical properties of the fluid in which colloidal particles are transported, and medium structure are dominant parameters in determining colloidal particle deposition in porous media. It is often written that an increase in ionic strength causes an increase in the retention of colloidal particles. Indeed, an increase in ionic strength increases colloidal particle aggregation. The influence of this factor has been extensively studied e.g. [9] - [14] .
Porous medium structure is a determining factor for the straining phenomenon. While the geometric criteria for straining depend on the relative size of soil pores to those of the colloidal particles (dcol/dpor). This phenomenon becomes significant when the ratio between the size of the colloidal particles and the median pore size (dcol/dpor) is greater than 0.05 [15] . It has been shown that straining depends not only on the ratio of sizes but also on the irregularity of particles [16] [17] , the concentration of colloidal particles in solution [18] [19] and ionic strength [20] . Porous medium structure also plays an important role in the retention process of colloidal particles in the sense that it can generate areas of low flow where the hydrodynamic effect is less important than the electrostatic attachment [21] .
Much work has been done in recent years to study the effect of porous medium structure on the retention of colloidal particles, but they are mainly carried out in water saturated homogeneous soil. Nevertheless, in general in situ flows occur in unsaturated conditions and are in heterogeneous porous media. In this context, the ability to accurately predict the fate of colloidal particles in a real porous medium is limited by incomplete understanding of the retention mechanisms [18] .
The objective of this paper is to study in laboratory conditions the influence of heterogeneous porous media structure in unsaturated conditions on the retention of colloidal particles using a new nanoparticle fluorescent tracer (SiO2-Au-FluoNPs). The materials used reproduce a common lithofacies present in a predominantly glaciofluvial deposit in the region of Lyon (France). The originality of this research lies in the choice of materials namely porous medium, and the choice of a fluorescent nanotracer specially developed for this study.
2. Theory
The chosen model for colloidal particle transfer was that of non-equilibrium hydrodynamic fractionation of water into two phases mobile and immobile. Transport in the mobile region is described by the convection-disper- sion equation and the exchange of colloidal particles between mobile and immobile regions by diffusion using a first order law for kinetics. In this study, diffusion and dispersion in the immobile phase were ignored. For a stationary hydraulic regime, the colloidal particles transfer equations are written as follows:
 (1)
(1)
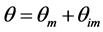 (2)
(2)
 (3)
(3)
where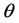 ,
, 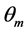 and
and  are respectively the volumetric water content in the mobile and immobile phases; fm and fim are fractions of respectively mobile
are respectively the volumetric water content in the mobile and immobile phases; fm and fim are fractions of respectively mobile  and immobile
and immobile  water;
water; 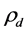 (g∙cm−3) is the dry bulk density; frac the fraction of sites in contact with mobile water; Cm and Cim are respectively colloidal particles concentrations in the mobile and immobile aqueous phases (g∙L−1); Sm and Sim are concentrations of the solid phase in contact with mobile and immobile water in grams of colloidal particles per gram of dry soil (gcol∙gsoil−1); q is the Darcy flow velocity in the mobile phase (cm∙min−1);
(g∙cm−3) is the dry bulk density; frac the fraction of sites in contact with mobile water; Cm and Cim are respectively colloidal particles concentrations in the mobile and immobile aqueous phases (g∙L−1); Sm and Sim are concentrations of the solid phase in contact with mobile and immobile water in grams of colloidal particles per gram of dry soil (gcol∙gsoil−1); q is the Darcy flow velocity in the mobile phase (cm∙min−1); 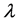 is the dispersivity (cm); and
is the dispersivity (cm); and 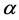 (min−1) is the exchange coefficient of colloidal particles from mobile and immobile phases.
(min−1) is the exchange coefficient of colloidal particles from mobile and immobile phases.
Colloidal particles partition between the liquid and solid phase is described by:
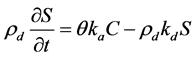 (4)
(4)
where C refers to total resident concentration of colloidal particles in the liquid phase and S total resident concentration of colloidal particles attached to solid phase. Indeed, colloidal particles in solution can attach in solid phase by first-order kinetics (attachment coefficient ka in g∙cm−3) and detach also by first-order kinetics (detachment coefficient kd in min−1).
3. Materials and Methods
The choice of materials was made to replicate a glaciofluvial type soil similar to that observed in an unsaturated zone, in the region of Lyon (France) [22] [23] : that is to say, having the same particle size distribution and the same chemical composition (Table 1). The selected materials are sand (0 - 0.2 cm) and gravel (0.4 - 1.1 cm) with which a bimodal mixture, which was formed in mass fraction 50% - 50% (Figure 1). These materials are known not to be chemically reactive in contact with nanoparticles. The pore size distributions were estimated for the three porous media. For the sand, the sand sieved at 300 mm and the gravel, the pore size distributions were derived from particle size distribution using the Arya and Paris model [24] . Then, for the bimodal porous media, we considered the total porosity as the combination of two porosities, i.e. the micro-porosity related to fine material (sand sieved or not) and the macro-porosity due to the presence of coarse material (gravel). The total pore size distributions were then derived from the combination of the two pore size distributions (micro- and macro-porosities) considering that the micro-porosity occupies 50% of the total porosity since the mixture is made of 50% of sand and 50% of gravel. It must be borne in mind that pore size distributions give pieces of information about both pore size and number of pores but complementary information is needed regarding the characterization of pore geometry or connectivity. The different pore size distributions are discussed with regards to colloidal particles retention.
3.1. Bromide Tracer and Colloidal Particle
The flow tracer chosen is an anionic tracer, bromide ion (Br−). This ion was chosen for certain qualities: it is very soluble, easy to collect, store and analyze and does not degrade. A neutral solution of sodium nitrate (NaNO3) at a concentration of 10−2 M is used for the percolation test. The tracer solution consisted of the neutral solution to which is added potassium bromide (KBr) at a concentration of 10−2 M. The concentration of bromide is measured by an ion chromatograph (ICS 1100, Dionex Thermoscientific, Bannockburn, USA) via electric conductivity detection.
Figure 1. Particle size distribution for the sand and gravel that forms bimodal material (by mixing 50% by mass of the sand and the gravel). The sand and the mixture are then used for leaching column experiments.
Table 1. Chemical composition of three soil types under study, the compound is a bimodal mixture of 50% sand and 50% gravel by mass.
The colloidal particles being studied are nanoparticles (Figure 2) of silica (SiO2-Au-FluoNPs). They are dispersed in aqueous solution, labeled by organic molecules: fluorescein. Each particle is formed of a gold heart about 10 nm in diameter, coated with a layer of polysiloxane (modified silica matrix), into which are grafted, by direct covalent grafting, organic fluorophores. The hydrodynamic diameters of the nanoparticles are between 50 and 60 nm. The nanoparticles are surface grafted with specific functional groups of hydroxyl (OH−) that make mono-dispersed solution, that is to say, they retain their single particle nature in pure water. The concentration of colloidal particles is fixed at 0.2 g∙L−1 in NaNO3 solution (10−2 M), this concentration is sufficient to have an analyzable response after dilution in the column. A UV visible fluorimeter (Cary Eclipse BIO, VARIAN, Santa Clara, USA) is used to determine the concentration of colloidal particles in water. The excitation light is emitted by a UV-visible flash lamp at 495 ± 2.5 nm and emission is around 515 ± 2.5 nm.
3.2. Experimental Set-Up and Experiments
Columns of PVC (Poly Vinyl Chloride) were used, measuring 10 cm in diameter and 30 cm in length (Figure 3). Several columns have been developed: 1) with sand (0 - 0.2 cm), 2) with the bimodal blend (0 - 1.1 cm) and 3) with the same bimodal mixture without its finer particle fraction (0.03 - 1.1 cm). In this text, the sand will be designated by (S), the bimodal mixture (B1) and the sieved bimodal (B2). Glass beads of 0.5 cm in diameter are placed at the bottom and top of the column in a layer of approximately 1.5 cm thick. They provide good distri-
Figure 2. Image of nanoparticles obtained by transmission electronic microscopy (TEM), each particle (gray) with a heart of gold that appears black.
Figure 3. Schematic diagram of leaching experimental set-up.
bution and homogenization of the solution at the inlet and outlet of the column. A filter of 0.45 microns and PVC grids surround the glass beads in order to limit leaching of fine soil particles. The interior of the column is coated with silicone grease before the introduction of materials to limit wall flow. Before use, the materials are dried for 48 h at 60˚C, and then moistened to a mass water content of 7%. The column packing is carried out in layers of 3 cm thick. Each layer is compacted uniformly using a pestle. Good contact between the layers is ensured by roughening a small thickness of the surface prior to deposition of the next layer. The bulk densities of the three types of dry materials S, bimodal B2 and bimodal B1, respectively are 1.70 ± 0.04 g∙cm−3, 1.78 ± 0.04 g∙cm−3 and 1.79 ± 0.04 g∙cm−3. The whole pore volume in each column, noted V0, is 510 mL for the sand, 515 mL for the bimodal B1 and 512 mL for the bimodal B2. This volume V0 includes pore volume between the glass beads, called dead volume, and the pore volume in the material. To ensure the proper conduct of the test, i.e. the establishment of a permanent flow regime, the outflow was measured at regular intervals and compared with the imposed inflow. The total volume of water in the column was measured before and after each test in order to ascertain any changes in saturation. A peristaltic pump imposes a rate of 600 mL∙h−1 (i.e. Darcy velocity 0.13 cm∙min−1) at the input of the column (Figure 3). After the first drops begin to fall, the pump is connected to the outlet of the column to facilitate the water flow and ensure continuous steady flow in the column. A pulse tracer either of Br− solution or colloidal solution is applied once the steady state is reached. A three-way valve allows the continuous switching from one solution to another. Samples were collected at the exit with an automated fraction collector (Gilson, FC204, Middleton, USA) every 6 minutes before determination of bromide and colloidal particles concentrations.
Three tests were performed for each material with a single Darcy velocity of 0.13 cm∙min−1. For each test, after reaching steady state flow, a pulse 2/3 of V0 was applied for bromide or colloidal particle solution. Under these conditions, 9 tests were performed, three for each type of material, namely, one with only the colloidal particles, one with the bromide and one with the colloidal particles and bromide injected simultaneously.
3.3. Moment Method
The moment method and MIM code were used to analyze elution curves of the tracer and colloidal particles. The input signal is either a pulse of bromide solution, of concentration C0,s or a pulse of colloidal particle solution, concentration C0,p of 
The moment of order N is defined by:

with C(t) the concentration of bromide or colloidal particles at the instant t. The solute mass balance, MB is calculated from the moment of order 0:

where 


Two different characteristic times of flow were also estimated. These are the convection time Tm, which is the time taken by the bromide or nanoparticles to cross the mobile volume of water present in the porous medium, and the transfer time TM which is the average exchange time between mobile and immobile phases [25]


where L is column length in cm.
Variance, s2, for assessing spreading magnitude of the elution curve is given by:

3.4. Determination of Model Transfer Parameters
The transfer of bromide and colloidal particles is modeled using Hydrus 1D [26] . This program allows the numerical solution of Equations (1)-(3) for different initial and boundary conditions of the column experiments: i.e. concentration known at entry, zero gradient concentration at column outlet and no initial solute or colloidal particles concentration at time t = 0. Transfer parameters are estimated by the inverse analysis method, by fitting calculated data to experimental data and using the method of non-linear least squares optimization based on the Levenberg-Maquardt algorithm [27] .
When adjusting, dispersivity λ has been considered as an intrinsic hydrodispersive characteristic of soil [28] on the same order of magnitude as the maximum soil particle size of the porous matrix. These data are fixed into Hydrus 1D; inverse analysis of experimental data provides other model parameters.
To determine retention coefficients ka and kd, we assimilate retention to a first-order kinetic rate process S:

where 


4. Results and Discussion
The results are discussed successively in terms of the effect of medium structure on the transfer of the bromide and colloidal particles.
4.1. Tracer Experiments and Flow
The bromide can characterize flow in terms of water fractionation and quantification of hydrodispersive parameters relative to convection and dispersion. Mass balance of bromide in all tests reveals a total restitution at column outlet (Table 2). In all cases, bromide mass balance is above 0.96, the difference of 4% can be explained by the inaccuracy in the determination of bromide concentration. The conservative nature of bromide is fully respected. The retardation factor of bromide, R, is greater than 0.97 while remaining lower than 1, thus validating the use of these anionic molecules to trace out water flow. It may be noted that the low percentage of fine particles (diameter < 0.02 mm) in the materials limits anionic exclusion. Thus, the difference in the retardation factor of 1 is likely related to the presence of a small fraction of water completely isolated from the flow.
The MIM model can adequately model bromide breakthrough curves (Figure 4). The model fit to experimental data validates the proposed approach to describe flow in the column. The model fit compared to the solute breakthrough curves is obtained with a regression coefficient higher than 0.99 and leads to reliable estimations on hydrodispersive parameters (Table 2). The dispersivity obtained is greater than the mean soil particle diameter, but will remain in the same order of magnitude. In unsaturated conditions and in contrast to the saturated conditions, the presence of air pockets in the pore space can make the path more tortuous for water and solutes and thus increase the apparent tortuosity and dispersivity of the medium [35] . The calculated mobile water fraction (Table 2) is larger in the sand than in the bimodal B1 and B2. This proves that the flow is more heterogeneous in bimodal media than in sand. For example, the fraction of mobile water in the sand is 71%; it was 57% in the bimodal medium B1.
This means that, in the sand, the pores are more accessible to flow than in the medium B1 of bimodal particle size where a large volume of pores remains inaccessible to the flow. Indeed, flow is dependent on pore size distribution in the medium. The pore structure of the medium may generate more or less rapid flow areas, smallpores may represent immobile areas where the bromide exchanges by diffusion but does not allow a convec-
Table 2. Hydrodispersive parameters of bromide for the three porous media.
Figure 4. Measured (symbols) and fitted (lines) breakthrough curves of bromide for three media, sand S, bimodal B1 and sieved bimodal B2.
tive flow. The estimated exchange coefficient between mobile and immobile phases is lower in the B1 bimodal medium, which leads to a smaller exchange compared to the other two media (Table 2). This means that the solute takes longer to exchange between the mobile and immobile phases in this medium. Solute exchange time is then significantly higher than the convection time, which justifies that the spread between mobile and immobile water zones is limited and that the flow is actually fractioned. This effect is observed for all three media.
4.2. Transfer and Retention of Colloidal Particles
Breakthrough curves of colloidal particles are asymmetric considering that distribution of pore space is non- uniform and hence produces preferential flows. This observation is made for all three media being studied. It is a characteristic of heterogeneous, dispersive flows [36] . Mass balance of colloidal particles is between 0.69 and 0.96 (Table 3), attesting to irreversible retention of colloidal particles in porous medium.
As conventionally used in transfer modeling [25] [37] [38] and as a first attempt, it was considered that hydrodispersive parameters applied to reactive solutes. The model was then fitted to experimental data by optimizing only the reactive parameters. The hydrodispersive bromide parameters have been used for a first approach to modeling colloidal particle transport and the model fit obtained proved poor. This means that bromide and colloidal particles do not follow the same path. Indeed, the colloidal particles show a very different behavior compared to the bromide. In sand, the mobile water fraction for colloidal particles is 96% while in the case of bromide is 71%. This means that the network of pores visited by colloidal particles is not the same as for bromide. A rapid perception of colloidal particles is observed in the elution curves (Figure 5) Three hypotheses are proposed in literature to explain this phenomenon: 1) colloidal particles have a molecular diffusion coefficient lower than bromide which excludes areas of low flow velocity [39] 2) they can be excluded from a part of porosity where pores size is smaller than colloidal particles [40] , therefore their path is less tortuous; this phenomenon has already been observed in a sandy soils [41] ; and 3), in a pore with a large enough radius, colloidal particles are transported usually through the center of the pore where the flow rates are highest in contrast to solutes which may approach the pore walls [42] . This is qualified as the steric exclusion phenomenon, which explains the rapid flow of colloidal particles. This hydrodynamic effect results in an average velocity of colloidal particles higher than the average carrier fluid velocity [6] [43] ; the latest is also the average velocity of the bromide. These three hypotheses also suggest a reduction of particle hydrodynamic dispersion. However, the tail of the colloidal particle elution curve is greater than that of bromide. This may be due to the remobilization of colloidal particles followed by slow exchange from the immobile to the mobile water phase.
4.3. Effect of Pore Structure on the Transfer of Colloidal Particles
Calculated mobile water fractions (Table 3) show a more heterogeneous colloidal particles transfer in bimodal B1 than in the sand. This remark can also be drawn from analyzing breakthrough curves these being more spread out in the bimodal media B1. The difference in the transfer of the three media can be related to their pore sizes distribution (Figure 6). Sand is characterized by a narrow particle size distribution (Figure 1) favoring a homo-
Figure 5. Colloidal particle experimental elutions: (a) Measured (symbols) and fitted (lines) breakthrough curves for three media, sand S, bimodal B1 and sieved bimodal B2, (b) exemple of injection of colloidal particle without C and with the tracer (C + T).
Table 3. Hydrodispersive and retention parameters of colloidal particles for three porous media; firstly for colloidal particles (C) alone, and secondly, colloidal particles together with the tracer (T + C).
geneous pore size distribution. Thus, water, solutes and colloidal particles are transferred in a medium consisting of capillary pores of comparable size. This configuration generates a homogeneous flow. In contrast, for the bimodal media, bimodal particle size distribution (Figure 1) favors bimodal pore size distributions with the concurrence of small and larger pore sizes (Figure 6) as already suggested by previous studies [24] . This configuration can induce a specific heterogeneous flow. Indeed, small pores, due to their large capillary force tend to easily fill with water while larger pores can drain easily. For B1 bimodal medium, only 75% of total water is involved in colloidal particle transport. In this medium, the finest fraction (0 - 0.03 cm) facilitates the creation of very small pores that promote increased immobile water. In addition, when the pore velocity increases, the mobile fraction of water decreases. This increases the velocity gradient at the interface between mobile and immobile water hampering the exchange of solutes at the immobile/mobile interface. The dependence of flow in relation to the physical characteristics of the media therefore has an effect on the transfer velocity of the colloidal particles.
Despite a less homogeneous flow, the retention of colloidal particles is greater in media of bimodal particle size distribution. Taking for example the tests on colloidal particles without the presence of bromide, mass balance in sand is 0.96, in bimodal B1 is 0.74 and in the bimodal B2 is 0.95. Values of Kd (Table 3) found by fitting
Figure 6. Pore size distributions: cumulative frequencies (FF) for the three porous media (sand S, bimodal B1 and sieved bimodal B2) (a); frequencies (fr) for sand (b) and for the bimodals B1 and B2 (d) and percetanges of pore radius below the two thresholds of 0.5 µm and 12.5 µm.
the experimental data to the model are increasing going from sand to bimodal medium B2 and then to bimodal medium B1. This is probably due to the trapping capacity resulting from pore size distribution. These results are consistent with pore size distributions since, in the sand, the pores are larger than in media of bimodal particle size and therefore the trapping phenomenon is reduced. The Figure 6 presents the cumulative pore size distribution (Figure 6(a)), pore size frequencies (Figure 6(c) and Figure 6(d)) and links this information with two thresholds pore sizes regarding colloidal particles retention. Clearly, the sand contains a smaller pore size. The pore size distribution shows a main mode between 50 and 100 mm (Figure 6(c)). The two bimodal porous media exhibit dual porosities with the first mode corresponding to the sand and the second mode of pore size between 100 mm and 1 mm (Figure 6(d)). Sieving the sand at 300 mm reduces the fraction of the smallest pores (Figure 6(d), bimodal B2 versus B1). We considered that the colloidal particles entrapment was predominant and that in this case the key factor was the ratio between the colloidal particles radius (27.5 mm) and the pore radius (r). Pores able to entrap the colloidal particles were supposed to be the pores small enough, i.e. with a radius that was below the threshold rp,lim with rcol/rp,lim ≥ Rlim. According to a literature review, two thresholds are considered. Herzig et al. [15] considered that a threshold Rlim of 0.05 was sufficient to retain particles. Bradford et al. [18] considered that colloidal particles could aggregate and form packs with an apparent the colloidal particle size larger than the size of the colloidal particles. Then, colloidal particles entrapment could occur even for ratios in pore radius rcol/rp,lim as low as 0.002. Then, we considered the two thresholds leading to two values for maximum pore size: 0.5 and 12.5 mm, respectively for Herzig et al. [15] and Bradford et al. [18] criteria. We then computed the cumulative frequency of pores with radius below the two thresholds 0.5 and 12.5 mm (Figure 6(b)). The comparison of bimodals B1 and B2 regarding pore size is logical. Bimodal B2 has smaller pores and colloidal particle entrapment should logically be smaller. This assumption is in full agreement with experimental data. The sand exhibits the largest fractions of small pores with more than 60% of pores below 12.5 mm and close to 5% of pores smaller than 0.5 mm in radius. For the bimodal B1 and B2, these frequencies fall to around 30% for 12.5 mm and around 3% for 0.5 mm. These results suggest that the sand should entrap much more colloidal particles than the bimodal porous media. Yet experimental results show that colloidal particles entrapment is more significant in the porous media B1.
This information shows that pore size distribution is not the sole key parameter to explain colloidal particles retention. Microstructure is strongly dependent on the geometry of pores and pore connections. This geometrical aspect must be important regarding colloidal particles entrapment as suggested by [44] . In addition, under unsaturated conditions, the geometry of water films around particles is strongly affected by the geometry of pores. Film straining (colloidal particles entrapment by water films and at the interface water-air) must be strongly impacted by the geometry of pores. This suggests that the arrangement of particles in bimodal porous media is favorable to a specific geometry of microporosity and thereby to colloidal particles entrapment.
Microstructure plays a key role regards flow and thus with regards to the transfer of colloidal particles that results from the coupling between flow and retention mechanisms [45] [46] . The degree of flow heterogeneity impacts the access of pollutants to adsorption sites [36] [37] [47] and even the access of colloidal particles to trapping and adsorption sites [45] [46] . In unsaturated conditions, the small pores have a large capillary force that pulls out colloidal particles trapped in constrictions. The presence of air-water interfaces in unsaturated conditions is an additional cause for trapping colloids [34] . Colloidal particles that are weakly attached to the water-solid interface can be drawn to immobile flow zones by hydrodynamic forces [34] [48] . This effect creates a more important colloidal particles concentration in the immobile phase. Microstructure plays both on the hydrodynamic process and on the retention trapping mechanisms, resulting in very significant differences in elution and retention colloidal particles.
4.4. Influence of Potassium Bromide on the Retention of Colloidal Particles
Increasing ionic strength between the solution of colloidal particles and the colloidal solution with bromide directly causes an increase in deposition of colloidal particles (Figure 5(b)). In the sand S, mass balance goes from 0.96 to 0.72, a 25% increase of retention due to the presence of potassium bromide. Several authors have shown the influence of this factor on the retention of colloidal particles e.g. [9] -[14] [20] . Attachment due to ionic strength is partially reversible. When the ionic strength decreases, a part of the colloidal particles can be released. In bimodal B2, decrease of mass balance due to increased ionic strength of the solution proves that retention by increases 20%. In contrast, in the bimodal medium B1, the retention is increased by only 1%. This small increase in retention could be explained by the fact that the effect of straining was already strongly influenced by the structure even with the absence of potassium bromide. Indeed, the colloidal particles under the influence of the ionic strength increase, due to the presence of bromide, can agglomerate. The apparent diameter of the agglomerate increases and the colloidal particles are more easily retained. The agglomeration effect is visible to the sand and bimodal B2 as their pore size distributions did not allow an optimal retention in the absence of bromide. When the colloidal particles are agglomerated, they are thus retained in greater quantity in the sand and in the bimodal B2, reducing the eluted mass at column outlets.
5. Conclusions
In this study, we examined the effect of the structure of three unsaturated porous media on the transport of bromide and colloidal particles. Bromide allows the water flow to be traced and the fluorescent silica nanoparticles (SiO2-Au-FluoNPs) allow the simulation of colloidal particles to transfer. Bromide and colloidal particles break- through curves were correctly modeled by considering the hydrodynamic non-equilibrium and split of water in two regions, mobile and immobile (MIM).
It was observed that bromide flow is closely dependent on medium structure. The hydrodispersive parameters obtained for bromide show that the flow is more heterogeneous in bimodal media than that in sand. The heterogeneous flow in both bimodal media B1 and B2 is due to their structure. These flows have been linked to the microstructure of materials. Within a monomodal-pore structure in terms of pore radius a more homogeneous flow of water was observed into the sand. Another result concerns the application of hydrodispersive parameters on colloidal transfers. Parameters obtained by tracing water flow do not correctly model colloidal particle transport, thus showing that the bromide path in the column is different from that of the colloidal particles.
Colloidal particles undergo irreversible retention during their transportation. Retention increases, going from sand to bimodal B1 and bimodal medium B2. The presence of fine particles favors the presence of very much smaller pores. Thus, despite a heterogeneous flow, porous media with bimodal particle size offer more capacity for colloidal particle retention. The model shows that retention is greater in the immobile region relative to the mobile region particularly for sand and bimodal B1 medium. Capillary forces in unsaturated conditions cause colloidal particles to pass through into the smallest pores because they are more constricted and then promote their blocking. Working in unsaturated conditions seems to increase chances of colloidal trapping at the air-wa- ter interface. As these colloidal particles are loosely attached, they are easily mobilized to immobile zones by hydrodynamic forces. Another factor playing heavily on retention of colloids is the ionic strength of solution. The modification of the ionic strength of the solution due to the presence of potassium bromide produces a 25% decrease in sand mass balance. This effect is related to increase in cluster size of particles formed by aggregation of colloidal particles following the change in ionic strength of particles. They are then more easily trapped in the pores.
These results show that the structure of unsaturated porous media has a strong influence on the retention of colloidal particles and validates the use of the nanoparticles as a new colloidal particle tracer. These nanoparticles, owing to their easy detection and stability in water, open a new way forward in the development of mechanistic studies of colloidal transfer in heterogeneous unsaturated porous media.
Acknowledgements
We would like to thank the Society Nano-H (www.nanoh.com, Saint-Quentin Fallavier, France) for their contribution to nanoparticles development. The practical assistance of Marc Danjean and Thérèse Bastide, and specially in conducting the column experiment, is highly appreciated. The first author received a PhD scholarship from the Government of the Republic of Haiti.
References
- Wiesner, M.R., Lowry, G.V., Alvarez, P., Dionysiou, D. and Biswas, P. (2006) Progress and Research Needs towards Assessing the Risks of Manufactured Nanomaterials. Environmental Science & Technology, 40, 4336-4345. http://dx.doi.org/10.1021/es062726m
- Kretzschmar, R., Borkovec, M., Grolimund, D. and Elimelech, M. (1999) Mobile Subsurface Colloids and Their Role in Contaminant Transport. Advances in Agronomy, 66, 121-193. http://dx.doi.org/10.1016/S0065-2113(08)60427-7
- Fried, J.J. (1975) Groundwater Pollution. Elsevier Scientific, Amsterdam.
- DeNovio, N.M., Saiers, J.E. and Ryan, J.N. (2004) Colloid Movement in Unsaturated Porous Media. Recent Advances and Future Directions. Vadose Zone Journal, 3, 338-351.
- Torkzaban, S., Hassanizadeh, S.M., Schijven, J.F. and van den Berg, H.H.J.L. (2006) Role of Air-Water Interfaces on Retention of Viruses under Unsaturated Conditions. Water Resources Research, 42. http://dx.doi.org/10.1029/2006WR004904
- van der, Lee J., Ledoux, E., de Marsily, G., de Cayeux, M.D., van der Weerd, H., Fraters, B., Doods, J., Rodier, E., Sardin, M. and Hernandez, A. (1994) A Bibliographical Review of Colloid Transport through the Geosphere. Nuclear Science and Technology, European Commission.
- Fang, J., Shan, X.Q., Wen, B., Lin, J.M. and Owens, G. (2009) Stability of Titania Nanoparticles in Soil Suspensions and Transport in Saturated Homogeneous Soil Columns. Environmental Pollution, 157, 1101-1109. http://dx.doi.org/10.1016/j.envpol.2008.11.006
- Solovitch, N., Labille, J., Rose, J., Chaurand, P., Borschneck, D., Wiesner, M.R. and Bottero, J.-Y. (2010) Concurrent Aggregation and Deposition of TiO2 Nanoparticles in a Sandy Porous Media. Environmental Science & Technology, 44, 4897-4902. http://dx.doi.org/10.1021/es1000819
- Compère, F., Porel, G. and Delay, F. (2001) Transport and Retention of Clay Particles in Saturated Porous Media. Influence of Ionic Strength and Pore Velocity. Journal of Contaminant Hydrology, 49, 1-21. http://dx.doi.org/10.1016/S0169-7722(00)00184-4
- Redman, J.A., Walker, S.L. and Elimelech, M. (2004) Bacterial Adhesion and Transport in Porous Media: Role of the Secondary Energy Minimum. Environmental Science & Technology, 38, 1777-1785. http://dx.doi.org/10.1021/es034887l
- Tufenkji, N. and Elimelech, M. (2004) Deviation from Colloid Filtration Theory in the Presence of Repulsive Electrostatic Interactions: Implications to Microbial Transport. National Meeting—American Chemical Society Division of Environmental Chemistry, 44, 773-774.
- Torkzaban, S., Bradford, S.A., van Genuchten, M.Th. and Walker, S.L. (2008) Colloid Transport in Unsaturated Porous Media: The Role of Water Content and Ionic Strength on Particle Straining. Journal of Contaminant Hydrology, 96, 113-127. http://dx.doi.org/10.1016/j.jconhyd.2007.10.006
- Jacobs, A., Lafolie, F., Herry, J.M. and Debroux, M. (2007) Kinetic Adhesion of Bacterial Cells to Sand: Cell Surface Properties and Adhesion Rate. Colloids and Surfaces B—Biointerfaces, 59, 35-45. http://dx.doi.org/10.1016/j.colsurfb.2007.04.008
- Majdalani, S., Michel, E., Di Pietro, L., Angulo-Jaramillo, R. and Rousseau, M. (2007) Mobilization and Preferential Transport of Soil Particles during Infiltration: A Core-Scale Modeling Approach. Water Resources Research, 43.
- Herzig, J.P., Leclerc, D.M. and LeGoff, P. (1970) Flow of Suspension through Porous Media: Application to Deep Filtration. Industrial & Engineering Chemistry Research, 62, 8-35. http://dx.doi.org/10.1021/ie50725a003
- Tufenkji, N. and Elimelech, M. (2004) Deviation from the Classical Colloid Filtration Theory in the Presence of Repulsive DLVO Interactions. Langmuir, 20, 10818-10828. http://dx.doi.org/10.1021/la0486638
- Torkzaban, S., Kim, H.N., Simunek, J. and Bradford, S.A. (2010) Hysteresis of Colloid Retention and Release in Saturated Porous Media during Transients in Solution Chemistry. Environmental Science & Technology, 44, 1662-1669. http://dx.doi.org/10.1021/es903277p
- Bradford, S.A. and Bettahar, M. (2006) Concentration Dependent Transport of Colloids in Saturated Porous Media. Journal of Contaminant Hydrology, 82, 99-117. http://dx.doi.org/10.1016/j.jconhyd.2005.09.006
- Foppen, J.W., van Herwerden, M. and Schijven, J. (2007) Transport of Escherichia coli in Saturated Porous Media: Dual Mode Deposition and Intra-Population Heterogeneity. Water Research, 41, 1743-1753. http://dx.doi.org/10.1016/j.watres.2006.12.041
- Shen, C.Y., Huang, Y.F., Li, B.G. and Jin, Y. (2008) Effects of Solution Chemistry on Straining of Colloids in Porous Media under Unfavorable Conditions. Water Resources Research, 44, Published Online. http://dx.doi.org/10.1029/2007WR006580
- Bradford, S.A., Torkzaban, S., Leij, F.J., Šimůnek, J. and van Genuchten, M.T. (2009) Modeling the Coupled Effects of Pore Geometry and Velocity on Colloid Transport and Retention. Water Ressources Research, 45, Published Online.
- Bien, L.B., Predelus, D., Lassabatere, L., Winiarsky, T. and Angulo-Jaramillo, R. (2013) Combined Effect of Infiltration, Capillary Barrier and Sloping Layered Soil on Flow and Solute Transfer in a Heterogeneous Lysimeter. Open Journal of Modern Hydrology, 3, 138-153. http://dx.doi.org/10.4236/ojmh.2013.33018
- Goutaland, D., Winiarski, T., Dubé, J.S., Bièvre, G., Buoncristiani, J.F., Chouteau, M. and Giroux, B. (2008) Hydrostratigraphic Characterization of Glaciofluvial Deposits Underlying an Infiltration Basin Using Ground Penetrating Ra- dar. Vadose Zone Journal, 7, 194-207. http://dx.doi.org/10.2136/vzj2007.0003
- Arya, L.M. and Paris, J.F. (1981) A Physicempirical Model to Predict the Soil Moisture Characteristic from Particle- Size Distribution and Bulk-Density Data. Soil Science Society of America Journal, 45, 1023-1030. http://dx.doi.org/10.2136/sssaj1981.03615995004500060004x
- Hanna, K., Lassabatere, L. and Bechet, B. (2012) Transport of Two Naphtoic Acids and Salicylic Acid in Soil: Experimental Study and Empirical Modeling. Water Research, 46, 4457-4467.
- Šimůnek, J. and van Genuchten, M.T. (2008) Modeling Nonequilibrium Flow and Transport Processes Using Hydrus Version 4.0. HYDRUS 1D. Department of Environmental Sciences, University of California, Riverside, 7, 782-797.
- Marquardt, D.W. (1963) An Algorithm for Least-Squares Estimation of Nonlinear Parameters. Journal of the Society for Industrial and Applied Mathematics, 11, 431-441. http://dx.doi.org/10.1137/0111030
- Bear, J. (1972) Dynamics of Fluids in Porous Media. American Elsevier, New York.
- Brusseau, H.L., Jessup, R.E. and Rao, P.S.C. (1989) Modeling the Transport of Solutes Influenced by Multiprocess Nonequilibrium. Water Resources Research, 25, 1971-1988. http://dx.doi.org/10.1029/WR025i009p01971
- Selim, H.M., Ma, L. and Zhu, H. (1999) Predicting Solute Transport in Soils: Second-Order Two-Site Models. Soil Science Society of America Journal, 63, 768-777. http://dx.doi.org/10.2136/sssaj1999.634768x
- Bradford, S.A., Bettehar, M., Šimůnek, J. and van Genuchten, M.T. (2004) Straining and Attachment of Colloids in Physically Heterogeneous Porous Media. Vadose Zone Journal, 3, 384-394. http://dx.doi.org/10.2113/3.2.384
- Pot, V., Šimůnek, J., Benoit, P., Coquet, Y., Yra, A. and Martínez-Cordón, M.J. (2005) Impact of Rainfall Intensity on the Transport of Two Herbicides in Undisturbed Grassed Filter Strip Soil Cores. Journal of Contaminant Hydrology, 81, 63-88. http://dx.doi.org/10.1016/j.jconhyd.2005.06.013
- Gargiulo, G. Bradford, S.A. Šimůnek, J. Ustohal, P., Vereecken, H. and Klumpp, E. (2007) Bacteria Transport and Deposition under Unsaturated Conditions: The Role of the Matrix Grain Size and the Bacteria Surface Protein. Journal of Contaminant Hydrology, 92, 255-273.
- Gargiulo, G. Bradford, S.A. Šimůnek, J. Ustohal, P., Vereecken, H. and Klumpp, E. (2008) Bacteria Transport and Deposition under Unsaturated Conditions: The Role of Water Content and Bacteria Surface Hydrophobicity. Vadose Zone Journal, 7, 406-419. http://dx.doi.org/10.2136/vzj2007.0068
- Torkzaban, S., Tazehkand, S.S., Walker, S.L. and Bradford, S.A. (2008) Transport and Fate of Bacteria in Porous Media: Coupled Effects of Chemical Conditions and Pore Space Geometry. Water Resources Research, 44, Published Online. http://dx.doi.org/10.1029/2007WR006541
- Sardin, M., Schweich, D., Leij, F.J. and van Genuchten, M.T. (1991) Modeling the Nonequilibrium Transport of Linearly Interacting Solutes: A Review. Water Resources Research, 27, 2287-2307. http://dx.doi.org/10.1029/91WR01034
- Lassabatere, L., Spadini, L., Delolme, C., Février, L., Cloutier, R.G. and Winiarski, T. (2007) Concomitant Zn-Cd and Pb Retention in a Carbonated Fluvio-Glacial Deposit under Both Static and Dynamic Conditions. Chemosphere, 69, 1499-1508. http://dx.doi.org/10.1016/j.chemosphere.2007.04.053
- Hanna, K., Rusch, B., Lassabatere, L., Hofmann, A. and Humbert, B. (2010) Reactive Transport of Gentisic Acid in a Hematite-Coated Sand Column: Experimental Study and Modeling. Geochimica et Cosmochimica Acta, 74, 3351-3366. http://dx.doi.org/10.1016/j.gca.2010.03.022
- Reimus, P.W., Robinson, B.A., Nuttall, H.E. and Kale, R. (1995) Simultaneous Transport of Synthetic Colloids and Nonsorbing Solute through Single Saturated Natural Fractures. Materials Research Society Symposium Proceedings, 353, 363-370. http://dx.doi.org/10.1557/PROC-353-363
- Sirivithayapakorn, S. and Keller, A. (2003) Transport of Colloids in Saturated Porous Media: A Pore-Scale Observation of the Size Exclusion Effect and Colloid Acceleration. Water Resources Research, 39, Published Online. http://dx.doi.org/10.1029/2002WR001583
- Bradford, S.A., Simunek, J., Bettahar, M., van Genuchten, M.T. and Yates, S.R. (2003) Modeling Colloid Attachment, Straining, and Exclusion in Saturated Porous Media. Environmental Science & Technology, 37, 2242-2250. http://dx.doi.org/10.1021/es025899u
- Powelson, D.K., Gerba, C.P. and Yahya, M.T. (1993) Virus Transport and Removal in Wastewater during Aquifer Re- charge. Water Research, 27, 583-590. http://dx.doi.org/10.1016/0043-1354(93)90167-G
- Keller, A.A. and Auset, M. (2007) A Review of Visualization Techniques of Biocolloid Transport Processes at the Pore Scale under Saturated and Unsaturated Conditions. Advances in Water Resources, 30, 1392-1407. http://dx.doi.org/10.1016/j.advwatres.2006.05.013
- Li, X., Scheibe, T.D. and Johnson, W.P. (2004) Apparent Decreases in Colloid Deposition Rate Coefficient with Distance of Transport under Unfavorable Deposition Conditions: A General Phenomen. Environmental Science & Techno- logy, 38, 5616-5625. http://dx.doi.org/10.1021/es049154v
- Lamy, E., Lassabatere, L., Bechet, B. and Andrieu, H. (2010) Flow and Colloidal Transfer in a Dual Porosity Medium. La Houille Blanche, 86-92. http://dx.doi.org/10.1051/lhb/2010022
- Lamy, E., Lassabatere, L., Bechet, B. and Andrieu, H. (2013) Effect of a Nonwoven Geotextile on Solute and Colloid Transport in Porous Media under Both Saturated and Unsaturated Conditions. Geotextiles and Geomenbranes, 36, 55- 65. http://dx.doi.org/10.1016/j.geotexmem.2012.10.009
- Lassabatere, L., Winiarski, T. and Galvez-Cloutier, R. (2004) Retention of Three Heavy Metals (Zn, Pb, and Cd) in a Calcareous Soil Controlled by the Modification of Flow with Geotextiles. Environmental Science & Technology, 38, 4215-4221. http://dx.doi.org/10.1021/es035029s
- Johnson, W.P., Tong, M. and Li, X. (2007) On Colloid Retention in Saturated Porous Media in the Presence of Energy Barriers: The Failure of Alpha, and Opportunities to Predict Eta. Water Resources Research, 43, Published Online. http://dx.doi.org/10.1029/2006WR005770








