Journal of Water Resource and Protection
Vol. 3 No. 12 (2011) , Article ID: 16400 , 9 pages DOI:10.4236/jwarp.2011.312098
Assessing the Influence of Global Climate and Anthropogenic Activities on the Water Balance of an Andean Lake
1Universidad de Antioquia, Grupo GAIA, Medellín, Colombia
2Department of Hydrology and Water Resources, The University of Arizona, Tucson, USA
E-mail: jecanon@udea.edu.co
Received September 27, 2011; revised October 28, 2011; accepted November 28, 2011
Keywords: Water Balance, Andean Lakes, Climate Teleconnections
ABSTRACT
Tropical regions along the Andean Cordillera face an uncertain future as mountain lakes and snow peaks exhibit receding trends associated with factors such as climatic precursors and local anthropogenic activities. Tota, the largest mountain lake in the Colombian Andes, exemplifies the role played by these factors on the lake's hydrologic evolution. A monthly water balance in Tota Lake was performed using available hydrological information from 1958 to 2007 to address interannual and multiannual level fluctuations associated with human activities and climatic precursors. The balance shows that net water uses fluctuated around 2 m3/s during this period with a pattern that, although constrained during years of severe decline in lake levels, is able to explain most of the multiannual decaying trend of 1.5 cm/year in the last 50 years. The lake’s naturalized levels were used to determine the influence of climate precursors on the lake evolution. Using Multichannel Singular Spectrum Analysis (M-SSA), significant five-year ENSO and 20-year PDO related quasi-oscillations were detected, explaining 54% of the variance associated with mean annual naturalized level fluctuations. ENSO is markedly in-phase with lake levels, with critical declines associated with low precipitation and high evaporation rates during El Niño years, whereas the PDO signal exhibits a phase opposition with lake levels, with low naturalized levels during a positive PDO phase and high levels during a negative PDO phase (an important result to consider given the current cooling trend of the PDO signal).
1. Introduction
Countries in tropical and subtropical regions, as along the Andean Cordillera in South America, are facing the depletion of important water bodies such as mountain lakes and snow peaks that exhibit receding trends associated with both global climate factors and local anthropogenic activities [1,2]. The understanding of how these factors affect the storage in these water bodies is crucial for the communities that depend on them for their survival. In this paper, we study the water balance of the largest natural mountain lake in Colombia, the Tota Lake, over the past 50 years. The lake has experienced a continuous descending trend in its seasonal levels associated with sustained extractions—for irrigation, industry, and urban supply—and climate forcing mechanisms.
Tota is located at 3015 masl in the eastern branch of the Andean Cordillera, between 5˚30' and 5˚40' North latitude and 72˚50' and 73˚ East longitude (Figure 1). The lake is a natural reservoir of glacial origin with an area of 60 km2 and an average depth of 30 m. The entire basin encompasses a total area of 201 km2 and its natural outflow gives origin to the Upía River, a tributary of the Orinoco. The lake is also the main source for irrigation within the basin and supplies the urban and industrial needs of more than 200,000 people in ten municipalities.
Reference [3] made the first hydrologic assessment of the lake, the results of which were adopted as a reference for water management in the basin for 20 years. According to this study, the expected uses of water were projected to be 1.6 m3/s by 2010 and 2.9 m3/s by 2030 (as will be shown later, these projections were significantly below the mean derivations calculated in the present assessment). Other studies in the basin included a land use assessment [4], which determined agriculture (primarily dedicated to onion, potato, and cereals) to be the main economic activity followed by cattle growing and fishery. At present, the expansion of the agricultural frontier toward the wetlands along the lake’s shoreline is one of the major conservation issues faced by local authorities. Reference [5] performed an approximate mass water balance showing that the levels in the lake are directly affected by precipitation and evaporation cycles, and that more emphasis should be given to determining flows derived from the lake to meet human requirements. The study also reviewed the main civil works that control and convey water for irrigation, industry and urban supplies, highlighting the derivation tunnel at Cuitiva (with a capacity of 0.9 m3/s) and the spillway located at El Desaguadero, in the Upía basin at a spill level of 3015 masl (see Figure 1).
The continuous level descent experienced by the lake in the 1990s and the uncertainty about the actual factors driving such drawdown motivated the interest for this new water balance assessment to determine the influence of variables such as groundwater outflows, anthropogenic activities and climate precursors on the storage fluctuations. Regarding the groundwater contributions, an isotopic balance of 180 and 2H performed between September of 1999 and November of 2000 showed no significant groundwater outflows from the lake [6].
To study the lake fluctuations as a result of anthropogenic activities and the associations with climate precursors we performed a water balance based on hydrological time series of precipitation, stream discharges and evaporation, adopting overall rainfall-runoff and tank evaporation coefficients as calibration parameters. Based on the results of the balance, we developed a Multichannel Singular Spectrum Analysis (M-SSA) to determine common
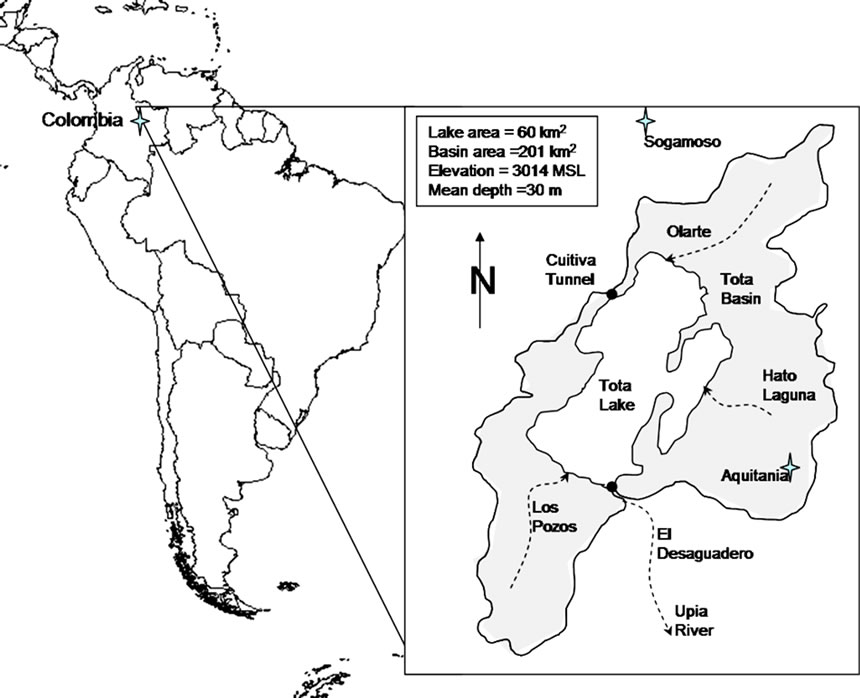
Figure 1. Tota Lake location and major features.
oscillatory responses among the normalized values of the monthly naturalized lake levels, the Bivariate ENSO Timeseries (BEST) [7], and the Pacific Decadal Oscillation (PDO) [8].
2. Hydrology of the Basin
2.1. Precipitation and Evaporation in the Basin
Rainfall and evaporation series are monomodal with higher precipitations (lower evaporation rates) occurring between June and August. The box and whisker plots of rainfall and evaporation monthly averages in Figure 2 show the negative correlation between these two series (r = –0.58). For the series of monthly precipitation a normal distribution was adopted starting from the first two statistical moments as  ,where Pi is the rainfall expected in the month i, mi is the mean multiannual rainfall value at month i, si is the standard deviation of the month i, and z is a standard normal variable with mean zero and unit variance.
,where Pi is the rainfall expected in the month i, mi is the mean multiannual rainfall value at month i, si is the standard deviation of the month i, and z is a standard normal variable with mean zero and unit variance.
The basin has a mean multiannual relative humidity (RH) of 82%. The RH values increase slightly to 90% during the rainy season in June and decrease to 70% during the dry season, mainly in January. Both evaporation and relative humidity were expressed by means of a normal function similar to the one adopted for precipitation.
Evaporation measurements were corrected by a coefficient calibrated in the balance model as will be described later. Thiessen polygons were used also to calculate aggregated values of precipitation and evaporation according to the length of records available from different stations within the basin.

Figure 2. Box and Whisker diagrams of (a) monthly evaporation (mm), (b) rainfall over the basin (mm), and (c) average monthly inflows to the lake (m3/s).
2.2. Rainfall-Runoff Coefficients
The mean monthly discharges to the lake are shown in Figure 2(c). On an individual basis, the discharges at Tobal River, which drains the waters of the municipality of Aquitania on the east side of the lake and runs over relatively impervious strata, are high compared to those of Hato Laguna and Olarte streams, the other two important inflows to the lake. The general inflow hydrograph from the streams that drain towards the lake was calculated with datasets from 1990 to 1997. An aggregate flow from minor streams (Donsiquirá, Pérez, Puerta, Dayto and Llano Alarcón) equivalent to 0.32 m3/s on annual average for the same period was also included in the calculations.
As in the case of the discharges at Hato Laguna, the other streams show monomodal responses associated with precipitation, exhibiting peak flows between June and August. The discharge of the rivers Olarte and Tobal in particular are higher during the rainy season, supporting the idea of a lack of baseflow during dry months, which is characteristic of seasonal streams with rapid responses to rainfall episodes.
Monthly comparisons of the relationship between basin precipitation and the corresponding flows to the lake determined that in January and February the baseflow effect prevails on streams such as Hato Laguna and Tobal, with rainfall-runoff coefficients greater than one, whereas rainfall-runoff coefficients oscillate around 0.5 in subsequent months (see Table 1).
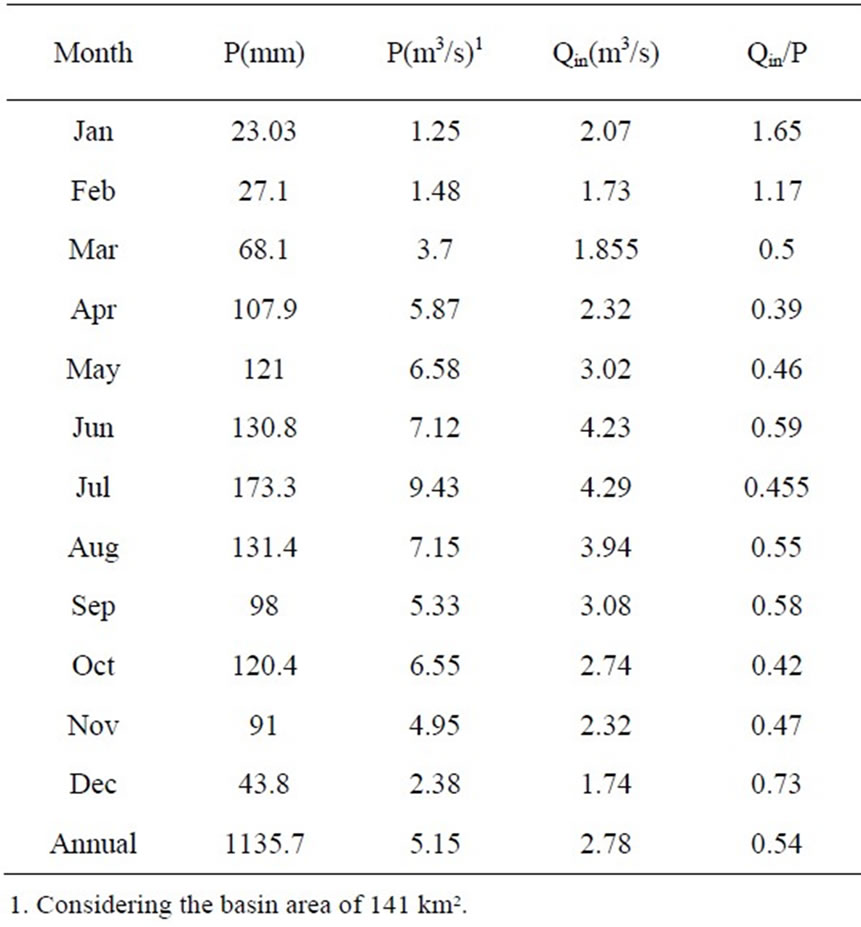
Table 1. Rainfall-runoff monthly coefficients.
The average annual rainfall-runoff coefficient is 0.54. It is assumed that an important part of the remaining 46% either evapotranspires in the course of the same month or infiltrates to surge again as springs during dry months.
2.3. Rainfall, Evaporation and Monthly Differential Changes in Lake Levels
Figure 3 illustrates Tota lake monthly level fluctuations over the last fifty years (from 1958 to 2004). This information is used to determine flows derived from the lake, based on the water balance equation. The differential changes on mean monthly levels registered in the lake are closely related to rainfall and evaporation values as illustrated in Figure 4 (El Niño events have been included as dashes at the bottom of the graph for comparison purposes). Notice that the main differential changes in lake levels have occurred during years in which El Niño was considered severe in the region.
Notice also the good correlation between rainfall peaks and the major differential monthly level increments (0.68), as well as between evaporation peaks and the major differential monthly level downdrafts (–0.52). An equally important correlation (0.70) is observed between differential monthly level changes and monthly inputs given by (P-E). These results are relevant for the analysis of the effects of evaporation rates in the monthly balance (other variables such as the derived flows for human consumption may also explain part of the correlation residue).
The mean monthly level series in Figures 3 and 4 exhibit the following important features:
- For the magnitude of the changes, the year 1998 and the period between 1972 and 1977 may be considered critical descents. Other years with extreme low levels were 1961, 1984-1985, and 1990-1992. The levels have experienced a favorable recovery since 1999. Notice also that strong level drops have occurred at 15-year intervals, in 1961, 1975 and 1990.
- A five-year fluctuation can be inferred from a 12- month moving average of the levels that filters the observed seasonal effects and suggests the ENSO influence, as will be analyzed in section 5.
- Pronounced differential monthly level downdrafts (Figure 4) have also coincided approximately with some El Niño episodes in 1965-1966, 1970, 1972- 1975, 1984-1986, 1990-1992, and 1997-1998.
- The linear decaying trend of the levels in the last fifty years, with a depletion rate equivalent to 1.5 cm/year from 1958 to 2004 is deduced from the slope of the best fit line of the levels during the entire period. It stands out that, starting from the critical drop of 1975, the lake was not able to recover the levels of previous years until 1999, which is significant considering the water management policies adopted in Tota since 1978. A year after the critical descent of 1998, the lake had a notorious recovery and has kept levels similar to those of the 1980s till 2004.

Figure 3. Monthly mean levels of the lake, 12-month moving average and linear trend of annual levels.

Figure 4. Monthly differential level changes and monthly rainfall and evaporation series.
3. Proposed Balance
Monthly balances are used mainly to simulate and to predict monthly runoff values to reconstruct the hydrological history of the basins; to determine the impact of climatic changes in the environment; and to assess the seasonal and geographical patterns of water supply for different purposes [9]. In principle, monthly water balances may be formulated in simple terms, using a few sets of parameters (i.e. soil field capacity and evapotranspiration coefficients) to accurately describe water flows in the basin. Since the rainfall-runoff relationship was appropriately identified in the basin and the measured evaporation has a relatively long and reliable record, we developed the monthly water balance based on two parameters: the seasonal rainfall-runoff coefficient and the correction factor for evaporation measured in a class A tank.
The inflows from different streams to the lake are estimated as a fraction of the monthly rainfall that becomes runoff, while the residue is considered part of the ground storage that evapotranspires or finally flows back to the lake. The derived flow is considered on a monthly basis to achieve the corresponding balance. The balance is performed to fit both the levels recorded at the monthly scale (including the linear decay trend) and the differential changes between consecutive months from 1958 to 2004 to encompass the available datasets. The equations involved in the calculations are nonlinear, since the derived flows are included as unknowns to be solved. The sequence of calculations is described below:
1) The initial level (h0) and volume (V0) in the lake are established for the first month in the calculations (using the level-capacity curve adopted from [5].
2) Averaged values of total rainfall Pt and Evaporation Et for the month t are calculated using Thiessen polygons. A correction factor ki is applied to the values of tank A evaporation such that Et = ki Et.
3) Calibrate the parameters considered in the balance as follows:
• Assume a monthly rainfall-runoff coefficient Ct, applied to the rainfall Pt in the basin (141 km2) to calculate the monthly discharge Qt = Ct Pt. To define Ct a single selected value C is affected by a periodic function (1 + AC*cos(2pt/12)), such that larger coefficients are obtained during dry months (October-March) and smaller during wet ones, maintaining an annual average value of C of approximately 0.54, as determined from the rainfallrunoff analysis. AC is a coefficient that fits the values of Ct in Table 1. The coefficient C is calibrated during the process.
• The fraction of precipitation that does not become runoff is temporarily stored in the basin as a residue Rt = (1 – Ct) Pt.
• Monthly mean rainfall values Pi directly over the lake (60 km²) are not affected by any coefficient.
4) The proportion of the stored residue Ri, expressed in volume, that is lost as evapotranspiration is calculated as follows:
• When Abasin (1 – Ct) Pt + Rt – 1 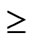 Et Abasin, all the evapotranspiration is covered by the accumulated residue and Vt = Vt – 1 + Abasin Ct Pt + Alake Pt – Et – Alake – VDt, with VDt = derivated volume in month t.
Et Abasin, all the evapotranspiration is covered by the accumulated residue and Vt = Vt – 1 + Abasin Ct Pt + Alake Pt – Et – Alake – VDt, with VDt = derivated volume in month t.
• When Abasin (1 – Ct) Pt + Rt – 1 < Et Abasin, evapotranspiration exceeds the volume of the accumulated residue and Vt = Vt–1+ Abasin Ct Pt + Alake Pt – (Et + Eexcess) Alake – VDt, where Eexcess is the excess of evaporation at month t.
5) The derived flow QDt at each month is determined in a way that all the calculated volumes and differential changes in storage are within 1% error respect to the measured values. The resulting balance is then:
6) 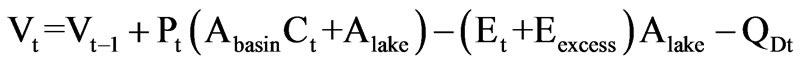
7) Calculate fitting errors and the sum of mean square errors for volumes and differential changes in storage as eV(%) = 100(Vmeas. – Vcalc.)/Vmeas.
8) Chose a new set of parameters at step 3 and repeat steps 4 to 6 to determine the sensibility of the balance to the coefficients and to calibrate the water balance by minimizing the sum of mean square errors. Level (volume) fitting and derived flows (QD) were evaluated by visual inspection in addition to minimizing the sum of mean square errors.
As expected, the values of the coefficient C that better fit the levels of the last fifty years oscillate between 0.50 and 0.55. The level fittings and changes of storage achieved with the balance are satisfactory given that only two parameters, the factor of correction of the evaporation and the rainfall-runoff coefficient C, were considered in the calibration. In addition to the adjustments it was verified that the linear decay trend is the same for both the historic and the calculated values.
Figure 5 compares the mean monthly levels calibrated to those measured. The adjustment was especially good for values recorded after 1978, when information from gauge stations at Olarte, Las Cintas, and Potrerito became available. This result is important in recommending a rational and efficient use of the meteorological information, since efforts may be concentrated on maintaining these three stations in good operating conditions.
Derived flows, shown in Figure 6, are consistent with mean annual values measured at CORPOBOYACA (the regional entity in charge of environmental management and with jurisdiction over the basin). The calculated values are above projections made by [3] but close to estimates made by [5], with an average outflow of 2 m3/s and a small increasing linear tendency between 1958 and 2004.
Two important results emerge from the analysis of Figures 5 to 7: during the period of the most critical level descent registered in the lake (1973-1977), human consumption was not the decisive factor while the evaporation had a remarkable impact on the depletion as it is shown by the residuals for the same period (in fact, consumption stayed within the limits allowed and it even diminished in 1977). Conversely, the balance during 1998-1999 shows the direct effect of consumption on the drastic drawdown and posterior recovery of lake levels. These two outcomes indicate the combined response of the lake as a system to the effects of climate and human intervention.
Another important consideration that arises from the

Figure 5. Measured and calculated Tota lake levels.

Figure 6. Monthly derived flows QD from the lake (m3/s).

Figure 7. Monthly cumulative water residues according to the balance.
series of derived flows shown in Figure 6 deals with the minimum values required to meet the balance. From the estimates, it is not apparent that an outflow may be directly attributed to infiltration losses, since residential use may explain the 0.4 m3/s of minimum consumption. Therefore, the infiltration rate is very low when compared with estimates proposed by [3,5,10]. These results are in agreement with the isotopic balance by [6], which indicates that groundwater outflows are not significant in the basin.
From a practical viewpoint, the calculation of derived flows (QD) by using the balance allows the local entities responsible for distributing the water to estimate the consumption derived during the year based primarily on hydrological information regarding rainfall, evaporation, and lake levels. After doing the balance, the naturalized lake levels are calculated by adding the derived volumes (VD) to the lake volumes at each month t.
4. Influence of Climate Precursors
The influence of global climate precursors in Tota is addressed via multichannel singular spectrum analysis (MSSA) of the annual normalized series of the lake’s naturalized levels, the bivariate ENSO signal [7] and the Pacific Decadal Oscillation [8]. The connection of these indices with the climatology of the Colombian Andes has been previously studied by [11]. References [12,13] describe the use of M-SSA to identify low frequency associations among different hydrologic variables and indices. References [14,15] provide a detailed mathematical framework of the M-SSA. A Singular Value Decomposition of the three series (channels) was performed, using a convolution window of 25 years, to obtain the percentage of variance explained by significant eigenvalues (above red noise series) and to detect pairs of eigenvectors working in quadrature (phase), which would explain common oscillations of the evaluated series with frequencies of oscillation within the 25 year window. The significant eigenvectors were then reconstructed to compare with the original series.
Figure 8 shows the results of applying M-SSA to the three series considered in their mean annual values (naturalized levels were normalized before the analysis). A significant percentage of the variance, up to 54% over red noise signal, is explained by the first six eigenvectors which represent low frequency oscillation modes at five years (ENSO related) and 20 years (PDO related). The reconstructed components from the first six significant eigenvectors clearly resemble the trends of the original signals, indicating a markedly opposite phase between PDO and the lake levels in which a positive PDO phase coincides with low mean annual levels whereas a negative PDO phase coincides with high mean annual levels. This result corroborates similar findings by [11], suggesting negative correlations between the PDO signal and precipitation series in the Northern Andean region.
5. Conclusive Remarks
Tota lake levels are influenced by unimodal climatic patterns in the precipitation and evaporation. As a conse-
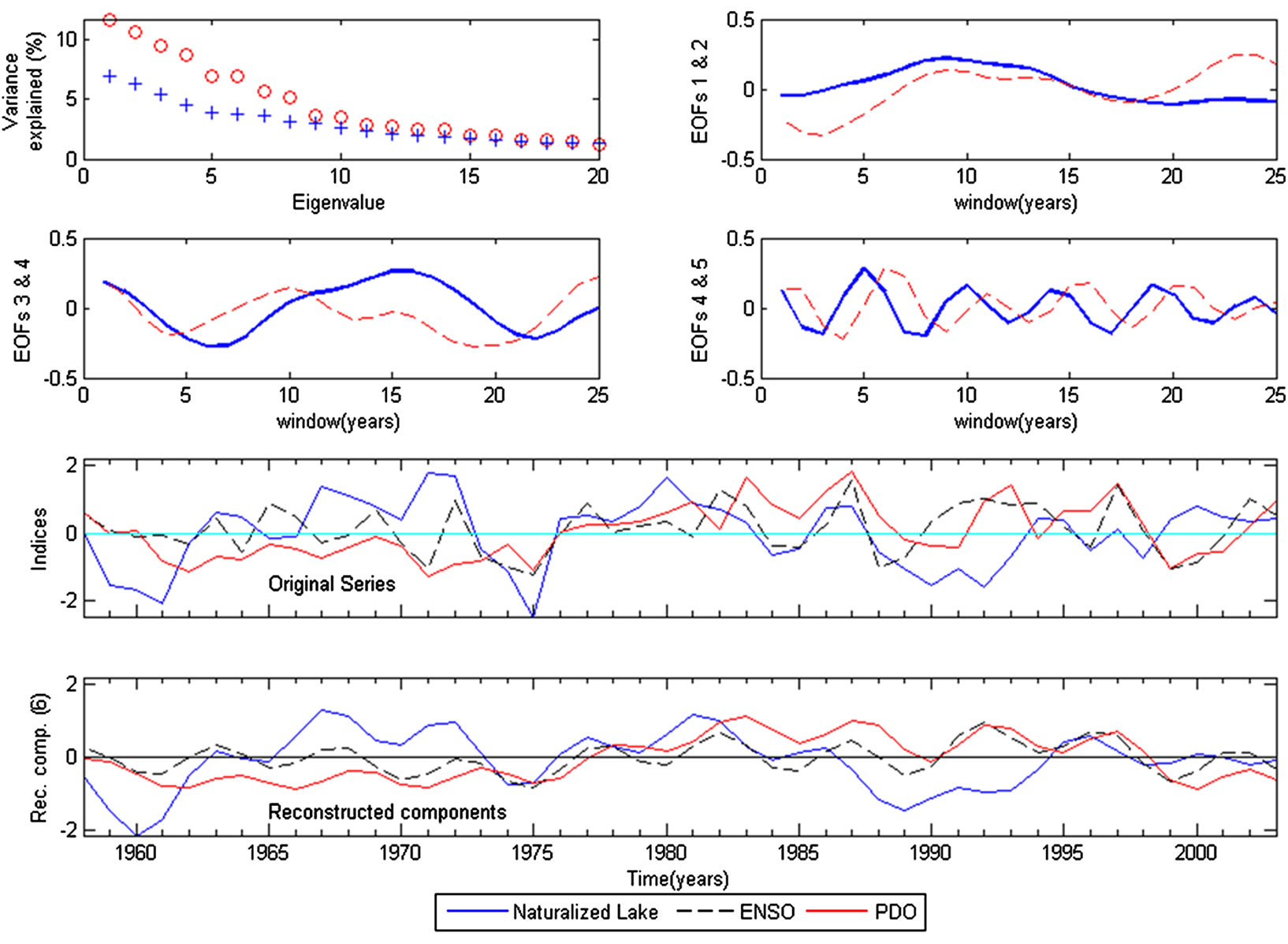
Figure 8. M-SSA analysis of common oscillations among ENSO, PDO and normalized values of Tota Lake naturalized levels.
quence of this influence, a seasonal fluctuation occurs in which low levels correspond to dry months (between November and March) and high levels to wet months (between April and October). Anthropogenic activities modify this annual cycle by accentuating monthly level variations, especially during dry months when demands increase.
The water balance considered two spatially aggregated parameters: the rainfall-runoff coefficient and the evaporation correction factor. The ranges in which these coefficients produced the best adjustments were between 0.50 and 0.55 for the former and between 0.75 and 0.80 for the later.
The water balance indicates that anthropogenic activities take full advantage of the available water in the lake at any time, overexploiting the resource during years of relative abundance and restricting usage during severe descents. The derived flows calculated in this study are 2 m3/s on average, with a maximum of 4 m3/s and a minimum of 0.50 m3/s. The average value is well above initial projections made by [3], indicating an overexploittation in the long run that has been sporadically constrained during periods of severe drawdown. Supply restrictions during sharp declines are likely to be conesquence of hydraulic controls exerted by the derivation tunnel that supplies the Sogamoso Aqueduct and the spillway located at El Desaguadero. Consumptive uses, on the other hand, occur within the basin and their flows eventually return to the lake.
In a multiannual scale, the lake exhibit a statistically significant correlation with global climate mechanisms associated with ENSO and PDO signals that affects levels at intervals of five and 20 years, respectively. The critical descent episodes registered in 1972-1975, 1984- 86, 1990-1992, and 1997-1999 were associated with a decrease in precipitation and an increase in evaporation rates during El Niño years. A remarkable contrast between the PDO signal and the mean annual naturalized lake levels indicates that negative phases of PDO are likely associated with increments in the lake levels whereas positive phases of PDO are related to descents in the naturalized lake levels. It is therefore expected that, under the event of a current transition to a negative phase of the PDO signal, the lake would exhibit an increase in its naturalized levels. This does not necessarily means that observed levels will increase, since derivations (QD) also accentuate the intra and interannual level fluctuations.
6. Acknowledgements
The authors thank CORPOBOYACA for supplying the meteorological and limnological information necessary for this study.
REFERENCES
- G. Casassa, W. Haeberlib, G. Jones, G. Kaser, P. Ribstein, A. Rivera and C. Schneider, “Current Status of Andean Glaciers,” Global and Planetary Change, Vol. 59, No. 1- 4, 2007, pp. 1-9. doi:10.1016/j.gloplacha.2006.11.013
- M. Vuille, B. Francou, P. Wagnon, I. Juen, G. Kaser, B. Mark and R. Bradley, “Climate Change and Tropical Andean Glaciers: Past, Present and Future,” Earth-Science Reviews, Vol. 89, No. 3-4, 2008, pp. 79-96. doi:10.1016/j.earscirev.2008.04.002
- Hidroestudios, “Tota Lake Watershed Management and Conservation Assessment,” Consultant Final Report, Regional Autonomous Corporation CAR, FONADE, Bogotá, 1978.
- IGAC, “Estudio General de Suelos de Los Municipios de Aquitania, Cuítiva, Firavitoba, Iza, Monguí, Nobsa, Sogamoso, Tibasosa, Tópaga y Tota,” Institutional Report, Departamento de Boyacá, Bogotá, 1980.
- P. Laserna, “Implementing Tota GIS Management Software,” Master’s Thesis, Universidad de Los Andes, Bogotá, 1996.
- J. Cañón, “Tota Lake Water Balance and Preliminary Study of Lake’s Hydraulics,” Master’s Thesis, School of Engineering, Universidad Nacional de Colombia, 2002.
- NOAA, “Climate Diagnostic Center: Climate Indices,” 2005. http://www.cdc.noaa.gov/ClimateIndices
- N. Mantua, “The Pacific Decadal Oscillation. Updated Standardized Values for the PDO Index,” 2005. http://jisao.washington.edu/pdo/PDO.latest
- L. Xiong and G. Shenglian, “Two Parameter Monthly Water Balace Model and Its Application,” Journal of Hydrology, Vol. 216, No. 1-2, 1998, pp. 111-123. doi:10.1016/S0022-1694(98)00297-2
- I. Vergara, J. Buitrago and C. Rodríguez, “Tota Lake Hydrogeology Survey,” Third Colombian Symposium of Hydrogeology, Cartagena, 1998, pp. 1-17.
- G. Poveda, J. Velez, O. Mesa, C. Hoyos, J. Mejia, O. Barco and P. Correa, “Influence of Macroclimatic Phenomenon on the Annual Hydrologic Cycle of Colombia: Linear, Non-Linear and Percentage Probability,” Meteorología Colombiana, Vol. 6, 2002, pp. 121-130.
- T. Shun and C. Duffy, “Low-Frequency Oscillations in Precipitation, Temperature and Runoff on a West Facing Mountain Front: A Hydrogeologic Interpretation,” Water Resources Research, Vol. 35, No.1, 1999, pp. 191-201. doi:10.1029/98WR02818
- J. Cañón, J. González and J. Valdés, “Precipitation in the Colorado River Basin and Its Low Frequency Associations with PDO and ENSO Signals,” Journal of Hydrology, Vol. 333, No. 2-4, 2007, pp. 252-264. doi:10.1016/j.jhydrol.2006.08.015
- G. Plaut and R. Vautard, “Spells of Low Frequency Oscillations and Weather Regimes in the Northern Hemisphere,” Journal of Atmospheric Sciences, Vol. 51, No.2, 1994, pp. 210-236. doi:10.1175/1520-0469(1994)051<0210:SOLFOA>2.0.CO;2
- R. Vautard, P. Yiou and M. Ghil, “Singular Spectrum Analysis: A Toolkit for Short, Noisy Chaotic Signals,” Physica D: Nonlinear Phenomena, Vol. 58, No. 1, 1992, pp. 95-95. doi:10.1016/0167-2789(92)90103-T

