Journal of Water Resource and Protection
Vol. 2 No. 6 (2010) , Article ID: 2066 , 5 pages DOI:10.4236/jwarp.2010.26061
Transport of Suspended Solids in Dammam (Saudi Arabia) Coastal Areas: Fish Market Works
Department of Mathematics, Tafila Technical University, Tafila, Jordan
E-mail: hussam@ttu.edu.jo
Received February 23, 2010; revised April 15, 2010; accepted May 4, 2010
Keywords: Numerical Modeling, TSS, Arabian Gulf, Sediment Transport
ABSTRACT
Some new projects are considered in the eastern coasts of Dammam city, Saudi Arabia Dredging operations would significantly alter coast hydrological and sediment transport processes. It is important that the project areas must keep flushing the fresh sea water in and out with good water quality parameters, which are currently facing increased pressure from urbanization and navigation requirements in conjunction with industrial developments. A suspended solids or sediments are expected to affect the flora and fauna in that area. A numerical modeling study in needed to study the effect of dredging and in particular the suspended sediments concentrations (mg/L) changed in the region. The results were obtained using finite element method and Newton-Raphson iterations.
1. Introduction
Dredging is critical to maritime trade and many recreational pursuits. Extensive dredging and gravel extraction in those coastal areas are for the purpose of extending the coasts, to build a new fish market, and for other purposes. Effective sediment management tools are of fundamental importance for coastal and water authorities to reduce the costs for maintenance dredging and waterway building activities. In this context reliable in situ data of siltation rates and suspended solid concentrations are a precondition to understand the mechanisms that control sediment transport and to optimize for example strategies for dredging and dumping material. Also for numerical computer models the availability of appropriate validation datasets is essential.
During dredging and disposal operations, there is an increase in the total suspended solids (TSS) in the area of activity. TSS, is sometimes referred to as suspended solids, is a simple measure of the dry-weight mass of nondissolved solids suspended per unit volume of water (usually expressed in mg/L). TSS includes inorganic solids such as clay, silt, sand, etc. as well as organic solids such as algae, zooplankton, and detritus [1]. These resuspended sediments can adverse impact biota. To study the effects of sediment transport in the Dammam coastal areas, it is necessary to understand and predict the sediment concentration and fate of these sediments using numerical models.
Following the progress in surveying technology for field data and computer application, models in 1-D, 2-D and 3-D for sediment transportation have been developed in the cases of rivers, estuaries, lakes and reservoirs (e.g., [2-4]). Fassnacht (1997, [5]) listed a table containing eight suspended sediment models with various applications. These models were applied to various settings; each model has its own pros and cons resulted from particular waterbody, specific boundary conditions and affecting factors; and a universal one may not be applicable in other cases. An integrated modeling study was completed to assess the magnitude of the potential impacts of suspended sediment plumes. The model was validated against previous dredging works in Dammam coastal areas [6] and then used to simulate the fish market dredging works. This research maybe used in other areas of new projects that require massive dredging works.
2. Methods
The proposed fish market location at the eastern part of Dammam city coasts is shown in Figure 1, while the study area is divided into 241 nodes that made finite-element mesh as described in Figure 2. Sediment transportation in estuary is influenced by many factors such as source of sand, tidal flow, wave, and particles flocculation

Figure 1. Study area; proposed fish market at the eastern coast of Dammam city.
 (a) (b)
(a) (b)
Figure 2. 241 nodes representing fish market area (left) and finite element triangles of that area (right).
culation, deposition/re-suspension and erosion [7]. It is not practical to cover all the factors in one model. This research is the first attempt to build up a dynamical 2D model for the transportation of suspended solids in Dammam coastal areas. A two-dimensional sediment transport model was applied to the shallow coastal areas of Damman due to dredging operations was developed. The shallow-water hydrodynamic equations used for one-dimensional depth average flow consist of the equations for the conservation of mass, momentum, and energy. For most applications, the conservation of momentum and conservation of energy equation produce identical results. Sediment transportation in estuary is influenced by many factors such as source of sand, tidal flow, wave, particles flocculation, deposition/re-suspension and erosion. Every estuary has particular dominant agent among all the factors controlling the sediment transportation there. It is not practical to cover all the factors in one model.
The equation of continuity is given by Kolar et al. 1994, [8]:

where
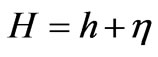
h is mean water depth, m is change in water level, m H is total water depth, m U is velocity component in x-direction, m/s V is velocity component in y-direction, m/s T is time, s Q is injected water, m3/s.
As the continuity equation includes three unknown variables u, v, and h, we need two more equations to complete the solution of the problem. These are given by the momentum equations in two directions
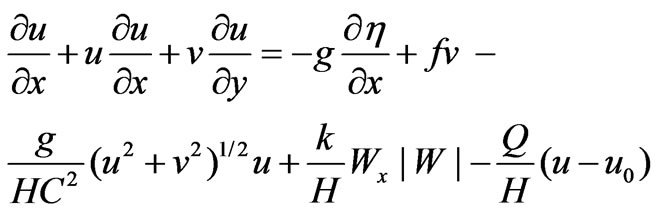
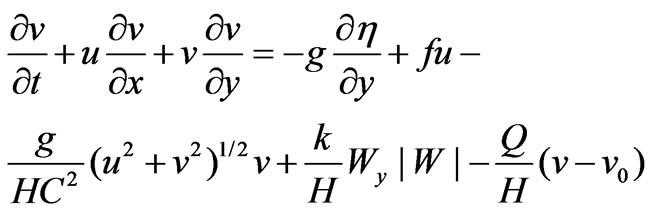
The Coriolis parameter f, is defined as
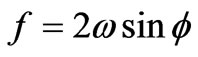
where is the latitude and is the Earth’s rate of rotation equal to 7.2722 × 10-5 s-1. The wind shear stress parameter, k, is defined as:
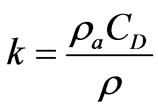
and:
Change in water level, m
H Total water depth, m
u Velocity in x-direction, m/s
v Velocity in y-direction, m/s
t Time, s
g Acceleration of gravity, m/s2
The Earth’s rate of rotation, s-1
Latitude, deg
C Chézy bottom friction coefficient, m1/2/s
a Density of air, kg/m3
CD Wind drag coefficient
Fluid density, kg/m3
Wx Wind velocity in x-direction, m/s
Wy Wind velocity in y-direction, m/s
W Wind speed, m/s
uo Velocity of injected water in x-direction, m/s
vo Velocity of injected water in y-direction, m/s.
The momentum equations together with the equation of continuity complete the specification of the shallow water flow problem.
The area of study is divided into small regions of finite elements consisting of 241 nodes (Figure 2(a)). A mesh is generated using the aquasea software to obtain this mesh (Figure 2(b)).
Two types of inputs exist; either input for each node or input on areal regions. Inputs at boundary nodes were given values so that we obtain a wave fluctuation of 0.5 m mean sea level (MSL). Each node has two unknowns, the flow rate Q and the water surface elevation z.
For N nodes in an inlet system, the total numbers of unknowns are 2N, thus, 2N equations are needed to determine values of the unknowns. The finite difference representations of the shallow-water equations with the boundary conditions and the junction conditions constitute a system of 2N nonlinear algebraic equations. To solve these equations we use the generalized NewtonRaphson iteration method [9]. Iteration is continued until the differences in water surface elevation and discharge between successive iterations at any node fall below specified tolerance values. Areal data such as wind speed, wind direction, chezy coefficient and others were also taken into consideration.
3. Results and Discussions
Initial results of the model regarding flow directions show that it depends mostly on wind direction and geometry of the region bed (Figure 3). The dredged area –the proposed fish market - will result in concentrations of suspended solids. Two nodes were picked for studying total suspended solid concentration in a time-series manner. Nodes number 223 and 87 were chosen at the exit of area of study Figure 2(a).
The model was verified by measured data of TSS contents at sites Dammam eastern coasts [10]. Model results for both selected nodes show that TSS will come back to normal levels within a maximum period of 6 days in the dredged area (Figures 4 and 5). This shows that dredging operations have no effect on the long terms on water quality in the area. This is consistent with results that dredging activities often generate no more increased suspended sediments than commercial shipping operations, bottom fishing or generated during severe storms [11]. Furthermore, natural events such as storms, floods and large tides can increase suspended sediments over much larger areas, for longer periods than dredging operations. It is therefore often very difficult to distinguish the environmental effects of dredging from those
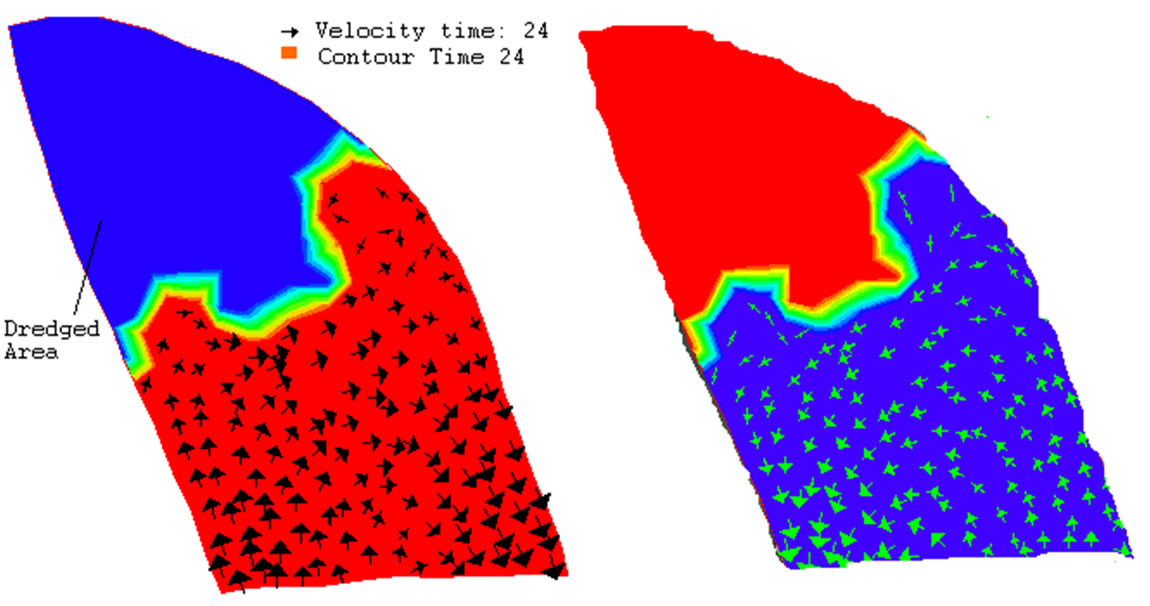
Figure 3. Flow direction within 1 day (left) and 10 days (right) of simulation.
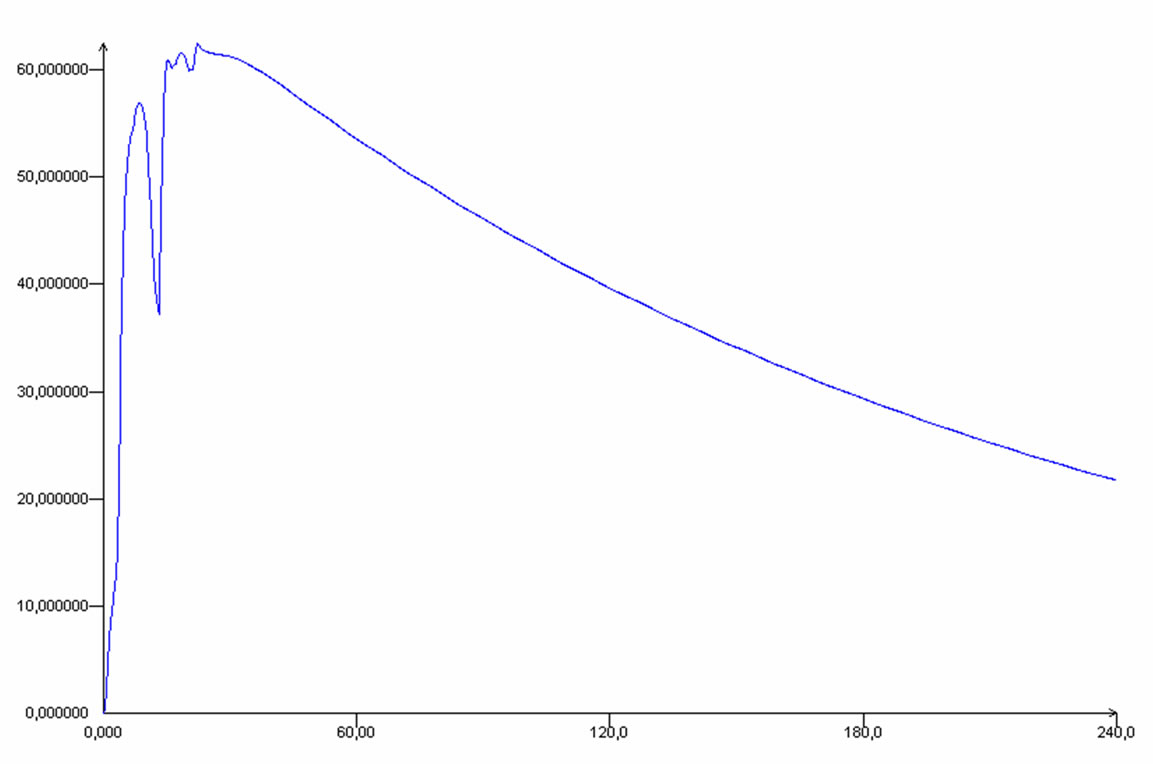
Figure 4. Suspended sediments concentration (mg/L) during 10 days after dredging operations at node 223.
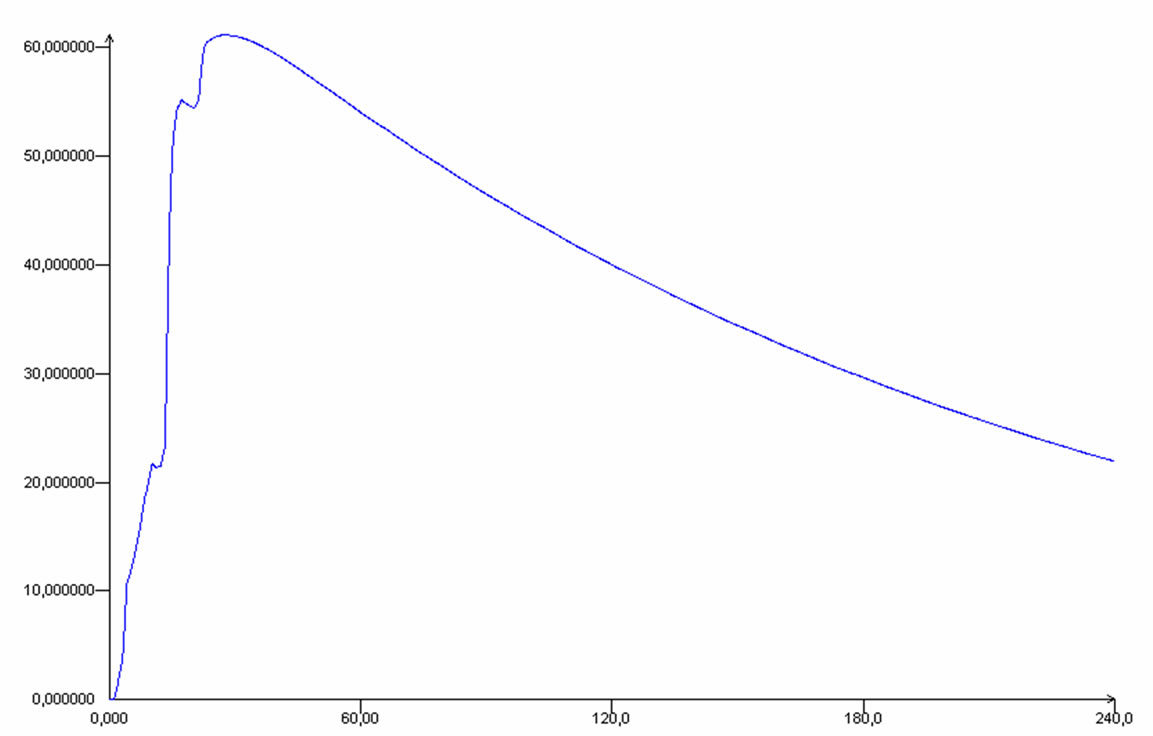
Figure 5. Suspended sediments concentration (mg/L) during 10 days after dredging operations at node 87.
resulting from natural processes or normal navigation activities [12].
4. Conclusions
The transportation of suspended solids Dammam coastal areas are jointly controlled by region inflow, tidal current and bottom vertical shear near the seabed. In this work, a 2D model to simulate the transportation of suspended solids was developed in which the mechanisms of advection, diffusion, flocculation settling of particles, scouring and silting of the seabed and the carrying capacity of wave and tide were involved. The model was run for 10 executive days to simulate sediment transportation and was verified with normal field data. The results showed that the modeled contents of suspended solids matched well with the existing readings. Modeled distributions of suspended reflected basically the overall behaviors of sediment transportation.
REFERENCES
- APHA, “Standard Methods for the Examination of Water and Wastewater,” 18th Edition, American Public Health Association, American Water Works Association, Water Pollution Control Federation, Washington, DC, 1992.
- E. Hayter and A. J. Metha, “Modeling Cohesive Sediment Transport in Estuary Waters,” Applied Mathematical Modelling, Vol. 10, No. 4, August 1986, pp. 294-303.
- L. C. van Rijn, H. van Rossum and P. Termes, “Field Verification of 2-D and 3-D Suspended-Sediment Models,” Journal of Hydrologic Engineering, ASCE, Vol. 116, No. 10, 1990, pp. 1270-1288.
- R. A. Falconer and B. Lin, “Three-Dimensional Modeling of Water Quality in the Humber Estuary,” Water Research, Vol. 31, No. 5, 1997, pp. 1092-1102.
- S. R. Fassnacht, “A Multi-Channel Suspended Sediment Transport Model for the Mackenzie Delta, Northwest Territories,” Journal of Hydrologycal, Vol. 197, No. 1-4, 1997, pp. 128-145.
- H. A. Al-Rabai’ah, “Numerical Modelling of Water Flow in a Dead-End Tidal Inlet at Dammam Coastal Areas, Saudi Arabia,” Journal of Applied Science and Environmental Sanitation, Vol. 3, No. 3, 2008, pp. 127-136.
- X. H. Chen, Y. Q. Chen and G. Y. Lai, “Modeling Transportation of Suspended Solids in Zhujiang River Estuary, South China,” Chinese Journal of Ocean and Lim, Vol. 23, No. 1, 2005, pp. 1-10.
- R. L. Kolar, J. J. Westerink, M. E. Cantekin and C. A. Blain, “Aspects of Nonlinear Simulations Using Shallow Water Models Based on the Wave Continuity Equation,” Computers and Fluids, Vol. 23, No. 3, 1994, pp. 523-538.
- A. M. Cialone, M. Amein and 1. Dynlet, “Model Formulation and User’s Guide,” U.S. Department of Transportation, Federal Highway Administration, Atlanta, 1993.
- H. A. Nasr-El-Din, A. M. Al-Mohammad, A. A. Al-Shurei, N. K. Merwat, M. M. Erbiland and M. Samuel, “Restoring the Injectivity of Water Disposal Wells Using a Viscoelastic Surfactant-Based Acid,” Journal of Petroleum Science and Technology, Vol. 54, No. 1-2, 2006, pp. 10-24.
- W. Parr, S. J. Clarke, P. Van Dijk and N. Morgan, “Turbidity in English and Welsh Tidal Waters,” 1998, WRc Report No. CO 4301/1 to English Nature.
- J. G. S. Pennekamp, R. J. C. Epskamp, W. F. Rosenbrand, A. Mullie, G. L. Wessel, T. Arts and I. K. Deibel, “Turbidity Caused by Dredging: Viewed in Perspective,” Terra et Aqua, Vol. 64, 1996, pp. 10-17.

