Journal of Water Resource and Protection
Vol. 1 No. 4 (2009) , Article ID: 759 , 6 pages DOI:10.4236/jwarp.2009.14032
Research on Plane 2-D Sediment Model of a Watercourse on Yangtze River
Water Conservancy and Hydropower Institute of Hohai University, Nanjing, China
E-mail: fyhhu@126.com
Received June 16, 2009; revised September 3, 2009; accepted September 17, 2009
Keywords: sand excavation, water-sand mathematic model, flood control safety
ABSTRACT
To provide basis for sand excavation of hydraulic fill and land forming in Daohukou region in a watercourse (Wuhan reach) on Yangtze River, a 2-D water-sand mathematic model of this river reach is established. The variation of water levels of this reach and the back silting of watercourse after sand excavation are calculated. The rationality of the results calculated by this model and the measured data are validated and analyzed. The results show that, this model is reasonable and reliable.
1. Introduction
To comprehensively renovate and exploit the flood control and environment of the new and old Wujin dike inner section in Daohuhou region of Wuchang District, hydraulic fill and land forming project is constructed by the government of Wuhan City. The main sand source region is located at the right of Yangsiji channel bar, Heposhan point bar, and the right of Baishazhou tail. Engineering hydraulic fill and sand excavation is mainly utilized. According to the landform data of the hydraulic fill area provided by Wuhan City, this area is relatively low with some fish ponds and cultivated land, including some residential area, etc. The land elevation varies from 23.0 to 27.0mm, and the area is about 0.65km2. This project is located at the urban area of Wuhan, so the source of soil materials in surrounding areas is very tense. The transportation distance from the soil field is far and the cost is high. To solve this problem, lower the engineering cost and reduce the impact to surrounding ecology and environment, sand will be excavated from the river in Wuhan reach on Yangtze River for hydraulic fill. It is estimated that about 2 million cubic meters of sand will have to be filled for this area. After sand excavation, the river regime of this river reach will be adjusted and the riverbed scouring and silting will be changed. Potential adverse effects may be brought to the flood control safety, navigation safety, water ecology, environment, and others of this reach. To reduce these adverse effects, the sand excavation location, scheme and countermeasures should be reasonably determined on the basis of analyzing and predicating the evolution law and development trend of watercourse of the sand excavation reach. Therefore, the feasibility of this sand excavation project should be demonstrated to provide referencing basis for the examination and approval by the water administrative department.
On the basis of considering the synchronous impact and continuous effect for riverbed evolution by sand excavation, mathematic control equations, which describe the water-sand movement in river in detail, are introduced. The mathematic model of plane 2-D sediment of the sand excavation river is established. The variation of water-sand movement in the sand excavation river is simulated in detail. Except specially noted, the Beijing coordinate system in 1954 will be used as the plane coordinates. The elevation standard in 1985 is used as the elevations of water levels and landform.
2. Calculation and Analysis of Plane 2-D Sediment Model
Through comprehensively considering the river regime, engineering study contents, hydrology data, and other factors, the scope of calculated reach of the 2-D mathematic model is selected as: Xiaojunshan is selected as the inlet section on the upstream, Yangluo is selected as the outlet control section on the downstream, and the total length is about 55km; and the influx of Hanjiang River is considered.
2.1. Plane 2-D Sediment Mathematic Model
Plane 2-D current and sediment equations under orthogonal curvilinear coordinate system are adopted.
1) Continuity equation and motion equation of current:
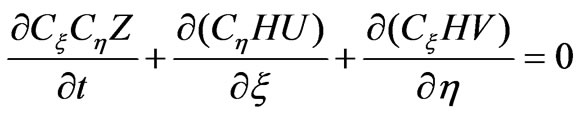 (1)
(1)
2) Motion equation [1,2] of current:
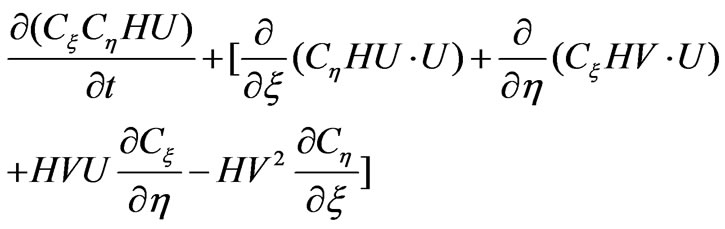
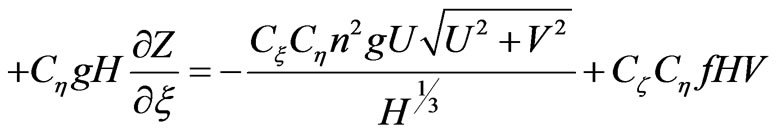
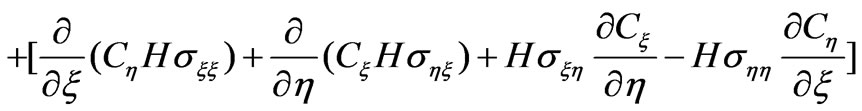 (2)
(2)
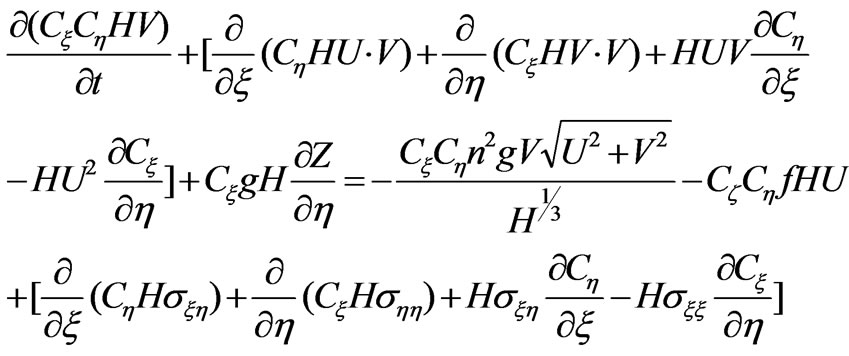 (3)
(3)
Where, U and V represent the velocity components in ξ and η directions; Z represents the water level; g represents the acceleration of gravity; σξξ, σηη, σξη, σηξ are stresses, which expressions are as follows:
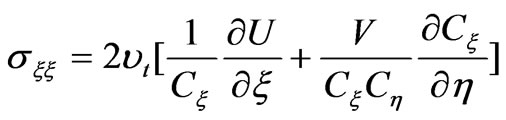 (4)
(4)
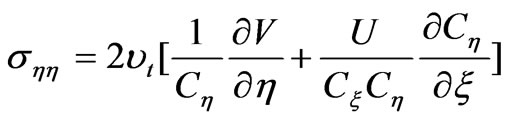 (5)
(5)
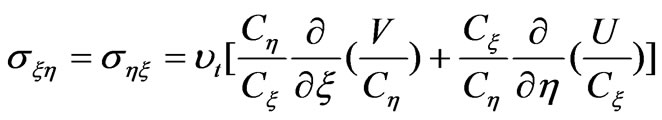 (6)
(6)
Cξ, Cη are Lame coefficients in the physical orthogonal curvilinear coordinate system:
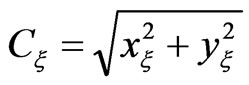 ,
, (7)
(7)
3) Suspended sediment transport equation:
 (8)
(8)
Where, i represents the group of sediment; Si and Si* represent the sediment concentration and sediment carrying capacity; εξ and εη represent the sediment diffusion coefficient in coordinate direction.
The grouping sediment carrying capacity Si*=Pi*·S*, is controlled by current strength and bed sand gradation. S* represents the sediment carrying capacity of current with the average settling speed of ωm; Pi* represents the gradation of grouping sediment carrying capacity [3].
4) Riverbed deformation equation [4,5] is:
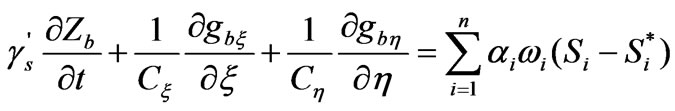 (9)
(9)
2.2. Model Numerical Method and Calculation Program
While solving the differential equation, finite volume method is adopted for the numerical discrete of control Equations (1–9). The solution of discrete equations is based on SIMPLEC arithmetic. The Gauss-Seidel iteration is used as the main iterative algorithm in the solution process. Over-relaxation and under-relaxation techniques [6] are used.
2.3. Treatment of Problems Relevant to Mathematical Calculation
2.3.1. Division of Calculating Grid
Body-fitted orthogonal curvilinear grid at the boundary of watercourse is adopted as the 2-D calculating grid. The quantity of grid nodes is 289×70. The space between grids in the direction of the current varies from 60 to 300m, and the space in the direction vertical to the current varies from 10 to 80m.
2.3.2. Treatment of Moving Boundary
According to the depths of water calculated in each time, distinguish the calculating nodes of water area and land area; boundary partition wall method is adopted for the treatment of calculating nodes at bank boundary; a small keel clearance is maintained for the calculating nodes at bank boundary to make the calculation possible; water level extension [7] at alongshore water area is adopted by the land area water level.
2.3.3. Roughness, and Other Parameters and Coefficients
The roughness in the calculating river reach is reversely calculated by using the measured hydrological data in general. According to the local landform, it is debugged in blocks according to the element. The calculated roughness coefficient in this paper varies from 0.018 to 0.022 in riverbed part and from 0.022 to 0.035 in bottomland.
The turbulent viscosity coefficient νt of the current is related to the turbulent stress in the current. In general situations, equation with constant coefficients is used to simplify the calculation. Its empirical correlation is νt= cu*h, where c represents the empirical constant (the value range is from 0.25 to 1.0) [8,9]. In this calculation, c is taken as 1.0. For sediment turbulent diffusion coefficient, its value is generally taken as the same of current turbulent viscosity coefficient, that is to say εx, εy=νt.
2.3.4. Model Definite Conditions
The definite conditions of the model include boundary conditions and initial conditions. Constant flow boundary conditions are adopted. Flux, sediment concentration, gradation, and others are provided for the upper reach; water level is provided for the lower reach; the velocity and sediment concentration at bank boundary are taken as zero. The initial landforms of riverbed and bed sand gradations of the calculated river reach are given.
Initial conditions: the initial velocity field is given as zero, and the initial water level is given according to the water surface profile gradient ratio. The errors brought by the initial values will be disappeared soon in the calculation.
3. Analysis of Mathematic Modes Calculation under the Influence of Sand Excavation
The influences to flood control, deposition, and others of Yangtze River by this project are evaluated through the calculation of variations of water levels, velocities, flow regimes, riverbed sediment depositions before and after the sand excavation project in this section.
3.1. Analysis for the Variation of Plane Velocity Field and Flow Regime
The main streamlines of the river reach of this project before and after the excavation of sand are compared in Figure 1. The engineering local flow fields before and after the excavations of sand are shown in Figure 2 and Figure 3. From Figure 1 to Figure 3 we can see that, the main streamlines of this engineering river reach are

Figure 1. Comparison of mainstreams before and after.
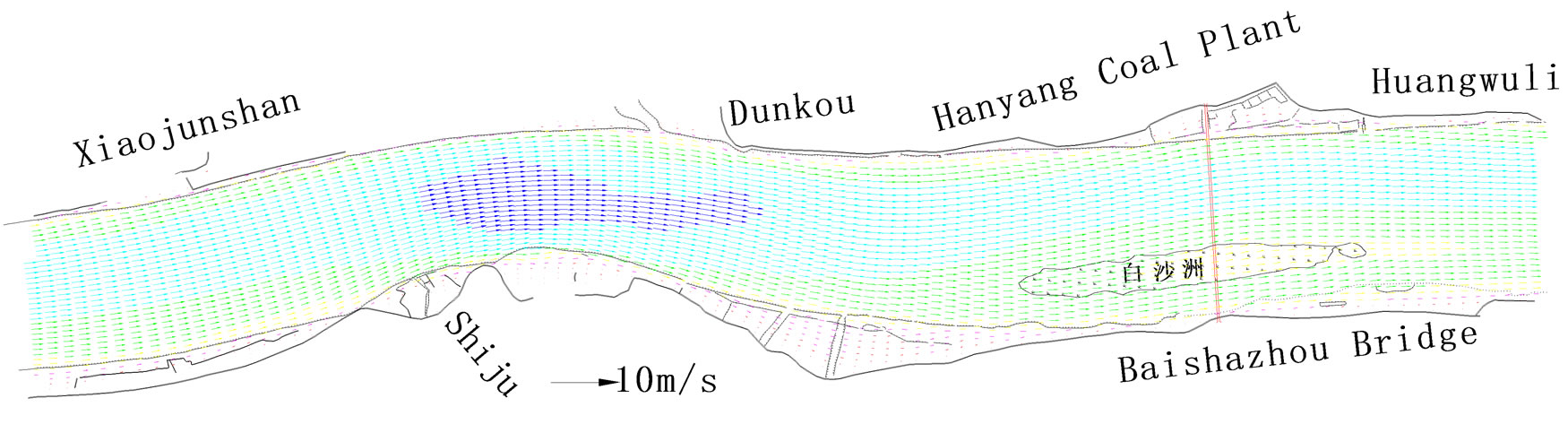
Figure 2. Local flow field before implementing this project (Q=76,100m3/s).

Figure 3. Local flow field after implementing this project (Q=76,100m3/s).
straightening with the increasing of flux, and are restricted by the river channel, both banks’ embankment revetment works and river beach. Except the area of this project, the positions of main streamlines are not changed obviously before and after the excavation of sand. The plane velocity field and flow regime of the engineering river reach are not changed obviously.
3.2. Analysis of Water Level Variation
To compare and analyze the water levels before and after implementing this project, 40 water level analyzing points are selected and arranged near the water area of this planned sand excavation project to plot the contour map for the variation of water levels before and after implementing this project. Through analyzing the variation of water levels of all analyzing points and the contour map for the variation of water levels of this river reach, the potential influences to the water levels of the watercourse by the sand excavation project are studied. The calculating results are shown in Figure 4 (variation of water level field). The calculating results show that, the variation of water levels is different quantitatively but consistent qualitatively after the implementing of this project.
3.3. Analysis of Sediment Back Silting Quantity in Sand Excavation Area
The back silting of sediment is calculated by selecting the water-sand data in three typical years of 2004 (medium flow and less sand). From the calculating results (Figure 5) we can see that, the back silting rates under different incoming water and incoming sediment conditions of the excavation areas vary greatly. Generally, the larger of the incoming sediment is, the higher the back silting rate will be. The first excavation area is located at the broadening section between Junshan Longchuanji node and Shiju node. The annual back silting rate of this area basically maintains at 54.9 to 79.8% in the year with large incoming sediment from the upper reach. And it can also maintain at about 27% in the year with small sediment. The second excavation area is located at the upper of the broadening section at the downstream of Shiju node. This area is greatly influenced by the swing of mainstream. The back silting rate in the year with medium flow and medium sediment will reach to 41.5%, and it will be below 15% in other years in general. The third excavation area is located at the slack water area at the tail of the right branch of Baishazhou. Compared with the two other areas at the upper reach, the variation of annual back silting rate is small even if the incoming water and sediment conditions are changed. It can maintain at 24.4 to 39.4% in general.

Figure 4. Variation scope of water levels after the implementing of sand excavation project (Q=76,100m3/s).
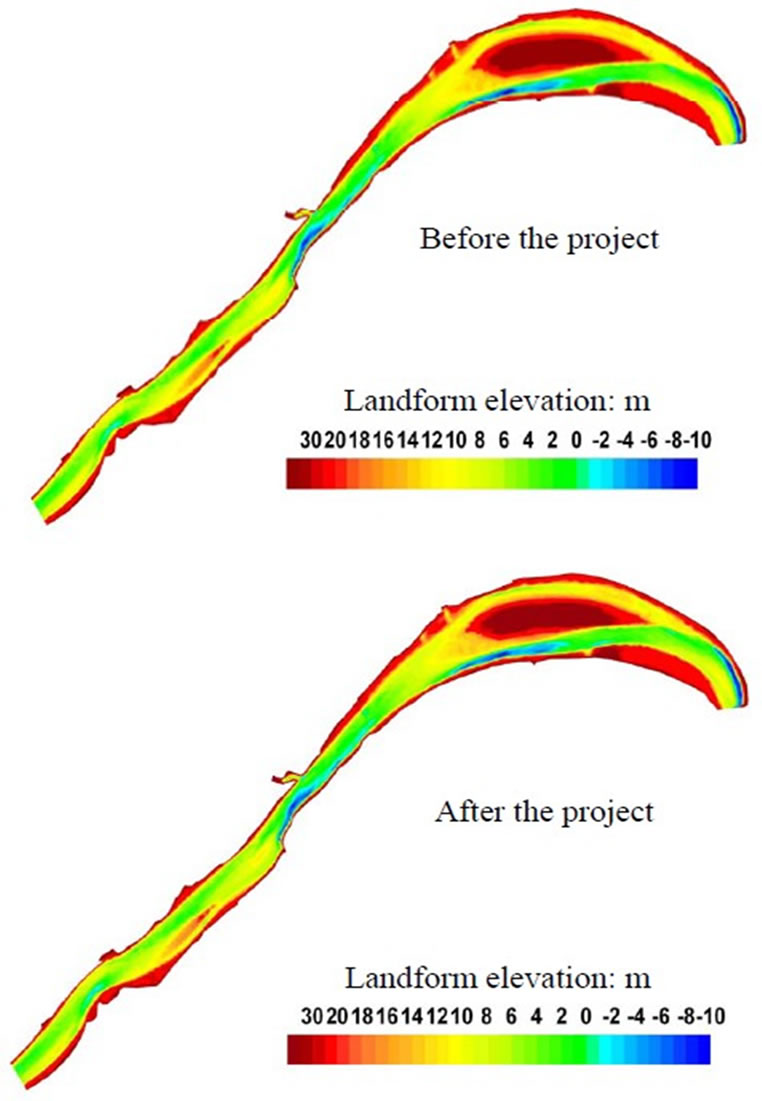
Figure 5. Comparison of landform of the engineering river reach after scouring and silting before and after the excavation of sand (2004).
4. Conclusions
We can see from the calculation results of the above model that:
1) If the incoming water, incoming sediment and boundary conditions are not varied greatly, Wuhan reach can still maintain the current river regime pattern. Due to the control of both banks by the nodes and the construction of revetment works on Wuhan reach, the current general river regime is relatively stable, which provides favorable river regime conditions for the excavation of sand.
2) The selected excavation area is far from the Yangtze River embankment and shoreline. The nearest distance to the embankment is 340m. There are wide high floodplains outside the embankment. The calculation results of the mathematic model show that, the positions of the mainstream line are not changed obviously before and after the sand excavation, except slight change in the engineering area. There are basically no significant changes in the plane velocity field and flow state of the engineering river reach. After the implementation of sand excavation project, the influence to the diversion ratio between Baishazhou inlet and Qianzhou channel is small, and the diversion ratio of Tianxingzhou inlet is not affected. After the implementation of sand excavation project, the velocity values in the excavation area are all reduced, and the overall performance of the water level is slightly banked-up. The maximum banked-up value of water level occurs at the lower reach of the excavation area. However, the maximum bank-up value of all threeexcavation areas is not exceeding 2.3cm. The implementation of the sand excavation project causes the redistribution of wetted cross-section unit width flux. The velocities a the left and right of the excavation area are reduced, while the velocities within certain scope of the upper reach and lower reach of the excavation area are slightly increased. After the implementation of sand excavation project, the changes of riverbank near embankment at the left of this project, the water level in coastal water, and the velocity are small (slightly reduced). The influences to the water level and velocity are mainly concentrated at local coastal segments at the right near this project. The influence is limited because the sand excavation area is far from the main water-related project in the engineering river reach.
Through rating and validation of measured water levels along Wuhan reach, the rating and validation of velocity distribution and sediment distribution in typical cross sections, the validation results of scouring and silting amount and distribution of the riverbed, we can see that, the adopted plane 2-D water-sand mathematic model and the treatment of its parameters and coefficients are reasonable and feasible. The model can preferably reflect the movement characters of water and sediment in the river reach, as well as the scouring and silting variation law of riverbed. Therefore, this model can be used for calculating and analyzing the impact to watercourse current and river regime by the excavation of sand.
REFERENCES
- X. L. Liu, L. Xun and Q. Zheng, “Computational fluid dynamics,” Harbin: Harbin Press, 1998.
- D. SilvaA, “Turbulent flow in sine generated meandering channel,” Queen’s University, Kingston, Ontario, Canada, March 1995.
- A. Vanoni, “Sediment engineering,” Beijing: Water Conservancy Press, 1981.
- T. Y. Li, “Research and preliminary application of sediment mathematic model in fluctuating backwater area of Three Gorges Reservoir [M],” Wuhan: Wuhan Industrial Press, 1993.
- Z. L. Wei, “A finite element solution of current and sediment problems in watercourse [J],” Journal of Wuhai Water Conservancy and Hydroelectric Power, 1990.
- J. H. Xie. “River simulation [M],” Beijing: Water Conversancy & Power Press, 1990.
- Y. L. Zhao and X. F. Zhang, “Hydrology [M],” Beijing: China Architecture & Building Press, 2001.
- X. Q. Zhou, “Computational Hydraulics [M],” Beijing:
- Tsinghua University Press, 1995.
- Y. C. Chang, “Lateral mixing in meandering channels,” PhD dissertation, The Department of mechanics and Hydraulics, University of Iowa, 200.

