Journal of Biomedical Science and Engineering
Vol.08 No.08(2015), Article ID:58841,8 pages
10.4236/jbise.2015.88048
Thermal Fluctuation Induced Piezoelectric Effect in Cytoskeletal Microtubules: Model for Energy Harvesting and Their Intracellular Communication
Arindam Kushagra1,2
1Centre for Research in Nanotechnology and Science, IIT Bombay, Mumbai, India
2Centre of Excellence in Nanoelectronics, IIT Bombay, Mumbai, India
Email: arindam.kushagra@iitb.ac.in, arindam.kushagra@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 July 2015; accepted 14 August 2015; published 17 August 2015
ABSTRACT
Cytoskeletal microtubules have long been conjectured to have piezoelectric properties. They have been shown to behave as nematic liquid crystals which oscillate along their director axis due to the prevalent thermal fluctuations. In this work, we develop a theoretical model of the mechanics of microtubules in the cytosolic space based on the buckling of its structure due to these thermal fluctuations. This cytosolic space has been considered as a viscoelastic medium in which microtubule oscillations have been considered. As a result of resilience of cytosol and neighbouring filaments from the axial force due to thermal fluctuations, the surface traction acting laterally on the microtubule structure has been further used to elucidate its piezoelectric behaviour in vivo. After the piezoelectric properties induced by thermal fluctuations (in addition to the buckling) of microtubules have been discussed, we propose a model discussing how microtubules behave as energy harvesters and communicate via electromagnetic radiation, with each other, in an intracellular environment.
Keywords:
Piezoelectricity, Cytoskeletal Microtubules, Intracellular Communication, Buckling, Thermal Fluctuations

1. Introduction
Microtubules are ubiquitous cytoskeletal elements that provide rigidity to otherwise blobby and gel-like living cell. They also participate in the intracellular transport of motor proteins by acting as rail-roads for dyenin & kinesin [1] . There are flexural compressions in the microtubule structure due to the transport of such proteins and also due to the turgidity of the cytosolic surroundings along with other filamental counterparts [2] . Theoretically, it has been proposed by Tuszynski and coauthors that microtubules possess piezoelectric properties as a result of the coupling of electrical and elastic degrees of freedom of the microtubule structure [3] . Experimental proof of piezoelectric properties of microtubules is yet to be obtained, as it will require intricate intracellular probing of microtubules while they are undergoing buckling (as will happen in case of cytoplasmic streaming or during the process of mitotic spindle formation). Thus, this work is based on the theoretical premise that microtubules display piezoelectric behaviour as discussed by Tuszynski [3] .
In this work, we explore the piezoelectric properties by analogizing the microtubules with collagen type-1 protein and propose a model by which microtubules behave as energy harvesters and may communicate with each other in a closed biological environment. For this work, we have considered the buckling behaviour of microtubules in a viscoelastic environment provided by the cytoskeletal components in addition to surrounding cytoplasm. The novelty in this work is that we have incorporated the impact of inherent thermal fluctuations due to the filament’s dynamic instability in calculating the piezoelectric behaviour of microtubules and the subsequent proposal of energy harvesting model and intracellular communication of microtubules.
Buckling and flexing of microtubules has been extensively studied [2] [4] -[15] by several groups. These studies concentrate on the continuum analyses of microtubules using shell theory [6] [8] [11] , elastic foundation [14] and beam model [4] [5] [7] [9] [10] [12] [13] [15] , to name a few major tools used to study the buckling behaviour of microtubules. Here, we would consider the analytically infinitesimal elastic behaviour to study the effects of thermal fluctuations in addition to the regular buckling forces on microtubules acting as cellular railroads [5] [9] . Due to the high aspect ratio of the microtubule filament structure, which is in the order of ~400 (assumed average length: 1 μm; diameter: 25 nm), Euler’s buckling model (static beam theory) can be applied for the impending analyses.
According to the Euler’s model, a filament of microtubule is considered as a very thin elastic rod which is buckled due to the loading forces acting on it due to its functionality as a cytoskeletal element. When this buckling happens, the neighbouring cytosol tries to restore the microtubule filament to its original position owing to the viscoelastic properties of the cytosolic space. We have also considered the effect of thermal fluctuations (Figure 1) that causes some bending which is countered by the viscoelasticity of cytosol.
Figure 1. Schematic of the microtubule filament buckled under the loading (buckling) force. As a result, cytosol exerts a restoring traction force. Thermal fluctuations also cause some bending of filament, analogous to the buckling force.
After analyzing the traction force induced piezoelectric behaviour of microtubules, we propose a mechanism by which microtubules can interact with each other as long as the dynamic instability process of addition of GTP-tubulin and secession of GDP-tubulin subunits is taking place.
2. Methodology
2.1. Buckling Mechanism in Viscoelastic Conditions
Cytosol has been considered as a viscoelastic medium which retaliates to any mechanical movement inside it, as expected. As discussed earlier, the shear traction force, Ftraction, could be described by using Euler’s beam theory as in Equation (1):
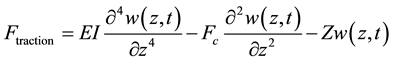 (1)
(1)
where E denotes the elastic modulus of the microtubule filament, I denotes the second moment of area, Z is a measure of viscoelastic resilience of the surrounding cytosol which is approximated to 2.7 times the shear modulus of the cytosol (μe: in the order of 1 - 3 kPa). w(z, t) suggests the wave propagation along the filament due to the application of critical buckling force (interchangeably termed as critical force in this paper), Fc, hereafter. We assume that the amplitude of wave-like perturbation due to buckling force varies only with time and is sinusoidal in the direction of propagation i.e. w(z, t) is broken into two parts by variable-separable methods as
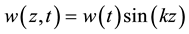 (2)
(2)
where k is the wavenumber of the perturbation propagating along the filament axis (z). The assumption made in Equation (2) reduces the Equation (1) into the following form.
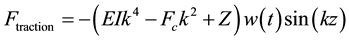 (3)
(3)
As we have mentioned earlier that the surrounding cytosol is assumed to be viscoelastic, this property either amplifies the buckling oscillations along the filament or dampens it. Hence Equation (3) could be re-written as
 (4)
(4)
Here α could assume either positive or negative values that would define whether the oscillations due to buckling force get bigger or accentuate with time. The significance of this parameter is discussed further in this paper.
We could deduce from the Equation (4) that Ftraction assumes the zero value in either of the following conditions:
1)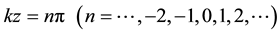 ;
;
2) 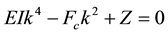
The buckling of microtubule is restricted between certain wavenumbers k1 and k2 of the buckling kink, known as critical wavenumbers. These two critical wavenumbers k1 and k2 are given by
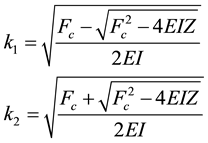 (5)
(5)
which are the distinct positive roots of the equation (as mentioned in the second condition discussed above)
 (6)
(6)
For all other wavenumbers above and below, there is no buckling as there is an inflexion in the value of the exponential coefficient α beyond those critical wavenumbers on either side i.e.
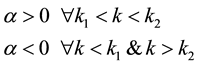 (7)
(7)
where α is the growth rate of perturbation that happens because of the critical force acting along the axis of microtubule, which takes care of the viscosity and shear modulus of the cytoplasm. The physical significance of the growth rate α could be that within the limits of k1 & k2, the wave propagation grows exponentially with time whereas beyond these wavenumbers on either side, temporal under-damping of sinusoidal oscillations along the filament is expected to happen.
Previously, we stated that there is no buckling beyond k1 and k2 because these are the two wavenumber values where Ftraction is reduced to zero. Since the expression for Ftraction contains a minus sign (Equation (4)), indicating that it is increasing at the first root, k1, of the Equation (6) and decreasing at the second root, k2, of the same equation i.e. the traction force is positive only between k1 and k2 and negative elsewhere. This condition is under the assumption that sin(kz) > 0.
2.2. Critical Buckling Force & Impact of Thermal Fluctuations
When some axial buckling force is applied on the filament due to intracellular loading processes, it is assumed to be countered by the shear traction force due to the viscoelastic properties of the surrounding medium (Figure 1). Intuitively, we could state that there has to be a minimum amount of axial force that needs to be applied for the buckling to take place, Fc. As we could figure out, the force required to buckle the microtubule filament would incorporate the elastic modulus of the filament, its second moment of area & shear modulus of the cytosol. The critical force required for the buckling of microtubules housed in viscoelastic cytosol, in addition to the impact of thermal fluctuations [9] [16] is given as follows:
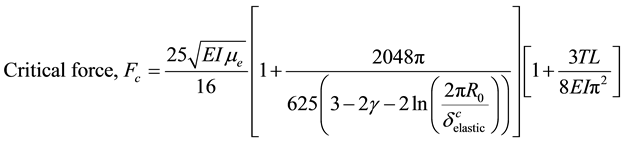 (8)
(8)
where,
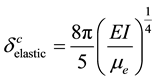 (9)
(9)
is the critical wavelength generated by the critical force 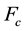 acting on the microtubules;
acting on the microtubules; 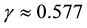 is the Euller’s constant and R0 is the radius of microtubule structure. Equation (8) incorporates the thermal fluctuations occurring in the filament, denoted by T. This is energy equivalent of thermal fluctuations. It is assumed that this thermal component T accounts for the in vivo free energy of GTP hydrolysis, though thermal fluctuations in absence of nucleotide hydrolysis have also been reported [17] .
is the Euller’s constant and R0 is the radius of microtubule structure. Equation (8) incorporates the thermal fluctuations occurring in the filament, denoted by T. This is energy equivalent of thermal fluctuations. It is assumed that this thermal component T accounts for the in vivo free energy of GTP hydrolysis, though thermal fluctuations in absence of nucleotide hydrolysis have also been reported [17] .
As discussed earlier, microtubules have been predicted to possess piezoelectric properties. Due to the aforementioned bending mechanisms, there would be an expected electric potential generation along the structure of microtubules. Shao et al. [18] have proposed the continuum model of piezoelectric behaviour in ZnO nanorods. We would extrapolate the same model to determine the potential distribution in microtubules. ZnO nanorods have been chosen as model system to depict the cytoskeletal microtubules as ZnO nanorods grown chemically via zinc nitrate reacting with alkali nitrate-halide salt mix at high temperatures (500˚C) for substantially long time (0.5 - 8 hours), demonstrate microtubule-like structures [19] . Thus we assume structural homology of microtubules with ZnO nanorods. We propose that the same distribution relation (as that of ZnO nanorods) holds valid for microtubules too. The analogy is depicted as a schematic in Figure 2.
Though the piezoelectric deformation matrix elements for microtubules need to be determined using more advanced measurements on single molecules. The model for piezoelectric potential distribution is as follows
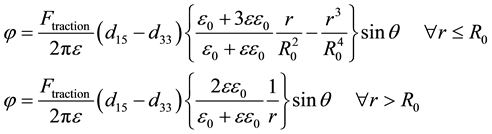 (10)
(10)
Figure 2. Schematic showing analogy between the compressive forces applied on the ZnO nanrods by AFM tip and the buckling force on the microtubule filament due to its cytoskeletal functions. The traction forces thus generated, give rise to the piezoelectric behaviour in ZnO nanorods and microtubules.
where θ is the angle in the x-y plane, ε is the dielectric constant of microtubules & R0 is the radius of the microtubule structure. To deduce the numerical piezoelectric characteristics of microtubules, we consider the fastest buckling growth wavenumber
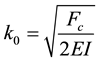
and the time value to calculate the traction force viz. t = 0, 0.5/α, 1.0/α, 1.5/α & 2/α (to be put in Equation (5)) from the proposed model in this work. Time values were chosen as multiples of α to avoid calculation complexity. To get the numerical trends from the proposed model, we chose the following parameters:
w0 = 1.0; R0 = 12.5 ´ 10−9 m; d15 = −0.3 ´ 10−12 C/N; d33 = 0 C/N; ε = 3.0; me = 1 ´ 103 Pa; L = 1 ´ 10−6 m; T (in vivo ΔGGTP-GDP) = 8.68 ´ 10−20 J; EI = 5 ´ 10−24 N∙m2.
Collagen and microtubule-associated protein tau have been demonstrated to share crystalline homology with each other [20] . Thus we assume that the piezoelectric potential generation due to similar forces would be analogous in the two proteins. Hence, the values of shear piezoelectric coefficient d15 & longitudinal piezoelectric coefficient d33 were assumed to be in close approximation with those of the collagen fibril [21] . We define r/R0 = γ & 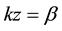

Based on the potential generated (as in Equation (12)) in the microtubules’ lattice, the energy stored (i.e. harvested) in it could be approximated to the energy stored in the capacitive electrical double layer (EDL) surrounding the microtubules in the ionic cytoplasmic environment. It is given by the following relation (Equation (13)) & holds valid only for values of γ < 1, for it is this range in which the piezoelectric potential generation actually takes place.
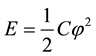
Intracellular communication model applicable to microtubules has been described in detail in the next section. Detailed mathematical analysis of the same has been discussed in reference 24.
3. Results and discussion
3.1. Piezoelectric Potential Distribution
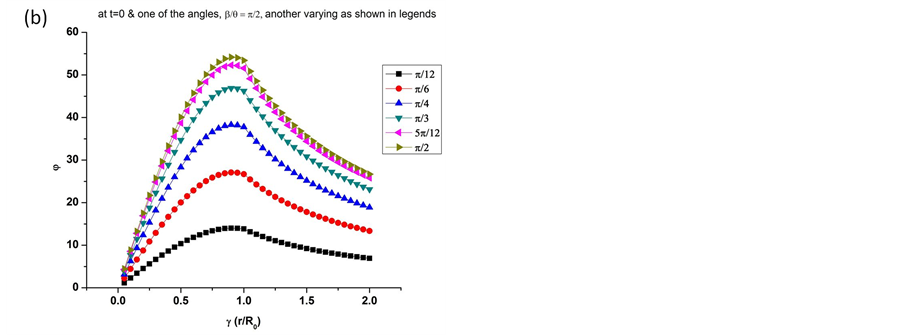
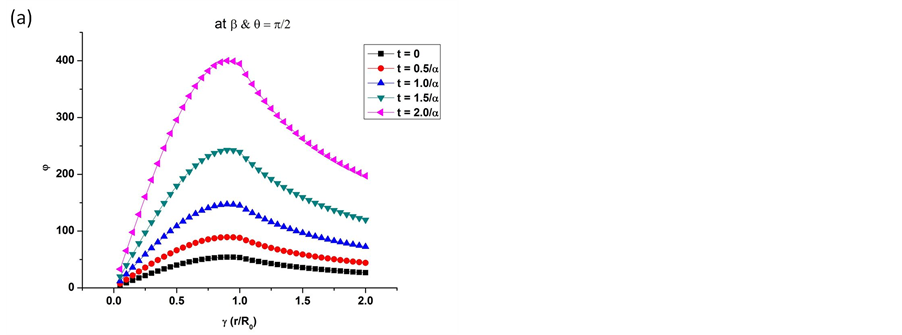
Equation (12) shows the distribution of piezoelectric potential inside the microtubule filament as well as outside. The potential distribution follows a cubic trend within the microtubule structure w.r.t the distance from the centre. As we move out of the structure, the potential starts dropping as it is inversely proportional to the distance from the centre-radius ratio. The same can be seen graphically in Figure 3.
The values shown in Figure 3 are significant because we can infer that the potential generated reaches its maximum at the surface of the microtubule filament. This gives inherent electrical stability to the structure due to the potential generated causing minimum damage, if any, at the core of the protein filament. This study sheds light on the quantitative aspect of piezoelectric behaviour of microtubules.
3.2. Energy Harvesting & Intracellular Communication of Microtubules
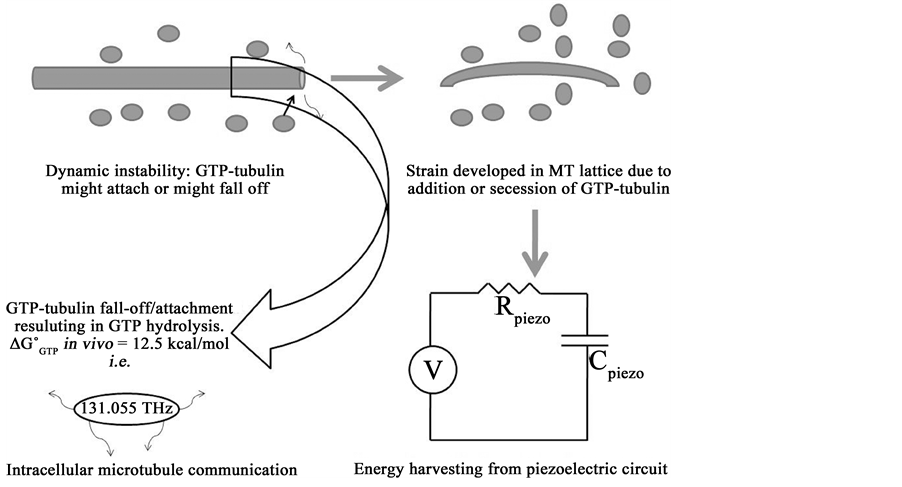
We also propose a model via which the microtubules could harvest energy and also communicate with neighbouring microtubules in the cytoskeleton. As we know, microtubules tend to display dynamic instability i.e. random lengthening and shortening of plus-end because of either addition or secession of GTP-tubulin. When GTP-tubulin binds to the cylindrical framework, there develops a compressive strain in the structure due to the preferential axial orientation of GTP-tubulin (parallel to the cylindrical axis) and GDP-tubulin (tilted w.r.t. the cylindrical axis) [22] . This strain build-up causes a voltage bias generation along the axis owing to the piezoelectric behaviour. The number of times this development of strain happens in the microtubule’s cylindrical lattice, it accounts for the number of cycles that would harness the energy in terms of stored charge due to piezoelectricity. This would result in a perpetual device that harnesses energy from its own movement/developed strain. As shown in Figure 4, this strain production is caused by either GTP-tubulin adding to the cylindrical structure or falling off from it. During the process of dynamic instability in microtubules, GTP hydrolysis takes place. The reported value of in vivo free energy of GTP hydrolysis is ~12.5 kcal/mol [23] i.e. amounting to 131.055 THz electromagnetic radiation. As per the model [24] , the ZnO nanorods have been shown to behave as nanogenerators of energy which also consume energy due to inter-ZnO-nanorod communication via terahertz (THz) range electromagnetic communication. Earlier in this paper, we have cited the structural homology of ZnO nanorods synthesised chemically with microtubules. Microtubules have also been analysed as piezoelectric filaments which are very densely packed within the cell. Hence, we propose a mechanism in which microtubules behave as energy harvesters which also consume energy due to communication via terahertz (131.055 THz) electromagnetic radiation. Schematic of the proposed model is shown in Figure 4. Mathematical treatise of the model could be found in the seminal work by Jornet and Akyildiz [24] . Details of the model (within the scope of this work) have been discussed in the next few paragraphs.
Figure 3. Graphs show the gradual increase of piezoelectric potentials w.r.t. the ratio of distance from the centre-radius (γ < 1) and inversely proportional to the ratio (γ > 1). (a) Values of angles are fixed to π/2 and the time parameter was varied to get the different amplitudes of piezoelectric potential generated; (b) At the start of the vibrations along the filament axis due to critical force, the values are plotted for varying angles along the x-y plane as well as on the z-axis.
Figure 4. Schematic proposes the model indicating microtubules harvesting energy from dynamic instability process utilizing their piezoelectric property. While GTP hydrolysis happens during dynamic instability, the in vivo free energy of GTP hydrolysis is proposed to be used for intracellular communication between the microtubules’ network. The energy of such communications is stipulated to be ~131 THz.
Energy harvesting in microtubules could be done when electric potential is generated in its lattice due to buckling (cytoplasmic loading & streaming, during the formation of mitotic spindles). Due to its intracellular ionic environment and prevalent negative charge, microtubules have an EDL formed around it by the positive ions. When the buckling happens, some amount of electric potential is generated in the microtubule lattice owing to its piezoelectric behaviour as discussed in the previous section. Henceforth we propose that this electric potential gets stored as energy in capacitive form in the EDL formed by the positive ions around microtubules.
Intracellular communication of microtubules is proposed to happen via electromagnetic radiation. The frequency of such communication is believed to be 131.055 THz. It represents the exact amount of energy that is generated by the in vivo free energy of GTP hydrolysis during dynamic instability of microtubules. Terahertz band, despite been absorbed by the molecules in the vicinity of microtubules causing a significant distortion (i.e. generating noise), are proposed to support very high bit-rates (in the order of 102 terabits/sec) within the cellular dimensions. This process would enable microtubules to faithfully transfer the information between each other to coordinate their collective behaviour as cytoskeletal elements. Testing of such a communication model is reported in detail in reference 24.
4. Conclusions
In this paper, we have studied the piezoelectric effect in cytoskeletal microtubules using ZnO nanorods as a model system and for the first time we have generated a quantitative estimate of the buckling that happens due to thermal fluctuations during dynamic instability i.e. GTP hydrolysis. Thermal fluctuations, as it appears from Equation (8), have miniscule effects on the critical force required for buckling. Based on the values of various parameters assumed, the effect comes out to be ~0.066%. Due to paucity of experimental data for microtubules, we have used collagen type-1 fibril, which is homologous to microtubule-associated-protein tau to approximate the shear and longitudinal piezoelectric coefficients.
We also propose a new model that describes how microtubules can function as energy harvesters and communicate with each other inside the cell at the expense of the in vivo free energy of GTP hydrolysis. This model is an inspiration generated from a similar work [24] on a cluster of ZnO nanorods. Energy harvesting mechanism has been proposed via the energy storage in the capacitive EDL, due to the electrical potential generation by the piezoelectric response of microtubules due to buckling. Intracellular mechanism has been proposed to take place via electromagnetic radiation at a very high bit-rate. Terahertz band communication has been proposed to faithfully transfer the information via the cytosol, despite its absorption by different molecules in the vicinity of microtubules. It can shed some light into the hypothetical mechanisms by which intracellular components interact with each other and into the energy efficiency of living systems.
Acknowledgements
The author is thankful to CEN (Phase-II) project at IIT Bombay (Project Code: 11DIT005) funded by Department of Information Technology, Ministry of Communication and Information Technology, Government of India. The author acknowledges the kind efforts of Prof. V. Ramgopal Rao, Dept. of Electrical Engineering at IIT Bombay for giving valuable suggestions in writing the manuscript and plotting the data & Dr. Shivani Srivastava, a post-doctoral fellow in Dept. of Mechanical Engineering at IIT Madras, for proofreading the manuscript.
Cite this paper
ArindamKushagra,11, (2015) Thermal Fluctuation Induced Piezoelectric Effect in Cytoskeletal Microtubules: Model for Energy Harvesting and Their Intracellular Communication. Journal of Biomedical Science and Engineering,08,511-519. doi: 10.4236/jbise.2015.88048
References
- 1. Fuchs, E. and Karakesisoglou, I. (2001) Bridging Cytoskeletal Intersections. Genes & Development, 15, 1-14.
http://dx.doi.org/10.1101/gad.861501 - 2. Mehrbod, M. and Mofrad, M.R.K. (2011) On the Significance of Microtubule Flexural Behavior in Cytoskeletal Mechanics. PLoS ONE, 6, e25627.
http://dx.doi.org/10.1371/journal.pone.0025627 - 3. Tuszynski, J.A. and Kurzynski, M. (2003) Introduction to Molecular Biophysics. CRC Press LLC, Boca Raton.
http://dx.doi.org/10.1201/9780203009963 - 4. Das, M., Levine, A.J. and Mackintosh, F.C. (2008) Buckling and Force Propagation along Intracellular Microtubules. Europhysics Letters, 84, Article ID: 18003.
http://dx.doi.org/10.1209/0295-5075/84/18003 - 5. Li, T. (2008) A Mechanics Model of Microtubule Buckling in Living Cells. Journal of Biomechanics, 41, 1722-1729.
http://dx.doi.org/10.1016/j.jbiomech.2008.03.003 - 6. Gao, Y. and An, L. (2010) A Nonlocal Elastic Anisotropic Shell Model for Microtubule Buckling Behaviors in Cytoplasm. Physica E, 42, 2406-2415.
http://dx.doi.org/10.1016/j.physe.2010.05.022 - 7. Jin, M.Z. and Ru, C.Q. (2013) Localized Buckling of a Microtubule Surrounded by Randomly Distributed Cross Linkers. Physical Review E, 2013, 88, Article ID: 012701.
http://dx.doi.org/10.1103/PhysRevE.88.012701 - 8. An, L. and Gao, Y. (2010) Mechanics Behavior of Microtubules Based on Nonlocal Anisotropic Shell Theory. IOP Conference Series: Materials Science and Engineering, 10, Article ID: 012181.
http://dx.doi.org/10.1088/1757-899x/10/1/012181 - 9. Ziang, H. and Zhang, J.J. (2008) Mechanics of Micro-tubule Buckling Supported by Cytoplasm. Journal of Applied Mechanics: Transactions of the ASME, 75, Article ID: 061019.
http://dx.doi.org/10.1115/1.2966216 - 10. Brangwynne, C.P., MacKintosh, F.C., Kumar, S., Geisse, N.A., Talbot, J., Mahadevan, L., Parker, K.K., Ingber, D.E. and Weitz, D.A. (2006) Microtubules Can Bear Enhanced Compressive Loads in Living Cells Because of Lateral Reinforcement. The Journal of Cell Biology, 173, 733-741.
http://dx.doi.org/10.1083/jcb.200601060 - 11. Adali, S. (2014) Variational Principles for Buckling of Microtubules Modeled as Nonlocal Orthotropic Shells. Computational and Mathematical Methods in Medicine. 2014, Article ID: 591532.
http://dx.doi.org/10.1155/2014/591532 - 12. Kikuchi, N., Ehrlicher, A., Koch, D., Kas, J.A., Ramaswamy, S. and Rao, M. (2009) Buckling, Stiffening, and Negative Dissipation in the Dynamics of a Biopolymer in an Active Medium. Proceedings of National Academy of Sciences, USA, 106, 19776-19779.
http://dx.doi.org/10.1073/pnas.0900451106 - 13. Civalek, O. and Akgoz, B. (2010) Free Vibration Analysis of Microtubules as Cytoskeleton Components: Nonlocal Euler-Bernoulli Beam Modelling. Scientia Iranica: Transaction B: Mechanical Engineering, 17, 367-375.
- 14. Taj, M. and Zhang, J.Q. (2012) Analysis of Vibrational Behaviors of Microtubules Embedded within Elastic Medium by Pasternak Model. Biochemical and Biophysical Research Communications, 424, 89-93.
http://dx.doi.org/10.1016/j.bbrc.2012.06.072 - 15. Wang, C.Y., Li, C. and Adhikari, S. (2009) Dynamic Behaviors of Microtubules in Cytosol. Journal of Biomechanics, 42, 1270-1274.
http://dx.doi.org/10.1016/j.jbiomech.2009.03.027 - 16. Baczyński, K.K. (2009) Buckling Instabilities of Semiflexible Filaments in Biological Systems. Ph.D. Thesis, Max Planck Institute of Colloids and Interfaces, Golm.
- 17. Hunt, A.J. and Howard, J. (1993) Kinesin Swivels to Permit Microtubule Movement in any Direction. Proceedings of National Academy of Sciences, USA, 90, 11653-11657.
http://dx.doi.org/10.1073/pnas.90.24.11653 - 18. Shao, Z.Z., Wen, L.Y., Wu, D.M., Wang, X.F., Zhang, X.A. and Chang, S.L. (2010) A Continuum Model of Piezoelectric Potential Generated in a Bent ZnO Nanorod. Journal of Physics D: Applied Physics, 43, Article ID: 245403.
http://dx.doi.org/10.1088/0022-3727/43/24/245403 - 19. Afanasiev, P. (2012) Snapshots of Zinc Oxide Formation in Molten Salt: Hollow Microtubules Generated by Oriented Attachment and the Kirkendall Effect. The Journal of Physical Chemistry C, 116, 2371-2381.
http://dx.doi.org/10.1021/jp210862y - 20. De Garcini, E.M., Carrascosa, J.L., Nieto, A. and Avila, J. (1990) Collagenous Structures Present in Brain Contain Epitopes Shared by Collagen and Microtu-bule-Associated Protein Tau. Journal of Structural Biology, 103, 34-39.
http://dx.doi.org/10.1016/1047-8477(90)90083-O - 21. Harnagea, C., Vallières, M., Pfeffer, C.P., Wu, D., Olsen, B.R., Pignolet, A., Légaré, F. and Gruverman, A. (2010) Two-Dimensional Nanoscale Structural and Functional Imaging in Individual Collagen Type I Fibrils. Biophysical Journal, 98, 3070.
http://dx.doi.org/10.1016/j.bpj.2010.02.047 - 22. Prodan, E. and Prodan, C. (2009) Topological Phonon Modes and Their Role in Dynamic Instability of Microtubules. Physical Review Letters, 109, Article ID: 248101.
http://dx.doi.org/10.1103/PhysRevLett.103.248101 - 23. Desai, A. and Mitchison, T.J. (1997) Microtubule Polymerization Dynamics. Annual Review of Cell and Developmental Biology, 13, 83-117.
http://dx.doi.org/10.1146/annurev.cellbio.13.1.83 - 24. Jornet, J.M. and Akyildiz, I.F. (2012) Joint Energy Harvesting and Communication Analysis for Perpetual Wireless Nanosensor Networks in the Terahertz Band. IEEE Transactions on Nanotechnology, 11, 570-580.
http://dx.doi.org/10.1109/TNANO.2012.2186313