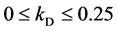Journal of Biomedical Science and Engineering
Vol.07 No.12(2014), Article ID:50660,10 pages
10.4236/jbise.2014.712097
An Efficient Liver-Segmentation System based on a Level-Set Method and Consequent Processes
Walita Narkbuakaew1, Hiroshi Nagahashi2, Kota Aoki2, Yoshiki Kubota3
1Interdisciplinary Graduate School of Science and Engineering, Tokyo Institute of Technology, Kanagawa, Japan
2Imaging Science and Engineering Laboratory, Tokyo Institute of Technology, Kanagawa, Japan
3Gunma University Heavy-Ion Medical Center, Gunma, Japan
Email: narkbuakaew.w.aa@m.titech.ac.jp, longb@isl.titech.ac.jp, aoki.k.af@m.titech.ac.jp, y_kubota@gunma-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 August 2014; revised 1 October 2014; accepted 16 October 2014
ABSTRACT
This paper presents an efficient liver-segmentation system developed by combining three ideas under the operations of a level-set method and consequent processes. First, an effective initial process creates mask and seed regions. The mask regions assist in prevention of leakage regions due to an overlap of gray-intensities between liver and another soft-tissue around ribs and vertebrae. The seed regions are allocated inside the liver to measure statistical values of its gray-inten- sities. Second, we introduce liver-corrective images to represent statistical regions of the liver and preserve edge information. These images help a geodesic active contour (GAC) to move without obstruction from high level of image noises. Lastly, the computation time in a level-set based on reaction-diffusion evolution and the GAC method is reduced by using a concept of multi-resolution. We applied the proposed system to 40 sets of 3D CT-liver data, which were acquired from four patients (10 different sets per patient) by a 4D-CT imaging system. The segmentation results showed 86.38% ± 4.26% (DSC: 91.38% ± 2.99%) of similarities to outlines of manual delineation provided by a radiologist. Meanwhile, the results of liver segmentation only using edge images presented 79.17% ± 5.15% or statistical regions showed 74.04% ± 9.77% of similarities.
Keywords:
Liver Segmentation, Level-Set, Geodesic Active Contour, Speed Images, Statistical Thresholds

1. Introduction
Liver image segmentation is an important procedure in the computer-aided diagnosis (CAD) and surgery (CAS). For example, it is used to determine the liver’s volume [1] that is essential information of liver surgery for primary hepatic tumors, metastatic lesions, and transplantation. Liver segmentation in computed tomography (CT) images is a challenging topic because of large variations in shapes and sizes. Moreover, gray-intensities of liver generally overlap another soft tissue. Occasionally, some CT data sets present high levels of image noises, some artifacts, and low image contrast due to the conditions of image acquisition and respiratory status [2] .
Many algorithms have been proposed to give high efficiency and reduce user involvement as presented in [3] - [5] . The level-set method is an interesting solution because it possibly gives high accuracy with small intervention from a user. However, it is normally formulated by a complicated energy-function. This sophisticated formulation may slightly improve performance of liver segmentation, but it consumes more computation cost due to an additional term. Further, it may require many data sets of manual delineation to produce extraordinary information from training data sets.
Alternatively, improvement in a quality of anatomical representations in a given image can give good segmentation results. For instance, in [6] , the level-set speed image was introduced to represent clear boundaries of a liver’s volume before performing the segmentation. This method performs well when image noises are suppressed. Thus, an advanced filter may be required to reduce image noise without deterioration in edges of anatomical structures. Further, in [7] , liver’s regions were described by a statistical distribution model of gray-in- tensities. Nonetheless, this method excludes gradient information that possibly assists in the segmentation.
Consequently, we are motivated to create an efficient liver-segmentation system from a combination of three main ideas. It is intended to perform under the conditions of a level-set method and consequent processes. These three ideas are presented to achieve several purposes as follows.
· The effective initial-process is proposed for excluding all information outside the ribcage and creating seed regions in axial images. The exclusion process assists in prevention of leakage regions when a given curve moves near ribs and vertebrae. The seed regions are completely allocated inside the liver for measuring statistical values of gray intensities. Further, it helps to obtain the start and stop indexes of axial images that contain liver regions.
· Liver-corrective images are created to represent statistical regions of the liver and preserve the edge information. These liver-corrective images help a level-set method based on reaction-diffusion (RD) evolution and a geodesic active contour (GAC) model to cope with high level of image noises. Further, an advanced image- filter is unnecessary.
· We use a concept of multi-resolution to combine with the RD-GAC based level-set method in order to reduce computation time.
We applied the proposed system to 40 sets of 3D CT-liver data, which were acquired from four patients by using a 4D-CT imaging system. The 10 different sets of 3D CT data were collected in a free-breathing cycle for each patient. In addition, we compared the proposed system with the liver-segmentation methods using only edge or statistical-region representation.
The rest of paper is organized as follows. Section 2 briefly describes related methods, and section 3 explains details of the proposed system. Next, the experimental results are illustrated and discussed. Finally, we conclude this study in the last section.
2. Related Methods
2.1. A Liver-Segmentation Approach Based on Edge Images
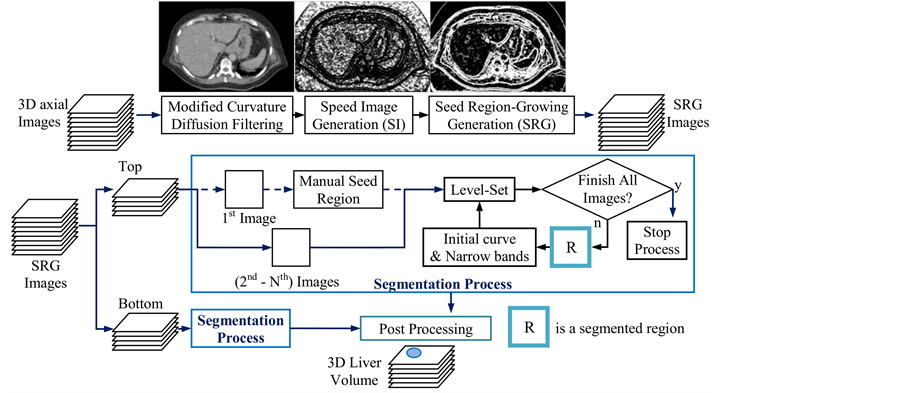
This approach transforms given images into edge images before performing liver segmentation. We refer to Lee, J. et al. [6] , who proposed a liver-segmentation method based on level-set speed images (LSSI). It contains two main processes as shown by a simple diagram in Figure 1. First, boundaries of anatomical structures are extracted. It begins with noise reduction by using a modified curvature diffusion filter [8] . Next, a speed image
(SI) is constructed from a gradient magnitude image 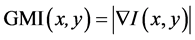 and a sigmoid formulation as
and a sigmoid formulation as
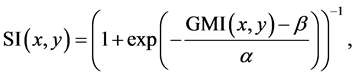 (1)
(1)
Figure 1. A diagram of liver segmentation based on the LSSI technique.
where 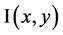 is a given image. The parameter
is a given image. The parameter 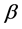 and
and  present center and width of the sigmoid function,
present center and width of the sigmoid function,
respectively. By choosing proper 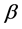 and
and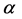 , it is possible to make pixels inside the homogeneous regions to be towards 1.0 and pixels beside edges to be around zero, respectively. Next, a threshold
, it is possible to make pixels inside the homogeneous regions to be towards 1.0 and pixels beside edges to be around zero, respectively. Next, a threshold 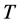 is required to gener-
is required to gener-
ate an inverted binary image called seed region growing as 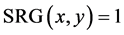 if
if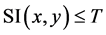 . After SRG images
. After SRG images
are constructed from all axial-images, a level-set method is applied to segment the liver’s region in each axial image.
However, this approach is inappropriate for the curve propagation in an inward direction. Thus, it is necessary to create an initial region for constructing a zero level-set function (LSF) inside the liver’s region. Further, for 3D CT data, liver regions in axial images expand from the top to around the middle; then, they shrink to small regions at the bottom of the volume. Consequently, each 3D CT data set needs to be divided at least two sections in z-axis (top-to-bottom) for placing initial curves inside the liver’s regions. Then, the first image in each section requires manual drawings of seed regions to initialize the zero LSF. In addition, complexity of edge information is reduced by using a segmentation result of previous image slice as an initial curve for a consecutive image. Further, the narrow bands are applied to limit areas of the curve propagation.
2.2. A Liver-Segmentation Approach Based on Statistical Regions
This approach statistically describes liver regions by measuring mean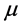 and standard deviation
and standard deviation of its gray intensities. These measures were mentioned in [7] [9] and we called them the statistical thresholding (ST) technique. According to those papers, this method starts from using a mean-shift filter [10] to reduce image noise. Next, statistical regions of liver are extracted when gray-intensities are in a range of
of its gray intensities. These measures were mentioned in [7] [9] and we called them the statistical thresholding (ST) technique. According to those papers, this method starts from using a mean-shift filter [10] to reduce image noise. Next, statistical regions of liver are extracted when gray-intensities are in a range of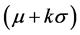 . The variable
. The variable is a constant that identifies a distribution rate. Subsequently, connected component labeling is applied and liver regions are selected. Next, these regions are refined by an active contour method. However, this approach needs good sampled regions to obtain the statistical values. Thus, liver segmentation based on the ST technique is performed as shown in Figure 2. The seed regions produced by our proposed system (section 3.4) are used to measure statistical values. Then, the statistical regions of liver are extracted by a range of
is a constant that identifies a distribution rate. Subsequently, connected component labeling is applied and liver regions are selected. Next, these regions are refined by an active contour method. However, this approach needs good sampled regions to obtain the statistical values. Thus, liver segmentation based on the ST technique is performed as shown in Figure 2. The seed regions produced by our proposed system (section 3.4) are used to measure statistical values. Then, the statistical regions of liver are extracted by a range of  and these statistical regions are used to segment a liver’s volume by using the level-set method.
and these statistical regions are used to segment a liver’s volume by using the level-set method.
2.3. A RD-GAC based Level-Set Method
Generally, a level-set method requires a re-initialization process to preserve an accurate numerical-solution, but this process consumes high computation cost as mentioned in [11] - [14] . The reaction-diffusion (RD) evolution [12] was introduced to remove this re-initialization process. Further, it supports a variety of forces for controlling the curve propagation. In summary, the RD technique requires two main steps for propagating the curve under a concept of two-step splitting method [15] . In the first step, the level-set evolution (LSE) equation is used
Figure 2. A diagram of liver segmentation based the ST technique.
to produce the reaction term. If a geodesic active contour (GAC) model [16] is applied, the reaction term is
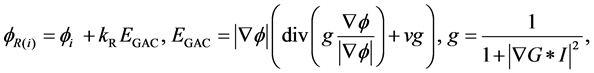
where 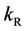
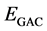
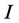
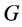
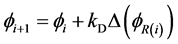
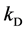
3. Proposed System
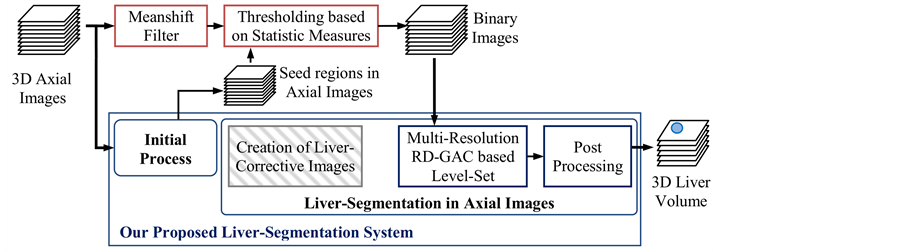
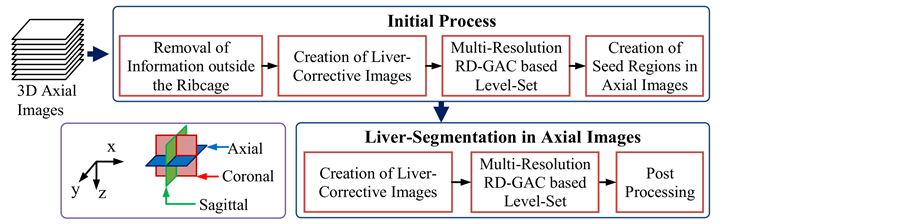
The proposed system (see Figure 3) is organized from five different processes and two types of combinations. These processes are: removal of information outside the ribcage, creation of liver-corrective images, multi-res- olution RD-GAC based level set, creation of seed regions in axial images, and post processing. The first combination called an initial process includes the first four processes. Meanwhile, the second combination is used to segment liver’s regions in axial images, and it is created from integration of the second, third, and fifth pro- cesses.
3.1. Removal of Information outside the Ribcage
To exclude all information outside the ribcage, we create a mask region for each axial image by performing the following procedures. First, a median filter is used to reduce noise. Then, a two-stage multi-thresholding Otsu’s (TSMO) method [17] improved by our proposed range constraint is applied to a filtered image. The result of the thresholding presents five segments containing background, three levels of soft tissues, and hard-tissue regions. Next, the hard-tissue regions represent ribs and vertebrae, and a template of seed points is created to cover these regions (see Figure 4). Subsequently, we move these seed points to boundaries of hard-tissue regions, and use straight lines to connect these points together in order to generate a mask region. However, regions of ribs and vertebrae are not always clearly displayed in some axial images (see a red arrow in Figure 4). Thus, we use a combination of soft-tissue regions instead of hard-tissue regions. In fact, this combined region is often larger than a boundary of the ribcage. Therefore, morphological erosion is required to shrink this combined region after connecting all seed points together.
Indeed, the original TSMO method [17] was introduced to accelerate computation without changing the results of a traditional Otsu’s method [18] . Conversely, these results are not good to present hard-tissue regions in our data sets as shown in Figure 5. Therefore, we need a range-constraint to improve the results. Indeed, an assignment of a range-constraint is often mentioned [19] - [21] , but it depends on a specific pattern of gray-inten- sities in a given image. In this study, we present a simple idea to define a range constraint by cutting gray intensities below the water (0 HU). The CT images describe gray intensities as CT standard numbers in the Houns-
Figure 3. An overview of a proposed liver-segmentation system.
Figure 4. An example of mask-region creation. (a) and (d) Two sample images, (b) and (e) templates of seed points, (c) and (f) mask regions.
Figure 5. An example of five-class clustering on a 16-bits CT image (a) using TSMO method (b) and including a proposed range-constraint (c).
field unit (HU) computed from the linear attenuation coefficient of materials [22] . Further, CT numbers of liver and bone are higher than the water.
3.2. Creation of Liver-Corrective Images
We perform the following steps to represent statistical regions of liver and preserve edge information in a given image. First, some samples of liver regions are measured their means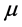
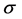
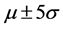
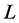
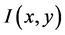
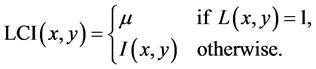
Moreover, we use the selected region to construct a zero LSF 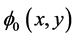
tion, that is 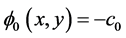
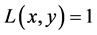
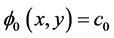
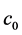
3.3. Multi-Resolution RD-GAC based Level-Set Segmentation method
As for the RD-GAC based level-set method in section 2.3, we combine it with a concept of multi-resolution as shown in Figure 6. In this study, three levels of 25%, 50%, and 100% of the original resolutions were performed. First, the edge detector function and the zero LSF are obtained at the original resolution. Then, they are scaled
Figure 6. A concept of multi-resolution RD-GAC based level-set method.
down to the lowest resolution. Next, the level-set method is operated. Afterwards, the result is used to construct the zero LSF in the higher resolution. Meanwhile, the edge detector function at the original resolution is scaled down to the desirable resolution. Then, the level-set method is repeatedly calculated to continue propagating the given curve from the lower resolution. Similarly, the process of segmentation is repeated until a final contour at the original resolution is released.
3.4. Creation of seed regions in axial images
After we remove all regions outside the ribcage (section 3.1) in a given 3D CT volume, coronal images are reconstructed by cutting the 3D CT volume in x-z planes (see Figure 7). Then, coronal images at the middle of the 3D data are sampled. Next, we define the region of interest (ROI), and create the liver-corrective images (section 3.2) from these samples of coronal images. Afterwards, the multi-resolution level-set method (section 3.3) is performed. The segmentation results represent the liver’s regions in coronal-image planes. Thus, if we compute the parallel projection of these segmentation results onto vertical axes of the coronal images, we will be able to obtain the start and stop indexes of axial images that include liver’s regions. Further, if these results are cut in horizontal planes (x-y planes), we will get seed regions in axial images.
3.5. Liver Segmentation in axial images
This process contains three main operations. First, we use seed regions produced by the process in section 3.4 to create liver-corrective images (section 3.2) in axial-image planes. Afterwards, the multi-resolution level-set method (section 3.3) is utilized to segment a liver’s volume.
3.6. Post Processing
From the segmentation results in section 3.5, they are refined by applying a Gaussian smooth filter to coronal and sagittal image planes. In addition, we use a hole-filling method to get outside boundaries of the liver regions. However, we can preserve hole-regions by intersecting these hole-filling regions with regions of holes.
4. Experiments and Results
4.1. Data Sets
We applied the proposed system to 40 sets of 3D CT-liver data, which were acquired from four patients by a 4D-CT imaging system (a GE Discovery ST machine and a Varian RPM system) in a cine mode. In each patient, 10 different sets of 3D CT data corresponded to a breathing cycle, which were counted from 0% to 90% phases of a breathing cycle with an equal different time phase. These data sets are provided by the MIDAS community, http://midas.kitware.com/community/view/47. Each 3D-CT data set includes 136, 120, 150, and 120 slices of 16-bits axial-images for patient A, B, C and D. The size of each axial image is 512 × 512 pixels with resolution 0.98 square millimeters, and slice thickness is 2.5 millimeters.
4.2. Parameter Setting for the Level-Set Method
When we used a GAC model to control the curve propagation and allocated the boundaries of the zero LSF inside the liver, the following three conditions were used to adjust parameters. First, the reaction factor of the RD method (section 2.3) should be large enough to move a given curve in the outward direction. However, if this reaction factor were over defined, the curve would easily move outwards from boundaries of liver. We set it to
Figure 7. An example of some steps in creation of seed regions in axial images from coronal images.
be 0.005 and 0.03 for coronal and axial images, respectively. Next, the diffusion factor should be
as mentioned in [12] . Further, it should be a small value to get an accurate result when a given image includes high level of image noise. We assigned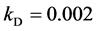
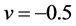
In addition, we simply defined the maximum number of iterations to stop the curve propagation as 300 iterations. However, if we segment liver’s regions in axial images, it will be possible to reduce the number of iterations. We automatically adjusted the number of iteration by performing parallel projection of liver-segmentation results in coronal images onto the vertical axes of coronal images. Actually, a position on the vertical axis is equivalent to the index of axial image. If the projection data at the position 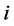
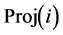
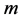
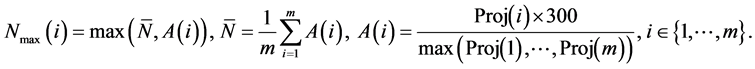
4.3. Results and Discussion
In this study, we validated similarities between the segmentation results of the proposed system and liver’s volumes delineated by a radiologist. Further, these segmentation results were compared with the liver-segmenta- tion methods based on the level-set speed image (LSSI) and statistical thresholding (ST) techniques, which were implemented in accordance with diagrams in section 2.1 and section 2.2, respectively.
4.3.1. Qualitative comparison
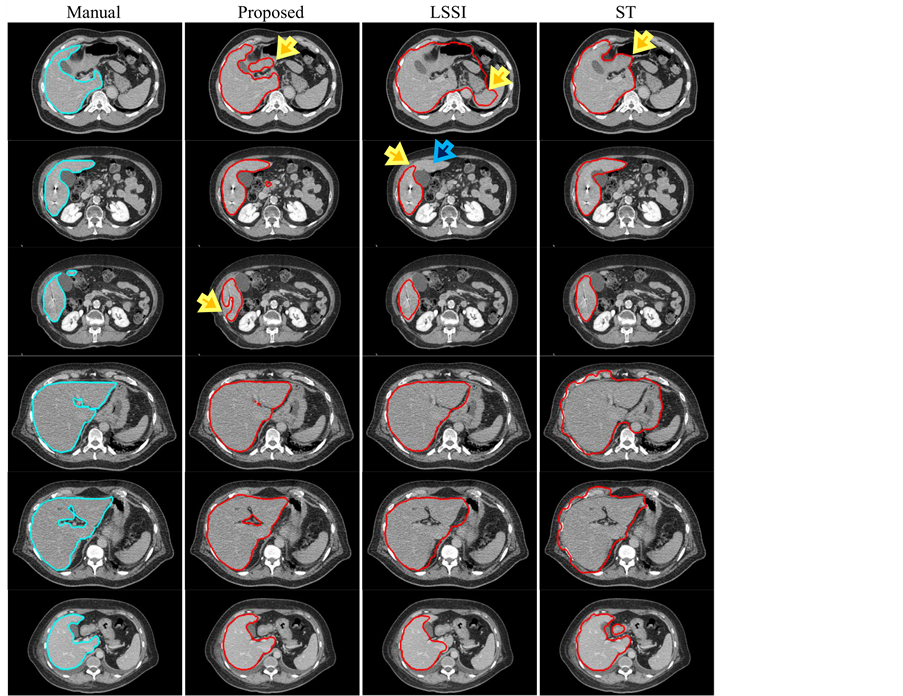
In Figure 8, an accumulated error from previous images and an overlap of gray-intensities between liver and another soft tissue caused some over-segmentations in all methods as shown in the first row. Liver segmentation based on the LSSI technique met a problem of the curve propagation in thin regions (see a yellow arrow in the second row). The given curve was unable to move into the remaining part of the liver’s region as indicated by a blue arrow. From observation, this problem occurred after a liver’s region in a given image was separated into two parts by edges in a speed image of the LSSI technique, and an initial region of the zero LSF was created inside the only one part. When we compared our proposed method with the LSSI and ST techniques, the proposed method achieved the best fitting boundaries of liver’s regions. These comparisons are illustrated in the remaining rows. However, these results did not clearly display hole-regions as shown in the outlines of manual delineation.
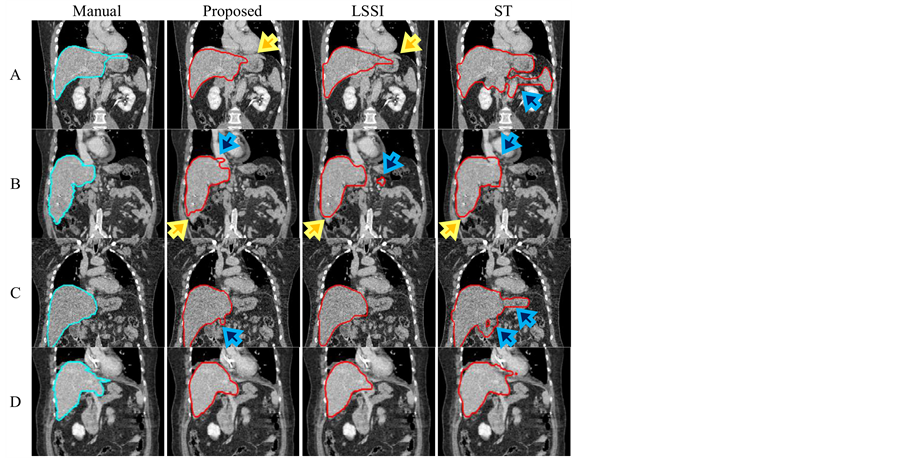
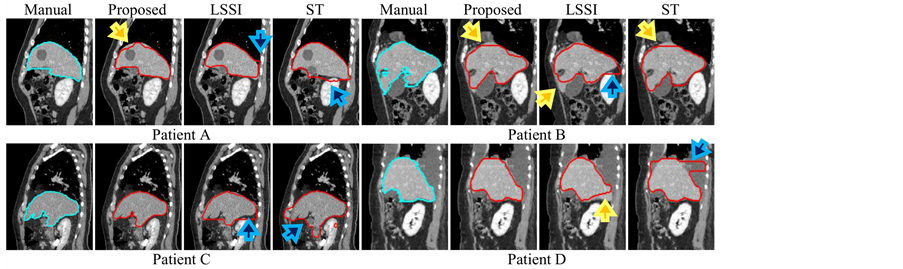
Next, Figure 9 shows examples of liver’s boundaries in coronal and sagittal images. The under-segmentation was a major problem of the proposed method as indicated by yellow arrows. This problem arises when an initial process creates extremely small seed-regions. Next, the results of liver segmentation based on the LSSI technique contained over or under-segmentations when some boundaries of anatomical structures were not extracted well in the speed images. Moreover, a critical problem of liver segmentation based on the ST technique is to cause a kind of over-segmentation as shown by blue arrows. In our opinion, this problem occurs when data sets include large variation in averages of gray-intensities among different axial-images. Further, sizes and locations of seed regions used in statistical measures occasionally fail to give good approximate liver’s regions.
4.3.2. Quantitative measures
This study validated the segmentation results by using relative absolute volume similarity (RAVS), volume overlapped coefficient (VOC) and dice similarity coefficient (DSC) [23] . Moreover, the quantities of over-and
Figure 8. Six examples of liver-segmentation results in axial-images of patient A (phase 0 slice 66), B (phase 20 slices 73 and 83), C (phase 0 slices 94 and 100), D (phase 50 slice 50), which are presented from top to bottom.
under-segmentations are measured by false positive rate (FPR) and false negative rate (FNR) [24], respectively.
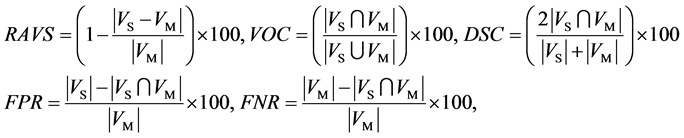
where 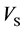
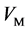
4.3.3. Computation time
The proposed system was operated under MATLAB environment on 3.40 GHz Intel(R) Core(TM) i7 2006 CPU. It spent around seven minutes 35 seconds to compute in the effective initial process. Further, liver segmentation in axial images consumed about 16 minutes and six seconds. Thus, the proposed system required around 23 mi-
Figure 9. Eight examples of liver-segmentation results: (Top) outlines in coronal images, and (bottom) outlines in sagittal images. The results show at slice 160 in patient A (phase 70), B (phase 30), C (phase 50), and D (phase 90).
Table 1. Comparison of average similarities and errors measured in all 40 data sets (unit: %).
Table 2. Comparison of average similarities and errors measured in patient A, B, C, and D (unit: %).
nutes and 41 seconds to segment a liver volume from 3DCT data that consists of 120 - 150 axial-image slices.
5. Conclusions
This study proposes an efficient liver-segmentation system based on a level-set method and consequent processes. The proposed system is composed of three main ideas. First, an effective initial process prevents the leakage of regions outside the ribcage when a given curve propagates near ribs and vertebrae. Further, it generates seed regions completely inside a liver’s volume for measuring statistical values of gray-intensities. Second, liver-corrective images are created to represent statistical regions of liver and preserve the edge information. The objective of these images is to improve accuracy of liver-segmentation. Lastly, computation time in the RD- GAC based level-set method is reduced by using a concept of multi-resolution.
We applied the proposed system to 40 sets of 3D CT-liver data, which were acquired by a 4D-CT imaging system from four patients. For each patient, 10 different sets of 3D CT were collected in different time phases of a breathing cycle. The segmentation results were compared with livers’ volumes, which were manually delineated by a radiologist. An average of similarity measures presented around 86.38 ± 4.26 percent. Further, the proposed system showed the highest accuracy compared with the liver-segmentation methods based on edge or statistical region information. However, the major problem found in the proposed method is a kind of under- segmentation. It appeared when liver’s regions were small and dirty edge information was produced by some artifacts. Thus, this problem will be addressed in the future work.
References
- Nakayama, Y., Li, Q., Katsuragawa, S., Ikeda, R., Hiai, Y., Awai, K., Kusunoki, S., Yamashita, Y., Okajima, H., Inomata, Y., et al. (2006) Automated Hepatic Volumetry for Living Related Liver Transplantation at Multisection CT 1. Radiology, 240, 743-748. http://dx.doi.org/10.1148/radiol.2403050850
- Jiang, S.B. (2006) Radiotherapy of Mobile Tumors. Seminars in Radiation Oncology, 16, 239-248. http://dx.doi.org/10.1016/j.semradonc.2006.04.007
- Campadelli, P., Casiraghi, E. and Esposito, A. (2009) Liver Segmentation from computed Tomography Scans: A Survey and a New Algorithm. Artificial Intelligence in Medicine, 45, 185-196. http://dx.doi.org/10.1016/j.artmed.2008.07.020
- Heimann, T., van Ginneken, B., Styner, M.A., et al. (2009) Comparison and Evaluation of Method for Liver Segmentation from CT Datasets. IEEE Transactions on Medical Imaging, 28, 1251-1264. http://dx.doi.org/10.1109/TMI.2009.2013851
- Mharib, A.M., Ramli, A.R., Mashohor, S. and Mahmood, R.B. (2012) Survey on Liver CT Image Segmentation Methods. Artificial Intelligence Review, 37, 83-95. http://dx.doi.org/10.1007/s10462-011-9220-3
- Lee, J., Kim, N., Lee, H., Seo, J.B., Won, H.J., Shin, Y.M., Shin, Y.G. and Kim, S.-H. (2007) Efficient Liver Segmentation Using a Level-Set Method with Optimal Detection of the Initial Liver Boundary from Level-Set Speed Images. Computer Methods and Programs in Biomedicine, 88, 26-38. http://dx.doi.org/10.1016/j.cmpb.2007.07.005
- Casciaro, S., Franchini, R., Massoptier, L., Casciaro, E., Conversano, F., Malvasi, A. and Lay-Ekuakille, A. (2012) Fully Automatic Segmentations of liver and Hepatic Tumors from 3-D Computed Tomography Abdominal Images: Comparative Evaluation of Two Automatic Methods. IEEE Sensors Journal, 12, 464-473. http://dx.doi.org/10.1109/JSEN.2011.2108281
- Whitaker, R.T. and Xue, X. (2001) Variable-Conductance, Level-Set Curvature for Image Denoising. Proceedings of International Conference on Image Processing, 7-10 October 2001, Thessaloniki, 142-145.
- Massoptier, L. and Casciaro, S. (2007) Fully Automatic Liver Segmentation through Graph-Cut Technique. Proceeding of the 29th Annual International Conference of the IEEE EMBS, Lyon, 23-26 August 2007, 5243-5246.
- Comaniciu, D. and Meer, P. (2002) Mean Shift: A Robust Approach toward Feature Space Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, 603-619. http://dx.doi.org/10.1109/34.1000236
- Osher, S. and Sethian, J.A. (1988) Fronts Propagating with Curvature-Dependent Speed: Algorithms Based on Hamilton-Jacobi Formulations. Journal of Computational Physics, 79, 12-49. http://dx.doi.org/10.1016/0021-9991(88)90002-2
- Zhang, K.H., Zhang, L., Song, H.H. and Zhang, D. (2013) Reinitializaion-Free Level Set Evolution via Reaction Diffusion. IEEE Transactions on Image Processing, 22, 258-271. http://dx.doi.org/10.1109/TIP.2012.2214046
- Li, C.M., Xu, C.Y., Gui, C.F. and Fox, M.D. (2005) Level Set Evolution without Re-Initialization: A New Variational Formulation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1, 430-436.
- Li, C.M., Xu, C.Y., Gui, C.F. and Fox, M.D. (2010) Distance Regularized Level Set Evolution and Its Application to Image Segmentation. IEEE Transactions on Image Processing, 19, 3243-3254. http://dx.doi.org/10.1109/TIP.2010.2069690
- Merriman, B., Bence, J.K. and Osher, S.J. (1994) Motion of Multiple Junctions: A Level Set Approach. Journal of Computational Physics, 112, 334-363. http://dx.doi.org/10.1006/jcph.1994.1105
- Caselles, V., Kimmel, R. and Sapiro, G. (1997) Geodesic Active Contours. International Journal of Computer Vision, 22, 61-79. http://dx.doi.org/10.1023/A:1007979827043
- Huang, D.Y., Lin, T.W. and Hu, W.C. (2011) Automatic Multilevel Thresholding Based on Two-Stage Otsu’s Method with Cluster Determination by Valley Estimation. ICIC International Journal of Innovative Computing, Information and Control, 7, 5631-5644.
- Otsu, N. (1979) A Threshold Selection Method from Gray-Level Histograms. IEEE Transactions on System, Man and Cybernetics, 9, 62-66.
- Hu, Q.M., Hou, Z.J. and Nowinski, W.L. (2006) Supervised Range-Constrained Thresholding. IEEE Transactions on Image Processing, 15, 228-240. http://dx.doi.org/10.1109/TIP.2005.860348
- Qiao, Y., Hu, Q.M., Qian, G.Y., Luo, S.H. and Nowinski, W.L. (2007) Thresholding Based on Variance and Intensity Contrast. Pattern Recognition, 40, 596-608. http://dx.doi.org/10.1016/j.patcog.2006.04.027
- Xu, X.Y., Xu, S.Z., Jin, L.H. and Song, E. (2011) Characteristic Analysis of Otsu Threshold and Its Applications. Pattern Recognition Letters, 32, 956-961. http://dx.doi.org/10.1016/j.patrec.2011.01.021
- Smith, N.B. and Webb, A. (2010) Introduction to Medical Imaging: Physics, Engineering and Clinical Applications. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511760976
- Dice, L.R. (1945) Measures of the Amount of Ecologic Association between Species. Ecology, 26, 297-302. http://dx.doi.org/10.2307/1932409
- Balafar, M. (2011) Spatial Based Expectation Maximizing (EM). Diagnostic Pathology, 6, 1-14. http://dx.doi.org/10.1186/1746-1596-6-103