Journal of Biomedical Science and Engineering
Vol.7 No.1(2014), Article ID:42426,10 pages DOI:10.4236/jbise.2014.71005
Predicting residue contacts for protein-protein interactions by integration of multiple information
![]()

1Graduate School of Natural Science and Technology, Kanazawa University, Kanazawa, Japan
2Institute of Science and Engineering, Kanazawa University, Kanazawa, Japan
Email: *kienltt@hnue.edu.vn, hirose@se.kanazawa-u.ac.jp, tvatva2002@gmail.com, thammakorn.kmutt@gmail.com, lananh257@gmail.com, thodx@hnue.edu.vn, ndluu@blu.edu.vn, mkubo@t.kanazawa-u.ac.jp, youichi@t.kanazawa-u.ac.jp, ken@t.kanazawa-u.ac.jp
Copyright © 2014 Tu Kien T. Le et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Tu Kien T. Le et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received 26 November 2013; revised 28 December 2013; accepted 12 January 2014
KEYWORDS:Residue-Residue Contacts; Domain-Domain Interactions; Protein-Protein Interactions; Domain Interfaces; Residue Co-Evolution; Contact Potentials
ABSTRACT
Detailed knowledge of interfacial region between interacting proteins is not only helpful in annotating function for proteins, but also very important for structure-based drug design and disease treatment. However, this is one of the most difficult tasks and current methods are constrained by some factors. In this study, we developed a new method to predict residue-residue contacts of two interacting protein domains by integrating information about evolutionary couplings andamino acid pairwise contact potentials, as well as domain-domain interaction interfaces. The experimental results showed that our proposed method outperformed the previous method with the same datasets. Moreover, the method promises an improvement in the source of template-based protein docking.
1. INTRODUCTION
Proteins take part in many biological processes such as DNA replication, gene expression, catalyzing metabolic reactions, and transporting molecules in living cells. To implement their functions, proteins often interact with other proteins to form permanent or transient protein complexes. The regions where proteins interact with each other are called protein interfaces. The knowledge of these regions is not only helpful for providing insights into the biological functions of the protein at proteomic level, but also for structure-based drug discovery and therapeutics development. Biophysical methods such as NMR (Nuclear Magnetic Resonance) and X-ray crystallography can provide detailed information about structure of protein-protein complexes, but their costs are still high. Therefore, it is motivated to develop computational methods in characterizing protein-protein interactions (PPIs).
The first approach that aims to investigate the interface of interacting proteins is prediction of PPI binding sites. Developed methods of this approach [1-7] are often based on sequence, structure, and physico-chemical characteristics to discriminate the interface residues from non-interface residues in a single protein. However, one protein may have two or more interfaces and each of them has specificity to some partner proteins. Hence it is also needed to develop methods that can infer residue contacts: contacts between residues of two interacting proteins [8]. Docking methods are able to meet this demand, but current docking methods require a time-consuming computational process and are difficult to define the best solution [9]. In addition, the conformation changes of monomers during the formation of proteinprotein complexes are also a challenge in them [8]. Recently, some docking methods combined knowledge of PPI binding sites with the docking process to improve their performance [8,10], but their applicability is still limited. Because of these limitations, it is difficult to predict large protein complexes consisting of many structure units (e.g., domains and monomers) by docking methods. In this circumstance, the development of new and better methods is therefore urgent [8].
Covariance-based methods of sequence analysis are other approaches to identifying interacting residues between interacting proteins or domains [11-14]. This approach relies on the premise that amino acid substitution patterns between interacting residues are constrained and correlated to each other. These couplings can be detected through mutual constraint of the amino acid substitutions in the two columns of a multiple sequence alignment. Solely depending on sequence information, this approach promises an application to the prediction of large-scale protein complexes, especially to predict transient ones. However, it requires a large set of binary PPIs or domain-domain interactions (DDIs) between protein members of two protein or domain families.
Recently, González et al. [15] introduced a method that relies on interaction profile hidden Markov model (ipHMM) proposed in [6] to predict residue contacts for two interacting protein domains. They used two ipHMMs to learn interaction sites from observed DDI interfaces of two interacting domain families and then applied the trained ipHMMs to predict interfaces of other unknown interacting domain pairs. The prediction results showed that their methods achieved high accuracy, true positive rate, and AUC (area under the ROC curve).
In this study, we aim to develop a new method to predict residue-residue contacts (RRCs) in interacting domain pairs, which not only uses domain interfaces like [15], but also integrates the other constrains in interacting residue pairs to improve performance of the predictor. In our novel method, the advantages of the previous researches are combined. Firstly, it inherits the advantage of using ipHMM proposed by Friedrich et al. [6] to transfer interaction information among members within a protein (or domain) family. Secondly, it utilizes an advanced covariance-based method to capture the coevolution relationship of residue pairs of PPIs. Finally, it integrates contact potentials of amino acids, which are often used in docking protein complexes and in protein structure prediction. The experimental results showed that our method outperformed the method of Gonzáslez et al. [15]. In addition, it accurately predicts residue contacts of hetero DDIs in the KBDOCK database [16], a source of the template-based protein docking.
The rest of this paper is organized as follows: Section 2 introduces frameworks of our novel method; Section 3 presents how we processed data; Section 4 shows the experimental results and compares the performances of our proposed method with the previous method. Finally, conclusions are described in Section 5.
2. METHOD
Figure 1 illustrates the general framework of our method. It includes three main steps for data filtering, feature construction, and classification. Here, it is expected that proteins with similar sequences often interact in similar ways [17] and one domain family may contain one or more interfaces [16,18]. Hence, we assumed that interaction between the query domain sequences are more likely to resemble DDIs that have the highest sequence identity with them. Based on this assumption, in the first step, we filtered out a subset of known interface DDIs such that the number of substitutions between their sequences and query domain sequences is smaller than a given threshold t. In the second step, the filtered DDIs were used to estimate two ipHMMs. Then, interaction probability (interactability) of residues, which belong to the query DDI and the filtered DDIs, were obtained from the estimated ipHMMs. Besides, we computed coevolution scores and contact potential scores for residue pairs based on direct coupling analysis algorithm (mfDCA) [19] and amino acid pairwise contact potentials (AAPCPs) [20], respectively. Subsequently, feature vector of residue pairs were formed. In the last step, we trained an SVM classifier and then used it to classify class label for residue pairs of the query DDI. The final output is a characterized query DDI: residue pairs of two given domain sequences contacting with each other. More details of our method are shown in two algorithms below. The algorithm 1 represents how we filtered out DDIs and trained ipHMMs, while the algorithm 2 represents how we coordinated information sources to construct feature vectors, and how we trained and tested a residue-residue contact classifier with SVM. In the next subsections, we first
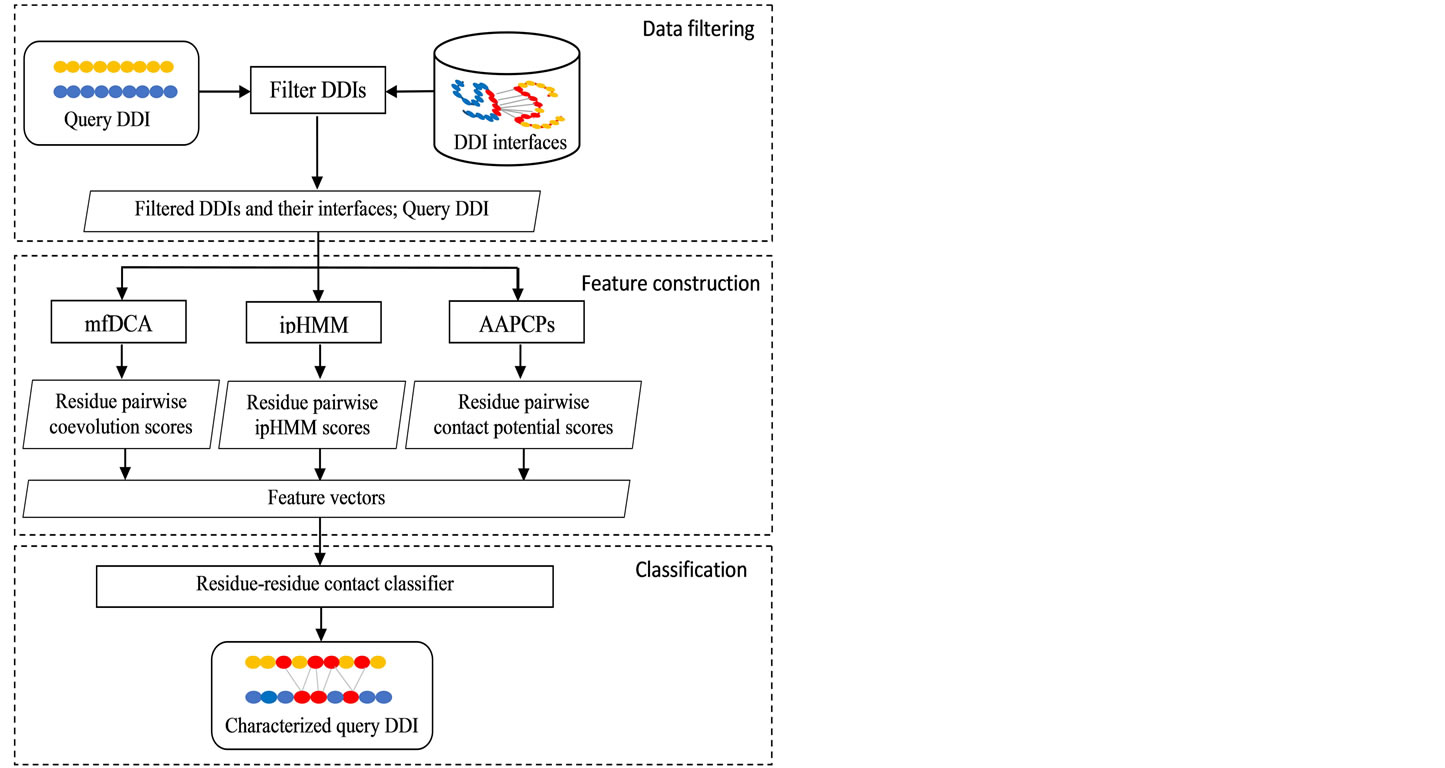
Figure 1. The framework of proposed prediction method. It includes three main steps: data filtering, feature construction, and classification.
describe more about ipHMMs and their applications tothe prediction of DDIs and residue contacts. We then describe how to calculate co-evolution scores and contact potential scores.
2.1. Interaction Profile Hidden Markov Models and Its Applications
In a multiple sequence alignment of homologous proteins, the conserved regions manifest structure and function of protein sequences [21]. Profile hidden Markov model (pHMM) is a kind of hidden Markov model which converts a multiple sequence alignment into a position-specific scoring system to model protein families [22]. Based on pHMM, Friedrich et al. proposed ipHMM to predict binding sites for protein domains [6]. ipHMM embeds interaction information of protein domain sequences extracted from Protein Data Bank (PDB) to a domain family by dividing each match state of the pHMM into two states: that is interacting and noninteracting match states. Each interaction match state presents posterior interaction probability of residues aligned at that position. The ability of ipHMM is that it can transfer the binding site information among the member in the domain family. In other words, using only known binding sites of sequences to estimates its parameters, it can infer binding sites of other sequence members that are solely known as sequences. This advantage is inherited from pHMM and it makes ipHMM a scalable method. However, like other PPI binding site prediction methods, ipHMM is only applied tothe prediction of binding sites in a single protein.
Taking the advantages of ipHMM into account, González and Liao [23,24] applied it to predict binary DDIs (i.e., do two domain sequences interact?). The probability features in the ipHMM are extracted and then transferred into a Fisher vector, which represents the derivatives of the probability for a query sequence to belong to the domain family. Therefore, the feature vector of a pair of domain sequences is formed by the concatenation of two Fisher vectors. Then, the singular value decomposition and support vector machine were employed to do the feature selection and binary classification of DDIs and nonDDIs. What is interesting in their method is that they used two leaning models ipHMM and SVM in tandem. ipHMM was used to transfer the binding site information among the member in the family, while the SVM was used to classify DDIs and nonDDIs. More recently, they extended their method to predict residue-residue contacts for a given binary interaction domain pair [15]. In [15], each residue in a domain sequence are represented by a Fisher vector of size 20 corresponding the number of amino acids such as:
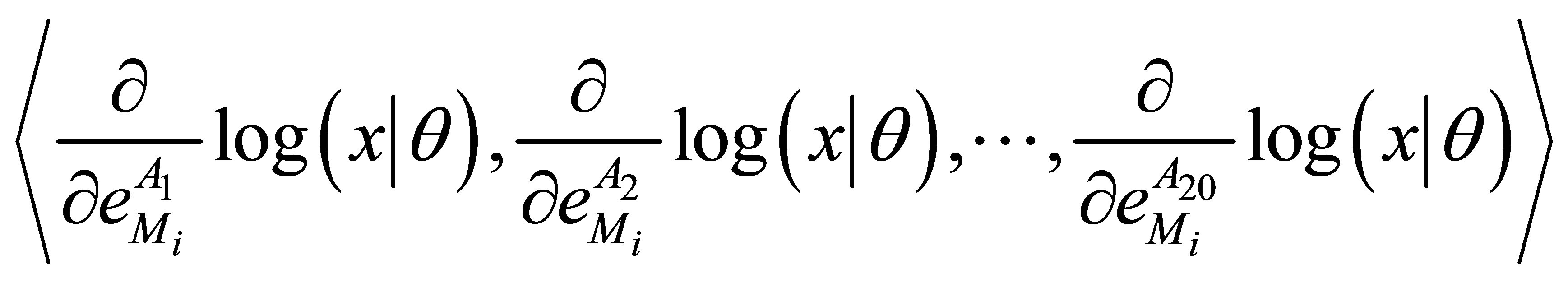
 where
where 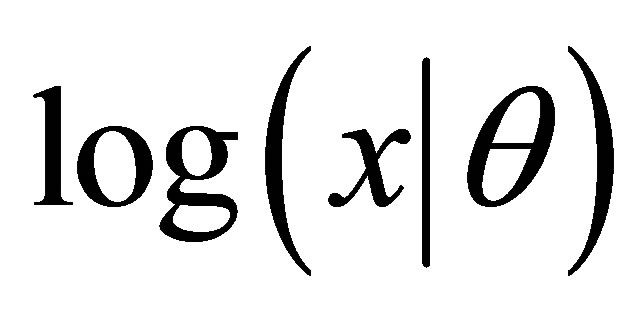 is the probability of the domain
is the probability of the domain 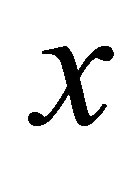 given the model
given the model . Here,
. Here,  is a parameter of an ipHMM that represents a domain family.
is a parameter of an ipHMM that represents a domain family. ,
,  is the emission probability of amino acid
is the emission probability of amino acid 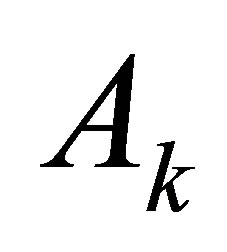 at the interacting or noninteracting match state
at the interacting or noninteracting match state . Hence, a concatenation of two Fisher vector representsa feature vector for a pair of residues. In addition, their method uses solely binding sites information.
. Hence, a concatenation of two Fisher vector representsa feature vector for a pair of residues. In addition, their method uses solely binding sites information.
Like [15], in this study, we also apply the approach of using the ipHMM to transfer binding sites among members in a domain family and the SVM to classify residue contacts and nonresidue contacts. However, unlike their method, our method has the following differences:
1)Introduce a threshold parameter t to filter out DDIs except the ones that have most similar interaction interfaces with the query domain sequences to train ipHMM.
2)Integrate more interaction constraints for residue pairs, i.e. evolutionary couplings of PPIs and amino acid pairwise contact potentials, to improve the performance of the predictor.
In Section 4, the effect of the threshold parameter t and the improvement of the performance are shown.
2.2. Direct Coupling Analysis
In the analyses of protein structures and protein-protein interactions, covariance-based methods have been used for defining residue contacts in intraand inter-proteins. The basic concept of covariance is defined as a relationship between a correlated substitution pattern and residue-residue contacts. If two residues of a protein or a pair of interacting proteins have an attractive interaction, the change of amino acid by substitution at one position may leads to the change at another position in order to maintain their contact [19]. For example, given a multiple sequence alignment (MSA) of a set homologous protein, the correlation of two columns i and j in the MSA can be defined by the mutual information
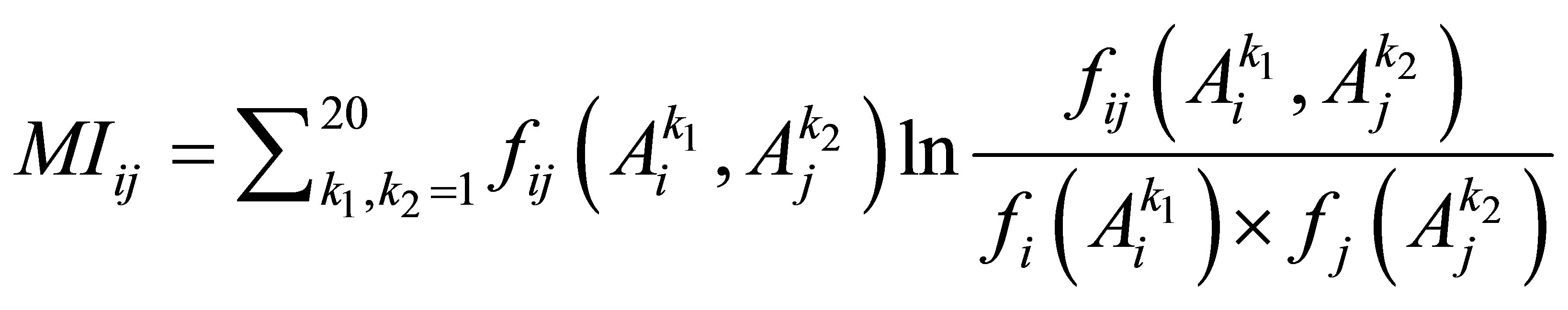 , (1)
, (1)
where ,
, 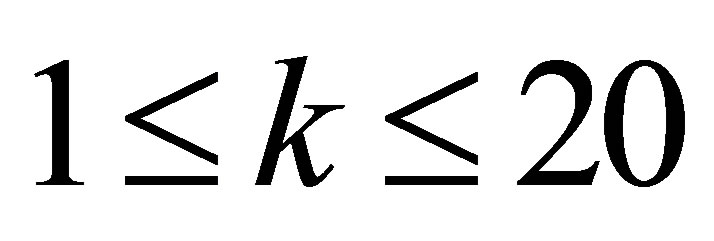 is the frequency of the amino acid
is the frequency of the amino acid 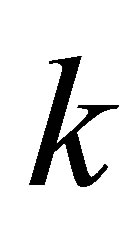 in the column i;
in the column i; 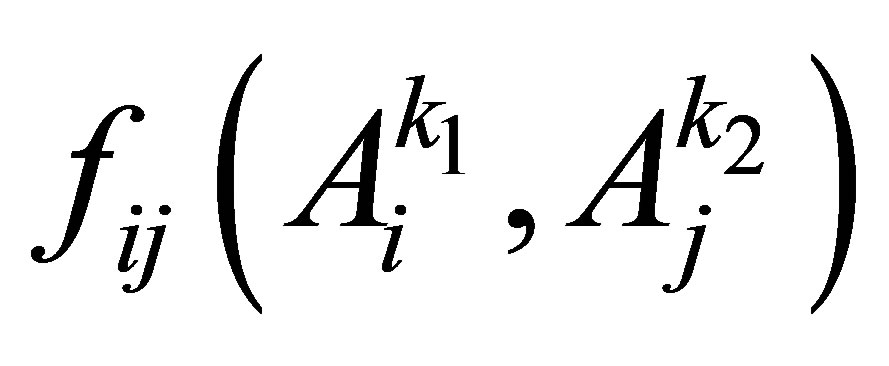 is the co-occurrence frequency of two amino acids
is the co-occurrence frequency of two amino acids 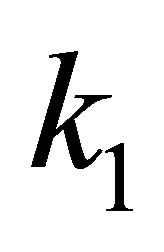 and
and 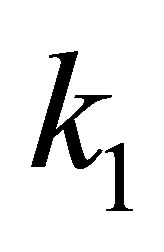 at column i and column j, respectively.
at column i and column j, respectively.
However, Eq.1 could not distinguish direct correlations from indirect correlations [13,14]. Hence, Weigt and his colleagues recently have developed an algorithm named direct coupling analysis (DCA) based on maximum-entropy modeling to capture direct information of residue pairs [14,19]. Their experimental results indicated that DCA method could obtain a large number of correctly predicted contacts, generalize the global structure of the contact maps between protein domains, and especially detect clear signals beyond intra-domain residue contacts and inter-domain interaction in protein oligomers, etc. Furthermore, the scalability of DCA method is confirmed by the research group of Marks et al. [25,26] through the successful utilization of it to predict the three dimensional structure of membrane proteins, that is one of the main challenge in predicting protein structure. Another important application of the DCA is that it can be applied to define PPI interface of a pair of proteins rather than single protein [19]. Currently, DCA is applied to define the residue contacts for PPIs of the bacterial two-component signal transduction system [14, 27].
Figure 2 and 3 illustrate how we applied mfDCA algorithm proposed in [19] to obtain pairwise residue coevolution scores. In Figure 2, sequences of observed DDIs between two domain families M and N are firstly aligned to the corresponding pHMM built in the Pfam database [28]. These aligned sequences are then concatenated to form a multiple alignment (concatenated MSA). In Figure 3, two query sequences belonging to M and N are also aligned and concatenated to form an aligned query sequence, then put into the mfDCA. Based on the concatenated MSA (Figure 2), the mfDCA computes the correlation between two residues i and j, which belong to the query sequences of domain families M and N, respectively. Note that the mfDCA returns both local correlation (i.e., mutual information, Eq.1) and global correlation (i.e., direct information). We used both of them as the features for residue pairs.
2.3. Statistical Amino Acid Pairwise Contact Potentials
Amino acid pairwise contact potentials are energy functions derived from interfacial regions of protein structures by statistical analysis. They are collected and organized in AAindex database [20]. In this study, we chose 12 contact potentials to integrate into our method as features for each residue pairs (Table 1). Each of chosen contact potentials is a matrix of size 20 × 20 where each entry presents energy relationship of a pair of amino acids. Since the contact potentials have different value ranges, we normalized them into the same scale before using.
3. DATA PROCESSING
For each pair of Pfam families, we obtained interaction information of DDIs from a database of 3D Interacting Domains (3did) [29] (as of December 2011). 3did used known 3D structure protein complexes in Protein Data Bank (PDB) to extract protein-protein interaction interfaces at domain and residue levels. A residue pair belonging to two domain sequences is considered to be contacting if it meets at least five contacts of vander Waals, electrostatic, and hydrogen bonds. Then, we mapped Pfam domain information organized in 3did to
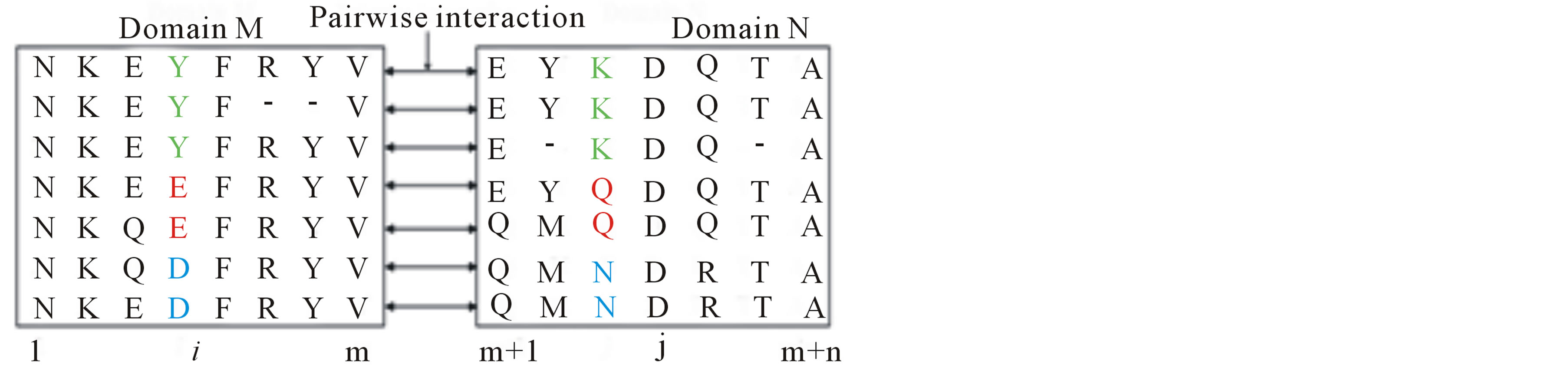
Figure 2. An example of concatenated multiple alignment formed by domain-domain interactions between two domain families M and N. The sequences of a set of DDIs are aligned to correspond pHMM built in the Pfam database and then are concatenated together to form a multiple alignment. Correlation between two columns i and j in the concatenated MSA is evaluated based on the frequency of amino acids in a single column or pairs of amino acids in the two columns.

Figure 3. Computational pipeline for pairwise residue-residue co-evolution scores. A given sequence pair of two domain families M and N is firstly aligned to their pHMMs and then is concatenated to form query concatenated sequence to put into the mfDCA model. Based on the concatenated MSA, the mfDCA will calculate direct information for residue pairs.

Table 1. List of contact potentials.
PDB database to retrieve domain sequences for DDIs.
The DDIs in the 3did can be classified into three types: intra DDI is the DDI where two domains belong to a single protein chain, homo DDI is the DDI where two domains belongs to two different instances of the same protein chain, and hetero DDI is the DDI where two domains belongs to two different protein chains [16]. Because the intra DDIs may be caused by the formation of protein structure rather than by biological function, we eliminated them from our obtained DDI data. In addition, because of many duplicated DDIs existing in a PDB entry, we clustered the remaining DDIs between domain family pairs into groups that sequence members are at least 95% similar. In each groups, we chose a DDI as a representative.
Furthermore, for satisfying statistical analysis, sufficient amount of DDI data is needed in the calculation of the residue co-evolution score by DCA. Based on the analysis in [19], we kept domain family pairs that have at least 100 DDIs remaining after the data processing. Table 2
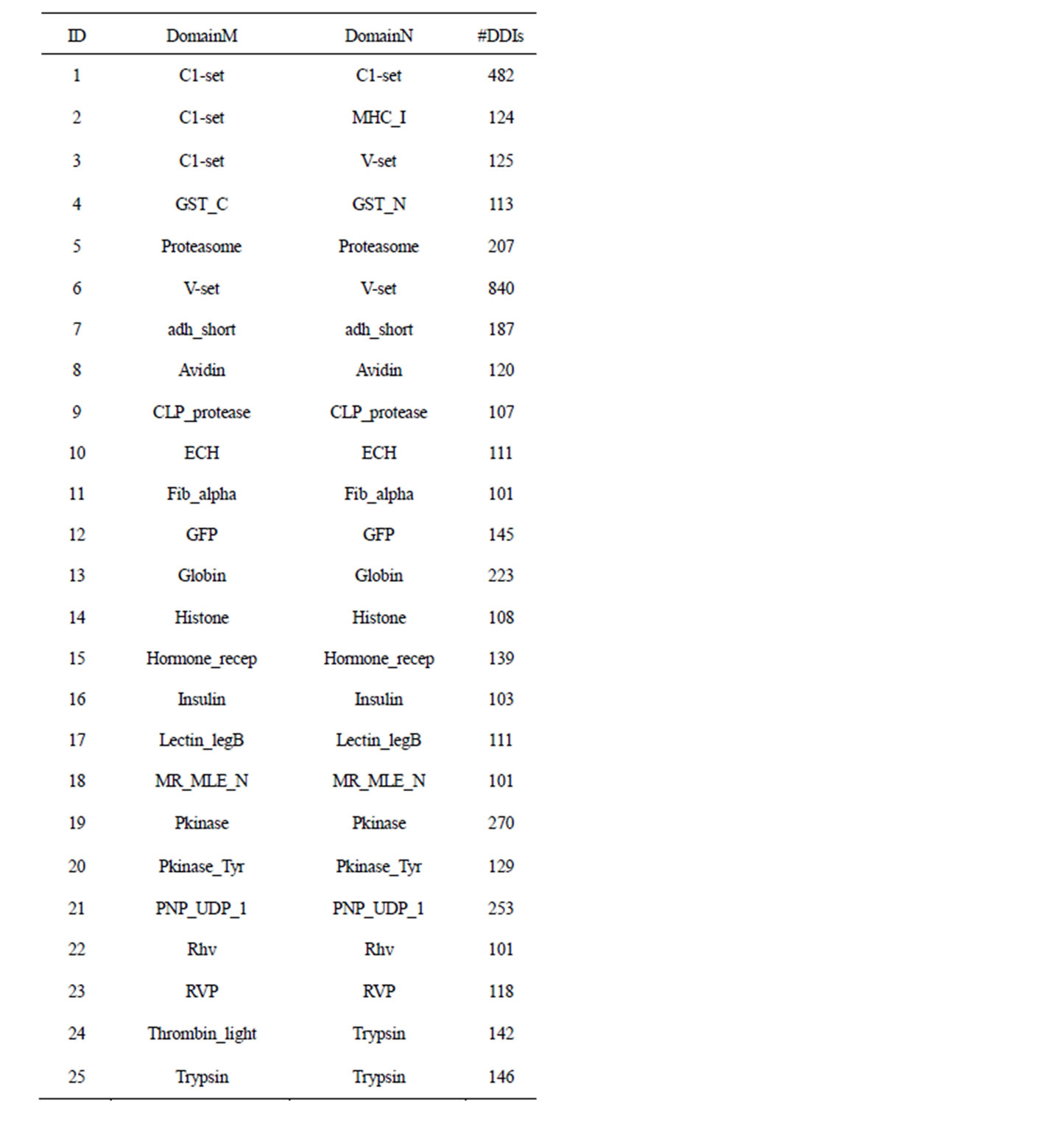
Table 2. Datasets used for experiments.
lists the names of 25 domain family pairs and the number of their DDIs that we used to do experiments. In the rest of this paper, each domain family pair is simply called a dataset.
4. RESULTS
To evaluate the performance of our methods, we conducted experiments investigating the following three aspects.
1)The effect of the threshold t to the predicted results.
2)The improvement of the performance comparing with the method proposed in [15] when we integrated more information.
3)The application of our method enriches the data source for template -based protein docking Additionally, we also attempted to know whether the transfer of posterior interaction probability of residues into Fisher vectors is more effective than directly using posterior interaction probability from the ipHMM (hereinafter called Fisher score and ipHMM score, respectively). Hence, a combination of three different feature sets was tested. The first feature set consists of Fisher scores proposed in [15]. The second feature set consists of the ipHMM score, the co-evolution scores, and the contact potentials. The last feature set is the combination of the Fisher scores, the co-evolution score, and the contact potentials. We named these three feature sets are named ipFis_RRC, ipCoEP_RRC, and ipCombine_RRC, respectively.
For each dataset in Table 2 and for each value of the threshold t described in Section 2, we repeated cross validation procedure five times for three feature sets ipFis_RRC, ipCoEP_RRC, and ipCombine_RRC based on the framework in Figure 1 and two algorithms described in Section 2. However, the number of possible residue pairs generated from two domain sequences is often large and highly imbalanced (i.e., the number of contact residue pairs is much smaller than the number of noncontact residue pairs). Therefore, when the value of the threshold t is large, the number of filtered DDIs also increases and the training set becomes so large. To tackle this problem, we decreased the size of training data in two approaches. The first approach is that we randomly took 10 DDIs from filtered DDIs to generate training data if the size of the set was greater than 10 (otherwise, all filtered DDIs were used). The second approach is that we firstly generated residue pairs from all filtered DDIs and randomly sampled noncontact residue pairs equal to the number of contact residue pairs. For short, we call the former sampling DDI case and the latter sampling nonRRC case.
The predictive performance was evaluated using three measures: true positive rate (TPR), false positive rate (FPR), and the Matthew correlation coefficient (MCC). They are defined as:

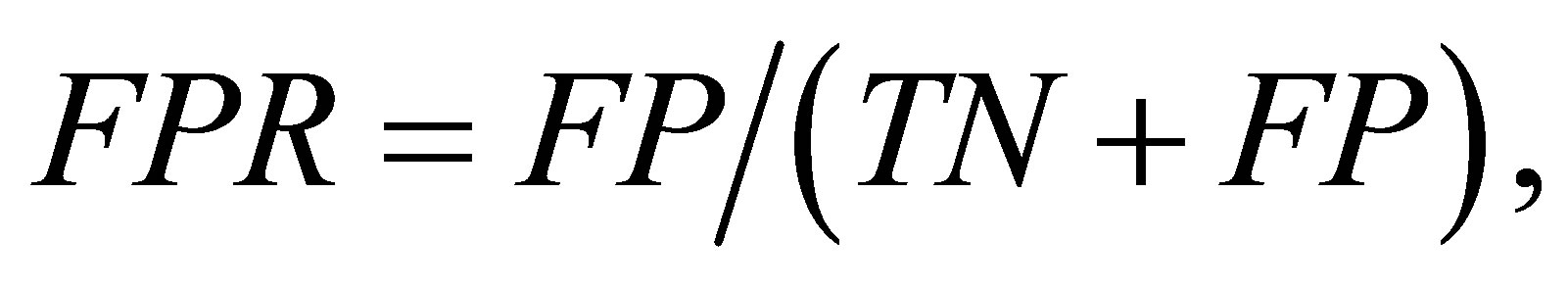
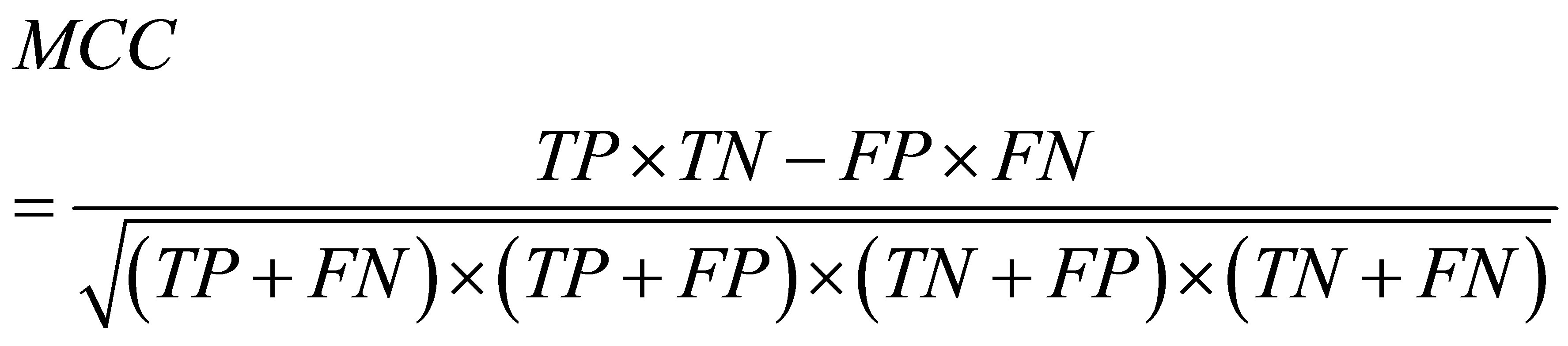
where TP and TN are the number of contact residue pairs and noncontact residue pairs predicted correctly, and FN and FP are the number of contact residue pairs and noncontact residue pairs predicted incorrectly. The higher TPR (or MCC) is better, while the lower FPR is better. In addition, MCC is a balanced measure that takes all TP, TN, FP, and FN into account and therefore it is a good measure when the data is imbalanced. Here, because the datasets are imbalanced, we gave a primary significance to MCC in comparing the performance of methods.
Figure 4 shows the averages of TPR, FPR, and MCC of predicted results of all three feature sets on 25 datasets with various values of the threshold tin both cases of sampling DDIs (Figure 4, left column) and sampling nonRRC (Figure 4, right column). In this figure, we made the following observations:
1)The lower value of the threshold t leads to the better TPR, FPR, and MCC. This result demonstrates that the sequence distance affects to the predicted results.
2)The TPRs in the case of sampling nonRRC is much better than the case of sampling DDIs. Otherwise, the FPRs of the sampling DDIs are better than the sampling nonRRC.
3)The average MCCs show that the ipCoEP_RRC is the worst predictor, while the ipCombine_RRC is better than the ipFis_RRC. This suggests that transferring probabilities from ipHMM to the Fisher scores is better than directly using them. Moreover, the integration of residue co-evolution and contact potentials improves the performance. It also confirms that our proposed method outperforms the one in [15].
In addition, we obtained some hetero DDIs of a pair of domain families C1-set/MHC-I from KBDOCK database as the queries and tried to predict their residue contacts. KBDOCK [16] is a database that integrates 3did, PDB, and Pfam into one, then uses spatial clustering technique to cluster binding sites for proteins. It extracts only hetero DDIs of 3did for supporting knowledge-based protein docking. Then, we conducted the experiments of predicting residue contacts for hetero DDIs by the feature set ipFisCoR_RRC and sampling nonRRC with various values of the threshold t. Table 3 shows the prediction performance with the value of the threshold t = 0.5. It can be seen that our method can accurately predict residue contacts for hetero DDIs. Hence, this demonstrates that the method may be utilized to enrich the data source of template-based protein docking.
5. CONCLUSIONS
In this study, a new method to predict residue-residue contacts was presented. The method follows an approach that has ability to aggregate the ipHMM and SVM for
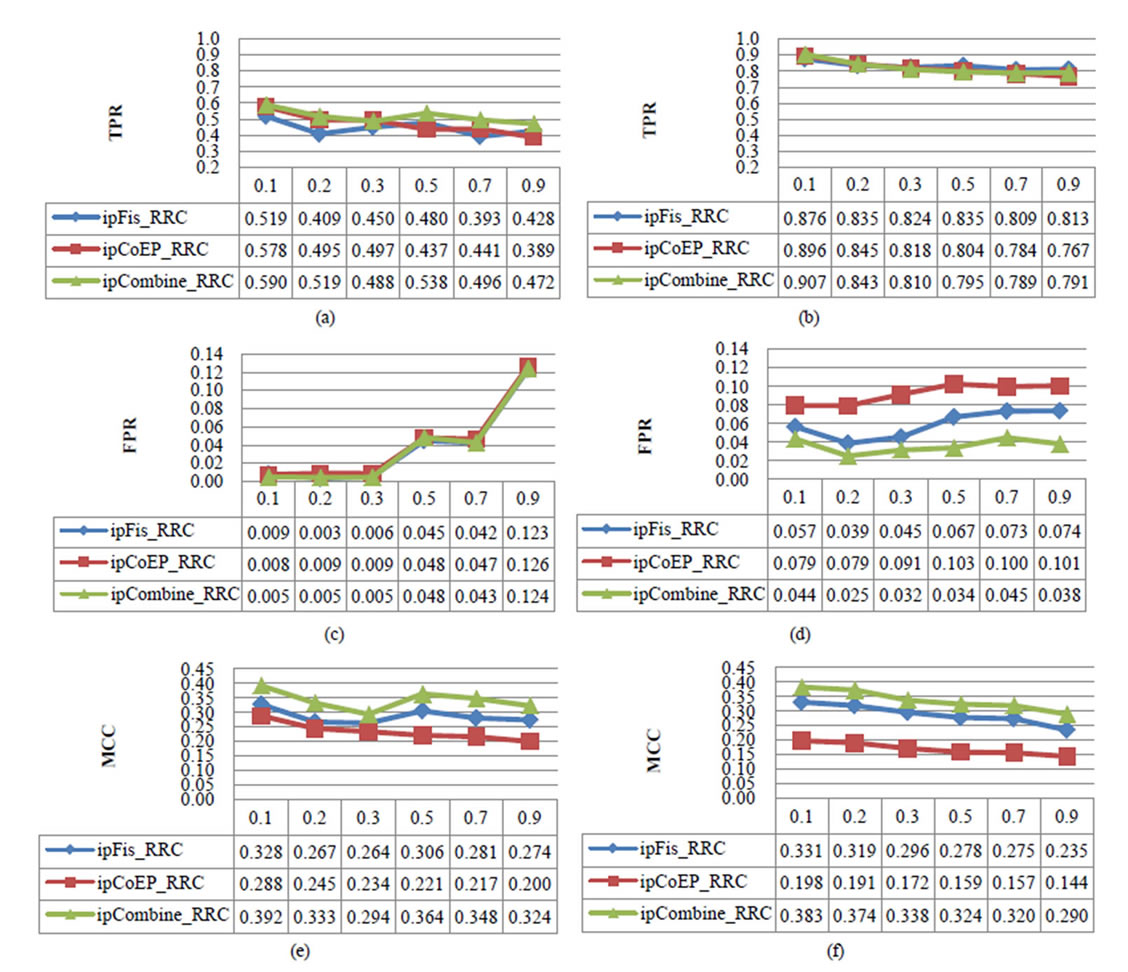
Figure 4. Comparison of TPR, FPR, and MCC by three methods ipFis_RCC, ipCoEP_RCC, and ioCombine_RCC predicting results in two cases: (a), (c), and (e) for sampling DDIs; and (b), (d), and (f) for sampling nonRRC.
inferring residue-residue contacts between interactive domains. The ipHMM was used to transfer binding site information among members in a domain family, while SVM was used to classify RRCs and nonRRCs. Besides binding site information, our proposed method utilized information of residue co-evolution and amino acid pairwise contact potentials to empower the classifier. It improved the performance of the predictor when comparing with the previous method.
On the other hand, we restricted the calculation of co-evolution of residue pairs by the observed DDIs in 3did. This may lead to decreasing its effectiveness to the performance and detracting the scalability of our method. These limitations could be overcome by collecting extra DDIs from binary PPI data. However, it is known that PPI data contain high false positive and high false negative, so we need to validate them before using.
In addition, the current trends in docking methods integrate knowledge of protein interfaces to improve their performance. The initial results of applying our method to predict residue contacts of some hetero DDIs in the KBDOCK database demonstrate that our method promises to enrich the source of template-based protein docking.
ACKNOWLEDGEMENTS
The authors wish to thank Friedrich et al., Gonzáslez et al., Morcos et al., and Hopf et al. for making available their Matlab implementations. In this research, the super-computing resource was provided by Human Genome Center, the Institute of Medical Science, the University of Tokyo. Additional computation time was provided by the super computer system in Research Organization of Information and Systems

Table 3. Prediction performance of hetero DDIs of the domain family pair C1-set/MHC-I in the KBDOCK (t = 0.5).
(ROIS), National Institute of Genetics (NIG).
REFERENCES
- Chen, C.-T., Peng, H.-P., Jian, J.-W., Tsai, K.-C., Chang, J.-Y., Yang, E.-W., Chen, J.-B., Ho, S.-Y., Hsu, W.-L. and Yang, A.-S. (2012) Protein-protein interaction site predictions with three-dimensional probability distributions of interacting atoms on protein surfaces. PloS ONE, 7, e37706. http://dx.doi.org/10.1371/journal.pone.0037706
- Jordan, A.R., El-Manzalawy, Y., Dobbs, D. and Honavar, V. (2012) Predicting protein-protein interface residues using local surface structural similarity. BMC Bioinformatics, 13, 41. http://dx.doi.org/10.1186/1471-2105-13-41
- Bradford, J.R. and Westhead, D.R. (2005) Improved prediction of protein-protein binding sites using a support vector machines approach. Bioinformatics, 21, 1487-1494. http://dx.doi.org/10.1093/bioinformatics/bti242
- Zhou, H.X. and Shan, Y. (2001) Prediction of protein interaction sites from sequence profile and residue neighbor list. Proteins, 44, 336-343. http://dx.doi.org/10.1002/prot.1099
- Burgoyne, N.J. and Jackson, R.M. (2006) Predicting protein interaction sites: Binding hot-spots in protein-protein and protein-ligand interfaces. Bioinformatics, 22, 1335- 1342. http://dx.doi.org/10.1093/bioinformatics/btl079
- Friedrich, T., Pils, B., Dandekar, T. and Muller, T. (2006) Modelling interaction sites in protein domains with interaction profile hidden Markov models. Bioinformatics, 22, 2851-2857. http://dx.doi.org/10.1093/bioinformatics/btl486
- Ofran, Y. and Rost, B. (2003) Predicted protein-protein interaction sites from local sequence information. FEBS Letters, 544, 236-239. http://dx.doi.org/10.1016/S0014-5793(03)00456-3
- Zhou, H.-X. and Qin, S. (2007) Interaction-site prediction for protein complexes: A critical assessment. Bioinformatics, 23, 2203-2209. http://dx.doi.org/10.1093/bioinformatics/btm323
- Ritchie, D.W. (2008) Recent progress and future directions in protein-protein docking. Current Protein and Peptide Science, 9, 1-15. http://dx.doi.org/10.2174/138920308783565741
- Li, B. and Kihara, D. (2012) Protein docking prediction using predicted protein-protein interface. BMC Bioinformatics, 13, 7. http://dx.doi.org/10.1186/1471-2105-13-7
- Thattai, M., Burak, Y. and Shraiman, B.I. (2007) The origins of specificity in polyketide synthase protein interactions. PLoS Computational Biology, 3, 1827-1835. http://dx.doi.org/10.1371/journal.pcbi.0030186
- Burger, L. and Van Nimwegen, E. (2008) Accurate prediction of protein-protein interactions from sequence alignments using a Bayesian method. Molecular Systems Biology, 4, 1-14. http://dx.doi.org/10.1038/msb4100203
- White, R.A., Szurmant, H., Hoch, J.A. and Hwa, T. (2007) Features of protein-protein interactions in two-component signaling deduced from genomic libraries. Methods in Enzymology, 422, 75-101. http://dx.doi.org/10.1016/S0076-6879(06)22004-4
- Weigt, M., White, R.A., Szurmant, H., Hoch, J.A. and Hwa, T. (2009) Identification of direct residue contacts in protein-protein interaction by message passing. PNAS, 106, 67-72. http://dx.doi.org/10.1073/pnas.0805923106
- González, A.J., Liao, L. and Wu, C.H. (2013) Prediction of contact matrix for protein-protein interaction. Bioinformatics, 29, 1018-1025. http://dx.doi.org/10.1093/bioinformatics/btt076
- Ghoorah, A.W., Devignes, M.-D., Smaïl-Tabbone, M. and Ritchie, D.W. (2011) Spatial clustering of protein binding sites for template based protein docking. Bioinformatics, 27, 2820-2827. http://dx.doi.org/10.1093/bioinformatics/btr493
- Aloy, P., Ceulemans, H., Stark, A. and Russell, R.B. (2003) The relationship between sequence and interaction divergence in proteins. Journal of Molecular Biology, 332, 989-998. http://dx.doi.org/10.1016/j.jmb.2003.07.006
- Keskin, O. and Nussinov, R. (2007) Similar binding sites and different partners: Implications to shared proteins in cellular pathways. Structure, 15, 341-354. http://dx.doi.org/10.1016/j.str.2007.01.007
- Morcos, F., Pagnani, A., Lunt, B., Bertolino, A., Marks, D.S., Sander, C., Zecchina, R., Onuchic, J.N., Hwa, T. and Weigt, M. (2011) Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proceedings of the National Academy of Sciences of the United States of America, 108, E1293- E1301. http://dx.doi.org/10.1073/pnas.1111471108
- Kawashima, S., Pokarowski, P., Pokarowska, M., Kolinski, A., Katayama, T. and Kanehisa, M. (2008) AAindex: Amino acid index database, progress report 2008. Nucleic Acids Research, 36, D202-D205. http://dx.doi.org/10.1093/nar/gkm998
- Krogh, A., Brown, M., Mian, I.S., Jokander, K. and David, H. (1994) Hidden Markov Models in Computational Biology Applications to Protein Modeling. Journal of Molecular Biology, 235, 1501-1531. http://dx.doi.org/10.1006/jmbi.1994.1104
- Eddy, S.R. (1998) Profile hidden Markov models. Bioinformatics Review, 14, 755-763.
- González, A.J. and Liao, L. (2010) Predicting domaindomain interaction based on domain profiles with feature selection and support vector machines. BMC Bioinformatics, 11, 537. http://dx.doi.org/10.1186/1471-2105-11-537
- González, A.J. and Liao, L. (2009) Constrained fisher scores derived from interaction profile hidden Markov models improve protein to protein interaction. Proceedings of the First International Conference BICoB 2009, New Orleans, 8-10 April 2009, 236-247.
- Hopf, T.A., Colwell, L.J., Sheridan, R., Rost, B., Sander, C. and Marks, D.S. (2012) Three-dimensional structures of membrane proteins from genomic sequencing. Cell, 149, 1607-1621. http://dx.doi.org/10.1016/j.cell.2012.04.012
- Marks, D.S., Colwell, L.J., Sheridan, R., Hopf, A.T., Pagnani, A., Zecchina, R. and Sander, C. (2011) Protein 3D structure computed from evolutionary sequence variation. PloS ONE, 6, e28766. http://dx.doi.org/10.1371/journal.pone.0028766
- Procaccini, A., Lunt, B., Szurmant, H., Hwa, T. and Weigt, M. (2011) Dissecting the specificity of protein-protein interaction in bacterial two-component signaling: orphans and crosstalks. PloS ONE, 6, e19729. http://dx.doi.org/10.1371/journal.pone.0019729
- Punta, M., Coggill, P.C., Eberhardt, R.Y., Mistry, J., Tate, J., Boursnell, C., Pang, N., Forslund, K., Ceric, G., Clements, J, Heger, A., Holm, L., Sonnhammer, E.L.L., Eddy, S.R., Bateman, A. and Finn, R.D. (2012) The Pfam protein families database. Nucleic Acids Research, 40, D290-D301. http://dx.doi.org/10.1093/nar/gkr1065
- Stein, A., Russell, R.B. and Aloy, P. (2005) 3did: Interacting protein domains of known three-dimensional structure. Nucleic Acids Research, 33, D413-D417. http://dx.doi.org/10.1093/nar/gki037
NOTES
*Corresponding author.





