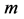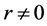Journal of Biomedical Science and Engineering
Vol.07 No.08(2014), Article ID:47340,23 pages
10.4236/jbise.2014.78050
Modeling Mechanical Patterns for Striated Muscles
Valery B. Kokshenev
Departamento de Fisica, Instituto de Ciencias Exatas, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil
Email: valery.kokshenev@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2014; revised 25 May 2014; accepted 7 June 2014
ABSTRACT
Muscles show a surprisingly large variety of functions when they mechanically respond to different environmental requests. However, the in vivo workloop studies distinguish well only four patterns of skeletal muscles, producing positive, negative, almost zero and zero net works, that qualifies them respectively as motors, brakes, struts, and springs. While much effort of comparative biologists has been done in searching for muscle design patterns, no fundamental concepts underlying such four primary patterns were established. In this interdisciplinary study, continuum mechanics is applied to the problem of muscle structure in relation to function. The known ability of a powering muscle as whole to be tuned via natural (resonant) frequency to the efficient locomotion is now modeled through the non-linear elastic muscle moduli, controlling both the contraction frequency and velocity. When incorporated in activated skeletal and cardiac (striated) muscles via the mechanical similarity between loaded and reaction forces, further exploration of elastic force patterns (borrowed from solid state physics) yields an explicit rationalization for currently known locomotor muscle patterns. Besides explanation of the origin of allometric exponents derived for leg muscles in animals adapted to fast running and wing muscles in flying birds, the skeletal and cardiac muscles are patterned through the primary and secondary high power activities. Further applications are expected to be useful in designing of artificial muscles and modeling living and extinct animals.
Keywords:
Continuum Mechanics, Modeled Muscles, Workloops, Scaling Elastic Effects, Allometry, Active Stiffness

1. Introduction
The mechanical role of muscles varies widely with their architecture and activation conditions. Striated (skeletal and cardiac) muscles are diverse in their contractive interspecific and intraspecific functional properties observed among and within animal species, nevertheless, in all cases “the smaller muscles and muscles of smaller animals are quicker” [1] . After Hill [1] who first noted this generic feature of the design of skeletal muscles, their physiological adaptation, resulting in beneficial changes in muscle function, has been recognized by a number of investigators. For example, it was learned that long-fibre muscles commonly contract at over larger length ranges and relatively higher velocities producing the greatest muscle forces the lowest relative energetic costs [2] . Muscles having shorter fibres expose smaller length change, but their cost of force generation is relatively less, e.g. [3] . Searching for determinants of evolution of shape, size, and force output of cardiac and skeletal muscle, a little is known about the regulation of directional processes of mass distribution [4] [5] . Although skeletal muscles grow in length as the bones grow, most studies only involve force increasing with respect to cross-sectional area. Following the idea that the muscle force production function is a critical evolutionary determinant [5] , I develop a physical study of the muscle form adaptation to a certain primary activity with growth of size (length and cross-sectional area) under evident condition of the preservation of muscle shape.
When designing architecture of the striated muscle built from repeating units (fibres and sarcomeres) at least three distinct muscle activities should be distinguished [5] : the concentric contraction defined as the production of active tension while the muscle is shortening and performing positive work, the eccentric contraction defined as contraction during lengthening performing negative work in a controlled fashion, and the isometric contraction when the muscle force output is produced without changing of length and performing almost zero or zero net work. The corresponding mechanical work patterns called by Russel et al. [5] as “concentric work” and “eccentric work” (that might be extended here by “isometric work”) were carefully studied via in vivo measurements of length-force cycling (workloops) of individual skeletal muscles in active animals. Presented (in Figure 3 in [6] ) by the pectoralis in flying birds, leg extensors in running cockroaches, gastrocnemius in the level running turkey, and intrinsic wing muscles in insects, the corresponding muscle locomotor patterns are known as the motor, brake, strut and spring muscles [6] .
The seminal research by Hill [1] on dynamics of electrically stimulated isolated muscles was restricted to a single isotonic shortening. The studies of the relevant motor function resulted in famous force-inverse-velocity master curve presenting the major dynamic constraint of all real (slow-fibre, fast-fibre, and superfast) muscles [7] and computationally modeled muscles, e.g. [8] . Besides, other two fundamental rules of muscle dynamics were noted by Hill [1] . Examining hovering humming and sparrow birds, he recognized that the “frequencies of wings are roughly in inverse proportion to the cube roots of the weights, i.e. to linear size”. Moreover, because the linear proportionality between the stroke period 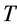 and body length
and body length 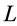 was equally established in in vivo and electrically stimulated isolated muscles, the corresponding frequency-inverse-length scaling rule
was equally established in in vivo and electrically stimulated isolated muscles, the corresponding frequency-inverse-length scaling rule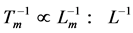 , shown for a given muscle
, shown for a given muscle , is likely more universal than previously appreciated and associated with the nervous control. Second velocity-inverse-length Hill’s constraint states that “the intrinsic speed of muscle has to vary inversely to length”, i.e.
, is likely more universal than previously appreciated and associated with the nervous control. Second velocity-inverse-length Hill’s constraint states that “the intrinsic speed of muscle has to vary inversely to length”, i.e. . Both Hill’s scaling rules still remain a challenge to viscoelastic models of transient-state muscle mechanics and other theories of muscle contraction, e.g. [9] .
. Both Hill’s scaling rules still remain a challenge to viscoelastic models of transient-state muscle mechanics and other theories of muscle contraction, e.g. [9] .
The earliest theories of muscle motor function supposed muscle to be an elastic body which, when stimulated, was converted in an active state containing elastic energy causing the muscle to shorten. Such elastic-energy theories failed to explain mechanisms of the force production in terms of viscoelastic characteristics. To a certain extent, poor experimental approaches providing often conflicting clues to muscle structure in relation to function may explain a little progress in understanding of contractile properties of a muscle [4] [9] . Moreover, physiological muscle properties accounted for macroscopic theories, i.e. (developed at macroscopic scale of consideration of muscle contractions, are primarily focused on the reproduction of force-velocity curve [9] . Besides, the existing phenomenological frameworks such as Hill-type muscle models only mimic the proper mechanical characteristics of muscles by means of passive viscoelastic springs attached to muscle contractive element in series [3] [10] [11] or in parallel [12] and recruited when muscle is activated. Such kind of models ignores the fact that the force production is followed by the process of force transmission throughout the same muscle organ. In other words, Hill-type muscle models employ Hill’s principal constraints of muscle dynamics, not being able to explain them. In line with the experimental evidences of the adaptive ability of skeletal muscle to exchange elastic strain energy during force production [2] , it was communicated on the force-similarity approach to modeling of the four primary muscle patterns via the adaptive muscle elasticity [13] .
In the present paper, I develop an integrative theoretical approach to the problem of active forces, mechanically adapted design, and contractive linear and non-linear dynamics of striated muscles. Instead of Hill-type modeling of in vitro motor function (e.g. [3] ), brake function (e.g. [2] [12] ), and strut function (e.g. [14] ), or study of muscle design by means of simulation of phenomenological force-length and/or force-velocity constraints [8] , the powerful method of continuum mechanics generally providing macroscopic characterization and modeling of soft tissues (e.g. [15] [16] ) is employed. As a further exploration of the elastic force patterns, I propose a self-consistent depiction of the three dynamically-distinct point characteristics of typical in vivo force- length loops of the naturally activated skeletal muscles. Unlike the earliest elastic theories based on minimization of energy, I develop the physical concept of similarity between the force output and reaction active elastic forces that permits one to avoid the molecular-scale details of the muscle activation process. The theory is validated by a comparison to phenomenological scaling rules including both mentioned Hill’s dynamic constraints and therefore may be hopefully helpful in designing artificial muscles [15] and modeling living and extinct organisms [17] .
2. Theory
2.1. Theoretical Background
2.1.1. McMahon’s Scaling to Body Weight
The engineering models by McMahon [18] [19] develop previous Hill’s approach to the problem of scaling quantities of animal performance to body weight . Using Hill’s geometric similarity models [1] [19] equally applied to animal body, long bone, or individual muscle, each one was approximated by a cylinder of longitudinal length
. Using Hill’s geometric similarity models [1] [19] equally applied to animal body, long bone, or individual muscle, each one was approximated by a cylinder of longitudinal length 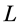 and cross-sectional area
and cross-sectional area  (or diameter
(or diameter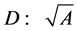 ). Moreover, the assumption on the weight-invariance of for the tissue density was adopted, namely
). Moreover, the assumption on the weight-invariance of for the tissue density was adopted, namely
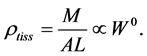 (1)
(1)
In mammalian long-bone allometry, this invariant was verified and observed with a high precision [20] . Mechanical models of bending bones and shortening muscles were introduced by McMahon via the weight-inva- riant elastic modulus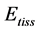 , tissue stress
, tissue stress 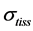 and strain
and strain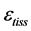 , namely
, namely
 (2)
(2)
Here 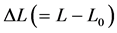 is the length change accompanied by the force change
is the length change accompanied by the force change 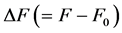 counted off from the resting length
counted off from the resting length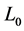
While searching for functional mechanical patterns of biological systems determined by maximal forces using Equation (1) and Equation (2), the maximal-amplitude stress/strain scaling relations
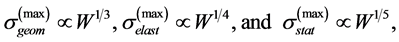
could be readily derived from McMahon’s geometric (isometric elastic stress), elastic (buckling elastic stress) and static (bending elastic stress) similarity models distinguished through McMahon’s scaling relations
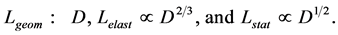
Instead, the maximum stress and strain

were postulated (in Table 4 in [19] ) thereby groundlessness extending McMahon’s exact result for the mean stress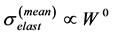
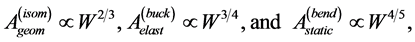
when applied to Equation (2), along with McMahon’s idea on the dominating role of gravitational forces in bones, muscles, and bodies, i.e.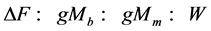
The patterns of long bones are generally driven by the peak muscle forces, but not by gravity, as repeatedly noted by many authors, proven [20] and exemplified by all mammals as whole [21] . Nevertheless, one amazing case of the experimental evidence of McMahon’s elastic similarity is due to limb bones in African elephants which, in contrast to Asian elephants, are most likely adapted for axial bone compression, influenced by gravitational reaction forces [21] .
Although the evolution of locomotor trends of terrestrial giants are likely driven by body weight [22] , the idea on the origin of locomotion patterns of animals (running, flying, and swimming) based on minimization of useful energy in the gravitational field [23] , was also confronted with the new idea of maximum body efficiency in the muscular field [24] .
2.1.2. Muscle Shape and Structure
After Alexander [25] , the physiologic cross-sectional area 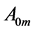
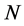
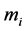
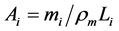


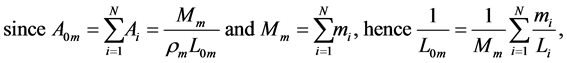
As shown [25] [26] , the sum of areas of the muscle and the muscle length 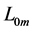
In scaling models, the evolution of the muscle structures across different-sized animals of body mass 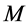
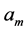
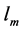
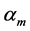
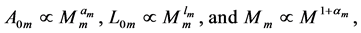
where the muscle mass index 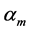
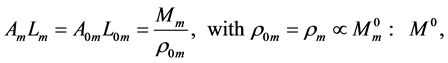
holding in all muscle activities, plays the role of the muscle mechanical invariant. This statement is ensured by the functional variation of density 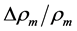
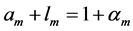
straightforwardly follows from Equation (8) and Equation (9). Likewise the case of hindlimb mammalian bones of the mean structure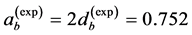
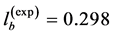
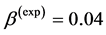
2.2. General Muscle Characterization
2.2.1. Maximal Force and Stress
Using the in vivo workloops, the muscle locomotor patterns can be generally specified regardless of details of activation-deactivation conditions. In Figure 1, the linear-slope characteristics 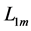
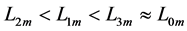
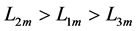
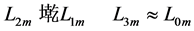
Moreover, such a qualitative general characterization of the activated individual muscle 


Figure 1. The qualitative analysis of the in vivo muscle force-length data. The muscle motor function is presented by gastrocnemius powering during shortening in uphill running turkey (inset a, adapted from [31] ). The lateral gastrocnemius and plantaris act as brake (inset b) and strut (inset c) in hopping tammar wallabies [28] . The solid (and dashed) arrows indicate rasing (and decreasing) of the exerted force near its maximum magnitude
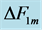

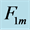

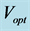
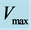
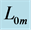
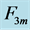
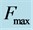

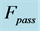
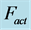
introduced by the maximum force 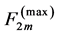

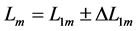
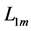
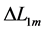
First, the linearization of the in vivo muscle force-length curve allows one to determine the trial peak stress and strain by
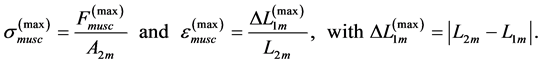
The corresponding force change 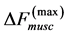
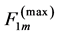
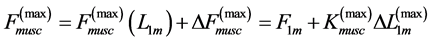
that in turn determinates effective muscle stiffness 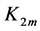
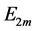
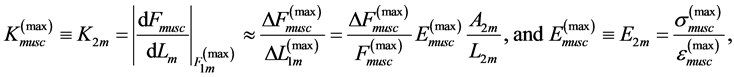
following from Equation (12) and Equation (13).
2.2.2. Active Stiffness and Resonant Muscle Mechanics
Secondly, treating the maximum-force crossover state as the generic transient-neutral state [30] , the resonant frequency 
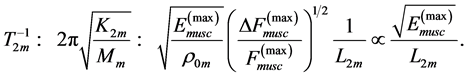
One can see that Equation (15) yields first Hill’s frequency-inverse-length constraint discussed in Introduction. However, the following three observation conditions of this constraint are required: 1) the preservation of dynamic functional volume (see Equation (9)), 2) the weight-invariance of the elastic modulus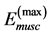
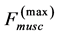
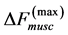
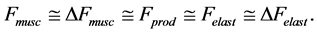
Here the active elastic force 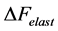

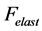
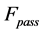
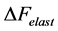
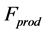
Given that the peak active muscle stress 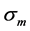
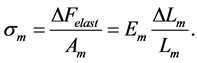
Unlike the trial peak stress in Equation (12), 
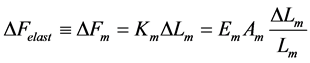
and in turn provides the corresponding active muscle stiffness
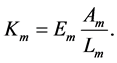
The underlying mechanical sarcomere elastic stiffness 

originated from end-to-end intercellular overlapping [12] [35] .
The muscle energy change

stored or released during active-period contraction provides the mechanical cost of energy
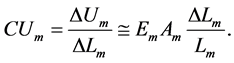
These relations demonstrate how the observable mechanical characteristics can be linked to the underlying muscle elastic forces using the force-similarity principle formulated in Equation (16). In turn, the contraction velocity
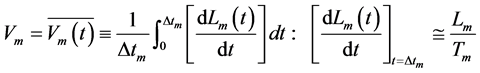
is defined by the instant velocity 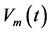

2.2.3. Fast and Slow Activated Muscles
According to the most general classification of diverse muscles, three types are conventionally distinguished: red (slow fibre) muscles, white (fast fibre) muscles, and intermediate type, mixed fibre muscles. Although collective mechanisms of muscle contractions are poor understood, e.g. [36] , physically, two limiting situations of the dynamic accommodation of local forces generated by cross bridge attachments can be generally rationalized. As schematically drawn in the inset d in Figure 1 for an activated muscle, the dynamic process of equilibration between the production intrinsic forces and external loads (not shown) is followed by the spatiotemporal relaxation of elastic forces. For the simplest case of slow muscles, the dynamic equilibration occurs via the slow channel of relaxation, supposedly common for both active, 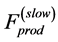
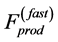
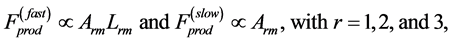
is proposed through the force-size scaling rules, for all three distinct states shown in Figure 1, hereafter distinguished by symbol r.
The linear-displacement regime with 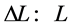

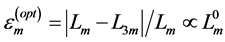
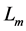
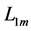
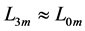
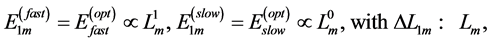
characteristic of the fast and slow muscles. Such a muscle description follows from the principle of similarity (see Equation (16)) between the active elastic force 
Likewise, the bilinear-displacement moderate-velocity regime 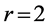
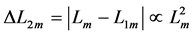
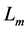
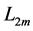
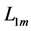

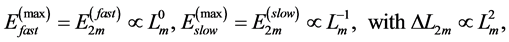
adjusted with the muscle production function on the basis of force similarity principle. Finally, the trilinear high-velocity regime 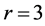
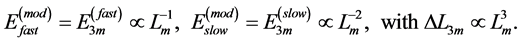
This condition specifies point 3 in Figure 1, along with the underlying cubic-power muscle displacements 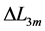
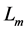
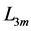
2.3. Muscle Functions
Likewise the naturally curved mammalian long bones biomechanically adapted to the maximum longitudinally bending [20] [30] , the muscle motor function is assigned to locomotor muscles showing concentric positive work exerted by elastic bending forces. Given that the elastic force patterns coincide for bending and torsion [30] , both kinds of unpinnate and uni-pinnate skeletal muscles, having respectively close to zero and non-zero fixed pinnate angles, may be expected to be structured by the same motor function. The specific-function mechanical characterization is described in Appendix B and results are summarized in Table 2.
Table 1. General mechanical characteristics of the striated muscles tuned to linear-displacement dynamic regime scaled to dynamic fibre length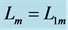
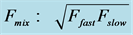
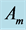

Table 2. Scaling to mass of mechanical characteristics of muscles adapted to different locomotor functions. The allometric exponents related to animal's body mass (via Equation (8)) are presented in terms of muscle mass index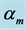
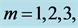
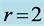
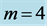
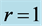
3. Results
Assumptions and Predictions
The following assumptions are made regarding elastic striated muscles in fully activated states:
1) The powering individual muscles considered at macroscopic scale are treated as regime-dependent homogeneous solid-like organs. Within the scope of continuum medium mechanics, the macroscopic coarse-grained description ignores details of heterogeneous microstructure, including those resulting in pinnate angles.
2) When activated under different boundary loading conditions, the muscles do not undergo changes in shape and whole volume. The emerging muscular active-force fields [24] [38] follow the same patterns as passive elastic-force fields known in continuum medium mechanics of solids.
3) The mechanical similarity between the extrinsic forces exerted by the muscle and intrinsic elastic reaction forces, established above as the observation condition, can provide dynamic similarity features (for contraction velocities and frequencies), which can be theoretically and experimentally observable, at least in biomechanically equivalent states.
4) The natural ability of the non-linear elastic tuning of fast and slow muscles [34] can be characterized by the regime-dependent elastic moduli sensitive to evolving dynamic observable characteristics, e.g. the muscle length change.
One can deduce from Table 1, that the mechanical characterization of slow, fast and mixed muscles attributed to the linear-displacement regime 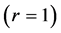
In Table 2, the scaling rules driving mass distribution in a given muscle 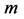
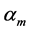
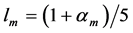
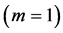
In Table 3, the scaling rules shown in Table 2 are compared with those for the optimal-force state related to the exponents 
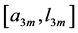
Table 3. Locomotor functions predicted by dynamic structured for slow and fast striated muscles tuned to distinct dynamic regimes. The primary functions 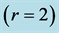
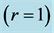
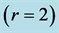
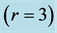
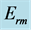


Table 4. Dynamic characterization of the red (slow) and white (fast) striated muscles in the optimum-, moderate-, and maximum-velocity dynamic regimes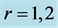
Some consequences of the proposed muscle scaling dynamic theory are:
1) The peak forces generated in all regimes scales as muscle volume or PCSA, respectively, in fast or slow muscles.
2) A general, function-independent mechanical description of the striated muscle activated in the liner-displacement regime is predicted for each type of muscles (Table 1).
3) The muscle-type independent locomotor functions and related mechanical and dynamic characteristics of the striated muscle activated in the bilinear regime are predicted (Table 2).
4) The muscle-type independent varied dynamic structures are predicted for all muscle regimes and functions (Table 3).
5) The function-independent dynamic scaling characteristics are obtained in Table 4 for all type of muscles.
In what follows, all theoretical findings are tested by available from the literature data.
4. Analysis and Discussion
Aiming to shed light on some important problems in the field of muscle dynamics, let me cite Louis Sullivan quoted in [5] : “What determines the shape, size, and force output of cardiac and skeletal muscle?”. Broadly, within the provided coarse-grained description of conservative striated muscles, the proposed theory suggests that the size-dependent peak elastic forces, emerging during the force production preserving muscle shape, are responsible for the muscle patterns observed via the functionally adapted structures. Moreover, the peak force output, which is described through the corresponding elastic force, is therefore determined by the muscle volume and cross-sectional area, respectively for white and red muscles, regardless of muscle functional specialization.
4.1. Function against Structure
4.1.1. General Muscle Characterization
Being composed of bundles of muscle fibres and other contractible components (neural, vascular, and collagenous reticulum), the striated muscle is thought of as a heterogeneous continuum medium transmitting the produced tension internally and externally, e.g. [39] . Primarily, I address the problem of mechanical design of striated muscle to a general, function-independent characterization of the individual muscle organ loaded by tension, reaction, and gravity through tendons, ligaments, and bones. My non-energetic approach is physically grounded by the existence of linear force-length regions (shown by the solid arrows in the workloops in Figure 1) revealed in all in vivo workloops regardless of dynamic details of approaching to the peak exerted force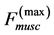
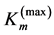
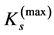
The analytical justification of Hill’s frequency-inverse-length constraint results from the analysis of Equation (15) that eventually requires the usage of the similarity between all intrinsic muscle forces, Equation (16). The constraint 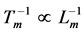
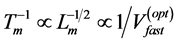

Thereby, it has been demonstrated that the dynamic similarity establishes a link between the body-propulsion speed and locomotor-muscle contraction velocity, earlier described by Rome et al. [43] . Being united with the muscle-force similarity, both constraints lead to the mechanical similarity, as the basic principle explored in this research. More general approach to the problem of dynamic similarity in animal locomotion shows that the concept of mechanical similarity [24] and obtained above findings naturally follow from the key principle of analytical mechanics applied to the resonant (in frequency and phase) efficient cyclic locomotion [38] .
4.1.2. Maximum Force Output against Structure and Velocity
In muscle physiology, the functional effect of muscle conceptual architecture simply states that muscle force output is proportional to PCSA. It may seem that the proposed study of the adaptation of muscle structure via force production function is in qualitative agreement with this statement, because in both cases of fast and slow muscles exposed in Equation (24) the muscle force output is proportional to
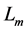
Although the proposal on scaling of the maximum production force (and active stress) with muscle size shown in Equation (24) is a challenge for further research, the provided fairly general physical grounds are supported by empirical observations by Marden and Allen [44] . They statistically established that the peak force output in all biological (and human-made) motors falls into two fundamental scaling laws: 1) in fast-cycling motors, presented by flying insects, bats and birds, swimming fishes, and running animals the peak force scales as (motor mass)1 and 2) in slow-cycling motors, such as myosin molecules, muscle cells, and some (unspecified) “whole muscles” the force output scales as (motor mass)2/3; where the role of “motor mass” plays muscle (like fuel) mass. Within this context, the studied individual muscles are treated as complex biological motors, working due to actomyosin linkages (cross bridges), interacting in both longitudinal and transverse directions [5] [13] . The fact that muscle motors were observed from sarcomere to whole muscle organ passing through the single-fibre level of muscle organization, makes a basis for the introduced below micro-macro scale correspondence.
The study of the in vivo force-length curves is provided here in terms of the three distinct characteristic points (shown in Figure 1) characterized by the force and velocity inequalities
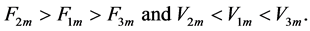
These three function-independent generic states are associated with the linear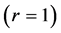


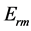
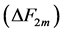
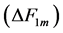
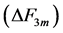
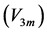
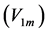
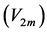
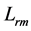
4.1.3. Muscle Functions against Size and Shape
Searching for answer on “what features make a muscular system well-adapted to a specific function?” [32] , it has been communicated [13] that the natural conditions of stabilization of the moderate-velocity regime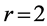
Likewise [13] , the elastic-force patterns, underlying concentric, eccentric, isometric, and cardiac contractions and determining eventually specific functions, are suggested, respectively in Equation (35), Equation (39), Equation (42), and Equation (44). The solutions to the muscle-force and muscle-shape constraints are accumulated in Table 2 as patterned functions well distinguished through the muscle structure parameter 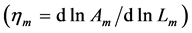
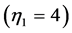
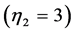
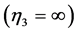
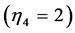
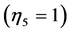
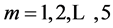
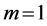
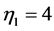
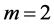
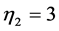
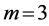
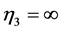
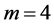
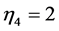
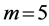
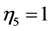
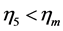
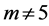
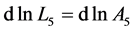
In Table 3, conceivable stable dynamic structures corresponding to muscle activity in different dynamic regimes are analyzed. As in the case of Table 2, the solutions to dynamic constraints follow from the similarity between the force output Equation (16) and elastic-force patterns. The resulting dynamic states are considered in terms of the scaling exponents for the muscle dynamic structure 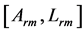


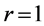
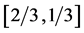
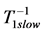
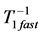


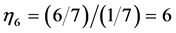

4.2. Direct Observations of Muscle Specialization
“If a muscle is specialized for a particular mechanical role how this is reflected in it architecture?” [45] . The proposed solution to stated problem is demonstrated below by the comparative analysis between the muscle architecture observed by allometric exponents and that predicted by the adaptation to a particular mechanical function.
4.2.1. Isolated Muscles in Hindlimb of Mammals and Birds
In Table 5 we analyze the morphometric data on the allometric exponents derived from the mean cross-sec- tional area 

First, let us verify the cylinder-shape similarity of skeletal muscles described by Equation (9). The muscle mass index 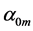
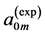

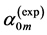
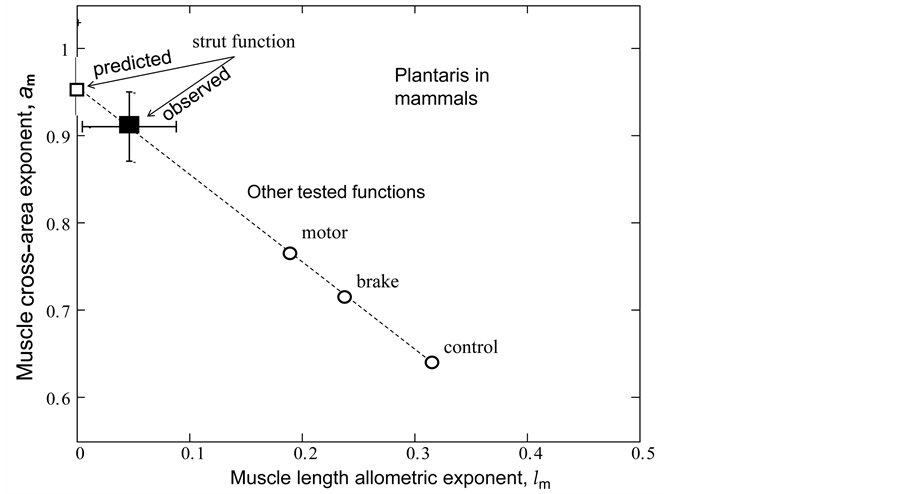
In Figure 2 and Figure 3, the method of determination of the primary mechanical function is illustrated: the adapted muscle structure is indicated by the appropriate theoretical point located most closely to the datapoint.
The found reliable estimates 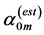

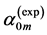
Secondly, the analysis in Figure 2 and Figure 3 indicates strong correlations between the morphometrically characterized structure of skeletal muscle and one of the primary locomotor functions described in Table 2. The primary functions indicated in Table 5 are found with a high degree of certainty. Indeed, as illustrated in Figure 2, the deviations of distances measured along the dashed line, corresponding to a given muscle, between the datapoint and distant challengers for the primary function, from the smallest distance indicating the primary candidate, always exceed the experimental uncertainty.
Thirdly, the found muscle mechanical specifications do not conflict with the physiological categorization established for joint extensors and flexors, which muscle structures are shown to be adapted to the brake and motor functions via activation of eccentric and concentric elastic forces. The found structure parameter 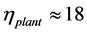
Table 5. The analysis of the allometric data by Pollock and Shadwick [26] provided on the basis of Equation (10) and Table 2. The shown statistical error is approximated by the symmetrized 95% confidence interval. The methodology of the analysis is illustrated in Figure 2. The primary functions found in Figure 2 and Figure 3 are described following Table 2, with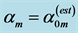
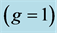
Figure 2. The indirect observation of the primary activity of mammalian plantaris. The solid symbol is the datapoint [26] presented in Table 5 and the bars indicate experimental error. The open symbols are theoretical estimates for stable dynamic struc- tures established for the motor, brake, strut, or control functions described in Table 2, with 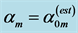
Figure 3. The observation of the primary mechanical function in some isolated individual muscles in mammals. The analysis and notations correspond to those in Figure 2. The experimental (and theoretical) data for gastrocnemius, DDF (deep digital flexor), and CDE (common digital extensor) are shown, respectively, by the closed (and open) inverted triangles, regular triangles, and circles. All the data are taken from Table 5.
no changing their support function in non-linear regimes. In contrast, the gastrocnemius in mammals manifests their motor, strut, and brake functions in, respectively, uphill, level, and incline running of animals. Through the motor adapted structure with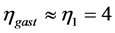
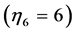
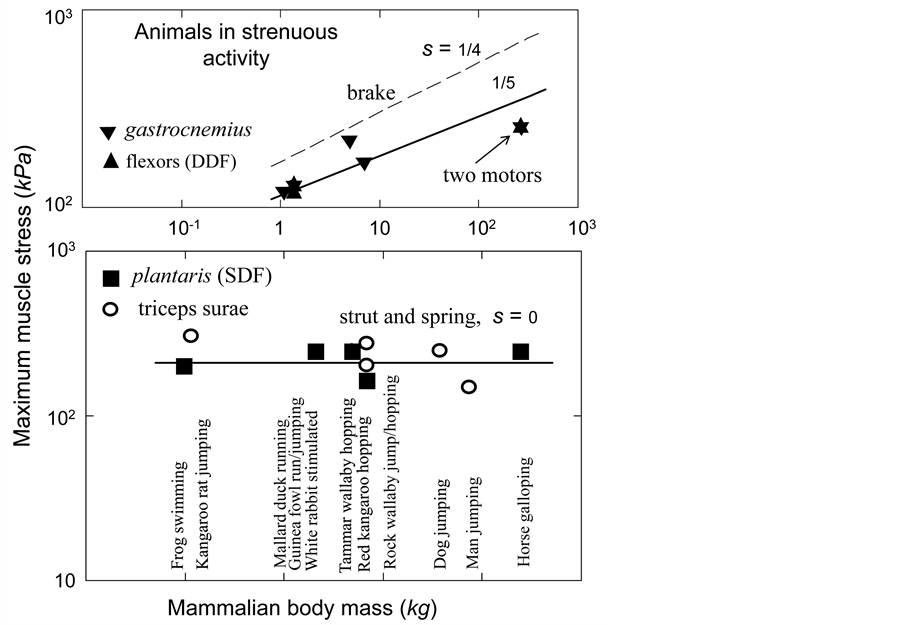
In Figure 4, the overall muscle peak stress data measured in limb muscles of animals in strenuous activity, reviewed by Biewener [29] , are re-examined and re-analyzed accounting for the primary functions of hindlimb muscles established in Table 5.
The uphill-motor specialization of gastrocnemius is independently supported by the compressive-stress analysis made in Figure 4 for fast running, jumping, and hopping mammals. The stress scaling exponents 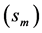
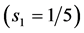
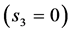

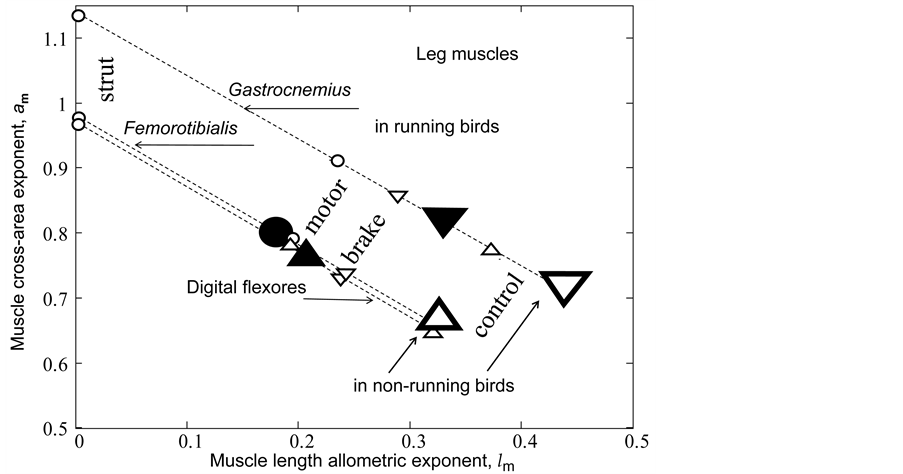
I have also investigated an interesting question: whether the primary function established for a certain leg muscle in mammals specialized to fast running coincides with that for the same muscle in birds? The pioneering data on individual leg muscles in 8 running birds, ranging in size from 0.1 kg quail to 40 kg ostrich, are analyzed in Table 6 and Figure 5.
In running and non-running birds (Figure 5), the gastrocnemius is employed as the brake and spring, in contrast to the motor function in mammals (Table 5). This is in accord with Bennett [27] , who noted that “the full force-generated capacity of gastrocnemius is only used occasionally, such as during take-off, when a bird attempts to throw itself into the air”. This explains our indirect observation: the primary function of the gastrocnemius in running specialists is attributed to the foot flexor in mammals and ankle extensor in birds (Table 6). In non-running birds, the legs are designed to control the ground locomotion (Figure 5), whereas their wings may share motor and brake functions (Table 3), in accord with that reviewed by Dickinson et al. [6] .
Figure 4. The qualitative study of the in vivo data on the peak stress in individual leg muscles of animals in strenuous activity. The symbols employed above in Figure 2 and Figure 3 are extended by the open circles (triceps) for the data on peak muscle stress taken from Table 1 in [29] , with the exclusion of the slow-mode data on cantering goat and trotting cat. The data [46] on the activated isometric stress in isolated white rabbit tibialis are added. The dashed line shows the brake-functional stress indicated by the stress scaling exponent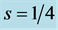

Table 6. The analysis of the allometric data by Maloiy et al. [47] . The shown large error is due to relatively wide confidence limits. The mean exponents 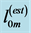
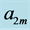
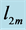
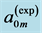
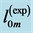
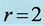
Figure 5. The analysis of the primary mechanical functions for leg muscles in running and non-running birds. The measured (and estimated) data taken from Table 6 (and Table 2) for gastrocnemius, femorotibialis, and digital flexors are shown by the closed (and open) inverted triangles, circles, and regular triangles, respectively. The semi-open triangles are the data by Bennett [27] for non-running birds.
4.2.2. Micro-Macro Scale Correspondence
There are many striking examples when skeletal muscles expose adaptation to a specific function, e.g. [3] [48] . The striated muscles anatomically suited to concentric or eccentric work [2] are structurally distinct having, respectively, long thin cells or short wide cells [5] . This observation suggests the microscopic level of muscle-cell adaptation introduced here by
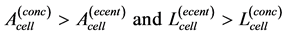
for the cellular cross-sectional area 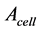
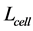
A general question arises whether allometric coefficients of proportionality omitted above in all structure- function power-law (scaling) relations are also attributed to active elastic strains accompanying maximum force production? Or, alternatively, other microscopically justified mechanisms, c.f. [49] , or additional parameters (such as pinnate angle) may result in different general macroscopic consequences? Given the highly conservative nature of contractive units of skeletal muscles and their well pronounced organization [29] , the specific-function trends of the muscle cross-sectional area
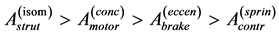
and muscle-fibre length
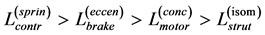
are generally expected from Table 2. The suggested trends become observable via the primary functions established in Table 5 for gastrocnemius
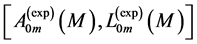
tion: 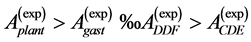
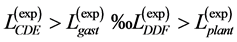
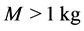
Similarly, the trend for active stiffness
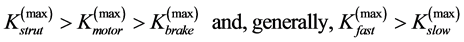
straightforwardly follows from Table 2. Given that the optimum velocity for fast fibres 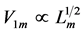
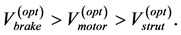
Moreover, a crude estimate for the cost energy
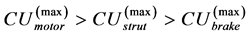
follows from 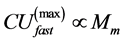
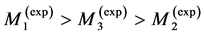
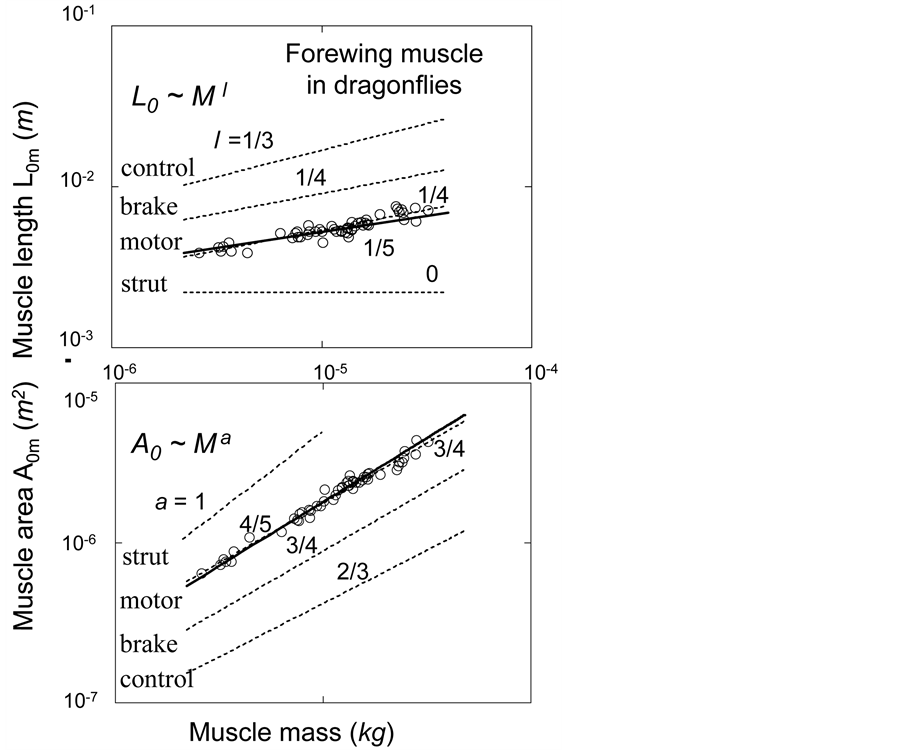
4.2.3. Muscle Dynamics of Mammalian Legs and Dragonfly Wings
Given that mammalian leg extensors are active mostly during lengthening [2] , the brake primary function (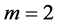
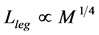
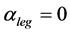
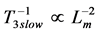

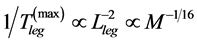

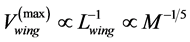
tion velocity, and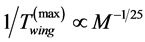
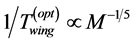
locity regime (see Table 4). Hence, analytically revealed Hill’s constraint becomes observable via the empirical regression data by Medler [48] : on the maximum-amplitude contraction velocities for the locomotor muscles in leg of terrestrial animals, 
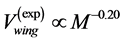
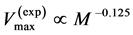
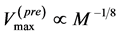


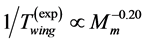
In the same optimum-velocity regime (Table 1), the maximum-amplitude static muscle force 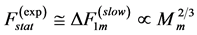
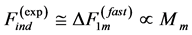
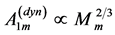
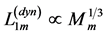
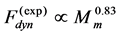
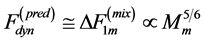
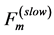
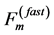
5. Conclusions
A theoretical framework for the mechanical characterization of the three activated states of the striated muscle introduced via force-length cycling in terms of the three well distinguished dynamic transient regimes is proposed. The explicit analytical description of muscle locomotor functions and related mechanical characteristics is provided on the basis of two concepts: 1) the preservation of dynamic muscle volume associated with self-preservation of the spindle-type shape in skeletal muscles and egg-type shape in cardiac muscles 2) the mechanical similarity between action (loading) and reaction (elastic) forces takes place in biomechanically equivalent states. Exploring a full set of a few numbers of patterns known for elastic forces from the continuum mechanics, the macroscopic study of the force production and its functional-structural accommodation in the loaded muscle organs provides the following major outcomes.
1) It is demonstrated how the generic principle of mechanical (force and velocity) similarity provides the dynamic (frequency-velocity) constraints for the muscle contractions, first observed by Hill in hovering birds and then revealed in locomotor muscles of running animals and flying birds, bats, and insects.
Figure 6. Scaling of the basalar structure to muscle mass in male dragonflies (Odonata and Anisoptera, listed in Figure 5 in [50] ). The datapoints for muscle length 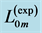
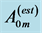



2) It is shown how the standard relations from classical mechanics of solids may successfully work in soft tissue mechanics. The study is grounded by the active-force muscle stiffness well distinguished in muscle work- loops near the maximum-amplitude exerted forces. At a fixed muscle shape, the muscle active stiffness, underlaid by sarcomere stiffness, is shown to be driven by the elastic moduli, which encompass all contractive elements arranged here as the elastic continuum medium.
3) The provided analysis of direct empirical observations of the maximal forces exerted by muscles in legs of mammals and birds and the scaling analysis of the resting muscle structures corroborates the major hypothesis of the study: the force output amplitude in high powering fast and slow individual muscles is linear with, respectively, muscle volume and cross-sectional area, regardless of their muscle’s specialization specified by primary functions.
4) The study reveals that the mechanical similarity applied to locomotor skeletal muscles specialized in spring, brake, and motor activities resembles McMahon’s “geometric”, “elastic”, and “static” stress similarities. It is not striking since the employed here scaling patterns for reaction elastic forces are well established in continuum mechanics of solids regardless of the nature of origin of other mechanical forces, e.g. external “passive” gravitational-field forces or internal “active” muscular-field forces. As the result, several observations of empirical data matching McMahon’s predictions, e.g. [48] [49] , are illuminated in terms of distinct muscle dynamic regimes.
5) The macroscopic structures of locomotor skeletal muscles revealed by the muscle allometry are found to be well adapted to the dynamic state with generation of maximum force at moderate velocity contractions. The relevant bilinear-displacement muscle dynamics, involving both fast-twitch and slow-twitch powering muscle fibres sheds light on the origin of allometric power laws and explains muscle specialization. The adapted structures examined via the available empirical data indicate that the leg muscles are brakes in mammals and springs in non-running birds, whereas the wing muscles are motor-brake engines in flying species. A new pump function suggested for the cardiac muscles needs further experimental tests.
6) The provided study of the muscle specialization in mammalian hindlimb indicates that the force production function is a dominated factor in the accommodation of muscle structure. When the mechanical scaling exponents are compared with the relatively small muscle-mass index, this finding likely indicates the predominating role in mass distribution due to mechanical adaptation effects over that due to biological adaptive mechanisms. As the result, a new tool for the investigation of indirect effects of the biomechanical adaptation of individual locomotor muscles is suggested through the regression analysis of in vivo muscle stresses in synergists scaled across different-sized animals.
7) The assumption on that the muscle tuning muscle ability of animals can be modeled by active elastic forces via non-linear muscle elastic moduli is validated through the observation of theoretical predictions made in muscle dynamics for legs and wings in running and flying specialists. Predictions are also provided for the experimental testing of the primary and secondary functions realized by the tuning the cycling muscle to the proper natural frequency.
8) The conservative character of architecture and related mechanical characteristics of striated muscles suggests general trends following from the mechanical and shape constraints. The trends dictated by the primary functions explain, in particular, why the muscles having larger fibre and sarcomere lengths and suited to efficient eccentric work, tend toward higher optimum contraction velocities, but show lower maximum stiffness and mechanical energy cost.
9) As an intriguing outcome of the analysis of maximal contraction muscle velocities and frequencies, the maximum-speed steady locomotion is revealed to be controlled by non-linear elasticity of slow-fibre muscles generating moderated force. This finding deserves further evaluation in finite muscle element analysis when studying top speeds of living and extant animals.
Acknowledgements
The author thanks Robert McN. Alexander, Andrew A. Biewener and James H. Marden for careful reading of the first versions of this study and helpful critical comments. Rudolf J. Schilder is appreciated for the datapoints on dragonflies. This work was in part sponsored by the national agency CNPq.
References
- Hill, A.V. (1950) The Dimensions of Animals and Their Muscular Dynamics. Science Progress, 38, 209-230.
- Lindstedt, S.L., Trude, E.R., Paul, K. and Paul, C.L. (2002) Do Muscle Function as Adaptable Locomotor Springs? Journal of Experimental Biology, 205, 2221-2216.
- Lichtwark, G.A. and Wilson, A.M. (2005) Effects of Series Elasticity and Activation Conditions on Muscle Power Output and Efficiency. Journal of Experimental Biology, 208, 2845-2853. http://dx.doi.org/10.1242/jeb.01710
- Squire, J.M. (1997) Architecture and Function in the Muscle Sarcomere. Current Opinion in Structural Biology, 7, 247-257. http://dx.doi.org/10.1016/S0959-440X(97)80033-4
- Russell, B., Motlagh, D. and Ashley, W.W. (2000) Form Follows Function: How Muscle Shape Is Regulated by Work. Journal of Applied Physiology, 88, 1127-1132. http://www.jappl.org/content/88/3/1127.full
- Dickinson, M.H., Farley, C.T., Full, J.R., Koehl, M.A.R., Kram, R. and Lehman, S. (2000) How Animals Move: An Integrative View. Science, 288, 100-106. http://dx.doi.org/10.1126/science.288.5463.100
- Rome, L.C. (2006) Design and Function of Superfast Muscles: New Insights into the Physiology of Skeletal Muscle. Annual Review of Physiology, 68, 193-221. http://dx.doi.org/10.1146/annurev.physiol.68.040104.105418
- Medler, S. and Hulme, K. (2009) Frequency-Dependent Power Output and Skeletal Muscle Design. Comparative Biochemistry and Physiology Part A: Molecular & Integrative Physiology, 152, 407-417. http://dx.doi.org/10.1016/j.cbpa.2008.11.021
- Jontes, J.D. (1995) Theories of Muscle Contraction. Journal of Structural Biology, 115, 119-143. http://dx.doi.org/10.1006/jsbi.1995.1037
- Cole van den, G.K., Bogert, A.J., Herzog, W. and Gerritsen, K.G.M. (1996) Modelling of Force Production in Skeletal Muscle Undergoing Stretch. Journal of Biomechanics, 29, 1091-1104. http://www.ingentaconnect.com/content/els/00219290/1996/00000029/00000008/art00005
- Alexander, R.McN. (1977) Allometry of the Limbs of Antelopes (Bovidae). Journal of Zoology (London), 183, 125- 146. http://dx.doi.org/10.1111/j.1469-7998.1977.tb04177.x
- Forcinito, M., Epstein, M. and Herzog, W. (1998) Can a Rheological Muscle Model Predict Force Depression/En- hancement? Journal of Biomechanics, 31, 1093-1099. http://dx.doi.org/10.1016/S0021-9290(98)00132-8
- Kokshenev, V.B. (2008) A Force-Similarity Model of the Activated Muscle Is Able to Predict Primary Locomotor Functions. Journal of Biomechanics, 41, 912-915. http://dx.doi.org/10.1016/j.jbiomech.2007.11.005
- Jenkyn, T.R., Koopman, B., Huijing, P., Lieber, R.L. and Kaufman, K.R. (2002) Finite Element Model of Intramuscu- lar Pressure during Isometric Contraction of Skeletal Muscle. Physics in Medicine and Biology, 47, 4043-4061. http://dx.doi.org/10.1088/0031-9155/47/22/309
- Marra, S.P., Ramesh, K.T. and Douglas, A.S. (2003) Characterization and Modeling of Compliant Active Materials. Journal of the Mechanics and Physics of Solids, 51, 1723-1743. http://dx.doi.org/10.1016/S0022-5096(03)00055-3
- Skatulla, S., Arockiarajan, A. and Sansour, C. (2009) A Nonlinear Generalized Continuum Approach for Electro-Elas- ticity Including Scale Effects. Journal of Mechanics and Physics of Solids, 57, 137-160. http://dx.doi.org/10.1016/j.jmps.2008.09.014
- Dumont, E.R., Grosse, I.R. and Slater, G.J. (2009) Requirements for Comparing the Performance of Finite Element Models of Biological Structures. Journal of Theoretical Biology, 256, 96-103. http://dx.doi.org/10.1016/j.jtbi.2008.08.017
- McMahon, T.A. (1973) Size and Shape in Biology. Science, 179, 1201-1204. http://dx.doi.org/10.1126/science.179.4079.1201
- McMahon, T.A. (1975) Using Body Size to Understand the Structural Design of Animals: Quadrupedal Locomotion. Journal of Applied Physiology, 39, 619-627. http://www.deepdyve.com/lp/the-american-physiological-society/using-body-size-to-understand-the-structural-design-of-animals-ac2OYKkNgX
- Kokshenev, V.B. (2003) Observation of Mammalian Similarity through Allometric Scaling Laws. Physica A, 322, 491-505. http://dx.doi.org/10.1016/S0378-4371(02)01923-4
- Kokshenev, V.B. and Christiansen, P. (2010) Salient Features in Locomotion of Proboscideans Revealed via the Differential Scaling of Limb Long Bones. Biological Journal of Linnean Society, 100, 16-29. http://dx.doi.org/10.1111/j.1095-8312.2010.01415.x
- Kokshenev, V.B. and Christiansen, P. (2011) Evolution of Locomotor Trends in Extinct Terrestrial Giants Affected by Body Mass. In: Klika, V., Ed., Theoretical Biomechanics, InTech, Croatia, 49-74. http://cdn.intechweb.org/pdfs/22186.pdf
- Bejan, A. and Marden, J.H. (2006) Unifying Constructal Theory for Scale Effects in Running, Swimming and Flying. Journal of Experimental Biology, 209, 238-248. http://dx.doi.org/10.1242/jeb.01974
- Kokshenev, V.B. (2011) Physical Insights into Dynamic Similarity in Animal Locomotion. I. Theoretical Principles and Concepts; II. Observation of Continuous Similarity States. In: Klika, V., Ed., Theoretical Biomechanics, InTech, Croatia, 267-302. http://www.intechopen.com/download/get/type/pdfs/id/22195
- Alexander, R.McN. (1997) Optimum Muscle Design for Oscillatory Movements. Journal of Theoretical Biology, 184, 253-259. http://dx.doi.org/10.1006/jtbi.1996.0271
- Pollock, C.M. and Shadwick, R.E. (1994) Allometry of Muscle, Tendon, and Elastic Energy-Storage Capacity in Mammals. American Journal of Physiology, 266, R1022-R1031.
- Bennett, M.B. (1996) Allometry of the Leg Muscles in Birds. Journal of Zoology (London), 238, 435-443. http://dx.doi.org/10.1111/j.1469-7998.1996.tb05404.x
- Biewener, A.A., Konieczynski, D.D. and Baudinette, R.V. (1998) In Vivo Muscle Force-Length Behavior during Steady-Speed Hopping in Tammar Wallabies. Journal of Experimental Biology, 201, 1681-1694.
- Biewener, A.A. (2005) Biomechanical Consequences of Scaling. Journal of Experimental Biology, 208, 1665-1676. http://dx.doi.org/10.1242/jeb.01520
- Kokshenev, V.B. (2007) New Insights into Long-Bone Biomechanics: Are Limb Safety Factors Invariable across Mammalian Species? Journal of Biomechanics, 40, 2911-2918. http://dx.doi.org/10.1016/j.jbiomech.2007.03.007
- Roberts, T.J., Marsh, R.I., Weyand, P.G. and Taylor, C.R. (1997) Muscular Force in Running Turkey: The Economy of Minimizing Work. Science, 275, 1113-1115. http://dx.doi.org/10.1126/science.275.5303.1113
- Rome, L.C. (1997) Testing a Muscle’s Design. American Scientist, 85, 356-363. http://www.jstor.org/discover/10.2307/27856813?uid=3737664&uid=2&uid=4&sid=21103234444773
- Josephson, R.K. (1999) Dissecting Muscle Power Output. Journal of Experimental Biology, 202, 3369-3375.
- Ahlborn, B.K., Blake, R.W. and Megill, W.M. (2006) Frequency Tuning in Animal Locomotion. Zoology, 109, 43-53. http://dx.doi.org/10.1016/j.zool.2005.11.001
- Forcinito, M., Epstein, M. and Herzog, W. (1997) Theoretical Considerations on Myofibril Stiffness. Biophysical Journal, 72, 1278-1286. http://dx.doi.org/10.1016/S0006-3495(97)78774-5
- Robinson, J.M., Wang, Y., Kerrick, W.G.L., Kawai, R. and Cheung, H.C. (2002) Activation of Striated Muscle: Nearest- Neighbor Regulatory-Unit and Cross-Bridge Influence on Myofilament Kinetics. Journal of Molecular Biology, 322, 1065-1088. http://dx.doi.org/10.1016/S0022-2836(02)00855-0
- Landau, L.D. and Lifshitz, E.M. (1989) Theory of Elasticity. Pergamon Press, London.
- Kokshenev, V.B. (2010) Key Principle of the Efficient Running, Swimming, and Flying. Europhysics Letters, 90, 48005-p1-p5. http://dx.doi.org/10.1209/0295-5075/90/48005
- Kent, G.C. (1987) Comparative Anatomy of the Vertebrates. Wm. C. Brown Publishers, Dubuque.
- Rome, L.C., Runke, R.P., Alexander, R.M., Lutz, G., Aldridge, H., Scott, F. and Freadman, M. (1988) Why Animals Have Different Fibre Types. Nature, 335, 824-827. http://dx.doi.org/10.1038/335824a0
- Farley, C.T., Glasheen, J. and McMahon, T.A. (1993) Running Springs: Speed and Animal Size. Journal of Experimental Biology, 185, 71-86.
- Bejan, A. and Marden, J.H. (2006) Unifying Constructal Theory for Scale Effects in Running, Swimming and Flying. Journal of Experimental Biology, 209, 238-248.
- Rome, L.C., Sosnicki, A.A. and Goble, D.O. (1990) Maximum Velocity of Shortening of Three Fibre Types from Horse Soleus Muscle: Implications for Scaling with Body Size. Journal of Physiology, 431, 173-185.
- Marden, J.H. and Allen, L.R. (2002) Molecules, Muscles, and Machines: Universal Performance Characteristics of Motors. Proceedings of the National Academy of Sciences of the United States of America, 99, 4161-4166. http://dx.doi.org/10.1073/pnas.022052899
- Daley, M.A. and Biewener, A.A. (2003) Muscle Force-Length Dynamics during Level versus Incline Locomotion: A Comparison of in Vivo Performance of Two Guinea Fowl Ankle Extensors. Journal of Experimental Biology, 206, 2941-2958. http://dx.doi.org/10.1242/jeb.00503
- Davis, J., Kaufman, K.R. and Lieber, R.L. (2003) Correlation between Active and Passive Isometric Stress and Intra- muscular Pressure in the Isolated Rabbit Tibialis Anterior Muscle. Journal of Biomechanics, 36, 505-512. http://dx.doi.org/10.1016/S0021-9290(02)00430-X
- Maloiy, G.M.O., Alexander, R.McN., Njau, R. and Jayes, A.S. (1979) Allometry of Legs of Running Birds. Journal of Zoology (London), 187, 161-167. http://dx.doi.org/10.1111/j.1469-7998.1979.tb03940.x
- Medler, S. (2002) Comparative Trends in Shortening Velocity and Force Production in Skeletal Muscles. American Journal of Physiology-Regulatory Integrative and Comparative Physiology, 283, R368-R378.
- Seow, C.Y. and Ford, L.E. (1991) Shortening Velocity and Power Output of Skinned Muscle Fibres from Mammals Having a 25,000-Fold Range of Body Mass. Journal of General Physiology, 97, 541-560. http://dx.doi.org/10.1085/jgp.97.3.541
- Schilder, J.R. and Marden, J.H. (2004) A Hierarchical Analysis of the Scaling of Force and Power Production by Dra- gonfly Flight Motors. Journal of Experimental Biology, 207, 767-776. http://dx.doi.org/10.1242/jeb.00817
- Mendez, J. and Keys, A. (1960) Density and Composition of Mammalian Muscle. Metabolism, 9, 184-188.
Appendix A. List of Notations
Abbreviations
PCSA—physiologic cross-sectional area
Mathematical signs and symbols


Physical and geometrical notations
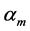
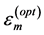
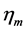
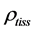
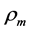
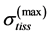
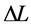
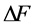
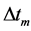


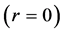
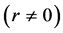
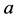
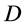
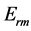
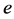
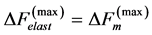
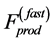
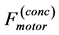
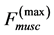
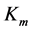
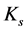
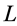
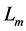
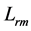
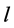
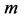
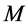
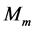
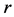
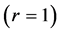
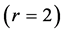
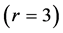

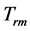
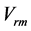

Appendix B. Scaling Muscle Functions
The motor function or motor activity is associated with the generation of the active force of amplitude 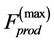
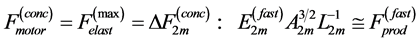
is described by the known universal pattern of the maximal elastic forces [37] emerging during pure bending, pure torsion, as well as complex bending-torsion loading of a long cylinder of length 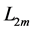
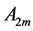
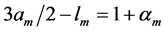
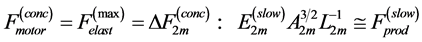
results in the slow-muscle-force constraint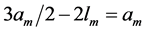

regardless of the fibre type content. This finding follows from both the muscle-force constraints solved with the help of the function-independent muscle-shape constraint shown in Equation (10). Moreover, as shown in [30] , the principal component of the compressive stress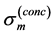
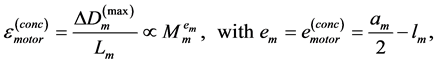
where 
Likewise, the maximum elastic eccentric force
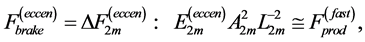
associated with the brake muscle function (see the inset b in Figure 1) provides the maximum elastic stress
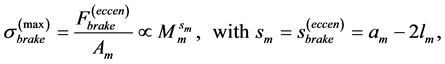
following from Equation (17) and Equation (39). The unique solution to both fast-muscle-force constraint, 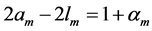
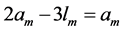
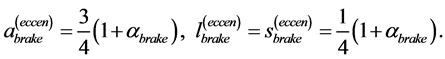
The strut muscle function treated as antagonistic to both motor and brake functions drives nearly isometric contractions characteristic of small, but non-zero length change 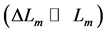

produce by fast muscles. Again, one solves the muscle strut constraints 
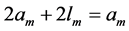
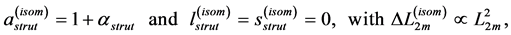
for any type of muscles.
A new antagonist (to strut muscle) tuned to the cardiac type contractions via active elastic force
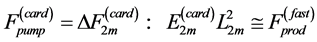
is associated with, say, pump function providing the fast-muscle-force constraint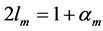
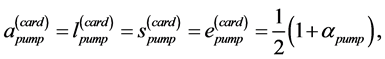
equally applied to slow-fibre muscles resulting in the slow-force constraint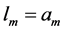
To complete the intrinsic-force description, the spring-type control function associated with the elastic force
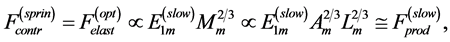
produced by slow-fibre muscles, results in
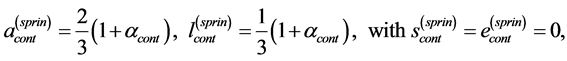
This solution follows from the slow-force and fast-force constraints 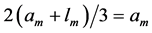

NOTES
1The correspondence sign