Journal of Biomedical Science and Engineering
Vol. 5 No. 3 (2012) , Article ID: 18102 , 8 pages DOI:10.4236/jbise.2012.53017
Characterization of a human brain cortical surface mesh using discrete curvature classification and digital elevation model
![]()
1LiSSi EA, Laboratory, Université Paris-Est Créteil (UPEC), Créteil, France
2LTSIRS Laboratory, National Engineering School, Tunis, Tunisia
Email: aloui_meteo@yahoo.fr, naitali@u-pec.fr, naceurs@yahoo.fr
Received 5 August 2011; revised 9 October 2011; accepted 19 October 2011
Keywords: Brain; Curvature; DEN; Level-Sets; MRI; Mapping; Surface Mesh
ABSTRACT
In this paper we present a novel approach for brain surfacec characterization based on convexity and concavity analysis of cortical surface mesh. Initially, volumetric Magnetic Resonance Images (MRI) data is processed to generate a discrete representation of cortical surface using low-level segmentation tools and LevelSets method. Afterward, pipeline procedure for brain characterization/labeling is developed. The first characterization method is based on discrete curvature classification. This is consists on estimating curvature information at each vertex in the cortical surface mesh. The second method is based on transforming the brain surface mesh into Digital Elevation Model (DEM), where each vertex is designed by its space coordinates and geometric measures related to a reference surface. In other word, it consists on analyzing the cortical surface as a topological map or an elevation map where the ridge or crest lines represent cortical gyri and valley lines represents sulci. The experimental results have shown the importance of these characterization methods for the detection of significant details related to the cortical surface.
1. INTRODUCTION
Segmentation of anatomical structures of the intracranial cavity is a preliminary and main step for the most analysis procedures for brain MRI images. When, the brain surface called also cortical surface is viewed, a human brain appears as a volume with a highly wrinkled boundary surface having numerous long furrows. The term sulci (plural of sulcus) is associated with these furrows and the term gyri (plural of gyrus) designates the regions between the sulci. Geometric modelling, mesh representation and mesh segmentation of anatomical structures in 3D images are becoming an increasingly important processing step. Segmentation of cortical surface should reduce the mesh into meaningful, connected pieces. “Meaningful” implies that the partitioned areas are relevant to the application at hand. In addition, visualization of brain structures such as brain surface, the segmentation allows the automatic identification and labeling of cortical sulci, which will be used in neuronavigation applications, understanding brain anatomy and function, neurosurgeon can easily track the features of interest. Also, segmented sulci from a brain mesh can serve as landmarks, which can be used to register the mesh with other brain meshes to make intra or inter-comparisons. For example, this could serve to measure brain growth and identify diseases.
The most common characterization or labeling of a cortical mesh is into sulcal and gyral regions. The brain gyri can be defined as the top surfaces of the brain folds (Ridges) or as convex regions. The barin sulci can be defined as the area within the brain folds (valleys) or as concave regions. Segmentation of a cortical surface in terms of sulci and gyri can occur in several ways. Classification or partitioning of the cortical surface in concave and convex regions can reduce the size of the Laplacian matrix, in the case of spectral analysis [1]. Also, it is useful to avoid the risk of main memory congestion, improve rendering speed and reduce the computational cost of rendering surface process that to be instantaneous.
In the last several years, many algorithms have been proposed in this growing area, offering several methods. For example, Rettmann’s works [2] involving the segmentation of sulci using watersheds. This work focuses on segmenting sulcale regions. This paper uses the geodesic depth of mesh points in the sulci regions as the height function of the watershed algorithm. Also Mangan and Whitaker [3] proposed an approach using the watershed algorithm for partitioning 3D surface meshes when total curvature is computed and used in segmentation.
We propose in this paper a pipeline steps for the problem of 3D mesh characterization of the brain in Magnetic Resonance Images. We have developed two techniques for cortical surface characterizing using discrete curvature computing and Digital Elevation Model (DEM). In the first technique, we segment the obtained surface meshes using a criteria based on discrete curvature. In the second technique, the cortical surface is labeled by transforming the surface mesh into Digital Elevation Model, where each vertex is designed by its space coordinates and geometric measures like orientation or altitude compared to a reference surface. In other word, it consists to analyzing the cortical surface as a topological map or an elevation map where the ridge lines represent cortical gyri and valley lines represents sulci. This last technique is done in three steps: first, extract cortical surface from volumetric brain MRI. Second, compute outer hull surface of brain using a simplified model of Level-Sets method. This outer hull surface will be used as a reference surface. Finally, Digital Elevation Model (DEM) is computed and cortical surface characterization/labeling is done.
This paper is organized as follows: in the next section, we present a 3D brain surface extraction from volumetric MR images using Level-Sets approach. In Section 3, the cortical surface characterization using discrete curvature information is described. In Section 4, we shows cortical surface labeling using Digital Elevation Model. Then, in the Section 5, we present our preliminary results by applying the proposed technique on a MRI images database. Finally, a discussion and a conclusion related to this work are given in Section 6.
2. BRAIN SURFACE EXTRACTION
Manually segmentation of volumetric images is a complex process which requires lot of time and much concentration to achieve a good quality extraction of regions of interest. For this reason, it is generally interesting to deal with automatic segmentation algorithms. For this purpose, a range of methods including edge based, region based, and knowledge based have been proposed for semiautomatic or automatic detection of various anatomical brain structures. Recently, several attempts have been made to apply deformable models [4-6] to brain image analysis. Indeed, deformable models refer to a large class of computer vision methods and have proved to be successful segmentation techniques for a wide range of applications. Moreover, they constitute an appropriate framework for merging heterogeneous information and they provide a consistent geometrical representation suitable for a surface based analysis.
In some particular Level-Sets [7], geometric deformable models provide an elegant solution for medical images processing [8-11]. In this paper, to extract brain surface from volumetric MRI images we will use a region-competition Level-Sets method as described in [12,13]. This algorithm overcomes classical Level-Sets problems by modulating the propagation term with a signed local statistical force, leading to a stable solution.
We propose a method which operates on 3D MRI scans to extract brain surface. First, the data volume is pre-processed with an anisotropic diffusion filtering method [14] to reduce noise and preserve edges. Then no-brain tissues are removed from the data volume using a simple thresholding. Afterwards, a 3D binary morphological erosion and dilation process [15] are applied to get an initial brain surface and finally we refine brain region extraction by using region-based information into the Level-Sets framework. These computational steps are illustrated in Figure 1.
The aim of the third step is to extract “exactly” the cerebral cortex surface representing the interface between the Gray Matter (GM) and the Cerebrospinal fluid (CSF). For this reason, we propose to use a deformable model algorithm based on the level set technique. We propose also to drive our model by region information instead boundary information, because it is more robust. The process requires an initialization step and speed function. Theoretically, the Level-Set snake is defined as the zero Level-Set of an implicit function 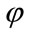 defined on the entire volume. This function will change over the time according to the speed term F. The evolution of
defined on the entire volume. This function will change over the time according to the speed term F. The evolution of 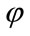 is defined as in [7] via a partial differential equation:
is defined as in [7] via a partial differential equation:
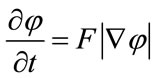 (1)
(1)
The classical speed term is defined as in [16,17]:
 (2)
(2)
Speed term is coupled with the image data through a multiplicative stopping term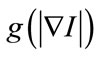 . The curvature k and the constant force v propagate curve near the region of interest surface.
. The curvature k and the constant force v propagate curve near the region of interest surface.
In this work, we use a simplified version of the Levelsets formulation [13]. The model shrinks when the boundary
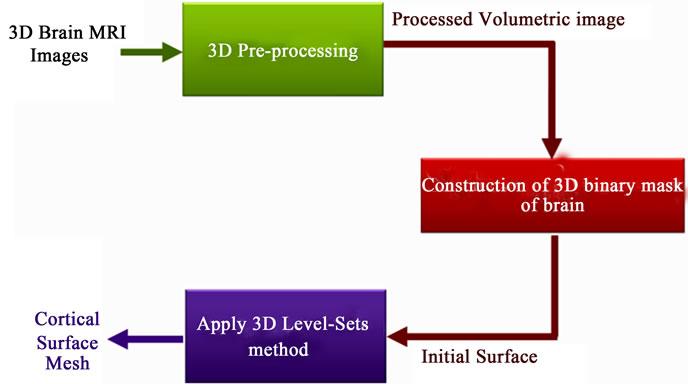
Figure 1. Proposed method for brain segmentation from 3D MRI data.
encloses parts of the background, and grows when the boundary is inside the brain region. Here, the speed function usually consists in a combination of two terms: curvature term for smoothness and data term for evolution. The snake evolves using the following equation:
 (3)
(3)
where D is a data term that forces the model to expand or contract toward desirable features in the input 3D MRI data. By making D positive in desired regions or negative in undesired regions. The term k is the means curvature of the surface, which forces the surface to have less area (and remain smooth), and 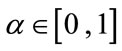 is a free parameter that controls the degree of smoothness.
is a free parameter that controls the degree of smoothness.
The speed function depends on the grayscale value input MRI data denoted D at the point x:
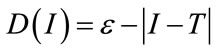 (4)
(4)
where T controls the brightness of the region to be segmented and  controls the range of grayscale values around T that could be considered inside the object. A model situated on voxels with grayscale values in the interval
controls the range of grayscale values around T that could be considered inside the object. A model situated on voxels with grayscale values in the interval 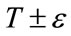 will expand to enclose that voxel, whereas a model situated on grayscale values outside that interval will contract to exclude that voxel.
will expand to enclose that voxel, whereas a model situated on grayscale values outside that interval will contract to exclude that voxel.
As represented in Figure 2, T describes the central intensity value of the region to be segmented, and 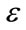 describes the intensity deviation around T that is a part of the desired segmentation. Therefore if a voxel has an intensity value within the
describes the intensity deviation around T that is a part of the desired segmentation. Therefore if a voxel has an intensity value within the 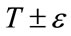 range, the model will expand; otherwise it will contract.
range, the model will expand; otherwise it will contract.
Consequently, the three user parameters that need to be specified for the segmentation are T, 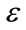 and
and . The initial surface obtained after pre-processing must be transformed into a signed distance [18] for the Level-Sets function is also required (Figure 3). The Level-Sets iteration can be terminated once
. The initial surface obtained after pre-processing must be transformed into a signed distance [18] for the Level-Sets function is also required (Figure 3). The Level-Sets iteration can be terminated once 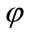 has converged, or after a certain number of iterations.
has converged, or after a certain number of iterations.
3. DISCRETE CURVATURE CLASSIFICATION
Curvatures can also be used as a height measure. The idea is that ridges and valleys have opposite signed curvatures, and the cortical surface is naturally divided between crest lines or ridges (gyri) and valley (sulci). For this reason, we compute gaussian curvature, mean curvature and the two principal curvatures, and later use them to classify the surface type of vertices. The major complication is that curvature cannot be directly evaluated for triangle meshes because it is mathematically defined for smooth surfaces only. However, discrete differential geometry operators have been developed which can estimate curvatures on traingulated manifolds [19,20]. We apply here some operators, which are derived recently by Meyer et al. [21], to estimate curvature information at each vertex in the mesh. We denote H and G, the Mean and the Gaussian discrete curvature operators. k1 et k2 the two principal curvatures operators. We calculate these operators according to the following formulae:
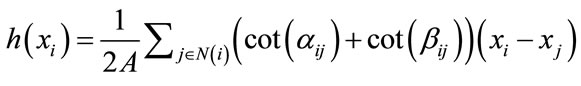 (5)
(5)
Mean curvature
 (6)
(6)

Figure 2. The speed term from [13].
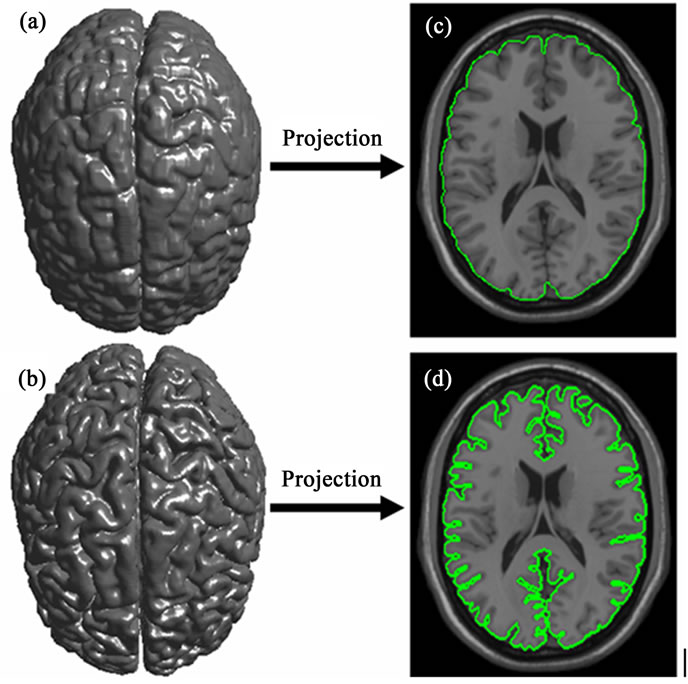
Figure 3. Cortical surface obtained after 3D segmentation of volumetric brain MR Images. (a) Initial cerebral cortex surface; (b) Shows 2D projection into 2D brain slice of initial surface; (c) Cerebral cortex surface obtained using 3D LevelSets method; (b) 2D projection of brain refined surface into 2D brain slice.
Gaussian curvature
 (7)
(7)
As shown in Figure 4,  and
and  are the two angles opposite to the edge in the two triangles sharing the edge
are the two angles opposite to the edge in the two triangles sharing the edge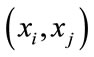 ,
,  is the angle of the
is the angle of the 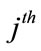 face at the vertex
face at the vertex  and
and 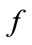 denotes the number of faces around this vertex. The two principal curvatures are expressed as shown by the following equations:
denotes the number of faces around this vertex. The two principal curvatures are expressed as shown by the following equations:
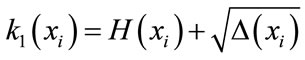 (8)
(8)
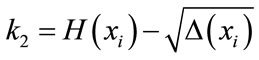 (9)
(9)
where
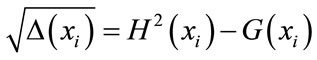 (10)
(10)
by examining discrete curvatures on triangular meshes, one can achieve the following analysis:
- Concave regions/valleys (sulci): 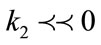 and
and 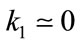
- Convex regions/crest lines (gyrus): 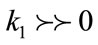 and
and 
- If the H value is negative, then we have a convex behavior (gyri), otherwise it is concave (sulci).
4. DIGITAL ELEVATION MODEL (DEM)
After the text edit has been completed, the paper is ready for the template. Duplicate the template file by using the Save as command, and use the naming convention prescribed by your journal for the name of your paper. In this newly created file, highlight all of the contents and import your prepared text file. You are now ready to style your paper.
In this second characterization method, we present a pipeline steps for cortical surface mesh labeling. Our

Figure 4. 1-ring neighbors and angles opposite to an edge.
method is based on transforming the brain surface mesh into Digital Elevation Model (DEM), where each vertex is designed by its space coordinated and geometric measures like orientation or altitude related to a reference surface. In other word, it consists to analyzing the cortical surface as a topological map or an elevation map where the ridge lines represent cortical gyri and valley lines represents sulci. The cortical surface characterization process is done in two steps: first, compute outer hull surface of brain using a simplified model of Level-Sets method. This outer hull surface will be used as a reference surface. Finally, Digital Elevation Model (DEM) is computed and cortical surface characterrization/labeling is done.
4.1. Outer Hall Surface Extraction
An outer hull surface, which wraps the brain surface, is computed using a simplified Level-Set model. This model is given as follows:
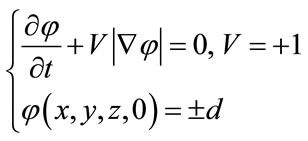 (11)
(11)
where V = +1 is a coefficient that controls the speed and direction of deformation (expands). This constant deformation plays the same role as the pressure force. This Levelsets model is implemented using entropy condition originally proposed in the area of interface propagation by Sethian [23,24].
After his stage, we have two discrete meshes surfaces: cortical surface denoted S and outer hull surface denoted  as show in Figures 5 and 6.
as show in Figures 5 and 6.
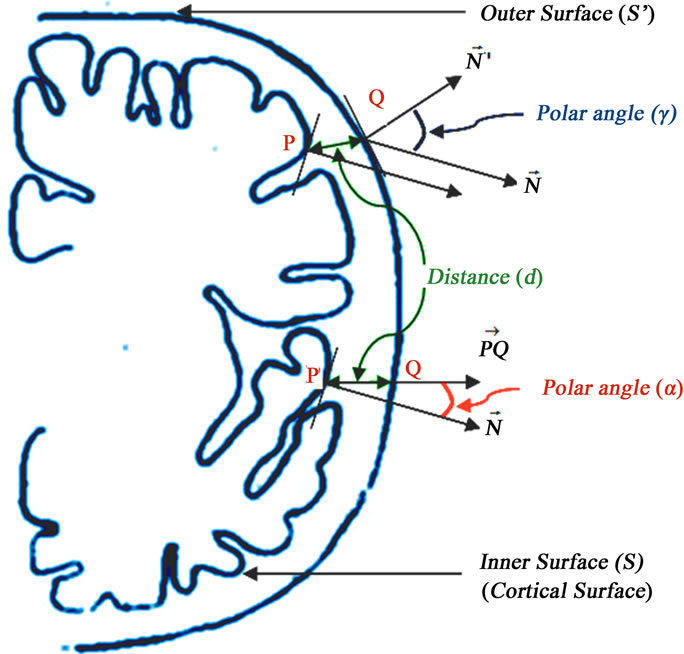
Figure 5. Geometric measures for characterizing the cortical surface denoted S. Minimum distance denoted d, the polar angle α and the polar angle γ.
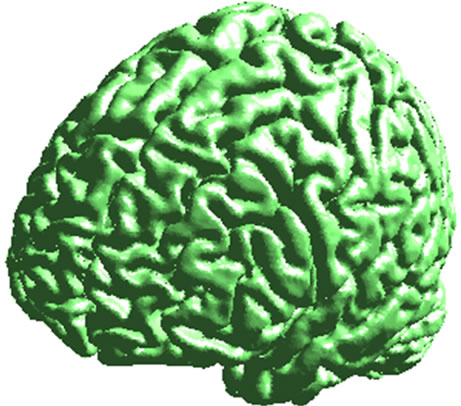


Figure 6. Cortical surface (left) and 2 views of outer hull surface (middle and right).
4.2. Digital Elevation Model Computing
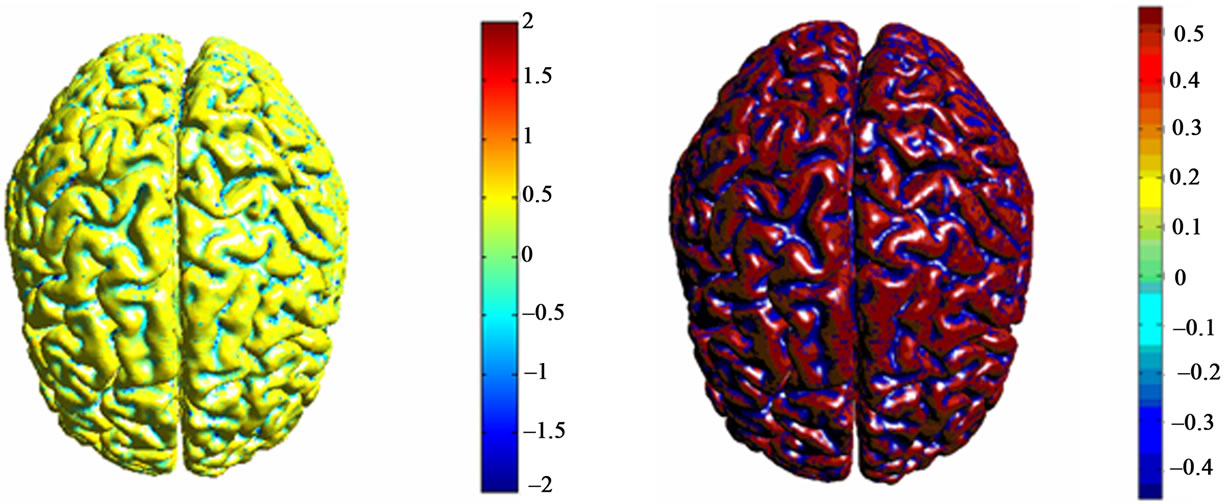
We have proposed to define three geometric measures for characterizing the cortical surface as shown on Figure 5. These measures are assigned to each cortical surface vertex. The first measure is the minimum distance denoted between vertex on the cortical surface and the outer hull surface. The second measure is the polar angle 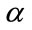 between the normal vector related to vertex P on cortical surface and the vector
between the normal vector related to vertex P on cortical surface and the vector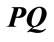 . Finally, the third measure is the polar angle
. Finally, the third measure is the polar angle 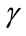 between the normal vector related to vertex P on the cortical surface and the normal vector related to vertex Q on the outer hull surface. Where Q is the nearest vertex belonging to the outer surface
between the normal vector related to vertex P on the cortical surface and the normal vector related to vertex Q on the outer hull surface. Where Q is the nearest vertex belonging to the outer surface  to vertex P on the cortical surface S. These measures are given as following:
to vertex P on the cortical surface S. These measures are given as following:
4.2.1. Elevation of Vertex d
Each vertex of the cortical surface receives the minimum distance that separates it from the outer surface. A vertex from cortical surface will be considered belonging to sulci or gyri according to its height and according to pre-fixed threshold.
4.2.2. Polar Angle α
The polar angle α is the angle between the normal vector 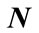 related to vertex P on cortical surface and the vector
related to vertex P on cortical surface and the vector 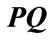 .
.
4.2.3. Polar Angle γ
The polar angle γ is the angle between the normal vector 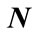 related to vertex P on the cortical surface and the normal vector
related to vertex P on the cortical surface and the normal vector 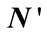 related to vertex Q on the outer hull surface. Where Q is the nearest vertex belonging to the outer surface
related to vertex Q on the outer hull surface. Where Q is the nearest vertex belonging to the outer surface  to vertex P on the cortical surface S.
to vertex P on the cortical surface S.
5. EXPERIMENTS RESULTS
We have performed a series of experiments on brain MR images from MeDEISA database [22]. Results of two different labeling methods of cortical surface are given. The mesh that represents cortical brain was created from T1-weighted MRI images using level-sets method. Results of cortical surface characterization by curvature classification are depicted in Figure 7. Discrete curvatures are used as a height measure. So that, gyri are considered as ridges and sulci are considered as basins which have opposite signed curvatures. Each label corresponds to a different color for each curvature operator. Then, results of cortical surface characterization using geometric measures computed from brain surface and outer haul surface are depicted in Figures 8 and 9:
- Figure 8 shows the classification result of the cortical surface into gyri and sulci using elevation of vertex.
- Figure 9 left shows the distribution of polar angle 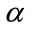 on the cortical surface, when gyri and sulci are very distinguishable and are divided into two different classes.
on the cortical surface, when gyri and sulci are very distinguishable and are divided into two different classes.
- Figure 9 right shows the distribution of polar angle 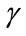 on the cortical surface, when gyri and sulci are very distinguishable and are divided into two different classes.
on the cortical surface, when gyri and sulci are very distinguishable and are divided into two different classes.
Through this classification process it will be easy to distinguish between gyri that are the surfaces top of the brain folds (ridges), and sulci that are the surface within the brain folds (basins). Each label corresponds to a different color for each geometric measure. An inherent difficultly in the interpretation of brain characterization is that there is no definition of what is correct. Some works use expert points of view from neurologists on where sulci and gyri exist. However, visual results given by Figures 7-9 can be interpreted given the idea that sulci are the surfaces within the brain folds (basins) and gyri are the surfaces at the top of the brain folds (ridges).
6. CONCLUSIONS
This paper proposes novel methods to decompose cortical surface represented by triangle meshes into separate parts based sulci and gyri using geometric measures computed from cortical surface and outer hull surface of the brain. Specially, the first approach use discrete curvature as height in order to distinguish brain sulci from gyru. The second approach is based on transforming the brain surface mesh into Digital Elevation Model (DEM), where each vertex
 (a)
(a)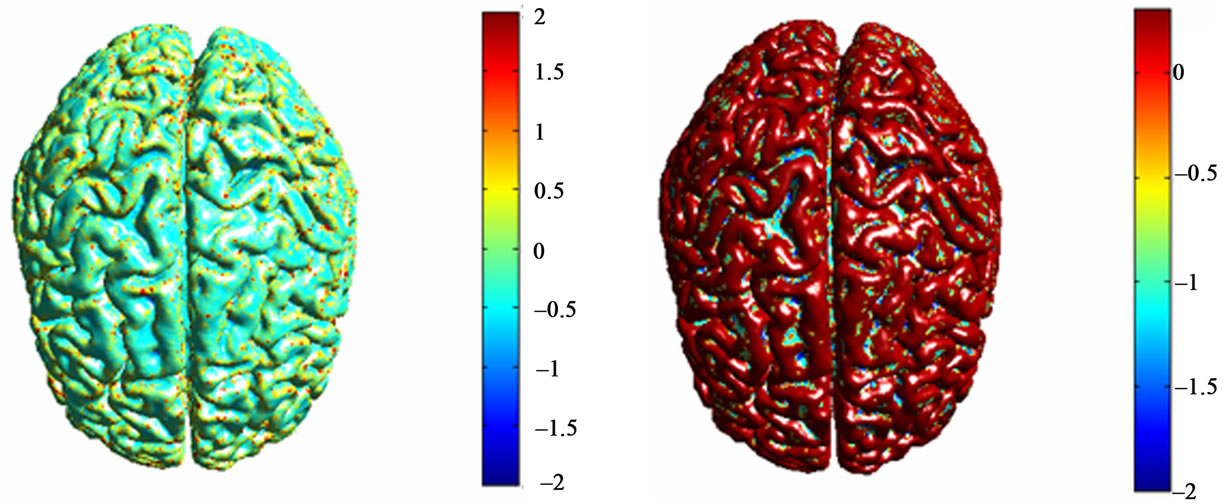 (b)
(b)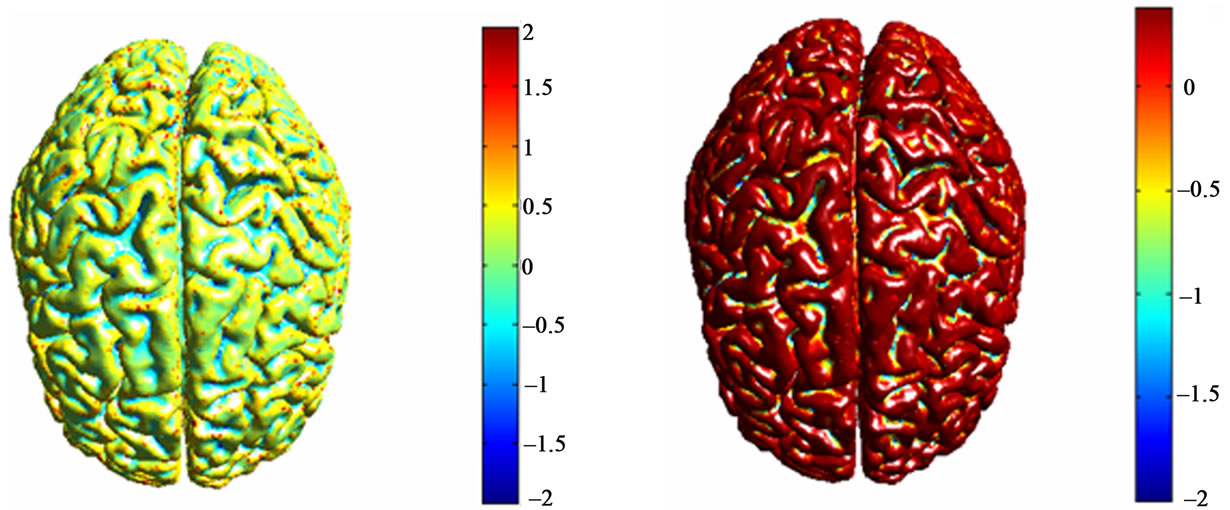 (c)
(c)
Figure 7. Corticale surface segmentation using discrete curvature classification into sulci and gyri. (a) Principal curvature k1; (b) Principal curvature k1 after thresholding; (c) Principal curvature k2; (b) Principal curvature k2 after thresholding; (a) Mean curavature H; (b) Mean curvature H after thresholding.
is designed by its space coordinates and geometric measures like polar angle α, polar angle γ and elevation of vertex d related to a reference surface. After that we will have, a cortical surface as a topological map, when gyri and sulci are very distinguishable and are divided into two different classes.
Visually appealing results can be interpreted given the idea that that sulci are the surfaces within the brain folds (basins) and gyri are the surfaces at the top of the brain folds (ridges). Thus, the prospects of this work would be

Figure 8. (Left) DEN computed from the altitude or the minimum distance for each vertex on the cortical surface that separates it from the outer hull surface. (Right) DEN after thresholding of vertex elevation on cortical surface.

Figure 9. (Left) Distribution of polar angle α on the cortical surface. (Right) the distribution of polar angle γ on the cortical surface.
to use our approach to address studies on asymmetry of brain anatomy, the inter-individual variability of brain anatomy, neurological dimension of certain mental diseases such as autism and schizophrenia, or, in the context of longitudinal studies on the characterization of brain development for healthy or pathological subject.
REFERENCES
- Lavoué, G. (2005) Compression de surfaces, basée sur la subdivision inverse, pour la transmission bas débit et la visualisation progressive. Thèse de Doctorat, Université Claude Bernard Lyon 1, Lyon.
- Mangan, A.P. and Whitaker, R. (1999) Partitioning 3d surface meshes using watershed segmentation. IEEE Transactions on Visualization and Computer Graphics, 5, 308- 321. doi:10.1109/2945.817348
- McInerney, T. and Terzopoulos, D. (1996) Deformable models in medical image analysis: A survey. Medical Image Analysis, 1, 91-108. doi:10.1016/S1361-8415(96)80007-7
- Kass, M., Witkin, A. and Terzopoulos, D. (1987) Snakes: Active contour models. International Journal of Computer Vision, 1, 321-331. doi:10.1007/BF00133570
- Xu, C., Pham, D. and Prince, J. (2000) Image segmentation using deformable models. Handbook of Medical Imaging, 2, 129-174.
- Sethian, J.A. (1996) Level set methods and fast marching methods. Cambridge University Press, Cambridge.
- Warfield, S.K., Kaus, M., Jolesz, F.A. and Kikinis, R. (2000) Adaptive, template moderated, spatially varying statistical classification. Medical Image Analysis, 20, 43- 55. doi:10.1016/S1361-8415(00)00003-7
- Baillard, C., et al. (2000) Cooperation between level set techniques and 3D registration for the segmentation of brain structures. International Conference on Pattern Recognition, Barcelona, 3-8 September 2000, 991-994.
- Suri, J.S., Singh, S. and Reden, L. (2002) Computer vision and pattern recognition techniques for 2-D and 3-D MR cerebral cortical segmentation (Part I): A state-ofthe-art review. Pattern Analysis & Applications, 5, 46- 764. doi:10.1007/s100440200005
- Liew, A.W.C. and Yan, H. (2006) Current methods in the automatic tissue segmentation of 3D magnetic resonance brain images. Current Medical Imaging Reviews, 2, 91-103. doi:10.2174/157340506775541604
- Ho, S., Bullitt, E. and Gerig, G. (2002) Level set evolution with region competition: Automatic 3-D segmentation of brain tumors. 16th International Conference on Pattern Recognition, 20, 532-535.
- Lefohn, A.E., Cates, J. and Whitaker, R. (2003) Interactive, GPU-based level sets for 3D brain tumor segmentation. Medical Image Computing and Computer Assisted Intervention, 564-572.
- P. Perona and Malik, J. (1990) Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Medical Imaging, 12, 629-639.
- Serra, J.P. (1982) Image analysis and mathematical morphology. Academic Press Inc., London.
- Caselles, V., Kimmel, R. and Sapiro, G. (1997) Geodesic active contours. International Journal of Computer Vision, 22, 61-97. doi:10.1023/A:1007979827043
- Malladi, R., Sethian, J.A. and Vemuri, B.C. (1995) Shape modeling with front propagation: A level set approach. IEEE Transactions on Pattern Analysis and Machine Intelligence, 17, 158-174. doi:10.1109/34.368173
- Osher, S. and Sethian, J.A. (1988) Fronts propagating with curvature dependent speed: Algorithms based on hamilton-jacobi formulations. Journal of Computational Physics, 79, 12-49. doi:10.1016/0021-9991(88)90002-2
- Hamman, B. (1993) Curvature approximation for traingulated surfaces. In: Gerald, F., et al., Eds., Geometric Modelling, Computing Supplementum, Springer-Verlag, Vienna, 139-153.
- Max, N. (1999) Weights for computing vertex normals from facet normals. Journal of Graphics Tools, 4, 1-6.
- Meyer, M., Desbrun, M. and Schroder, P. (2002) Discrete differential-geometry operators for triangulated 2-manifolds. International Workshop on Visualization and Mathematics, Berlin.
- Medical Database for the Evaluation of Image and Signal Processing (MeDEISA), 2011. www.medeisa.net.
- Sethian, J. (1982) An analysis of flame propagation. Ph.D. Thesis, University of California, Berkeley.
- Sethian, J. (1994) Curvature flow and entropy conditions applied to grid generation. Journal of Computational Physics, 115, 440-454. doi:10.1006/jcph.1994.1209
- Rettmann, M.E., Han, X., Xu, C. and Prince, J.L. (2002) Automated sulcal segmentation using watersheds on the cortical surface. NeuroImage, 15, 329-344,

