Journal of Cancer Therapy
Vol.1 No.2(2010), Article ID:2028,5 pages DOI:10.4236/jct.2010.12012
Analysis of Quality of Life in Cancer Patients by Structural Equation Model
![]()
Department of Mathematics, Wuhan University of Technology, Wuhan, China.
Email: tonghengqing@126.com
Received April 14th, 2010; revised May 8th, 2010; accepted May 27th, 2010.
Keywords: Quality of life, Structural equation model, Unit vector constraint, Definite linear algorithm
ABSTRACT
Many people have been dead of cancer. The life quality of patients with cancer has aroused great concern from the public and specialists. In this paper, an index system of life quality is proposed to evaluate the quality of life, which includes 6 first-level indexes and 34 second-level indexes. Then, a structural equation model (SEM) based on these indexes and relationships among them is constructed for the analysis of quality of life in cancer patients. Furthermore, we offer a definite linear algorithm for the calculation of SEM. This method is more objective and scientific compared with traditional methods, such as descriptive analysis, some simple test methods and so on.
1. Introduction
Nowadays, cancer has become the main threat to human health. For these diseases, it is hard to evaluate the treatment effect by cure rate, also survival rate is very limited. Compared with the traditional survival analysis method only considering survival rate or survival time, QOL evaluation focus more on subjective feeling, and can reflect the patient's health more fully. Considering that, the conception of QOL was accepted by the medical community in the 1970s,and there was ever a great upsurge in studies. QOL research of Clinical Oncology can go back to Karnofsky Performance Status (KPS) proposed by Karnofsky in the 1940s, which does not include the patient's subjective feelings, therefore, it is not a real QOL evaluation. The modern QOL research was initiated by Priestman and others with QOL measurement of breast cancer patients in 1976. QOL is an index system comprehensively evaluating individual physical, psychological, social support and demographic level.
QOL has been widely applied in various fields, and become an indispensable social important index and evaluation tool. The research of QOL has mainly three great effects in the treatment of cancer. 1) The evaluation of the effect of cancer treatment performs the selective therapy; 2) It has advantage of the selection and assessment of anti-cancer drug, antiemetic and anodyne and so on. U.S. FDA has decided that QOL must be the index in all anti-cancer drug evaluation, there should have the material both improving survival time and quality of life, when the efficacy of new medicine is not better than the old, new role can be found by QOL evaluation, which is good for drugs listed, it also helps to find new unexpected side effects or toxicity; 3) It helps to comprehend the long-term existing status of therapy in patients with cancer and assists to adopt the best management countermeasure in patients with late cancer. Now the basic principle of cancer radical treatment is the comprehensive treatment, the ultimate goal of which is to extend lifetime and improve the quality of life. But for most of the definite diagnosis of cancer patients, they already lost radical therapy and need palliative treatment, then improving QOL becomes the primary consideration. Therefore, study of QOL is of great significance in theoretically and practically, which needs further research.
At present, the evaluation of QOL is a very weak link, it is not maturity to measure QOL. Main systematic evaluation methods of Quality of Life, which are in common use are descriptive analysis method and some simple test methods, including Correlation Analysis and T test and so on. The assessment is seriously hindered by the complexity of QOL. In this paper, we build a related structural equation model (SEM) to reveal the potential factor of QOL, and the relationships between them, in which the summarizing coefficients are calculated by samples, so it is more objective and convincing, and could offer more deep analysis for the index systems. It will provide the suitable intervention methods in order to improve and enhance the quality of life in patients with cancer.
2. SEM for the QOL of the Cancer
SEM is a fast-growing embranchment of Application Statistics, widely used in psychology, sociology and other fields. This model not only studies the interior relationship among various factors, but also the relative and causal relations among latent variables. The QOL of the patients is controlled by psychological factor and physiological factor, whose values cannot be measured directly, so it is not suitable to use the usual statistical methods to analyze the influencing factors of the QOL. Considering that, this paper is the application of SEM to analyze the influencing factors of the QOL in patients with cancer.
There are always two systems of equations in a SEM. One is a structure system of equations among structural variables, and the other one is a measurement system of equations between structural variables and observed variables. Since the QOL of the patients with cancer cannot only reflect the curative effect, but also prevention and rehabilitation effects, it’s important and urgent to quantitative analysis and build effective QOL index immediately. In our model, there are 6 latent variables and 34 observed variables. The variables are listed in Table 1 as follows:
There are 6 structural variables ( ,
,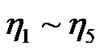 ) and 15 path relationships, which are expressed in Figure 1 below (The path coefficients from the exogenous latent variable
) and 15 path relationships, which are expressed in Figure 1 below (The path coefficients from the exogenous latent variable 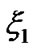 to the endogenous latent variables
to the endogenous latent variables  are
are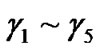 , expressed with dashed arrowheads; The relationships among independent variables are
, expressed with dashed arrowheads; The relationships among independent variables are 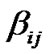 , expressed with real-line arrowheads).
, expressed with real-line arrowheads).
The structural equations are relationships among the latent variables. The structural equations can be expressed as follows:
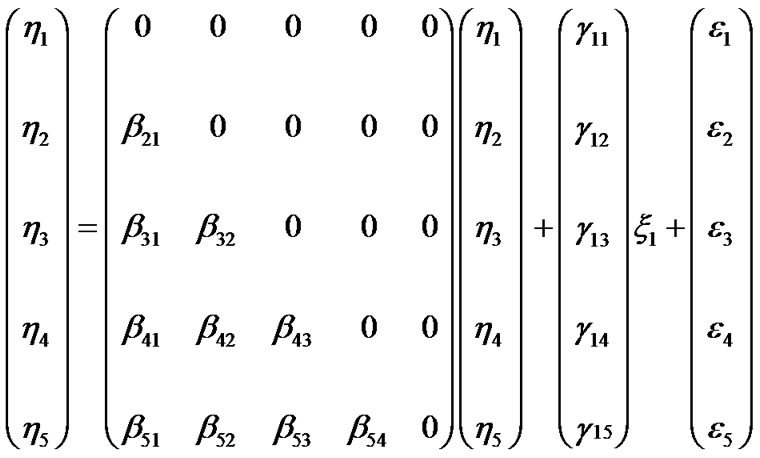
(1)
In general, vector and matrix are used to describe the structural equations. Let  and
and 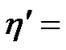
 .Then
.Then  square matrix
square matrix  is the coefficient matrix of
is the coefficient matrix of , then
, then  matrix
matrix 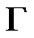 is the coefficient matrix of
is the coefficient matrix of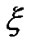 ,
,  is the residual vector, then the structural equations (1) may be extended as:
is the residual vector, then the structural equations (1) may be extended as:
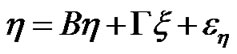 (2)
(2)
The structural variables are implicit and cannot be observed directly. Each structural variable is corresponding with many observed variables.
Suppose there are 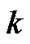 independent structural variables and
independent structural variables and 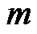 dependent structural variables. The observed variables corresponding to the independent structural variable
dependent structural variables. The observed variables corresponding to the independent structural variable  are denoted as
are denoted as ,
, 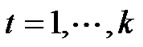 ,
, 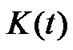
 , where
, where 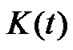 is the number of observed variables corresponding to the independent structural variable
is the number of observed variables corresponding to the independent structural variable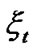 . In Figure 1,
. In Figure 1,  and
and . The observed variables corresponding to the dependent variable
. The observed variables corresponding to the dependent variable  are denoted as
are denoted as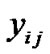 ,
, 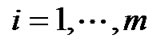 ,
, 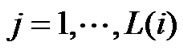 , where
, where 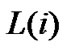 is the number of observed variables corresponding to the dependent structural variable
is the number of observed variables corresponding to the dependent structural variable . In Figure 1,
. In Figure 1, 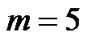 and
and .
.
The observation equations can be expressed as the relationship from the observed variables to the structural variables:
 ,
, (3)
(3)
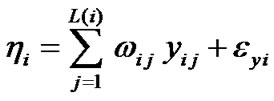 ,
, (4)
(4)
where 、
、 are the summarizing coefficients, and
are the summarizing coefficients, and  with subscript is a random error.
with subscript is a random error.
The relationships between the structural variables and the observed variables can also be expressed as follows:
 ,
,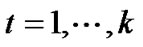 (5)
(5)
 ,
,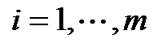 (6)
(6)
where 、
、 are the carrying coefficients, and
are the carrying coefficients, and 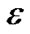 with subscript is still a random error.
with subscript is still a random error.
Denoting observation vectors as ,
, 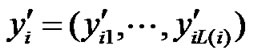 , and denoting coefficients as
, and denoting coefficients as

Table 1. Index of variables
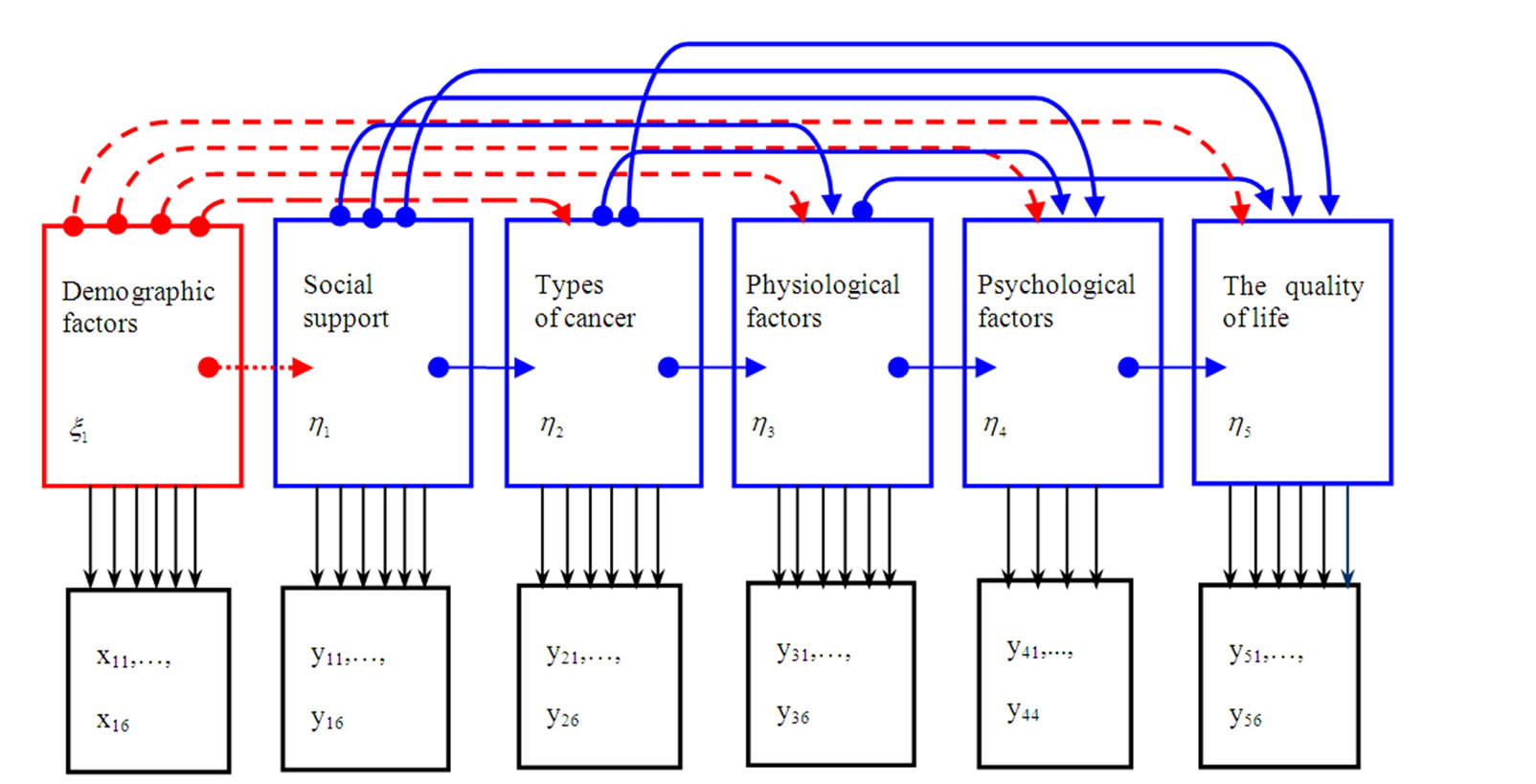
Figure 1. Model of QOL index
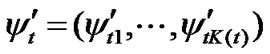 ,
,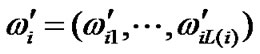 , then the equations (2)-(4) can be written into:
, then the equations (2)-(4) can be written into:
 (7)
(7)
We call 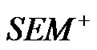 the structural equation model with positive observation.
the structural equation model with positive observation.
Letting ,
, 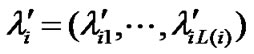 , then the observation equations (5) and (6) can be expressed as:
, then the observation equations (5) and (6) can be expressed as:
 ,
,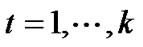 (8)
(8)
 ,
,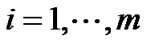 (9)
(9)
Combine the equations (2), (8) and (9) as:
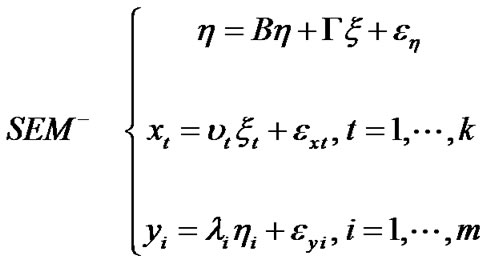 (10)
(10)
and call 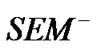 the structural equation model with converse observation.
the structural equation model with converse observation.
3. The Least Square Solution by the Modular Constraint of Structural Vector
By analyzing the observation equations of SEM carefully, we can discover the least square relationship between each structural variable and its observed variables, and obtain the least square solution of structural variable by the modular constraint of structural vector. Now, we give the MCLS algorithm of structural vector in SEM which is studied by penman as follows:
Algorithm 1. The modular constraint least square solution (MCLS) of structural vector in SEM.
Step 1. In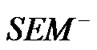 , suppose that
, suppose that  all are unit vectors, calculate the least square estimates of the coefficients between the structural variable and its observed variables:
all are unit vectors, calculate the least square estimates of the coefficients between the structural variable and its observed variables:
 ,
,  ,
,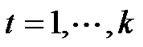 (11)
(11)
 ,
, 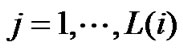 ,
, (12)
(12)
Step 2. In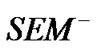 , calculate the least square estimates of structural variable by making use of
, calculate the least square estimates of structural variable by making use of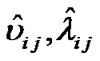 :
:
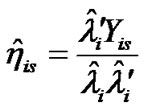
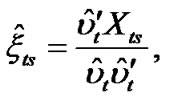 ,
,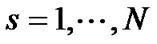 ,
,
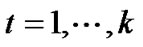 ,
,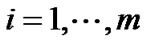 (13)
(13)
Here  are the transverse vector of the observation data matrix,
are the transverse vector of the observation data matrix, 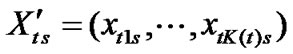 ,
, .
.
Step 3. In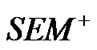 (or (3) and (4)), make use of
(or (3) and (4)), make use of  obtained in Step 2 to calculate regression coefficients
obtained in Step 2 to calculate regression coefficients 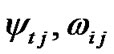 according to a common linear regression method.
according to a common linear regression method.
Step 4. In (or (2)),make use of
(or (2)),make use of  obtained in Step 2 to calculate the estimates of coefficient matrices
obtained in Step 2 to calculate the estimates of coefficient matrices .
.
Notice that (2) is a common linear regression equation system, we can use Two Step Least Square to calculate it.
4. Definite Linear Algorithm of Prescription Constraint
Since the solutions of 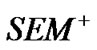 or
or 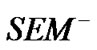 are not unique, and they may differ by a multiple (the proof is omitted). Therefore, in the structural equation (1) or (2), if each structural variable is multiplied by the same multiple, its coefficient solution is the same. Taking note of this, the solution of structural equations is irrelevant to the modular length of the structural variable. However, it is not reasonable to assume that the modular length of each structural variable is 1. On the other hand, if each modular length of the structural variable is not the same in the possibly existing optimal solution set, then MCLS is not good.
are not unique, and they may differ by a multiple (the proof is omitted). Therefore, in the structural equation (1) or (2), if each structural variable is multiplied by the same multiple, its coefficient solution is the same. Taking note of this, the solution of structural equations is irrelevant to the modular length of the structural variable. However, it is not reasonable to assume that the modular length of each structural variable is 1. On the other hand, if each modular length of the structural variable is not the same in the possibly existing optimal solution set, then MCLS is not good.
One reasonable way is to let each structural variable have an undetermined parameter of the modular length and combine the structural equation (1) or (2) to find the solution. The error square sum of this solution includes  modular length parameters. Changing these modular length parameters to minimize the error square sum, we can obtain a reasonable modular length of the structural variable.
modular length parameters. Changing these modular length parameters to minimize the error square sum, we can obtain a reasonable modular length of the structural variable.
Another possible way is to find a more reasonable constraint to replace the modular constraint. After getting MCLS, we can change the modular length of the structural variable in observation equations to make the path coefficient between structural variables and observation variables satisfy the prescription condition. In equations (3) and (4), the prescription conditions are:
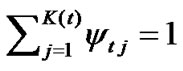 ,
,  ,
,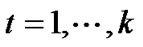 (14)
(14)
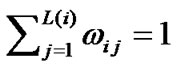 ,
, 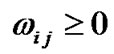 ,
, (15)
(15)
If the corresponding path coefficients of MCLS are non-negative at the beginning, then it is simple. We just need to divide the two sides of the equations (3) and (4) by a constant. This constant should be the sum of the corresponding path coefficients in MCLS. For example, in the equation (3), if , then the two sides of the equation (4) are divided by the constant
, then the two sides of the equation (4) are divided by the constant , so the modular length of structural variables becomes
, so the modular length of structural variables becomes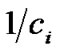 , and
, and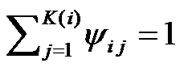 .
.
If the corresponding path coefficients of MCLS are negative at the beginning, we cannot copy the method of prescription regression proposed by Fang (1982, 1985), because regression dependent variables are not completely known. Now we know the direction of regression dependent variables, but the modular length is undetermined. According to the theorem in Fang (1982), if the initial regression coefficients have negative ones, whose prescription regression coefficient should be 0. So we can first make ordinary regression about MCLS, where the modular length of dependent variables is 1. If there are some non-positive terms in the initial regression coefficients, we can get rid of these variables, and thus the corresponding regression coefficient is 0. Then the two sides of the equations (3) and (4) can be divided by a constant that should be the sum of the corresponding path coefficients in MCLS, as discussed in the previous paragraph.
Of course we can improve the constraint of the prescription condition. If some regression coefficient is 0, its corresponding variable may be removed from the model, which is not a desired situation. To avoid this, we may change the prescription condition and let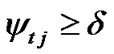 ,
, 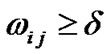 , where
, where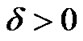 . If some initial regression coefficients are less than
. If some initial regression coefficients are less than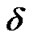 , they all are changed as
, they all are changed as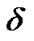 , and the corresponding independent variables with coefficient
, and the corresponding independent variables with coefficient  should be moved to the left side of the equation in regression process.
should be moved to the left side of the equation in regression process.
Summarizing the above discussion we can continue to improve the algorithm of MCLS.
Algorithm 2. Improvement on Step 3 of Algorithm 1.
Step 5. After getting the estimate of structural variables 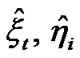 in Step 2, calculate the summarizing coefficients
in Step 2, calculate the summarizing coefficients 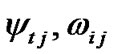 by prescription regression, and recalculate the estimates of
by prescription regression, and recalculate the estimates of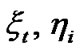 .
.
1) Make use of 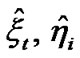 directly in Step 2 and calculate
directly in Step 2 and calculate  in
in 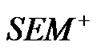 by common regression.
by common regression.
2) For any , if there are
, if there are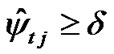 , (
, (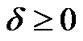 ) for all
) for all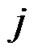 , and
, and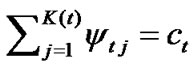 , then divide both sides of equation (3) by
, then divide both sides of equation (3) by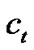 . Similarly, for any
. Similarly, for any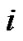 , if there are
, if there are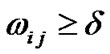 ,(
,(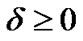 ) for all
) for all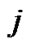 , and
, and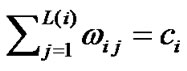 ,then divide both sides of equation (4) by
,then divide both sides of equation (4) by .
.
After checking all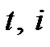 , go to Step 4 in Algorithm 1.
, go to Step 4 in Algorithm 1.
3) For any , if there is some
, if there is some  so that
so that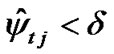 , or
, or , (
, (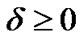 ), then let the corresponding term be fixed, i.e.,
), then let the corresponding term be fixed, i.e., 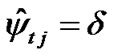 or
or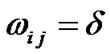 . After checking all
. After checking all , go to Step 1 and Step 2 in this algorithm.
, go to Step 1 and Step 2 in this algorithm.
Note that if some regression coefficient is fixed in common regression, the corresponding independent variables with its coefficient  should be moved to the left side of the equation and combined with the dependent variable to regression. After regression the corresponding independent variable with its coefficient
should be moved to the left side of the equation and combined with the dependent variable to regression. After regression the corresponding independent variable with its coefficient 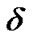 should be moved to the right side of the equation.
should be moved to the right side of the equation.
5. Conclusions and Discussions
In this paper, a structural equation model is proposed to analyze the quality of life in cancer patients. Besides, a definite linear algorithm for SEM based on the modular constraint of structural variable, the least square theorem, and the prescription regression method is introduced, this model is more objective and scientific compared with traditional methods, such as descriptive analysis method and some simple test methods, including Correlation Analysis and T test and so on, because the summarizing coefficients of this evaluation system are calculated by samples rather than designed arbitrarily. Therefore, we can have a better understanding of the relationships among the indexes, which will do a great favor to decision-making analysis of Quality of Life in Cancer Patients.
REFERENCES
- P. Ravasco, I. Monteiro-Grillo and M. E. Camilo, “Does Nutrition Influence Quality of Life in Cancer Patients Undergoing Radiotherapy?” Radiother Oncology, Vol. 67, No. 2, May 2003, pp. 213-220.
- C. C. Gotay, E. I. Korn, M. S. McCabe, et al., “Building Quality of Life Assessment into Cancer Treatment Studies,” Oncology, Vol. 6, 1992, pp. 25-28.
- D. F. Cella and E. A. Cherin, “Quality of Life during and after Cancer Treatment,” Comprehensive Therapy, Vol. 14, 2001, p. 69.
- F. Gu, “Quality of Life Measurement in 233 Cancer Patients,” Chinese Cancer, Vol. 8, No. 8, 1999, pp. 356-358.
- J. P. Wang and J. N. Cui, “Quality of Life and Factors that Influencing it among Cancer Patients in China,” Chinese Journal of Clinical Psychology, Vol. 8, No. 1, 2000, pp. 23-26.
- H. Q. Tong, “Data Analysis and Statistical Computation (DASC),” Electronic Publication, Science Press of China, Beijing, 2005.
- C. M. Wang and H. Q. Tong, “Best Iterative Initial Values for PLS in a CSI Model,” Mathematical and Computer Modeling, Vol. 46, No. 3-4, August 2007, pp. 439- 444.
- Y. H. Jiang, Z. Li and Y. F. Cheng, “The Relation of Psychological Factor and Cancer,” Chinese Journal of Clincal Rehabililation, Vol. 6, No. 1, 2002, pp. 92-93.

