Intelligent Information Management
Vol.07 No.04(2015), Article ID:58443,9 pages
10.4236/iim.2015.74019
K-Means Graph Database Clustering and Matching for Fingerprint Recognition
Vaishali Pawar, Mukesh Zaveri
Department of Computer Engineering, SVNIT, Surat, India
Email: vaishali_s_pawar@yahoo.com, mazaveri@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2015; accepted 27 July 2015; published 30 July 2015
ABSTRACT
The graph can contain huge amount of data. It is heavily used for pattern recognition and matching tasks like symbol recognition, information retrieval, data mining etc. In all these applications, the objects or underlying data are represented in the form of graph and graph based matching is performed. The conventional algorithms of graph matching have higher complexity. This is because the most of the applications have large number of sub graphs and the matching of these sub graphs becomes computationally expensive. In this paper, we propose a graph based novel algorithm for fingerprint recognition. In our work we perform graph based clustering which reduces the computational complexity heavily. In our algorithm, we exploit structural features of the fingerprint for K-means clustering of the database. The proposed algorithm is evaluated using realtime fingerprint database and the simulation results show that our algorithm outperforms the existing algorithm for the same task.
Keywords:
Pattern Recognition, Fingerprint Matching, Graph Matching, Clustering

1. Introduction
The graph is an important data structure for representing various multi-attributed data and their complex rela- tions. Pattern recognition is the area of computer science which intends to find a particular pattern in the given input. A variety of graph based techniques had been proposed as a powerful tool for pattern representation and classification in the past years. For a longer duration, graphs were considered to be computationally expensive tool. But recently the graph based pattern recognition and image processing is gaining popularity. It is a fact that the computational complexity of the graph based methods is becoming feasible due to high end new generations of the computers and the research advancements. In this work, we exploit graph based fingerprint recognition. Fingerprint plays a distinguishing role in biometrics. It gives unique identification to the individual. It is per- manent and non-changing character pattern over a long period of time. The fingerprint recognition consists of retrieving specific fingerprints from database. The characteristics or features of a fingerprint are extracted and used in identification. We have used attributed graph to represent the extracted features of the fingerprint. When the feature set size grows, graph matching becomes expensive. So we optimize the fingerprint database by K- Means clustering which drastically reduces the fingerprint matching time. In this section, we discuss some basic graph terminologies which are prerequisite for the further discussion. We also discuss the related literature in this section. In section 2, we present the proposed algorithm. Section 3 discusses simulation results and section 4 concludes the paper. A graph 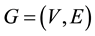 is a set of vertices V and edges E. V is the set of vertices and
is a set of vertices V and edges E. V is the set of vertices and 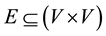 is the set of edges of graph G. The order or size of a graph G is defined as the number of vertices of G and it is represented as
is the set of edges of graph G. The order or size of a graph G is defined as the number of vertices of G and it is represented as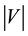 . If two vertices in G, say
. If two vertices in G, say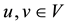 , are connected by an edge
, are connected by an edge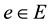 , this is denoted by
, this is denoted by  and the two vertices are said to be adjacent to each other. Edges can be directed or undirected. Graph matching can be applied to directed and undirected graphs both. A directed graph
and the two vertices are said to be adjacent to each other. Edges can be directed or undirected. Graph matching can be applied to directed and undirected graphs both. A directed graph  is called complete when there is always an edge
is called complete when there is always an edge 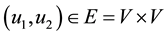 between any two vertices
between any two vertices 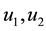 in the graph. When graphs are used to represent objects, images or fingerprints, vertices usually represent regions or features of the object or images, and edges between them represent the relations between the features.
in the graph. When graphs are used to represent objects, images or fingerprints, vertices usually represent regions or features of the object or images, and edges between them represent the relations between the features.
Graph vertices and edges can contain large complex information. When this information is a label or attributes of vertices and edges, the graph is called an attributed graph. Formally, an attributed graph is a graph with six-tuple , where
, where
・ V is a finite set of nodes,
・ 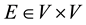 is a finite set of edges,
is a finite set of edges,
・ u is a labeling function for vertices, 
・ v is a labeling function for edges, 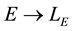
・  is a set of node labels, and
is a set of node labels, and
・ 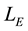 is a set of edge labels
is a set of edge labels
The two graphs G and 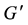 can be compared by determining a mapping function f which associates nodes and edges of G with nodes and edges of
can be compared by determining a mapping function f which associates nodes and edges of G with nodes and edges of 





1) 
2) for any edge 





Formally, two graphs are isomorphic to each other if they are equal. Practically, for most applications this mapping is too much restrictive. In practice, graph isomorphism is of limited use and more relaxing concepts are necessary. One such approach is subgraph isomorphism. An injective function 









where U is the set of all graphs that can be constructed from a given set 

2. The Proposed Algorithm
In this work we present a new algorithm for automated graph based fingerprint representation and matching. We achieve the promising results by clustering the graph feature set and then applying the graph isomorphism. The algorithm proves robust for noisy images as well. We extract various structural features like ridges, end points, bifurcations of the fingerprint. These end points and bifurcations are called as minutiae. Each fingerprint is represented as an attributed relational graph [19] where these features are represented as nodes of the graph. The edges of the graph represent relation attributes between the vertices of the graph. In this way the graph structure captures the structural relationships within the fingerprint graph. The algorithm is implemented and tested using a database of real fingerprint images. Most of the fingerprint recognition algorithms deal with large databases. So comparing the fingerprint with all images in the database takes long time and needs lots of computations. The algorithm performs two tier clustering of graphs. In the first level of clustering fingerprint features are clustered. In the second level the fingerprint graph database is clustered. The novelty of algorithm lies in the following considerations.
1) It uses graph as fingerprint data structure.
2) It optimizes fingerprint search by clustering fingerprint graph feature nodes (Tier 1 clustering).
3) It further optimizes the search by clustering fingerprint database (Tier 2 clustering).
2.1. Graph Based Fingerprint Recognition
This is a graph based approach to compare structural fingerprint features called as minutiae. We implement graph based algorithm given by [20] . The graph based representation of the features of the fingerprint make the procedure more flexible in nature. Each minutiae is represented as a vertex of the graph. We use attributed relational graph. Each minutiae is labeled with its own attributes and neighborhood features. An edge between two vertices indicates that they share neighborhood information between them. The graph isomorphism is applied to decide similarity or dissimilarity between the two graphs being compared.
The overall method involves following steps.
1) Fingerprint preprocessing
2) Features Extraction
3) Features representation as a graph
4) Graph isomorphism algorithm to classify the fingerprint. We are using ridge (R), ridge ending (E) and ridge bifurcation (B) minutiae for fingerprint recognition. Figure 1 shows some typical examples of ridges and features extracted. If the feature extraction phase detects “n” minutiae for the fingerprint, an attributed relational graph with “n” nodes is formed. The graph isomorphism is applied between the input fingerprint graph 



Figure 1. Ridges, end points and bifurcations.
2.2. Tier 1 Clustering: Graph Based Fingerprint Recognition by K-NN Clustering of the Minutiae
When the fingerprint minutiae are more in numbers, comparing each one of them becomes very expensive for the machine. So in this algorithm we cluster the graph data by using K-NN clustering based on Euclidean distance between the vertices of the graph. A features template for each fingerprint is build after clustering the neighborhood relative vertices in similar classes. The advantage of this type of clustering is that the graph comparison is first done with the cluster features template of the fingerprint instead of direct comparison of the vertices of the graph. If the cluster features match with the input fingerprint graph then further graph isomorphism is performed. Otherwise the next cluster is visited in a hope to get matching candidate in it. The algorithm involves following steps. The steps 1 to 3 are same as discussed in previous section.
1) Fingerprint preprocessing
2) Features extraction
3) Features representation as a graph
4) KNN based graph node clustering
5) Graph isomorphism algorithm to classify the fingerprint.
2.3. The K-Nearest Neighbor Clustering
The K-nearst-neighbor (KNN) clustering algorithm measures the distance between a query scenario and a set of scenarios in the data set. It cluster the K nearest neighbor minutiae in the fingerprint space. The distance between two scenarios is computed by using distance function

The Euclidean distance metric is chosen to determine the closeness between the minutiae (vertices). The Euclidean distance is defined as the K-NN distance because of the structural neighborhood properties of the minutiae ( or vertices). The Euclidean distance is given by:

The K-NN clustering proves to be the best due to its lesser execution time and good clustering accuracy. Generally a node is classified by a majority votes of its neighbors. The nodes are assigned to the class that is closest amongst its K nearest neighbors, where K is a small positive integer. If K = 1, then the node is assigned to the class of its nearest neighbor.
1) Each node within the feature set has a class label in the set,
2) The K-nearest neighbors are found by calculating the distance matrix where K is the number of neighbors.
3) The K-closest nodes are analyzed to determine which class label is the most common among the set.
4) The most common class label is then assigned to the node being analyzed.
After graph node clustering the graph based fingerprint matching is performed. The identification of the fingerprint is performed in this module. It reads each fingerprint clustered graph template from the database linearly and compares it with the clustered input fingerprint graph template. If the initial graph template matches then only the total graph isomorphism [20] is applied. The graph matching is continued till the input fingerprint is identified otherwise no match is found.
2.4. Tier 2 Clustering: Graph Based Fingerprint Recognition by K Means Graph Database Clustering
In the earlier section we cluster the features of each fingerprint prior to fingerprint matching. In K-means graph database clustering approach we cluster the fingerprint database based on K means clustering algorithm. It clusters the similar class of fingerprints in the database in similar clusters. It saves further matching time dra- stically as the fingerprint search needs to search a specific sub part of the database. We compare the perfor- mance of our algorithm with the graph based fingerprint recognition [20] which do not apply any database clustering.
3. Simulation Results
For the fingerprint detection we have tested the results on real life data set with 150 images. In fingerprint recognition we implemented following algorithms
Method 1: Fingerprint recognition with graph matching [20]
Method 2: Fingerprint recognition with K-NN clustering of the features and graph matching
Method 3: Fingerprint recognition with K means graph database clustering
The results are depicted in this section. We notice that the graph clustering is reducing the graph matching time drastically than the time taken by graph matching without clustering. Figure 2 shows sample database used.The features extraction phase extracts the minutiae in the fingerprint. It identifies ridges, endpoints and bifurcations present in the image. An attributed relational graph is build for each fingerprint. These features are stored as a characteristic template for each image. Figure 3 shows the features extracted from the image. Each minutia is identified by its (x, y) position, angle, and its type as end point, ridge, bifurcation etc. Each minutia is represented as a vertex and the features are attributes of the vertex.
In the experiments conducted, we recorded fingerprint processing time and fingerprint matching time as comparison criterions. Figure 4 shows the time difference for fingerprint graph processing/clustering for all the three methods for the same sample set. The graph processing clustering time taken for K-NN feature clustering is much higher than processing time taken by method 1 and method 3.
The graph processing/clustering time difference between method 1 and method 3 is not clearly distinguishable in Figure 4. Figure 5 elaborates the graph processing/clustering time difference between graph processing without clustering (method 1) and graph processing with K-means graph database clustering (method 3).
Figure 6 shows the significant time difference for fingerprint graph matching for all the three methods. Once the fingerprint database is clustered, fingerprint matching takes minimum time in method 3. The method 2 takes intermediate matching time in between method 1 and method 3. The method 1 where no clustering is applied, graph matching time the maximum.
4. Conclusions
In this work we have proposed two tier graph clustering and matching algorithms for fingerprint recognition. The fingerprints are preprocessed and structural features, the minutiae are extracted. The fingerprint is represented as an attributed graph by relating all the features with each other. When a query fingerprint image is given as an input for fingerprint matching, graph isomorphism is applied. For the graph of size “n” vertices the algorithm performs “n2” comparisons. When size of “n” becomes larger, graph matching proves expensive. So we apply tier-clustering; Euclidean distance based K-NN clustering of the feature set. It clusters the feature vertices in similar groups
Figure 2. Few examples of fingerprints used for testing.
Figure 3. Feature extraction like ridges, end points, bifurcations.
Figure 4. The difference in fingerprint processing time needed for all three methods. Method 1: Graph based fingerprint recognition (without clustering), Method 2: Graph based fingerprint recognition by K-NN clustering of the minutiae, Method 3: Graph based fingerprint recognition by K means graph database clustering.
Figure 5. The difference in fingerprint processing time needed for Method 1 and Method 3. Method 1: Graph based fingerprint recognition (without clustering) Method 3: Graph based fingerprint recognition by K means graph database clustering.
Figure 6. The difference in fingerprint matching time needed for Method 1, Method 2 and Method 3.
based on their neighborhood relationships. Because of the clustering, the algorithm compares cluster properties before comparing contents of the cluster individually. The approach drastically reduces the time taken by comparison without clustering. Further in tier-2, the fingerprint database is clustered with K-means algorithm. We have tested the results on real time data set available with 150 fingerprints. The observation is that graph clustering definitely reduces time needed for the graph matching purpose. The results of graph matching remain the same. The size of graph, we are considering is restricted due to memory limits of the processing machine. These techniques increase the processing time though. In that case, it is expected that the clustering of the databases is to be done off line prior to graph matching process for best results as a combination.
In the future work, we intend to analyze and test the results on larger data sets along with detail performance evaluation of the algorithms. Definitely graphs based algorithms have their own pros and cons. The selection of appropriate graphs for specific applications with appropriate graph matching algorithm is the key. It is always a challenge to achieve a general graph based platform for various applications and their needs.
Acknowledgements
We thank the Editor and the referee for their comments.
Cite this paper
VaishaliPawar,MukeshZaveri, (2015) K-Means Graph Database Clustering and Matching for Fingerprint Recognition. Intelligent Information Management,07,242-251. doi: 10.4236/iim.2015.74019
References
- 1. Jain, A.K., Prabhakar, S. and Hong, L. (1999) A Multichannel Approach to Fingerprint Classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 21, 348-358.
http://dx.doi.org/10.1109/34.761265 - 2. Rao, K. and Balck, K. (1980) Type Classification of Fingerprints: A Syntactic Approach. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2, 223-231.
http://dx.doi.org/10.1109/TPAMI.1980.4767009 - 3. Lumini, A., Maio, D. and Maltoni, D. (1999) Inexact Graph Matching for Fingerprint Classification. Journal of Machine Graphics and Vision, 8, 241-248.
- 4. Serrau, A., Marcialis, G.L., Bunke, H. and Roli, F. (2005) An Experimental Comparison of Fingerprint Classification Methods Using Graphs. Proceedings of the 5th International Workshop on Graph-Based Representations in Pattern Recognition GbR05, Poitiers, 11-13 April 2005, 281-290.
- 5. Cappelli, R., Maio, D., and Maltoni, D. (2002) A Multi-Classifier Approach to Fingerprint Classification. Pattern Analysis and Appllications, 5, 136-144. http://dx.doi.org/10.1007/s100440200012
- 6. Rao, K. and Balck, K. (1980) Type Classification of Fingerprints: A Syntactic Approach. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2, 223-231.
http://dx.doi.org/10.1109/TPAMI.1980.4767009 - 7. Neuhaus, M. and Bunke, H. (2005) A Graph Matching Based Approach to Fingerprint Classification Using Directional Variance. Proceedings of 5th International Conference on Audio and Video Based Biometric Person Authentication, AVBPA 05, Hilton Rye Town, 20-22 July 2005, 191-200.
- 8. Neuhaus, M. and Bunke, H. (2005) Graph-Based Multiple Classifier System—A Data Levels Fusion Approach. Proceedings of 13th International Conference on Image Analysis and Processing ICIAP05, Cagliari, 6-8 September 2005, 479-486.
- 9. Llados, J., Marti, E. and Villanueva, J.J. (2001) Symbol Recognition by Error-Tolerant Subgraph Matching between Region Adjacency Graphs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23, 1137-1143.http://dx.doi.org/10.1109/34.954603
- 10. Sanchez, G., Llados, J. and Tombre, K. (2002) An Error Correction Graph Grammar to Recognize Textured Symbols. In: Blostein, D. and Kwon, Y.-B., Eds., Graphics Recognition Algorithms and Applications, Springer, Berlin, 128-138.
- 11. Sossa, H. and Horaud, R. (1992) Model Indexing: The Graph-Hashing Approach. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Urbana, June 1992, 811-814.
- 12. Messmer, B.T. and Bunke, H. (2000) Efficient Subgraph Isomorphism Detection: A Decomposition Approach. IEEE Transactions on Knowledge and Data Engineering, 12, 307-323.
http://dx.doi.org/10.1109/69.842269 - 13. Hlaoui, A. and Wang, S. (2003) A New Median Graph Algorithm. In: Hancock, E. and Vento, E., Eds., Graph Based Representations in Pattern Recognition, Springer, Berlin, 225-234.
- 14. Ferrer, M. and Bunke, H. (2010) An Iterative Algorithm for Approximate Median Graph Computation. Proceedings of International Conference on Pattern Recognition, Turkey, 23-26 August 2010, 1562-1565. http://dx.doi.org/10.1109/icpr.2010.386
- 15. Riesen, K. and Bunke, H. (2009) Dissimilarity Based Vector Space Embedding of Graphs Using Prototype Reduction Schemes. Proceedings of the Machine Learning and Data Mining in Pattern Recognition, Leipzig, July 23-25 2009, 617-631.
- 16. Hlaoui, A. and Wang, S. (2004) Approximate Graph Matching and Computing Median Graph for Graph Clustering. Proceedings of the International Workshop on Multidisciplinary Image, Video, and Audio Retrieval and Mining, Quebec, 25-26 October 2004.
- 17. Isenor, D.K. and Zaky, S.G. (1986) Fingerprint Identification Using Graph Matching. Pattern Recognition, Elsevier, 19, 113-122. http://dx.doi.org/10.1016/0031-3203(86)90017-8
- 18. Pawar, V.S. and Zaveri, M.A. (2011) Graph Based Pattern Matching. Proceedings of the 8th International Conference FSKD 2011, Shanghai, 26-28 July 2011, 1022-1026.
http://dx.doi.org/10.1109/fskd.2011.6019722 - 19. Changhua, L., Bing, Y., Weixin, X. (2000) Online Hand-Sketched Graphics Recognition Based on Attributed Relational Graph Matching. Proceedings of the 3rd World Congress on Intelligent Control and Automation, Hefei, 28 June-2 July 2000, 2549-2553.
http://dx.doi.org/10.1109/wcica.2000.862507 - 20. Shapiro, L. and Haralick, R. (1982) Organization of Relational Models for Scene Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 3, 595-602.
http://dx.doi.org/10.1109/TPAMI.1982.4767312









