Intelligent Information Management
Vol.2 No.8(2010), Article ID:2503,4 pages DOI:10.4236/iim.2010.28058
Real-Time Traffic Signal Timing for Urban Road Multi-Intersection
College of Mechanical Engineering, Shanghai University of Engineering Science, Shanghai, China
E-mail: Donglin1985@hotmail.com
Received April 19, 2010; revised June 5, 2010; accepted July 19, 2010
Keywords: Traffic Signal Control, Traffic Flows, Real-Time Signal Timing, Release Matrix, Split, Passion Distribution
Abstract
Abstract—this paper develops a real-time traffic signal timing model which is to be integrated into a single intersection for urban road, thereby solving the problem of traffic congestion. We analyze the current situation of the traffic flow with release matrix firstly, and then put forward the basic models to minimize total delay time of vehicles at the intersection. The optimal real-time signal timing model (non-fixed cycle and non-fixed split) is built with the Webster split optimal model. At last, the simulated results, which are compared with conventional model, manifest the promising properties of proposed model.
1. Introduction
Traffic congestion is a severe problem at an intersection in urban, having been causing many critical problems and challenges in major and most populated cities around the world. Indeed, signal timing is the technique to appropriately decide the signal cycle and effective green time or other factors, with respect to various intersections, phases, traffic flows and others. The conventional signal timing model by using fixed cycle and fixed split algorithm is less efficiencies to cause congestion problem. Therefore, the design of real-time signal timing model for a single intersection in urban traffic networks is important to improve service function of road. A lot of ground can be gained in this area. Indeed, a model of signal timing, proposed in [1-3], is constructed with respect to minimization of vehicle average delay and number of stops at an intersection. Other study, for example [4], the reinforcement learning method, which defining the state sets, action sets and reward function, is introduced to the intersection signal control system. Critical Intersection Control (CIC) [5], is using real-time traffic data to better assign green times to conflicting movements. A real-time dynamic model on multiphase traffic flows, as in [6-13], is that each phase time in next cycle is determined with GA optimizing method. Using data of the traffic flow in the current cycle and the cycle before, and the traffic flows in the next cycle may be estimated through the linear pre-estimation method.
Based on the above research, this paper develops a real-time signal timing model (non-fixed cycle and non-fixed split). According to real-time traffic flows, the model decides the signal cycle and effective green to relieve the congestion problem. Due to the random and complexity, the accurate models is hard to find to describe the traffic flow system. So, the release matrix is introduced to analyze the current situation of the traffic flow. The fixed cycle and non-fixed split model is put forward to minimize total delay time of vehicles, which use the maximum road capacity as the control level. Finally, integrated with the Webster split optimal model, the optimal real-time signal timing model (non-fixed cycle and non-fixed split) is obtained.
2. Modeling of Real-Time Signal Timing
This section is to focus on presenting the real-time optimized signal timing model, including signal state description, delay estimation, mathematical formulation and others.
2.1. Fixed Cycle and Non-Fixed Split Model
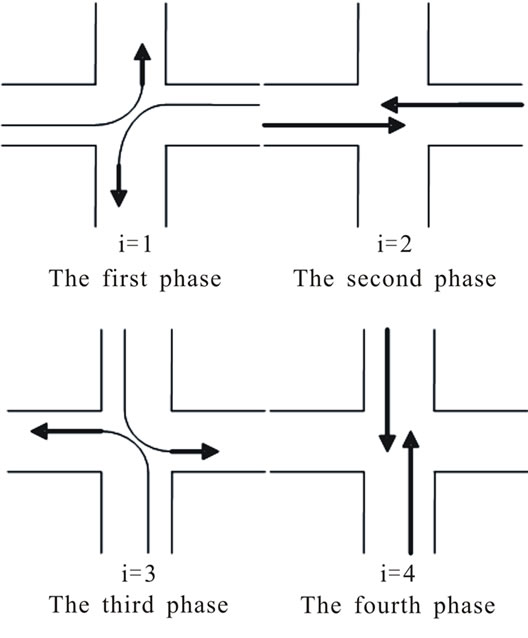
As is shown in Figures 1(a-c), a movement state of a vehicle at a single intersection, denoted by the release matrix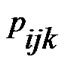 , is defined by the follow information: 1) a phase (i), 2) a direction (j), and 3) a road-lane (k). The release matrix
, is defined by the follow information: 1) a phase (i), 2) a direction (j), and 3) a road-lane (k). The release matrix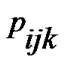 , which describes the current traffic situation, is given by:
, which describes the current traffic situation, is given by:
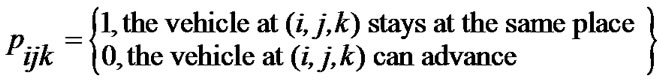 (1)
(1)
where i values 1, 2, 3 and 4 represent respectively the first, second, third and fourth phase. Correspondingly, the j values 1, 2, 3 and 4 represent respectively the direction of south, west and north respectively. And k values 1, 2 and 3 represent respectively turning left, directing and turning right.
Therefore, the release matrix  in Figure 1 can be written as:
in Figure 1 can be written as:
 (2)
(2)
Now that vehicle travel delay is the main index for estimating intersection Level of Service (LOS), accuracy of the delay estimation directly affects the effectiveness of the signal control. So, a calculation for the total delay of vehicles uses mathematical analysis for traffic flow and stop equation. We assume that ti (I = 1, 2, 3, 4) is the green phase at the single intersection.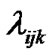 is the arrive ratio of vehicle at (i, j, k). Then, the total number of vehicles at (i, j, k), which flow-into the intersection, is as follow:
is the arrive ratio of vehicle at (i, j, k). Then, the total number of vehicles at (i, j, k), which flow-into the intersection, is as follow:

 (3)
(3)
During the green time, we assume that the ratio of flow-out vehicle at (i, j, k) is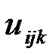 . In one cycle, the total number of flow-out vehicles at (i, j, k) can be given by:
. In one cycle, the total number of flow-out vehicles at (i, j, k) can be given by:
 (4)
(4)
The total number of delay vehicles at (i,j,k) in one cycle is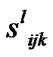 , then:
, then:
 (5)
(5)
where 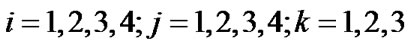 and
and  is the total number of delay vehicles at (i, j, k) in l-1 cycle. Indeed, total number of delay vehicles at the end of l cycle at the single intersection can be written as:
is the total number of delay vehicles at (i, j, k) in l-1 cycle. Indeed, total number of delay vehicles at the end of l cycle at the single intersection can be written as:
 (6)
(6)
Based the above analysis, we put forward the fixed cycle and non-fixed split model to minimize total delay time of vehicles to maximize the capacity of traffic flow at the intersection. Therefore, the objective function realizing
 (a)
(a)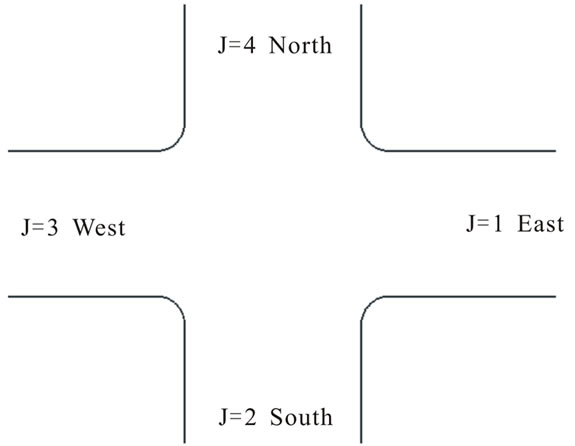 (b)
(b) (c)
(c)
Figure 1. Current traffic flow analysis at a single intersection.
the minimum delay can be given by:
 (7)
(7)
Subject to:
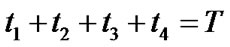 (8)
(8)
where T denotes the cycle time at the single intersection.
Taking the security of pedestrians crossing the road at the intersection into account, the green time of one phase is supposed to be less than a specific value e ( , generally). So, the green time of each phase is supposed to be subject to the (9):
, generally). So, the green time of each phase is supposed to be subject to the (9):
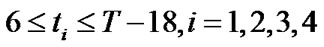 (9)
(9)
The , which describe the maximum vehicle at the road, is a constant up to 1.5 veh/s. and T is up to 120 s. Generally, the effective green time will follow on the yellow time. So, the yellow time is supposed to be considered as a part of green time to simplify the calculation.
, which describe the maximum vehicle at the road, is a constant up to 1.5 veh/s. and T is up to 120 s. Generally, the effective green time will follow on the yellow time. So, the yellow time is supposed to be considered as a part of green time to simplify the calculation.
2.2. Optimized Model
The “Webster” split algorithm is that the green time is determined by the traffic flow ratio in adjoining phases after determining the signal cycle. The equation can be written as:
 (10)
(10)
where 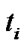 is the green time of i phase.
is the green time of i phase. is the constant up to 1.5 veh/s.
is the constant up to 1.5 veh/s.  is traffic flow ratio at i phase and key road-lane.
is traffic flow ratio at i phase and key road-lane. 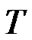
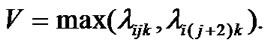 denotes the cycle time, and,
denotes the cycle time, and, 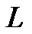 is the lost time.
is the lost time.
We simplified the (10) to (11) for easy calculation:
 (11)
(11)
Therefore, the relationship between T and traffic flow can be written as:
 (12)
(12)
Based on the above calculation, the ultimate goal function can be written as:
 (13)
(13)
where 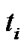 is The green time of i phase,
is The green time of i phase,  is traffic flow ratio at i phase and key road-lane,
is traffic flow ratio at i phase and key road-lane,  = 1.5 veh/s,
= 1.5 veh/s, 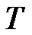 is the cycle time, and
is the cycle time, and  is lost time in a cycle respectively.
is lost time in a cycle respectively.
2.3. Simulation
Because the traffic pattern in the simulation is stochastic, the traffic flow based on the Poisson distribution is applied to obtain the estimates of model performance. The parameters of Poisson distribution are accurately determined by the analysis of traffic flow at high demand level from Songjiang road, Shanghai. Simulation results will be presented as follow.
The model 1, 2 and 3, as in Tables 1, 2 and 3, represent the fixed cycle and fixed split model, fixed cycle and non-split cycle model and real-time signal timing model respectively. The detailed performance improvement at high demand compare the results of three models based on the total vehicle delay for all movement at each time step and the cumulated delay over three cycles. From Table 1, the simulation results indicate that the real-time signal timing model limit the ratio of delay vehicle within 30%. Indeed, the optimal model out performance conventional model by approximately 10%. The simulation results present that the proposed real-time model is more efficient and fairness than the others at the high demand level.
3. Conclusions
The paper developed the real-time signal timing model (non-fixed cycle and non-fixed split) to relieve the traffic congestion. Introducing the release matrix to analyze the situation of traffic flow, the basic model was proposed to minimize total delay time of vehicles. Then, the optimal real-time signal model was realized by combining the Webster split optimal model. Finally, based on simulated

Table 1. the simulation of fixed cycle and fixed split model.
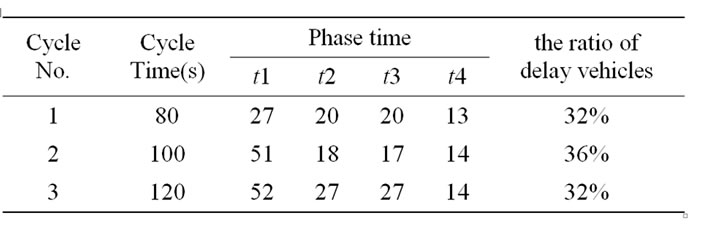
Table 2. the simulation of fixed cycle and non-fixed split model.

Table 3. the simulation of non-fixed cycle and non-fixed split model.
data using Passion distribution, result was showed that the “non-fixed cycle, non-fixed split” model out performance and is more cost effective than “fixed cycle, fixed split” model and “fixed cycle, non-fixed timing”. This research gives useful suggestions on signal control to prevent the traffic congestion.
4. References
[1] G. F. Qu, S. Y. Chen, Q. B. Zhu and Y. Zhang, “Determine Traffic Signal Timing Plan with Particle Swarm Optimization,” Journal of Computational Information Systems, Vol. 4, No. 6, December 2008, pp. 2809-2816.
[2] D. Mariagrazia, F. M. Pia and M. Carlo, “A Signal Timing Plan Formulation for Urban Traffic Control,” Control Engineering Practice, Vol. 14, No. 11, November 2006, pp. 1297-1311.
[3] E. D. Ferreira, E. Subrahmanian and D. Manstretten, “Intelligent Agent in Decentralized Traffic Control,” IEEE Intelligent Transportation System Conference Proceedings, Oakland, August 2001, pp. 707-711.
[4] K. Lu, J. M. Xu and Y. S. Li, “An Optimization Method for Single Intersection’s Signal Timing Based on SARSA (λ) Algorithm,” Control and Decision Conference, July 2008, pp. 5146-5150.
[5] S. Alexander, B. R. Gallagher and K. P. Patel, “Determining Capacity Benefits of Real-Time Signal Control at an Intersection,” Transportation Research Record, Vol. 16, No. 1, November 2007, pp. 78-83.
[6] Y. X. Huang and K. C. Shi, “Real-Time Control of Traffic Signal with Genetic Algorithms Optimizing in Urban Intersection,” Systems Engineering-Theory & Pratice, Vol. 21, No. 3, 2001, pp. 102-106.
[7] B. Wolshon and W. C. Taylor, “Analysis of Intersection Delay under Real-Time Adaptive Signal Control,” Transportation Research Part C: Emerging Technologies, Vol. 7, No. 1, February 1999, pp. 53-72.
[8] D. A. Roozemond and J. L. H. Rogier, “Agent Control Traffic Lights,” ESIT2000, Aachen, 2000.
[9] M. Nazmi, N. Hanim and S. Takaba, “Simulation and Evaluation for Solving the Traffic Flows Problem at Four Intersection in Malaysia,” Proceedings for the 24th JSST Conference, Chester, July 2005.
[10] M. Higashikubo, T. Hinenoya and K. Takeuchi, “Traffic Queue Length Measurement Using an Image Processing Sensor,” The 3rd ITSWorld Conference, Budapest, 1996.
[11] R. L. Kelsey and K. R. Bisset, “A Simulation Environment for Fuzzy Control of Traffic Systems,” 12th IFACWorld Congress, Sydney, Austria, Vol. 5, 18-23 July 1993, pp. 553-556.
[12] C. C. Lee, “Fuzzy Logic in Control System: Fuzzy Logic Controller - Part I & II,” IEEE Transactions on Systems, Man and Cybernetics, Vol. 20, No. 2, 1990, pp. 404-435.
[13] J. Favilla, A. Machion and F. Gomide, “Fuzzy Traffic Control: Adaptive Strategy,” Proceedings of the 2nd IEEE International Conference on Fuzzy Systems, San Francisco, March 1993, pp. 1371-1376.

